A Convex Combination Approach for Artificial Neural Network of Interval Data
Abstract
:1. Introduction
2. Reviews of Existing Methods
2.1. Linear Regression Based on Center Method
2.2. Linear Regression Based on Center-Range Method
2.3. Linear Regression Based on Convex Combination Method
2.4. Regularized Artificial Neural Network (RANN)
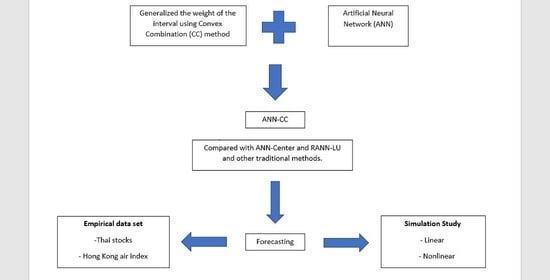
3. The Proposed Method Artificial Neural Network with Convex Combination (ANN-CC)
| Algorithm1. Pseudo code for the proposed ANN-CC with one predictor and one response |
| , where and are the set of candidate weight of input and output , respectively, within [0, 1]. |
| #Serach the optimal |
| For each in |
| Calculateand |
| #Define the loss function of ANN structure |
| , = Parameters( ) |
| # Follow the gradients until convergence |
| repeat |
| until convergence |
| end for |
| #Choose the with the lowest as the optimal |
| Calculateand |
| # Compute the loss function of ANN structure using and |
| # Follow the gradients until convergence |
| repeat |
| until convergence |
4. Simulation Study
4.1. Linear Structure
4.2. Nonlinear Structure
5. Application to Real Data
5.1. Capital Asset Pricing Model: Thai Stocks
5.2. Comparison Results
5.3. Hong Kong Air Quality Monitoring Dataset
5.4. Discussion
- (1)
- Regarding the prediction performance, our ANN-CC was superior to other traditional models in all datasets.
- (2)
- We note that the symmetric weight within the interval data should not be . We found that the prediction result was sensitive to the weight ; thus, the weight should not be a fixed parameter.
- (3)
- Our model outperformed the ANN-LU and RANN-LU models in situations in which the interval series had linear and nonlinear behavior.
- (4)
- We also studied the sensitivity of each activation function and found that the quality of the prediction model was not very sensitive in many cases. However, careful assessment needs to be made when choosing the activation function.
- (5)
- Even though the exponential activation function seemed to be the best fit one in the ANN architecture, it was noticed that other activation functions performed well in some cases. Although the exponential activation function performed very well in the selected three stocks, it may not be reliable in other stocks or under other ANN structures.
- (6)
- However, we can draw an important conclusion that our ANN-CC is a promising model for interval-valued data forecasting. The ANN-CC method has the advantages of not assuming constraints for the weight nor fixing reference points. The ANN-CC model is adaptive and adjusts itself for the best fit. The fitted model allows the behavior analysis of response lower and upper bounds based on the variation of the reference points of input and output intervals.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maciel, L.; Ballini, R. A fuzzy inference system modeling approach for interval-valued symbolic data forecasting. Knowl. Based Syst. 2019, 164, 139–149. [Google Scholar] [CrossRef]
- Ma, X.; Dong, Y. An estimating combination method for interval forecasting of electrical load time series. Expert Syst. Appl. 2020, 158, 113498. [Google Scholar] [CrossRef]
- Chou, J.S.; Truong, D.N.; Le, T.L. Interval forecasting of financial time series by accelerated particle swarm-optimized multi-output machine learning system. IEEE Access 2020, 8, 14798–14808. [Google Scholar] [CrossRef]
- Lauro, C.N.; Palumbo, F. Principal component analysis of interval data: A symbolic data analysis approach. Comput. Stat. 2000, 15, 73–87. [Google Scholar] [CrossRef]
- Branzei, R.; Branzei, O.; Gök, S.Z.A.; Tijs, S. Cooperative interval games: A survey. Cent. Eur. J. Oper. Res. 2010, 18, 397–411. [Google Scholar] [CrossRef]
- Kiekintveld, C.; Islam, T.; Kreinovich, V. Security games with interval uncertainty. In Proceedings of the 2013 International Conference on Autonomous Agents and Multi-Agent Systems, Paul, MN, USA, 6–10 May 2013; pp. 231–238. [Google Scholar]
- Billard, L.; Diday, E. Regression analysis for interval-valued data. In Data Analysis, Classification, and Related Methods; Springer: Berlin/Heidelberg, Germany, 2000; pp. 369–374. [Google Scholar]
- Neto, E.D.A.L.; de Carvalho, F.D.A. Centre and range method for fitting a linear regression model to symbolic interval data. Comput. Stat. Data Anal. 2008, 52, 1500–1515. [Google Scholar] [CrossRef]
- Souza, L.C.; Souza, R.M.; Amaral, G.J.; Silva Filho, T.M. A parametrized approach for linear regression of interval data. Knowl. Based Syst. 2017, 131, 149–159. [Google Scholar] [CrossRef]
- Chanaim, S.; Sriboonchitta, S.; Rungruang, C. A Convex Combination Method for Linear Regression with Interval Data. In Integrated Uncertainty in Knowledge Modelling and Decision Making. IUKM 2016; Huynh, V.N., Inuiguchi, M., Le, B., Le, B., Denoeux, T., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2016; Volume 9978, pp. 469–480. [Google Scholar] [CrossRef]
- Phadkantha, R.; Yamaka, W.; Tansuchat, R. Analysis of Risk, Rate of Return and Dependency of REITs in ASIA with Capital Asset Pricing Model. In Predictive Econometrics and Big Data. TES 2018; Kreinovich, V., Sriboonchitta, S., Chakpitak, N., Eds.; Studies in Computational Intelligence; Springer: Cham, Switzerland, 2018; Volume 753, pp. 536–548. [Google Scholar] [CrossRef]
- Buansing, T.T.; Golan, A.; Ullah, A. An information-theoretic approach for forecasting interval-valued SP500 daily returns. Int. J. Forecast. 2020, 36, 800–813. [Google Scholar] [CrossRef]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Mondal, P.; Shit, L.; Goswami, S. Study of effectiveness of time series modeling (ARIMA) in forecasting stock prices. Int. J. Comput. Sci. Eng. Appl. 2014, 4, 13. [Google Scholar] [CrossRef]
- McMillan, D.G. Nonlinear predictability of stock market returns: Evidence from nonparametric and threshold models. Int. Rev. Econ. Financ. 2001, 10, 353–368. [Google Scholar] [CrossRef] [Green Version]
- Nyberg, H. Predicting bear and bull stock markets with dynamic binary time series models. J. Bank. Financ. 2013, 37, 3351–3363. [Google Scholar] [CrossRef] [Green Version]
- Pastpipatkul, P.; Maneejuk, P.; Sriboonchitta, S. Markov Switching Regression with Interval Data: Application to Financial Risk via CAPM. Adv. Sci. Lett. 2017, 23, 10794–10798. [Google Scholar] [CrossRef]
- Phochanachan, P.; Pastpipatkul, P.; Yamaka, W.; Sriboonchitta, S. Threshold regression for modeling symbolic interval data. Int. J. Appl. Bus. Econ. Res. 2017, 15, 195–207. [Google Scholar]
- Hiransha, M.; Gopalakrishnan, E.A.; Menon, V.K.; Soman, K.P. NSE stock market prediction using deep-learning models. Procedia Comput. Sci. 2018, 132, 1351–1362. [Google Scholar]
- Haykin, S.; Principe, J. Making sense of a complex world [chaotic events modeling]. IEEE Signal Process. Mag. 1998, 15, 66–81. [Google Scholar] [CrossRef]
- Zhang, G.; Patuwo, B.E.; Hu, M.Y. Forecasting with artificial neural networks: The state of the art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Leung, D.; Abbenante, G.; Fairlie, D.P. Protease inhibitors: Current status and future prospects. J. Med. Chem. 2000, 43, 305–341. [Google Scholar] [CrossRef]
- Cao, Q.; Leggio, K.B.; Schniederjans, M.J. A comparison between Fama and French′s model and artificial neural networks in predicting the Chinese stock market. Comput. Oper. Res. 2005, 32, 2499–2512. [Google Scholar] [CrossRef]
- San Roque, A.M.; Maté, C.; Arroyo, J.; Sarabia, Á. iMLP: Applying multi-layer perceptrons to interval-valued data. Neural Process. Lett. 2007, 25, 157–169. [Google Scholar] [CrossRef]
- Maia, A.L.S.; de Carvalho, F.D.A.; Ludermir, T.B. Forecasting models for interval-valued time series. Neurocomputing 2008, 71, 3344–3352. [Google Scholar] [CrossRef]
- Maia, A.L.S.; de Carvalho, F.D.A. Holt’s exponential smoothing and neural network models for forecasting interval-valued time series. Int. J. Forecast. 2011, 27, 740–759. [Google Scholar] [CrossRef]
- Yang, Z.; Lin, D.K.; Zhang, A. Interval-valued data prediction via regularized artificial neural network. Neurocomputing 2019, 331, 336–345. [Google Scholar] [CrossRef] [Green Version]
- Mir, M.; Nasirzadeh, F.; Kabir, H.D.; Khosravi, A. Neural Network-based interval forecasting of construction material prices. J. Build. Eng. 2021, 39, 102288. [Google Scholar]
- Moore, R.E. Methods and Applications of Interval Analysis; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1979. [Google Scholar]
- Humphrey, G.B.; Maier, H.R.; Wu, W.; Mount, N.J.; Dandy, G.C.; Abrahart, R.J.; Dawson, C.W. Improved validation framework and R-package for artificial neural network models. Environ. Model. Softw. 2017, 92, 82–106. [Google Scholar] [CrossRef] [Green Version]
- Sharpe, W.F. Capital asset prices: A theory of market equilibrium under conditions of risk. J. Financ. 1964, 19, 425–442. [Google Scholar]
- Lintner, J. Security prices, risk, and maximal gains from diversification. J. Financ. 1965, 20, 587–615. [Google Scholar]
- Maneejuk, P.; Yamaka, W. Significance test for linear regression: How to test without P-values? J. Appl. Stat. 2021, 48, 827–845. [Google Scholar] [CrossRef]
- Hansen, P.R.; Lunde, A.; Nason, J.M. The model confidence set. Econometrica 2011, 79, 453–497. [Google Scholar] [CrossRef] [Green Version]







| ANN-CC | ANN-Center | RANN-LU | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Scenario 1 | MAE | MSE | RMSE | MAE | MSE | RMSE | MAE | MSE | RMSE |
| tanh | 2.4011 (0.1548) | 10.8590 (1.3251) | 3.2951 (1.2434) | 2.3154 (0.1215) | 9.4115 (1.1154) | 3.0681 (1.0859) | 3.1244 (1.1245) | 14.2251 (2.3414) | 3.7729 (1.5521) |
| sigmoid | 2.5870 (0.1211) | 10.9894 (1.3511) | 3.3154 (1.2433) | 2.4023 (0.1011) | 9.5558 (1.1584) | 3.0917 (1.0756) | 3.1148 (1.3584) | 12.5441 (3.6974) | 3.5423 (1.2532) |
| linear | 2.7244 (0.1513) | 12.0524 (1.1125) | 3.4723 (1.3234) | 2.4488 (0.1254) | 10.3554 (1.0015) | 3.2184 0028) | 3.5415 (1.2121) | 14.3554 (1.5487) | 3.7890 (1.1112) |
| exp | 2.5980 (0.1148) | 11.3486 (1.981) | 3.3693 (1.2113) | 2.4223 (0.1011) | 10.0215 (1.1057) | 3.1661 (1.0723) | 3.1057 (1.2554) | 12.5015 (3.4548) | 3.5361 (0.9723) |
| Scenario 2 | MAE | MSE | RMSE | MAE | MSE | RMSE | MAE | MSE | RMSE |
| tanh | 2.1350 (0.1254) | 7.0789 (1.3258) | 2.6610 (1.1123) | 3.1332 (2.1254) | 9.0173 (2.4848) | 3.0021 (1.4434) | 3.5445 (1.3145) | 15.1541 (2.6879) | 3.8935 (1.2329) |
| sigmoid | 2.3328 (0.1158) | 8.6030 (1.2217) | 2.9337 (1.0283) | 4.2214 (3.3141) | 10.6030 (1.6278) | 3.2565 (1.3233) | 2.5847 (1.2597) | 9.6984 (3.3354) | 3.1154 (1.2810) |
| linear | 2.7825 (0.1698) | 8.9356 (1.1369) | 2.9894 (1.0022) | 4.3112 (2.6545) | 10.9356 (2.3679) | 3.3078 (1.2232) | 4.1125 (1.3541) | 14.0778 (1.1548) | 3.7533 (1.0012) |
| exp | 2.4625 (0.1354) | 8.5072 (1.2589) | 2.9173 (0.9233) | 3.5845 (2.3651) | 10.4072 (2.2589) | 3.2269 (1.1129) | 3.4797 (1.5479) | 10.3155 (1.1554) | 3.2129 (0.9928) |
| Scenario 3 | MAE | MSE | RMSE | MAE | MSE | RMSE | MAE | MSE | RMSE |
| tanh | 2.1049 (0.1112) | 6.9441 (1.5159) | 2.6352 (0.6333) | 3.4488 (2.1254) | 9.9410 (4.3549) | 3.1539 (1.6727) | 2.4141 (1.0413) | 8.5454 (2.5444) | 2.9245 (1.5529) |
| sigmoid | 2.1249 (0.1874) | 7.0088 (1.6511) | 2.6468 (0.7843) | 3.9784 (2.3743) | 15.0113 (5.4035) | 3.8730 (1.2270) | 2.5454 (1.1115) | 10.5544 (2.1125) | 3.2456 (1.2332) |
| linear | 2.8524 (0.1369) | 12.9612 (1.3594) | 3.6013 (1.0091) | 3.8411 (2.6588) | 14.9023 (5.8941) | 3.8607 (1.3410) | 2.9445 (0.8797) | 13.1154 (2.1112) | 3.6210 (1.2221) |
| exp | 2.4489 (0.1364) | 10.4617 (1.5114) | 3.2344 (0.8833) | 4.8778 (4.2643) | 16.4107 (5.4113) | 4.0511 (2.0013) | 3.0124 (1.0694) | 11.3547 (1.9967) | 3.2683 (1.1009) |
| ANN-CC | ANN-Center | RANN-LU | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Scenario 1 | MAE | MSE | RMSE | MAE | MSE | RMSE | MAE | MSE | RMSE |
| tanh | 3.6341 (0.3015) | 14.8140 (2.3840) | 3.8491 (1.0023) | 3.1258 (0.2474) | 9.8741 (2.0126) | 3.1438 (0.9343) | 3.9874 (1.4126) | 14.9874 (3.2158) | 3.8715 (0.9323) |
| sigmoid | 3.4558 (0.3114) | 10.9894 (5.0114) | 3.3155 (0.9833) | 3.2154 (0.2099) | 9.9741 (2.3654) | 3.1582 (0.8834) | 4.9845 (1.9136) | 15.3898 (5.1145) | 3.9245 (0.9823) |
| linear | 5.3155 (1.4259) | 17.1148 (5.6584) | 4.1377 (1.0824) | 5.2145 (1.3978) | 16.4213 (3.3665) | 4.0523 (1.1112) | 5.4136 (2.0113) | 17.8854 (5.7897) | 4.2295 (1.2334) |
| exp | 4.6211 (0.8797) | 16.3123 (2.8557) | 4.0391 (1.0067) | 3.1158 (0.9788) | 14.1314 (2.6547) | 3.7599 (0.9823) | 4.8654 (1.3541) | 17.0198 (3.9844) | 4.1256 (1.2220) |
| Scenario 2 | MAE | MSE | RMSE | MAE | MSE | RMSE | MAE | MSE | RMSE |
| tanh | 3.2250 (0.8453) | 9.1588 (3.6941) | 3.0372 (0.8832) | 3.9788 (2.5481) | 10.5448 (4.6641) | 3.2475 (1.1234) | 3.7888 (1.1255) | 9.8368 (3.6879) | 3.1367 |
| sigmoid | 4.0581 (1.3511) | 13.5154 (3.6444) | 3.6765 (0.8734) | 5.3698 (2.4145) | 20.3688 (4.3658) | 4.5139 (2.4449) | 4.3781 (1.8746) | 16.1556 (5.1034) | 4.0197 |
| linear | 4.8744 (2.5584) | 17.9981 (4.3398) | 4.2428 (0.9734) | 6.1142 (3.9451) | 27.6548 (10.4891) | 5.2597 (2.1240) | 5.6684 (2.9876) | 22.8314 (6.3598) | 4.7783 |
| exp | 4.1158 (0.7446) | 15.4458 (3.3658) | 3.9311 (0.9872) | 5.4101 (2.3155) | 20.0123 (4.4115) | 4.4744 (2.1098) | 4.2666 (1.3659) | 14.9155 (1.4231) | 3.8628 |
| Scenario 3 | MAE | MSE | RMSE | MAE | MSE | RMSE | MAE | MSE | RMSE |
| tanh | 3.4589 (0.7894) | 9.3158 (4.1158) | 3.0544 (0.9239) | 5.8115 (3.0125) | 21.1930 (10.3661) | 4.6033 (1.2323) | 3.5012 (1.2458) | 9.4125 (4.2320) | 3.0681 (1.9383) |
| sigmoid | 4.1585 (1.3841) | 14.3651 (3.9887) | 3.7901 (1.1112) | 5.9884 (2.3688) | 20.0113 (10.4035) | 4.4730 (1.2223) | 4.3685 (1.5645) | 14.8554 (4.3598) | 3.8544 (1.2234) |
| linear | 4.8664 (2.1355) | 16.6557 (6.0123) | 4.0814 (1.0389) | 5.9424 (2.6871) | 25.1253 (10.3211) | 5.0131 (1.4980) | 4.9785 (1.8994) | 16.9974 (5.3145) | 4.1229 (1.4409) |
| exp | 4.2556 (1.2154) | 14.4456 (4.1106) | 3.8009 (0.9227) | 6.6698 (5.1155) | 31.4107 (12.9987) | 5.6044 (1.3409) | 4.8664 (2.0115) | 15.5024 (2.1258) | 3.9377 (1.2284) |
| SET_ u | SET_ l | PTT_ u | PTT_ l | SCC_ u | SCC_ l | CPALL_ u | CPALL_ l | |
|---|---|---|---|---|---|---|---|---|
| Mean | 0.012 | −0.011 | 0.019 | −0.018 | 0.018 | −0.017 | 0.021 | −0.019 |
| Median | 0.010 | −0.009 | 0.016 | −0.015 | 0.016 | −0.015 | 0.017 | −0.016 |
| Maximum | 0.097 | 0.025 | 0.136 | 0.033 | 0.113 | 0.027 | 0.185 | 0.032 |
| Minimum | −0.019 | −0.106 | −0.027 | −0.128 | −0.016 | −0.105 | −0.058 | −0.172 |
| Std. Dev. | 0.010 | 0.010 | 0.016 | 0.015 | 0.014 | 0.013 | 0.017 | 0.016 |
| Skewness | 1.894 | −1.812 | 1.576 | −1.564 | 1.653 | −1.475 | 2.038 | −2.280 |
| Kurtosis | 12.247 | 11.383 | 7.981 | 8.775 | 8.337 | 7.522 | 12.824 | 15.743 |
| Jarque—Bera | 7659.845 | 6398.846 | 2665.961 | 3308.472 | 3022.738 | 2235.950 | 8677.507 | 14,052.600 |
| MBF Jarque-Bera | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Observations | 1841 | 1841 | 1841 | 1841 | 1841 | 1841 | 1841 | 1841 |
| Unit root test | −2.230 | −3.454 | −2.125 | −2.125 | −2.661 | −2.385 | −2.307 | −3.255 |
| MBF-unit root | 0.083 | 0.003 | 0.105 | 0.105 | 0.029 | 0.058 | 0.070 | 0.005 |
| One Hidden Node | Weight Parameter | MAE | MSE | RMSE | ||||
| PTT | out | in | out | in | out | in | ||
| tanh | 0.648521 | 0.999000 | 0.014094 | 0.013565 | 0.000315 | 0.000298 | 0.017751 | 0.017265 |
| sigmoid | 0.608577 | 0.962942 | 0.011501 | 0.011931 | 0.000249 | 0.000237 | 0.015792 | 0.015362 |
| linear | 0.611678 | 0.999000 | 0.013707 | 0.013696 | 0.000303 | 0.000301 | 0.017401 | 0.017378 |
| exp | 0.607746 | 0.999000 | 0.010572 | 0.010023 | 0.000221 | 0.000209 | 0.014862 | 0.014465 |
| SCC | out | in | out | in | out | In | ||
| tanh | 0.510112 | 0.927919 | 0.011382 | 0.011377 | 0.000218 | 0.000211 | 0.014768 | 0.014533 |
| sigmoid | 0.513121 | 0.910014 | 0.010506 | 0.011060 | 0.000190 | 0.000160 | 0.013781 | 0.012658 |
| linear | 0.519982 | 0.920239 | 0.011793 | 0.011423 | 0.000235 | 0.000232 | 0.015343 | 0.015238 |
| exp | 0.509987 | 0.930019 | 0.010734 | 0.011065 | 0.000193 | 0.000168 | 0.013897 | 0.012970 |
| CPALL | out | in | out | in | out | In | ||
| tanh | 0.412312 | 0.481917 | 0.013848 | 0.013835 | 0.000391 | 0.000384 | 0.019765 | 0.019588 |
| sigmoid | 0.461660 | 0.500013 | 0.012627 | 0.012231 | 0.000235 | 0.000191 | 0.015343 | 0.013832 |
| linear | 0.386464 | 0.342022 | 0.013619 | 0.012975 | 0.000353 | 0.000277 | 0.018756 | 0.016650 |
| exp | 0.461668 | 0.500101 | 0.013608 | 0.012891 | 0.000342 | 0.000269 | 0.018489 | 0.016413 |
| Two Hidden Nodes | Weight Parameter | MAE | MSE | RMSE | ||||
| PTT | out | in | out | in | out | In | ||
| tanh | 0.398420 | 0.398420 | 0.014168 | 0.013570 | 0.000328 | 0.000294 | 0.018121 | 0.017151 |
| sigmoid | 0.409278 | 0.409278 | 0.010203 | 0.009748 | 0.000167 | 0.000157 | 0.012934 | 0.012535 |
| linear | 0.421373 | 0.421373 | 0.013431 | 0.013755 | 0.000315 | 0.000298 | 0.017763 | 0.017269 |
| exp | 0.389728 | 0.389728 | 0.009030 | 0.009085 | 0.000151 | 0.000145 | 0.012275 | 0.012040 |
| SCC | out | in | out | in | out | In | ||
| tanh | 0.358503 | 0.358503 | 0.012146 | 0.011344 | 0.000242 | 0.000201 | 0.0155543 | 0.014181 |
| sigmoid | 0.387659 | 0.387659 | 0.010360 | 0.010467 | 0.000162 | 0.000168 | 0.012736 | 0.012977 |
| linear | 0.359730 | 0.359730 | 0.010858 | 0.010981 | 0.000172 | 0.000190 | 0.013121 | 0.013779 |
| exp | 0.351820 | 0.351820 | 0.010011 | 0.010006 | 0.000156 | 0.000155 | 0.012494 | 0.012469 |
| CPALL | out | in | out | in | out | In | ||
| tanh | 0.423709 | 0.423709 | 0.014073 | 0.013789 | 0.000318 | 0.000319 | 0.017836 | 0.017856 |
| sigmoid | 0.376741 | 0.376741 | 0.012700 | 0.012163 | 0.000255 | 0.000262 | 0.015960 | 0.016191 |
| linear | 0.431735 | 0.431735 | 0.015190 | 0.013474 | 0.000393 | 0.000301 | 0.019825 | 0.017356 |
| exp | 0.427827 | 0.427827 | 0.011830 | 0.011123 | 0.000212 | 0.000201 | 0.014567 | 0.014183 |
| Three Hidden Nodes | Weight Parameter | MAE | MSE | RMSE | ||||
| PTT | out | in | out | in | out | In | ||
| tanh | 0.394010 | 0.394010 | 0.012486 | 0.011650 | 0.000279 | 0.000215 | 0.016751 | 0.014672 |
| sigmoid | 0.387755 | 0.387755 | 0.010510 | 0.009682 | 0.000192 | 0.000151 | 0.013866 | 0.012291 |
| linear | 0.425890 | 0.425890 | 0.012102 | 0.011565 | 0.000258 | 0.000222 | 0.016080 | 0.014912 |
| exp | 0.383586 | 0.383586 | 0.010312 | 0.009675 | 0.000180 | 0.000150 | 0.013425 | 0.012256 |
| SCC | out | in | out | in | out | In | ||
| tanh | 0.363167 | 0.363167 | 0.011112 | 0.011669 | 0.000183 | 0.000215 | 0.013529 | 0.014668 |
| sigmoid | 0.337693 | 0.337693 | 0.010553 | 0.010319 | 0.000175 | 0.000161 | 0.013230 | 0.012692 |
| linear | 0.364510 | 0.364510 | 0.011384 | 0.011578 | 0.000187 | 0.000214 | 0.013677 | 0.014633 |
| exp | 0.367622 | 0.367622 | 0.010887 | 0.010341 | 0.000179 | 0.000164 | 0.013381 | 0.012815 |
| CPALL | out | in | out | in | out | In | ||
| tanh | 0.399262 | 0.399262 | 0.014182 | 0.013737 | 0.000397 | 0.000306 | 0.019931 | 0.017499 |
| sigmoid | 0.410937 | 0.410937 | 0.012159 | 0.012331 | 0.000261 | 0.000261 | 0.016160 | 0.016158 |
| linear | 0.415327 | 0.415327 | 0.013745 | 0.012910 | 0.000319 | 0.000282 | 0.017865 | 0.016780 |
| exp | 0.423794 | 0.423794 | 0.011926 | 0.012321 | 0.000231 | 0.000252 | 0.015185 | 0.015873 |
| One Hidden Node | Weight Parameter | MAE | MSE | RMSE | ||||
| PTT | out | in | out | in | out | in | ||
| tanh | 0.500000 | 0.500000 | 0.019527 | 0.019337 | 0.000626 | 0.000593 | 0.025023 | 0.024332 |
| sigmoid | 0.500000 | 0.500000 | 0.019831 | 0.019362 | 0.000639 | 0.000596 | 0.025286 | 0.024424 |
| linear | 0.500000 | 0.500000 | 0.019064 | 0.019355 | 0.000597 | 0.000583 | 0.024441 | 0.02415 |
| exp | 0.500000 | 0.500000 | 0.012656 | 0.011672 | 0.000261 | 0.000225 | 0.016154 | 0.015011 |
| SCC | out | in | out | in | out | in | ||
| tanh | 0.500000 | 0.500000 | 0.017691 | 0.017901 | 0.000479 | 0.000496 | 0.021866 | 0.022275 |
| sigmoid | 0.500000 | 0.500000 | 0.017738 | 0.017932 | 0.000506 | 0.000499 | 0.022495 | 0.022342 |
| linear | 0.500000 | 0.500000 | 0.017561 | 0.017892 | 0.000465 | 0.000486 | 0.021569 | 0.022032 |
| exp | 0.500000 | 0.500000 | 0.017469 | 0.017703 | 0.000455 | 0.000472 | 0.021335 | 0.021737 |
| CPALL | out | in | out | in | out | in | ||
| tanh | 0.500000 | 0.500000 | 0.021078 | 0.020439 | 0.000801 | 0.000631 | 0.028314 | 0.025126 |
| sigmoid | 0.500000 | 0.500000 | 0.021049 | 0.020295 | 0.000797 | 0.000626 | 0.028236 | 0.025027 |
| linear | 0.500000 | 0.500000 | 0.021850 | 0.020635 | 0.000857 | 0.000658 | 0.029283 | 0.025666 |
| exp | 0.500000 | 0.500000 | 0.022129 | 0.020771 | 0.000891 | 0.000733 | 0.029861 | 0.027078 |
| Two Hidden Nodes | Weight Parameter | MAE | MSE | RMSE | ||||
| PTT | out | in | out | in | out | in | ||
| tanh | 0.500000 | 0.500000 | 0.018938 | 0.019209 | 0.000558 | 0.000556 | 0.023622 | 0.023830 |
| sigmoid | 0.500000 | 0.500000 | 0.019426 | 0.019363 | 0.000608 | 0.000611 | 0.024658 | 0.024490 |
| linear | 0.500000 | 0.500000 | 0.018735 | 0.018200 | 0.000548 | 0.000541 | 0.023434 | 0.023269 |
| exp | 0.500000 | 0.500000 | 0.019611 | 0.019322 | 0.000629 | 0.000595 | 0.025092 | 0.024391 |
| SCC | out | in | out | in | out | in | ||
| tanh | 0.500000 | 0.500000 | 0.017883 | 0.017851 | 0.000472 | 0.000487 | 0.021731 | 0.022073 |
| sigmoid | 0.500000 | 0.500000 | 0.018067 | 0.017798 | 0.000517 | 0.000476 | 0.022742 | 0.021825 |
| linear | 0.500000 | 0.500000 | 0.018658 | 0.017653 | 0.000546 | 0.000461 | 0.023375 | 0.021481 |
| exp | 0.500000 | 0.500000 | 0.013203 | 0.012860 | 0.000291 | 0.000281 | 0.017057 | 0.016770 |
| CPALL | out | in | out | in | out | in | ||
| tanh | 0.500000 | 0.500000 | 0.020415 | 0.020792 | 0.000690 | 0.000681 | 0.026271 | 0.026090 |
| sigmoid | 0.500000 | 0.500000 | 0.021457 | 0.020544 | 0.000752 | 0.000665 | 0.027426 | 0.025781 |
| linear | 0.500000 | 0.500000 | 0.020851 | 0.020698 | 0.000644 | 0.000692 | 0.025382 | 0.026314 |
| exp | 0.500000 | 0.500000 | 0.015538 | 0.014341 | 0.000472 | 0.000386 | 0.021739 | 0.019653 |
| Three Hidden Nodes | Weight Parameter | MAE | MSE | RMSE | ||||
| PTT | out | in | out | in | out | in | ||
| tanh | 0.500000 | 0.500000 | 0.019384 | 0.019376 | 0.000581 | 0.000607 | 0.024115 | 0.024637 |
| sigmoid | 0.500000 | 0.500000 | 0.019355 | 0.019373 | 0.000608 | 0.000600 | 0.024667 | 0.024495 |
| linear | 0.500000 | 0.500000 | 0.019215 | 0.019423 | 0.000603 | 0.000602 | 0.024549 | 0.024536 |
| exp | 0.500000 | 0.500000 | 0.009504 | 0.009139 | 0.000178 | 0.000165 | 0.013344 | 0.012845 |
| SCC | out | in | out | in | out | in | ||
| tanh | 0.500000 | 0.500000 | 0.017898 | 0.017843 | 0.000493 | 0.000482 | 0.022213 | 0.021961 |
| sigmoid | 0.500000 | 0.500000 | 0.017337 | 0.017988 | 0.000458 | 0.000491 | 0.021412 | 0.022166 |
| linear | 0.500000 | 0.500000 | 0.017841 | 0.017864 | 0.000489 | 0.000483 | 0.022121 | 0.021968 |
| exp | 0.500000 | 0.500000 | 0.012653 | 0.012585 | 0.000273 | 0.000267 | 0.016530 | 0.016353 |
| CPALL | out | in | out | in | out | in | ||
| tanh | 0.500000 | 0.500000 | 0.014358 | 0.014825 | 0.000393 | 0.000414 | 0.019813 | 0.020359 |
| sigmoid | 0.500000 | 0.500000 | 0.020873 | 0.020682 | 0.000718 | 0.000674 | 0.026790 | 0.025967 |
| linear | 0.500000 | 0.500000 | 0.021531 | 0.020515 | 0.000791 | 0.000655 | 0.028131 | 0.025598 |
| exp | 0.500000 | 0.500000 | 0.014286 | 0.014245 | 0.000413 | 0.000385 | 0.020323 | 0.019629 |
| One Hidden Neuron | MAE | MSE | RMSE | |||
| PTT | out | in | out | in | out | in |
| tanh | 0.020572 | 0.020551 | 0.000699 | 0.000633 | 0.026443 | 0.025164 |
| sigmoid | 0.019717 | 0.019512 | 0.000641 | 0.000612 | 0.025322 | 0.024745 |
| linear | 0.011574 | 0.014203 | 0.000348 | 0.000239 | 0.018662 | 0.015467 |
| exp | 0.011498 | 0.014183 | 0.000347 | 0.000204 | 0.018634 | 0.014291 |
| MAE | MSE | RMSE | ||||
| SCC | out | in | out | in | out | In |
| tanh | 0.017615 | 0.017566 | 0.000461 | 0.000463 | 0.021466 | 0.021522 |
| sigmoid | 0.017725 | 0.017619 | 0.000529 | 0.000470 | 0.023012 | 0.021684 |
| linear | 0.018800 | 0.017891 | 0.000541 | 0.000487 | 0.023267 | 0.022070 |
| exp | 0.018008 | 0.017821 | 0.000519 | 0.000480 | 0.022791 | 0.021915 |
| MAE | MSE | RMSE | ||||
| CPALL | out | in | out | in | out | in |
| tanh | 0.020698 | 0.020667 | 0.000679 | 0.000673 | 0.026053 | 0.025945 |
| sigmoid | 0.020784 | 0.020711 | 0.000735 | 0.000675 | 0.027123 | 0.025978 |
| linear | 0.020946 | 0.020754 | 0.000785 | 0.000730 | 0.028028 | 0.027032 |
| exp | 0.018078 | 0.016966 | 0.000571 | 0.000516 | 0.023883 | 0.022729 |
| Two Hidden Neurons | MAE | MSE | RMSE | |||
| PTT | out | in | out | in | out | in |
| tanh | 0.020031 | 0.019463 | 0.000657 | 0.000611 | 0.025640 | 0.024736 |
| sigmoid | 0.009529 | 0.009196 | 0.000186 | 0.000165 | 0.013632 | 0.012854 |
| linear | 0.019771 | 0.019383 | 0.000608 | 0.000610 | 0.024667 | 0.024689 |
| exp | 0.009449 | 0.009187 | 0.000184 | 0.000160 | 0.013573 | 0.012657 |
| MAE | MSE | RMSE | ||||
| SCC | out | in | out | In | out | In |
| tanh | 0.018178 | 0.017976 | 0.000517 | 0.000506 | 0.022743 | 0.022488 |
| sigmoid | 0.013537 | 0.013251 | 0.000314 | 0.000294 | 0.017732 | 0.017155 |
| linear | 0.013337 | 0.013334 | 0.000295 | 0.000300 | 0.017182 | 0.017329 |
| exp | 0.013058 | 0.013048 | 0.000285 | 0.000281 | 0.016898 | 0.016773 |
| MAE | MSE | RMSE | ||||
| CPALL | out | in | out | in | out | in |
| tanh | 0.014284 | 0.014469 | 0.000359 | 0.000406 | 0.018953 | 0.020149 |
| sigmoid | 0.014353 | 0.014793 | 0.000393 | 0.000415 | 0.019832 | 0.020377 |
| linear | 0.020375 | 0.020873 | 0.000663 | 0.000698 | 0.025759 | 0.026432 |
| exp | 0.020621 | 0.020821 | 0.000675 | 0.000696 | 0.025989 | 0.026378 |
| Three Hidden Neurons | MAE | MSE | RMSE | |||
| PTT | out | in | out | in | out | in |
| tanh | 0.019891 | 0.019421 | 0.000646 | 0.000611 | 0.025424 | 0.024728 |
| sigmoid | 0.019574 | 0.019510 | 0.000602 | 0.000621 | 0.024545 | 0.024933 |
| linear | 0.009158 | 0.009339 | 0.000173 | 0.000171 | 0.013169 | 0.013071 |
| exp | 0.009113 | 0.009108 | 0.000162 | 0.000156 | 0.012731 | 0.012481 |
| MAE | MSE | RMSE | ||||
| SCC | out | in | out | in | out | in |
| tanh | 0.017995 | 0.018026 | 0.000514 | 0.000507 | 0.022674 | 0.022523 |
| sigmoid | 0.014593 | 0.013787 | 0.000355 | 0.000315 | 0.018857 | 0.017751 |
| linear | 0.018369 | 0.017916 | 0.000524 | 0.000503 | 0.022878 | 0.022455 |
| exp | 0.013318 | 0.013200 | 0.000296 | 0.000295 | 0.017223 | 0.017189 |
| MAE | MSE | RMSE | ||||
| CPALL | out | in | out | in | out | in |
| tanh | 0.020252 | 0.020950 | 0.000637 | 0.000713 | 0.025246 | 0.026711 |
| sigmoid | 0.020111 | 0.020974 | 0.000604 | 0.000719 | 0.024565 | 0.026829 |
| linear | 0.020553 | 0.020850 | 0.000651 | 0.000705 | 0.025521 | 0.026563 |
| exp | 0.014032 | 0.014000 | 0.000364 | 0.000393 | 0.019083 | 0.019832 |
| Number | MAE | MSE | RMSE | |||||
| PTT | Activation | Hidden Neuron | out | in | out | in | out | in |
| ANN-CC | exp | 2 | 0.009030 (1.0000) | 0.009085 (1.0000) | 0.000151 (1.0000) | 0.000145 (1.0000) | 0.012275 (1.0000) | 0.012040 (1.0000) |
| ANN-Center | linear | 2 | 0.018735 (0.0000) | 0.018200 (0.0000) | 0.000548 (0.0000) | 0.000541 (0.0000) | 0.023434 (0.0000) | 0.023269 (0.0000) |
| RANN-LU | exp | 3 | 0.009113 (0.2012) | 0.009108 (0.1015) | 0.000162 (0.2450) | 0.000156 (0.0010) | 0.012731 (0.3232) | 0.012481 (0.0000) |
| IF | 0.017932 (0.0000) | 0.017817 (0.0000) | 0.000513 (0.0000) | 0.000501 (0.0000) | 0.022652 (0.0000) | 0.022383 (0.0000) | ||
| PM | 0.018212 (0.0000) | 0.018326 (0.0000) | 0.000523 (0.0000) | 0.000561 (0.0000) | 0.022873 (0.0000) | 0.0236861 (0.0000) | ||
| Center | 0.021453 (0.0000) | 0.020541 (0.0000) | 0.000751 (0.0000) | 0.000664 (0.0000) | 0.027410 (0.0000) | 0.025771 (0.0000) | ||
| Center-range | 0.019877 (0.0000) | 0.01532 (0.0000) | 0.000717 (0.0000) | 0.000602 (0.0000) | 0.026771 (0.0000) | 0.024538 (0.0000) | ||
| MAE | MSE | RMSE | ||||||
| SCC | out | in | out | in | out | in | ||
| ANN-CC | exp | 2 | 0.010011 (1.0000) | 0.010006 (1.0000) | 0.000156 (1.0000) | 0.000155 (1.0000) | 0.012494 (1.0000) | 0.012469 (1.0000) |
| ANN-Center | exp | 3 | 0.012653 (0.0000) | 0.012585 (0.0000) | 0.000273 (0.0000) | 0.000267 (0.0000) | 0.016530 (0.0000) | 0.016353 (0.0000) |
| RANN- LU | exp | 2 | 0.013058 (0.0000) | 0.013048 (0.0000) | 0.000285 (0.0000) | 0.000281 (0.0000) | 0.016898 (0.0000) | 0.016773 (0.0000) |
| IF | 0.012455 (0.0000) | 0.012101 (0.0000) | 0.000250 (0.0000) | 0.000236 (0.0000) | 0.015813 (0.0000) | 0.015366 (0.0000) | ||
| PM | 0.013013 (0.0000) | 0.012992 (0.0000) | 0.000271 (0.0000) | 0.000263 (0.0000) | 0.016464 (0.0000) | 0.016221 (0.0000) | ||
| Center | 0.014044 (0.0000) | 0.014021 (0.0000) | 0.000285 (0.0000) | 0.000281 (0.0000) | 0.016877 (0.0000) | 0.016765 (0.0000) | ||
| Center-range | 0.013221 (0.0000) | 0.013019 (0.0000) | 0.000277 (0.0000) | 0.000275 (0.0000) | 0.016642 (0.0000) | 0.016581 (0.0000) | ||
| MAE | MSE | RMSE | ||||||
| CPALL | out | in | out | in | out | in | ||
| ANN-CC | exp | 2 | 0.011830 (1.0000) | 0.011123 (1.0000) | 0.000212 (1.0000) | 0.000201 (1.0000) | 0.014567 (1.0000) | 0.014183 (1.0000) |
| ANN-Center | exp | 3 | 0.014286 (0.0000) | 0.014245 (0.0000) | 0.000413 (0.0000) | 0.000385 (0.0000) | 0.020323 (0.0000) | 0.019629 (0.0000) |
| RANN- LU | exp | 3 | 0.014032 (0.0000) | 0.014000 (0.0000) | 0.000396 (0.0000) | 0.000393 (0.0000) | 0.019083 (0.0000) | 0.019832 (0.0000) |
| IF | 0.013251 (0.0000) | 0.013656 (0.0000) | 0.000372 (0.0000) | 0.000369 (0.0000) | 0.019291 (0.0000) | 0.019205 (0.0000) | ||
| PM | 0.015130 (0.0000) | 0.014561 (0.0000) | 0.000431 (0.0000) | 0.000426 (0.0000) | 0.020763 (0.0000) | 0.02071 (0.0000) | ||
| Center | 0.016125 (0.0000) | 0.015365 (0.0000) | 0.00510 (0.0000) | 0.000439 (0.0000) | 0.071423 (0.0000) | 0.020961 (0.0000) | ||
| Center-range | 0.019877 (0.0000) | 0.01532 (0.0000) | 0.000717 (0.0000) | 0.000602 (0.0000) | 0.026762 (0.0000) | 0.024524 (0.0000) | ||
| Number | MAE | MSE | RMSE | |||||
|---|---|---|---|---|---|---|---|---|
| PTT | Activation | Hidden Neuron | out | in | out | in | out | in |
| ANN-CC | sigmoid | 2 | 2.6374 (1.0000) | 2.7092 (1.0000) | 7.3232 (1.0000) | 7.4085 (1.0000) | 2.7078 (1.0000) | 2.7225 (1.0000) |
| ANN-Center | sigmoid | 2 | 2.9833 (0.0000) | 2.8363 (0.0000) | 8.1092 (0.0000) | 8.3233 (0.0000) | 2.8483 (0.0000) | 2.8854 (0.0000) |
| RANN-LU | sigmoid | 3 | 2.7762 (0.0000) | 2.7423 (0.0000) | 7.6403 (0.0000) | 7.5409 (0.0510) | 2.7656 (0.0000) | 2.74613 (0.0000) |
| IF | 2.8532 (0.0000) | 2.7821 (0.0000) | 8.5110 (0.0000) | 8.3368 (0.0000) | 2.9161 (0.0000) | 2.8866 (0.0000) | ||
| PM | 2.7011 (0.0000) | 2.6893 (0.0000) | 7.5215 (0.0000) | 7.4212 (0.0000) | 2.7427 (0.0000) | 2.7240 (0.0000) | ||
| Center | 3.0029 (0.0000) | 2.9861 (0.0000) | 8.7334 (0.0000) | 8.7433 (0.0000) | 2.9543 (0.0000) | 2.9571 (0.0000) | ||
| Center-range | 2.8763 (0.0000) | 2.7823 (0.0000) | 8.5532 (0.0000) | 8.3499 (0.0000) | 2.9239 (0.0000) | 2.8883 (0.0000) | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamaka, W.; Phadkantha, R.; Maneejuk, P. A Convex Combination Approach for Artificial Neural Network of Interval Data. Appl. Sci. 2021, 11, 3997. https://0-doi-org.brum.beds.ac.uk/10.3390/app11093997
Yamaka W, Phadkantha R, Maneejuk P. A Convex Combination Approach for Artificial Neural Network of Interval Data. Applied Sciences. 2021; 11(9):3997. https://0-doi-org.brum.beds.ac.uk/10.3390/app11093997
Chicago/Turabian StyleYamaka, Woraphon, Rungrapee Phadkantha, and Paravee Maneejuk. 2021. "A Convex Combination Approach for Artificial Neural Network of Interval Data" Applied Sciences 11, no. 9: 3997. https://0-doi-org.brum.beds.ac.uk/10.3390/app11093997