DFT Characteristics of Charge Transport in DBTP-Based Hole Transport Materials
Abstract
:1. Introduction
2. Computational Methods
3. Results and Discussions
3.1. Geometry and Frontier Molecular Energy Level
3.2. Density of States (DOS) and Frontier Molecular Orbitals (FMOs)
3.3. Ionization Potential (IP), Electron Affinity (EA), and Reorganization Energy
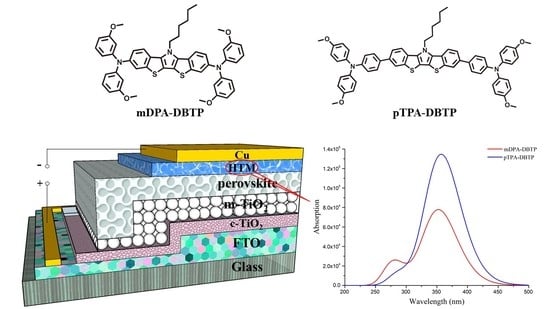
3.4. Absorption Spectra
3.5. Charge Transport
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Yang, W.S.; Noh, J.H.; Jeon, N.J.; Kim, Y.C.; Ryu, S.; Seo, J.; Seok, S.I. High-performance photovoltaic perovskite layers fabricated through intramolecular exchange. Science 2015, 348, 1234–1237. [Google Scholar] [CrossRef] [PubMed]
- Völker, S.F.; Collavini, S.; Delgado, J.L. Organic Charge Carriers for Perovskite Solar Cells. ChemSusChem 2015, 8, 3012–3028. [Google Scholar] [CrossRef] [PubMed]
- Collavini, S.; Völker, S.F.; Delgado, J.L. Understanding the Outstanding Power Conversion Efficiency of Perovskite-Based Solar Cells. Angew. Chem. Int. Ed. 2015, 54, 9757–9759. [Google Scholar] [CrossRef] [PubMed]
- Marinova, N.; Valero, S.; Delgado, J.L. Organic and perovskite solar cells: Working principles, materials and interfaces. J. Colloid Interface Sci. 2017, 488, 373–389. [Google Scholar] [CrossRef] [PubMed]
- Matsui, T.; Petrikyte, I.; Malinauskas, T.; Domanski, K.; Daskeviciene, M.; Steponaitis, M.; Gratia, P.; Tress, W.; Correa-Baena, J.-P.; Abate, A.; et al. Additive-Free Transparent Triarylamine-Based Polymeric Hole-Transport Materials for Stable Perovskite Solar Cells. ChemSusChem 2016, 9, 2567–2571. [Google Scholar] [CrossRef] [PubMed]
- Calio, L.; Kazim, S.; Salado, M.; Zimmermann, I.; Nazeeruddin, M.K.; Ahmad, S. Design of cyclopentadithiophene-based small organic molecules as hole selective layers for perovskite solar cells. Sustain. Energy Fuels 2018, 2, 2179–2186. [Google Scholar] [CrossRef]
- Petrus, M.L.; Schutt, K.; Sirtl, M.T.; Hutter, E.M.; Closs, A.C.; Ball, J.M.; Bijleveld, J.C.; Petrozza, A.; Bein, T.; Dingemans, T.J.; et al. New Generation Hole Transporting Materials for Perovskite Solar Cells: Amide-Based Small-Molecules with Nonconjugated Backbones. Adv. Energy Mater. 2018, 8, 1801605. [Google Scholar] [CrossRef]
- Zhang, D.; Xu, P.; Wu, T.; Ou, Y.; Yang, X.; Sun, A.; Cui, B.; Sun, H.; Hua, Y. Cyclopenta [hi] aceanthrylene-based dopant-free hole-transport material for organic–inorganic hybrid and all-inorganic perovskite solar cells. J. Mater. Chem. A 2019, 7, 5221–5226. [Google Scholar] [CrossRef]
- Jung, I.H.; Kim, J.-H.; Nam, S.Y.; Lee, C.; Hwang, D.-H.; Yoon, S.C. Development of New Photovoltaic Conjugated Polymers Based on Di(1-benzothieno)[3,2-b:2′,3′-d]pyrrole: Benzene Ring Extension Strategy for Improving Open-Circuit Voltage. Macromolecules 2015, 48, 5213–5221. [Google Scholar] [CrossRef]
- Li, Z.; Ye, T.; Tang, S.; Wang, C.; Ma, D.; Li, Z. Triphenylamine-based π-conjugated dendrimers: Convenient synthesis, easy solution processability, and good hole-transporting properties. J. Mater. Chem. C 2015, 3, 2016–2023. [Google Scholar] [CrossRef]
- Azmi, R.; Nam, S.Y.; Sinaga, S.; Akbar, Z.A.; Lee, C.-L.; Yoon, S.C.; Jung, I.H.; Jang, S.-Y. High-performance dopant-free conjugated small molecule-based hole-transport materials for perovskite solar cells. Nano Energy 2018, 44, 191–198. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef] [Green Version]
- Zong, H.; Wang, J.; Mu, X.; Xu, X.; Li, J.; Wang, X.; Long, F.; Sun, M. Physical mechanism of photoinduced intermolecular charge transfer enhanced by fluorescence resonance energy transfer. Phys. Chem. Chem. Phys. 2018, 20, 13558–13565. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Runge, E.; Gross, E.K.U. Density-Functional Theory for Time-Dependent Systems. Phys. Rev. A Gen. Phys. 1987, 35, 442. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision A.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Li, Y.; Pullerits, T.; Zhao, M.; Sun, M. Theoretical Characterization of the PC60BM:PDDTT Model for an Organic Solar Cell. J. Phys. Chem. C 2011, 115, 21865–21873. [Google Scholar] [CrossRef]
- Ashassi-Sorkhabi, H.; Salehi-Abar, P.; Kazempour, A. Effect of electron-donating groups on the electrochemical and optical properties of indoline substituents as hole transport materials: A computational study. Sol. Energy 2019, 180, 146–151. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Zhang, J.; Li, J.; Wu, W.; Wang, L. Constructive effects of the interfacial properties: A strategy to design hole transport materials for high performance perovskite solar cells. Org. Electron. 2018, 62, 591–597. [Google Scholar] [CrossRef]
- Ren, P.; Sun, C.; Shi, Y.; Song, P.; Yang, Y.; Li, Y. Global performance evaluation of solar cells using two models: From charge-transfer and recombination mechanisms to photoelectric properties. J. Mater. Chem. C 2019, 7, 1934–1947. [Google Scholar] [CrossRef]
- Li, Y.; Xu, B.; Song, P.; Ma, F.; Sun, M. D–A−π–A System: Light Harvesting, Charge Transfer, and Molecular Designing. J. Phys. Chem. C 2017, 121, 12546–12561. [Google Scholar] [CrossRef]
- Ashassi-Sorkhabi, H.; Salehi-Abar, P. How the change of OMe substituent position affects the performance of spiro-OMeTAD in neutral and oxidized forms: Theoretical approaches. RSC Adv. 2018, 8, 18234–18242. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Chen, C.; Wang, L.; Zhang, J. Design new hole transport materials for efficient perovskite solar cells by suitable combination of donor and core groups. Org. Electron. 2017, 49, 255–261. [Google Scholar] [CrossRef]
- Jeon, N.J.; Lee, H.G.; Kim, Y.C.; Seo, J.; Noh, J.H.; Lee, J.; Seok, S.I. o-Methoxy Substituents in Spiro-OMeTAD for Efficient Inorganic-Organic Hybrid Perovskite Solar Cells. J. Am. Chem. Soc. 2014, 136, 7837–7840. [Google Scholar] [CrossRef]
- Mor, G.K.; Kim, S.; Paulose, M.; Varghese, O.K.; Shankar, K.; Basham, J.; Grimes, C.A. Visible to Near-infrared Light Harvesting in TiO2 Nanotube Array-P3HT Based Heterojunction Solar Cells. Nano Lett. 2009, 9, 4250–4257. [Google Scholar] [CrossRef]
- Ashassi-Sorkhabi, H.; Salehi-Abar, P. Design of two novel hole transport materials via replacing the core of spiro-OMeTAD with tetrathiafulvalene and tetraazafulvalene for application in perovskite solar cells. Solar Energy 2018, 173, 132–138. [Google Scholar] [CrossRef]
- Yang, L.; Ren, A.M.; Feng, J.K.; Wang, J.F. Theoretical investigation of optical and electronic property modulations of pi-conjugated polymers based on the electron-rich 3,6-dimethoxy-fluorene unit. J. Org. Chem. 2005, 70, 3009–3020. [Google Scholar] [CrossRef]
- Cheng, Y.; Qi, Y.; Tang, Y.; Zheng, C.; Wan, Y.; Huang, W.; Chen, R. Controlling Intramolecular Conformation through Nonbonding Interaction for Soft-Conjugated Materials: Molecular Design and Optoelectronic Properties. J. Phys. Chem. Lett. 2016, 7, 3609–3615. [Google Scholar] [CrossRef]
- Wang, X.; Yang, H.; Wen, Y.; Wang, L.; Li, J.; Zhang, J. Comprehension of the Effect of a Hydroxyl Group in Ancillary Ligand on Phosphorescent Property for Heteroleptic Ir(III) Complexes: A Computational Study Using Quantitative Prediction. Inorg. Chem. 2017, 56, 8986–8995. [Google Scholar] [CrossRef]
- Koese, M.E.; Mitchell, W.J.; Kopidakis, N.; Chang, C.H.; Shaheen, S.E.; Kim, K.; Rumbles, G. Theoretical studies on conjugated phenyl-cored thiophene dendrimers for photovoltaic applications. J. Am. Chem. Soc. 2007, 129, 14257–14270. [Google Scholar] [CrossRef]
- Deng, W.-Q.; Sun, L.; Huang, J.-D.; Chai, S.; Wen, S.-H.; Han, K.-L. Quantitative prediction of charge mobilities of π-stacked systems by first-principles simulation. Nat. Protoc. 2015, 10, 632. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Yang, Y.; Wang, L.; Li, Y. Introducing Asymmetry Induced by Benzene Substitution in a Rigid Fused π Spacer of D−π–A-Type Solar Cells: A Computational Investigation. J. Phys. Chem. C 2019, 123, 4007–4021. [Google Scholar] [CrossRef]
- Chi, W.-J.; Sun, P.-P.; Li, Z.-S. A strategy to improve the efficiency of hole transporting materials: Introduction of a highly symmetrical core. Nanoscale 2016, 8, 17752–17756. [Google Scholar] [CrossRef] [PubMed]
- Marcus, R.A. Chemical and Electrochemical Electron-Transfer Theory. Annu. Rev. Phys. Chem. 2003, 15, 155–196. [Google Scholar] [CrossRef]
- Deng, W.Q.; Goddard, W.A. Predictions of hole mobilities in oligoacene organic semiconductors from quantum mechanical calculations. J. Phys. Chem. B 2004, 108, 8614–8621. [Google Scholar] [CrossRef]



| Molecule | IP | EA | η | λh | λe |
|---|---|---|---|---|---|
| mDPA-DBTP | 4.53 | 1.40 | 1.56 | 0.30 | 0.36 |
| pTPA-DBTP | 4.57 | 1.92 | 1.33 | 0.22 | 0.33 |
| Molecule | mDPA-DBTP | pTPA-DBTP | ||||
|---|---|---|---|---|---|---|
| Field | 0 | 5 | 10 | 0 | 5 | 10 |
| r | 4.33 | 4.30 | 4.17 | 4.48 | 4.38 | 4.30 |
| vh | 0.021 | 0.074 | 0.130 | 0.013 | 0.047 | 0.073 |
| ve | 0.033 | 0.081 | 0.140 | 0.010 | 0.044 | 0.082 |
| kh (×1012) | 0.74 | 9.17 | 28.32 | 0.67 | 8.94 | 22.05 |
| ke (×1012) | 0.97 | 5.92 | 16.66 | 0.12 | 2.32 | 8.20 |
| µh | 0.027 | 0.33 | 0.95 | 0.026 | 0.33 | 0.79 |
| µe | 0.035 | 0.20 | 0.56 | 0.0048 | 0.086 | 0.29 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, M.; Pei, W.; Lu, Q.; Li, Z.; Li, Y.; Liang, J. DFT Characteristics of Charge Transport in DBTP-Based Hole Transport Materials. Appl. Sci. 2019, 9, 2244. https://0-doi-org.brum.beds.ac.uk/10.3390/app9112244
Qiu M, Pei W, Lu Q, Li Z, Li Y, Liang J. DFT Characteristics of Charge Transport in DBTP-Based Hole Transport Materials. Applied Sciences. 2019; 9(11):2244. https://0-doi-org.brum.beds.ac.uk/10.3390/app9112244
Chicago/Turabian StyleQiu, Ming, Weiwei Pei, Qiuchen Lu, Zhuo Li, Yuanzuo Li, and Jianping Liang. 2019. "DFT Characteristics of Charge Transport in DBTP-Based Hole Transport Materials" Applied Sciences 9, no. 11: 2244. https://0-doi-org.brum.beds.ac.uk/10.3390/app9112244