1. Introduction
The measurement, simulation, and evaluation of species distributions in thermodynamic equilibria and potentiometric titration curves are of special interest in research as they indicate the behavior of reactions taking place at different pH values, cf. [
1,
2]. The stability constants of the considered reactions and the concentration distribution of the given species over the pH values are of particular interest. For example, in the electrolyte design, a major indicator of the deposition speed is the free metal concentration in thermodynamic equilibrium in the electrolyte at a certain pH value, see [
3]. Additionally, the free metal concentrations in thermodynamic equilibrium are commonly used as boundary data for simulations of metal deposition while electro plating, see [
4,
5,
6,
7]. For this the stability constants are needed, which are commonly computed from titration curves, see [
8,
9,
10,
11,
12].
A common way to compute stability constants, as applied in the work of Xu et al. [
8] and the work of Zanonato et al. [
9], is through the application of DFT (density functional theory) methods as described in the work of Becke [
10], which is based on the approximation of the density functional describing the exchange-energy density of atomic and molecular systems. Although this strategy is time-efficient, in this paper a numerical strategy will be constructed to unify the calculation of titration curves with the inverse calculation of the stability constants by reconstructing the titration curves themselves. In addition to the unification of the approaches for the computation of titration curves and stability constants, the approach chosen in this paper has three major additional advantages. The first advantage is that the presented algorithm and model immediately produces concentration distributions over the pH values without additional computation steps. The second advantage is the closeness of the theoretical model to the measured chemical process. The third advantage is that the approach discussed in this paper yields a robust numerical strategy for the inverse problem, which is known to be unstable, see [
13,
14].
The model for the computation of the titration curve used in this paper is based on the model formulation in the articles of Alderighi et al. and Gans et al. [
11,
12] and in the work of Langtangen [
15], but it will be equivalently reformulated to stabilize the model formulation. This is needed since inverse problems such as the one used to calculate the stability constants tend to be unstable from a mathematical perspective, see Hinze et al. [
13] and Richter [
14]. In the work of Alderighi [
11], the numerical scheme is described by a simple application of the Newtonian algorithm, which is known to be unstable, see the book of Mäkelä et al. and Lange [
16,
17], in this paper, an algorithm will be discussed which is more stable based on homotopy methods, see [
18,
19].
Similar to as in the book of Martell [
20], the simulated titration curves are used to calculate the stability constants from measured titration curves. However, in contrast to the numerical scheme described in [
11,
12,
20], the numerical scheme described in this article is based on the treatment of the stabilized formulation of the titration curve.
Due to the stabilized formulation of the titration curve, an increase in robustness and reliability of the results of the stability constants is gained.
An important application for the evaluation of titration curves, inverse calculated stability constants, and the species distributions under the pH value is given by the work of Cesiulis [
3], which gives a methodology to identify the pH-value with the current density
j during electrodeposition with the stability constants being used to compute the free metal concentrations. This requires chemical and numerical considerations. To accomplish this, a closer look at the electrolyte is needed, in particular in terms of the chemical equilibrium and the law of mass action, see [
21]. The law of mass action, also referred to as the mass-conservation law, forms the basis for both equilibrium and kinetic investigations. This is based on activities. However, the experiments and calculations presented in this paper are based on concentrations. The difference between concentration and activity is determined by the activity coefficient, which is difficult to determine experimentally [
22]. By default, this difficulty is circumvented by working with constant ionic strength, since the activity coefficients are largely dependent on it, and equilibrium constants can thus be more easily recorded. However, the ionic strength does not stay constant during a reaction. Additionally, the addition of “inert” salts could influence the reaction. The desired equilibrium constants could be determined with infinite dilution; from a practical perspective, however, infinite dilution is unfeasible/impossible. The attractive forces between the ions acting in more concentrated solutions result in dissolved particles no longer moving completely independently of each other, as would be the case for ideal solutions [
23]. In an ideally diluted solution of an electrolyte, the probability of encountering another cation or anion in the vicinity of a cation should be equally high because the ions do not influence each other. As the concentration increases, more orderly ratios gradually begin to form, i.e., an anion is more likely to be found in the vicinity of the cation and vice versa. In real solutions, the dissolved particles are no longer completely free to move. Therefore, lower concentrations are simulated. However, only the mean activity coefficient can be determined. This is not only dependent on the concentration of the own ions but also on the concentration of all ions present in the solution. The determination of the equilibrium constant using the law of mass action, as shown in this work, takes all the species present into account. Since these are dependent on the established chemical equilibrium, it is assumed that once a stable equilibrium system has been reached at any point on the titration curve, the determination of the activity can be dispensed with in favor of observing the concentrations in the case of equilibrium. Similar to the contribution of Karimvand et al. [
24], this article proposes an approach where thermodynamic equilibrium constants are determined directly from the analysis of potentiometric pH titrations. However, this approach avoids the use of activity coefficients by determining the individual points of the potentiometric titration at any time in thermodynamic equilibrium. For this purpose, the adjustment of the equilibrium is monitored “intelligently” by letting the system reach its equilibrium before the base is added in the next titration step. From this, a simulation of the titration curves is carried out by means of a robust numerical method, and the thermodynamic stability constants are calculated from the law of mass action.
2. Experimental Methodology-Intelligent Potentiometric Titration
Two real-life problems are discussed in this work to validate the framework of the models described. For this purpose, potentiometric pH titrations were performed. The ”intelligent“, i.e., automatically controlled, potentiometric pH titration was carried out at a constant temperature of 25 °C and with the intake of argon (
, Alphagaz™Air Liquide), shown in
Figure 1. These were performed first with an electrolyte containing only citric acid and then with a citric acid-nickel electrolyte. Each titration was performed in
L ultrapure water (
, Barnstead™Smart2Pure™, Thermo Fisher Scientific Inc. Waltham, MA, USA). For the first titration of pure citric acid, a quantity of
citric acid (
, >99.5%, Th. Geyer GmbH & Co. KG.) was added and the solution was adjusted to
using sodium hydroxide (NaOH,
, 99.99%, ABCR GmbH). Afterwards,
NaOH was added in stages (doses) in areas with fast equilibrium setting and
NaOH in areas with slow equilibrium setting. For the titration of citric acid-nickel, a solution with
citric acid and
nickel from nickel chloride (
, >99.8%, ABCR GmbH) was provided and carried out in the same way as with the previous titration. All measurements were repeated three times for statistical confirmation and significance.
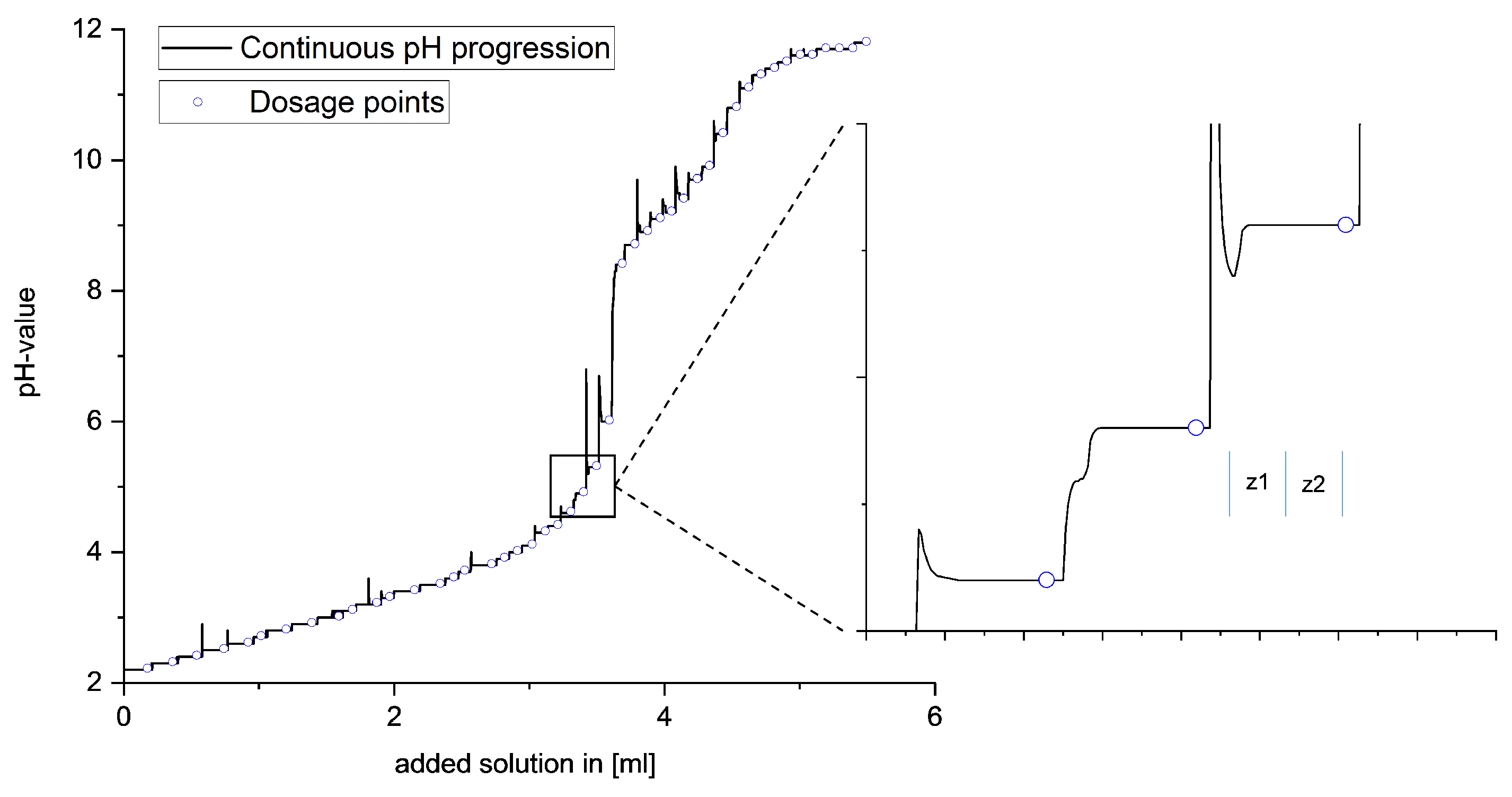
A special feature of this titration procedure is the ability to adjust the timing of the next dose of the respective base based on real-time observation of the equilibrium setting, as shown in
Figure 2. After each addition, the equilibrium setting was monitored by means of automated measurement of the potential curve. Only when the potential curve showed no further increase was the next dosage carried out. This is necessary to guarantee the final adjustment of the equilibrium state, depending on thermodynamic and kinetic reaction influences. To exclude the influence of the background noise of the potential measurement, two ranges with time comparison values
and
are defined in the potential curve after the dosing
, and the increases of these two ranges are compared with each other. If the curve shows the same increase in both time periods, the equilibrium setting continues to run evenly, and two new time units are formed during the potential. Only when the rise of the second time unit approaches zero is the equilibrium setting complete and the next dose given. Due to the variability regarding the timing of the base addition, the optimum amount of base can always be given.
Based on this experimental system, the following numerical considerations could be made.
3. Modeling
This section is devoted to the derivation of a stable and robust model formulation for the simulation of thermodynamic equilibria, titration curves, and the inverse determination of the associated Michaelis constants, referred to as stability constants in this paper. Although the model type discussed in this article will be confined to aqueous media, other generalized models and concepts are conceivable but would require minor modifications from the discussion below.
3.1. Concentrations in Thermodynamic Equilibria
First, assuming that there are
ligands
, …,
and
metals
, …,
, protons
and hydroxide ions
are given in solution as educts. Furthermore, assume that the following
reactions take place in the electrolyte:
where for all
the species
denote the product of the
-th reaction. Furthermore, let
be the stoichiometric index of the
j-th ligand in the
-th reaction. Analogously, let
be the stoichiometric index of the
k-th metal in the
-th reaction. In addition, the stoichiometric index of
in the
-th reaction is denoted by
and
denotes the stoichiometric index of
in the
-th reaction.
For the simplicity of the notation of the following discussion, define the educts
, …,
,
, …,
,
, and
. The stoichiometric indices
denote the respective stoichiometric indices of the single species. In this notation, the reaction (
1) reduces to the simpler formula given below:
As a foundation of the model discussed in this paper, the following mass-conservation laws, see [
15], for given total masses
, including free species concentrations and species in complexes, of the educt
is given by:
In the notation above, the values denote the free masses of the educt , and denotes the masses of the complexes .
One obtains a system of
N non-linear equations in
variables. The system above can be solvable but not uniquely. To obtain a system of uniquely solvable equations, one needs to add
R additional equations. In this setting, one directly uses the definition of the stability constant, which is equivalent to the following system of equations, see [
15]:
In fact, Equations (
3a) and (
3b) directly build up a model for thermodynamic equilibria due to the reactions given in (
2). Please note that one can also equivalently formulate the non-linear Equations (
3a) and (
3b) in terms of concentrations rather than in terms of masses.
Due to the fact that the stability constants can reach values up to , the model formulation tends to be unstable from a numerical perspective. Hence, a further reformulation of the model must be made to stabilize the mathematical formulation.
For the mathematical reformulation, note that under the assumptions
there exist
,
and
such that the following identities hold true:
Using the identities above, especially (
4c) and (
4d), the model described by Equations (
3a) and (
3b) transforms to the following model equations:
The resulting formulation of a single thermodynamic equilibrium yields a more stable formulation of the mass-conservation law.
For the solution of (
5a) and (
5b), the formulation for the determination of roots of the function
, reflecting (
5a) and (
5b) regarding the variables (
4c) and (
4d).
Remark 1. The following remarks must be made:
- 1.
The models corresponding to Equations (5a) and (5b) and (3a) and (3b) both correspond to a search of roots of non-linear functions. The corresponding mathematical problems are constructed to be equivalent, meaning that each solution of (5a) and (5b) can uniquely be identified to a solution to (3a) and (3b) and vice versa, see (4c) and (4d). - 2.
For the well-posedness of the model given through Equations (5a) and (5b) the following assumptions are sufficient. - (A1)
The variables are independent, i.e., the single variables are referring to unique concentration.
- (A2)
The single equations are (linear) independent from each other, i.e., describe the behavior of a uniquely determined setting, i.e., there is no doubling in the reactions (2). - (A3)
The total masses are positive for each .
- 3.
In general, the numerical treatment of the model associated with Equations (5a) and (5b) becomes necessary as it follows from the mathematical theory that there is no general formula to calculate roots of polynomials with coefficients in for a polynomial degree larger or equal to 5, see [25]. - 4.
Please note that the model associated with Equations (5a) and (5b) where derived from (3a) and (3b), under the assumption of positive concentrations, by changing the variables into logarithms. The advantage, besides the numerical stability of the new formulation it grants intrinsic positive species concentrations. This is for (3a) and (3b) in general not given, since there usually exist negative roots to (3a) and (3b), see [25]. Please note that the species distributions and the inclusion of complexes guarantee the positivity of the complex formation constants. This avoids the necessity to use more complicated and more cost-intensive numerical methods, such as described in this paper, such as augmented Lagrangian algorithms, see [26,27]. - 5.
The model formulation used in this paper (5a) and (5b) differs not only in the introduction of logarithms into the problem formulation, but it also differs from the model formulations used in the works of Alderighi et al., Gans et al. and Martell [11,12,20], by considering the complexes as well. This is commonly omitted by inserting (3b) into (3a).
3.2. A Model of Titration Curves with Vertices in Thermodynamic Equilibrium
The aim of this section is the modeling of the potentiometric titration curves as they are obtained from the experimental set-up described in
Section 2. First, assume that ligands
, …,
, metals
, …,
, hydroxide ions
, and protons
are given in the original electrolyte. Additionally, suppose that
reactions in the form of (
1) take place.
As described in the experimental set-up described in
Section 2, a starting volume
of electrolyte is assumed to be given, with given total masses
, in mol of the ligand
, for
, total masses
of the metal
, for
, and the total mass of hydroxide ions
in mol of
as well as the total masses of the protons
in the electrolyte.
Furthermore, suppose that
additions of a solution, with molar concentration
in
of
concentration, and suppose that no additional species other than
,
and
are interacting with the assumed system of reactions (
1). Additionally, suppose that the solution is added in the following volume steps:
.
Due to the experimental set-up, it can be assumed that in each chosen measurement, a state close to the thermodynamic equilibrium is reached. Due to the assumptions above, one can describe the concentrations in each measured state through the model given by Equations (
5a) and (
5b). To describe the respective models, it is left to describe the total masses
,
,
, and
in each added volume
for
of the solution above.
Due to the assumptions about the added solution described above, one finds that the masses
and
do not change over the titration, i.e., for all
, for all
, and all
, i.e., one obtains
Furthermore, under the usage of
, and for
where
is the complex formation constant of water, the exact value for 25 °C is given in Equation (
19), where
is the deprotonation constant and
where
denotes the concentration of the hydroxide ions of the added solution and
the concentration of the protons. Then, the total masses
and
of the electrolyte after the
z-th addition of the given solution are described by
Combining the model with the RHS (
6a)–(
6f), one obtains for each measurement point
a model for the thermodynamic equilibrium. This yields a complete model for the titration curve, under the assumption that the stability constants
are given for each reaction
.
This set-up yields a set of
Z systems of
non-linear equations which directly describe the molar masses of the species as variables for the RHS as input data, which must be solved to obtain the molar masses at each step, i.e., one has to solve a system of non-linear equations in the following form:
where
is, for all
, the function given by the non-linear model (
5a) and (
5b), with variables as denoted by (
4c) and (
4d) and RHS given by (
6a)–(
6f) for fixed stability constants
The Equation (
7) can be used to fit the titration curve regarding the variables
, …,
to the measured titration curve as given by the measurement as described in
Section 2.
3.3. Calculation of the Total Masses and
In many relevant cases, the total masses of and are unknown. In this section, a way to calculate and will be detailed. For this, it should be noted that in the measurement of the titration curve, the pH value of the initial volume of the electrolyte is given. Hence, the concentrations and are known. These values will be used to determine and .
The way to calculate the values of
and
is to take the first equation, corresponding to the 0-th addition during titration, as given in
Section 3.2 and with the interpretation of
and
as variables and then interpret the given values of
and
as input data to finally obtain a system of
equations in
variables which must be solved. As part of the corresponding solution, one obtains values for
and
.
When formalizing the strategy above, one obtains a non-linear system of equations in the following form:
In the equation above, the function
is the function associated with the model given by (
5a) and (
5b) where the variables
, …,
are corresponding to
Additionally, the variables
and
are given through
This yields a system of functions from which and can be determined.
3.4. Formulating an Inverse Problem
As discussed in the introduction, this paper aims at a method to calculate the stability constants
associated with the reactions given in (
2). In this section, an inverse problem, as in the books of Hinze et al., Richter [
13,
14] or in the book of Mäkelä [
16], will be derived.
Assume that
measurements of the pH values
are given. Furthermore, for an arbitrary fixed
, let the vector
be the solution to (
7). Then, the to
b associated pH values
can be interpreted as the image of a vector-valued function
Then, one seeks a
for which the following residual is minimal:
In many cases, the values of b can be restrained. For most applications, stability constants can be restricted to .
When translating the setting above into a restrained minimization problem, one seeks the solution
b to the following restrained minimization problem:
Then, the stability constants
are given as
Hence, a minimization problem was derived whose solution can be reformulated into the searched stability constants.
3.5. An Inherent Method to Validate the Assumed Reaction System
In practice, an important question is how to validate an assumed system of reactions. In the following, a way to validate the system of reactions (
1) will be discussed:
Suppose that the reaction
is considered in the calculations of the thermodynamic equilibrium and the minimization (
14). Then, at room-temperature, the identity
holds true. For the discussion, it should be noted that the molar weight of water is given by the molar weights of two protons, which has a molar weight of
and an oxygen atom, which has a molar weight of
. With the data above and taking into account that one liter of water has a weight of 1000 g, one obtains the following concentration of water in water:
With the equation above and the usage of the deprotonation constant of water
, one obtains the following verification identity:
Although the calculation above was done for the concentration of pure water of , the value of can be used to validate the reaction systems and additional stability constants.
4. Numerical Methodology
In this section, the numerical strategy to simulate the thermodynamic equilibria, titration curves, and the inverse problems will be discussed. Based on the simulation of thermodynamic equilibria, see
Section 4.1, a method for the prediction of titration curves will be derived, see
Section 4.2. Additionally, in
Section 4.3, the calculation of the RHS parts associated with
and
will be discussed as well as the numerical methodology of the evaluation of the inverse problem in
Section 4.4.
4.1. Simulation of Thermodynamic Equilibria
This section is devoted to the description of the numerical treatment and approximation of the non-linear systems of equations associated with the model (
5a) and (
5b), as given by the determination of roots of the function
as it is defined in
Section 3.1.
An initial idea for the treatment of the zero search could be, as done in the work of Alderighi et al. or Martell [
11,
20], a direct application of a Newtonian scheme, see [
28]. Since the convergence of classical Newtonian schemes is only granted when the starting value
of the algorithm is member of a sufficient close neighborhood of the searched zero
, see [
17,
29],
for
must be fulfilled. The major issue is that
and
are generally unknown. Since a sufficiently good starting value is unknown in the first instance, the Newtonian scheme cannot be applied directly in most cases. A solution to this problem is the usage of stabilized Newtonian schemes as described in [
30].
The stabilized Newtonian schemes converge for each given , but the efficiency of the stabilized Newton methods still depends on the initial value, although it is relatively complicated. In practice, the stabilized Newton methods need rather long computation times.
Therefore, it is not a stabilized Newton scheme described in this article but instead an easier method based on a homotopy method, see [
18,
19]. The basic idea of the homotopy method is to calculate an appropriate initial value for the Newtonian scheme. A central point is the use of continuous deformation from a simpler function
, for which a zero is known, to
.
In this paper, the function
g is the identity function. Furthermore, a deformation in the form
is used.
Now, let a decomposition , with and be given. Then in each step the system of nonlinear equations is solved:
Find
Then, one applies the following Algorithm 1:
| Algorithm 1: Homotopy Loop |
Input: Initial value , tolerance , a decomposition , length of the decomposition and set .
Output: Approximate solution to .
Perform the following steps:
- S 1
Approximate a solution of x, with tolerance , and initial value to the following problem with the Newtonian scheme given in Appendix A. Find such that it fulfills ( 21). As output of the Newtonian scheme, one obtains an approximation of and an error . - S 2
Ifand set , and go to S 1. If and then go to S 4. If then go to S 3. - S 3
Use a finer decomposition of than beforehand, meaning with greater length , and set , and set .
|
Remark 2. 1. Please note that the identities and directly imply that the output of Algorithm 1 is a sufficiently good approximation of the initially searched zero of .
- 2.
Additionally, note that the stability issues of the Newtonian scheme are solved by the homotopy Algorithm 1 if the decomposition is sufficiently fine, and one can grant convergence independently from the initial value.
- 3.
In contrast to the numerical schemes described in Alderighi et al., Gans et al., or Martell [11,12,20], where a simple Newtonian scheme is used, in this paper the homotopy Algorithm 1 was introduced, which grants convergence of the numerical scheme in any case. Although the convergence of the numerical schemes is granted due to the introduction of the homotopy loop 1 if the decomposition is sufficiently fine, but the efficiency of the algorithm is still dependent of the initial value of the numerical scheme and the number of nodes in .
With Algorithm 1, one has a stable, robust and convergent numerical method to simulate thermodynamic equilibria.
4.2. Simulation of Titration Curves
In this section, a way to simulate the titration curve, i.e., how to approximately find the roots of (
7), is discussed.
As the discussion in
Section 3.2 already noted, the model of the titration curve is fully decoupled, i.e., the concentrations in each addition
are mathematically independent from the concentrations associated with each other addition. Thus, it is sufficient to solve the thermodynamic equilibrium in each addition
separately.
Additionally, note that Algorithm 1 is applicable to the search of zeros of instead of zeros of ; hence, the direct approach of applying Algorithm 1 to treat the equations for all the equations is an easy and efficient way to simulate titration curves.
4.3. Calculation of and
Before a method for the approximation of the inverse problem (
14) can be discussed in
Section 4.4, the calculation of
and
will briefly be discussed in this subsection.
As formulated in Equation (
9) in
Section 3.3, one must find a root of the function
. This root can be calculated by the same Algorithm 1 as for the calculation of thermodynamic equilibria but with one simple adaptation as described above. This adaptation is to treat
instead of
in the corresponding algorithm.
4.4. Treating the Inverse Problem
In this section, a way to treat the minimization problem (
14) will be discussed.
As studied in
Section 3.4, one must evaluate the residual
to calculate the stability constants (Michaelis constants); that is, the map
, given through
must be evaluated. The evaluation of
g is done through the evaluation of the thermodynamic equilibria described by the zero search given by (
7) described in
Section 3.2. Then, the pH values
for all
can be given by
, where
is the solution to
, as described in
Section 3.2. Furthermore,
is the initial volume and
is the total added volume in addition
z. The corresponding values can be obtained as discussed in
Section 4.2.
As the evaluation of the residual res has already been discussed, now the treatment of the restrained minimization problem (
14) can now be described. The common solution theory of restrained minimization problem is based on the treatment of KKT theory (Karush–Kuhn–Tucker theory), see [
31], and multiple methods are known to treat such problems as augmented Lagrangian methods, see [
26], which are made especially for large scale problems. However, the problem types discussed in this paper are of medium type. For that, SQP methods are much more efficient. The corresponding method applied in this section is described in [
32].
Remark 3. One major question is how to reduce the numerical effort to approximate a solution to (14). Please note that the following model reductions to (14) can be used. - (i)
Please note that the measured pH values, as given through the experimental method described in Section 2, can be interpreted as evaluations of a function , where is the maximal added volume, which can be approximated via its interpolant due to the measured points. A way to reduce the effort is to use a set of data points for with instead of the measured data points for ; is the interpolation of the titration curve pH onto the corresponding data points. - (ii)
As discussed in Section 3.4, the residual , as defined in (13), can also be defined as a function in a lower dimension by interpreting for a subindex set the values as variable and leaving the remaining values of b as constant. With this adaptation, one is enabled to search for specific stability constants. - (iii)
Combining the points (i) and (ii), one must use at last points in (i) to find unique approximations for the stability constants searched for in (ii).
- (iv)
Warning:Using the reduction (ii), one must be very careful, due to the fact that by keeping several stability constants fixed, one assumes that the fixed stability constants are known known exactly, but most of the stability constants are not known exactly. It immediately follows that this assumption will lead to error propagation.
This discussion completes the section and all numerical schemes for this article are assembled.
7. Discussion and Conclusions
The given paper contributes to the field of simulation thermodynamic equilibria, titration curves and the determination of stability constants from titration curves. The current work remodels a standard approach of describing thermodynamic equilibria described in [
11,
12,
20], to guarantee positive species concentrations and stability constants, as well as to stabilize the applied numerical schemes. Furthermore, a numerical method was introduced which converges and is stable regarding the initial value. The numerical scheme and the revised model are validated in this work.
In this paper, in
Section 2, a type of measurement was introduced for which, for every measured pH value, one can assume a thermodynamic equilibrium. In
Section 3, a model for the description of thermodynamic equilibria was equivalently reformulated to gain numerical stability. Based on this formulation, models for titration curves, the calculation of
,
, and the inverse computation of stability constants were obtained.
Additionally, in
Section 4, numerical schemes for the simulation of thermodynamic equilibria titration curves are discussed in addition to the inverse calculation of
,
, and the stability constants were described. The methodology was designed for the greatest possible simplicity, stability, and robustness.
Furthermore, numerical examples were given in
Section 5, by which the functionality of the algorithmic approach and the convergence of the schemes were validated.
On the algorithmic approach, some remarks must be made. First, the efficiency of the numerical schemes for the simulation of the titration curves is highly dependent on the model to which the numerical scheme was applied. For instance, the time needed for computation, especially for the required number of iterations in the homotopy loop, is dependent on the number of educts in which reactions are formulated, the number of products (reactions), the stoichiometric indices, the total masses of the educts , and especially the stability constants. The large number of possible varieties in the considered model makes the estimation of needed computation time difficult.
Due to the use of the simulation of titration curves for the inverse problem, the factors described above also have an influence on the time efficiency of the numerical treatment of the inverse problem (
14). Furthermore, the efficiency of the underlying calculations is also dependent on the initial values given for the SQP method. That means, the better the stability constants can be estimated before the actual optimization starts, the less time the calculations will take.
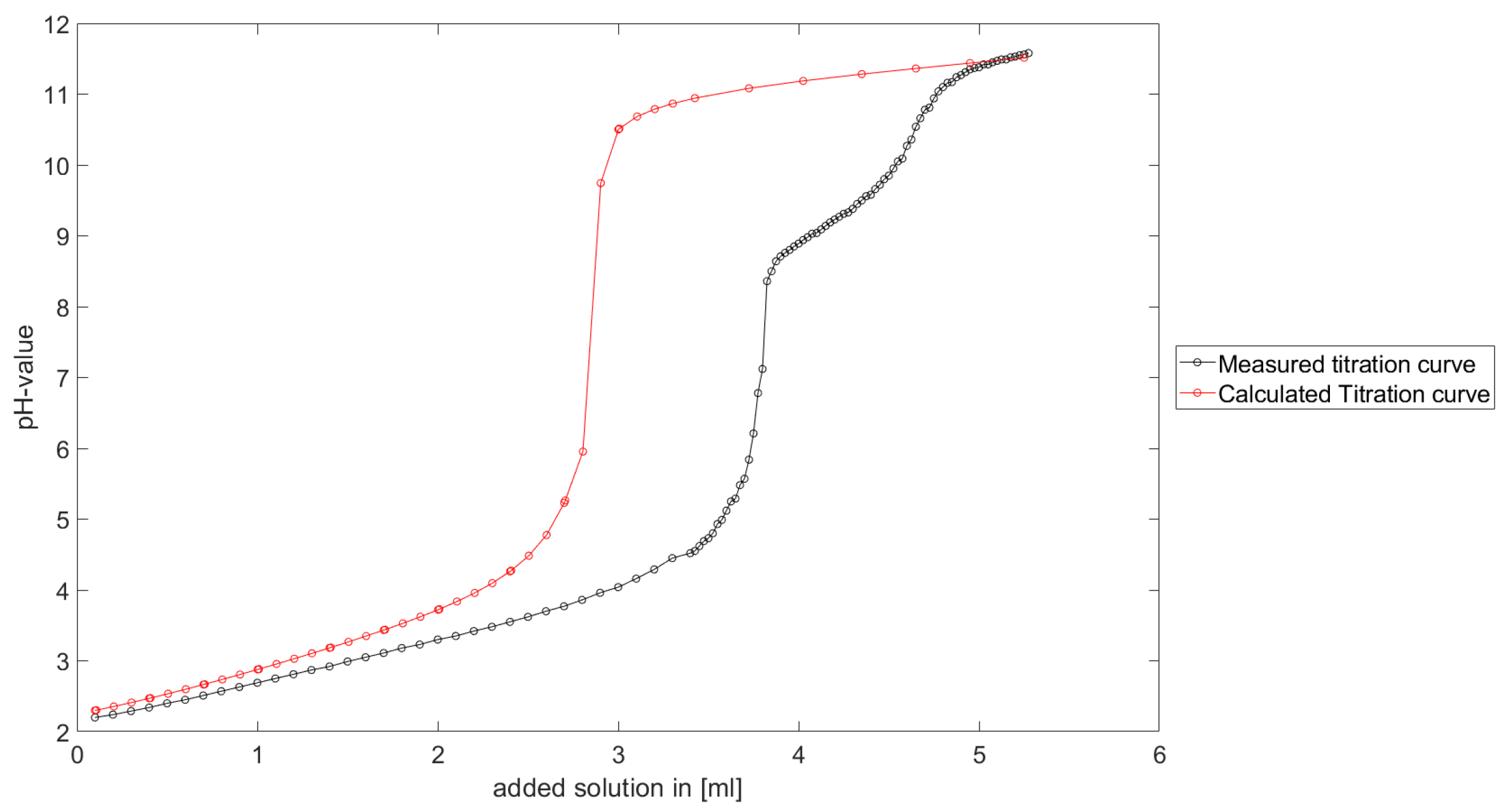
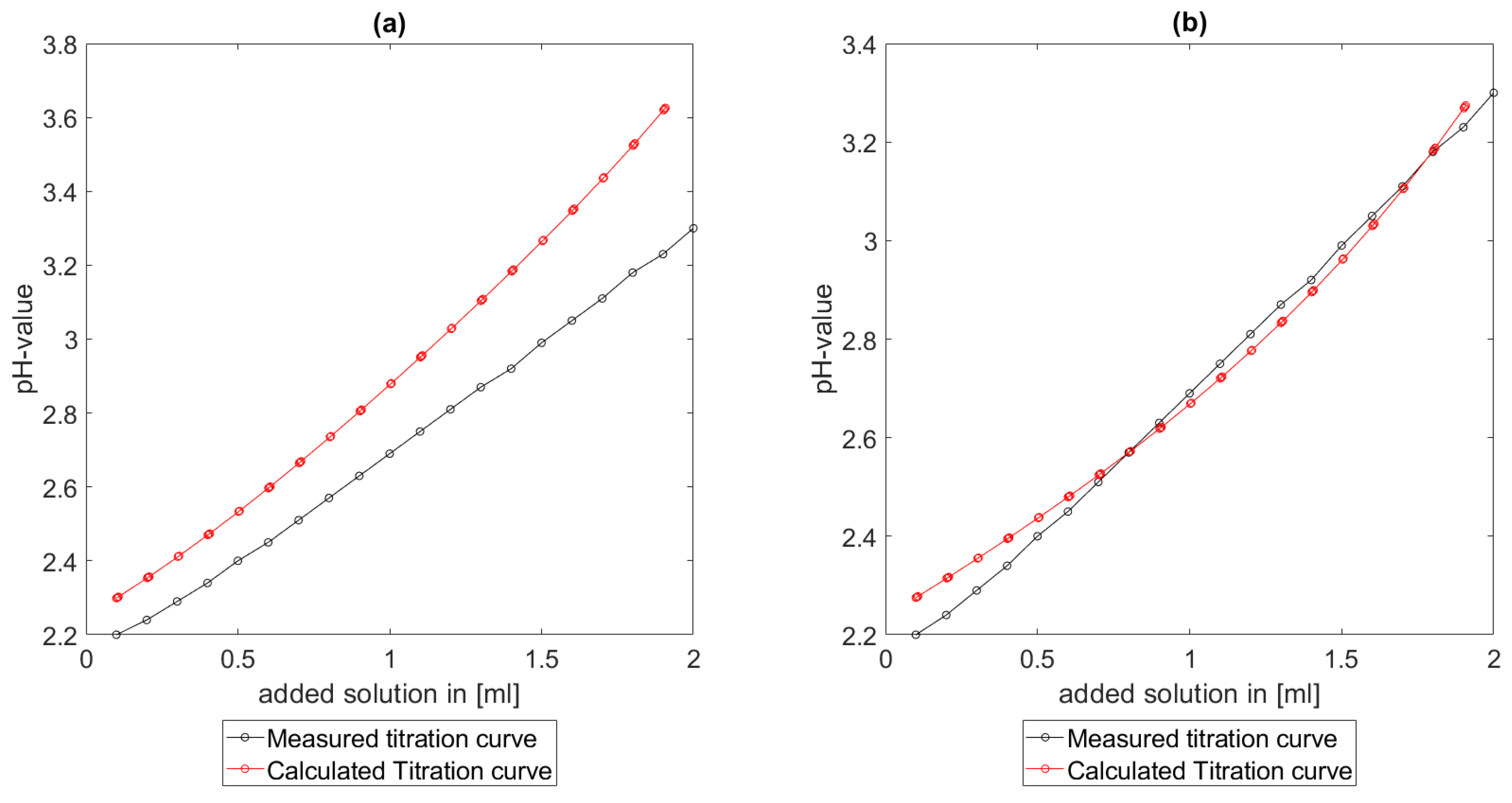
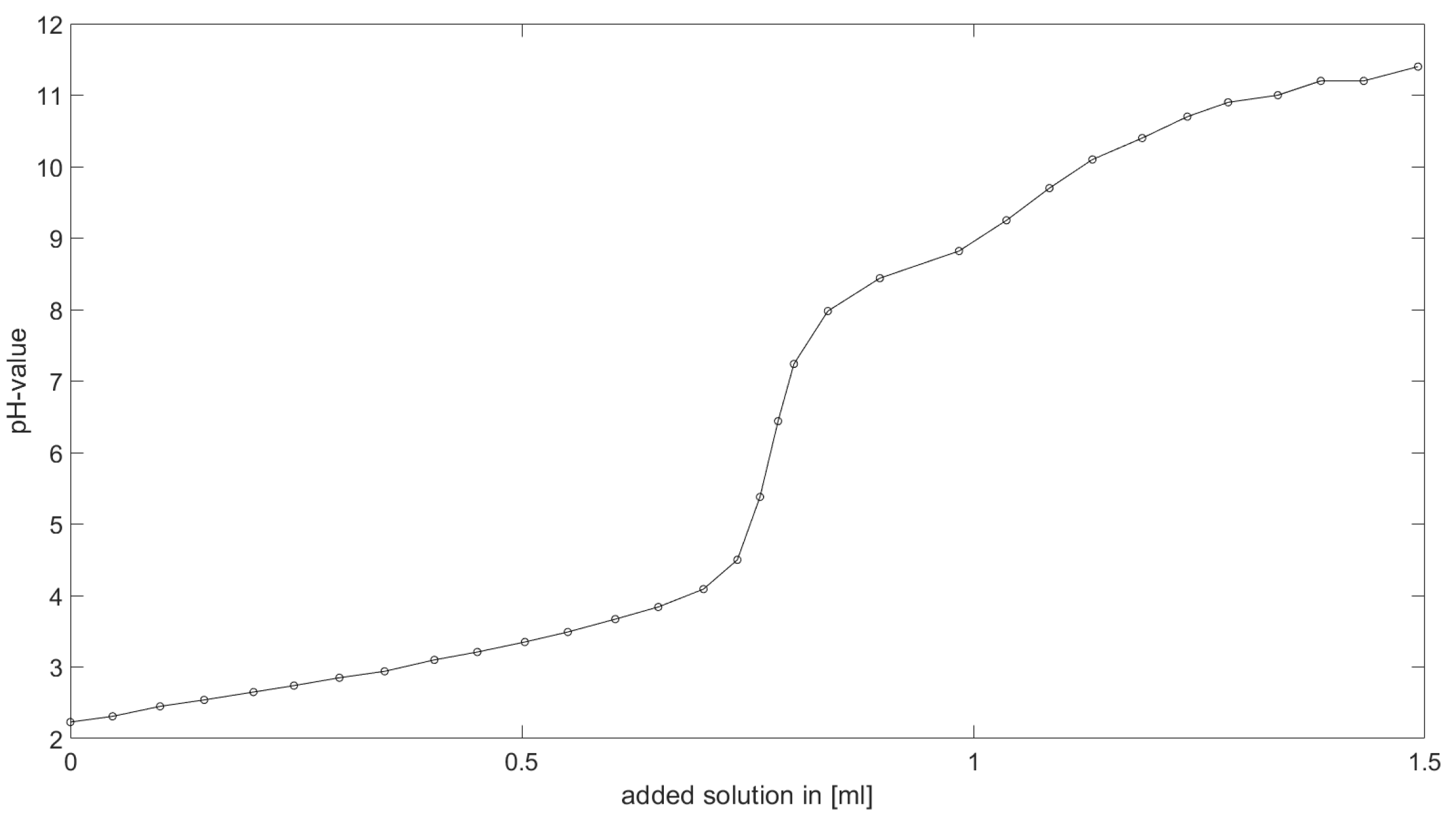
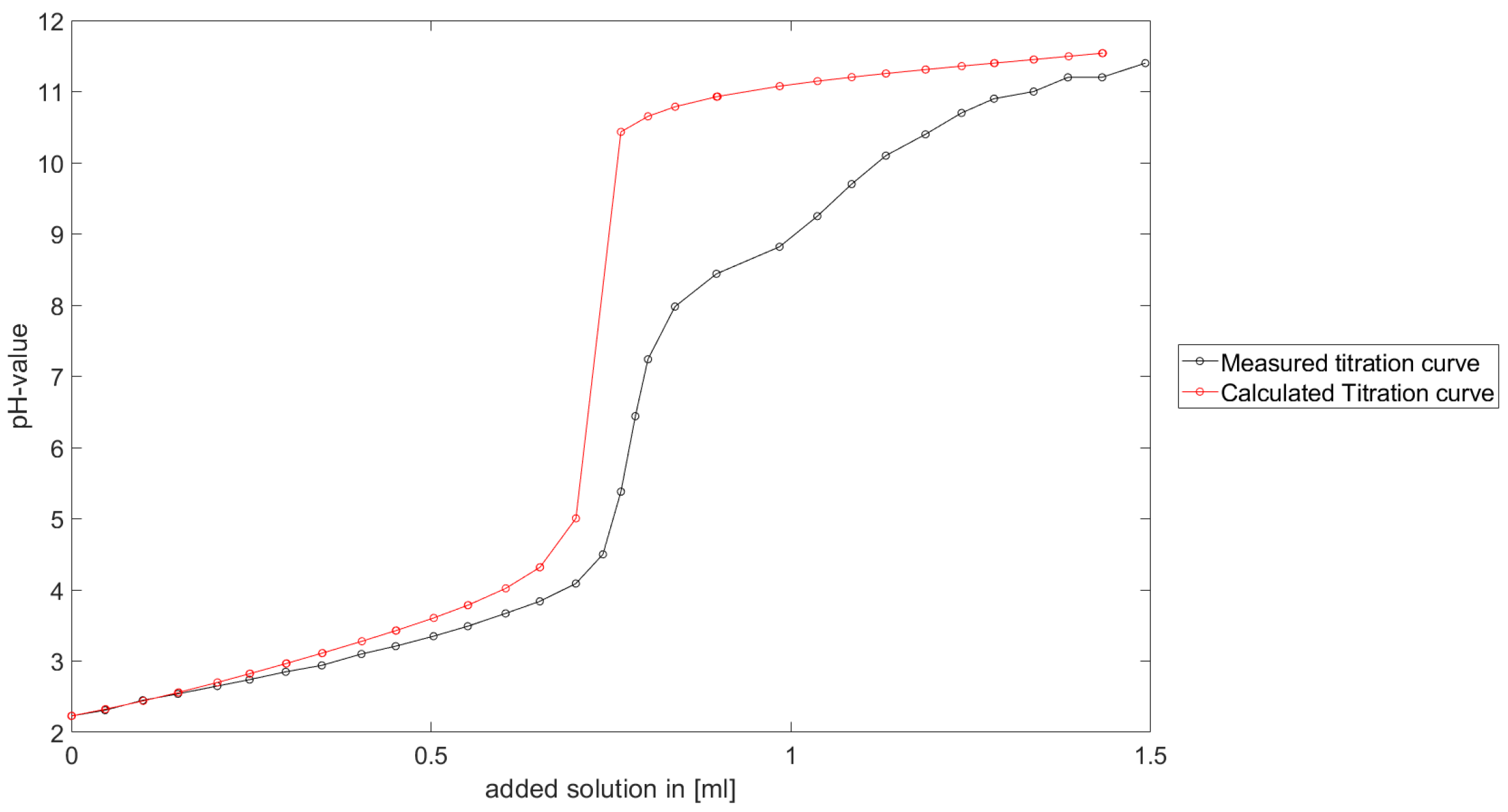
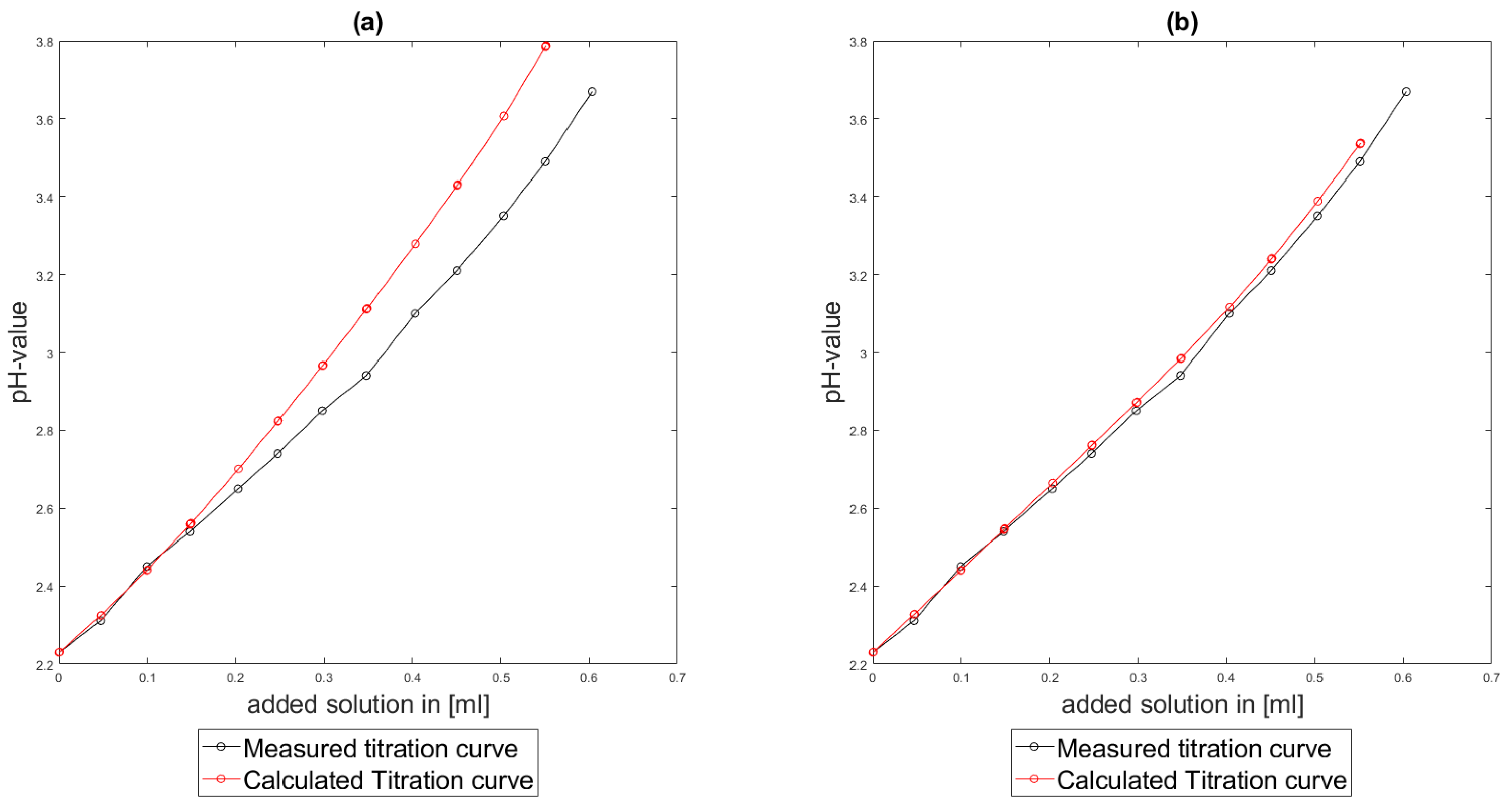
As could be seen from the treatment of the titration of citric acid Cit, see
Section 6.1, the measured titration curve is close to the one predicted by the software with stability constants and reactions from literature. Additionally, applying the algorithm for the inverse problem, one observes stability constants close to the values found in the literature.
Furthermore, in
Section 6.2 and
Section 6.3, the software was applied to the titration of a Cit-Ni-electrolyte. In both cases, that of the self-measured titration curve and the one from literature, a gap between the simulated and measured titration curves can be observed. When fitting the whole titration curve, one obtains different stability constants from the values in the literature. However, good agreement between simulated and measured curves is obtained for lower additions and pH values. Satisfactory results of the inverse calculations of the titration curves were obtained.
The behavior discussed above can be explained through the possibility of missing reactions. An error in the software or the general model can be excluded since the simulations in the case of the titration of the Cit-electrolyte and for both Cit-Ni cases for low additions of solutions are plausible, which would not be the case if major mistakes in the modeling or the implementation were done.
Summarizing the results, one obtains a methodology to compute stability constants, which is stable, convergent and guarantees positive stability constants. The computed stability constants are comparable to the results given in the literature. Although the calculated complex formation constants differ from the values in the literature, it is shown that the calculated values are plausible for a significant number of examples. Furthermore, the gap between the measured titration curve and computed titration curve for the Cit-Ni electrolytes indicate some error in the assumed reactions. However, the strength of the methodology described in this article is the adjusted numerical scheme to the experimental setting, in addition to the robustness of the numerical scheme.
For further scientific work besides the identification of stability constants, a study to explain the gap between measurement and simulation is needed. Taking additionally the times of measurements into account the associated kinetic constants of the reactions (
2) can be accessible. A further extension of the underlying model on the space component, through diffusion-reaction models, and taking the place of measurement and addition of the titrant, could make diffusion coefficients acceptable.