Improved Equilibrium Optimization Algorithm Using Elite Opposition-Based Learning and New Local Search Strategy for Feature Selection in Medical Datasets
Abstract
:1. Introduction
- An improved version of the original EOA, named IEOA is proposed for FS problems in wrapper mode.
- Two main improvements were introduced to the original EOA to solve its limitations:
- EOBL technique is applied at the initialization phase of EOA to improve its population diversity.
- A novel local search mechanism is proposed and integrated with EOA to prevent trapping in local optima and to improve the EOA exploitation search.
- The performance of IEOA was evaluated using classification accuracy, selected features, fitness value, and p-value. In addition, IEOA results were compared with the results of other well-known and recent optimization algorithms, including particle swarm optimization (PSO), genetic algorithm (GA), whale optimization algorithm (WOA), grasshopper optimization algorithm (GOA), ant lion optimizer (ALO), slime mould algorithm (SMA), and butterfly optimization algorithm (BOA). In these experiments, 21 benchmark biomedical datasets from the UCI repository were used. The conducted experiments revealed the superior performance of IEOA in comparison to these baseline algorithms.
2. Related Works
3. Preliminaries
3.1. Equilibrium Optimization Algorithm (EOA)
3.1.1. Initialization Phase
3.1.2. Exploration Phase
3.1.3. Exploitation Phase
3.2. Elite Opposition Based-Learning (EOBL)
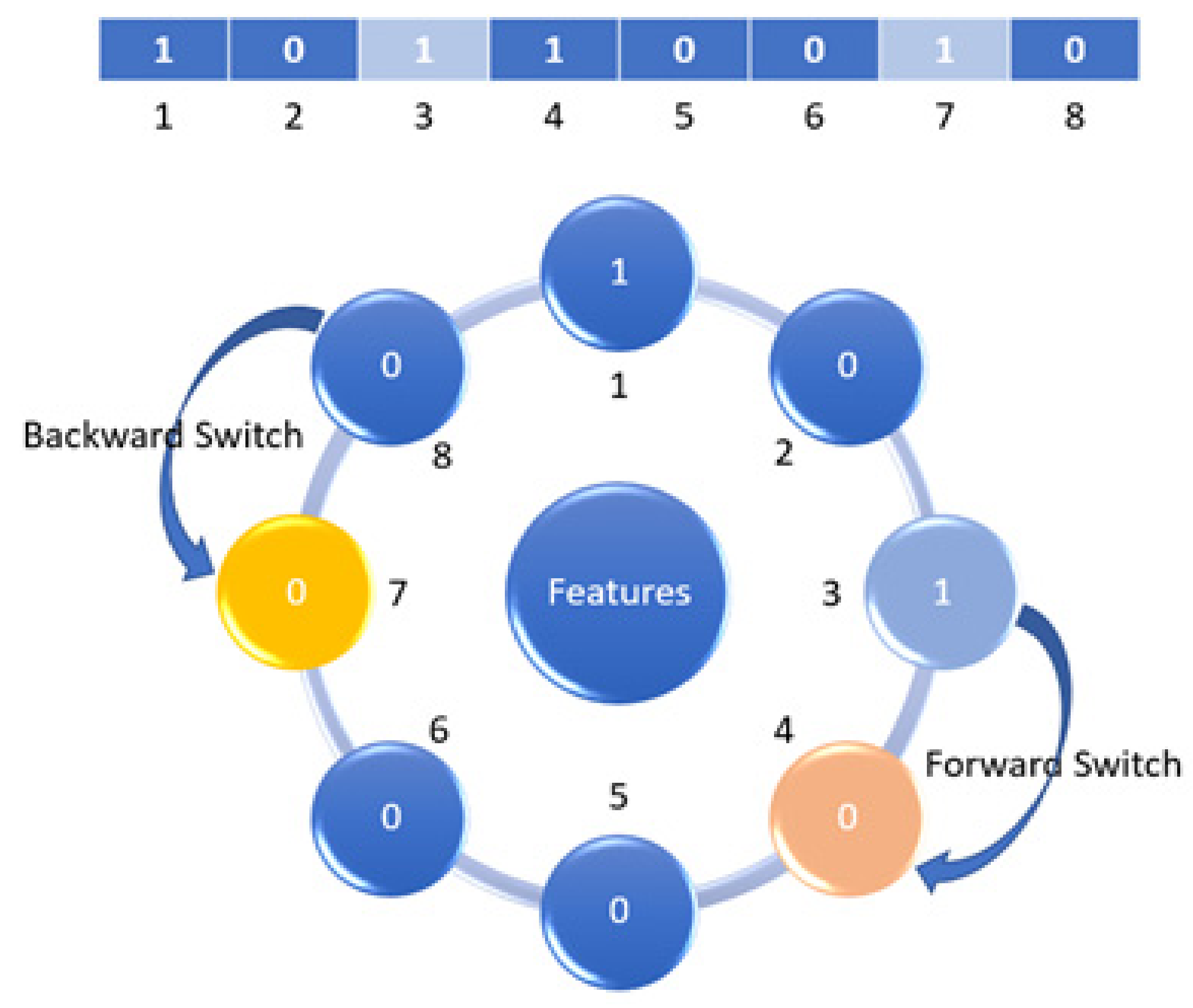
3.3. The Mutation Search Strategies (MSS)
3.3.1. Mutation
3.3.2. Mutation Neighborhood Method (MNM)
3.3.3. Backup Method (BM)
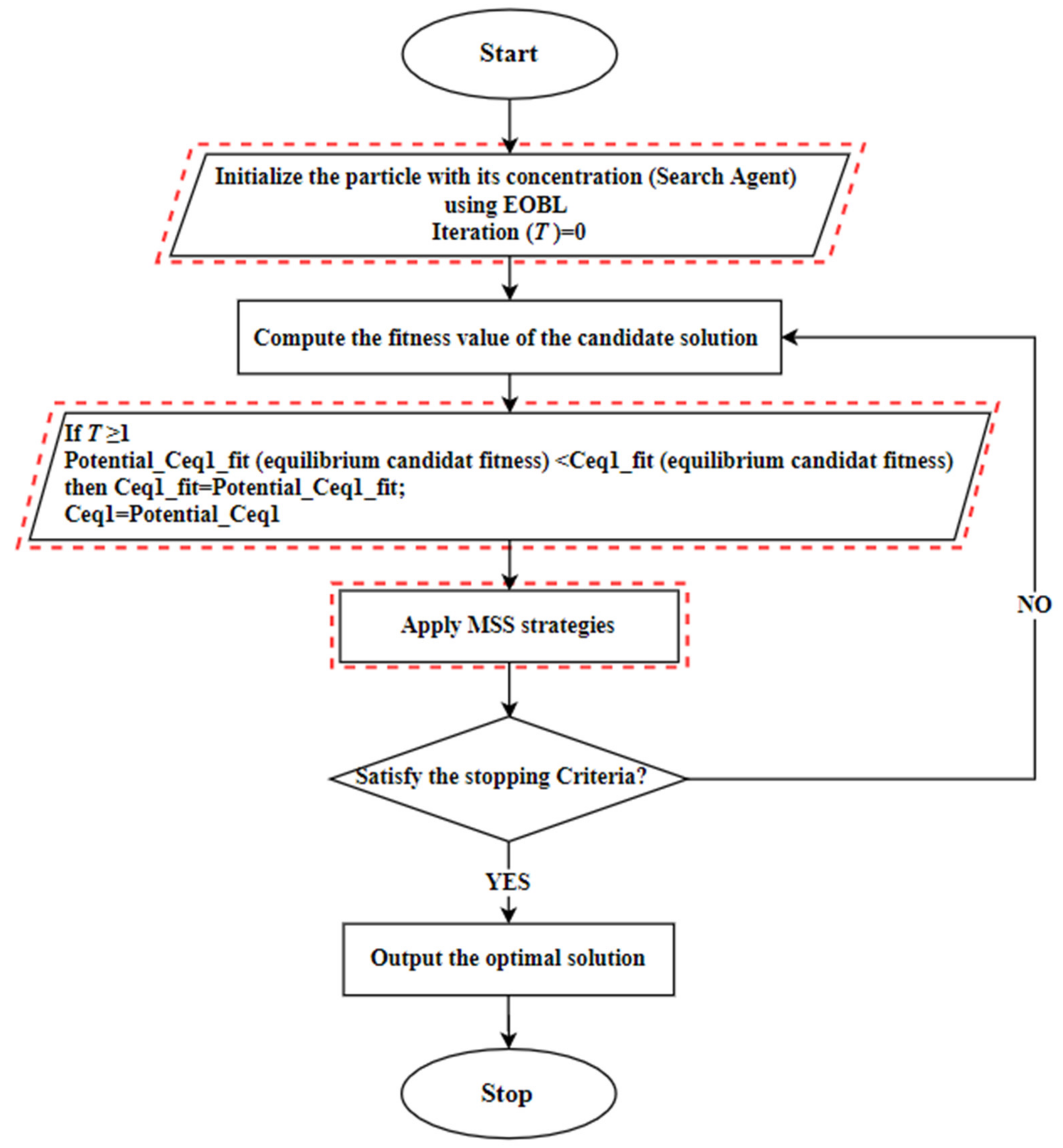
4. Improved Equilibrium Optimization Algorithm (IEOA)
- In the first step: the particle population C is initialized using the random generation function with the size N, as defined in Equation (2) and the equilibrium candidate’s fitness is assigned with a large number. In this step, each generated particle (search-agent) is regarded as a possible solution, which includes a random set of features from the complete set of features.
- In the second step: compute the fitness value of each solution and find the elite position from the initial population. After that, the EOBL method creates the opposite elite solutions, as defined in Equation (15), then selects the best N solution.
- In the third step: the EOA algorithm is executed to update the location of each particle in the population and to find the best current location based on the best fitness value, as defined in Equation (13). IEOA works based on KNN classification accuracy and the feature selection is based on the wrapper mode.
- In the fourth step: MSS strategies are employed to improve the current location. Here, a potential best solution is considered; if the fitness value of a new location is better than the current one, then the MNM is executed for further improvement.
- The next iteration of EOA is executed and the current best solution compared with the potential solution in the fifth step. Here, the BM strategy is used if the current best solution is better than the potential location. Otherwise, the current best location is changed to be equal to the potential solution
- In the sixth step: The proposed solution proceeds with the iterations until the stopping criteria is met. The pseudocode of the proposed IEOA is illustrated in Algorithm 1.
| Algorithm 1. Pseudo code of IEOA Algorithm. |
| Input: Initialize the particle’s population randomly, T: the maximum number of iterations. Output: The equilibrium state and its fitness value. Apply EOBL method to find the bestopposite solutions, then select the fittestsolutions, according to Equations (14)–(16) Assign free parameters Calculate the fitness of the particle locations. %MSS %BM Apply mutation strategy to current best location using Equations (17) and (18) Return the best location |
5. Experiments
5.1. Platform
5.2. Benchmark Datasets
5.3. Algorithms and Experiment Parameter Setting
5.4. Computational Complexity
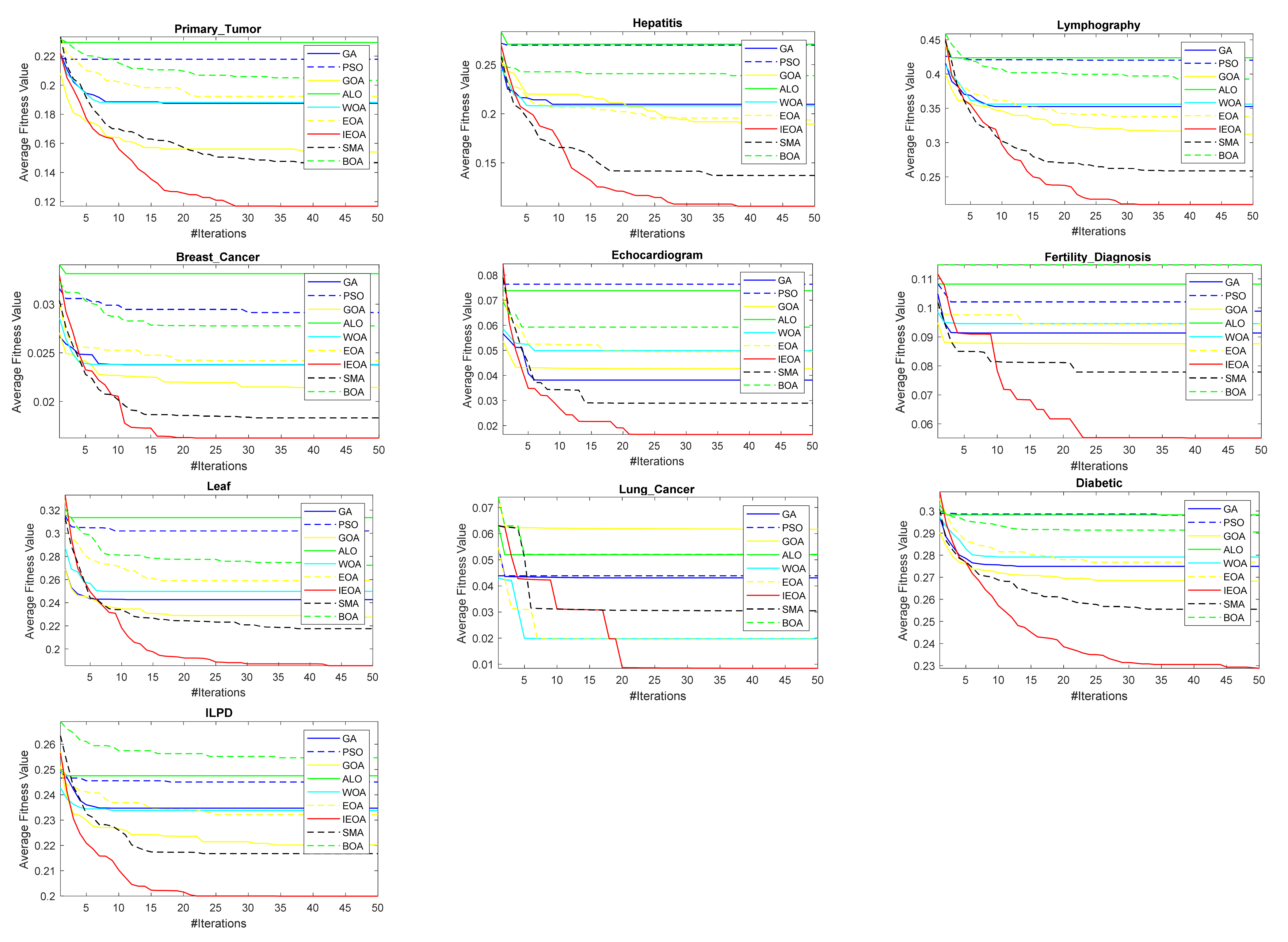
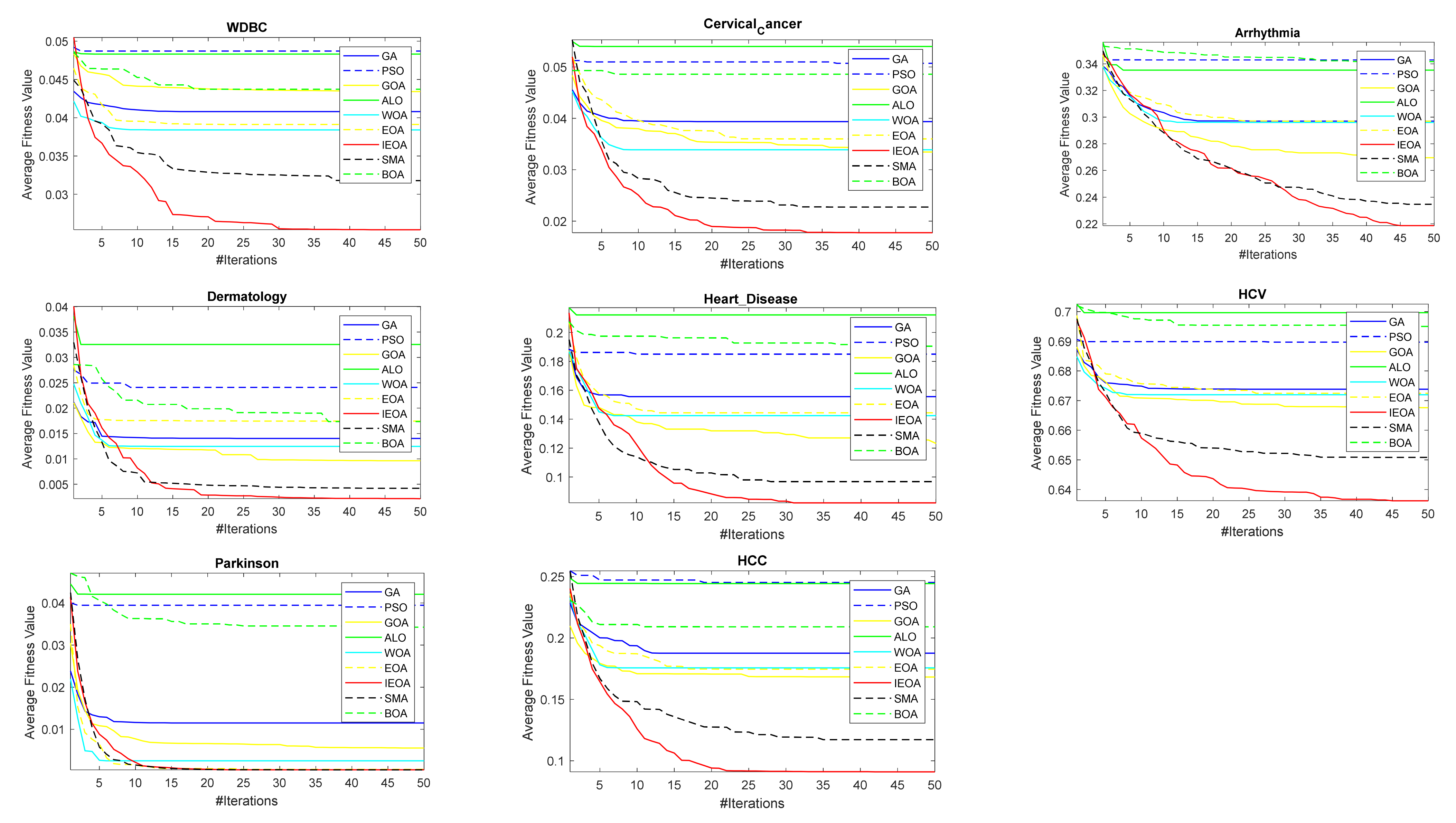
6. Results and Analysis
6.1. Comparison of EOA and IEOA
6.2. Comparison of IEOA Algorithm with Other Optimization Algorithms
6.3. Limitations of the Proposed IEOA
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Devanathan, K.; Ganapathy, N.; Swaminathan, R. Binary Grey Wolf Optimizer based Feature Selection for Nucleolar and Centromere Staining Pattern Classification in Indirect Immunofluorescence Images. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019. [Google Scholar]
- Lin, K.C.; Hung, J.C.; Wei, J. Feature selection with modified lion’s algorithms and support vector machine for high-dimensional data. Appl. Soft Comput. J. 2018, 68, 669–676. [Google Scholar] [CrossRef]
- Rao, H.; Shi, X.; Rodrigue, A.K.; Feng, J.; Xia, Y.; Elhoseny, M.; Yuan, X.; Gu, L. Feature selection based on artificial bee colony and gradient boosting decision tree. Appl. Soft Comput. J. 2019, 74, 634–642. [Google Scholar] [CrossRef]
- Al-Sharhan, S.; Bimba, A. Adaptive multi-parent crossover GA for feature optimization in epileptic seizure identification. Appl. Soft Comput. J. 2019, 75, 575–587. [Google Scholar] [CrossRef]
- Elgamal, Z.M.; Yasin, N.B.M.; Tubishat, M.; Alswaitti, M.; Mirjalili, S. An Improved Harris Hawks Optimization Algorithm With Simulated Annealing for Feature Selection in the Medical Field. IEEE Access 2020, 8, 186638–186652. [Google Scholar] [CrossRef]
- Moradi, P.; Gholampour, M. A hybrid particle swarm optimization for feature subset selection by integrating a novel local search strategy. Appl. Soft Comput. 2016, 43, 117–130. [Google Scholar] [CrossRef]
- Faris, H.; Mafarja, M.M.; Heidari, A.A.; Aljarah, I.; Al-Zoubi, A.M.; Mirjalili, S.; Fujita, H. An efficient binary Salp Swarm Algorithm with crossover scheme for feature selection problems. Knowl. Based Syst. 2018, 154, 43–67. [Google Scholar] [CrossRef]
- Tubishat, M.; Idris, N.; Shuib, L.; Abushariah, M.A.M.; Mirjalili, S. Improved Salp Swarm Algorithm based on opposition based learning and novel local search algorithm for feature selection. Expert Syst. Appl. 2020, 145, 113122. [Google Scholar] [CrossRef]
- Mafarja, M.; Mirjalili, S. Whale optimization approaches for wrapper feature selection. Appl. Soft Comput. J. 2018, 62, 441–453. [Google Scholar] [CrossRef]
- Too, J.; Abdullah, A.R.; Saad, N.M.; Ali, N.M.; Tee, W. A new competitive binary grey wolf optimizer to solve the feature selection problem in EMG signals classification. Computers 2018, 7, 58. [Google Scholar] [CrossRef] [Green Version]
- Too, J.; Abdullah, A.R.; Mohd Saad, N. Hybrid binary particle swarm optimization differential evolution-based feature selection for EMG signals classification. Axioms 2019, 8, 79. [Google Scholar] [CrossRef] [Green Version]
- Chantar, H.; Mafarja, M.; Alsawalqah, H.; Heidari, A.A.; Aljarah, I.; Faris, H. Feature selection using binary grey wolf optimizer with elite-based crossover for Arabic text classification. Neural Comput. Appl. 2019, 32, 12201–12220. [Google Scholar] [CrossRef]
- Too, J.; Abdullah, A.R.; Saad, N.M.; Ali, N.M. Feature selection based on binary tree growth algorithm for the classification of myoelectric signals. Machines 2018, 6, 65. [Google Scholar] [CrossRef] [Green Version]
- Too, J.; Abdullah, A.R.; Saad, N.M.; Tee, W. EMG feature selection and classification using a Pbest-guide binary particle swarm optimization. Computation 2019, 7, 12. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.; Kong, X.; Xu, J.; Xue, Z.; Zhai, R.; Zhang, S. A Hybrid Gene Selection Method Based on ReliefF and Ant Colony Optimization Algorithm for Tumor Classification. Sci. Rep. 2019, 9, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Taradeh, M.; Mafarja, M.; Heidari, A.A.; Faris, H.; Aljarah, I.; Mirjalili, S.; Fujita, H. An evolutionary gravitational search-based feature selection. Inf. Sci. 2019, 497, 219–239. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl. Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Chang, V.; Mohamed, R. A Novel Equilibrium Optimization Algorithm for Multi-Thresholding Image Segmentation Problems; Springer: London, UK, 2020. [Google Scholar]
- Elsheikh, A.H.; Shehabeldeen, T.A.; Zhou, J.; Showaib, E.; Abd Elaziz, M. Prediction of laser cutting parameters for polymethylmethacrylate sheets using random vector functional link network integrated with equilibrium optimizer. J. Intell. Manuf. 2020, 32, 1–12. [Google Scholar] [CrossRef]
- Shaheen, A.M.; Elsayed, A.M.; El-Sehiemy, R.A.; Abdelaziz, A.Y. Equilibrium optimization algorithm for network reconfiguration and distributed generation allocation in power systems. Appl. Soft Comput. 2021, 98, 106867. [Google Scholar] [CrossRef]
- Tubishat, M.; Abushariah, M.A.M.; Idris, N.; Aljarah, I. Improved whale optimization algorithm for feature selection in Arabic sentiment analysis. Appl. Intell. 2019, 49, 1688–1707. [Google Scholar] [CrossRef]
- Gou, J.; Lei, Y.X.; Guo, W.P.; Wang, C.; Cai, Y.Q.; Luo, W. A novel improved particle swarm optimization algorithm based on individual difference evolution. Appl. Soft Comput. J. 2017, 57, 468–481. [Google Scholar] [CrossRef]
- Arora, S.; Anand, P. Binary butterfly optimization approaches for feature selection. Expert Syst. Appl. 2019, 116, 147–160. [Google Scholar] [CrossRef]
- Guo, M.W.; Wang, J.S.; Zhu, L.F.; Guo, S.S.; Xie, W. Improved Ant Lion Optimizer Based on Spiral Complex Path Searching Patterns. IEEE Access 2020, 8, 22094–22126. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, W.; Pan, Y. Enhancing electronic nose performance by feature selection using an improved grey wolf optimization based algorithm. Sensors 2020, 20, 4065. [Google Scholar] [CrossRef]
- Ewees, A.A.; Abd Elaziz, M.; Houssein, E.H. Improved grasshopper optimization algorithm using opposition-based learning. Expert Syst. Appl. 2018, 112, 156–172. [Google Scholar] [CrossRef]
- Park, J.; Park, M.W.; Kim, D.W.; Lee, J. Multi-population genetic algorithm for multilabel feature selection based on label complementary communication. Entropy 2020, 22, 876. [Google Scholar] [CrossRef] [PubMed]
- Brezočnik, L.; Fister, I.; Podgorelec, V. Swarm intelligence algorithms for feature selection: A review. Appl. Sci. 2018, 8, 1521. [Google Scholar] [CrossRef] [Green Version]
- Pichai, S.; Sunat, K.; Chiewchanwattana, S. An asymmetric chaotic competitive swarm optimization algorithm for feature selection in high-dimensional data. Symmetry 2020, 12, 1782. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Nagpal, S.; Arora, S.; Dey, S.; Shreya, S. Feature Selection using Gravitational Search Algorithm for Biomedical Data. Procedia Comput. Sci. 2017, 115, 258–265. [Google Scholar] [CrossRef]
- Gao, Y.; Zhou, Y.; Luo, Q. An Efficient Binary Equilibrium Optimizer Algorithm for Feature Selection. IEEE Access 2020, 8, 140936–140963. [Google Scholar] [CrossRef]
- Abdul-hamied, D.T.; Shaheen, A.M.; Salem, W.A.; Gabr, W.I.; El-sehiemy, R.A. Equilibrium optimizer based multi dimensions operation of hybrid AC/DC grids. Alexandria Eng. J. 2020, 59, 4787–4803. [Google Scholar] [CrossRef]
- Too, J.; Mirjalili, S. General Learning Equilibrium Optimizer: A New Feature Selection Method for Biological Data Classification. Appl. Artif. Intell. 2020, 35, 1–17. [Google Scholar]
- Ghosh, K.K.; Guha, R.; Bera, S.K.; Sarkar, R.; Mirjalili, S. BEO: Binary Equilibrium Optimizer Combined with Simulated Annealing for Feature Selection. ResearchSquare 2020. [Google Scholar] [CrossRef]
- Tizhoosh, H.R. Opposition-Based Learning: A New Scheme for Machine Intelligence. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vienna, Austria, 28–30 November 2005; pp. 695–701. [Google Scholar]
- Sihwail, R.; Omar, K.; Ariffin, K.A.Z.; Tubishat, M. Improved Harris Hawks Optimization Using Elite Opposition-Based Learning and Novel Search Mechanism for Feature Selection. IEEE Access 2020, 8, 121127–121145. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, R.; Luo, Q. Elite opposition-based flower pollination algorithm. Neurocomputing 2016, 188, 294–310. [Google Scholar] [CrossRef]
- Zhang, S.; Luo, Q.; Zhou, Y. Hybrid Grey Wolf Optimizer Using Elite Opposition-Based Learning Strategy and Simplex Method. Int. J. Comput. Intell. Appl. 2017, 16, 1–37. [Google Scholar] [CrossRef]
- Mostafa Bozorgi, S.; Yazdani, S. IWOA: An improved whale optimization algorithm for optimization problems. J. Comput. Des. Eng. 2019, 6, 243–259. [Google Scholar] [CrossRef]
- Huang, K.; Zhou, Y.; Wu, X.; Luo, Q. A cuckoo search algorithm with elite opposition-based strategy. J. Intell. Syst. 2015, 2015, 567–593. [Google Scholar] [CrossRef]
- Wang, H.; Wu, Z.; Rahnamayan, S.; Liu, Y.; Ventresca, M. Enhancing particle swarm optimization using generalized opposition-based learning. Inf. Sci. 2011, 181, 4699–4714. [Google Scholar] [CrossRef]
- Marinakis, Y.; Migdalas, A.; Sifaleras, A. A hybrid Particle Swarm Optimization–Variable Neighborhood Search algorithm for Constrained Shortest Path problems. Eur. J. Oper. Res. 2017, 261, 819–834. [Google Scholar] [CrossRef]
- Nekkaa, M.; Boughaci, D. Hybrid Harmony Search Combined with Stochastic Local Search for Feature Selection. Neural Process. Lett. 2016, 44, 199–220. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Manogaran, G.; El-Shahat, D.; Mirjalili, S. A hybrid whale optimization algorithm based on local search strategy for the permutation flow shop scheduling problem. Futur. Gener. Comput. Syst. 2018, 85, 129–145. [Google Scholar] [CrossRef] [Green Version]
- Yan, C.; Ma, J.; Luo, H.; Patel, A. Hybrid binary Coral Reefs Optimization algorithm with Simulated Annealing for Feature Selection in high-dimensional biomedical datasets. Chemom. Intell. Lab. Syst. 2019, 184, 102–111. [Google Scholar] [CrossRef]
- Toksari, M.D. A hybrid algorithm of Ant Colony Optimization (ACO) and Iterated Local Search (ILS) for estimating electricity domestic consumption: Case of Turkey. Int. J. Electr. Power Energy Syst. 2016, 78, 776–782. [Google Scholar] [CrossRef]
- Mafarja, M.M.; Mirjalili, S. Hybrid Whale Optimization Algorithm with simulated annealing for feature selection. Neurocomputing 2017, 260, 302–312. [Google Scholar] [CrossRef]
- Tubishat, M.; Idris, N.; Abushariah, M. Explicit aspects extraction in sentiment analysis using optimal rules combination. Futur. Gener. Comput. Syst. 2021, 114, 448–480. [Google Scholar] [CrossRef]
- Das, S.; Abraham, A.; Chakraborty, U.K.; Konar, A. Differential evolution using a neighborhood-based mutation operator. IEEE Trans. Evol. Comput. 2009, 13, 526–553. [Google Scholar] [CrossRef] [Green Version]
- Tubishat, M.; Ja’afar, S.; Alswaitti, M.; Mirjalili, S.; Idris, N.; Ismail, M.A.; Omar, M.S. Dynamic Salp swarm algorithm for feature selection. Expert Syst. Appl. 2021, 164, 113873. [Google Scholar] [CrossRef]
- Sayed, G.I.; Khoriba, G.; Haggag, M.H. A novel chaotic salp swarm algorithm for global optimization and feature selection. Appl. Intell. 2018, 48, 3462–3481. [Google Scholar] [CrossRef]
- Khan, T.A.; Zain-Ul-Abideen, K.; Ling, S.H. A Modified Particle Swarm Optimization Algorithm Used for Feature Selection of UCI Biomedical Data Sets. In Proceedings of the 60th International Scientific Conference on Information Technology and Management Science of Riga Technical University (ITMS), Riga, Latvia, 3–5 October 2019. [Google Scholar]
- Ghosh, M.; Guha, R.; Alam, I.; Lohariwal, P.; Jalan, D.; Sarkar, R. Binary Genetic Swarm Optimization: A Combination of GA and PSO for Feature Selection. J. Intell. Syst. 2019, 29, 1598–1610. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary ant lion approaches for feature selection. Neurocomputing 2016, 213, 54–65. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Futur. Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Salgotra, R.; Singh, U.; Saha, S.; Gandomi, A.H. Improving Cuckoo Search: Incorporating Changes for CEC 2017 and CEC 2020 Benchmark Problems. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–7. [Google Scholar]


| Dataset | Features | Sample | Dimensionality |
|---|---|---|---|
| Primry_Tumer | 17 | 339 | Average |
| Hepatitis | 20 | 155 | Average |
| Lymphography | 19 | 148 | Average |
| Breast_Cancer | 10 | 699 | Average |
| Echocardiogram | 12 | 132 | Average |
| Fertility | 10 | 100 | Average |
| Leaf | 16 | 340 | Average |
| Lung_Cancer | 57 | 32 | Average |
| Diabetic | 20 | 1151 | Average |
| ILPD | 11 | 583 | Average |
| Cortex_Nuclear | 82 | 1080 | High |
| Epileptic_Seizure | 179 | 11,500 | High |
| Promoter-gene | 58 | 116 | High |
| WDBC | 31 | 569 | High |
| Cervical cancer | 36 | 858 | High |
| Arrhythmia | 279 | 452 | High |
| Dermatology | 35 | 366 | High |
| Heart Disease | 75 | 303 | High |
| HCV | 29 | 1385 | High |
| Parkinson | 29 | 1040 | High |
| HCC | 50 | 165 | High |
| Parameter | Value |
|---|---|
| Population size | 10 |
| Number of iterations | 50 |
| Dimension | Number of Feature |
| Number of runs for each method | 30 |
| α | 0.99 |
| β | 0.01 |
| Algorithm | Parameters | Reference |
|---|---|---|
| PSO | Inertia Weight value 0.9 Inertia Weight Damping Ratio 0.4 Accelerating-constant values are C1 = 2, C2 = 2 | [53] |
| GA | Crossover Ratio 0.9 Mutation Rate 0.2 | [54] |
| WOA | A [2, 0] | [21] |
| GOA | cMax = 1 cMin = 0.00004 | [26] |
| ALO | K = 500 | [55] |
| SMA | z = 0.03 | [56] |
| BOA | Probability-switch 0.8 Power exponent = 0.1 Sensory modality = 0.01 | [57] |
| Dataset | Classification Accuracy | Selected Feature | Fitness | EOA p-Value | |||
|---|---|---|---|---|---|---|---|
| EOA | IEOA | EOA | IEOA | EOA | IEOA | ||
| Primry_Tumer | 0.85556 | 0.88604 | 6.3667 | 6.8667 | 0.14675 | 0.11686 | 0.0398 |
| Hepatitis | 0.86319 | 0.89514 | 3.3 | 3.1 | 0.13717 | 0.10587 | 0.00203 |
| Lymphography | 0.74192 | 0.79155 | 6.8333 | 5.0333 | 0.25874 | 0.20972 | 0.0624 |
| Breast_Cancer | 0.98476 | 0.98714 | 3.3 | 3.1667 | 0.018308 | 0.016247 | 0.296 |
| Echocardiogram | 0.90586 | 0.9185 | 1.9 | 1.1 | 0.028925 | 0.016475 | 0.0474 |
| Fertility | 0.72333 | 0.74667 | 1.7667 | 2.1 | 0.077863 | 0.055133 | 0.0541 |
| Leaf | 0.78373 | 0.81634 | 5.1333 | 5.1333 | 0.21753 | 0.18558 | 0.0112 |
| Lung_Cancer | 0.53611 | 0.55833 | 1.4 | 1.1 | 0.0305 | 0.008446 | 0.0384 |
| Diabetic | 0.99697 | 0.99697 | 7.1 | 5.5333 | 0.004268 | 0.003988 | 0.146 |
| ILPD | 0.55061 | 0.55119 | 25 | 26.7333 | 0.4463 | 0.44605 | 0.912 |
| Cortex_Nuclear | 0.98152 | 1 | 6.8 | 6.4667 | 0.019493 | 0.001135 | 0.0189 |
| Epileptic_Seizure | 0.96895 | 0.97539 | 3.1333 | 3.0333 | 0.03178 | 0.025379 | 0.0966 |
| Promoter-gene | 0.97475 | 0.98096 | 2.9333 | 2.9333 | 0.022737 | 0.017753 | 0.27 |
| WDBC | 0.99635 | 1 | 8.4333 | 6.9667 | 0.006098 | 0.002966 | 0.00898 |
| Cervical cancer | 0.90494 | 0.91975 | 3.4667 | 3.5 | 0.096778 | 0.082137 | 0.357 |
| Arrhythmia | 0.34425 | 0.35914 | 4.4333 | 4.4 | 0.65086 | 0.63621 | 0.0211 |
| Dermatology | 1 | 1 | 1.0333 | 1 | 0.000369 | 0.000357 | 0.334 |
| Heart Disease | 0.76492 | 0.78154 | 54 | 54.9333 | 0.23467 | 0.21861 | 0.0252 |
| HCV | 0.7482 | 0.77193 | 5.1333 | 5.0333 | 0.25199 | 0.24217 | 0.00302 |
| Parkinson | 0.78403 | 0.80118 | 2.9333 | 3.1333 | 0.21674 | 0.19997 | 0.0684 |
| HCC | 0.8826 | 0.90882 | 5 | 3.8667 | 0.11725 | 0.091054 | 0.0771 |
| Dataset | IEOA | GOA | GA | PSO | ALO | WOA | BOA | SMA |
|---|---|---|---|---|---|---|---|---|
| Primry_Tumer | 0.88604 | 0.77302 | 0.8153 | 0.84878 | 0.81438 | 0.80945 | 0.78586 | 0.80059 |
| Hepatitis | 0.89514 | 0.73056 | 0.79181 | 0.81153 | 0.79222 | 0.80694 | 0.73264 | 0.76389 |
| Lymphography | 0.79155 | 0.57721 | 0.64861 | 0.68843 | 0.64447 | 0.66259 | 0.58146 | 0.60909 |
| Breast_Cancer | 0.98714 | 0.97143 | 0.98048 | 0.98238 | 0.98 | 0.98 | 0.97667 | 0.97667 |
| Echocardiogram | 0.9185 | 0.86282 | 0.89799 | 0.89267 | 0.88535 | 0.88516 | 0.86007 | 0.87766 |
| Fertility | 0.74667 | 0.69333 | 0.71 | 0.71333 | 0.70667 | 0.70667 | 0.70333 | 0.68667 |
| Leaf | 0.81634 | 0.68839 | 0.75952 | 0.7742 | 0.75276 | 0.7432 | 0.70144 | 0.7314 |
| Lung_Cancer | 0.55833 | 0.51667 | 0.525 | 0.50556 | 0.54722 | 0.54722 | 0.525 | 0.51667 |
| Diabetic | 0.99697 | 0.80606 | 0.90273 | 0.95 | 0.92485 | 0.93091 | 0.81515 | 0.81939 |
| ILPD | 0.55119 | 0.49977 | 0.51701 | 0.52188 | 0.52762 | 0.52696 | 0.49661 | 0.49919 |
| Cortex_Nuclear | 1 | 0.78848 | 0.87333 | 0.94364 | 0.91576 | 0.92667 | 0.81667 | 0.82606 |
| Epileptic_Seizure | 0.97539 | 0.95547 | 0.96192 | 0.95841 | 0.96426 | 0.9625 | 0.95605 | 0.95547 |
| Promoter-gene | 0.98096 | 0.9162 | 0.93019 | 0.93523 | 0.93406 | 0.93172 | 0.9201 | 0.92204 |
| WDBC | 1 | 0.96189 | 0.98448 | 0.99094 | 0.99089 | 0.98549 | 0.98181 | 0.98358 |
| Cervical cancer | 0.91975 | 0.79012 | 0.84691 | 0.87901 | 0.85926 | 0.85679 | 0.81852 | 0.81235 |
| Arrhythmia | 0.35914 | 0.29806 | 0.32258 | 0.32837 | 0.32376 | 0.32355 | 0.30884 | 0.30309 |
| Dermatology | 1 | 0.96218 | 0.99167 | 0.99647 | 0.9984 | 1 | 0.96538 | 0.97083 |
| Heart Disease | 0.78154 | 0.66622 | 0.70459 | 0.73192 | 0.70461 | 0.70283 | 0.65969 | 0.66047 |
| HCV | 0.77193 | 0.67662 | 0.71719 | 0.72008 | 0.70907 | 0.7053 | 0.68271 | 0.69169 |
| Parkinson | 0.80118 | 0.75471 | 0.76685 | 0.78117 | 0.7674 | 0.76858 | 0.75761 | 0.7479 |
| HCC | 0.90882 | 0.75784 | 0.81409 | 0.83284 | 0.82426 | 0.82488 | 0.75784 | 0.79387 |
| Mean value (F-test) | 0.840313 | 0.745098 | 0.783917 | 0.799373 | 0.788918 | 0.789877 | 0.752545 | 0.759456 |
| Overall ranking | 1 | 8 | 5 | 2 | 4 | 3 | 7 | 6 |
| Dataset | GOA | GA | PSO | ALO | WOA | BOA | SMA |
|---|---|---|---|---|---|---|---|
| Primry_Tumer | 4.64 × 10−8 | 4.92 × 10−5 | 3.92 × 10−3 | 1.01 × 10−5 | 1.80 × 10−5 | 8.41 × 10−9 | 3.51 × 10−5 |
| Hepatitis | 8.84 × 10−10 | 9.49 × 10−7 | 2.58 × 10−5 | 1.98 × 10−6 | 3.35 × 10−5 | 3.80 × 10−10 | 1.30 × 10−6 |
| Lymphography | 5.99 × 10−8 | 2.06 × 10−5 | 1.76 × 10−3 | 9.50 × 10−6 | 1.17 × 10−4 | 9.24 × 10−9 | 2.84 × 10−5 |
| Breast_Cancer | 5.29 × 10−6 | 1.71 × 10−2 | 6.59 × 10−2 | 2.18 × 10−2 | 2.01 × 10−2 | 3.41 × 10−4 | 5.00 × 10−2 |
| Echocardiogram | 2.85 × 10−6 | 1.77 × 10−3 | 3.83 × 10−3 | 1.77 × 10−3 | 1.02 × 10−2 | 2.10 × 10−6 | 3.62 × 10−3 |
| Fertility | 5.51 × 10−2 | 1.42 × 10−1 | 4.34 × 10−1 | 2.19 × 10−1 | 2.21 × 10−1 | 4.89 × 10−2 | 8.41 × 10−2 |
| Leaf | 3.00 × 10−7 | 1.40 × 10−3 | 2.65 × 10−2 | 1.14 × 10−3 | 3.27 × 10−4 | 6.73 × 10−6 | 5.59 × 10−3 |
| Lung_Cancer | 4.30 × 10−2 | 4.30 × 10−2 | 4.14 × 10−2 | 4.51 × 10−1 | 8.58 × 10−1 | 4.30 × 10−2 | 8.77 × 10−2 |
| Diabetic | 3.18 × 10−11 | 5.79 × 10−11 | 3.47 × 10−10 | 1.80 × 10−5 | 2.36 × 10−5 | 3.52 × 10−11 | 6.36 × 10−10 |
| ILPD | 4.07 × 10−11 | 2.67 × 10−9 | 8.88 × 10−10 | 4.44 × 10−7 | 1.36 × 10−7 | 3.02 × 10−11 | 5.59 × 10−9 |
| Cortex_Nuclear | 2.88 × 10−11 | 2.88 × 10−11 | 4.28 × 10−11 | 1.62 × 10−6 | 9.40 × 10−7 | 2.89 × 10−11 | 5.30 × 10−11 |
| Epileptic_Seizure | 4.61 × 10−7 | 7.50 × 10−6 | 3.69 × 10−6 | 1.72 × 10−4 | 8.14 × 10−4 | 9.90 × 10−7 | 2.74 × 10−6 |
| Promoter-gene | 1.91 × 10−8 | 1.10 × 10−6 | 3.45 × 10−5 | 2.03 × 10−5 | 6.04 × 10−5 | 5.65 × 10−9 | 6.10 × 10−6 |
| WDBC | 5.95 × 10−11 | 2.00 × 10−10 | 8.41 × 10−9 | 1.90 × 10−9 | 7.90 × 10−10 | 1.08 × 10−10 | 2.74 × 10−10 |
| Cervical cancer | 1.09 × 10−10 | 2.47 × 10−7 | 1.16 × 10−3 | 4.21 × 10−5 | 1.05 × 10−5 | 1.21 × 10−8 | 7.34 × 10−7 |
| Arrhythmia | 8.95 × 10−11 | 2.77 × 10−7 | 2.68 × 10−5 | 2.02 × 10−7 | 2.28 × 10−7 | 2.19 × 10−7 | 7.96 × 10−7 |
| Dermatology | 1.21 × 10−12 | 1.19 × 10−12 | 4.36 × 10−12 | 3.06 × 10−4 | 2.15 × 10−2 | 1.21 × 10−12 | 5.35 × 10−11 |
| Heart Disease | 9.83 × 10−8 | 7.20 × 10−5 | 5.08 × 10−3 | 3.83 × 10−5 | 2.13 × 10−4 | 9.06 × 10−8 | 9.53 × 10−5 |
| HCV | 3.45 × 10−10 | 4.42 × 10−7 | 1.38 × 10−5 | 2.10 × 10−7 | 8.81 × 10−7 | 2.15 × 10−10 | 2.06 × 10−7 |
| Parkinson | 2.93 × 10−5 | 7.04 × 10−4 | 2.49 × 10−2 | 7.43E × 10−4 | 9.42 × 10−3 | 2.75 × 10−5 | 4.03 × 10−4 |
| HCC | 6.65 × 10−10 | 2.55 × 10−7 | 1.63 × 10−5 | 9.74 × 10−6 | 3.06 × 10−6 | 2.58 × 10−10 | 1.21 × 10−7 |
| Dataset | IEOA | GOA | GA | PSO | ALO | WOA | BOA | SMA |
|---|---|---|---|---|---|---|---|---|
| Primry_Tumer | 6.3667 | 7.9 | 7.9667 | 7.4667 | 7.5 | 6.2667 | 9.9333 | 10.0333 |
| Hepatitis | 3.3 | 7.9333 | 6.7333 | 5.6333 | 4.4 | 4.7333 | 9.7333 | 9.5 |
| Lymphography | 6.8333 | 9.1333 | 8.3333 | 6.8667 | 7.5333 | 7.4 | 10.4333 | 10.3667 |
| Breast_Cancer | 3.3 | 4.3667 | 4 | 3.6 | 3.6 | 3.9333 | 5.4333 | 4.2 |
| Echocardiogram | 1.9 | 4.3667 | 3.4667 | 2.6667 | 2.6 | 2 | 4.2667 | 4.6 |
| Fertility | 1.7667 | 2.3333 | 2.0333 | 1.6667 | 1.9667 | 1.8333 | 2.8667 | 2.3667 |
| Leaf | 5.1333 | 7.5333 | 6.8 | 5.9667 | 7.6333 | 7.3 | 9.7 | 9.8 |
| Lung_Cancer | 1.4 | 13.6 | 10.1 | 6.7333 | 3.1 | 1.7333 | 14.7333 | 14.3667 |
| Diabetic | 7.1 | 24.8333 | 23.8333 | 17.9667 | 10.9 | 10.7333 | 31.3 | 27.1667 |
| ILPD | 25 | 86.5667 | 84 | 86.7333 | 28.7 | 20.1 | 94.4 | 92.1333 |
| Cortex_Nuclear | 6.8 | 26.7333 | 25.4 | 19.1667 | 10.8 | 10.3 | 33.1 | 30.9333 |
| Epileptic_Seizure | 3.1333 | 12.7 | 9.2667 | 6.7 | 9.1 | 5.9667 | 15.6 | 14.5333 |
| Promoter-gene | 2.9333 | 14.1 | 11.4 | 8.0667 | 5.6667 | 4.9333 | 16.1333 | 15.3667 |
| WDBC | 8.4333 | 16.9667 | 15.0667 | 11.4667 | 15.5333 | 14.3333 | 21.2 | 18.8667 |
| Cervical cancer | 3.4667 | 5.7 | 5.2 | 4.4667 | 4.1 | 3.4 | 6.9333 | 6.1333 |
| Arrhythmia | 4.4333 | 13.3 | 9 | 7.5333 | 6.9333 | 7.8 | 15.3 | 14.2 |
| Dermatology | 1.0333 | 12.9667 | 9.1333 | 5.7333 | 2.5333 | 1.3667 | 14.5333 | 15.0333 |
| Heart Disease | 54 | 133.5333 | 128.5 | 116.0333 | 100.1667 | 76.7667 | 167.2 | 153.5 |
| HCV | 5.1333 | 9.5333 | 7.6333 | 6.9667 | 8.3 | 7 | 11.5 | 9.9667 |
| Parkinson | 2.9333 | 4.6667 | 3.9 | 3.5333 | 3.5333 | 3.1 | 5.0667 | 5.0333 |
| HCC | 5 | 22.7667 | 17.3 | 13.5333 | 8.1667 | 6.0333 | 27.0667 | 24.7667 |
| Mean value (F-test) | 7.590467 | 21.0254 | 19.00317 | 16.59524 | 12.0365 | 9.858724 | 25.06825 | 23.46984 |
| Overall ranking | 1 | 6 | 5 | 4 | 3 | 2 | 8 | 7 |
| Dataset | IEOA | GOA | GA | PSO | ALO | WOA | BOA | SMA |
|---|---|---|---|---|---|---|---|---|
| Primry_Tumer | 0.11686 | 0.22935 | 0.18754 | 0.1541 | 0.18818 | 0.19233 | 0.21784 | 0.20331 |
| Hepatitis | 0.10587 | 0.27093 | 0.20966 | 0.18955 | 0.20802 | 0.19362 | 0.26981 | 0.23875 |
| Lymphography | 0.20972 | 0.42363 | 0.35251 | 0.31227 | 0.35616 | 0.33815 | 0.42015 | 0.39276 |
| Breast_Cancer | 0.016247 | 0.033138 | 0.023773 | 0.021443 | 0.0238 | 0.02417 | 0.029137 | 0.027767 |
| Echocardiogram | 0.016475 | 0.073777 | 0.038146 | 0.042677 | 0.049869 | 0.049505 | 0.076406 | 0.059303 |
| Fertility | 0.055133 | 0.10819 | 0.091359 | 0.087652 | 0.094585 | 0.094437 | 0.098885 | 0.11483 |
| Leaf | 0.18558 | 0.31352 | 0.24261 | 0.22752 | 0.24986 | 0.2591 | 0.30204 | 0.27245 |
| Lung_Cancer | 0.008446 | 0.051929 | 0.043054 | 0.061702 | 0.019804 | 0.01956 | 0.043881 | 0.052065 |
| Diabetic | 0.003988 | 0.19643 | 0.10056 | 0.052708 | 0.076346 | 0.070317 | 0.18859 | 0.18365 |
| ILPD | 0.44605 | 0.50009 | 0.48287 | 0.47821 | 0.46927 | 0.46944 | 0.50366 | 0.50098 |
| Cortex_Nuclear | 0.001135 | 0.21409 | 0.12986 | 0.059163 | 0.085295 | 0.074407 | 0.18731 | 0.17763 |
| Epileptic_Seizure | 0.025379 | 0.048316 | 0.040793 | 0.043411 | 0.038411 | 0.039114 | 0.048714 | 0.043717 |
| Promoter-gene | 0.017753 | 0.053989 | 0.039372 | 0.033431 | 0.033897 | 0.036003 | 0.05071 | 0.048573 |
| WDBC | 0.002966 | 0.042722 | 0.019792 | 0.012341 | 0.013587 | 0.018585 | 0.024247 | 0.021801 |
| Cervical cancer | 0.082137 | 0.21216 | 0.15556 | 0.12321 | 0.14249 | 0.14439 | 0.185 | 0.1905 |
| Arrhythmia | 0.63621 | 0.69967 | 0.67386 | 0.66761 | 0.67196 | 0.67247 | 0.68971 | 0.69501 |
| Dermatology | 0.000357 | 0.042073 | 0.011512 | 0.005538 | 0.002491 | 0.000488 | 0.03946 | 0.034244 |
| Heart Disease | 0.21861 | 0.33523 | 0.29706 | 0.26956 | 0.29603 | 0.29695 | 0.3429 | 0.34164 |
| HCV | 0.24217 | 0.32516 | 0.284 | 0.28079 | 0.29239 | 0.29543 | 0.32017 | 0.31047 |
| Parkinson | 0.19997 | 0.2475 | 0.23472 | 0.22017 | 0.23381 | 0.23221 | 0.24504 | 0.25462 |
| HCC | 0.091054 | 0.24438 | 0.18758 | 0.16825 | 0.17564 | 0.1746 | 0.24526 | 0.20912 |
| Mean value (F-test) | 0.12772 | 0.222204 | 0.183152 | 0.167205 | 0.177233 | 0.175966 | 0.215663 | 0.208247 |
| Overall ranking | 1 | 8 | 5 | 2 | 4 | 3 | 7 | 6 |
| Algorithms | Accuracy | Features | Fitness |
|---|---|---|---|
| EOA | 1.69% | 0.203% | 1.59% |
| GOA | 9.52% | 13.43% | 9.45% |
| GA | 5.64% | 11.41% | 5.54% |
| PSO | 4.09% | 9.003% | 3.95% |
| ALO | 5.14% | 4.44% | 4.95% |
| WOA | 5.04% | 2.26% | 4.82% |
| BOA | 8.78% | 17.47% | 8.79% |
| SMA | 8.09% | 15.87% | 8.05% |
| Average | 6.00% | 9.26% | 5.89% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elgamal, Z.M.; Yasin, N.M.; Sabri, A.Q.M.; Sihwail, R.; Tubishat, M.; Jarrah, H. Improved Equilibrium Optimization Algorithm Using Elite Opposition-Based Learning and New Local Search Strategy for Feature Selection in Medical Datasets. Computation 2021, 9, 68. https://0-doi-org.brum.beds.ac.uk/10.3390/computation9060068
Elgamal ZM, Yasin NM, Sabri AQM, Sihwail R, Tubishat M, Jarrah H. Improved Equilibrium Optimization Algorithm Using Elite Opposition-Based Learning and New Local Search Strategy for Feature Selection in Medical Datasets. Computation. 2021; 9(6):68. https://0-doi-org.brum.beds.ac.uk/10.3390/computation9060068
Chicago/Turabian StyleElgamal, Zenab Mohamed, Norizan Mohd Yasin, Aznul Qalid Md Sabri, Rami Sihwail, Mohammad Tubishat, and Hazim Jarrah. 2021. "Improved Equilibrium Optimization Algorithm Using Elite Opposition-Based Learning and New Local Search Strategy for Feature Selection in Medical Datasets" Computation 9, no. 6: 68. https://0-doi-org.brum.beds.ac.uk/10.3390/computation9060068






