Effects of A Magnetic Field on the Transport and Noise Properties of a Graphene Ribbon with Antidots
Abstract
:1. Introduction
2. Method
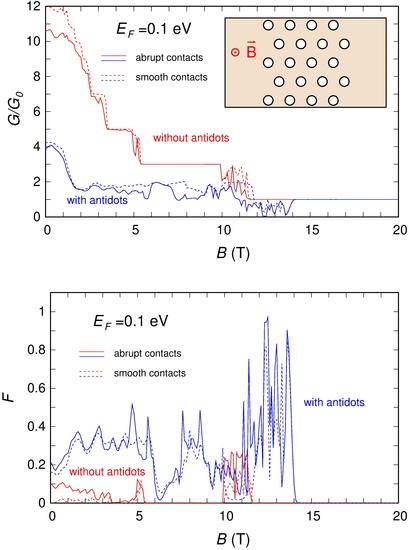
3. Numerical Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–169. [Google Scholar] [CrossRef] [Green Version]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Katsnelson, M.I. Graphene: Carbon in Two Dimensions; Cambridge University Press: Cambridge, UK, 2012; ISBN 052-119-5403. [Google Scholar]
- Foa Torres, L.E.F.; Roche, S.; Charlier, J.-C. Introduction to Graphene-Based Nanomaterials: From Electronic Structure to Quantum Transport; Cambridge University Press: Cambridge, UK, 2020; ISBN 110-703-0838. [Google Scholar]
- Enoki, T.; Ando, T. Physics and Chemistry of Graphene: Graphene to Nanographene; Jenny Stanford Publishing: Singapore, 2020; ISBN 981-480-0384. [Google Scholar]
- Bhimanapati, G.R.; Lin, Z.; Meunie, V.; Jung, Y.; Cha, J.; Das, S.; Xiao, D.; Son, Y.; Strano, M.S.; Cooper, V.R.; et al. Recent Advances in Two-Dimensional Materials beyond Graphene. ACS Nano 2015, 9, 11509–11539. [Google Scholar] [CrossRef]
- Miró, P.; Audiffreda, M.; Heine, T. An atlas of two-dimensional materials. Chem. Soc. Rev. 2014, 43, 6537–6554. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Marconcini, P.; Hossian, M.S.; Qiu, W.; Evans, R.J.; Macucci, M.; Skafidas, S. A tight binding and k·p study of monolayer stanene. Sci. Rep. 2017, 7, 12069. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Novoselov, K.S.; Fal’ko, V.I.; Colombo, L.; Gellert, P.R.; Schwab, M.G.; Kim, K. A roadmap for graphene. Nature 2012, 490, 192–200. [Google Scholar] [CrossRef]
- Avouris, P.; Dimitrakopoulos, C. Graphene: Synthesis and applications. Mater. Today 2012, 15, 86–97. [Google Scholar] [CrossRef]
- DiVincenzo, D.P.; Mele, E.J. Self-consistent effective-mass theory for intralayer screening in graphite intercalation compounds. Phys. Rev. B 1984, 29, 1685–1694. [Google Scholar] [CrossRef]
- Semenoff, G.W. Condensed-Matter Simulation of a Three-Dimensional Anomaly. Phys. Rev. Lett. 1984, 53, 2449–2452. [Google Scholar] [CrossRef]
- Ando, T. Theory of Electronic States and Transport in Carbon Nanotubes. J. Phys. Soc. Jpn. 2005, 74, 777–817. [Google Scholar] [CrossRef] [Green Version]
- Marconcini, P.; Macucci, M. The k·p method and its application to graphene, carbon nanotubes and graphene nanoribbons: The Dirac equation. Riv. Nuovo Cimento 2011, 34, 489–584. [Google Scholar] [CrossRef]
- Katsnelson, M.I.; Novoselov, K.S. Graphene: New bridge between condensed matter physics and quantum electrodynamics. Solid State Commun. 2007, 143, 3–13. [Google Scholar] [CrossRef] [Green Version]
- Katsnelson, M.I.; Novoselov, K.S.; Geim, A.K. Chiral tunnelling and the Klein paradox in graphene. Nat. Phys. 2006, 2, 620–625. [Google Scholar] [CrossRef] [Green Version]
- Beenakker, C.W.J. Colloquium: Andreev reflection and Klein tunneling in graphene. Rev. Mod. Phys. 2008, 80, 1337–1354. [Google Scholar] [CrossRef] [Green Version]
- Shytov, A.; Rudner, M.; Gu, N.; Katsnelson, M.; Levitov, L. Atomic collapse, Lorentz boosts, Klein scattering, and other quantum-relativistic phenomena in graphene. Solid State Commun. 2009, 149, 1087–1093. [Google Scholar] [CrossRef] [Green Version]
- Tworzydło, J.; Trauzettel, B.; Titov, M.; Rycerz, A.; Beenakker, C.W.J. Sub-Poissonian Shot Noise in Graphene. Phys. Rev. Lett. 2006, 96, 246802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Balandin, A.A. Low-frequency 1/f noise in graphene devices. Nat. Nanotech. 2013, 8, 549–555. [Google Scholar] [CrossRef]
- Pellegrini, B.; Marconcini, P.; Macucci, M.; Fiori, G.; Basso, G. Carrier density dependence of 1/f noise in graphene explained as a result of the interplay between band-structure and inhomogeneities. J. Stat. Mech. Theory Exp. 2016, 2016, 054017. [Google Scholar] [CrossRef]
- Macucci, M.; Marconcini, P. Theoretical comparison between the flicker noise behavior of graphene and of ordinary semiconductors. J. Sensors 2020, 2020, 2850268. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Jiang, Z.; Zhang, Y.; Morozov, S.V.; Stormer, H.L.; Zeitler, U.; Maan, J.C.; Boebinger, G.S.; Kim, P.; Geim, A.K. Room-Temperature Quantum Hall Effect in Graphene. Science 2007, 315, 1379. [Google Scholar] [CrossRef] [Green Version]
- Gusynin, V.P.; Sharapov, S.G. Unconventional Integer Quantum Hall Effect in Graphene. Phys. Rev. Lett. 2005, 95, 146801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Connolly, M.R.; Puddy, R.K.; Logoteta, D.; Marconcini, P.; Roy, M.; Griffiths, J.P.; Jones, G.A.C.; Maksym, P.A.; Macucci, M.; Smith, C.G. Unraveling Quantum Hall Breakdown in Bilayer Graphene with Scanning Gate Microscopy. Nano Lett. 2012, 12, 5448–5454. [Google Scholar] [CrossRef] [Green Version]
- Raza, H. Graphene Nanoelectronics: Metrology, Synthesis, Properties and Applications; Springer: Berlin, Germany, 2012; ISBN 978-3642-204-678. [Google Scholar]
- Murali, R. Graphene Nanoelectronics: From Materials to Circuits; Springer: New York, NY, USA, 2012; ISBN 146-140-5475. [Google Scholar]
- Wu, Y.; Farmer, D.B.; Xia, F.; Avouris, P. Graphene Electronics: Materials, Devices, and Circuits. Proc. IEEE 2013, 101, 1620–1637. [Google Scholar] [CrossRef]
- Yung, K.C.; Wu, W.M.; Pierpoint, M.P.; Kusmartsev, F.V. Introduction to graphene electronics—A new era of digital transistors and devices. Contemp. Phys. 2013, 54, 233–251. [Google Scholar] [CrossRef] [Green Version]
- Schwierz, F. Graphene Transistors. Nat. Nanotechnol. 2010, 5, 487–496. [Google Scholar] [CrossRef] [PubMed]
- Schwierz, F. Graphene Transistors: Status, Prospects, and Problems. Proc. IEEE 2013, 101, 1567–1584. [Google Scholar] [CrossRef]
- Marconcini, P.; Macucci, M. Approximate calculation of the potential profile in a graphene-based device. IET Circuits Devices Syst. 2015, 9, 30–38. [Google Scholar] [CrossRef] [Green Version]
- Brey, L.; Fertig, H.A. Electronic states of graphene nanoribbons studied with the Dirac equation. Phys. Rev. B 2006, 73, 235411. [Google Scholar] [CrossRef] [Green Version]
- Son, Y.W.; Cohen, M.L.; Louie, S.G. Energy Gaps in Graphene Nanoribbons. Phys. Rev. Lett. 2006, 97, 216803. [Google Scholar] [CrossRef] [Green Version]
- Jiao, L.; Wang, X.; Diankov, G.; Wang, H.; Dai, H. Facile synthesis of high-quality graphene nanoribbons. Nat. Nanotechnol. 2010, 5, 321–325. [Google Scholar] [CrossRef] [Green Version]
- Kolmer, M.; Steiner, A.-K.; Izydorcsyk, I.; Ko, W.; Engelund, M.; Szymonski, M.; Li, A.-P.; Amsharov, K. Rational synthesis of atomically precise nanoribbons directly on metal oxide surfaces. Science 2020, 369, 571–575. [Google Scholar] [CrossRef] [PubMed]
- Marconcini, P.; Cresti, A.; Roche, S. Effect of the Channel Length on the Transport Characteristics of Transistors Based on Boron-Doped Graphene Ribbons. Materials 2018, 11, 667. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, L.Z.; Tian, S.B.; Long, Y.Z.; Li, W.X.; Yang, H.F.; Li, J.J.; Gu, C.Z. Tunable periodic graphene antidot lattices fabricated by e-beam lithography and oxygen ion etching. Vacuum 2014, 105, 21–25. [Google Scholar] [CrossRef]
- Kim, M.; Safron, N.S.; Han, E.; Arnold, M.S.; Gopalan, P. Fabrication and characterization of large-area, semiconducting nanoperforated graphene materials. Nano Lett. 2010, 10, 1125–1131. [Google Scholar] [CrossRef]
- Bai, J.; Zhong, X.; Jiang, S.; Huang, Y.; Duan, X. Graphene nanomesh. Nat. Nanotechnol. 2010, 5, 190–194. [Google Scholar] [CrossRef]
- Wang, M.; Fu, L.; Gan, L.; Zhang, C.; Rümmeli, M.; Bachmatiuk, A.; Huang, K.; Fang, Y.; Liu, Z. CVD growth of large area smooth-edged graphene nanomesh by nanosphere lithography. Sci. Rep. 2013, 3, 1238. [Google Scholar] [CrossRef] [Green Version]
- Sinitskii, A.; Tour, J.M. Patterning graphene through the self-assembled templates: Toward periodic two-dimensional graphene nanostructures with semiconductor properties. J. Am. Chem. Soc. 2010, 132, 14730–14732. [Google Scholar] [CrossRef]
- Liang, X.; Jung, Y.-S.; Wu, S.; Ismach, A.; Olynick, D.L.; Cabrini, S.; Bokor, J. Formation of bandgap and subbands in graphene nanomeshes with sub-10 nm ribbon width fabricated via nanoimprint lithography. Nano Lett. 2010, 10, 2454–2460. [Google Scholar] [CrossRef]
- Yang, J.; Ma, M.; Li, L.; Zhang, Y.; Huang, W.; Dong, X. Graphene nanomesh: New versatile materials. Nanoscale 2014, 6, 13301–13313. [Google Scholar] [CrossRef]
- Fürst, J.A.; Pedersen, J.G.; Flindt, C.; Mortensen, N.A.; Brandbyge, M.; Pedersen, T.G.; Jauho, A.-P. Electronic properties of graphene antidot lattices. New J. Phys. 2009, 11, 095020. [Google Scholar] [CrossRef]
- Marconcini, P.; Macucci, M. Envelope-function based transport simulation of a graphene ribbon with an antidot lattice. IEEE Trans. Nanotechnol. 2017, 16, 534–544. [Google Scholar] [CrossRef]
- Zoghi, M.; Goharrizi, A.Y.; Saremi, M. Band Gap Tuning of Armchair Graphene Nanoribbons by Using Antidotes. J. Electron. Mater. 2017, 46, 340–346. [Google Scholar] [CrossRef]
- Shen, T.; Wu, Y.Q.; Capano, M.A.; Rokhinson, L.P.; Engel, L.W.; Ye, P.D. Magnetoconductance oscillations in graphene antidot arrays. Appl. Phys. Lett. 2008, 93, 122102. [Google Scholar] [CrossRef] [Green Version]
- Sandner, A.; Preis, T.; Schell, C.; Giudici, P.; Watanabe, K.; Taniguchi, T.; Weiss, D.; Eroms, J. Ballistic Transport in Graphene Antidot Lattices. Nano Lett. 2015, 15, 8402–8406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yagi, R.; Sakakibara, R.; Ebisuoka, R.; Onishi, J.; Watanabe, K.; Taniguchi, T.; Iye, Y. Ballistic transport in graphene antidot lattices. Phys. Rev. B 2015, 92, 195406. [Google Scholar] [CrossRef]
- Pedersen, J.G.; Pedersen, T.G. Hofstadter butterflies and magnetically induced band-gap quenching in graphene antidot lattices. Phys. Rev. B 2013, 87, 235404. [Google Scholar] [CrossRef] [Green Version]
- Power, S.R.; Thomsen, M.R.; Jauho, A.-P.; Pedersen, T.G. Electron trajectories and magnetotransport in nanopatterned graphene under commensurability conditions. Phys. Rev. B 2017, 96, 075425. [Google Scholar] [CrossRef] [Green Version]
- Thomsen, M.R.; Power, S.R.; Jauho, A.-P.; Pedersen, T.G. Magnetic edge states and magnetotransport in graphene antidot barriers. Phys. Rev. B 2016, 94, 045438. [Google Scholar] [CrossRef] [Green Version]
- Pedersen, J.G.; Pedersen, T.G. Dirac model of an isolated graphene antidot in a magnetic field. Phys. Rev. B 2012, 85, 035413. [Google Scholar] [CrossRef]
- Rakyta, P.; Tóvári, E.; Csontos, M.; Csonka, S.Z.; Csordás, A.; Cserti, J. Emergence of bound states in ballistic magnetotransport of graphene antidots. Phys. Rev. B 2014, 90, 125428. [Google Scholar] [CrossRef] [Green Version]
- Mills, S.M.; Gura, A.; Watanabe, K.; Taniguchi, T.; Dawber, M.; Averin, D.V.; Du, X. Dirac fermion quantum Hall antidot in graphene. Phys. Rev. B 2019, 100, 245130. [Google Scholar] [CrossRef] [Green Version]
- Logoteta, D.; Marconcini, P.; Bonati, C.; Fagotti, M.; Macucci, M. High-performance solution of the transport problem in a graphene armchair structure with a generic potential. Phys. Rev. E 2014, 89, 063309. [Google Scholar] [CrossRef] [Green Version]
- Marconcini, P.; Logoteta, D.; Macucci, M. Sinc-based method for an efficient solution in the direct space of quantum wave equations with periodic boundary conditions. J. Appl. Phys. 2013, 114, 173707. [Google Scholar] [CrossRef]
- Marconcini, P.; Macucci, M. Symmetry-dependent transport behavior of graphene double dots. J. Appl. Phys. 2013, 114, 163708. [Google Scholar] [CrossRef] [Green Version]
- Herbschleb, E.D.; Puddy, R.K.; Marconcini, P.; Griffiths, J.P.; Jones, G.A.C.; Macucci, M.; Smith, C.G.; Connolly, M.R. Direct imaging of coherent quantum transport in graphene p-n-p junctions. Phys. Rev. B 2015, 92, 125414. [Google Scholar] [CrossRef]
- Marconcini, P.; Macucci, M. Geometry-dependent conductance and noise behavior of a graphene ribbon with a series of randomly spaced potential barriers. J. Appl. Phys. 2019, 125, 244302. [Google Scholar] [CrossRef]
- Bala Kumar, S.; Jalil, M.B.A.; Tan, S.G.; Liang, G. Magnetoresistive effect in graphene nanoribbon due to magnetic field induced band gap modulation. J. Appl. Phys. 2010, 108, 033709. [Google Scholar] [CrossRef] [Green Version]
- Büttiker, M. Absence of backscattering in the quantum Hall effect in multiprobe conductors. Phys. Rev. B 1988, 38, 9375–9389. [Google Scholar] [CrossRef]
- Macucci, M.; Marconcini, P. Shot noise suppression due to a magnetic field in disordered conductors. J. Comput. Electron. 2015, 14, 107–113. [Google Scholar] [CrossRef]
- Berry, M.V.; Mondragon, R.J. Neutrino billiards: Time-reversal symmetry-breaking without magnetic fields. Proc. R. Soc. Lond. A 1987, 412, 53–74. [Google Scholar] [CrossRef]
- Macucci, M.; Marconcini, P.; Roche, S. Optimization of the Sensitivity of a Double-Dot Magnetic Detector. Electronics 2020, 9, 1134. [Google Scholar] [CrossRef]
- Fagotti, M.; Bonati, C.; Logoteta, D.; Marconcini, P.; Macucci, M. Armchair graphene nanoribbons: PT-symmetry breaking and exceptional points without dissipation. Phys. Rev. B 2011, 83, 241406. [Google Scholar] [CrossRef] [Green Version]
- Ando, T.; Uryu, S.; Ishizaka, S.; Nakanishi, T. Chaos and Quantum Transport in Antidot Lattices. Jpn. J. Appl. Phys. 1999, 38, 308–314. [Google Scholar] [CrossRef] [Green Version]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marconcini, P.; Macucci, M. Effects of A Magnetic Field on the Transport and Noise Properties of a Graphene Ribbon with Antidots. Nanomaterials 2020, 10, 2098. https://0-doi-org.brum.beds.ac.uk/10.3390/nano10112098
Marconcini P, Macucci M. Effects of A Magnetic Field on the Transport and Noise Properties of a Graphene Ribbon with Antidots. Nanomaterials. 2020; 10(11):2098. https://0-doi-org.brum.beds.ac.uk/10.3390/nano10112098
Chicago/Turabian StyleMarconcini, Paolo, and Massimo Macucci. 2020. "Effects of A Magnetic Field on the Transport and Noise Properties of a Graphene Ribbon with Antidots" Nanomaterials 10, no. 11: 2098. https://0-doi-org.brum.beds.ac.uk/10.3390/nano10112098