Understanding FBA Solutions under Multiple Nutrient Limitations
Abstract
:1. Introduction
2. Results
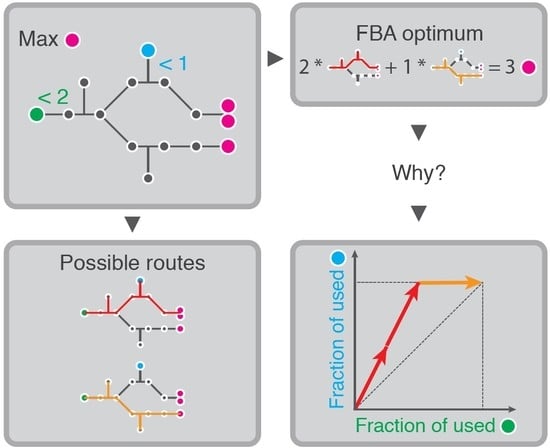
2.1. Small Models Show That FBA Solutions Are Not Just Selected for Maximal Yield
2.1.1. FBA with One Constraint Selects the Maximal-Yield EFM
2.1.2. Under Two Constraints, EMs Are Selected on Two Different Yields
2.2. FBA Solutions Can Be Rationalized Using Cost Vectors
2.3. Understanding FBA Solutions for Genome-Scale Models
2.3.1. A Core E. coli-Model as an Introduction
2.3.2. Optimal Solutions under Glucose- and Oxygen-Limitation of a Genome-Scale E. coli-Model Are Determined by Few Minimal Strategies
2.3.3. Lactococcus lactis in Rich Medium: Elementary Modes-Based Analysis Can Rationalize Solutions to Many-Constraint Optimizations
2.3.4. Lactobacillus plantarum
3. Discussion
4. Materials and Methods
4.1. The Use of ECMs Instead of EFMs
4.2. Different Levels of Detail Can Be Used to Study FBA Solutions
4.2.1. ECMs between All External Metabolites for the Full Network
4.2.2. ECMs between a Subset of External Metabolites for the Full Network
4.2.3. ECMs between a Subset of External Metabolites for the Active Network
4.3. Outline of the Code
- Load model and set constraints. Depending on the research question, one can leave the default constraints that are set in the model, or one can change them. This and the subsequent optimization steps are done with the cbmpy-package [39].
- Perform FBA. We initialize the model by performing an FBA. We use the minimization of the sum of absolute reaction rates as a secondary objective. This ensures that the number of Elementary Modes will indeed be bounded by the number of constraints.
- Perform reduced cost analysis. The reduced cost of a reaction can be defined as the derivative of the objective function with respect to the reaction value. The reduced costs thus capture what happens to the objective when the reaction value is increased. When a reduced cost is nonzero in the optimum, it must have hit a constraint, and these reactions are thus of interest to us. We then select only the inhomogeneous constraints, i.e., constraints with a bound that is nonzero. Now we are left with four categories of reactions: reactions can have a positive or a negative optimal rate, and the reduced cost can also be positive or negative. A positive rate with positive reduced cost indicates that the reaction is bounded from above, so this indicates a limited production. A positive rate with negative reduced cost indicates a forced production; negative rate with positive reduced cost indicates forced uptake, and negative rate with negative reduced cost means that this uptake is limited. We mark the reactions with forced production and uptake as secondary objectives, and the limited production and uptake reactions as constraints.
- Coupling an external metabolite to each constraint. Most constraints are on exchange reactions and therefore we can immediately use the exchange of the metabolite as a marker of the reaction flux when we compute ECMs. When an internal reaction rate is constrained, we use the tag-method of ecmtool to add an external metabolite that is produced in this reaction.
- Optional: Simplifying the network for ECM-enumeration. As explained above, we can use two simplifications: (1) we can choose to consider only the active network. This means that all reactions that are zero in the FBA-solution are deleted from the model. (2) We can choose to compute the ECMs only between the external metabolites related to a constraint. If we choose this option, we here find all ECMtool-indices of the metabolites that are to be hidden.
- ECM enumeration. For this step, we used ecmtool as a Python library (as opposed to running it via the command line), of which the code can be found at https://github.com/SystemsBioinformatics/ecmtool accessed on 14 April 2021. Our computations were done with a version available at 14 April 2021. It can also be installed via the Python package manager pip.
- Compute costs for all ECMs with respect to each constraint normalized to each objective. If we have ECMs, objects, and constraints, we thus eventually get tables of dimensions by . The rows of these tables give for each ECM the fraction of the various constraints that are used for the production of one unit objective.
- Calculation of the activities of the ECMs in the FBA solution. We first compute the overall conversion () that is induced by the FBA solution for the non-hidden metabolites. Then, we perform an LP that finds this conversion as a sum of ECMs: . We minimize the sum of the ’s in this LP under the constraint that for all i. In principle, we could also compute the -spectrum [47] for the various ECMs to see if they could contribute to the FBA solution, but we have not done that.
- For each ECM, find a corresponding EFM. Given an ECM , we can reconstruct an EFM by solving another LP: choose reaction rates such that , with , and where is minimized. The minimization of ensures that we get a minimal solution, which will be an EFM.
- Optional: reconstruct the full conversion if some metabolites were hidden. Given the EFM, , we can now reconstruct the full conversion by multiplying with the full stoichiometry matrix: . As such, we get for each ECM a possible conversion between all external metabolites (i.e., including the first hidden metabolites).
Code Availability
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FBA | Flux Balance Analysis |
| EFM | Elementary Flux Mode |
| ECM | Elementary Conversion Mode |
| EM | Elementary Mode |
Appendix A. An Upper Bound to the Number of Elementary Modes in the Optimum
Appendix B. Supplemental Figures



References
- Orth, J.D.; Thiele, I.; Palsson, B.Ø.O. What is flux balance analysis? Nat. Biotechnol. 2010, 28, 245–248. [Google Scholar] [CrossRef]
- Raman, K.; Chandra, N. Flux Balance Analysis of Biological Systems: Applications and Challenges. Brief. Bioinform. 2009, 10, 435–449. [Google Scholar] [CrossRef]
- Schuster, S.; Hilgetag, C. On Elementary Flux Modes in biochemical reaction systems at steady state. J. Biol. Syst. 1994, 2, 165–182. [Google Scholar] [CrossRef]
- Teusink, B.; Wiersma, A.; Jacobs, L.; Notebaart, R.A.; Smid, E.J. Understanding the adaptive growth strategy of Lactobacillus plantarum by in silico optimisation. PLoS Comput. Biol. 2009, 5, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Maarleveld, T.R.; Wortel, M.T.; Olivier, B.G.; Teusink, B.; Bruggeman, F.J. Interplay between constraints, objectives, and optimality for genome-scale stoichiometric models. PLoS Comput. Biol. 2015, 11, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Ibarra, R.U.; Edwards, J.S.; Palsson, B.O. Escherichia coli K-12 undergoes adaptive evolution to achieve in silico predicted optimal growth. Nature 2002, 420, 186–189. [Google Scholar] [CrossRef] [PubMed]
- Fong, S.S.; Joyce, A.R.; Palsson, B. Parallel adaptive evolution cultures of Escherichia coli lead to convergent growth phenotypes with different gene expression states. Genome Res. 2005, 15, 1365–1372. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schuster, S.; Pfeiffer, T.; Fell, D.A. Is maximization of molar yield in metabolic networks favoured by evolution? J. Theor. Biol. 2008, 252, 497–504. [Google Scholar] [CrossRef] [PubMed]
- Henry, C.S.; Broadbelt, L.J.; Hatzimanikatis, V. Thermodynamics-based metabolic flux analysis. Biophys. J. 2007, 92, 1792–1805. [Google Scholar] [CrossRef] [Green Version]
- Molenaar, D.; Berlo, R.V.; Ridder, D.D.; Teusink, B. Shifts in growth strategies reflect tradeoffs in cellular economics. Mol. Syst. Biol. 2009, 5, 323. [Google Scholar] [CrossRef]
- Postma, E.; Verduyn, C.; Scheffers, W.A.; Van Dijken, J.P.; Scheffers, A.W.; Van Dijken, J.P. Enzymic analysis of the Crabtree effect in glucose-limited chemostat cultures of Saccharomyces cerevisiae. Appl. Environ. Microbiol. 1989, 55, 468–477. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wolfe, A.J. The acetate switch. Microbiol. Mol. Biol. Rev. 2005, 69, 12–50. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Warburg, O. On the origin of cancer cells. Science 1956, 123, 309–314. [Google Scholar] [CrossRef] [PubMed]
- Thomas, T.D.; Ellwood, D.C.; Longyear, V.M. Change from homo- to heterolactic fermentation by Streptococcus lactis resulting from glucose limitation in anaerobic chemostat cultures. J. Bacteriol. 1979, 138, 109–117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Folsom, J.P.; Carlson, R.P. Physiological, biomass elemental composition and proteomic analyses of Escherichia coli ammonium limited chemostat growth, and comparison with iron- and glucose-limited chemostat growth. Microbiology 2015, 161, 1659–1670. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reed, J.L.; Vo, T.D.; Schilling, C.H.; Palsson, B.O. An expanded genome-scale model of Escherichia coli K-12 (iJR904 GSM/GPR). Genome Biol. 2003, 4. [Google Scholar] [CrossRef] [Green Version]
- Feist, A.M.; Henry, C.S.; Reed, J.L.; Krummenacker, M.; Joyce, A.R.; Karp, P.D.; Broadbelt, L.J.; Hatzimanikatis, V.; Palsson, B. A genome-scale metabolic reconstruction for Escherichia coli K-12 MG1655 that accounts for 1260 ORFs and thermodynamic information. Mol. Syst. Biol. 2007, 3. [Google Scholar] [CrossRef]
- Chen, Y.; van Pelt-KleinJan, E.; van Olst, B.; Douwenga, S.; Boeren, S.; Bachmann, H.; Molenaar, D.; Nielsen, J.; Teusink, B. Proteome constraints reveal targets for improving microbial fitness in nutrient-rich environments. Mol. Syst. Biol. 2021, 17, e10093. [Google Scholar] [CrossRef]
- Olivier, B.; Mendoza, S.N. SystemsBioinformaticsCbmpy-Metadraft: MetaDraft Is Now Available (Version v0.9.5). 2020. Available online: https://zenodo.org/record/2398336#.YH-T9egzZPY (accessed on 14 April 2021).
- Jamshidi, N.; Palsson, B. Investigating the metabolic capabilities of Mycobacterium tuberculosis H37Rv using the in silico strain iNJ661 and proposing alternative drug targets. BMC Syst. Biol. 2007, 1. [Google Scholar] [CrossRef] [Green Version]
- Mo, M.L.; Palsson, B.; Herrgård, M.J. Connecting extracellular metabolomic measurements to intracellular flux states in yeast. BMC Syst. Biol. 2009, 3. [Google Scholar] [CrossRef] [Green Version]
- Clement, T.J.; Baalhuis, E.B.; Teusink, B.; Bruggeman, F.J.; Planqué, R.; de Groot, D.H. Unlocking elementary conversion modes: Ecmtool unveils all capabilities of metabolic networks. Patterns 2021, 2. [Google Scholar] [CrossRef] [PubMed]
- Urbanczik, R.; Wagner, C. Functional stoichiometric analysis of metabolic networks. Bioinformatics 2005, 21, 4176–4180. [Google Scholar] [CrossRef] [PubMed]
- De Groot, D.H.; van Boxtel, C.; Planqué, R.; Bruggeman, F.J.; Teusink, B. The number of active metabolic pathways is bounded by the number of cellular constraints at maximal metabolic rates. PLoS Comput. Biol. 2019, 15, 1–26. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Edwards, J.S.; Palsson, B.O. Robustness analysis of the Escherichia coli metabolic network. Biotechnol. Prog. 2000, 16, 927–939. [Google Scholar] [CrossRef] [PubMed]
- Gagneur, J.; Klamt, S. Computation of elementary modes: A unifying framework and the new binary approach. BMC Bioinform. 2004, 5, 175. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mahadevan, R.; Schilling, C.H. The effects of alternate optimal solutions in constraint-based genome-scale metabolic models. Metab. Eng. 2003, 5, 264–276. [Google Scholar] [CrossRef]
- Kelk, S.M.; Olivier, B.G.; Stougie, L.; Bruggeman, F.J. Optimal flux spaces of genome-scale stoichiometric models are determined by a few subnetworks. Sci. Rep. 2012, 2, 580. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Klamt, S.; Stelling, J. Combinatorial complexity of pathway analysis in metabolic networks. Mol. Biol. Rep. 2002, 29, 233–236. [Google Scholar] [CrossRef] [PubMed]
- Klamt, S.; Müller, S.; Regensburger, G.; Zanghellini, J. A mathematical framework for yield (vs. rate) optimization in constraint-based modeling and applications in metabolic engineering. Metab. Eng. 2018, 47, 153–169. [Google Scholar] [CrossRef]
- Orth, J.D.; Palsson, B.Ø.; Fleming, R.M.T. Reconstruction and use of microbial metabolic networks: The core Escherichia coli metabolic model as an educational guide. EcoSal Plus 2010, 4. [Google Scholar] [CrossRef]
- Schilling, C.H.; Edwards, J.S.; Letscher, D.; Palsson, B.O. Combining pathway analysis with flux balance analysis for the comprehensive study of metabolic systems. Biotechnol. Bioeng. 2000, 71, 286–306. [Google Scholar] [CrossRef]
- de Groot, D.H.; Lischke, J.; Muolo, R.; Planqué, R.; Bruggeman, F.J.; Teusink, B. The common message of constraint-based optimization approaches: Overflow metabolism is caused by two growth-limiting constraints. Cell. Mol. Life Sci. 2020, 77, 441–453. [Google Scholar] [CrossRef] [Green Version]
- Jensen, P.R.; Hammer, K. Minimal requirements for exponential growth of Lactococcus lactis. Appl. Environ. Microbiol. 1993, 59, 4363–4366. [Google Scholar] [CrossRef] [Green Version]
- Teusink, B.; Molenaar, D. Systems biology of lactic acid bacteria: For food and thought. Curr. Opin. Syst. Biol. 2017, 6, 7–13. [Google Scholar] [CrossRef]
- Fernández, M.; Zúñiga, M. Amino acid catabolic pathways of lactic acid bacteria. Crit. Rev. Microbiol. 2006, 32, 155–183. [Google Scholar] [CrossRef]
- Goel, A.; Eckhardt, T.H.; Puri, P.; de Jong, A.; Branco dos Santos, F.; Giera, M.; Fusetti, F.; de Vos, W.M.; Kok, J.; Poolman, B.; et al. Protein costs do not explain evolution of metabolic strategies and regulation of ribosomal content: Does protein investment explain an anaerobic bacterial Crabtree effect? Mol. Microbiol. 2015, 97, 77–92. [Google Scholar] [CrossRef]
- Teusink, B.; Wiersma, A.; Molenaar, D.; Francke, C.; De Vos, W.M.; Siezen, R.J.; Smid, E.J. Analysis of growth of Lactobacillus plantarum WCFS1 on a complex medium using a genome-scale metabolic model. J. Biol. Chem. 2006, 281, 40041–40048. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Olivier, B.G. PySCeS CBMPy: Constraint Based Modelling in Python. 2011. Available online: http://cbmpy.sourceforge.net/ (accessed on 14 April 2021).
- Klamt, S.; Saez-Rodriguez, J.; Gilles, E.D. Structural and functional analysis of cellular networks with CellNetAnalyzer. BMC Syst. Biol. 2007, 1, 2. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schellenberger, J.; Que, R.; Fleming, R.M.; Thiele, I.; Orth, J.D.; Feist, A.M.; Zielinski, D.C.; Bordbar, A.; Lewis, N.E.; Rahmanian, S.; et al. Quantitative prediction of cellular metabolism with constraint-based models: The COBRA Toolbox v2.0. Nat. Protoc. 2011, 6, 1290–1307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rocha, I.; Maia, P.; Evangelista, P.; Vilaça, P.; Soares, S.; Pinto, J.P.; Nielsen, J.; Patil, K.R.; Ferreira, E.C.; Rocha, M. OptFlux: An open-source software platform for in silico metabolic engineering. BMC Syst. Biol. 2010, 4, 45. [Google Scholar] [CrossRef] [Green Version]
- Hoops, S.; Sahle, S.; Gauges, R.; Lee, C.; Pahle, J.; Simus, N.; Singhal, M.; Xu, L.; Mendes, P.; Kummer, U. COPASI–a COmplex PAthway SImulator. Bioinformatics 2006, 22, 3067–3074. [Google Scholar] [CrossRef] [Green Version]
- Francke, C.; Siezen, R.J.; Teusink, B. Reconstructing the metabolic network of a bacterium from its genome. Trends Microbiol. 2005, 13, 550–558. [Google Scholar] [CrossRef]
- Thiele, I.; Palsson, B. A protocol for generating a high-quality genome-scale metabolic reconstruction. Nat. Protoc. 2010, 5, 93–121. [Google Scholar] [CrossRef] [Green Version]
- Mendoza, S.N.; Olivier, B.G.; Molenaar, D.; Teusink, B. A systematic assessment of current genome-scale metabolic reconstruction tools. Genome Biol. 2019, 20, 158. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wiback, S.J.; Mahadevan, R.; Palsson, B. Reconstructing metabolic flux vectors from extreme pathways: Defining the α-spectrum. J. Theor. Biol. 2003, 224, 313–324. [Google Scholar] [CrossRef]
- Carlson, R.; Srienc, F. Fundamental Escherichia coli biochemical pathways for biomass and energy production: Creation of overall flux states. Biotechnol. Bioeng. 2004, 86, 149–162. [Google Scholar] [CrossRef] [PubMed]
- Carlson, R.; Srienc, F. Fundamental Escherichia coli biochemical pathways for biomass and energy production: Identification of reactions. Biotechnol. Bioeng. 2004, 85, 1–19. [Google Scholar] [CrossRef] [PubMed]
- De Groot, D.H.; Hulshof, J.; Teusink, B.; Bruggeman, F.J.; Planqué, R. Elementary Growth Modes provide a molecular description of cellular self-fabrication. PLoS Comput. Biol. 2020, 16, 1–33. [Google Scholar] [CrossRef] [Green Version]
- Lloyd, C.J.; Ebrahim, A.; Yang, L.; King, Z.A.; Catoiu, E.; O’Brien, E.J.; Liu, J.K.; Palsson, B.O. COBRAme: A computational framework for genome-scale models of metabolism and gene expression. PLoS Comput. Biol. 2018, 14, e1006302. [Google Scholar] [CrossRef] [PubMed]
- Gianchandani, E.P.; Chavali, A.K.; Papin, J.A. The application of flux balance analysis in systems biology. Wiley Interdiscip. Rev. Syst. Biol. Med. 2010, 2, 372–382. [Google Scholar] [CrossRef]
- Poolman, M.; Venkatesh, K.; Pidcock, M.; Fell, D. A method for the determination of flux in elementary modes, and its application to Lactobacillus rhamnosus. Biotechnol. Bioeng. 2004, 88, 601–612. [Google Scholar] [CrossRef]
- Wiback, S.J.; Mahadevan, R.; Palsson, B.Ø.O. Using metabolic flux data to further constrain the metabolic solution space and predict internal flux patterns: The Escherichia coli spectrum. Biotechnol. Bioeng. 2004, 86, 317–331. [Google Scholar] [CrossRef]
- Klamt, S.; Mahadevan, R. On the feasibility of growth-coupled product synthesis in microbial strains. Metab. Eng. 2015, 30, 166–178. [Google Scholar] [CrossRef] [PubMed]
- von Kamp, A.; Thiele, S.; Hädicke, O.; Klamt, S. Use of CellNetAnalyzer in biotechnology and metabolic engineering. J. Biotechnol. 2017, 261, 221–228. [Google Scholar] [CrossRef] [PubMed]
- Nookaew, I.; Meechai, A.; Thammarongtham, C.; Laoteng, K.; Ruanglek, V.; Cheevadhanarak, S.; Nielsen, J.; Bhumiratana, S. Identification of flux regulation coefficients from elementary flux modes: A systems biology tool for analysis of metabolic networks. Biotechnol. Bioeng. 2007, 97, 1535–1549. [Google Scholar] [CrossRef] [PubMed]
- Müller, S.; Regensburger, G. Elementary vectors and conformal sums in polyhedral geometry and their relevance for metabolic pathway analysis. Front. Genet. 2016, 7, 90. [Google Scholar] [CrossRef] [Green Version]





| Organism | Model | Number of Active Constraints |
|---|---|---|
| E. coli | iJR904 [16] | 2 |
| E. coli | iAF1260b [17] | 2 |
| L. lactis | [18] | 10 |
| L. plantarum | [19] | 4 |
| M. tuberculosis | iNJ661 [20] | 4 |
| S. cerevisiae | iMM904 [21] | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
van Pelt-KleinJan, E.; de Groot, D.H.; Teusink, B. Understanding FBA Solutions under Multiple Nutrient Limitations. Metabolites 2021, 11, 257. https://0-doi-org.brum.beds.ac.uk/10.3390/metabo11050257
van Pelt-KleinJan E, de Groot DH, Teusink B. Understanding FBA Solutions under Multiple Nutrient Limitations. Metabolites. 2021; 11(5):257. https://0-doi-org.brum.beds.ac.uk/10.3390/metabo11050257
Chicago/Turabian Stylevan Pelt-KleinJan, Eunice, Daan H. de Groot, and Bas Teusink. 2021. "Understanding FBA Solutions under Multiple Nutrient Limitations" Metabolites 11, no. 5: 257. https://0-doi-org.brum.beds.ac.uk/10.3390/metabo11050257