A Novel Simplified Algorithm for Bare Surface Soil Moisture Retrieval Using L-Band Radiometer
Abstract
:1. Introduction
2. Study Area and Datasets
2.1. Study Area
2.2. Microwave Data
2.3. Field Data
3. Methodology
3.1. Surface Emission Model
3.2. Soil Moisture Retrieval Model
4. Results and Discussion
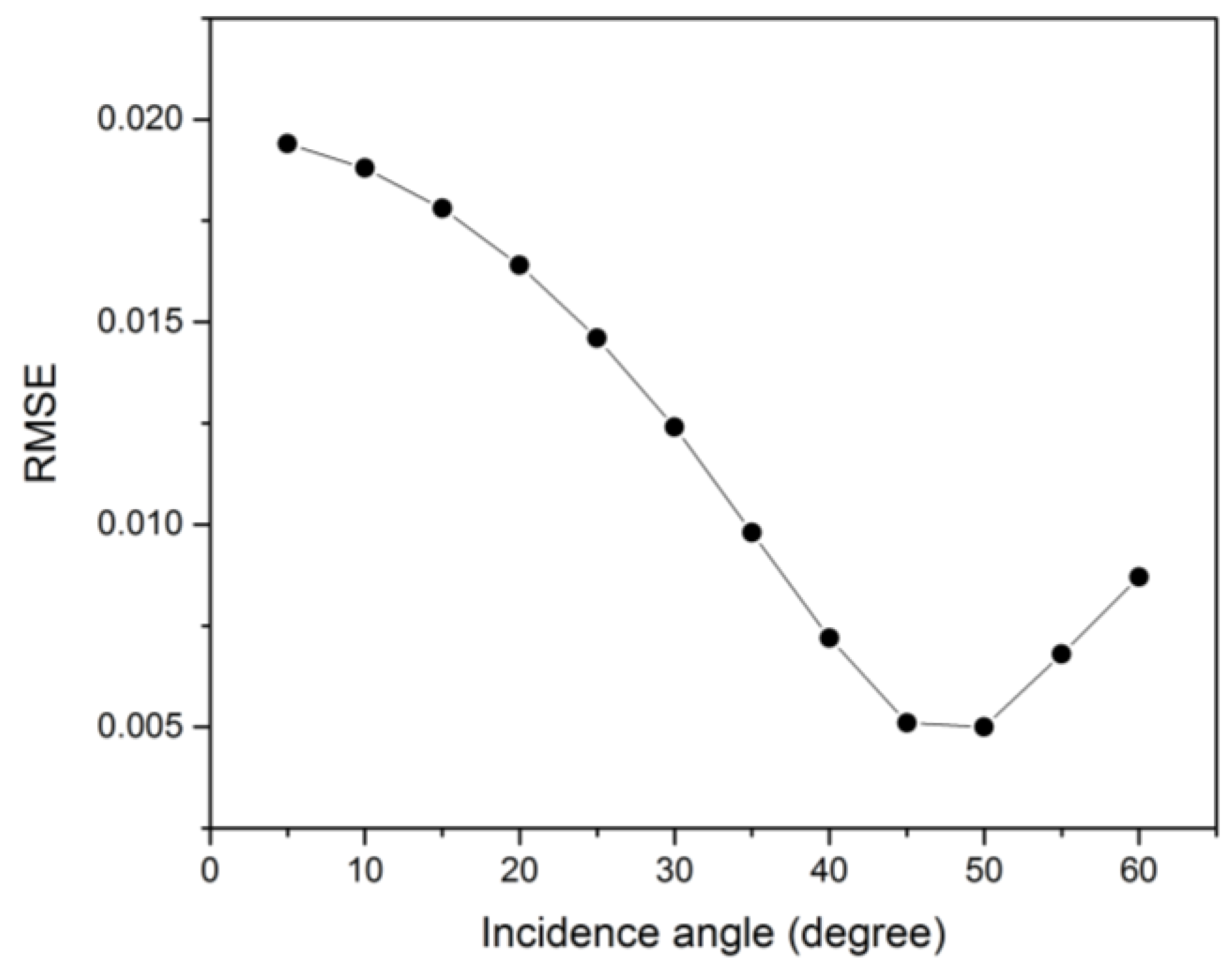
4.1. Soil Moisture Estimation with Simulated Data
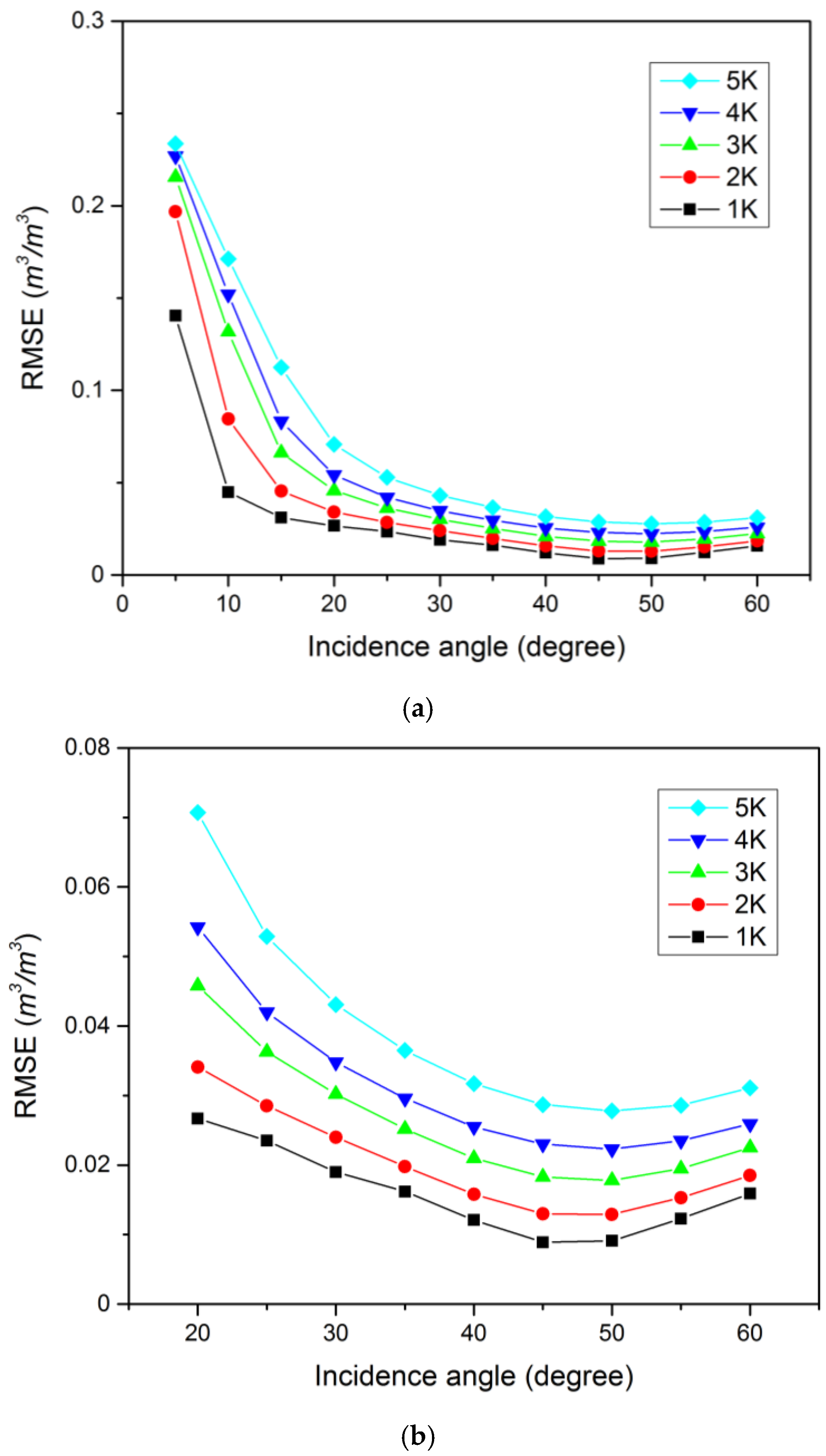
4.2. Sensitivity Analysis
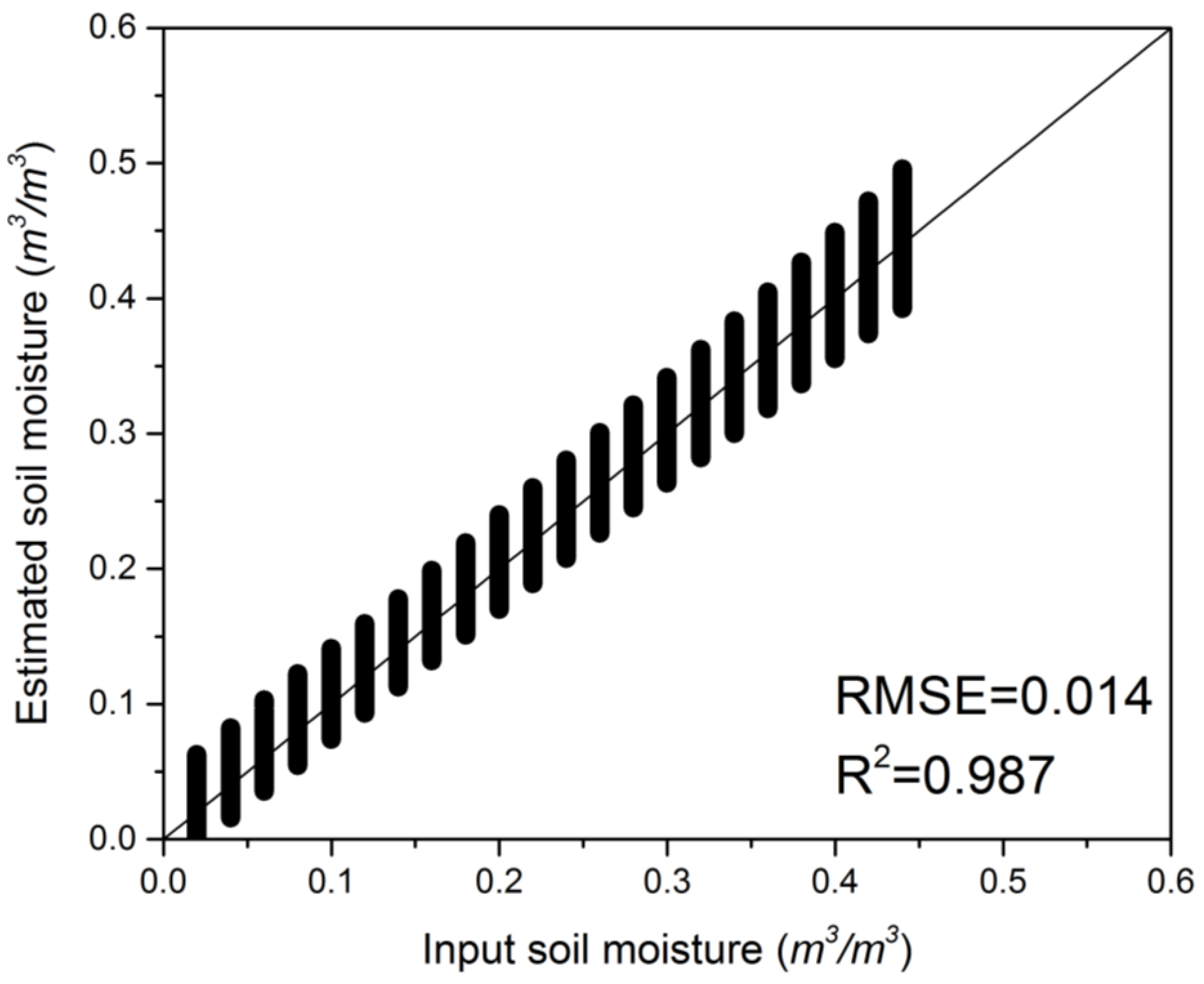
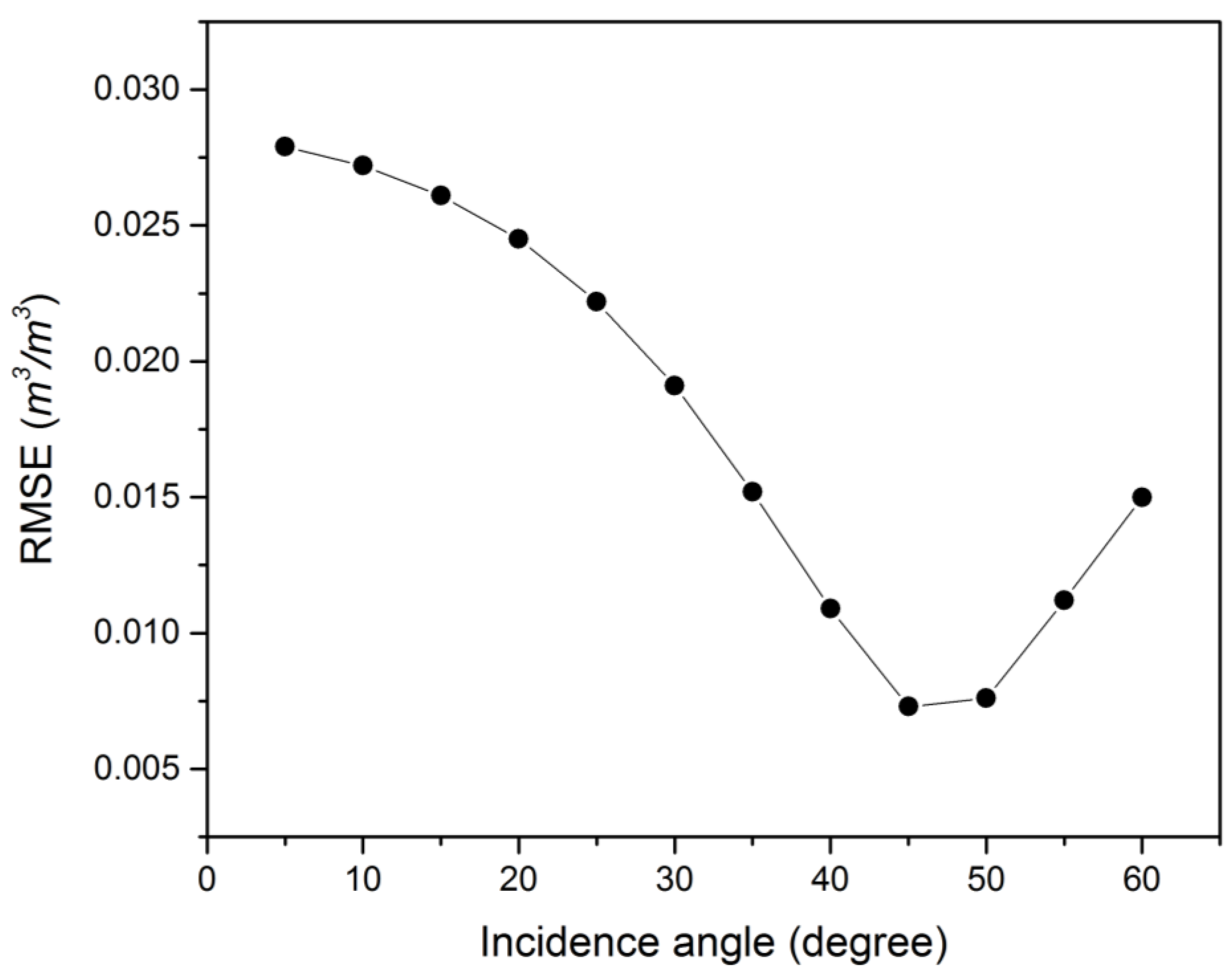
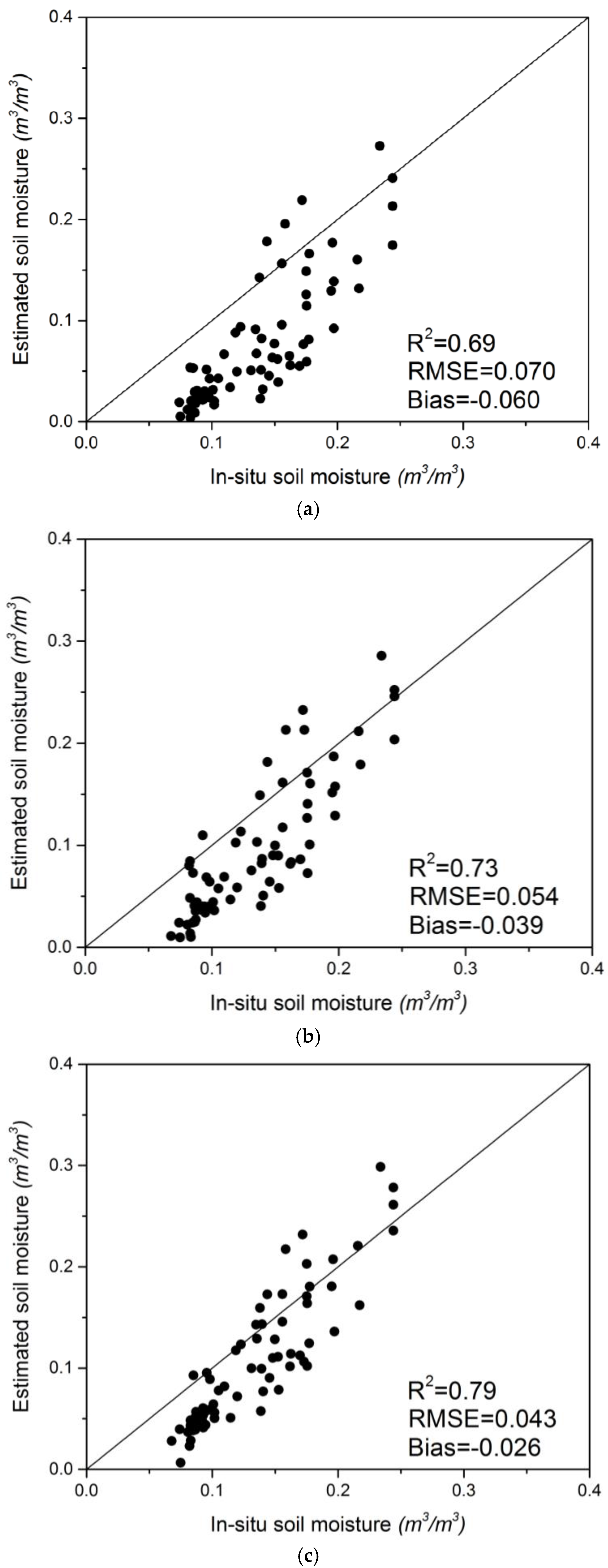
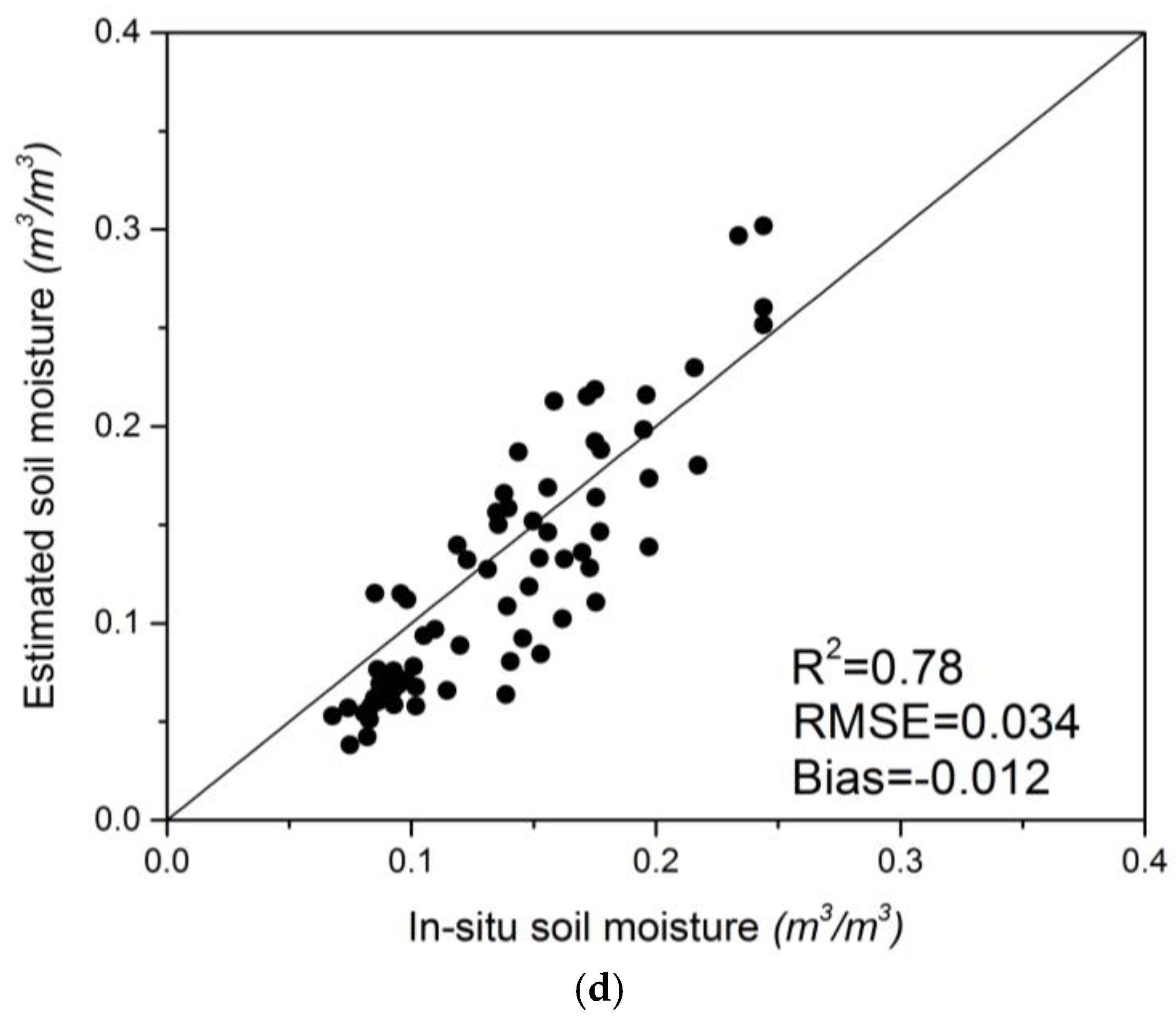
4.3. Soil Moisture Validation with in Situ Data
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements of the global water cycle. IEEE Proc. 2010, 98, 666–687. [Google Scholar] [CrossRef] [Green Version]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) mission. IEEE Proc. 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Gharechelou, S.; Tateishi, R.; Sharma, R.C.; Johnson, B.A. Soil moisture mapping in an arid area using a land unit area (LUA) sampling approach and geostatistical interpolation techniques. ISPRS Int. Geo-Inf. 2016. [Google Scholar] [CrossRef]
- Le Vine, D.A.; Lagerloef, G.S.E.; Colomb, F.R.; Yueh, S.H.; Pellerano, F.A. Aquarius: An instrument to monitor sea surface salinity from space. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2040–2050. [Google Scholar] [CrossRef]
- Shi, J.C.; Dong, X.L.; Zhao, T.J.; Du, J.Y.; Jiang, L.M.; Du, Y.; Liu, H.; Wang, Z.Z.; Ji, D.B.; Xiong, C.; et al. Wcom: The science scenario and objectives of a global water cycle observation mission. In Proceedings of the 2014 IEEE International Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; IEEE: New York, NY, USA, 2014; pp. 3646–3649. [Google Scholar]
- Chen, K.S.; Wu, T.D.; Tsang, L.; Li, Q.; Shi, J.C.; Fung, A.K. Emission of rough surfaces calculated by the integral equation method with comparison to three-dimensional moment method simulations. IEEE Trans. Geosci. Remote Sens. 2003, 41, 90–101. [Google Scholar] [CrossRef]
- Choudhury, B.J.; Schmugge, T.J.; Chang, A.; Newton, R.W. Effect of surface-roughness on the microwave emission from soils. J. Geophys. Res.-Oceans Atmos. 1979, 84, 5699–5706. [Google Scholar] [CrossRef]
- Shi, J.C.; Chen, K.S.; Li, Q.; Jackson, T.J.; O’Neill, P.E.; Tsang, L. A parameterized surface reflectivity model and estimation of bare-surface soil moisture with L-band radiometer. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2674–2686. [Google Scholar]
- Chen, L.; Shi, J.C.; Wigneron, J.P.; Chen, K.S. A parameterized surface emission model at L-band for soil moisture retrieval. IEEE Geosci. Remote Sens. Lett. 2010, 7, 127–130. [Google Scholar] [CrossRef]
- Guo, P.; Shi, J.C.; Liu, Q.; Du, J.Y. A new algorithm for soil moisture retrieval with L-band radiometer. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1147–1155. [Google Scholar] [CrossRef]
- Jia, Y.Y.; Tang, B.H.; Zhang, X.Y.; Li, Z.L. Estimation of land surface temperature and emissivity from AMSR-E data. In Proceedings of the IGARSS: 2007 Ieee International Geoscience and Remote Sensing Symposium, Vols 1–12: Sensing and Understanding Our Planet, Barcelona, Spain, 23–28 July 2007; IEEE: New York, NY, USA, 2007; pp. 1849–1852. [Google Scholar]
- Liu, Z.L.; Wu, H.; Tang, B.H.; Qiu, S.; Li, Z.L. An empirical relationship of bare soil microwave emissions between vertical and horizontal polarization at 10.65 GHz. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1479–1483. [Google Scholar]
- Jackson, T.J. Measuring surface soil-moisture using passive microwave remote-sensing. Hydrol. Process. 1993, 7, 139–152. [Google Scholar] [CrossRef]
- Wigneron, J.P.; Kerr, Y.; Waldteufel, P.; Saleh, K.; Escorihuela, M.J.; Richaume, P.; Ferrazzoli, P.; de Rosnay, P.; Gurney, R.; Calvet, J.C.; et al. L-band microwave emission of the biosphere (L-MEB) model: Description and calibration against experimental data sets over crop fields. Remote Sens. Environ. 2007, 107, 639–655. [Google Scholar] [CrossRef]
- Oneill, P.E. Microwave remote-sensing of soil-moisture—A comparison of results from different truck and aircraft platforms. Int. J. Remote Sens. 1985, 6, 1125–1134. [Google Scholar] [CrossRef]
- Wang, J.R. Effect of vegetation on soil-moisture sensing observed from orbiting microwave radiometers. Remote Sens. Environ. 1985, 17, 141–151. [Google Scholar] [CrossRef]
- Schmugge, T.; Oneill, P.E.; Wang, J.R. Passive microwave soil-moisture research. IEEE Trans. Geosci. Remote Sens. 1986, 24, 12–22. [Google Scholar] [CrossRef]
- Al-Yaari, A.; Wigneron, J.P.; Kerr, Y.; de Jeu, R.; Rodriguez-Fernandez, N.; van der Schalie, R.; Al Bitar, A.; Mialon, A.; Richaume, P.; Dolman, A.; et al. Testing regression equations to derive long-term global soil moisture datasets from passive microwave observations. Remote Sens. Environ. 2016, 180, 453–464. [Google Scholar] [CrossRef]
- Shi, J.C.; Du, Y.; Du, J.Y.; Jiang, L.M.; Chai, L.N.; Mao, K.B.; Xu, P.; Ni, W.J.; Xiong, C.; Liu, Q.; et al. Progresses on microwave remote sensing of land surface parameters. Sci. China-Earth Sci. 2012, 55, 1052–1078. [Google Scholar] [CrossRef]
- Wang, J.; Shiue, J.; Engman, E.; McMurtrey, J.; Lawless, I.P.; Schmugge, T.J.; Jackson, T.J.; Gould, W.; Fuchs, J.; Calhoon, C.; et al. Remote Measurements of Soil Moisture by Microwave Radiometers at BARC Test Site; NASA, NASA Tech. Memo: Greenbelt, MD, USA, 1980.
- Wang, J.; O’Neill, P.; Engman, E.; McMurtrey, J.; Lawless, I.P.; Schmugge, T.J.; Jackson, T.J.; Gould, W.; Fuchs, J.; Glazer, W. Remote Measurements of Soil Moisture by Microwave Radiometers at BARC Test Site II; NASA, NASA Tech. Memo: Greenbelt, MD, USA, 1982.
- Wang, J.; Jackson, T.J.; Engman, E.; Gould, W.; Fuchs, J.; Glazer, W.; O’Neill, P.; Schmugge, T.J.; McMurtrey, J. Microwave Radiometer Experiment of Soil Moisture Sensing at BARC Test Site Curing Summer 1981; NASA, NASA Tech. Memo: Greenbelt, MD, USA, 1984.
- O’Neill, P.; Jackson, T.J.; Blanchard, B.; van den Hoek, R.; Gould, W.; Wang, J.; Glazer, W.; McMurtrey, J. Soil Hydraulic Properties on Passive Microwave Sensing of Soil Moisture: Data Report for the 1982 Field Experiments; NASA, NASA Tech. Memo: Greenbelt, MD, USA, 1983.
- Hong, S. Retrieval of refractive index over specular surfaces for remote sensing applications. J. Appl. Remote Sens. 2009, 3, 033560. [Google Scholar] [CrossRef]
- Hong, S. Detection of small-scale roughness and refractive index of sea ice in passive satellite microwave remote sensing. Remote Sens. Environ. 2010, 114, 1136–1140. [Google Scholar] [CrossRef]
- Hong, S. Global retrieval of small-scale roughness over land surfaces at microwave frequency. J. Hydrol. 2010, 389, 121–126. [Google Scholar] [CrossRef]
- Hong, S. Surface roughness and polarization ratio in microwave remote sensing. Int. J. Remote Sens. 2010, 31, 2709–2716. [Google Scholar] [CrossRef]
- Liou, K.N. An Introduction to Atmospheric Radiation, 2nd ed.; Academic Press: New York, NY, USA, 2002. [Google Scholar]
- Sohn, B.J.; Lee, S.M. Analytical relationship between polarized reflectivities on the specular surface. Int. J. Remote Sens. 2013, 34, 2368–2374. [Google Scholar] [CrossRef]
- Hallikainen, M.T.; Ulaby, F.T.; Dobson, M.C.; Elrayes, M.A.; Wu, L.K. Microwave dielectric behavior of wet soil. 1. Empirical-models and experimental-observations. IEEE Trans. Geosci. Remote Sens. 1985, 23, 25–34. [Google Scholar] [CrossRef]
- Njoku, E.G.; Chan, S.K. Vegetation and surface roughness effects on AMSR-E land observations. Remote Sens. Environ. 2006, 100, 190–199. [Google Scholar] [CrossRef]
- Jones, M.O.; Jones, L.A.; Kimball, J.S.; McDonald, K.C. Satellite passive microwave remote sensing for monitoring global land surface phenology. Remote Sens. Environ. 2011, 115, 1102–1114. [Google Scholar] [CrossRef]
- Justice, C.O.; Vermote, E.; Townshend, J.R.G.; Defries, R.; Roy, D.P.; Hall, D.K.; Salomonson, V.V.; Privette, J.L.; Riggs, G.; Strahler, A.; et al. The moderate resolution imaging spectroradiometer (MODIS): Land remote sensing for global change research. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1228–1249. [Google Scholar] [CrossRef]

| Year | Location | Texture | Sand (%) | Silt (%) | Clay (%) |
|---|---|---|---|---|---|
| 1979 | Elinsboro | Sandy loam | 68 | 21 | 11 |
| 1980 | Elinsboro | Sandy loam | 68 | 21 | 11 |
| 1981 | Edmonston | Sandy loam | 67 | 18 | 15 |
| South Farm | Loam | 31 | 44 | 25 | |
| 1982 | Edmonston | Sandy loam | 68 | 21 | 11 |
| South Farm | Loam | 34 | 42 | 24 | |
| Gish | Loam/clay loam | 24 | 47 | 29 |
| Soil Parameters | Minimum | Maximum | Interval |
|---|---|---|---|
| Soil moisture (%) | 2 | 44 | 2 |
| RMS 1 height (cm) | 0.25 | 3 | 0.25 |
| Correlation length (cm) | 5 | 30 | 2.5 |
| Incidence angle (degree) | 5 | 60 | 5 |
| Incidence Angle | a | b | c |
|---|---|---|---|
| 5° | 0.953487 | 1.00148 | 0.054886 |
| 10° | 0.845617 | 1.004317 | 0.186599 |
| 15° | 0.718362 | 1.005721 | 0.352128 |
| 20° | 0.59251 | 1.003765 | 0.531698 |
| 25° | 0.46837 | 0.997595 | 0.728534 |
| 30° | 0.336077 | 0.987071 | 0.958948 |
| 35° | 0.178412 | 0.972665 | 1.250999 |
| 40° | −0.032488 | 0.955735 | 1.650921 |
| 45° | −0.346537 | 0.939325 | 2.240814 |
| 50° | −0.872675 | 0.929568 | 3.189056 |
| 55° | −1.929771 | 0.938026 | 4.934479 |
| 60° | −4.929332 | 0.986903 | 9.172908 |
| Soil Parameter | Minimum | Maximum | Interval |
|---|---|---|---|
| Soil moisture (%) | 2 | 44 | 2 |
| Bulk density (g/cm3) | 0.9 | 1.7 | 0.1 |
| Soil temperature (°C) | 5 | 40 | 1 |
| Sand content (%) | 5 | 95 | 5 |
| Clay content (%) | 5 | 95 | 5 |
| Coefficients | a0 | a1 | a2 | b0 | b1 | b2 | c0 | c1 | c2 |
|---|---|---|---|---|---|---|---|---|---|
| Value | 1.40 | 0.55 | 0.12 | 6.18 | 6.32 | 2.18 | 2.82 | −9.80 | −3.24 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, B.; Song, X.; Leng, P.; Sun, C.; Wang, R.; Jiang, X. A Novel Simplified Algorithm for Bare Surface Soil Moisture Retrieval Using L-Band Radiometer. ISPRS Int. J. Geo-Inf. 2016, 5, 143. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi5080143
Zhu B, Song X, Leng P, Sun C, Wang R, Jiang X. A Novel Simplified Algorithm for Bare Surface Soil Moisture Retrieval Using L-Band Radiometer. ISPRS International Journal of Geo-Information. 2016; 5(8):143. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi5080143
Chicago/Turabian StyleZhu, Bin, Xiaoning Song, Pei Leng, Chuan Sun, Ruixin Wang, and Xiaoguang Jiang. 2016. "A Novel Simplified Algorithm for Bare Surface Soil Moisture Retrieval Using L-Band Radiometer" ISPRS International Journal of Geo-Information 5, no. 8: 143. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi5080143





