Analysis of Burglary Hot Spots and Near-Repeat Victimization in a Large Chinese City
Abstract
:1. Introduction
2. Theoretical Background
2.1. Environmental Criminology
2.2. Repeat and Near-Repeat Victimization
2.3. Hot Spot and Near-Repeat Victimization
3. Materials
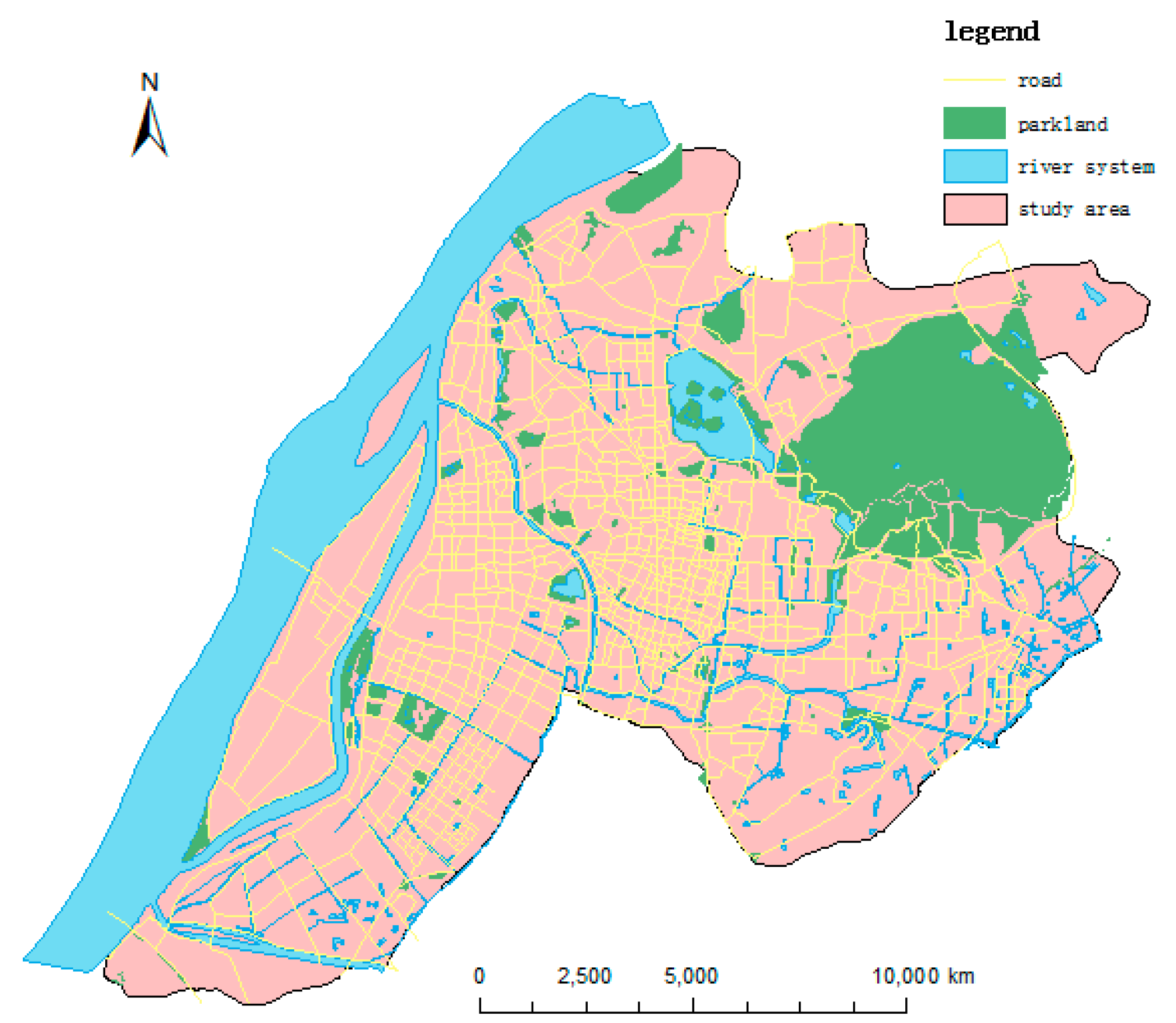
3.1. Study Area
3.2. Data Sources
4. Methods
4.1. Near-Repeat Matrix
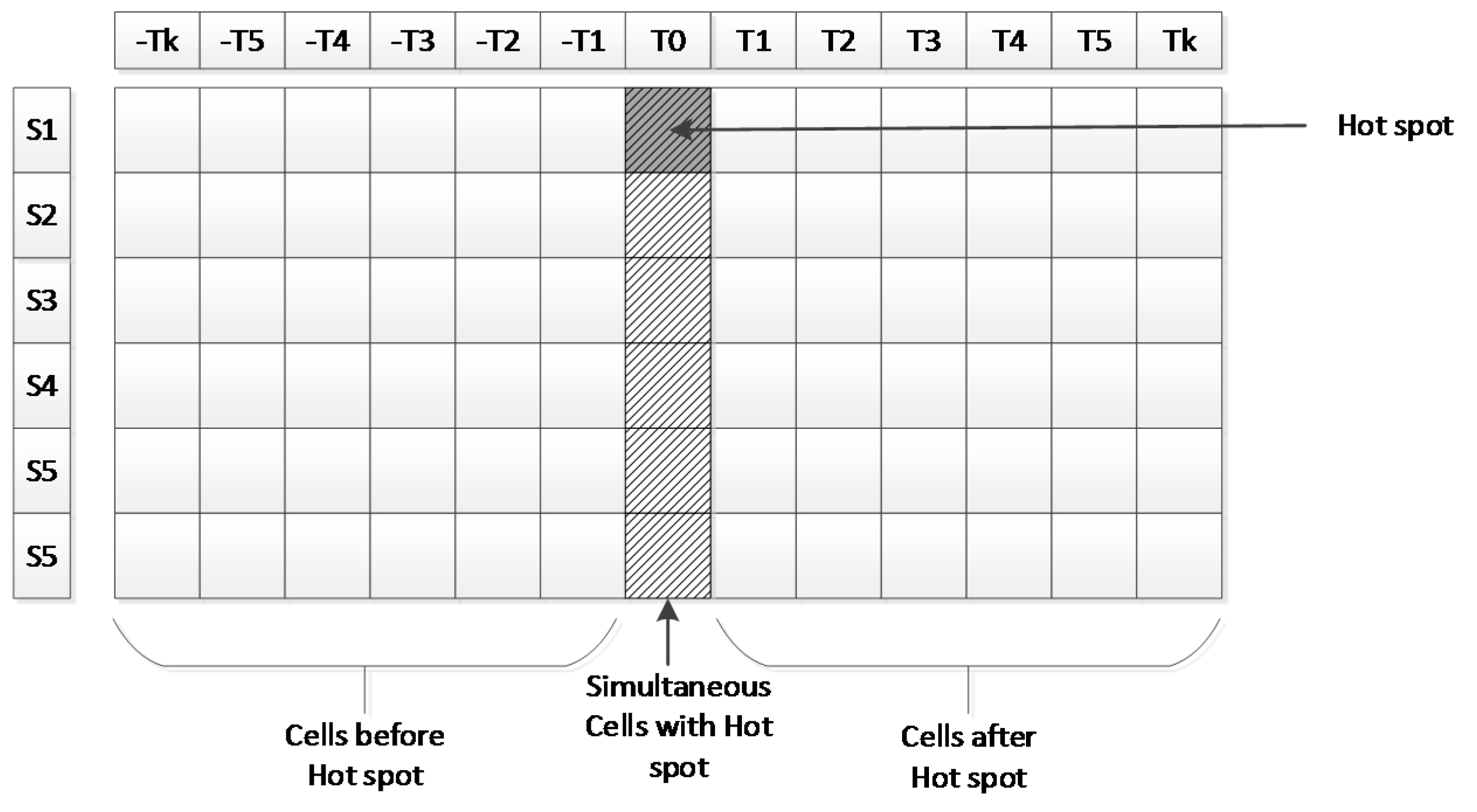
4.2. Temporal Expanded Near-Repeat Matrix
5. Case Studies
5.1. Near-Repeat Characteristics of Research Area
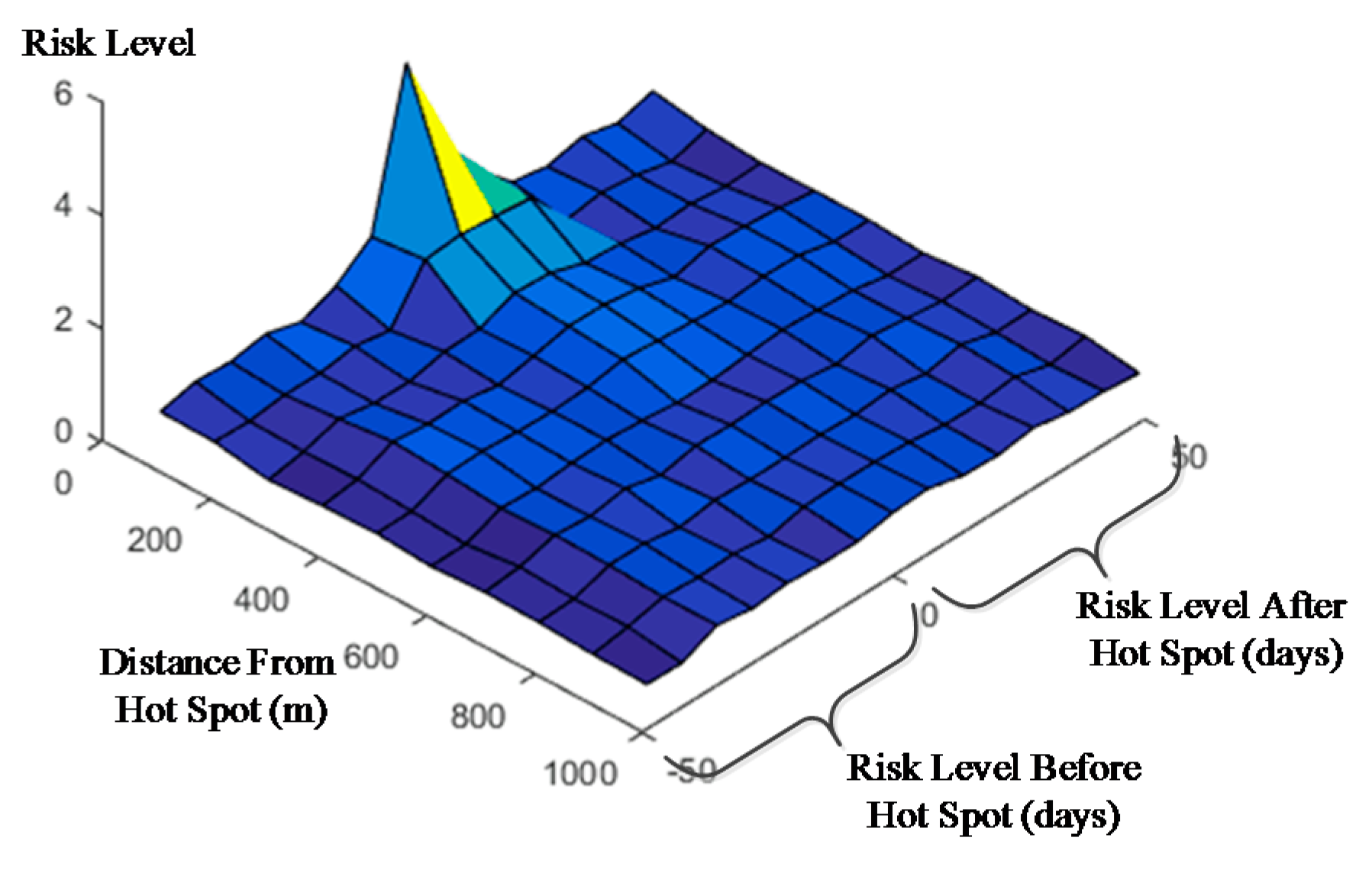
5.2. Contribution of Hot Spots in Repeat and Near-Repeat Victimizations
5.3. Distribution of Crime Incidents Based on Hot Spots
6. Discussion
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Johnson, S.D.; Bowers, K.J. The burglary as clue to the future: The beginnings of prospective hot-spotting. Eur. J. Criminol. 2004, 1, 237–255. [Google Scholar] [CrossRef]
- Townsley, M.; Homel, R.; Chaseling, J. Repeat burglary victimization: Spatial and temporal patterns. Aust. N. Z. J. Criminol. 2000, 33, 37–63. [Google Scholar] [CrossRef]
- Jochelson, R. Crime and Place: An Analysis of Assaults and Robberies in Inner Sydney; General Report Series; New SouthWales Bureau of Crime Statistics and Research: Sydney, Australia, 1997.
- Ratcliffe, J.H.; Rengert, G.F. Near-repeat patterns in Philadelphia shootings. Secur. J. 2008, 21, 58–76. [Google Scholar] [CrossRef]
- Shaw, C.R.; McKay, H.D. Social Factors in Juvenile Delinquency; Government Press: New York, NY, USA, 1931.
- Quetelet, A.J. Sur l’Homme et le Développement de ses Facultés, ou Essai de Physique Sociale; Bachelier: Paris, France, 1835. [Google Scholar]
- Mastrofski, S.D.; Weisburd, D.; Braga, A.A. Rethinking policing: The policy implications of hot spots of crime. In Contemporary Issues in Criminal Justice Policy, 2010Belmont; Natasha, F., Joshua, F., Todd, C., Eds.; CAWadsworth Cengage Learning: Boston, MA, USA, 2010; pp. 251–264. [Google Scholar]
- Cohen, L.E.; Felson, M. Social change and crime rate trends: A routine activity approach. Am. Sociol. Rev. 1979, 44, 588–608. [Google Scholar] [CrossRef]
- Clarke, R.V.G. Situational Crime Prevention: Successful Case Studies; Criminal Justice Press: Cincinnati, OH, USA, 1997. [Google Scholar]
- Rengert, G.F. The Journey to Crime: Conceptual Foundations and Policy Implications; Crime Policing Place: Essays in Environmental Criminology; Routledge: London, UK, 1992; pp. 109–117. [Google Scholar]
- Brantingham, P.L.; Brantingham, P.J. Crime pattern theory. In Environmental Criminology and Crime Analysis; Wortley, R., Mazerolle, L., Rombouts, S., Eds.; Willan Publishing: Cullompton, UK, 2008; pp. 78–93. [Google Scholar]
- Pease, K. Repeat Victimization: Taking Stock; Police Research Group: Crime Detection and Prevention Series Paper 90; The Home Office: London, UK, 1998.
- Morgan, F. Repeat burglary in a Perth suburb: Indicator of short-term or long-term risk? In Repeat Victimization; Farrell, G., Pease, K., Eds.; Monsey: New York, NY, USA, 2001; pp. 83–118. [Google Scholar]
- Johnson, S.D. Repeat burglary victimisation: A tale of two theories. J. Exp. Criminol. 2008, 4, 215–240. [Google Scholar] [CrossRef]
- Farrell, G.; Phillips, C.; Pease, K. Like taking candy: Why does repeat victimization occur? Br. J. Criminol. 1995, 35, 384–399. [Google Scholar] [CrossRef]
- Helbich, M.; Leitner, M. Frontiers in Spatial and Spatiotemporal Crime Analytics—An Editorial. ISPRS Int. J. Geo-Inf. 2017, 6, 73. [Google Scholar] [CrossRef]
- Sagovsky, A.; Johnson, S.D. When does repeat burglary occur? Aust. N. Z. J. Criminol. 2007, 40, 1–26. [Google Scholar] [CrossRef]
- Bowers, K.J.; Johnson, S.D. Who commits near repeats? A test of the boost explanation. Western Criminol. Rev. 2004, 5, 12–24. [Google Scholar]
- Johnson, S.D.; Summers, L.; Pease, K. Offender as forager? A direct test of the boost account of victimization. J. Quant. Criminol. 2009, 25, 181–200. [Google Scholar] [CrossRef]
- Knox, E.G.; Bartlett, M.S. The detection of space-time interactions. J. R. Stat. Soc. Series C (Appl. Stat.) 1964, 13, 25–30. [Google Scholar] [CrossRef]
- Townsley, M.; Homel, R.; Chaseling, J. Infectious burglaries: A test of the near repeat hypothesis. Br. J. Criminol. 2003, 43, 615–633. [Google Scholar] [CrossRef]
- Johnson, S.D.; Bernasco, W.; Bowers, K.J.; Elffers, H.; Ratcliffe, J.; Rengert, G.; Townsley, M. Space–time patterns of risk: A cross national assessment of residential burglary victimization. J. Quant. Criminol. 2007, 23, 201–219. [Google Scholar] [CrossRef]
- Johnson, S.D.; Bowers, K.J.; Birks, D.J.; Pease, K. Predictive mapping of crime by ProMap: Accuracy, units of analysis, and the environmental backcloth. In Putting Crime in Its Place; Springer: New York, NY, USA, 2009; pp. 171–198. [Google Scholar]
- Short, M.B.; D’Orsogna, M.R.; Brantingham, P.J.; Tita, G.E. Measuring and modeling repeat and near-repeat burglary effects. J. Quant. Criminol. 2009, 25, 325–339. [Google Scholar] [CrossRef]
- Bowers, K.J.; Johnson, S.D.; Pease, K. Prospective hot-spotting the future of crime mapping? Br. J. Criminol. 2004, 44, 641–658. [Google Scholar] [CrossRef]
- Johnson, S.D.; Birks, D.J.; McLaughlin, L.; Bowers, K.J.; Pease, K. Prospective Crime Mapping in Operational Context: Final Report; UCL, Jill Dando Institute of Crime Science: London, UK, 2007. [Google Scholar]
- Block, C.R. STAC hot-spot areas: A statistical tool for law enforcement decisions. In Crime Analysis Through Computer Mapping; Police Executive Research Forum: Washington, DC, USA, 1995; pp. 15–32. [Google Scholar]
- Ratcliffe, J.H.; McCullagh, M.J. Identifying repeat victimization with GIS. Br. J. Criminol. 1998, 38, 651–662. [Google Scholar] [CrossRef]
- Brunsdon, C.; Corcoran, J.; Higgs, G. Visualising space and time in crime patterns: A comparison of methods. Comput. Environ. Urban Syst. 2007, 31, 52–75. [Google Scholar] [CrossRef]
- Shiode, S.; Shiode, N. Network-based space-time search-window technique for hotspot detection of street-level crime incidents. Int. J. Geogr. Inf. Sci. 2013, 27, 866–882. [Google Scholar] [CrossRef]
- Haberman, C.P.; Ratcliffe, J.H. The predictive policing challenges of near repeat armed street robberies. Policing 2012, 6, 151–166. [Google Scholar] [CrossRef]
- Wu, L.; Xu, X.; Ye, X.; Zhu, X. Repeat and near-repeat burglaries and offender involvement in a large Chinese city. Cartogr. Geogr. Inf. Sci. 2015, 42, 178–189. [Google Scholar] [CrossRef]
- Nakaya, T.; Yano, K. Visualising crime clusters in a space-time cube: An exploratory data-analysis approach using space-time kernel density estimation and scan statistics. Trans. GIS 2010, 14, 223–239. [Google Scholar] [CrossRef]
- Leong, K.; Li, J.; Chan, S.C.; Ng, V. An application of the dynamic pattern analysis framework to the analysis of spatial-temporal crime relationships. J. UCS 2009, 15, 1852–1870. [Google Scholar]
- Piquero, A.R. Rational Choice and Criminal Behavior: Recent Research and Future Challenges; Routledge: London, UK, 2012. [Google Scholar]
- Paulsen, D.J.; Robinson, M.B. Spatial Aspects of Crime: Theory and Practice; Allyn & Bacon: Boston, MA, USA, 2004. [Google Scholar]
- Groff, E.R.; Johnson, L.; Ratcliffe, J.H.; Wood, J. Exploring the relationship between foot and car patrol in violent crime areas. Policing 2013, 36, 119–139. [Google Scholar] [CrossRef]
- Chen, P.; Yuan, H.; Li, D. Space-time analysis of burglary in Beijing. Secur. J. 2013, 26, 1–15. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, X.; Lu, J. Multiscale geographic analysis of burglary. ACTA Geogr. Sin. 2017, 72, 329–340. [Google Scholar]
- Xu, C.; Zhou, S.; Liu, L. Patterns of near-repeat street robbery in DP peninsula. Geogr. Res. 2015, 34, 384–394. [Google Scholar]
- Wang, Z.; Liu, X.; Wu, W.; Lu, J. Construction and spatial-temporal analysis of crime network: A case study on burglary. Geomatics and Information Science of Wuhan University. Available online: http://www.cnki.net/kcms/detail/42.1676.TN.20160714.1324.003.html (accessed on 9 May 2017).
- Ratcliffe, J.H.; McCullagh, M.J. Hotbeds of crime and the search for spatial accuracy. J. Geogr. Syst. 1999, 1, 385–398. [Google Scholar] [CrossRef]
- McLafferty, S.; Williamson, D.; McGuire, P.G. Identifying crime hot spots using kernel smoothing. In Analyzing Crime Patterns: Frontiers of Practice; SAGE Publications: Thousand Oaks, CA, USA, 2000; pp. 77–85. [Google Scholar]
- Block, R.L.; Block, C.R. Space, place and crime: Hot spot areas and hot places of liquor-related crime. Crime Place 1995, 4, 145–184. [Google Scholar]
- Levine, N. CrimeStat III: A Spatial Statistics Program for the Analysis of Crime Incident Locations (version 3.0); Ned Levine & Associates: Houston, TX, USA; National Institute of Justice: Washington, DC, USA, 2004.
- Duczmal, L.; Assuncao, R. A simulated annealing strategy for the detection of arbitrarily shaped spatial clusters. Comput. Stat. Data Anal. 2004, 45, 269–286. [Google Scholar] [CrossRef]
- Takahashi, K.; Kulldorff, M.; Tango, T.; Yih, K. A flexibly shaped space-time scan statistic for disease outbreak detection and monitoring. Int. J. Health Geogr. 2008, 7, 14. [Google Scholar] [CrossRef] [PubMed]
- Shiode, S. Street-level spatial scan statistic and STAC for analysing street crime concentrations. Trans. GIS 2011, 15, 365–383. [Google Scholar] [CrossRef]
- Glasner, P.; Leitner, M. Evaluating the Impact the Weekday Has on Near-Repeat Victimization: A Spatio-Temporal Analysis of Street Robberies in the City of Vienna, Austria. ISPRS Int. J. Geo-Inf. 2016, 6, 3. [Google Scholar] [CrossRef]
- Chen, P.; Shu, X.; Yan, J.; Yuan, H. Timing of criminal activities during the day. J. Tsinghua Univ. (Sci. Tech.) 2009, 49, 2036–2039. [Google Scholar]
- Andresen, M.A.; Malleson, N. Crime seasonality and its variations across space. Appl. Geogr. 2013, 43, 25–35. [Google Scholar] [CrossRef]

| Spatial Distance (m) | Temporal Distance (Day) | ||||||
|---|---|---|---|---|---|---|---|
| 0–7 | 8–14 | 15–21 | 22–28 | 29–35 | 35–42 | 42+ | |
| <100 | 2.85 ** | 1.77 ** | 1.70 ** | 1.72 ** | 1.45 ** | 1.29 ** | 1.05 |
| 100–200 | 1.81 ** | 1.50 ** | 1.41 ** | 1.32 ** | 1.15 ** | 1.02 | 1.02 |
| 200–300 | 1.72 ** | 1.54 ** | 1.37 ** | 1.34 ** | 1.20 ** | 1.09 | 1.09 |
| 300–400 | 1.48 ** | 1.35 ** | 1.28 ** | 1.26 ** | 1.19 ** | 1.11 * | 1.04 |
| 400–500 | 1.43 ** | 1.37 ** | 1.29 ** | 1.23 ** | 1.18 ** | 1.15 * | 1.12 |
| 500–600 | 1.28 ** | 1.28 ** | 1.19 ** | 1.17 * | 1.16 * | 1.16 * | 1.05 |
| 600–700 | 1.27 ** | 1.21 ** | 1.19 ** | 1.10 * | 1.05 | 1.03 | 1.01 |
| 700–800 | 1.24 ** | 1.20 ** | 1.12 * | 1.09 | 1.04 | 1.05 | 1.01 |
| 800–900 | 1.27 * | 1.19 * | 1.16 * | 1.11 * | 1.08 | 1.03 | 1.08 |
| 900–1000 | 1.20 * | 1.15 * | 1.08 | 1.13 * | 1.10 | 1.13 | 1.06 |
| Spatial Distance (m) | Temporal Distance (Day) | ||||||
|---|---|---|---|---|---|---|---|
| 0–7 | 8–14 | 15–21 | 22–28 | 29–35 | 35–42 | 42+ | |
| <100 | 62.2% | 34.7% | 33.9% | 29.5% | 28.9% | 27.5% | 26.6% |
| 100–200 | 37.0% | 30.3% | 26.1% | 26.2% | 26.3% | 27.3% | 26.6% |
| 200–300 | 29.2% | 28.2% | 26.1% | 25.5% | 24.4% | 26.2% | 22.6% |
| 300–400 | 25.8% | 24.9% | 24.6% | 25.6% | 24.4% | 25.4% | 24.8% |
| 400–500 | 26.9% | 23.4% | 24.4% | 22.7% | 25.6% | 26.4% | 22.6% |
| 500–600 | 26.5% | 25.5% | 24.7% | 24.0% | 24.3% | 24.4% | 25.1% |
| 600–700 | 25.3% | 23.9% | 25.4% | 24.2% | 24.3% | 23.6% | 24.0% |
| 700–800 | 25.4% | 24.4% | 25.2% | 25.0% | 24.2% | 24.7% | 23.5% |
| 800–900 | 25.7% | 24.9% | 24.2% | 24.1% | 25.4% | 24.6% | 24.1% |
| 900–1000 | 25.7% | 25.6% | 25.2% | 25.5% | 24.2% | 25.6% | 23.9% |
| Spatial Distance (m) | Temporal Distance (Day) | ||||||
|---|---|---|---|---|---|---|---|
| 0–7 | 8–14 | 15–21 | 22–28 | 29–35 | 35–42 | 42+ | |
| <100 | 100.0% | 98.5% | 79.3% | 72.0% | 70.6% | 64.2% | 61.1% |
| 100–200 | 100.0% | 99.3% | 78.7% | 71.5% | 71.9% | 65.7% | 60.1% |
| 200–300 | 74.9% | 74.4% | 74.9% | 64.1% | 62.4% | 56.4% | 53.8% |
| 300–400 | 71.4% | 70.7% | 68.3% | 61.5% | 60.2% | 54.5% | 49.8% |
| 400–500 | 66.3% | 66.8% | 65.9% | 58.3% | 57.6% | 51.3% | 46.0% |
| 500–600 | 64.2% | 64.8% | 63.1% | 55.0% | 56.3% | 46.5% | 45.0% |
| 600–700 | 63.9% | 60.7% | 60.9% | 52.5% | 49.8% | 44.8% | 41.3% |
| 700–800 | 57.0% | 58.4% | 57.7% | 50.0% | 47.5% | 38.1% | 38.0% |
| 800–900 | 55.7% | 57.6% | 54.5% | 50.0% | 46.8% | 41.9% | 37.8% |
| 900–1000 | 58.9% | 56.5% | 58.9% | 49.7% | 47.7% | 41.5% | 38.1% |
| Temporal Distance (Day) | Spatial Distance (m) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| <100 | 100–200 | 200–300 | 300–400 | 400–500 | 500–600 | 600–700 | 700–800 | 800–900 | 900–1000 | |
| −43–49 | 0.78 | 1.21 ** | 0.86 | 0.80 | 1.00 | 0.78 | 0.77 | 0.72 | 0.77 | 0.77 |
| −36–42 | 0.85 | 1.52 ** | 1.49 ** | 1.08 | 1.17 * | 1.01 | 0.98 | 1.03 | 0.89 | 0.79 |
| −29–35 | 1.30 ** | 1.47 ** | 1.24 ** | 0.98 | 1.11 * | 1.15 * | 1.08 | 1.08 | 0.94 | 1.00 |
| −22–28 | 1.60 ** | 0.84 | 1.00 | 1.09 | 1.11 * | 1.20 * | 0.74 | 1.13 | 1.07 | 0.99 |
| −15–21 | 1.46 ** | 1.49 ** | 1.38 ** | 1.08 | 1.07 | 1.12 | 1.04 | 1.03 | 1.09 | 0.97 |
| −8–14 | 0.93 | 1.27 ** | 1.17 | 0.97 | 1.21 * | 0.79 | 1.05 | 0.86 | 0.97 | 0.87 |
| 0–7 | 1.09 | 1.56 ** | 1.35 ** | 1.03 | 1.23 * | 0.97 | 0.74 | 1.04 | 1.16 | 1.00 |
| 0 | 4.84 ** | 2.16 ** | 1.47 ** | 1.02 | 1.53 ** | 1.13 * | 1.22 * | 1.34 * | 1.35 * | 0.94 |
| 0–7 | 2.06 ** | 2.00 ** | 1.51 ** | 1.05 | 1.50 ** | 1.17 * | 1.19 * | 1.26 * | 1.32 * | 0.94 |
| 8–14 | 1.06 | 1.45 ** | 1.37 * | 1.11 * | 1.16 * | 0.95 | 0.76 | 1.07 | 1.16 | 1.04 |
| 15–21 | 0.88 | 1.32 ** | 1.13 * | 0.93 | 1.15 | 0.80 | 1.02 | 0.88 | 0.99 | 0.85 |
| 22–28 | 1.84 ** | 1.49 ** | 1.37 * | 1.13 * | 1.18 * | 1.18 * | 1.01 | 0.99 | 1.09 | 0.98 |
| 29–35 | 1.33 ** | 0.80 | 1.01 | 1.03 | 1.05 | 1.17 | 0.86 | 1.16 | 1.08 | 0.95 |
| 36–42 | 1.20 ** | 1.50 ** | 1.36 * | 1.14 * | 1.13 * | 1.14 * | 1.01 | 1.05 | 0.92 | 1.01 |
| 43–49 | 1.02 | 1.50 * | 1.37 * | 0.93 | 1.20 | 1.03 | 0.97 | 1.04 | 0.87 | 0.78 |
| Temporal Distance (Day) | Spatial Distance (m) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| <100 | 100–200 | 200–300 | 300–400 | 400–500 | 500–600 | 600–700 | 700–800 | 800–900 | 900–1000 | |
| −43–49 | 0.98 | 0.97 | 0.81 | 0.87 | 0.90 | 0.83 | 0.89 | 0.87 | 0.82 | 0.80 |
| −36–42 | 1.13 * | 0.95 | 0.92 | 0.95 | 0.90 | 0.83 | 0.95 | 0.90 | 0.92 | 0.79 |
| −29–35 | 1.09 | 1.02 | 1.11 * | 1.23 * | 1.17 * | 1.08 | 1.12 | 1.11 | 1.06 | 1.08 |
| −22–28 | 1.20 * | 1.02 | 1.00 | 1.15 * | 1.18 * | 1.04 | 1.06 | 1.10 | 1.02 | 0.98 |
| −15–21 | 1.02 | 1.11 * | 0.99 | 1.17 * | 1.14 * | 1.10 * | 1.17 * | 1.00 | 1.04 | 1.04 |
| −8–14 | 1.27 * | 1.00 | 1.13 * | 1.06 | 1.11 | 1.12 | 1.01 | 1.09 | 0.95 | 1.00 |
| −0–7 | 1.75 ** | 1.86 ** | 1.15 * | 1.19 * | 1.15 * | 1.07 | 1.15 * | 1.06 | 1.10 | 1.00 |
| Hot spot | 4.44 ** | 1.91 ** | 1.40 * | 1.32 * | 1.25 * | 1.00 | 1.13 * | 1.06 | 1.12 | 1.13 |
| 0–7 | 2.66 ** | 1.85 ** | 1.36 * | 1.32 * | 1.20 * | 1.01 | 1.15 * | 1.08 | 1.11 | 1.16 |
| 8–14 | 1.77 ** | 1.78 ** | 1.15 * | 1.22 * | 1.15 * | 1.07 | 1.13 * | 1.05 | 1.08 | 1.01 |
| 15–21 | 1.16 * | 1.01 | 1.10 | 1.03 | 1.11 * | 1.13 * | 1.04 | 1.10 | 0.99 | 0.98 |
| 22–28 | 1.05 | 1.10 * | 0.99 | 1.19 * | 1.17 * | 1.09 | 1.16 * | 0.99 | 0.99 | 1.07 |
| 29–35 | 1.19 * | 1.03 | 1.03 | 1.15 * | 1.15 * | 1.05 | 1.07 | 1.12 * | 1.07 | 0.96 |
| 36-42 | 1.04 | 0.88 | 0.95 | 1.09 | 1.01 | 0.93 | 0.98 | 0.95 | 0.90 | 0.94 |
| 43-49 | 1.22 * | 1.06 | 0.98 | 1.00 | 1.00 | 0.93 | 1.02 | 0.96 | 1.01 | 0.87 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Liu, X. Analysis of Burglary Hot Spots and Near-Repeat Victimization in a Large Chinese City. ISPRS Int. J. Geo-Inf. 2017, 6, 148. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi6050148
Wang Z, Liu X. Analysis of Burglary Hot Spots and Near-Repeat Victimization in a Large Chinese City. ISPRS International Journal of Geo-Information. 2017; 6(5):148. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi6050148
Chicago/Turabian StyleWang, Zengli, and Xuejun Liu. 2017. "Analysis of Burglary Hot Spots and Near-Repeat Victimization in a Large Chinese City" ISPRS International Journal of Geo-Information 6, no. 5: 148. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi6050148






