Detecting Intra-Urban Housing Market Spillover through a Spatial Markov Chain Model
Abstract
:1. Introduction
- Interventions of local government on a housing market bubble only generate marginal influence on housing market spillover; they does not change the spillover transition in the long run.
- The driving forces of the housing market spillover are directed to two submarkets located around Tongzhou, a new city which is planned to be a major satellite city of Beijing and will be equipped with many valuable medical, educational, and administrative resources. Therefore, the direction of spillover transition in Beijing is highly consistent with policy preference.
- The driving forces and mechanism behind intra-urban spillover in Beijing are significantly distinct from those behind the widely-documented inter-urban spillover. The ripple form of spillover is no longer dominant. In contrast, the migration effect induced by price-gap and the spatial pattern are two major forces driving the intra-urban spillover in Beijing, although they are considered the least important forces in inter-urban spillover studies.
- This paper proposes a new space-time method to study housing price spillover by integrating Markov chain model and constrained clustering.
- The differences we reveal herein between the intra- and inter-urban housing market spillovers could promote future investigations, both theoretical and empirical.
- Various types of policy shocks can differ significantly in terms of affecting the long-run spillover mechanism, which provides insight for the field of housing market regulation.
2. Data and Methods
2.1. Data Description
2.2. Markov Chain Model
2.3. Constrained K-Means Clustering
2.4. Kernel Density Estimation and Hotspot Analysis
2.5. Hausdorff Distance
2.6. Evolution of Spillover Intensity
3. Results
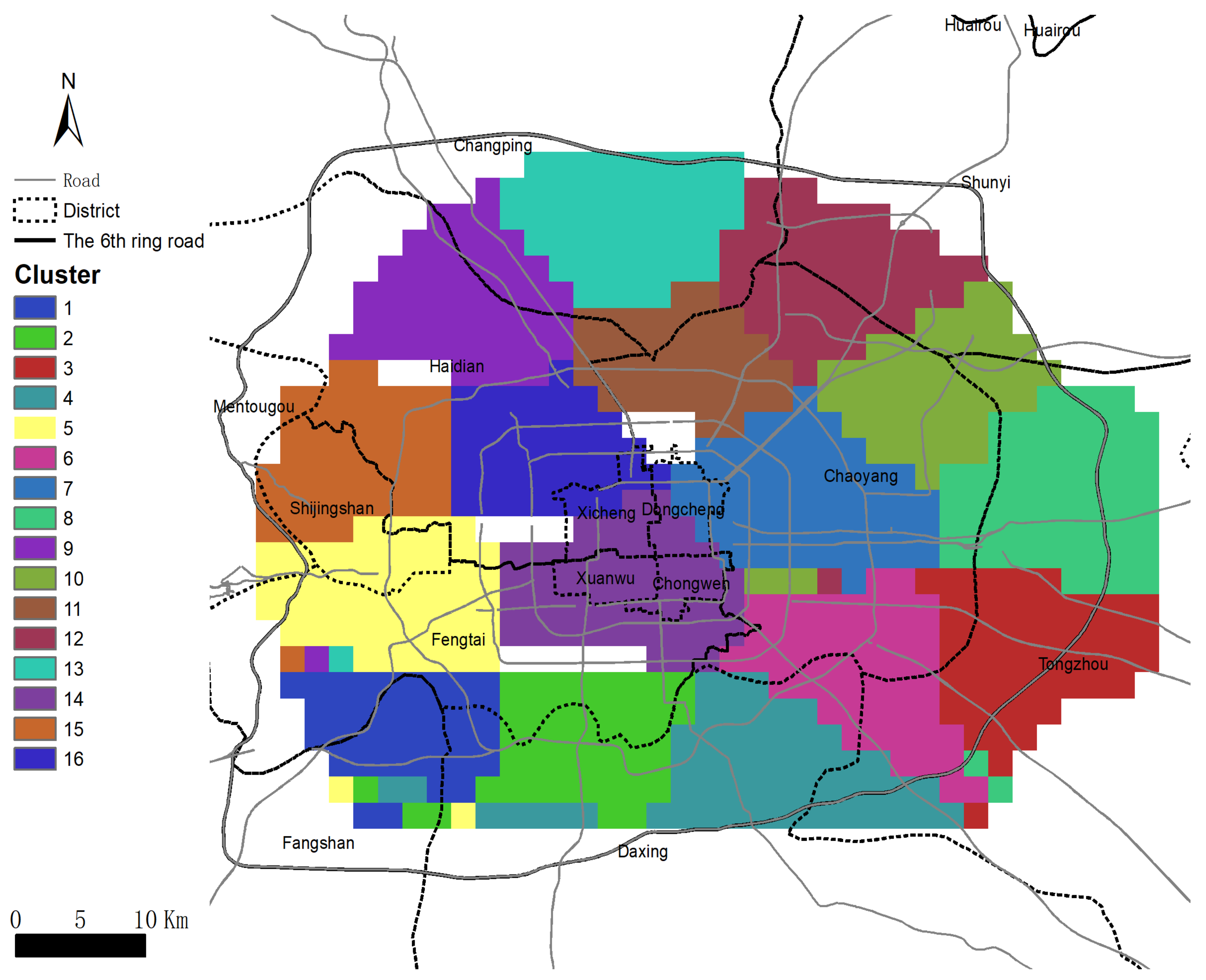
3.1. Study Area
3.2. Boundaries of Housing Market and Submarkets in Beijing
3.3. Robustness Analysis by Policy Shock
3.4. Factors Affecting Spillover
3.5. Transition Intensity of Multi-Period Spillovers
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Data Summary
| Beijing | |||||
|---|---|---|---|---|---|
| Variable | Meaning | Min | Max | Mean | Std. |
| Construction | |||||
| area (m2) | Construction area (m2) | 10.5 | 140 | 87.38 | 10.1 |
| age | The age (years) of the apartment unit (2017 minus the year built) | 0 | 59 | 12.23 | 6.98 |
| South | Whether the orientation direction includes south (south, southeast, southwest, etc., 1 = yes, 0 = no) | 0 | 1 | 0.8 | 0.4 |
| lobby num | The number of lobby rooms | 0 | 8 | 1.7 | 0.79 |
| room num | The number of bedrooms | 1 | 9 | 2.79 | 1.19 |
| floor | The floor level that an apartment is on | 1 | 57 | 4 | 3.9 |
| Public Transport | |||||
| dist subway | Distance (km) to the nearest metro station | 0.1 | 31.5 | 1.14 | 2.94 |
| dist bus | Distance (km) to the nearest bus station | 0.1 | 18.17 | 0.41 | 3.06 |
| num bus routes | Number of bus routes offered by the nearest bus station within 1 km | 0 | 312 | 84.42 | 58.84 |
| Neighborhood | |||||
| dist school | Distance (km) to nearest primary and middle school | 0.1 | 18.54 | 0.69 | 2.83 |
| dist mall | Distance (km) to nearest mall | 0.11 | 31.5 | 1.15 | 3.13 |
| dist hospital | Distance (km) to the nearest hospital | 0.16 | 29.67 | 2.44 | 0.29 |
References
- Ashworth, J.; Parker, S.C. Modelling regional house prices in the UK. Scott. J. Political Econ. 1997, 44, 225–246. [Google Scholar] [CrossRef]
- Peterson, W.; Holly, S.; Gaudoin, P.; Britain, G. Further Work on an Economic Model of the Demand and Need for Social Housing; Stationery Office: London, UK, 2002. [Google Scholar]
- Cook, S. The convergence of regional house prices in the UK. Urban Stud. 2003, 40, 2285–2294. [Google Scholar] [CrossRef]
- Du, Q.; Wu, C.; Ye, X.; Ren, F.; Lin, Y. Evaluating the Effects of Landscape on Housing Prices in Urban China. Tijdschriftvoor Economische En Sociale Geografie 2018, 109, 525–541. [Google Scholar] [CrossRef]
- Holmes, M.J.; Grimes, A. Is there long-run convergence among regional house prices in the uk? Urban Stud. 2008, 45, 1531–1544. [Google Scholar] [CrossRef] [Green Version]
- Barros, C.; Gil-Alana, L.; Payne, J. Tests of convergence and long memory behavior in us housing prices by state. J. Hous. Res. 2013, 23, 73–87. [Google Scholar]
- Chow, W.W.; Fung, M.K.; Cheng, A. Convergence and spillover of house prices in chinese cities. Appl. Econ. 2016, 48, 4922–4941. [Google Scholar] [CrossRef]
- DeFusco, A.; Ding, W.; Ferreira, F.; Gyourko, J. The role of price spillovers in the American housing boom. J. Urban Econ. 2018, 108, 72–84. [Google Scholar] [CrossRef]
- Cohen, J.P.; Zabel, J. Local house price diffusion. Real Estate Econ. 2018. early view. [Google Scholar] [CrossRef]
- Alper, O.; Ertugrul, H.; Coskun, Y. A dynamic model for housing price spillovers with an evidence from the US and the UK markets. J. Cap. Mark. Stud. 2018, 2, 70–81. [Google Scholar]
- Pijnenburg, K. The spatial dimension of US house prices. Urban Stud. 2017, 54, 466–481. [Google Scholar] [CrossRef]
- Won, J.; Lee, J.S. Investigating How the Rents of Small Urban Houses are Determined: Using Spatial Hedonic Modeling for Urban Residential Housing in Seoul. Sustainability 2018, 10, 31. [Google Scholar] [CrossRef] [Green Version]
- Rangan, G.; Sun, X. Housing market spillovers in South Africa: Evidence from an estimated small open economy DSGE model. Empir. Econ. 2018, 58, 1–24. [Google Scholar]
- Cakan, E.; Demirer, R.; Gupta, R.; Uwilingiye, J. Economic Policy Uncertainty and Herding Behavior: Evidence from the South African Housing Market. Adv. Decis. Sci. 2019, 23, 1–25. [Google Scholar]
- Li, S.; Ye, X.; Lee, J.; Gong, J.; Qin, C. Spatiotemporal Analysis of Housing Prices in China: A Big Data Perspective. Appl. Spat. Anal. Policy 2017, 10, 421–433. [Google Scholar] [CrossRef]
- Meen, G. Regional house prices and the ripple effect: A new interpretation. Hous. Stud. 1999, 14, 733–753. [Google Scholar] [CrossRef]
- Murphy, A.; Muellbauer, J. Explaining Regional House Prices in the UK; Department of Economics, University College Dublin: Dublin, Ireland, 1994. [Google Scholar]
- Tajani, F.; Morano, P.; Saez-Perez, M.P.; Di-Liddo, F.; Locurcio, M. Multivariate Dynamic Analysis and Forecasting Models of Future Property Bubbles: Empirical Applications to the Housing Markets of Spanish Metropolitan Cities. Sustainability 2019, 11, 3575. [Google Scholar] [CrossRef] [Green Version]
- Stein, J.C. Prices and trading volume in the housing market: A model with down-payment effects. Q. J. Econ. 1995, 110, 379–406. [Google Scholar] [CrossRef]
- Gordon, I. Housing and labour market constraints on migration across the north-south divide. Hous. Natl. Econ. 1990, 75–89. [Google Scholar]
- Holmans, A.E. House Prices: Changes through Time at National and Sub-National Level; Department of the Environment London: London, UK, 1990. [Google Scholar]
- Wu, C.; Ye, X.; Ren, F.; Wan, Y.; Ning, P.; Du, Q. Spatial and Social Media Data Analytics of Housing Prices in Shenzhen, China. PLoS ONE 2016, 11, e0164553. [Google Scholar] [CrossRef]
- Holmans, A. What has happened to the north-south divide in house prices and the housing market. Hous. Financ. Rev. 1995, 96, 25–31. [Google Scholar]
- Wu, C.; Ye, X.; Du, Q.; Luo, P. Spatial Effects of Accessibility to Parks on Housing Prices in Shenzhen, China. Habitat Int. 2017, 63, 45–54. [Google Scholar] [CrossRef]
- Hui, E.; Wang, Z. Market sentiment in private housing market. Habitat Int. 2014, 44, 375–385. [Google Scholar] [CrossRef]
- Munro, M.; Maclennan, D. Intra-urban changes in housing prices: Glasgow 1972–1983. Hous. Stud. 1987, 2, 65–81. [Google Scholar] [CrossRef]
- Fadiga, M.L.; Wang, Y. A multivariate unobserved component analysis of us housing market. J. Econ. Financ. 2009, 33, 13–26. [Google Scholar] [CrossRef]
- Zhang, M.; Meng, X.; Wang, L.; Xu, T. Transit development shaping urbanization: Evidence from the housing market in beijing. Habitat Int. 2014, 44, 545–554. [Google Scholar] [CrossRef]
- Zhang, S.; Guldmann, J.M. Accessibility, diversity, environmental quality and the dynamics of intra-urban population and employment location. Growth Chang. 2010, 41, 85–114. [Google Scholar] [CrossRef]
- Kirby, D.K.; LeSage, J.P. Changes in commuting to work times over the 1990 to 2000 period. Reg. Sci. Urban Econ. 2009, 39, 460–471. [Google Scholar] [CrossRef]
- Jones, C.; Leishman, C.; Watkins, C. Intra-urban migration and housing submarkets: Theory and evidence. Hous. Stud. 2004, 19, 269–283. [Google Scholar] [CrossRef]
- Schelling, T.C. Dynamic models of segregation. J. Math. Sociol. 1971, 1, 143–186. [Google Scholar] [CrossRef]
- Cui, C.; Geertman, S.; Hooimeijer, P. The intra-urban distribution of skilled migrants: Case studies of shanghai and nanjing. Habitat Int. 2014, 44, 1–10. [Google Scholar] [CrossRef]
- Zheng, S.; Peiser, R.B.; Zhang, W. The rise of external economies in beijing: Evidence from intra-urban wage variation. Reg. Sci. Urban Econ. 2009, 39, 449–459. [Google Scholar] [CrossRef]
- Partridge, M.D.; Rickman, D.S.; Ali, K.; Olfert, M.R. Agglomeration spillovers and wage and housing cost gradients across the urban hierarchy. J. Int. Econ. 2009, 78, 126–140. [Google Scholar] [CrossRef] [Green Version]
- Njoh, A.J. Interorganisational relations and effectiveness in a developing housing policy field. Habitat Int. 1996, 20, 253–264. [Google Scholar] [CrossRef]
- Li, Z.; Li, X.; Wang, L. Speculative urbanism and the making of university towns in china: A case of guangzhou university town. Habitat Int. 2014, 44, 422–431. [Google Scholar] [CrossRef]
- Krupka, D.J.; Noonan, D.S. Empowerment zones, neighborhood change and owner-occupied housing. Reg. Sci. Urban Econ. 2009, 39, 386–396. [Google Scholar] [CrossRef] [Green Version]
- Clayton, J.; Ling, D.; Naranjo, A. Commercial real estate valuation: Fundamentals versus investor sentiment. J. Real Estate Financ. Econ. 2009, 38, 5–37. [Google Scholar] [CrossRef]
- Zhou, J.; Anderson, R.I. An empirical investigation of herding behavior in the us reit market. J. Real Estate Financ. Econ. 2013, 47, 83–108. [Google Scholar] [CrossRef]
- Valentini, P.; Ippoliti, L.; Fontanella, L. Modeling us housing prices by spatial dynamic structural equation models. Ann. Appl. Stat. 2013, 7, 763–798. [Google Scholar] [CrossRef]
- Tsai, I.C. Spillover effect between the regional and the national housing markets in the UK. Reg. Stud. 2015, 49, 1957–1976. [Google Scholar] [CrossRef]
- Harding, J.P.; Rosenblatt, E.; Yao, V. The contagion effect of foreclosed properties. J. Urban Econ. 2009, 66, 164–178. [Google Scholar] [CrossRef]
- Daneshvary, N.; Clauretie, T.; Kader, A. Short-term own-price and spillover effects of distressed residential properties: The case of a housing crash. J. Real Estate Res. 2011, 33, 179–207. [Google Scholar]
- Leonard, T.; Murdoch, J. The neighborhood effects of foreclosure. J. Geogr. Syst. 2009, 11, 317. [Google Scholar] [CrossRef] [Green Version]
- Rogers, W. Declining foreclosure neighborhood effects over time. Hous. Policy Debate 2010, 20, 687–706. [Google Scholar] [CrossRef]
- Ihlanfeldt, K.; Mayock, T. The impact of REO sales on neighborhoods and their residents. J. Real Estate Financ. Econ. 2016, 53, 282–324. [Google Scholar] [CrossRef]
- Del Giudice, V.; De Paola, P.; Forte, F.; Manganelli, B. Real Estate Appraisals with Bayesian Approach and Markov Chain Hybrid Monte Carlo Method: An Application to a Central Urban Area of Naples. Sustainability 2017, 9, 2138. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Sharma, R. Housing submarket classification: The role of spatial contiguity. Appl. Geogr. 2012, 32, 746–756. [Google Scholar] [CrossRef]
- Wagstaff, K.; Cardie, C.; Rogers, S.; Schrödl, S. Constrained k-means clustering with background knowledge. Icml 2001, 1, 577–584. [Google Scholar]
- Basu, S.; Banerjee, A.; Mooney, R.J. Active semi-supervision for pairwise constrained clustering. In Proceedings of the 2004 SIAM International Conference on Data Mining, Lake Buena Vista, FL, USA, 22–24 April 2004; pp. 333–344. [Google Scholar]
- Diaz-Valenzuela, I.; Loia, V.; Martin-Bautista, M.J.; Senatore, S.; Vila, M.A. Automatic constraints generation for semisupervised clustering: Experiences with documents classification. Soft Comput. 2016, 20, 2329–2339. [Google Scholar] [CrossRef]
- Bonhomme, S.; Manresa, E. Grouped patterns of heterogeneity in panel data. Econometrica 2015, 83, 1147–1184. [Google Scholar] [CrossRef] [Green Version]
- Kang, W.; Rey, S.J. Conditional and joint tests for spatial effects in discrete markov chain models of regional income distribution dynamics. Ann. Reg. Sci. 2018, 61, 73–93. [Google Scholar] [CrossRef]
- Wu, C.; Ye, X.; Ren, F.; Du, Q. A Modified Data-Driven Framework for Housing Market Segmentation. J. Urban Plan. Dev. 2018, 144, 04018036. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. The analysis of spatial association by use of distance statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Ord, J.K.; Getis, A. Local spatial autocorrelation statistics: Distributional issues and an application. Geogr. Anal. 1995, 27, 286–306. [Google Scholar] [CrossRef]
- Girres, J.F.; Touya, G. Quality assessment of the french openstreetmap dataset. Trans. GIS 2010, 14, 435–459. [Google Scholar] [CrossRef]
- Deng, M.; Li, Z.; Chen, X. Extended hausdorff distance for spatial objects in gis. Int. J. Geogr. Inf. Sci. 2007, 21, 459–475. [Google Scholar]
- National Bureau of Statistics. China City Statistical Yearbook; Statistics Press: Beijing, China, 2016.
- Zhu, R.; Wu, X. Risks and Potentials in Beijing’s Real Estate Market. Biomed. J. Sci. Tech. Res. 2018, 9, 7406–7413. [Google Scholar]
- Wang, F.; Gao, X. The Transitional Spatial Pattern of Housing Prices in Beijing: Factors and Implication. Int. Rev. Spat. Plan. Sustain. Dev. 2014, 2, 46–62. [Google Scholar] [CrossRef] [Green Version]
- Lin, G.; Zhang, A. China’s metropolises in transformation: Neoliberalizing politics, land commodification, and uneven development in beijing. Urban Geogr. 2017, 38, 643–665. [Google Scholar] [CrossRef]
- Tajani, F.; Morano, P.; Torre, C.; Di Liddo, F. An Analysis of the Influence of Property Tax on Housing Prices in the Apulia Region (Italy). Buildings 2017, 7, 67. [Google Scholar] [CrossRef] [Green Version]
- Meen, G. Spatial aggregation, spatial dependence and predictability in the uk housing market. Hous. Stud. 1996, 11, 345–372. [Google Scholar] [CrossRef]
Sample Availability: Samples of this research are available from the authors. |



| City | Center Location (Lat, Lon) | GDP (billion RMB) | Population Size (million) | Built Area (km2) | # County-Level Administrative Units | # Subway Lines |
|---|---|---|---|---|---|---|
| Beijing | 39.9° N, 116.41° E | 2800 | 21.7 | 1419 | 16 | 18 up to Nov. 2017 |
| Before 2013 Q3 | After 2013 Q3 | |||||
|---|---|---|---|---|---|---|
| Cluster | Nearest-Distance | p-Value | 0.05 CI | Nearest-Distance | p-Value | 0.05 CI |
| 1 | 0.061 | 1 | 0.82 | 0.094 | 0.986 | 0.76 |
| 2 | 0.098 | 0.999 | 0.5 | 0.063 | 1 | 0.92 |
| 3 | 0.16 | 0.345 | 0.32 | 0.098 | 0.999 | 0.69 |
| 4 | 0.152 | 0.51 | 0.36 | 0.184 | 0.999 | 0.73 |
| 5 | 0.08 | 0.96 | 0.6 | 0.044 | 1 | 0.88 |
| 6 | 0.107 | 1 | 0.71 | 0.092 | 0.999 | 0.73 |
| 7 | 0.121 | 0.788 | 0.72 | 0.138 | 0.671 | 0.39 |
| 8 | 0.108 | 0.203 | 0.14 | 0.079 | 0.999 | 0.68 |
| 9 | 0.126 | 0.239 | 0.24 | 0.099 | 0.994 | 0.5 |
| 10 | 0.123 | 0.076 | 0.16 | 0.131 | 0.998 | 0.7 |
| 11 | 0.112 | 0.675 | 0.7 | 0.113 | 0.831 | 0.49 |
| 12 | 0.236 | 0.002 | 0.06 | 0.188 | 0.309 | 0.39 |
| 13 | 0.173 | 0.498 | 0.69 | 0.175 | 0.004 | 0.06 |
| 14 | 0.12 | 0.833 | 0.39 | 0.121 | 0.939 | 0.49 |
| 15 | 0.061 | 1 | 0.85 | 0.099 | 0.999 | 0.74 |
| 16 | 0.098 | 0.813 | 0.54 | 0.124 | 0.505 | 0.53 |
| Period | Test-Statistics | p-Value | 0.05_CI |
|---|---|---|---|
| Before 2013 Q3 | 501.523 | 0 | 294.321 |
| After 2013 Q3 | 208.79 | 0.986 |
| # | Var | Test-Statistics | p-Value |
|---|---|---|---|
| 1 | 13.002 | 0.0003 | |
| 2 | 12.307 | 0.0005 | |
| 3 | 11.871 | 0.0006 | |
| 4 | 11.682 | 0.0006 | |
| 5 | 11.589 | 0.0007 | |
| 6 | 11.42 | 0.0007 | |
| 7 | 10.849 | 0.001 | |
| 8 | 10.814 | 0.001 | |
| 9 | 10.575 | 0.001 | |
| 10 | 10.531 | 0.001 | |
| 11 | 10.384 | 0.001 | |
| 12 | 10.302 | 0.001 | |
| 13 | 9.991 | 0.002 | |
| 14 | 9.771 | 0.002 | |
| 15 | 7.722 | 0.005 | |
| 16 | 7.365 | 0.007 | |
| 17 | 6.777 | 0.009 | |
| 18 | 6.766 | 0.009 | |
| 19 | 6.746 | 0.009 | |
| 20 | 5.952 | 0.015 | |
| 21 | 5.083 | 0.024 | |
| 22 | 5.051 | 0.025 | |
| 23 | 4.708 | 0.03 | |
| 24 | 4.649 | 0.031 | |
| 25 | 4.476 | 0.034 | |
| 26 | 4.385 | 0.036 | |
| 27 | 4.341 | 0.037 | |
| 28 | 4.18 | 0.041 | |
| 29 | 4.018 | 0.045 | |
| 30 | 3.887 | 0.049 |
| Model Selected (20) | T | Model Selected (21) | |
|---|---|---|---|
| distance | 0.0135 ** | distance | ∼0 |
| price_dif | 0.0283 *** | price_dif | 0.0566 *** |
| area_dif | −0.0006 | area_dif | −0.0011 |
| out_lon | 0.0083 | diff_lon | −0.0291 *** |
| in_lon | 0.0029 | - | - |
| out_lat | −0.0187 *** | diff_lat | 0.0054 |
| in_lat | −0.0128 *** | - | - |
| Adj. R2 | 0.984 | Adj. R2 | 0.849 |
| F-statistic | 2275 *** | F-statistic | 287.8 *** |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Zhang, X.; Zheng, Y.; Ye, X.; Li, S.; Dai, Q. Detecting Intra-Urban Housing Market Spillover through a Spatial Markov Chain Model. ISPRS Int. J. Geo-Inf. 2020, 9, 56. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9010056
Zhang D, Zhang X, Zheng Y, Ye X, Li S, Dai Q. Detecting Intra-Urban Housing Market Spillover through a Spatial Markov Chain Model. ISPRS International Journal of Geo-Information. 2020; 9(1):56. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9010056
Chicago/Turabian StyleZhang, Daijun, Xiaoqi Zhang, Yanqiao Zheng, Xinyue Ye, Shengwen Li, and Qiwen Dai. 2020. "Detecting Intra-Urban Housing Market Spillover through a Spatial Markov Chain Model" ISPRS International Journal of Geo-Information 9, no. 1: 56. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9010056






