1. Introduction
Unsupervised representation learning has become an important domain with the advent of deep generative models which include the variational autoencoder (VAE) [
1] , generative adversarial networks (GANs) [
2], Long Short Term memory networks (LSTMs) [
3] , and others. Anomaly detection is a well-known sub-domain of unsupervised learning in the machine learning and data mining community. Anomaly detection for images and videos are challenging due to their high dimensional structure of the images, combined with the non-local temporal variations across frames.
We focus on reviewing firstly, deep convolution architectures for feature or representation learnt “end-to-end” and secondly, predictive and generative models specifically for the task of video anomaly detection (VAD). Anomaly detection is an unsupervised learning task where the goal is to identify abnormal patterns or motions in data that are by definition infrequent or rare events. Furthermore, anomalies are rarely annotated and labeled data rarely available to train a deep convolutional network to separate normal class from the anomalous class. This is a fairly complex task since the class of normal points includes frequently occurring objects and regular foreground movements while the anomalous class include various types of rare events and unseen objects that could be summarized as a consistent class. Long streams of videos containing no anomalies are made available using which one is required to build a representation for a moving window over the video stream that estimates the normal behavior class while detecting anomalous movements and appearance, such as unusual objects in the scene.
Given a set of training samples containing no anomalies, the goal of anomaly detection is to design or learn a feature representation, that captures “normal” motion and spatial appearance patterns. Any deviations from this normal can be identified by measuring the approximation error either geometrically in a vector space or the posterior probability of a given model which fits training sample representation vectors or by modeling the conditional probability of future samples given their past values and measuring the prediction error of test samples by training a predictive model, thus accounting for temporal structure in videos.
1.1. Anomaly Detection
Anomaly detection is an unsupervised pattern recognition task that can be defined under different statistical models. In this study we will explore models that perform linear approximations by PCA, non-linear approximation by various types of autoencoders and finally deep generative models.
Intuitively, a complex system under the action of various transformations is observed, the normal behavior is described through a few samples and a statistical model is built using the said normal behavior samples that is capable of generalizing well on unseen samples. The normal class distribution
is estimated using the training samples
, by building a representation
which minimizes model prediction loss
error over all the training samples, over all
i, is evaluated. Now the deviation of the test samples
under this representation
is evaluated as the anomaly score,
is used as a measure of deviation. For said models, the anomalous points are samples that are poorly approximated by the estimated model
. Detection is achieved by evaluating a threshold on the anomaly score
. The threshold is a parameter of the detection algorithm and the variation of the threshold w.r.t detection performance is discussed under the Area under ROC section. For probabilistic models, anomalous points can be defined as samples that lie in low density or concentration regions of the domain of an input training distribution
.
Representation learning automates feature extraction for video data for tasks such as action recognition, action similarity, scene classification, object recognition, semantic video segmentation [
4], human pose estimation, human behavior recognition and various other tasks. Unsupervised learning tasks in video include anomaly detection [
5,
6], unsupervised representation learning [
7], generative models for video [
8], and video prediction [
9].
1.2. Datasets
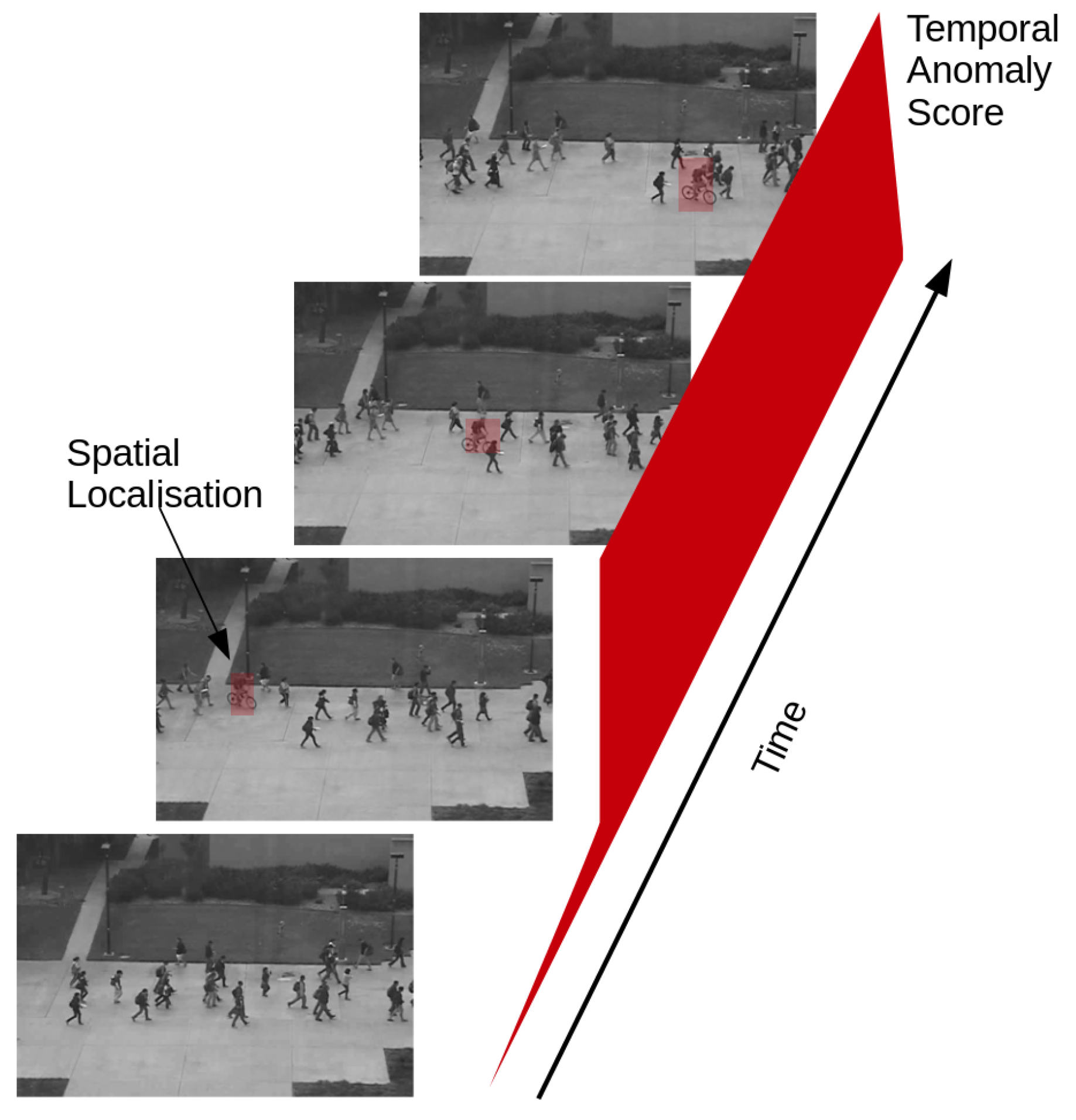
We now define the video anomaly detection problem setup. The videos considered come from a surveillance camera where the background remains static, while the foreground constitutes of moving objects such as pedestrians, traffic and so on. The anomalous events are the change in appearance and motion patterns that deviate from the normal patterns observed in the training set. We see a few examples demonstrated in
Figure 1.
Here we list the frequently evaluated datasets, though this is not exhaustive. The UCSD dataset [
5] consists of pedestrian videos where anomalous time instances correspond to the appearance of objects like a cyclist, a wheelchair, and a car in the scene that is usually populated with pedestrians walking along the roads. People walking in unusual locations are also considered anomalous. In CUHK Avenue Dataset [
10] anomalies correspond to strange actions such as a person throwing papers or bag, moving in unusual directions, and appearance of unusual objects like bags and bicycle. In the Subway entry and exit datasets people moving in the wrong direction, loitering and so on are considered as anomalies. UMN dataset [
11] consists of videos showing unusual crowd activity, and is a particular case of the video anomaly detection problem. The Train dataset [
12] contains moving people in a train. The anomalous events are mainly due to unusual movements of people in the train. And finally the Queen Mary University of London U-turn dataset [
13] contains normal traffic with anomalous events such as jaywalking and movement of a fire engine. More recently, a controlled environment based LV dataset has been introduced by [
14], with challenging examples for the task of online video anomaly detection.
2. Representation Learning for Video Anomaly Detection (VAD)
Videos are high dimensional signals with both spatial-structure, as well as local temporal variations. An important problem of anomaly detection in videos is to learn a representation of input sample space
, to
d-dimensional vectors. The idea of feature learning is to automate the process of finding a good representation of the input space, that takes into account important prior information about the problem [
15]. This follows from the No-Free-Lunch-Theorem which states that no universal learner exists for every training distribution
. Following work already established for video anomaly detection, the task concretely consists in detecting deviations from models of static background, normal crowd appearance and motion from optical flow, change in trajectory and other priors. Representation learning consists of building a parameterized model
, and in this study we focus on representations that reconstruct the input, while the latent space
is constrained to be invariant to changes in the input, such as change in luminance, translations of objects in the scene that don’t deviate normal movement patterns, and others. This provides a way to introduce prior information to reconstruct normal samples.
2.1. Taxonomy
The goal of this survey is to provide a compact review of the state of the art in video anomaly detection based on unsupervised and semi-supervised deep learning architectures. The survey characterizes the underlying video representation or model as one of the following:
Representation learning for reconstruction: Methods such as Principal component analysis (PCA), Autoencoders (AEs) are used to represent the different linear and non-linear transformations to the appearance (image) or motion (flow), that model the normal behavior in surveillance videos. Anomalies represent any deviations that are poorly reconstructed.
Predictive modeling: Video frames are viewed as temporal patterns or time series, and the goal is to model the conditional distribution . In contrast to reconstruction, where the goal is to learn a generative model that can successfully reconstruct frames of a video, the goal here is to predict the current frame or its encoded representation using the past frames. Examples include autoregressive models and convolutional Long-Short-Term-Memory models.
Generative models: Variational Autoencoders (VAE), Generative Adversarial Networks (GAN) and Adversarially trained AutoEncoders (AAE), are used for the purpose of modeling the likelihood of normal video samples in an end-to-end deep learning framework.
An important common aspect in all these models is the problem of representation learning, which refers to the feature extraction or transformation of input training data for the task of anomaly detection. We shall also remark the other secondary feature transformations performed in each of these different models and their purposes.
2.2. Context of the Review
A short review on the subject of video anomaly detection is provided here [
16]. To the best of our knowledge, there has not been a systematic study of deep architectures for video anomaly detection, which is characterized by abnormal appearance and motion features, that occur rarely. We cite below the other domains which do not fall under this study.
A detailed review of abnormal human behavior and crowd motion analysis is provided in [
17] and [
18]. This includes deep architectures such as Social-LSTM [
19] based on the social force model [
20] where the goal is to predict pedestrian motion taking into account the movement of neighboring pedestrians.
Action recognition is an important domain in computer vision which requires supervised learning of efficient representations of appearance and motion for the purpose of classification [
21]. Convolutional networks were employed to classify various actions in video quite early [
22]. Recent work involves fusing feature maps evaluated on different frames (over time) of video [
23] yielding state of the art results. Finally, convolutional networks using 3-D filters (C3D) have become a recent base-line for action recognition [
24].
Unsupervised representation learning is a well-established domain and the readers are directed towards a complete review of the topic in [
25], as well as the deep learning book [
26].
In this review, we shall mainly focus on the taxonomy provided and restrict our review to deep convolutional networks and deep generative models that enable end-to-end spatio-temporal representation learning for the task of anomaly detection in videos. We also aim to provide an understanding of what aspects of detection do these different models target. Apart from the taxonomy being addressed in this study, there have been many other approaches. One could cite work on anomaly detection based on K-Nearest Neighbors [
27], unsupervised clustering [
28], and object speed and size [
29].
We briefly review the set of hand-engineered features used for the task of video anomaly detection, though our focus still remains deep learning based architectures. Mixture of dynamic textures (MDT) is a generative mixture model defined for each spatio-temporal windows or cubes of the raw training video [
5,
6]. It models appearance and motion features and thus detects both spatial and temporal anomalies. Histogram of oriented optical flow and oriented gradients [
30] is a baseline used in anomaly detection and crowd analysis, [
31,
32,
33]. Tracklets are representation of movements in videos and have been applied to abnormal crowd motion analysis [
34,
35]. More recently, there has been work on developing optical flow acceleration features for motion description [
36].
Problem setup: Given a training sequence of images from a video,
, which contains only “normal motion patterns” and no anomalies, and given a test sequence
, which is susceptible to contain anomalies, the task consists in associating each frame with an anomaly score for the temporal variation, as well as a spatial score to localize the anomaly in space. This is demonstrated in
Figure 2.
The anomaly detection task is usually considered unsupervised when there is no direct information or labels available about the positive rare class. However the samples in the study with no anomalies are available, and thus is a semi-supervised learning problem.
For we have samples only with . The goal thus of anomaly detection is two-fold: first, find the representation of the input feature , for example, using convolutional neural networks (CNNs), and then the decision rule that detects anomalies, whose detection rate can be parameterized as per the application.
3. Reconstruction Models
We begin with an input training video , with N frames and pixels per frame, which represents the dimensionality of each vector. In this section, we shall focus on reducing the expected reconstruction error by different methods. We shall describe the Principal Component Analysis (PCA), Convolutional AutoEncoder (ConvAE), and Contractive AutoEncoders (CtractAE), and their setup for dimensionality reduction and reconstruction.
3.1. Principal Component Analysis
PCA finds the directions of maximal variance in the training data. In the case of videos, we are aiming to model the spatial correlation between pixel values which are components of the vector representing a frame at a particular time instant.
With input training matrix
X, which has zero mean, we are looking for a set of orthogonal projections that whiten/de-correlate the features in the training set:
where,
, with the constraint
representing an orthonormal reconstruction of the input
X. The projection
is a vector in a lower dimensional subspace, with fewer components than the vectors from
X. This reduction in dimensionality is used to capture the anomalous behavior, as samples that are not well reconstructed. The anomaly score is given by the Mahalanobis distance between the input and the reconstruction, or the variance scaled reconstruction error:
We associate each frame with continual optical flow magnitude, and learn atomic motion patterns with standard PCA on the training set, and evaluate reconstruction error on the test optical flow magnitude. This serves a baseline for our study. A refined version was implemented and evaluated in [
37] which evaluated the atomic movement patterns using a probabilistic PCA [
38], over rectangular regions over the image domain.
Optical flow estimation is a costly step of this algorithm, and there has been large progress in the improving its evaluating speed. Authors [
39], propose to trade of accuracy of for fast approximation of optical flow using PCA to interpolate flow fields.
3.2. Autoencoders
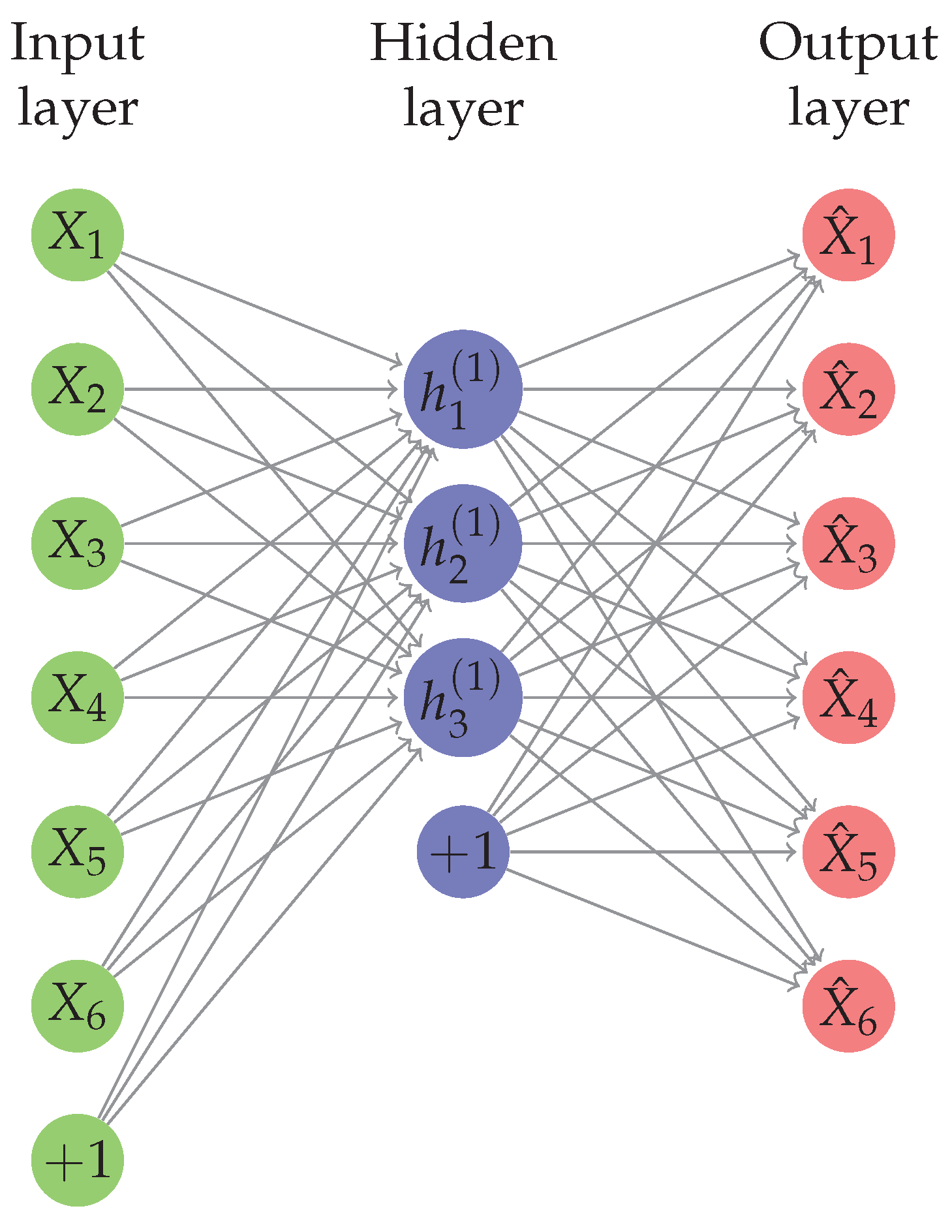
An Autoencoder is a neural network trained by back-propagation and provides an alternative to PCA to perform dimensionality reduction by reducing the reconstruction error on the training set, shown in
Figure 3. It takes an input
and maps it to the latent space representation
, by a deterministic application,
.
Unlike the PCA the autoencoder (AE) performs a non-linear point-wise transform of the input
, which is required to be a differentiable function. It is usually a rectified linear unit (ReLU) (
) or Sigmoid (
). Thus we can write a similar reconstruction of the input matrix given by:
The low-dimensional representation is given by , where represents the optimal linear encoding that minimizes the reconstruction loss above. There are multiple ways of regularizing the parameters . One of the constraints is the average value of the activations in the hidden layer, this enforces sparsity.
3.3. Convolutional AutoEncoders (CAEs)
Autoencoders in their original form do view the input as a signal decomposed as the sum of other signals. Convolutional AutoEncoders (CAEs) [
40], makes this decomposition explicit by weighting the result of the convolution operator. For a single channel input
(for example a gray-scale image), the latent representation of the
kth filter would be:
The reconstruction is obtained by mapping back to the original image domain with the latent maps
H and the decoding convolutional filter
:
where
is a point-wise non-linearity like the sigmoid or hyperbolic tangent function. A single bias value is broadcast to each component of a latent map. These
k-output maps can be used as an input to the next layer of the CAE. Several CAEs can be stacked into a deep hierarchy, which we again refer as a CAE to simplify the naming convention. We represent the stack of such operations as a single function
where the convolutional weights and biases are together represented by the weights
W.
In retrospect, the PCA, and traditional AE, ignore the spatial structure and location of pixels in the image. This is also termed as being permutation invariant. It is important to note that when working with image frames of few pixels, these methods introduce large redundancy in network parameters W, and furthermore span the entire visual receptive field. CAEs have fewer parameters on account of their weights being shared across many input locations/pixels.
3.4. CAEs for Video Anomaly Detection
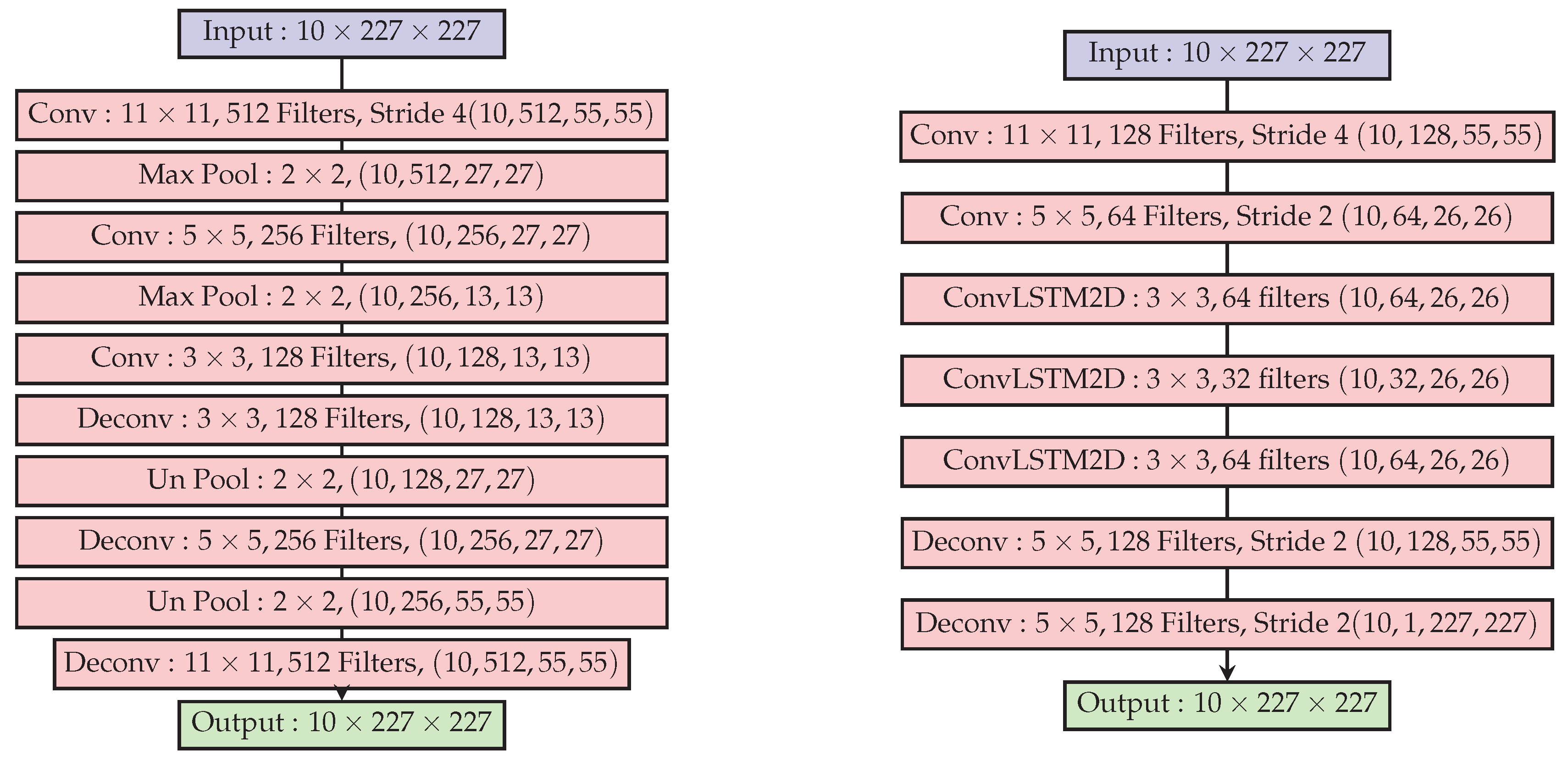
In the recent work by [
41], a deep convolutional autoencoder was trained to reconstruct an input sequence of frames from a training video set. We call this a Spatio-Temporal Stacked frame AutoEncoder (STSAE), to avoid confusion with similar names in the rest of the article. The STSAE in [
41] stacks
p frames
with each time slice treated as a different channel in the input tensor to a convolutional autoencoder. The model is regularized by augmenting the loss function with L2-norm of the model weights:
where the tensor
is a cuboid with spatial dimensions
are the spatial dimensions and
p is the number of frames temporally back into the past, with hyper-parameter
which balances the reconstruction error and norm of the parameters, and
N is the mini-batch size. The architecture of the convolutional autoencoder is reproduced in
Figure 4.
The image or tensor
reconstructed by the autoencoder enforces temporal regularity since the convolutional (weights) representation along with the bottleneck architecture of the autoencoder compresses information. The spatio-temporal autoencoder in [
42] is shown in the right panel of
Figure 4. The reconstruction error map at frame
t is given by
, while the temporal regularity score is given by the inverted, normalized reconstruction error:
where the ∑, min and max operators are across the spatial indices’s
. In other models, the normalized reconstruction error is directly used as the anomaly score. One could envisage the use of Mahalanobis distance here since the task is to evaluate the distance between test points from the points from the normal ones. This is evaluated as the error between the original tensor and the reconstruction from the autoencoder.
Robust versions of Convolutional AutoEncoders (RCAE) are studied in [
43], where the goal is to evaluate anomalies in images by imposing L2-constraints on parameters
W as well as adding a bias term. A video-patch (spatio-temporal) based autoencoder was employed by [
44] to reconstruct patches, with a sparse autoencoder whose average activations were set to parameter
, enforcing sparseness, following the work in [
45].
3.5. Contractive Autoencoders
Contractive autoencoders explicitly create invariance by adding the Jacobian of the latent space representation w.r.t the input of the autoencoder, to the reconstruction loss
. This forces the latent space representation to remain the same for small changes in the input [
46]. Let us consider the autoencoder with the encoder mapping the input image to the latent space
and the decoder mapping back to the input image space
. The regularized loss function is:
Authors in [
47] describe what regularized autoencoders learn from the data generating the density function, and show for contractive and denoising encoders that this corresponds to the direction in which density is increasing the most. Regularization forces the autoencoders to become less sensitive to input variation, though enforcing minimal reconstruction error keeps it sensitive to variations along the manifold having high density. Contractive autoencoders capture variations on the manifold, while mostly ignoring variations orthogonal to it. Contractive autoencoder estimates the tangent plane of the data manifold [
26].
3.6. Other Deep Models
De-noising AutoEncoders (DAE) and Stacked DAEs (SDAEs) are well-known robust feature extraction methods in the domain of unsupervised learning [
48], where the reconstruction error minimization criteria is augmented with that of reconstructing from corrupted inputs. SDAEs are used to learn representations from a video using both appearance, i.e. raw values, and motion information, i.e. optical flow between consecutive frames [
49]. Correlations between optical flow and raw image values are modeled by coupling these two SDAE pipelines to learn a joint representation.
Deep belief networks (DBNs) are generative models, created by stacking multiple hidden layer units, which are usually trained greedily to perform unsupervised feature learning. They are generative models in the sense that they can reconstruct the original inputs. They have been discriminatively trained using back-propagation [
50] to achieve improved accuracies for supervised learning tasks. The DBNs have been used to perform a raw image value based representation learning in [
51].
An early application of autoencoders to anomaly detection was performed in [
52], on non-visual data. The Replicating neural network [
52], constitutes of a feed-forward multi-layer perceptron with three hidden layers, trained to map the training dataset to itself and anomalies correspond to large reconstruction error over test datasets. This is an autoencoder setup with a staircase like non-linearity applied at the middle hidden layer. The activation levels of this hidden units are thus quantized into
N discrete values,
. The step-wise activation function used for the middle hidden layer divides the continuously distributed data points into a number of discrete-valued vectors. The staircase non-linearity quantizes data points into clusters. This approach identifies cluster labels for each sample, and this often helps interpret resulting outliers.
A rejection cascade over spatio-temporal cubes was generated to improve the performance speed of Deep-CNN based video anomaly detection framework by authors in [
53].
Videos can be viewed as a special case of spatio-temporal processes. A direct approach to video anomaly detection can be estimating the spatio-temporal mean and covariance. A major issue is estimating the spatio-temporal covariance matrix due to its large size
(where
N pixels ×
p frames). In [
54], space-time pixel covariance for crowd videos were represented as a sum of Kronecker products using only a few Kronecker factors,
. To evaluate the anomaly score, the Mahanalobis distance for clips longer than the learned covariance needs to be evaluated. The inverse of the larger covariance matrix needs to be inferred from the estimated one, by block Toeplitz extension [
55]. It is to be noted that this study [
54] only evaluates performance on the UMN dataset.
4. Predictive Modeling
Predictive models aim to model the current output frame
as a function of the past
p frames
. This is well-known in time series analysis under auto-regressive models, where the function over the past is linear. Recurrent neural networks (RNN) model this function as a recurrence relationship, frequently involving a non-linearity such as a sigmoid function. LSTM is the standard model for sequence prediction. It learns a gating function over the classical RNN architecture to prevent the vanishing gradient problem during backpropagation through time (BPTT) [
3]. Recently there have also been attempts to perform efficient video prediction using feed-forward convolutional networks for video prediction by minimizing the mean-squared error (MSE) between predicted and future frames [
9]. Similar efforts were performed in [
56] using a CNN-LSTM-deCNN framework while combining MSE and an adversarial loss.
4.1. Composite Model: Reconstruction and Prediction
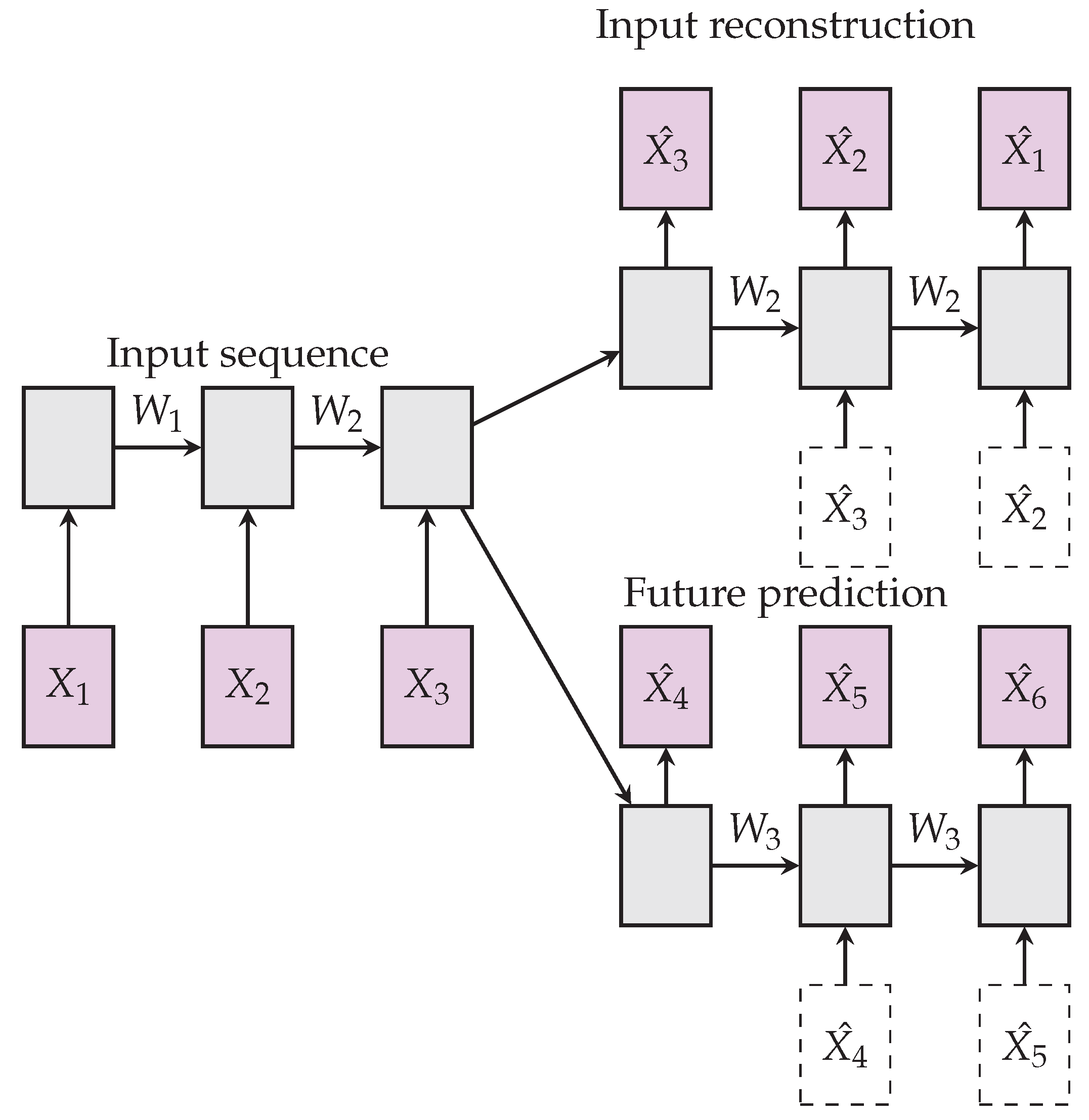
This composite LSTM model in [
7], combines an autoencoder model and predictive LSTM model, see
Figure 5. Autoencoders suffer learning trivial representations of input, by memorization, while memorization is not useful for predicting future frames. On the other hand, the future predictor’s role requires memory of temporally past few frames, though this would not be compatible with the autoencoder loss which is more global. The composite model was used to extract features from video data for the tasks of action recognition. The composite LSTM model is defined using a fully connected LSTM (FC-LSTM) layer.
4.2. Convolutional LSTM
Convolutional long short-term memory (ConvLSTM) model [
57] is a composite LSTM based encoder-decoder model. FC-LSTM does not take spatial correlation into consideration and is permutation invariant to pixels, while a ConvLSTM has convolutional layers instead of fully connected layers, thus modeling spatio-temporal correlations. The ConvLSTM as described in Equation (
10) evaluates future states of cells in a spatial grid as a function of the inputs and past states of its local neighbors.
Authors in [
57], consider a spatial grid, with each grid cell containing multiple spatial measurements, which they aim to forecast for the next
K future frames, given
J observations in the past. The spatio-temporal correlations are used as input to a recurrent model, the convolutional LSTM. The equations for input, gating and the output are presented below.
Here, ∗ refers to the convolution operation while ∘ refers to the Hadamard product, the element-wise product of matrices. Encoding network compresses the input sequence into a hidden state tensor while the forecasting network unfolds the hidden state tensor to make a prediction. The hidden representations can be used to represent moving objects in the scene, a larger transitional kernel captures faster motions compared to smaller kernels [
57].
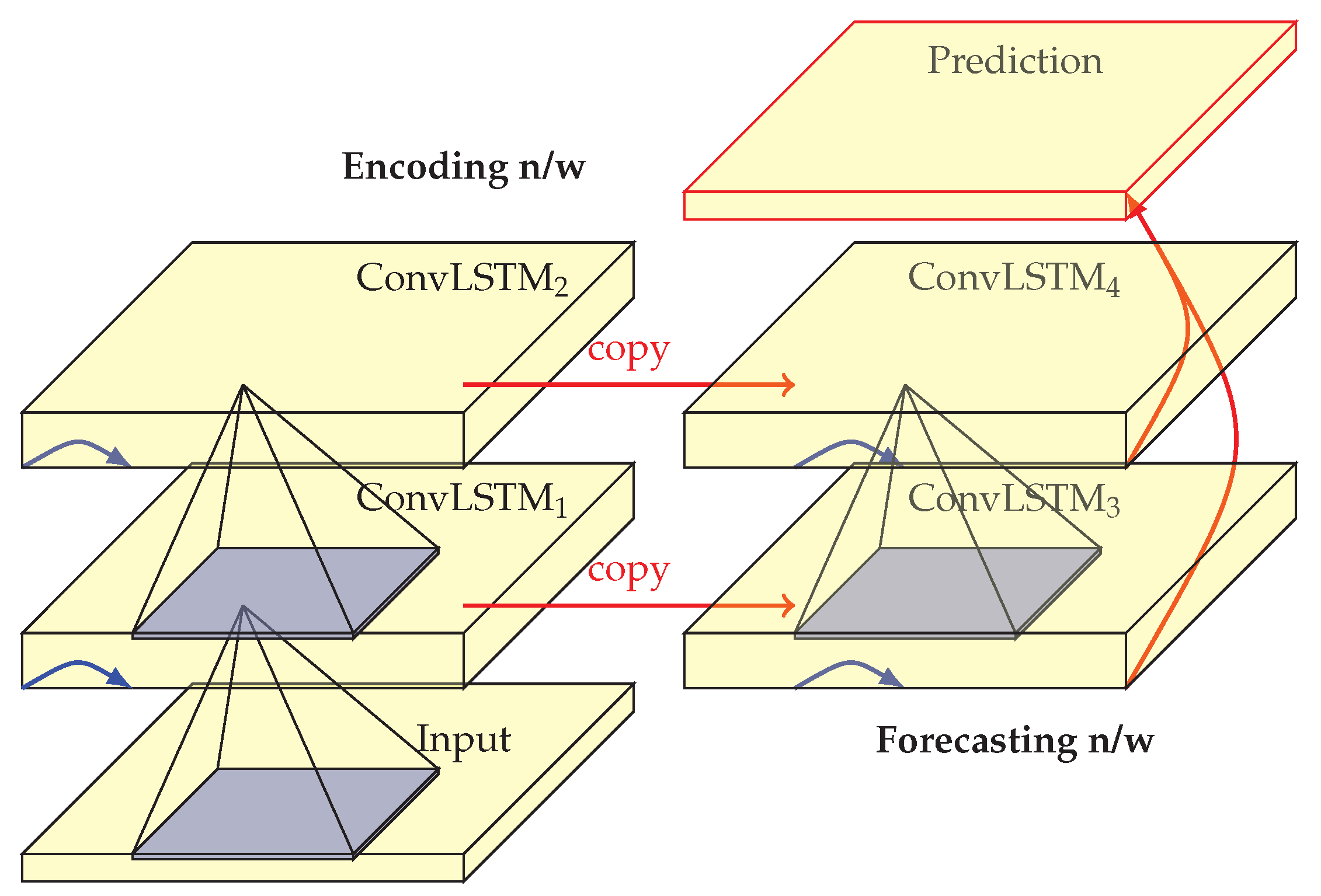
The ConvLSTM model was used as a unit within the composite LSTM model [
7] following an encoder-decoder, with a branch for reconstruction and another for prediction. This architecture, shown in
Figure 6, was applied to the VAD task by [
58,
59], with promising results.
In [
60], a convolutional representation of the input video is used as input to the convolutional LSTM and a de-convolution to reconstruct the ConvLSTM output to the original resolution. The authors call this a ConvLSTM Autoencoder, though fundamentally it is not very different from a ConvLSTM.
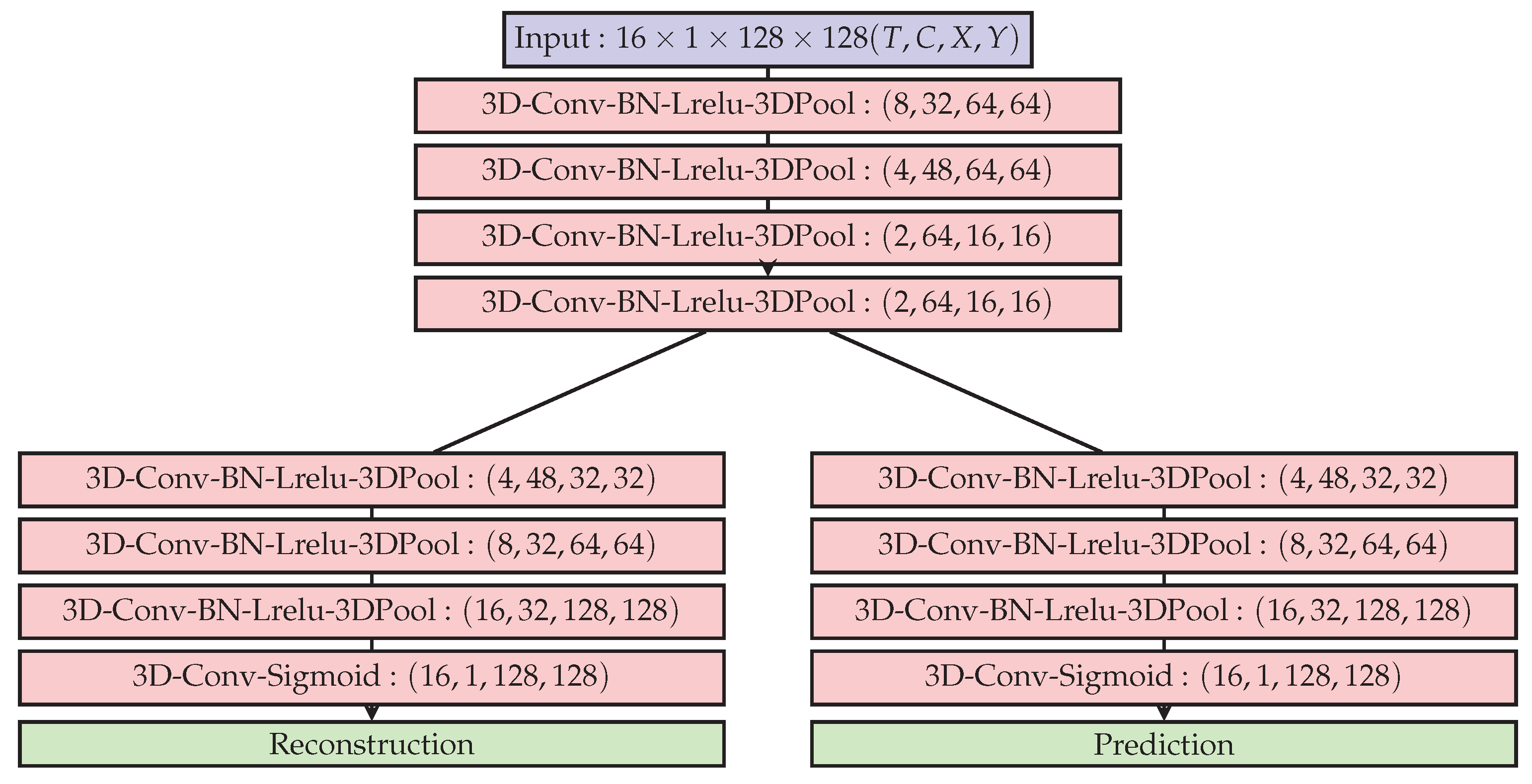
4.3. 3D-Autoencoder and Predictor
As remarked by authors in [
61], while 2D-ConvNets are appropriate representations learnt for image recognition and detection tasks, they are incapable of capturing the temporal information encoded in consecutive frames for video analysis problems. 3-D convolutional architectures are known to perform well for action recognition [
24], and are used in the form of an autoencoder. Such a 3D autoencoder learns representations that are invariant to spatio-temporal changes (movement) encoded by the 3-D convolutional feature maps. Authors in [
61] propose to use a 3D kernel by stacking T-frames together as in [
41], shown in
Figure 7. The output feature map of each kernel is a 3D tensor including the temporal dimension and are aimed to summarize motion information.
The reconstruction branch follows an autoencoder loss:
The prediction branch loss is inversely weighted by moving window’s length that falls off symmetrically w.r.t the current frame, to reduce the effect of past frames on the predicted frame:
Thus the final optimization objective minimized is:
Anomalous regions where spatio-temporal blocks, that even when poorly reconstructed by the autoencoder branch, would be well predicted by the prediction branch. The prediction loss was designed to enforce local temporal coherence by tracking spatio-temporal correlation, and not for the prediction of the appearance of new objects in the relatively long-term future.
4.4. Slow Feature Analysis (SFA)
Slow feature analysis [
62] is an unsupervised representation learning method which aims at extracting slowly varying representations of rapidly varying high dimensional input. The SFA is based on the
slowness principle, which states that the responses of individual receptors or pixel variations are highly sensitive to local variations in the environment, and thus vary much faster, while the higher order internal visual representations vary on a slow timescale. From a predictive modeling perspective SFA extracts a representation
of the high dimensional input
that maximizes information on the next time sample
. Given a high dimensional input varying over time,
SFA extracts a representation
which is a solution to the following optimization problem [
63]:
As seen in the constraints, the representation is enforced to have, zero mean to ensure a unique solution, while unit covariance to avoid trivial zero solution. Feature de-correlation removes redundancy across the features.
SFA has been well known in pattern recognition and has been applied to the problem of activity recognition [
64,
65]. Authors in [
66] propose an incremental application of SFA that updates slow features incrementally. The SFA is calculated using batch PCA, iterated twice. The first PCA to whiten the inputs. The second PCA is applied on the derivative of the normalized input to evaluate the flow features. To achieve a computationally tractable solution, a two-layer localized SFA architecture is proposed by authors [
67] for the task of online slow feature extraction and consequent anomaly detection.
Other Predictive Models: A convolutional feature representation was fed into an LSTM model to predict the latent space representation and its prediction error was used to evaluate anomalies in a robotics application [
68]. A recurrent autoencoder using an LSTM that models temporal dependence between patches from a sequence of input frames is used to detect video forgery [
69].
5. Deep Generative Models
5.1. Generative vs. Discriminative
Let us consider a supervised learning setup , where i indexes the number of samples in the dataset. Generative models estimate class conditional posterior distribution , which can be difficult if the input data are high dimensional images or spatio-temporal tensors. A discriminative model evaluates the class probability directly from the data to classify the samples X into different classes .
Deep generative models that can learn via the principle of maximum likelihood differ with respect to how they represent or approximate the likelihood. The explicit models are ones where the density is evaluated explicitly and the likelihood maximized.
In this section, we will review the stochastic autoencoders; the variational autoencoder and the adversarial autoencoder, and their applications to the problem of anomaly detection. And finally the generative adversarial networks to anomaly detection in images and videos.
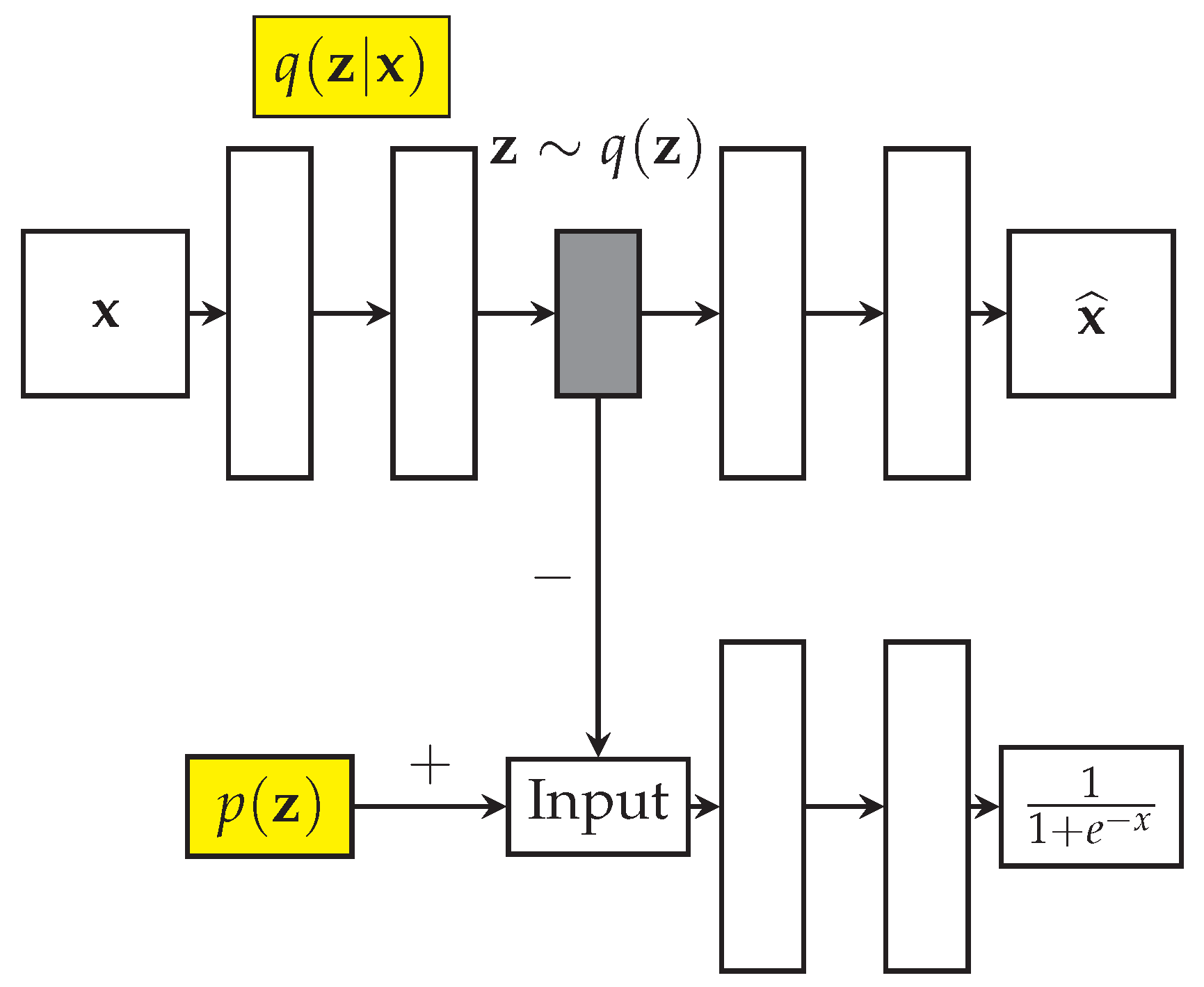
5.2. Variational Autoencoders (VAEs)
Variational Autoencoders [
1] are generative models that approximate the data distribution
of a high dimensional input
X, an image or video. The graphical mode of the VAE is reproduced from [
1] in
Figure 8. A variational approximation of the latent space
is achieved using an autoencoder architecture, with a probabilistic encoder
that produces Gaussian distribution in the latent space, and a probabilistic decoder
, which given a code produces distribution over the input space. The motivation behind variational methods is to pick a family of distributions over the latent variables with its own variational parameters
, and estimate the parameters for this family so that it approaches
.
The loss function constitutes of the KL-Divergence regularization term, and the expected negative reconstruction error with an additional KL-divergence term between the latent space vector and the representation with a mean vector and a standard deviation vector, that optimizes the variational lower bound on the marginal log-likelihood of each observation.
The function
maps sample
and noise vector
to a sample from the approximate posterior for that data-point
where,
. To solve this sampling problem authors [
1] propose the reparameterization trick. The random variable
is expressed as function of a deterministic variable
where
is an auxiliary variable with independent marginal
. This reparameterization rewrites an expectation w.r.t
such that the Monte Carlo estimate of the expectation is differentiable w.r.t.
. A valid reparameterization was the unit-Gaussian case
where
.
Specifically for a VAE, the goal is to learn a low dimensional representation
z by modeling
with a simpler distribution, a centered isotropic multivariate Gaussian, i.e.
. In this model both the prior
, and
are Gaussian; and the resulting loss function was described in Equation (
15).
5.3. Anomaly Detection Using VAE
Anomaly detection using the VAE framework has been studied in [
70]. Authors define the reconstruction probability as
. Once the VAE is trained, for a new test sample
, one first evaluates the mean and standard deviation vectors with the probabislistic encoder,
. Then samples
L latent space vectors,
. The parameters of the input distribution are reconstructed using these
L samples,
then the reconstruction probability for test sample
is given by:
Multiple samples drawn from the latent variable distribution, lets take into account the variability of the latent variable space, which is one of the essential distinctions between the stochastic variational autoencoder and a standard autoencoder, where latent variables are defined by deterministic mappings.
5.4. Generative Adversarial Networks (GANs)
A GAN [
2] consists of a generator
G, usually a decoder, and a discriminator
D, usually an binary classifier that assigns a probability of an image being generated (fake), or sampled from the training data (real). The generator
G in fact learns a distribution
over data
via a mapping
of samples
, 1D vectors of uniformly distributed input noise sampled from latent space
, to 2D images in the image space manifold
, which is populated by normal examples. In this setting, the network architecture of the generator
G is equivalent to a convolutional decoder that utilizes a stack of strided convolutions. The discriminator
D is a standard CNN that maps a 2D image to a single scalar value
. The discriminator output
can be interpreted as the probability that the given input to the discriminator
D was a real image
sampled from training data
X or a generated image using
by the generator
G.
D and
G are simultaneously optimized through the following two-player minimax game with value function
:
The discriminator is trained to maximize the probability of assigning real training examples the “real” and samples from
the “fake” label. The generator
G is simultaneously trained to fool
D via minimizing
, which is equivalent to maximizing
. During adversarial training, the generator improves in generating realistic images and the discriminator progresses in correctly identifying real and generated images. GANs are implicit models [
71], that sample directly from the distribution represented by the model.
5.5. GANs for Anomaly Detection in Images
This section reviews work done by authors [
72] who apply a GAN model for the task of anomaly detection in medical images. GANs are generative models that best produce a set of training data points
where
represents the probability density of the training data points. The basic idea in anomaly detection is to be able to evaluate the density function of the normal vectors in the training set containing no anomalies while for the test set we evaluate a negative log-likelihood score which serves as the final anomaly score. The score corresponds to the test sample’s posterior probability of being generated from the same generative model representing the training data points. GANs provide a generative model that minimizes the distance between the training data distribution and the generative model samples without explicitly defining a parametric function, which is why it is called an implicit generative model [
71]. Thus to be successfully used in an anomaly detection framework the authors [
72] evaluate the mapping
, i.e., Image domain → latent representation. This was done by choosing the closest point
using back-propagation. Once done the residual loss in the image space was defined as
.
GANs are generative models and to evaluate a likelihood one requires a mapping from the image domain to the latent space. This is achieved by authors in [
72], which we shall shortly describe here. Given a query image
, the authors aim to find a point
in the latent space that corresponds to an image
that is visually most similar to the query image
and that is located on the manifold
. The degree of similarity of
and
depends on to which extent the query image follows the data distribution
that was used for training of the generator.
To find the best , one starts randomly sampling from the latent space distribution and feeds it into the trained generator which yields the generated image . Based on the generated image we can define a loss function, which provides gradients for the update of the coefficients of resulting in an updated position in the latent space, . In order to find the most similar image , the location of in the latent space is optimized in an iterative process via back-propagation steps.
5.6. Adversarial Discriminators Using Cross-Channel Prediction
Here we shall review the work done in [
73] applied to anomaly detection in videos. The anomaly detection problem in this paper is formulated as a cross-channel prediction task, where the two channels are the raw-image values
and the optical flow vectors
for frames
in the videos. This work combines two architectures, the pixel-GAN architecture by [
74] to model the normal/training data distribution, and the Split-Brain Autoencoders [
75]. The Split-Brain architectures aims at predicting a multi-channel output by building cross-channel autoencoders. That is, given training examples
, we split data into
and
, where
, and the authors train multiple deep representations
and
, which when concatenated provided a reconstruction of the input tensor
X, just like an autoencoder. Various manners of aggregating these predictors have been explored in [
75]. In the same spirit as the cross-channel autoencoders [
75], Conditional GANs were developed [
74] to learn a generative model that learns a mapping from one input domain to the other.
The authors [
73] train two networks much in the spirit of the conditional GAN [
74] where:
which generates the raw image frames from the optical flow and
which generates the optical flow from the raw images.
are image frames with RGB channels and
are vertical and horizontal optical flow vector arrays. The input to discriminator
D is thus a 6-D tensor. We now describe the adaption of the cross-channel autoencoders for the task of anomaly detection.
The generators/discriminators follow a U-net architecture as in [
74] with skip connections. The two generators
are trained to map training frames and their optical flow to their cross-channel counterparts. The goal is to force a poor cross-channel prediction on test video frames containing an anomaly so that the trained discriminators shall provide a low probability score.
The trained discriminators
are patch-discriminators that produce scores
on a grid with resolution smaller than the image. These scores do not require the reconstruction of the different channels to be evaluated. The final score is
which is normalized between
based on the maximum value of individual scores for each frame. The U-net uses the Markovian structure present spatially by the skip connections shown between the input and the output of the generators in
Figure 9. Cross-channel prediction aims at modeling the spatio-temporal correlation present across channels in the context of video anomaly detection.
5.7. Adversarial Autoencoders (AAEs)
Adversarial Autoencoders are probabilistic autoencoders that use GANs to perform variational approximation of the aggregated posterior of the latent space representation [
76] using an arbitrary prior.
AAEs were applied to the problem of anomalous event detection over images by authors [
77]. In
Figure 10,
denotes input vectors from training distribution,
the encoder’s posterior distribution,
the prior that the user wants to impose on the latent space vectors
. The latent space distribution is given by
where
represents the training data distribution. In an AAE, the encoder acts like the generator of the adversarial network, and it tries to fool the discriminator into believing that
comes from the actual data distribution
. During the joint training, the encoder is updated to improve the reconstruction error in the autoencoder path, while it is updated by the discriminator of the adversarial network to make the latent space distribution approach the imposed prior. As prior distribution for the generator of the network, authors [
77] use the Gaussian distribution of 256 dimensions, with the dropout set to 0.5 probability. The method achieves close to state of the art performance. As the authors remark themselves, the AAE does not take into account the temporal structure in the video sequences.
5.8. Controlling Reconstruction for Anomaly Detection
One of the common problems using deep autoencoders is their capability to produce low reconstruction errors for test samples, even over anomalous events. This is due to the way autoencoders are trained in a semi-supervised way on videos with no anomalies, but with sufficient training samples, they are able to approximate most test samples well.
In [
78], the authors propose to limit the reconstruction capability of the generative adversarial networks by learning conflicting objectives for the normal and anomalous data. They use negative examples to enforce explicit poor reconstruction. Thus this setup is weakly supervised, not requiring labels. Given two random variables
with samples
, we want the network to reconstruct the input distribution
X while poorly reconstruct
Y. This was achieved by maximizing the following objective function:
where
refers to the autoencoders parameters. This setup assumes strong class imbalance, i.e.very few samples of the anomalous class
Y are available compared to the normal class
X. The motivation for negative learning using anomalous examples is to consistently provide poor reconstruction of anomalous samples. During the training phase, authors [
68] reconstruct positive samples by minimizing the reconstruction error between samples, while negative samples are forced to have a bad reconstruction by maximizing the error. This last step was termed as negative learning. The datasets evaluated were the reconstruction of the images from MNIST and Japanese highway video patches [
79].
In similar work by [
80], discriminative autoencoders aim at learning low-dimensional discriminative representations for positive (
) and negative (
) classes of data. The discriminative autoencoders build a latent space representation under the constraint that the positive data should be better reconstructed than the negative data. This is done by minimizing the reconstruction error for positive examples while ensuring that those of the negative class are pushed away from the manifold.
In the above loss function,
denotes as the label of the sample, and
the distance of that example to the manifold. Minimizing the hinge loss in Equation (
22) achieves reconstruction such that the discriminative autoencoders build a latent space representation of data that better reconstructs positive data compared to the negative data
6. Experiments
There are two large classes of experiments : first, reconstructing the input video on a single frame basis
, second the reconstruction of a stack of frames
. These reconstruction schemes are performed either on raw frame values, or on the optical flow between consequent frame pairs. Reconstructing raw image values modeled the back-ground image, since minimizing the reconstruction error was in fact evaluating the background. Convolutional autoencoders reconstructing a sequence of frames captured temporal appearance changes as described by [
41]. When learning feature representations on optical flow we indirectly operate on two frames, since each optical flow map evaluates the relative motion between two consequent frame pairs. In the case of predictive models the current frame
was predicted after observing the past
p frames. This provides a different temporal structure as compared to a simple reconstruction of a sequence of frames
, where the temporal coherence results from enforcing a bottleneck in the autoencoder architectures. The goal of these experiments were not evaluate the best performing model, and were intended as a tool to understand how background estimation and temporal appearance were approximated by the different models. A complete detailed study is beyond the scope of this review.
In this section, we evaluate the performance of the following classes of models on the UCSD and CUHK-Avenue datasets. As a baseline, we use the reconstruction of a dense optical flow calculated using the Farneback method in OpenCV 3, by principal component analysis, with around 150 components. For predictive models, as a baseline we use a vector autoregressive model (VAR), referred to as
LinPred. The coefficients of the model are estimated on a lower dimensional, random projection of the raw image or optical flow maps from the input training video stream. The random projection avoids badly conditioned and expensive matrix inversion. We compare the performance of Contractive autoencoders, simple 3D autoencoders based on C3D [
24] CNNs (C3D-AE), the ConvLSTM and ConvLSTM autoencoder from the predictive model family and finally the VAE from the generative models family. The VAE’s loss function consists of the binary cross-entropy (similar to a reconstruction error) between the model prediction and the input image, and the KL-divergence
, between the encoded latent space vectors and
multivariate unit-Gaussian. These models were built in Keras [
81] with Tensorflow back-end and executed on a K-80 GPU.
6.1. Architectures
Our Contractive and Variational AE (VAE) constitutes of a random projection to reduce the dimensionality to 2500 from an input frame of size 200 × 200. The Contractive AE constitutes of one fully connected hidden layer of size 1250 which map back to the reconstruction of the randomly projected vector of size 2500. While the VAE contains two hidden layers (dimensions: 1024, 32), which maps back to the output of 2500 dimensions. We use the latent space representation of the VAE to fit a multivariate Gaussian on the training dataset and evaluate the negative-log probability for the test samples.
6.2. Observations and Issues
The results are summarized in the
Table 1 and
Table 2. The performance measures reported are the Area Under Receiver-Output-Characteristics plot (AU-ROC), Area Under Precision-Recall plot. These scores are calculated when the input channels correspond to the raw image (raw) and the optical flow (flow), each of which has been normalized by the maximum value. The final temporal anomaly score is given by Equation (
8). These measures are described in the next section. We also describe the utility of these measures under different frequencies of occurrences of the anomalous positive class.
Reconstruction model issues: Deep autoencoders identify anomalies by poor reconstruction of objects that have never appeared in the training set, when raw image pixels are used as input. It is difficult to achieve this in practice due to a stable reconstruction of new objects by deep autoencoders. This pertains to the high capacity of autoencoders, and their tendency to well approximate even the anomalous objects. Controlling reconstruction using negative examples could be a possible solution. This holds true, but to a lower extent, when reconstructing a sequence of frames (spatio-temporal block).
AUC-ROC vs. AUC-PR: The anomalies in the UCSD pedestrian dataset have a duration of several hundred frames on average, compared to the anomalies in the CUHK avenue dataset which occur only for a few tens of frames. This makes the anomalies statistically less probable. This can be seen by looking at the AU-PR
Table 2, where the average scores for CUHK-avenue are much lower than for UCSD pedestrian datasets. It is important to note that this does not mean the performance over the CUHK-Avenue dataset is lower, but just the fact that the positive anomalous class is rarer in occurrence.
Rescaling image size: The models used across different experiments in the articles that were reviewed, varied in the input image size. In some cases the images were resized to sizes (128, 128), (224, 224), (227, 227). We have tried to fix this to be uniformly (200, 200). Though it is essential to note that there is a substantial change in performance when this image is resized to certain sizes.
Generating augmented video clips: Training the convolutional LSTM for video anomaly detection takes a large number of epochs. Furthermore, the training video data required is much higher and data augmentation for video anomaly detection requires careful thinking. Translations and rotations may be transformations to which the anomaly detection algorithm requires to be sensitive to, based on the surveillance application.
Performance of models: VAEs perform consistently as well as or better than PCA on optical flow. It is still left as a future study to understand clearly, why the performance of a stochastic autoencoder such as VAE is better. Convolutional LSTM on raw image values follow closely behind as the first predictive model performing as good as PCA but sometimes poorer. Convolutional LSTM-AE is a similar architecture with similar performance. Finally, the 3D convolutional autoencoder, based on the work by [
24], performs as well as PCA on optical flow, while modeling local motion patterns.
To evaluate the specific advantages of each of these models, a larger number of real world, video surveillance examples are required demonstrating the representation or feature that is most discriminant. In experiments, we have also observed that application of PCA on the random projection of individual frames performed well in avenue dataset, indicating that very few frames were sufficient to identify the anomaly; while the PCA performed poorly on UCSD pedestrian datasets, where motion patterns were key to detect the anomalies.
For single frame input based models, optical flow served as a good input since it already encoded part of the predictive information in the training videos. On the other hand, convolutional LSTMs and linear predictive models required input raw image values, in the training videos, to predict the current frame raw image values.
6.3. Evaluation Measures
The anomaly detection task is a single class estimation task, where 0 is assigned to samples with likelihood (or reconstruction error) above (below) a certain threshold, and 1 assigned to detected anomalies with low likelihood (high reconstruction error). Statistically, the anomalies are a rare class and occurs less frequently compared to the normal class. The most common characterization of this behavior is the expected frequency of occurrence of anomalies. We briefly review the anomaly detection evaluation procedure as well as the performance measures that were used across different studies. For a complete treatment of the subject, the reader is referred to [
82].
The final anomaly score is a value that is treated as a probability which lies in
,
,
T being the maximum time index. For various level sets or thresholds of the anomaly score
, one can evaluate the True Positives (TP, the samples which are truly anomalous and detected as anomalous), True Negatives (TN, the samples that are truly normal and detected as normal), False Positives (FP, the samples which are truly normal samples but detected as anomalous) and finally False Negatives (FN, the samples which are truly anomalous but detected as normal).
We require these measures to evaluate the ROC curve, which measures the performance of the detection at various False positive rates. That is ROC plots TPR vs FPR, while the PR plots precision vs. recall.
The performance of anomaly detection task is evaluated based on an important criterion, the probability of occurrence of the anomalous positive class. Based on this value, different performance curves are useful. We define the two commonly used performance curves: Precision-Recall (PR) curves and Receiver-Operator-Characteristics (ROC) curves. The area under the PR curve (AU-PR) is useful when true negatives are much more common than true positives (i.e., TN >> TP). The precision recall curve only focuses on predictions around the positive (rare) class. This is good for anomaly detection because predicting true negatives (TN) is easy in anomaly detection. The difficulty is in predicting the rare true positive events. Precision is directly influenced by class (im)balance since FP is affected, whereas TPR only depends on positives. This is why ROC curves do not capture such effects. Precision-recall curves are better to highlight differences between models for highly imbalanced data sets. For this reason, if one would like to evaluate models under imbalanced class settings, AU-PR scores would exhibit larger differences than the area under the ROC curve.
7. Conclusions
In this review paper, we have focused on categorizing the different unsupervised learning models for the task of anomaly detection in videos into three classes based on the prior information used to build the representations to characterize anomalies.
They are reconstruction based, spatio-temporal predictive models, and generative models. Reconstruction based models build representations that minimize the reconstruction error of training samples from the normal distribution. Spatio-temporal predictive models take into account the spatio-temporal correlation by viewing videos as a spatio-temporal time series. Such models are trained to minimize the prediction error on spatio-temporal sequences from the training series, where the length of the time window is a parameter. Finally, the generative models learn to generate samples from the training distribution, while minimizing the reconstruction error as well as distance between generated and training distribution, where the focus is on modeling the distance between sample and distributions.
Each of these methods focuses on learning certain prior information that is useful for constructing the representation for the video anomaly detection task. One key concept which occurs in various architectures for video anomaly detection is how temporal coherence is implemented. Spatio-temporal autoencoders and Convolutional LSTM learn a reconstruction based or spatio-temporal predictive model that both use some form of (not explicitly defined) spatio-temporal regularity assumptions. We can conclude from our study that evaluating how sensitive the learned representation is to certain transformations such as time warping, viewpoint, applied to the input training video stream, is an important modeling criterion. Certain invariances are as well defined by the choice of the representation (translation, rotation) either due to reusing convolutional architectures or imposing a predictive structure. A final component in the design of the video anomaly detection system is the choice of thresholds for the anomaly score, which was not covered in this review. The performance of the detection systems were evaluated using ROC plots which evaluated performance across all thresholds. Defining a spatially variant threshold is an important but non-trivial problem.
Finally, as more data is acquired and annotated in a video-surveillance setup, the assumption of having no labeled anomalies progressively turns false, partly discussed in the section on controlling reconstruction for anomaly detection. Certain anomalous points with well defined spatio-temporal regularities become a second class that can be estimated well; and methods to include the positive anomalous class information into detection algorithms becomes essential. Handling class imbalance becomes essential in such a case.
Another problem of interest in videos is the variation in temporal scale of motion patterns across different surveillance videos, sharing a similar background and foreground. Learning a representation that is invariant to such time warping would be of practical interest.
There are various additional components of the stochastic gradient descent algorithm that were not covered in this review. The Batch Normalization [
83] and drop-out based regularization [
84] play an important role in the regularization of deep learning architectures, and a systematic study is important to be successful in using them for video anomaly detection.