1. Introduction
In competitive markets with multiple sellers and buyers, prices are mostly driven by supply and demand, with price itself providing signals to ensure market equilibrium. However, meaningful price fluctuations come from exceptional events, causing distortions that may have effects on trends in the long-term. Furthermore, the strong push from governments to allow a smooth transition between an era dominated by fossil fuels and one focused on a low-carbon economy will continue to influence non-renewable pricing structures to reflect environmental attributes and energy-related megatrends.
Within this framework, the study of patterns in the energy time series becomes of great interest. This study assesses stochastic properties of the three energy commodities that account for the majority of global energy demand, i.e., crude oil, coal, and natural gas, in addition to gasoil and fuel oil, using a comprehensive approach. In this sense and to the best of our knowledge, this paper is the first that addresses a systematic review of endogenous testing procedures for non-renewable energy prices. Of separate interest are the results of the break dates estimates themselves and the insights gained from this using each test.
Our analysis is motivated by the fact that, as it is well known, the effects of major historical events find the balance of evidence in favor of the trend stationary hypothesis more often [
1]. More specifically, the purpose of this paper is threefold: firstly, to provide evidence for the presence of unit roots in time series in light of the most recent oil price crashes. Secondly, to examine the potential existence of breaks and the nature and impacts of those shocks on price developments, and thirdly, to properly address testing limitations providing a view towards improving modelling and forecasting techniques.
While maintaining a certain distance from the effects of the coronavirus pandemic—a rather unique phenomenon negatively affecting expectations for growth worldwide—our study focuses on two major events: Firstly, the credit crunch in 2008 associated with global economy uncertainty and a sharp reduction in global demand. Secondly, the collapse of oil prices since late 2014.
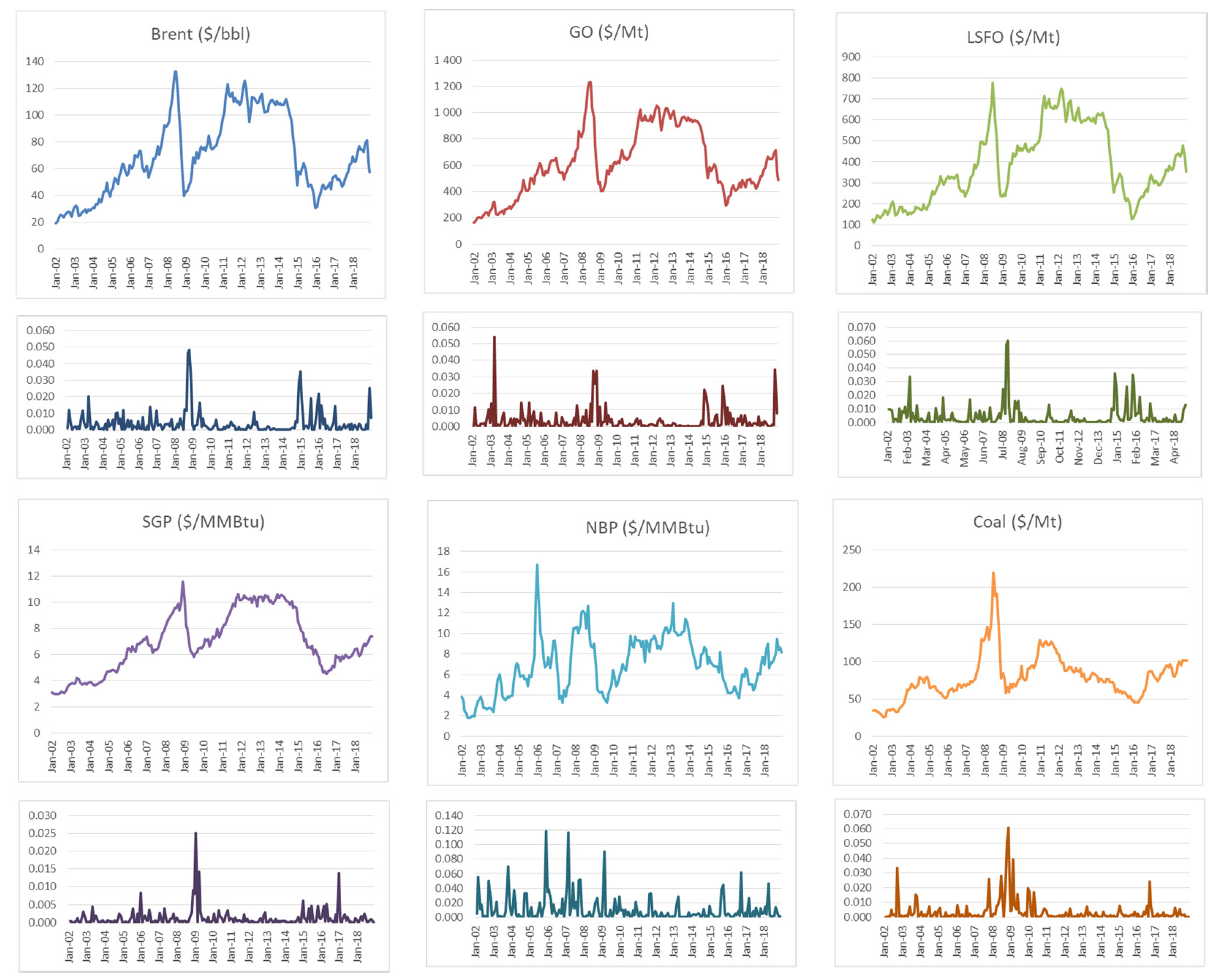
Figure 1 shows the developments in the prices of oil and oil products from 2002 until the end of 2018.
There are multiple similarities and differences among the two oil price crashes, although the differences are possibly more revealing of how traded oil markets behave. In the first place, the 2008–2009 crash was precipitated by global events, mainly the financial crisis, with oil prices during that crash being highly correlated with equity and exchange rate movements. Due to this interaction and the uncertainty regarding the health of the global economy, volatility spiked in 2008. However, the impact of shocks to equity markets on volatility during the recent crash was muted [
2]. As a matter of fact, that macroeconomic shocks are closely related to crude oil price variations does not come as a surprise [
3,
4,
5,
6,
7,
8]. In the second place, the decline in the second half of 2014 was considerably sharper for oil than for other commodities, whereas almost all commodity prices, including coal, metals, food commodities, and agricultural raw materials, declined by similar magnitudes in 2008 [
9]. The third and perhaps the most important factor from a market point of view: although after the financial crisis virtually all commodity prices rebounded, helped by production cuts and a strong emerging market demand, global oil supply started building up.
In terms of the benefits provided by the study, it makes three main contributions: (i) it provides an integrated framework in which the most representative endogenous unit root testing procedures are evaluated; (ii) it unravels the nature of non-renewable energy resources’ prices facilitating a more precise assessment of the effects of structural breaks in each variable using different alternatives; (iii) it improves decision-making by taking into account climate policy interventions and clarifies the potential for a smooth transition from fossil fuels to low-carbon energy sources. As is well-known, if price series exhibit trend stationary properties with breaks in the trends, that would suggest that price stabilization policies may be ineffective and difficult to implement.
The remainder of this paper is organized as follows.
Section 2 briefly explains the econometric methodology of this paper.
Section 3 provides the descriptive statistics of the sample data and the various testing methodologies’ results.
Section 4 discusses the empirical results. The final section includes some concluding remarks.
2. Materials and Methods
2.1. Data Definition
This study considers six time series, namely, crude oil Brent (Brent), gasoil (GO), low-sulfur fuel oil (LSFO), average Spanish gas import prices (SGP), national balancing point (NBP), and coal prices, all of which except SGP are variables widely traded around the world, providing producers and consumers with valuable financial products to protect themselves against the risk of price fluctuations in their respective markets. We also introduce Spanish gas import prices to expand the scope of investigation into oil-indexed gas supplies supported by the fact that Spain, with access to diverse, competing sources of gas, is an ideal reference to assess relationships between crude oil and long-term gas globally [
10,
11]. The data sets consist of the average monthly prices spanning from January 2002 to December 2018 (total 204 observations). The price series are converted into the logarithmic percentage return series for all sample indices, i.e., y
t = 100 × ln (P
t/P
t−1) for t = 1, 2,..., T, where y
t is the returns for each time series at time t, P is the current price, and P is the price from the previous month.
Figure 2 shows time variations of monthly prices and absolute returns over the study period for all the variables considered.
As can be seen, Brent crude oil and oil products data sets share large swings in common, and at the same time show similar upward trends in spite of the effects of shocks during 2008 and 2014 pulling down the trend line with no clear indication of mean reversion. Common peaks anticipating potential structural breaks were observed at the beginning of 2003 and the Iraq war, in mid-2008 as a result of the financial crisis, and at the end of 2014.
Table 1 provides of the descriptive statistics of the natural logarithm of the series.
As can be seen, on average, coefficients of variation (CV) are generally close, indicating a similar month-to month variation in all of the prices, with gasoil showing the lowest CV. Regarding the statistical distribution of natural logarithm levels, all variables reveal similar evidence of negative skewness, implying that the left tail is more extreme than in the Gaussian case. It is interesting to notice that coal shows the highest level of kurtosis among the energy products’ prices, implying that the distribution of coal prices has a tail that is thicker than the rest.
2.2. Methodological Issues
This section is concerned with methodological issues affecting unit root estimation in the study in the context of structural change. Our focus is on the conceptual issues about the different approaches to better understand the potential applicability to our investigation. It is important to highlight the impressive amount of research in the last few decades devoted to improving existing methodologies and to overcoming potential problems. The fact that unit root processes can sometimes be viewed as observationally equivalent to, or hardly distinguishable from, a trend stationary process with breaks lays at the heart of the debate [
12]. It has to be noted that since the seminal paper by Perron [
1] was published, several alternatives in addition to joint inference have been developed, and a complementary strand of literature is concerned with specific issues related to the detection and estimation of structural changes [
13,
14,
15,
16,
17,
18].
The basic model in the earlier articles of Perron [
1] and Hamilton [
19] leading to important development afterwards, considers a univariate process y
t generated by either additive (AO) or innovational outlier (IO) models, the distinction being how the impact of the break is distributed over time. In the AO model, the impact is complete over the period, whereas in the IO model the effect is distributed over time, implying a distinction between the short-run and long-run impacts of the break.
The data generating process (DGP) of the additive outlier (AO) model is:
where
with DU
t = B
t = 0 if t ≤ T
1 and DU
t = 1, B
t = t − T
1 if t > T
1.
The noise ut is such that A (L) ut = B (L) εt where εt ≈ i.i.d. (0, σ2), and A (L) and B (L) are polynomials in L of order p +1 and q, respectively.
The DGP of the innovational outlier (IO) model under the alternative is given by:
where
with φ* (L) and φ (L) such that φ* (L) = A* (L)
−1 B (L) and (1 − αL)
−1 φ* (L) = ϕ (L).
Models A1 and I1 are called “level shift” or “crash” models, A2 is a “changing growth” model, and A3 and I3 are “mixed” models. A changing growth model of the IO type is typically not considered because it is necessary to assume that no break occurs under the null hypothesis which imposes an asymmetric treatment in Perron’s framework.
A brief description of the specific testing methodology employed in this study follows, including abbreviations used later on:
- (i)
Zivot and Andrews (ZA) [
20] and Perron and Vogelsang (VP) [
21]. These unit root tests have in common that they endogenize the choice of the break point proposing to estimate the break date such that it gives the most weight to the trend stationary alternative, i.e., either minimizing the Dickey–Fuller statistic or optimizing a statistic which tests the significance of one or more of the coefficients on the trend break dummy variables.
- (ii)
Lumsdaine and Papell (LP) [
22]. This specification extends the ZA design to introduce a unit root testing procedure that allows for two structural breaks, although, unfortunately, it leads to results that are heavily dependent on break size [
23]; however, implementing this framework has clear advantages, as it provides less (or stronger) evidence against the unit root hypothesis than that given by Perron, plus it provides valuable information as to whether structural breaks have significantly contributed to a change in trend or not.
- (iii)
Saikkonen and Lütkepohl [
24] and Lanne et al. (LLS) [
25] extended Saikkonen and Lütkepohl [
26], and Lanne et al. [
27] tests respectively—these tests are considered in turn extensions of the tests of Elliot, Rothenberg and Stock [
28], which are based on estimating the deterministic term first by generalized least squares (GLS) and subtracting it from the time series. It has to be noted that [
26,
27] tests have the convenient feature that they allow for smooth transitions through different shift functions what may be more reasonable than assuming an abrupt shift. Moreover, tests statistics are easy to compute for quite general shift functions and allow the possibility to include seasonal dummies in addition to a constant or linear trend line.
- (iv)
Lee and Strazicich (LS) [
29,
30]. These testing methodologies propose one and two break Lagrange multiplier (LM) unit root tests as alternatives to the ZA and LP tests respectively. In contrast to the ADF (augmented Dickey–Fuller) type of tests, the LM unit root test has the advantage that it is unaffected by breaks under the null, and therefore solves the issue about the asymptotic validity of the null distributions described above. The breakpoint estimation scheme is similar to those in the ZA and LP tests; i.e., the breakpoints are determined to be where the test statistic is minimized. While the LM test offers an improvement over procedures that only allow for breaks under the trend stationary alternative, it is recognized to be substantially undersized for large breaks, whereas it has difficulties in identifying small break dates [
23]. As a result of continuous progress made on this area, Ming et al. [
31] proposed a new unit root test that adopts the residual augmented least squares (RALS) procedure to gain improved power when the error term follows a non-normal distribution. These new tests using the RALS procedure are more powerful than the usual LM test which does not incorporate information on non-normal errors, and it is not free of nuisance parameters that indicate the locations of a structural break.
- (v)
Kim and Perron [
32] (KP). These tests use research on structural change by Perron and Zhu [
33] and Perron and Yabu [
14], who developed new test procedures which allow a break in the trend function at an unknown time under both null and alternative hypotheses.
3. Results
In this section, we examine the unit root properties of the six selected variables and identify the months in which structural breaks occur. The results are then analyzed to explain similarities and consequences using alternative testing methodologies. As discussed, each testing method applied will result in different specifications for the null and alternative hypotheses and will have varying quality in line with the underlying data generating process. Furthermore, the structure of deterministic terms included in the maintained regression will influence the asymptotic distributions of the unit root test statistics. As can be seen in
Figure 1, all the variables under investigation, similarly to typical financial time series, seem to be better approached by a random walk like process with drift, implying that the differenced time series behave very much like a white noise process. In this sense, throughout the testing process, the alternative, including a linear trend in the maintained regression, seems the most plausible description of the data under both null and alternative hypotheses [
34]. The standard conventional level for inference used is 5%.
3.1. Generic Unit Root Tests
In this subsection, we analyze the integrational properties of natural log prices in levels and first differences using generic ADF and KPSS (Kwiatkowski–Phillips–Schmidt–Shin) tests in order to examine whether all the variables can be considered, at least initially, first-order integrated in levels.
Table 2 summarizes the results of the various tests to account for the alternative that the time series is stationary, rejecting the unit root null in favor of the alternative (ADF test) or accounting for a stationary null versus the unit root alternative (KPSS test). It has to be noted that although all indications are that time series under investigation do have trends, we have also included non-trending model results, as these show more power to reject the null hypothesis than models including trends which are not contained in the data. In order to specify the number of lagged difference terms, i.e., lag length to be added to the test regression, we used the Akaike information criterion (AIC). The usual Ljung–Box Q-test to assess serial autocorrelation at the selected lags proves that in all cases the number of lags is sufficient to remove serial correlation in the residuals (this not shown in the table).
Test results clearly indicate that none of the six variables are stationary at the 5% level or better with than without a trend. The ADF test does not reject the null hypothesis of a unit root for the levels of the three prices. The KPSS test, in which the null hypothesis is stationarity, indicates that the null hypothesis is clearly rejected. When both tests are applied to the first-differences of the variables, results strongly imply stationarity. As discussed before, unit root tests can be misleading when structural breaks remain unaccounted for, tending to lose dramatically against stationary alternatives with low-order moving average processes [
21].
We use five additional procedures to test the null hypothesis that each time series contains a unit root including one or two structural breaks.
3.2. Unit Root Tests with One Structural Break
Prior to further testing, two main choices related to the nature of the DGP need to be made. First is the question about how the effect of the breaks is incorporated into the process, and secondly comes how to characterize the form of the break under the trend-break stationary alternative, i.e., mainly deciding about the most relevant model for inference. In regard to the first question, we will use econometric models preferably allowing for smooth transitions from one level to some other level over an extended period of time, i.e., innovational models. We believe that in our case, smooth transitions, sometimes expanding for a few months, are a more realistic option than assuming abrupt shifts to new levels. Regarding the second question, we argue that selection in the form of the break is correlated with the data and therefore we will favor the break specification according to the most general mixed model; this decision is also supported by specific research on this matter [
37]. Central to our investigation is the fact that misspecification of the form of the break can be critical and the performances of the different tests used may vary significantly depending on the break model selection.
Following the decision to consider the break as unknown but also joint inference overall, the general-to-specific principle, widely used in model selection, seems best suited for our analysis. Therefore, we initially start with a general specification that incorporates a changing intercept (crash model) and then continue with a combined assumption for the break behavior including intercept and trend break (mixed model). We then evaluate the inference provided and the significance of the coefficients of the dummy variables.
Table 3 shows the empirical results for the location of the break and inference from the ZA (t
αZA) and VP unit root tests either minimizing the t-statistic for the intercept break coefficient using a crash model (t
θ) or over the maximum t-statistic for the absolute trend break coefficient t
IδI using a mixed model (t
|θ|). In all cases the method for deciding the number of additional lags in the autoregressive equation is given by BIC. Inferences on nonstationarity in cases of discrepancy between models indicate rejection or acceptance of the unit root null according to the models which show the most robust specifications. In addition, results from the LLS tests where the level shift point (τ) is viewed as an unknown valued parameter, from the KP tests (t
αλ) and from the minimum LM unit root test statistic (t
αLS), are also shown. It has to be noted that the presence of the endpoints causes the asymptotic distribution of the statistics to diverge towards infinity. Therefore, trimming is performed to remove endpoint values from consideration as the break date in all cases.
As can be seen, large negative values for the test statistics might reject the null hypothesis of a unit root, and therefore, according to this, we are unable to reject the unit null hypothesis for any of the variables except for fuel oil when applying VP tests and for NBP applying either LLS or KP tests at a significance level of 5%. These results show that market-related events may have stronger effects on some variables than others. The case of LSFO is very interesting considering the commodities price drop at the end of 2014 using the crash model—it led to higher power when the intercept break was large and the slope break was small, resulting in long-term stationarity. Perhaps the fact that LSFO is the least traded commodity of the oil-related commodities might be a reason for it.
In addition, some detailed considerations can be outlined.
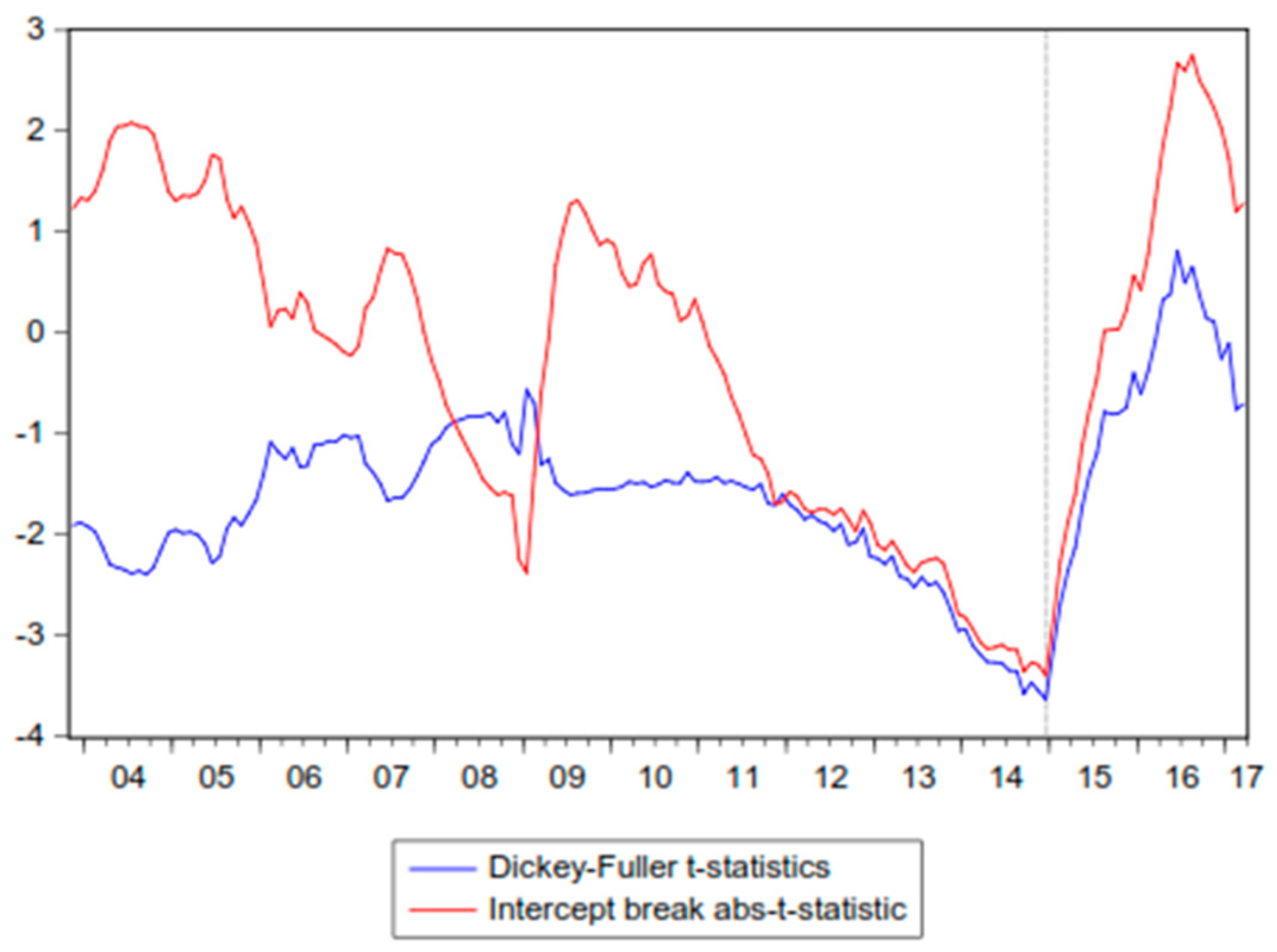
Figure 3 shows tests statistical results for Brent prices using the VP break date selection process while maximizing the intercept break of the abs-t-statistic (t
|θ|), and over the Dickey–Fuller (DF) t-statistic (this not shown on
Table 3). As can be seen, both methodologies clearly coincide in giving the most weight to an estimated breakpoint located at the end of 2014 rather than around 2008.
It has to be noted that in the case of LLS tests, selecting the AR order has proved to be critical in order not to jeopardize power of the test. During the testing process, overstating the AR order reduces power progressively, whereas severely understating the order makes power drop comparatively faster. In our case and following LLS indications, a reasonably large AR order, i.e., six, has been used to select the break date. In the case of the KP test, as discussed previously, the modelling approach concentrates on estimating the break date by minimizing the sum of squared residuals, and only the results from the innovational model test are shown, for consistency with the original strategy.
3.3. Unit Root Tests with Two Structural Breaks
The results of the Lumsdaine and Papell [
22] (LP) and Lee and Strazicich [
30] (LS) unit root tests with two structural breaks are presented in
Table 4.
As can be seen, all unit root tests with two structural breaks suggest nonstationarity for all the variables, which is an indication of the ability of the two-break test to expand on insights in regard to long periods of time [
14]. Regarding the locations of break dates, the effect of the sharp downturn in prices at the end of 2014 is overwhelmingly present in all the time series analyzed except for NBP and coal. Interestingly, the impact of the financial crisis in 2008 is only revealed when applying the two-break tests, possibly indicating that supply–demand fundamentals were the main driver of oil products’ dynamics over the whole period analyzed and in spite of 2008’s events. As can be seen from
Table 4 above, LLS tests’ break date selection picked breakpoints that slightly differ from other tests. In this sense, it is important to note that the rather different development of how to model the impact of the break, distributed over time, as in the case of VP or LS models, compared to the impact of the break being complete within the period TB + 1, as in the LLS case, may reasonably affect the nature of the results.
Again, NBP results reflect better gas market events, such as those in 2006, rather than the oil crash in 2008. In addition, although coal prices appear to be very reflective of 2008’s events, as would be expected of a global commodity, other coal market episodes captured do not coincide with oil-driven shocks. It has to be noted that detection of both intercept and slope breaks in the mixed model seems to work properly, especially for LP tests. Results from the LM tests are more difficult to reconcile and they show poorer break-detection capabilities than LP tests.
4. Discussion
This section provides a discussion on the key market factors underpinning price series evolution in view of the results shown. Over the period of interest, i.e., 2002 to 2018, there are three specific sub-periods to note. First, the period until mid-2008 with prices steadily increasing due to strong demand growth for crude oil driven by non-OECD countries, particularly China and India. Second, the period after the second half of 2008—the sharp decline of commodity prices—quickly followed by a surge in the price of oil and a period of relatively stable but historically high prices, and finally, the commodity price collapse between mid-2014 and early 2016, driven by a mounting supply glut followed by a rebound in investment and trade against a backdrop of benign global financing conditions overall. In line with this chronology of events, our investigation reveals key aspects of the response of each market to shocks considering both crash and mixed modelling developments.
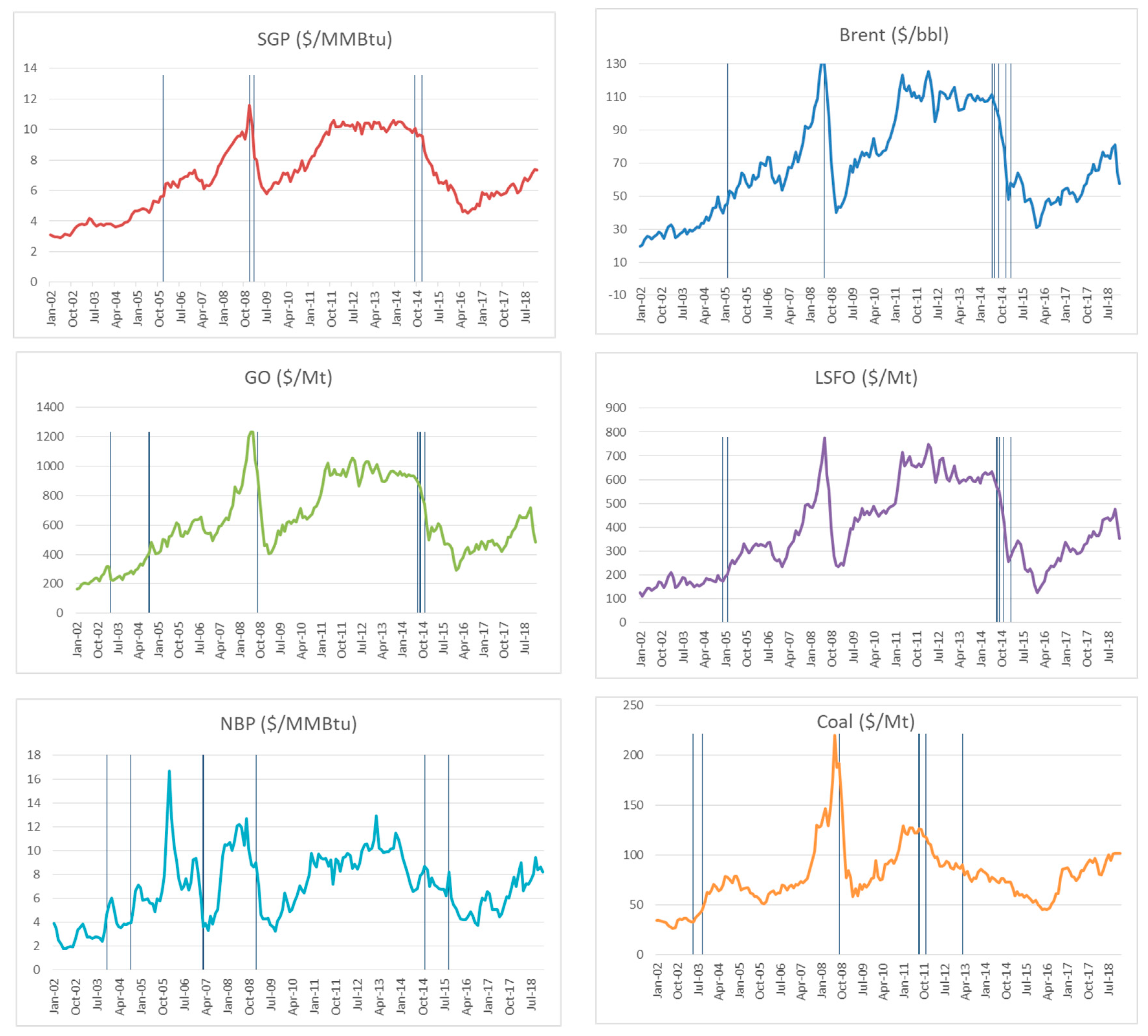
Table 5 and
Figure 4 show for each of the six variables analyzed the corresponding structural breaks according to the crash model effects, i.e., permitting a one or two-time change in the level of the time series. It is noted that allowing for two breaks produces a richer set of results, not necessarily more precise definition of the locations of break dates.
In general, the sequence of relevant outliers found for all the time series considered indicates that the 2014–2015 price crash was without any doubt the most influential event over the period for the crude oil and oil-related variables, including Spanish gas import prices. Only when the scope of the research is expanded upon with two breaks, does the 2008 financial crisis manifest itself—not for LSFO though. Interestingly, both NBP and coal prices typically show a response to their own market events and not to oil price shocks. In the case of NBP, periods of high volatility during the winters of 2003–2004 and 2004–2005, with actual shortages creating significant seasonal upward pressure on prices, seem to be more relevant than oil-related events over the whole period analyzed. Moreover, crash modelling for NBP prices reflects very vividly the gaps which opened between NBP and continental gas prices in the period of November 2006 to July 2007, and also in the fourth quarter of 2008 as a recession in the UK hit hard and the lag in long term contracts meant that falling oil prices were much slower to feed through into gas prices (see SGP chart over the same period). Finally, the analysis also reveals the highly relevant nature of gas-market events in the last part of 2015, not coinciding with the crude oil price drop in 2014.
In the case of coal, our analysis reflects the multidimensional nature of coal market-driven events, such as the coal price increase by 40–50% in one year between 2003 and 2004, as much as the fact that prices fell drastically in the wake of economic downturns starting in autumn 2008, affecting both coking coal and steam coal markets through lower automobile sales and electricity consumption decline [
38]. In particular, the trend of declining prices since 2011, by around 50% until 2015 [
39], due to increasing supply and subdued demand for thermal coal, is clearly shown in our results.
Table 6 and
Figure 5 show for each of the six variables analyzed the corresponding structural breaks according to the mixed model effects, i.e., permitting a one or two-time change in the level and in the rate of growth of the time series.
As it can be seen, for crude oil and oil-related products the influence of the downturn in 2014 is lower than in the crash model, and oil price recovery after 2008 events and into 2010–2011 seemed to be more important relative to changes in slope; the same goes for LSFO. Again, the NBP and coal’s different profile became evident. Viewed in perspective, this is not a minor issue and reinforces the case for the UK’s market having its own dynamics, in spite of the continental European oil linkage [
40]. As it can be noticed, exceptionally high gas prices in the UK during the winter 2005–2006 as a result of the January 2006 Russia–Ukraine crisis, followed by a spell of extremely cold weather and the fire at the UK’s Rough storage facility, were extremely relevant to a change in slope of NBP prices. Regarding coal market developments, breakpoints signaling meaningful changes of slope are emphasized more and more clearly in late 2008 as a result of weak global demand and easing supply conditions. Changes in slope during the declining trend since 2011 that continued into 2014–2015 are also detected. It is interesting to notice that since late 2014, the development of European spot prices of coal and gas show remarkable similarity, suggesting that the relative competitiveness of the two fuels remains stable.
5. Conclusions
It is now widely admitted that failing to check for the structural break effects in time series’ properties leads to confusing results in regard to the assessment of stationarity properties. In particular, traditional unit root tests may have little power when the true data generating process includes a broken trend and is stationary. In this research we investigated the stochastic properties and changing trends of six non-renewable resource prices throughout a structured strategy with a view toward optimize the testing quality, validity, and relevance of results in the presence of structural breaks. Our main innovation in this sense is that we brought together a wide-ranging panel of model specifications combining traditional endogenous testing approaches and pre-detection techniques.
Our main findings are as follows. When we applied generic tests, we were unable to reject the unit root null hypothesis for any of the six variables analyzed. However, when we applied the VP test allowing for one structural break, we found strong evidence for the stationarity of fuel oil and also for NBP when using either the LLS model or the KP model. These results confirm the findings of previous research revealing the high degree of persistence shown by crude oil and gasoil prices, but they also reveal the potential for a stationary trend process for fuel oil. In the case of NBP, the results found for stationarity when using pre-testing methodology led to us thinking that one of the main factors supporting the controversy over the persistence of market-related time series, such as UK gas prices, might be the considerations about the inference process itself and the approximation to assumed knowledge of the true break date.
Of separate interest are the break dates themselves. The results indicate that the 2014–2015 price downturn was without any doubt the most influential event over the period for all the non-renewable variables analyzed, and especially significant for the intercept of fuel oil, turning its long-term dynamics towards stationarity. Only when the scope of the research was expanded with the two-break tests, were the 2008 financial crisis’s effects manifest. Interestingly, both NBP and coal price trends show that their dynamics are mainly affected by their own market events and not directly by oil price shocks, this in spite of sharing common industry fundamentals on a timely basis, such as depressed demand or oversupply situations. As evidence of this, our results show that, even under the two-break tests, the effects of 2008 and 2014 downturns on NBP and coal prices are very limited. The case of coal prices’ drastic drop in the last part of 2015, not coinciding with crude oil price drop in the second half of 2014, is a good example of this.
The results have significant consequences for economic analysis, forecasting, and policy-making decisions. In particular, when modelling non-renewable energy resources, it will be critical to account for structural breaks while testing for unit roots. Moreover, our findings reveal that in developed markets long-term dynamics may be mainly achieved by genuine market dynamics resulting from the free interplay of market forces—this fact does not necessarily lead us to believe that less developed national markets behave like unit root processes. Further to this research, we suggest expanding investigations on the relationship between traditional energy resources’ prices and renewable generation prices, consistently interconnected through competition in gas and electricity markets. In line with this, an interesting issue not analyzed in the study is the evolution of the relationship between prices for natural gas and coal and in spite of price regulation for coal masking that relationship over long periods. Finally, and as another route of investigation worth exploring, we believe that cointegration and long-run equilibria of non-renewable energy variables, especially applying new methodological innovations in cointegration analysis, such as non-linear cointegration, could shed more light on the complex interactions analyzed in our study.