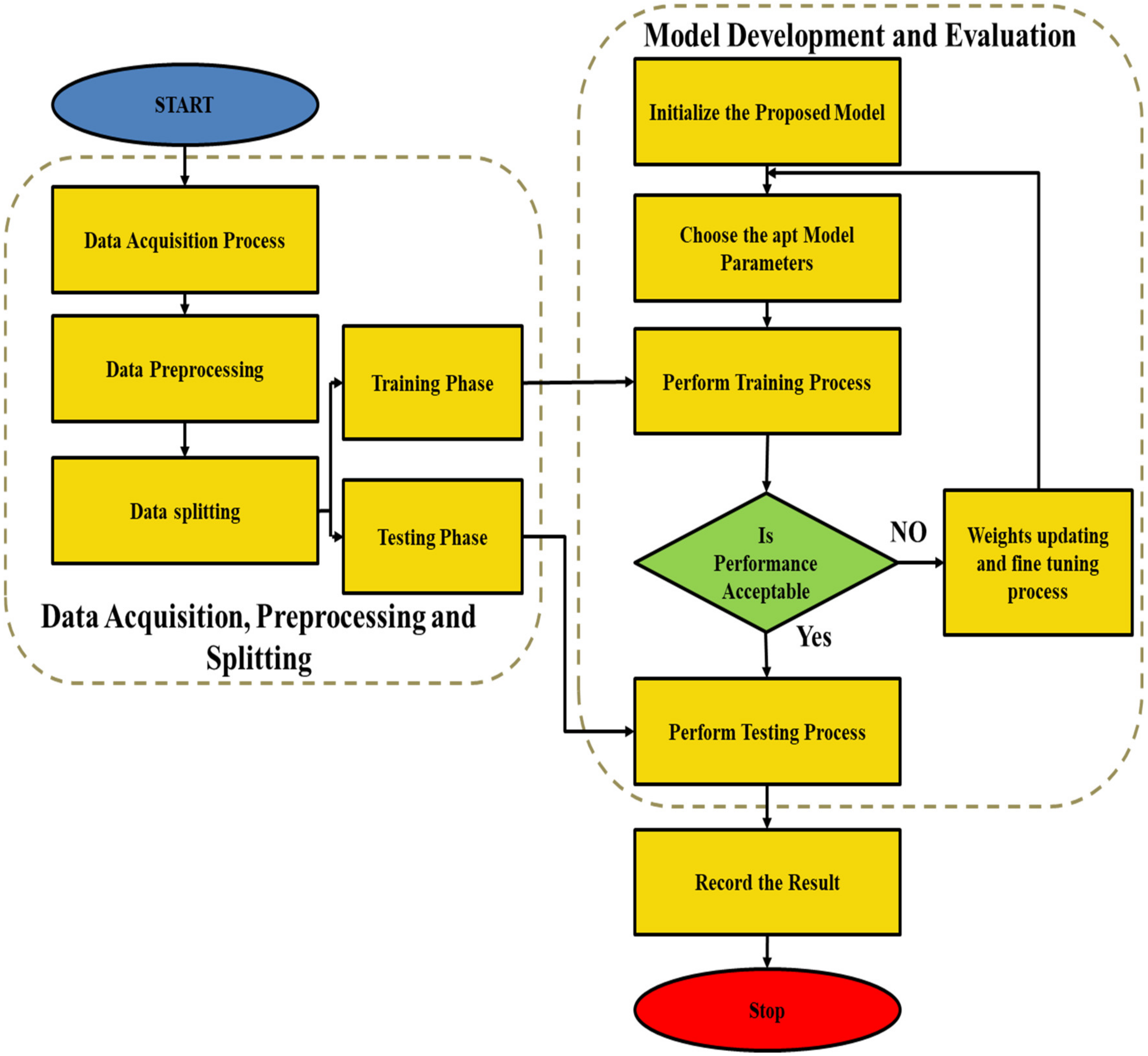
3. Proposed Model Result and Discussion
Electricity load forecast depends on various factors such as geographical location, atmospheric weather conditions, types of days and seasons, subsidies, and energy tariffs. Hence, it possesses irregularities and uncertainty; it creates demanding and challenging tasks for accurate electricity load forecasting. This paper endeavors an electricity load forecasting model using a multilayer perceptron neural network; the proposed model was experimentally conducted on the MATLAB platform. The proposed forecasting model was run on an Acer laptop with a Pentium (R) dual-core processor of 2.30 GHz, RAM: 2 GB. The presented forecasting model’s performance was validated using ERCOT data sets. ERCOT data sets and ENTSO-E data sets with different input parameters are collected and used as training and testing sets.
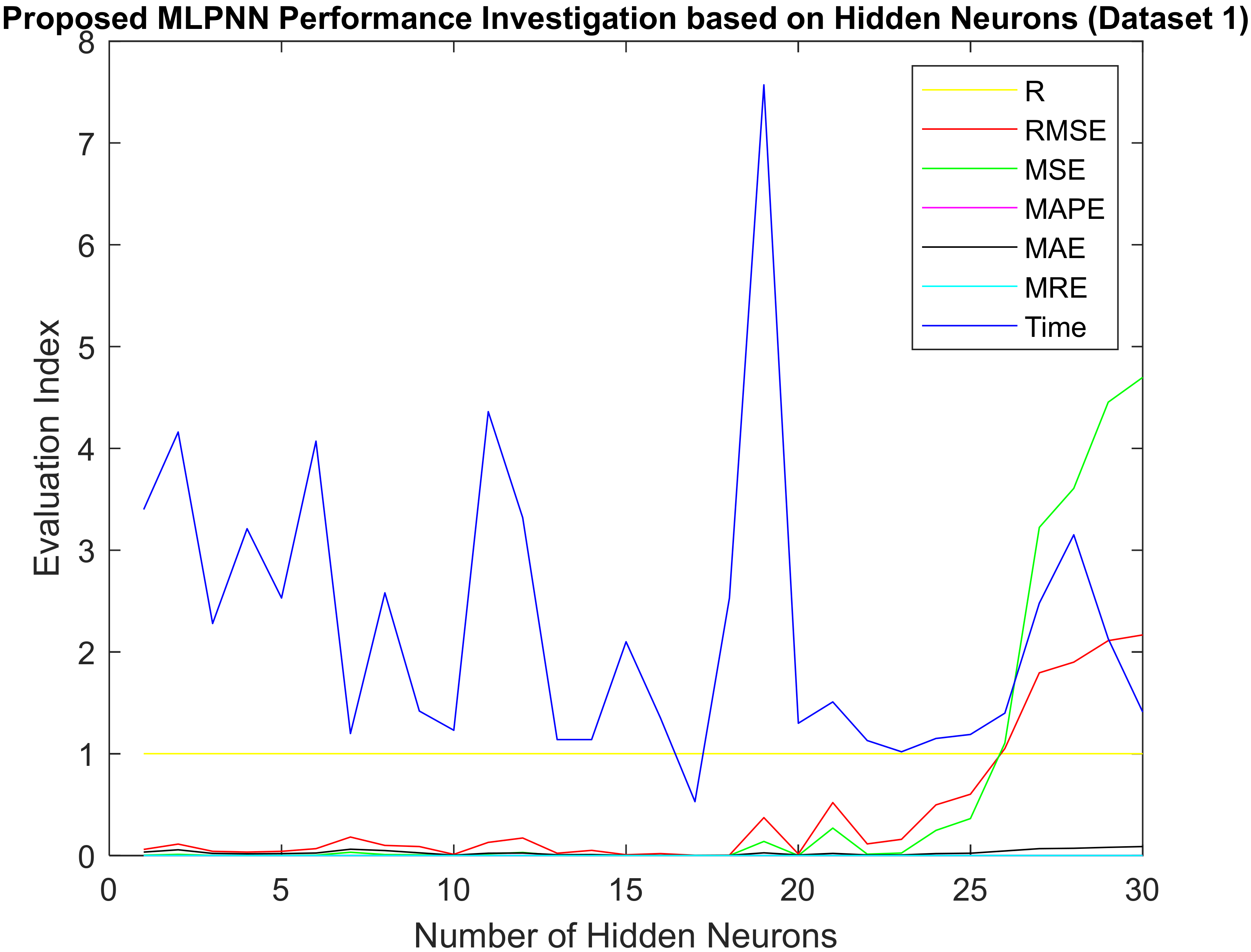
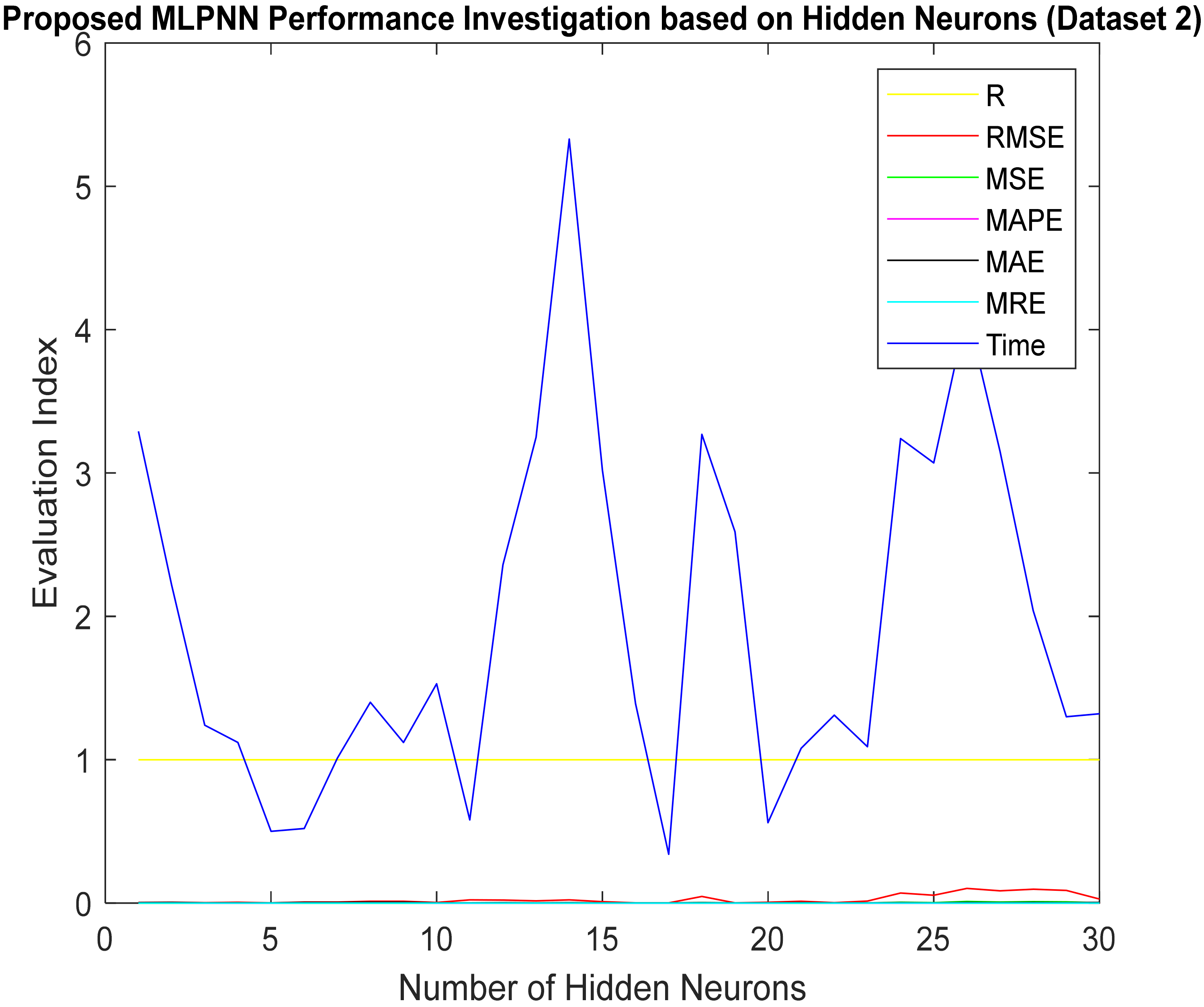
The hidden neurons possess a critical role in the artificial neural network’s stability and accuracy; improper selection of hidden neurons leads to poor performance, underfitting, and overfitting problems. Hence, this paper carried out a performance investigation concerning the various hidden neuron placements in the hidden layer of the proposed multilayer perceptron neural network to resolve the hidden neurons’ issues. The proposed model-based results regarding various hidden neurons concern the electricity load forecasting tabulated in
Table 3 and
Table 4.
The number of hidden neurons that influence the neural network is understood clearly from
Table 3 and
Table 4,
Figure 4 and
Figure 5, respectively, for Dataset 1 and Dataset 2, which shows that the hidden neurons are essential in neural network stability, and convergence.
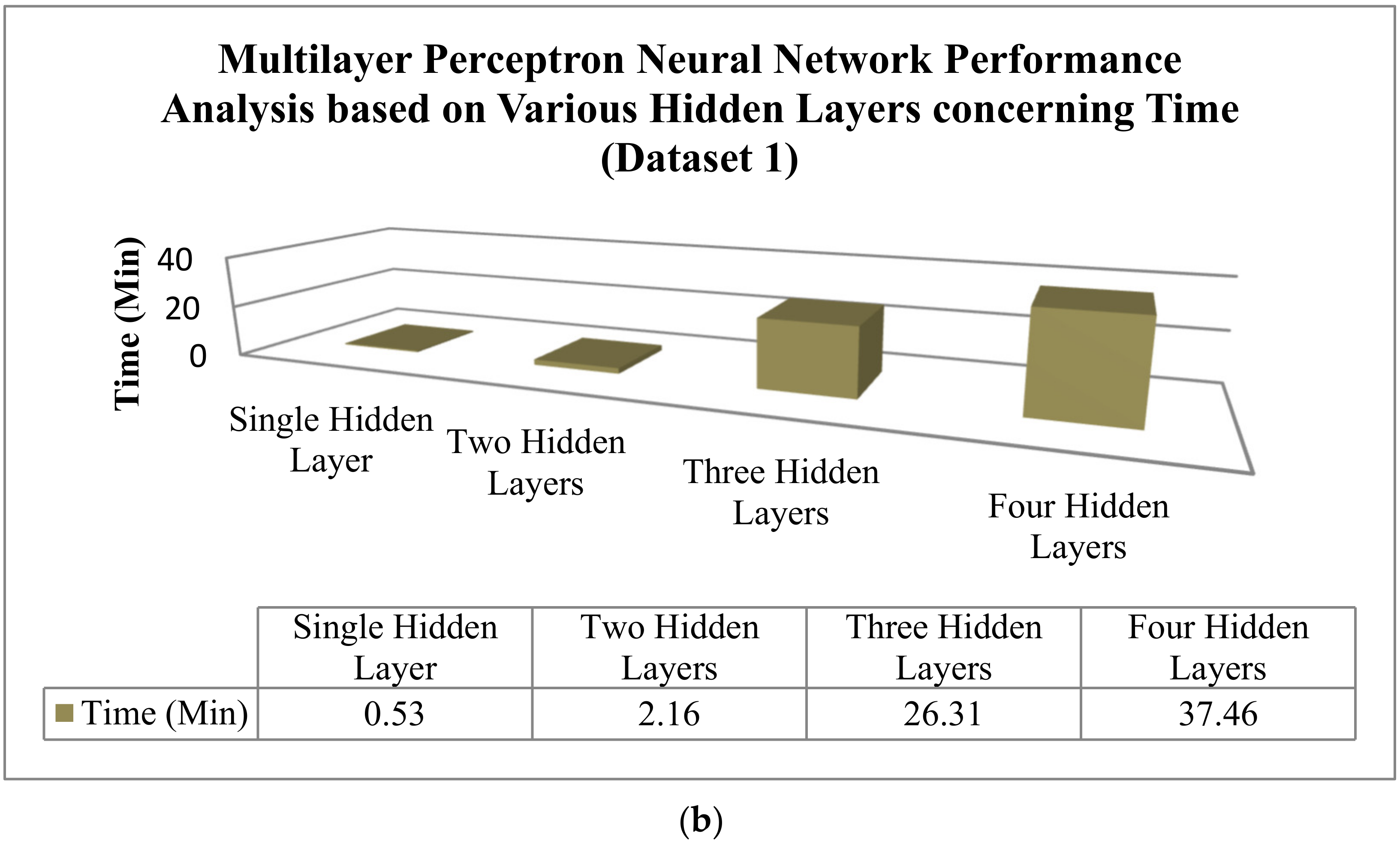
From the careful investigation of
Table 3 and
Table 4, it is noted that the proposed model with 17 hidden neurons in the hidden layer achieves the minimal evaluation index as RMSE = 0.0034, MSE = 1.1506 × 10
−05, MAPE = 2.3633 × 10
−05, MAE = 0.0021, MRE = 2.3633 × 10
−07 and R = 1, convergence time is 0.53 min for dataset 1, RMSE = 6.3358 × 10
−04, MSE = 4.0142 × 10
−07, MAPE = 7.5578 × 10
−05, MAE = 4.5615 × 10
−04, MRE = 7.5578 × 10
−07 and R = 1, convergence time is 0.34 min for dataset 2. Hence, this hidden neuron (17) was selected as the optimal hidden neuron. Further investigation concerning different forecasting horizons was performed based on the optimal hidden neurons based on the implemented proposed model.
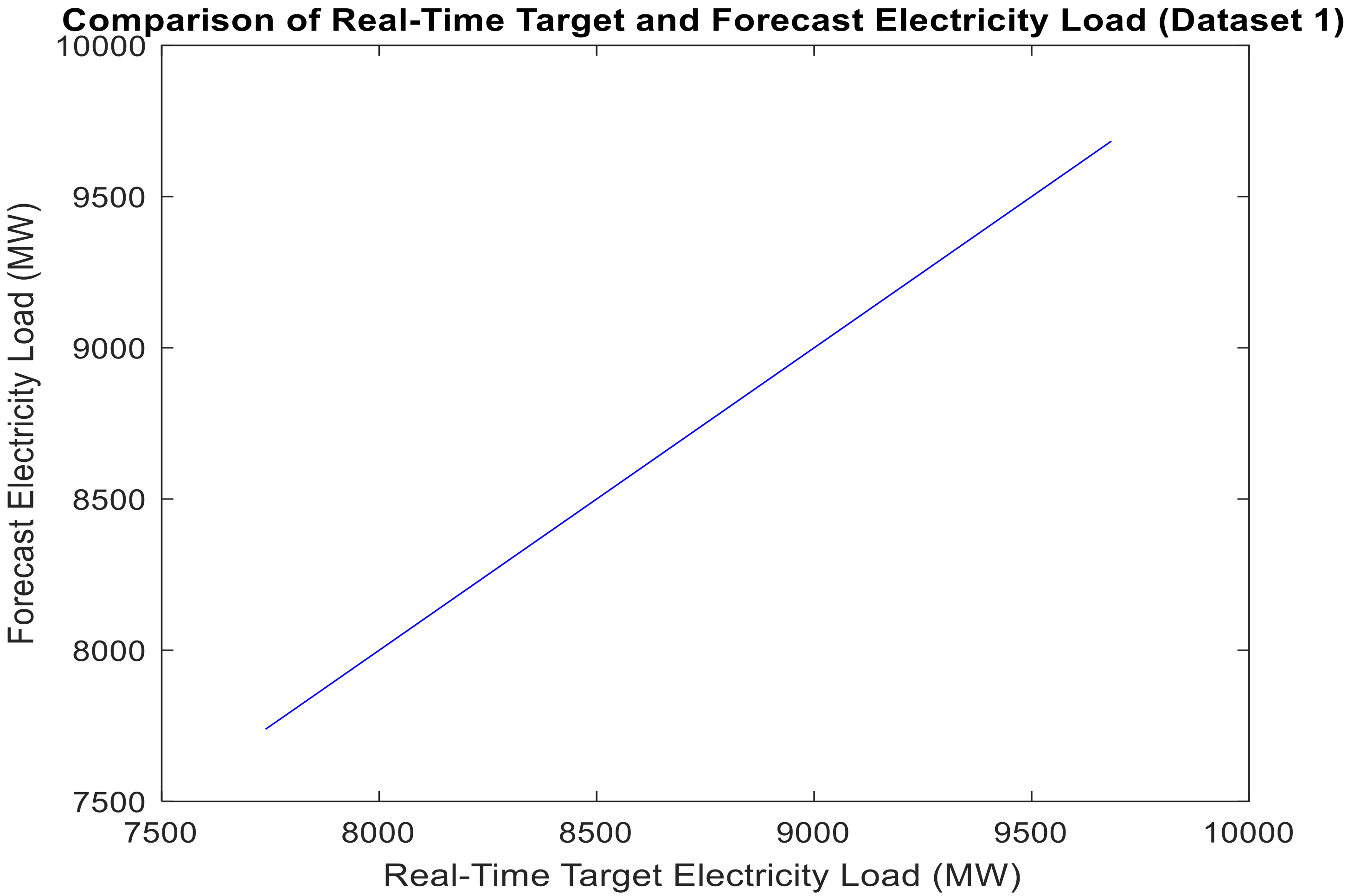
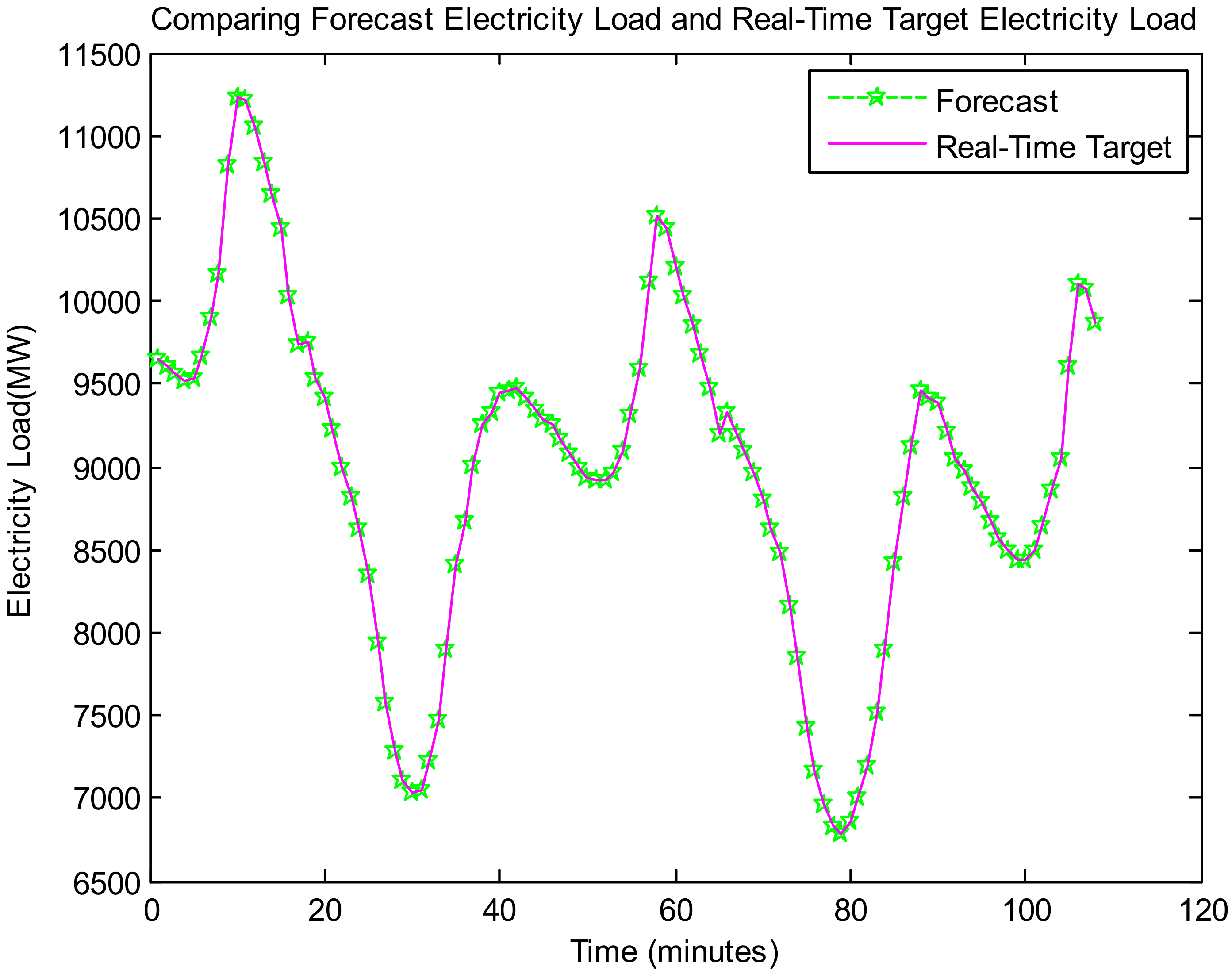
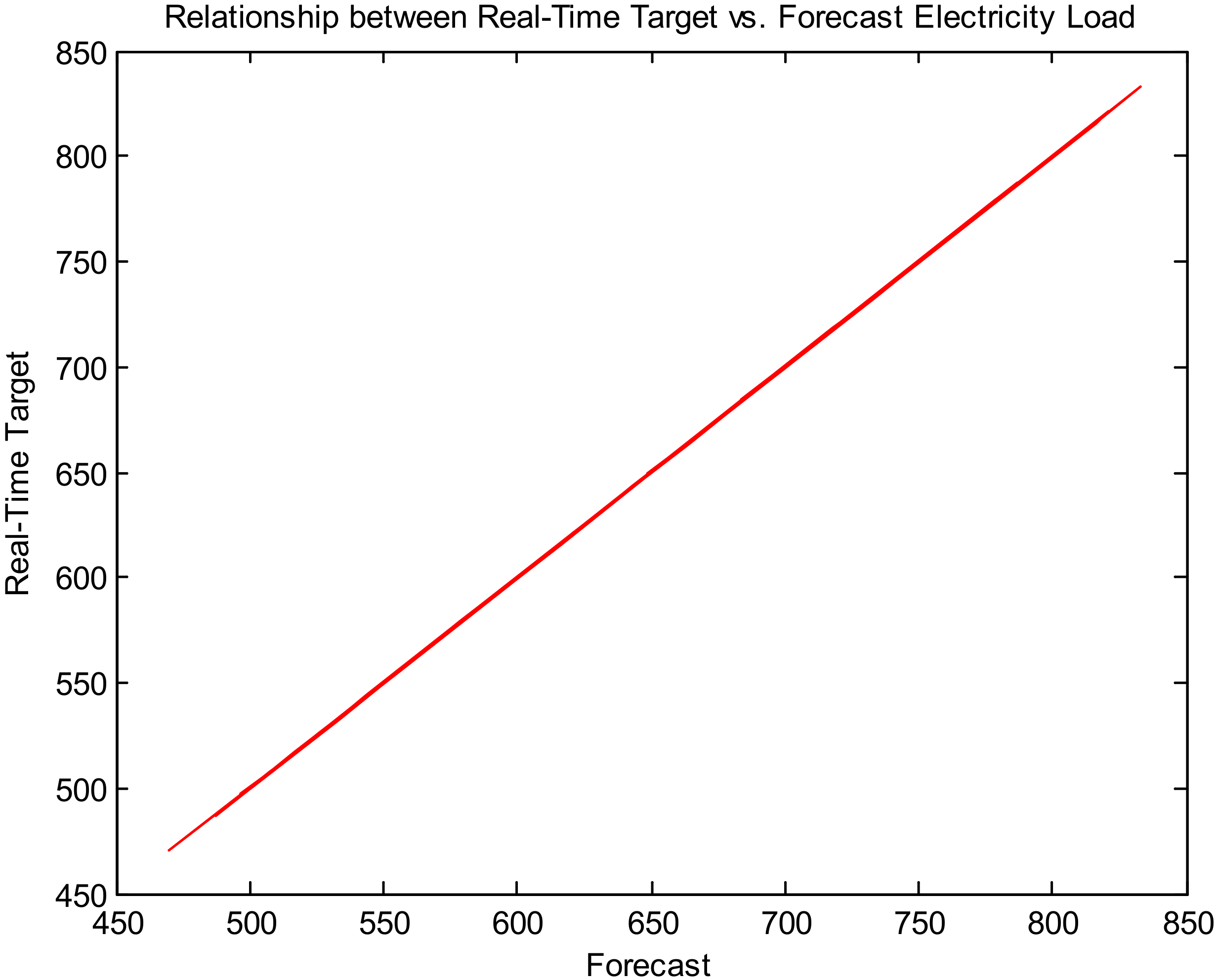
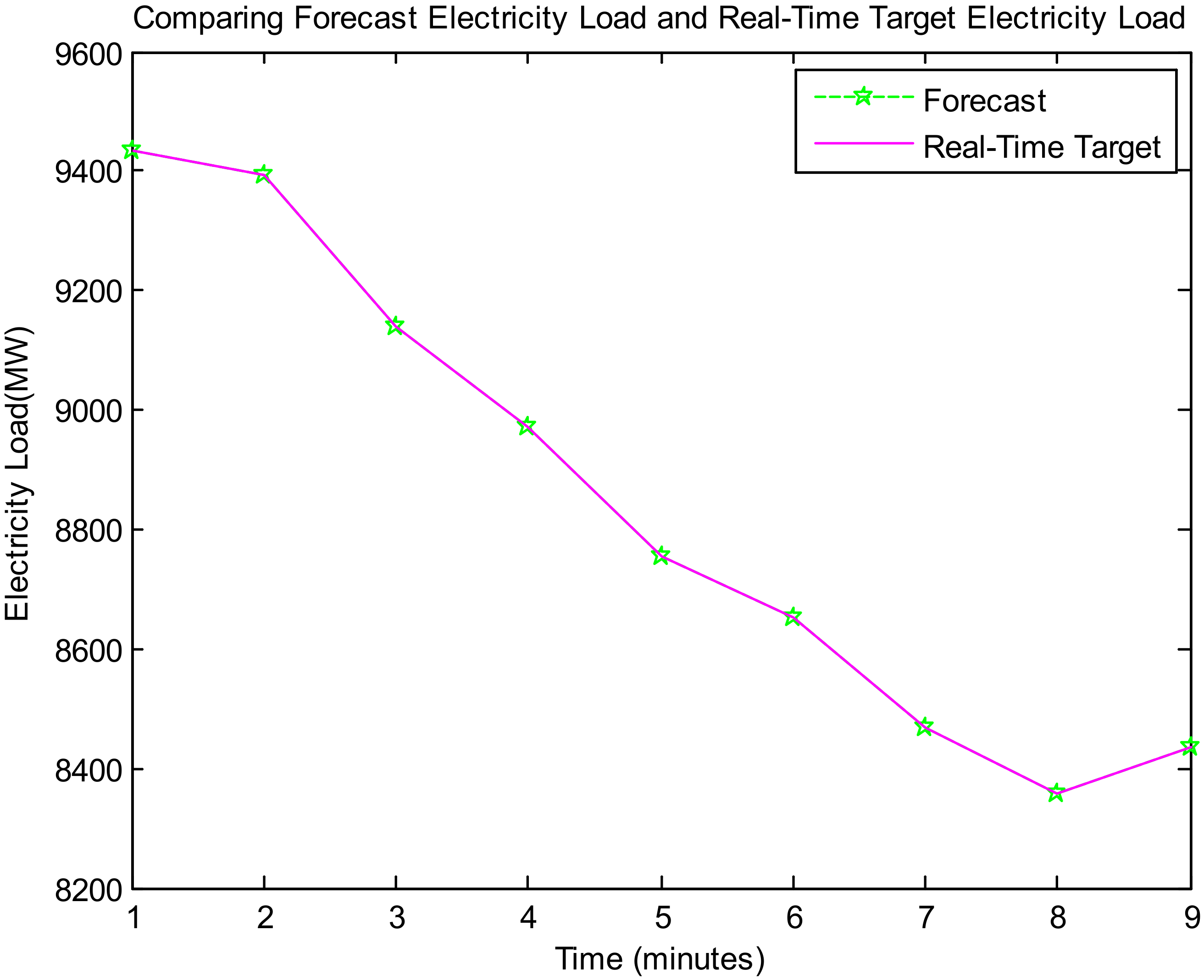
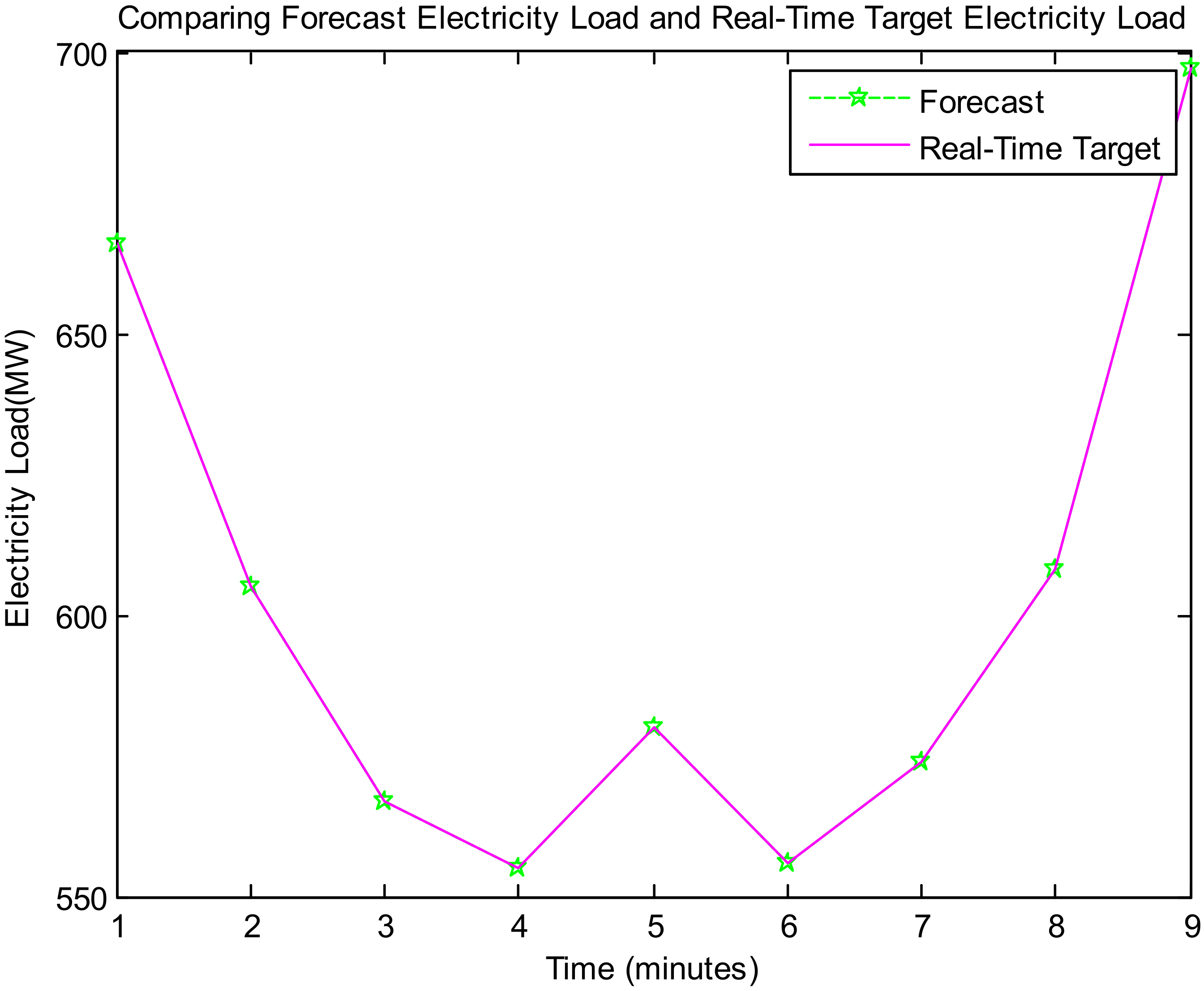
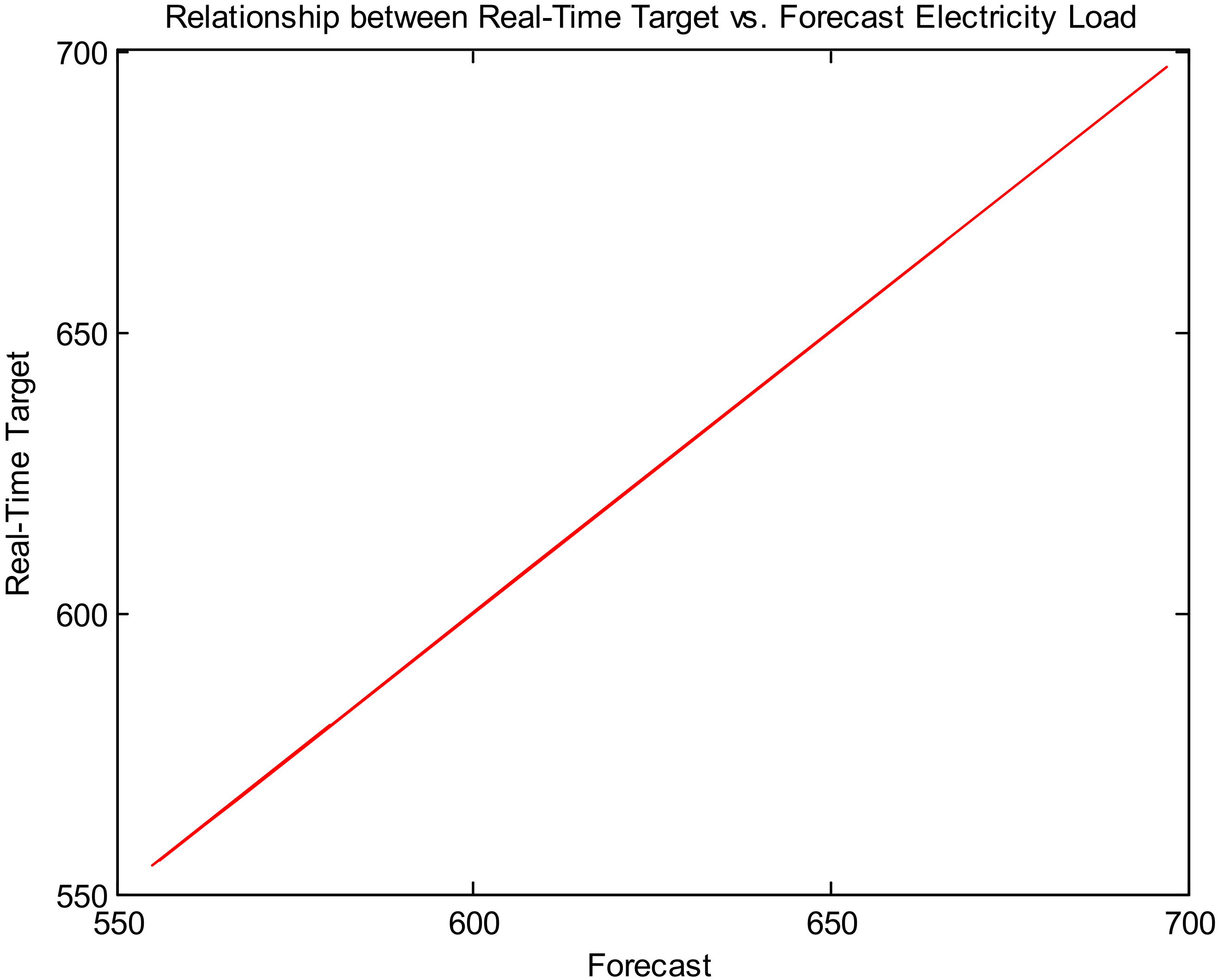
Table 5 and
Figure 6 present the comparison of real-time and forecast electricity load (Dataset 1).
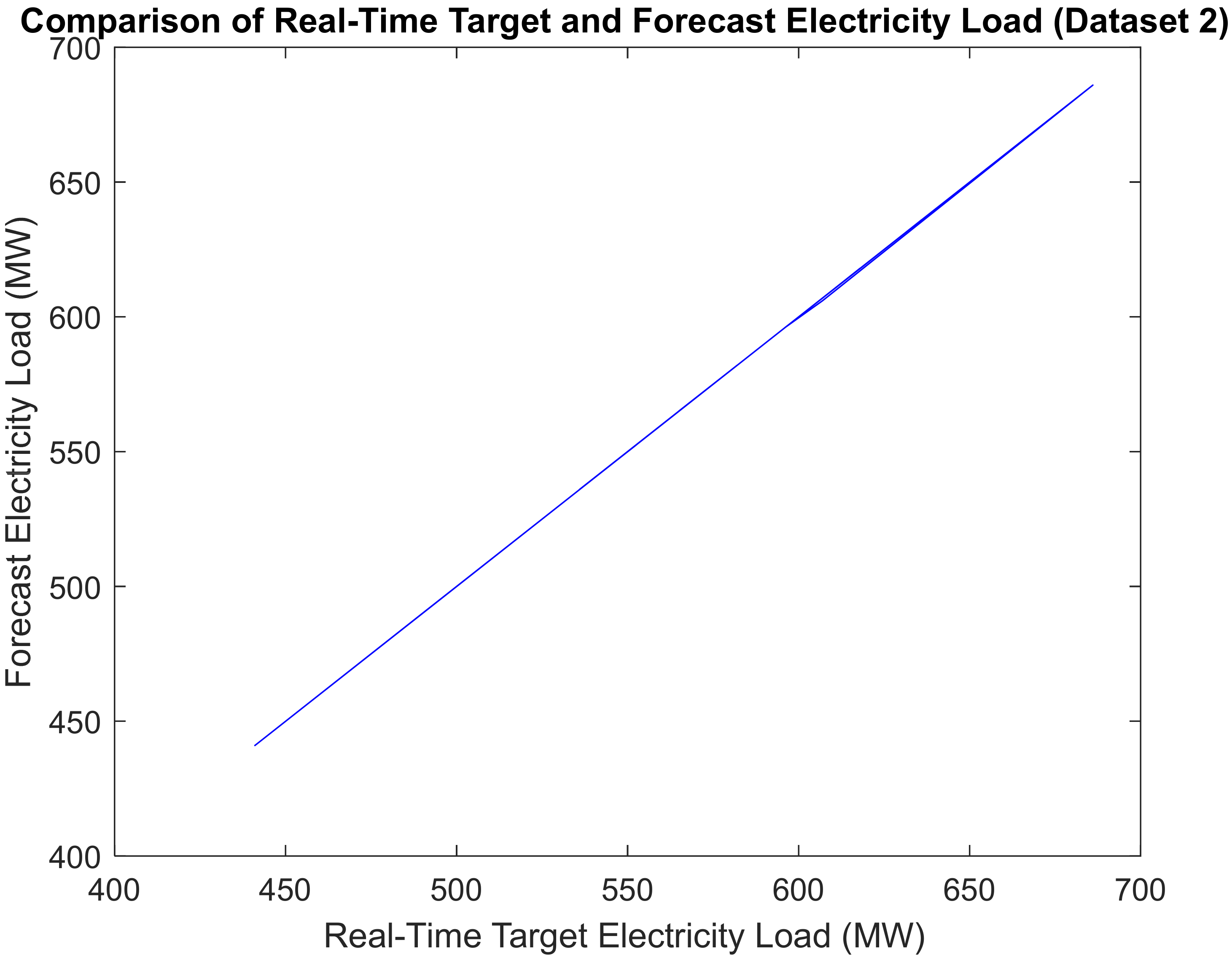
Table 6 and
Figure 7 depict the comparison of real-time and forecast electricity load (Dataset 2). As observed from the obtained simulation results shown in
Table 5 and
Table 6 and
Figure 6 and
Figure 7 is the proposed model to accurately match the forecast electricity load with the target real-time electricity load. It indicates the proposed model’s validity.
Decaying the power shortage issue and meeting the future electric energy requirement, different forecasting horizons based on electricity forecasting are obligatory. Our primary motive is to forecast the highly accurate load forecasting concern for various time horizons. The input electricity load depends on the time horizon forecast range. The output load is the ahead forecasting concern with different forecasting horizons compared with the real-time target load.
Long-term forecasting: The proposed long-term forecasting model can forecast the weekly/monthly/yearly ahead load forecast. Long-term load forecasting plays a significant role in power system planning, expansion, and operation management.
Medium-term load forecasting: The proposed medium-term load forecasting model forecasts 6 h to 24 h (1 day) ahead of the load forecast. Medium-term load forecasting is helpful for power system load scheduling, load balancing, reserve planning, and control.
Short-term load forecasting: The suggested short-term load forecasting model forecasts the load in 30 min to 6 h ahead of the load forecast. Short-term load forecasting is essential for unit commitment, economic dispatch, and the electricity market.
Very short-term load forecasting: The presented very short-term load forecasting covers a period of 1 min to 30 min ahead of the load forecast. Very short-term load forecasting is helpful for the deregulated power industry and energy prizing.
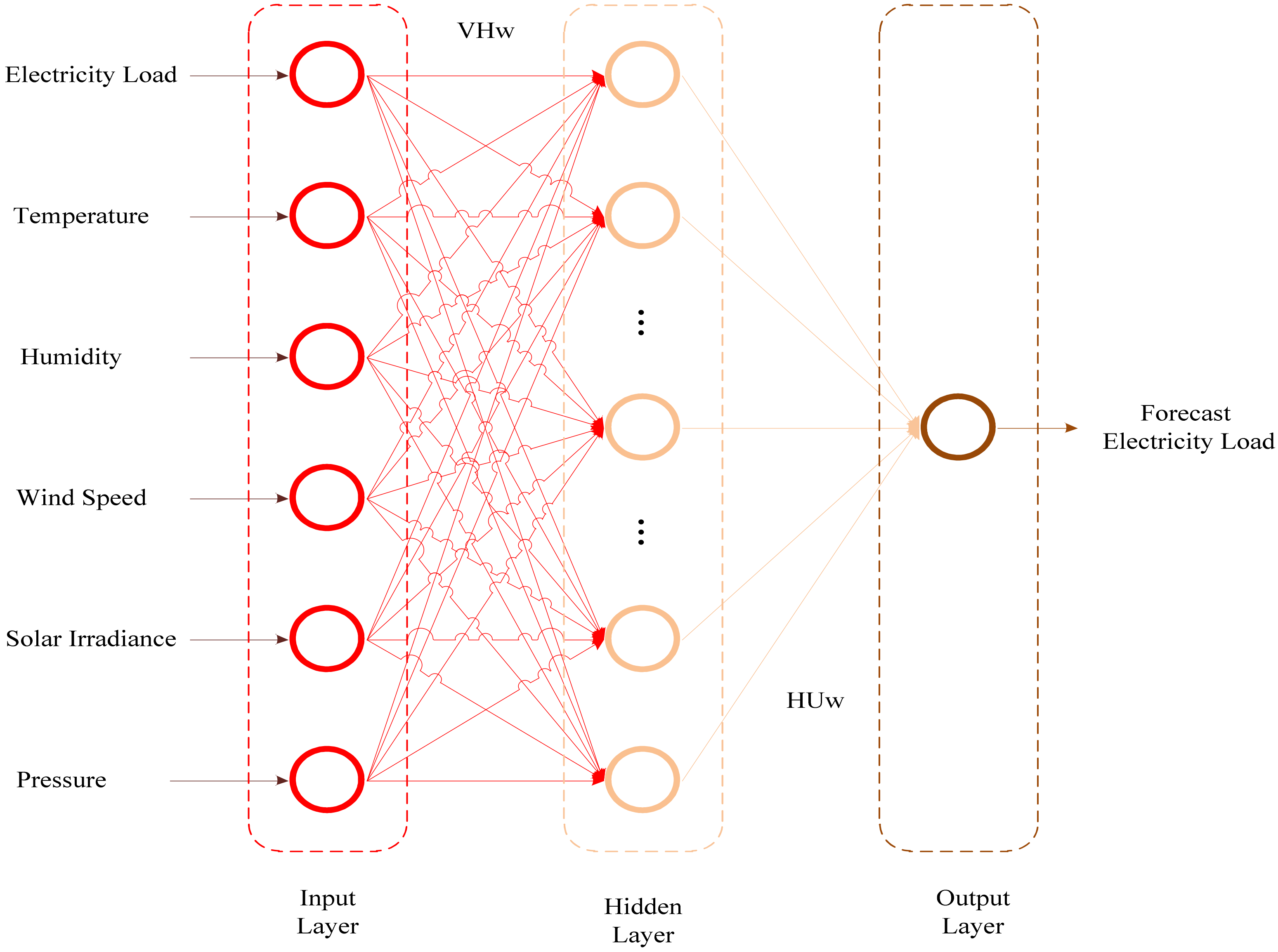
In this paper, the authors propose a different forecasting horizons model mentioned above, range or period ahead load forecasting, which overcomes the issues related to energy and load management and aids power system engineers. Although the authors already specified the proposed model inputs in
Table 1 and
Table 2 and
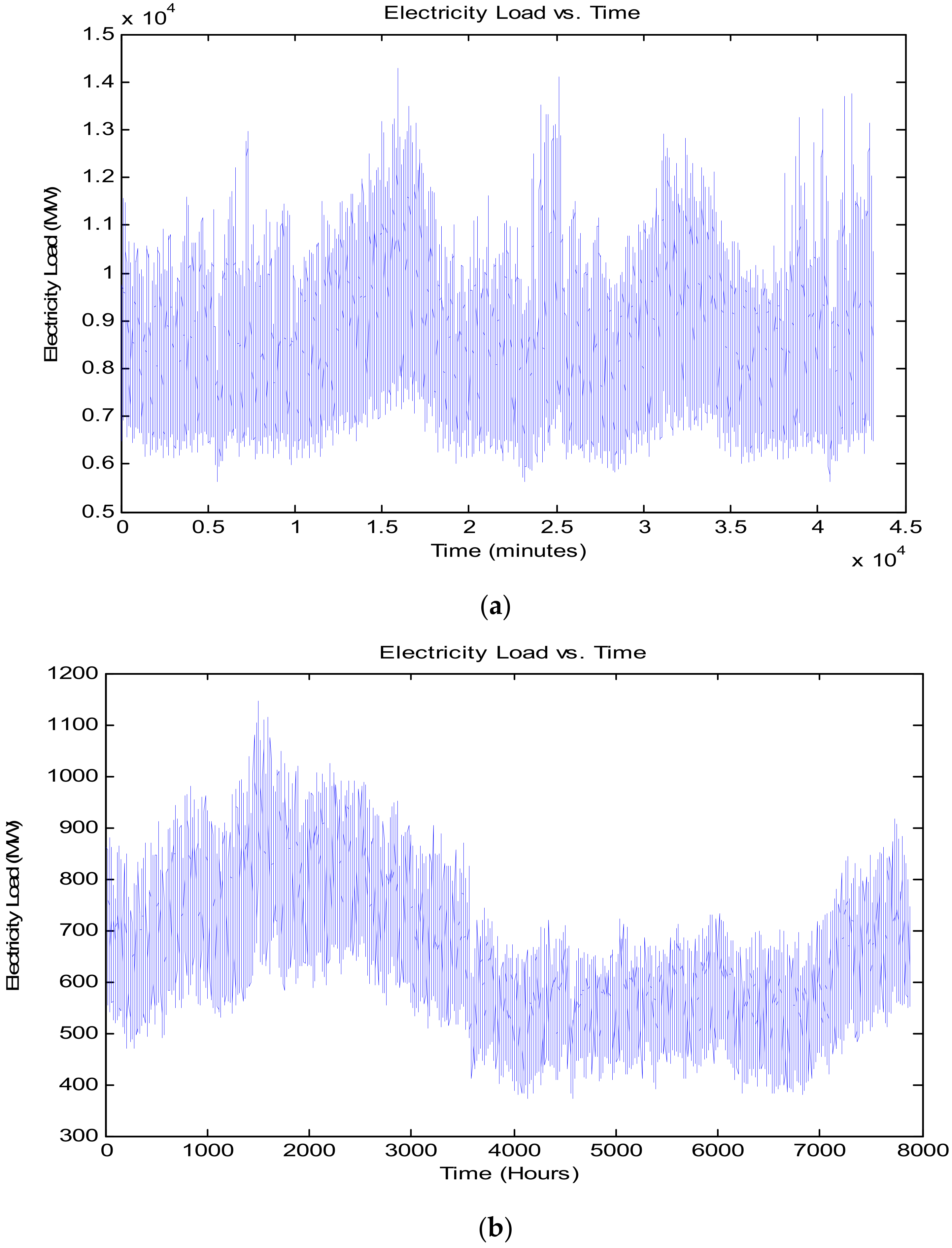
Figure 1 to make it clearly understood it was mentioned again as the proposed load forecasting model built based on six inputs, namely, electricity load (MW), temperature (°C), humidity (%), wind speed (m/s), solar irradiance (W/m), and pressure (bar). For Dataset 1 comprises 5.256 × 10
6 data points of each taken input variable, and Dataset 2 shall comprise 7.884 × 10
4 data points of each taken input variable. Depending on the time horizon, as mentioned above, the input time span varies.
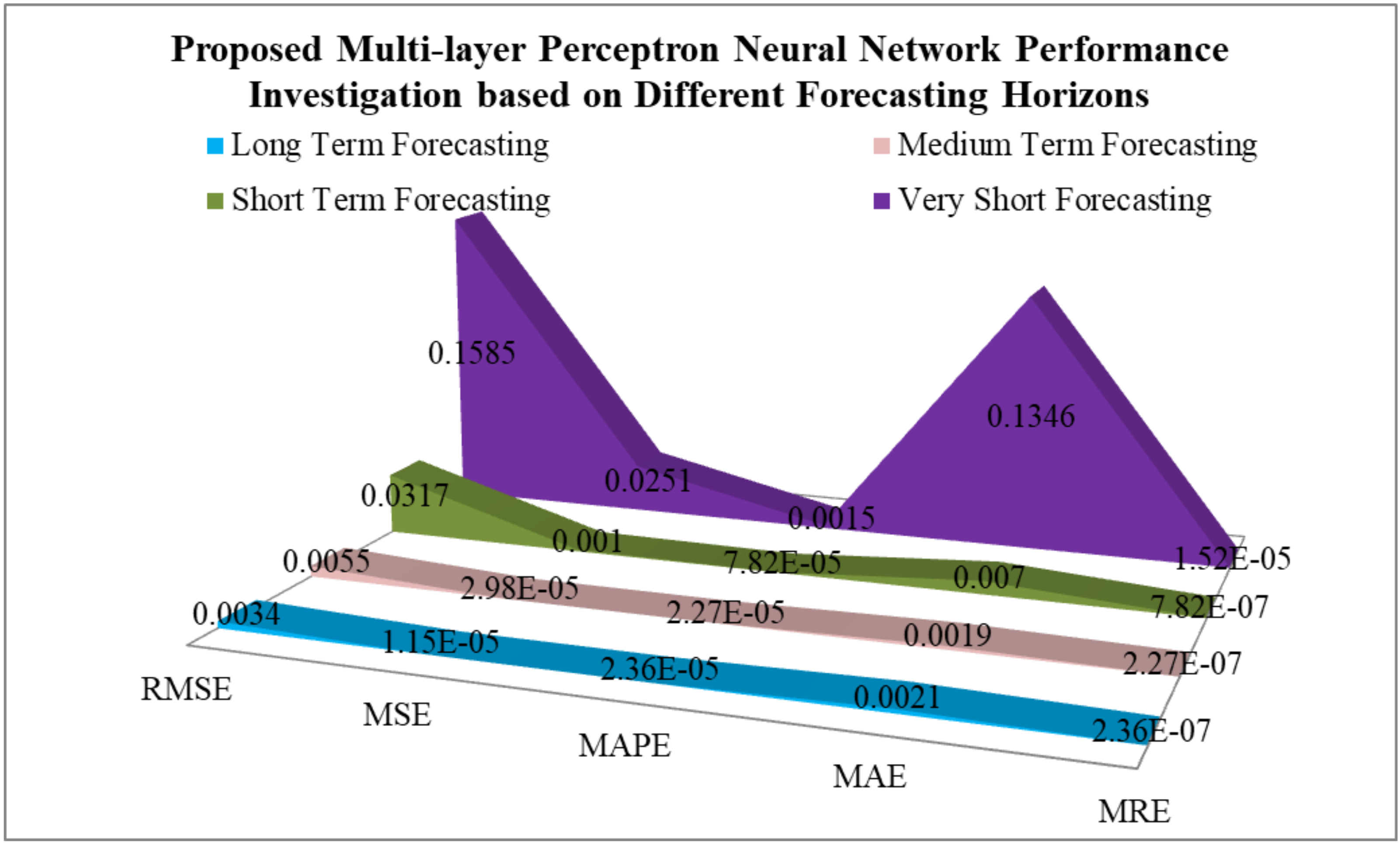
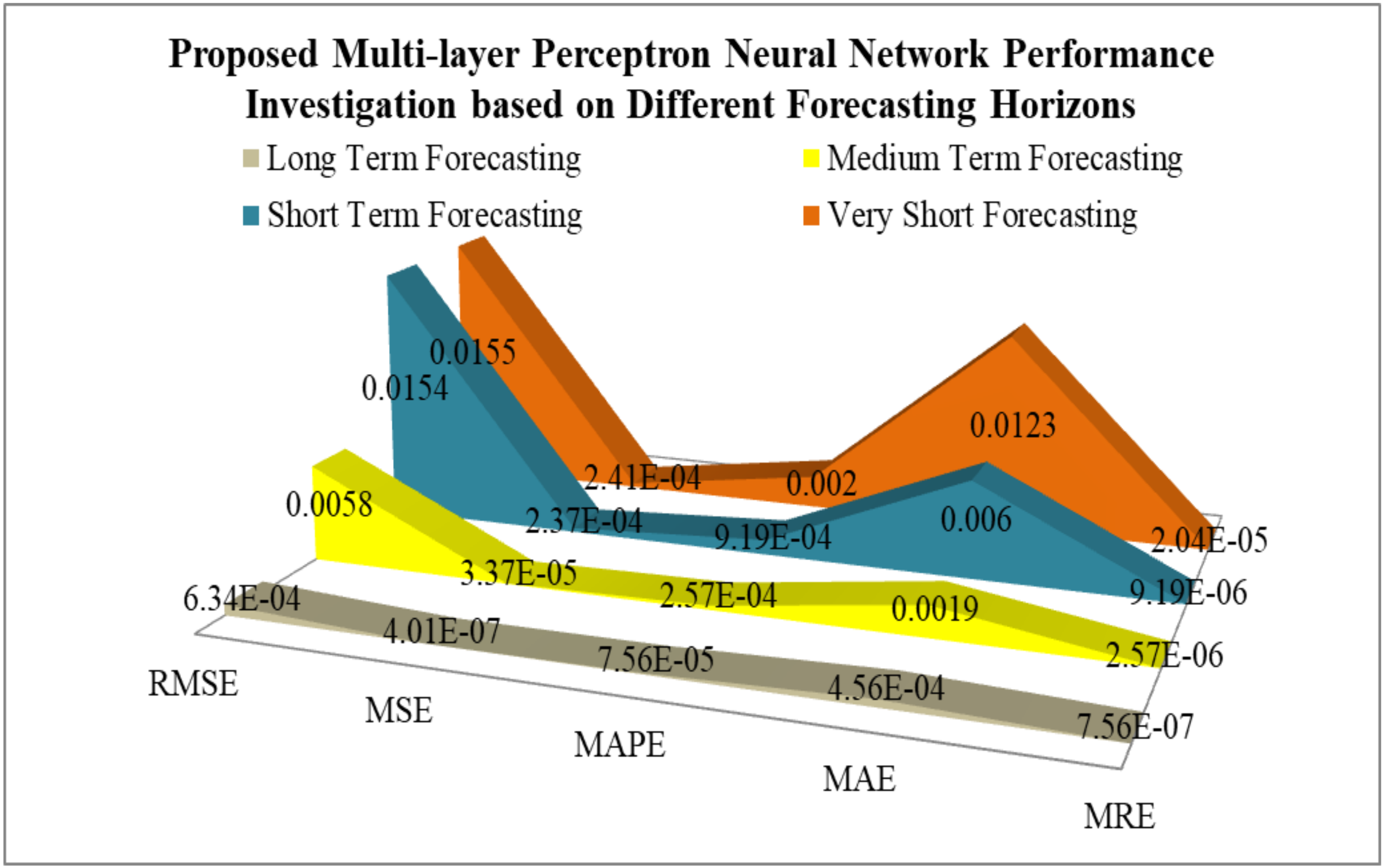
The horizon of long-term load forecasting is years ahead, the horizon of medium-term load forecasting is 24 h ahead, the horizon of short-term load forecasting is 6 h ahead, and the horizon of very short-term load forecasting is 30 min ahead. Therefore, the proposed multilayer perceptron neural network-based forecasting model performance was investigated with concern to the different forecasting horizons, namely long-term, medium-term, short-term, and very short-term electricity load forecasting. The obtained results based on the proposed model concern to different forecasting horizons presented in
Table 7 and
Table 8 show that the proposed model can forecast the electricity load in all time horizons, namely, long-term, medium-term, short-term, and very short-term, with minimum evaluation index (RMSE, MSE, MAPE, MAE, MRE) and converge faster for both datasets.
Figure 8,
Figure 9 and
Figure 10 show the results of long-term load forecasting concern on dataset 1.
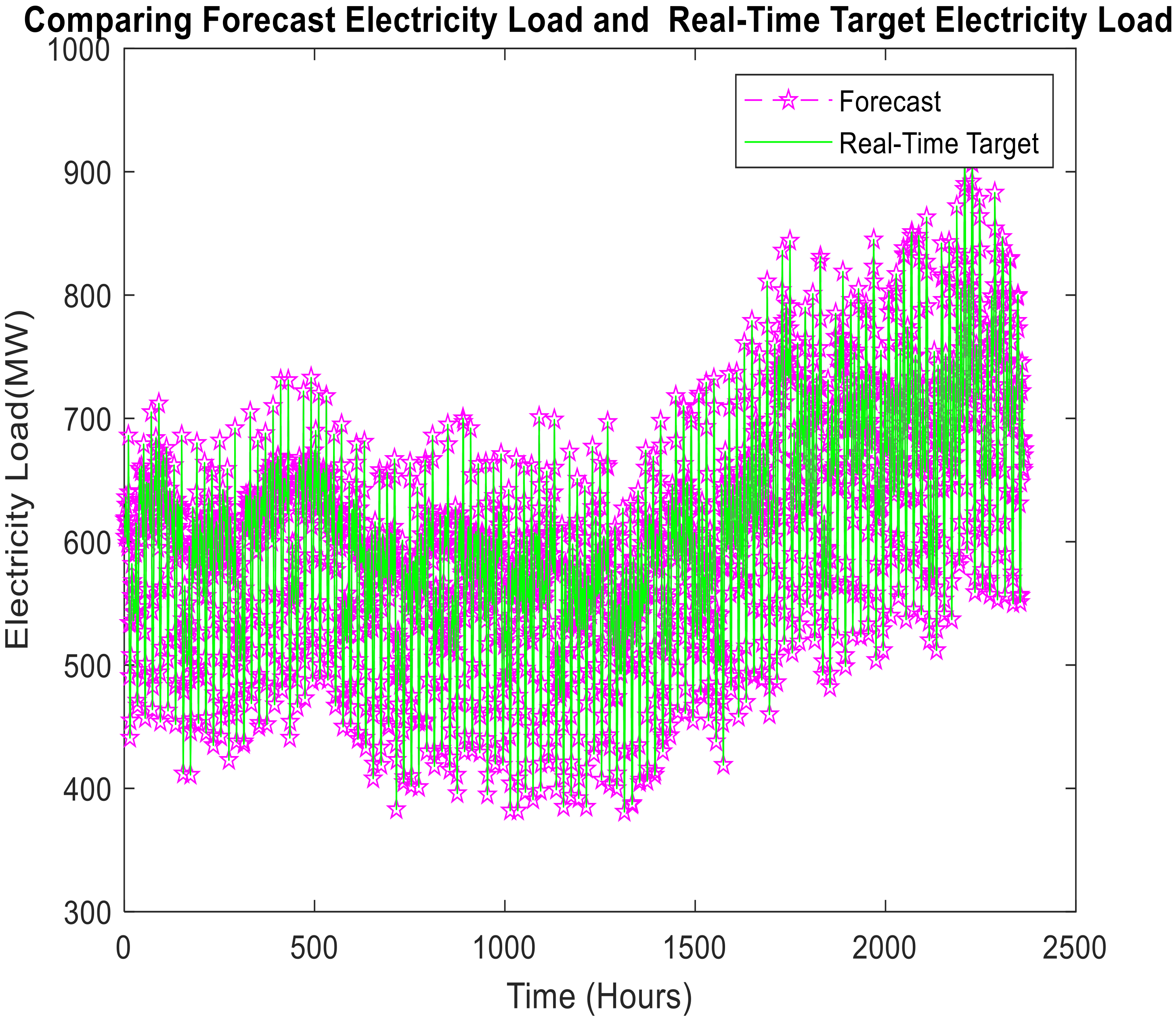
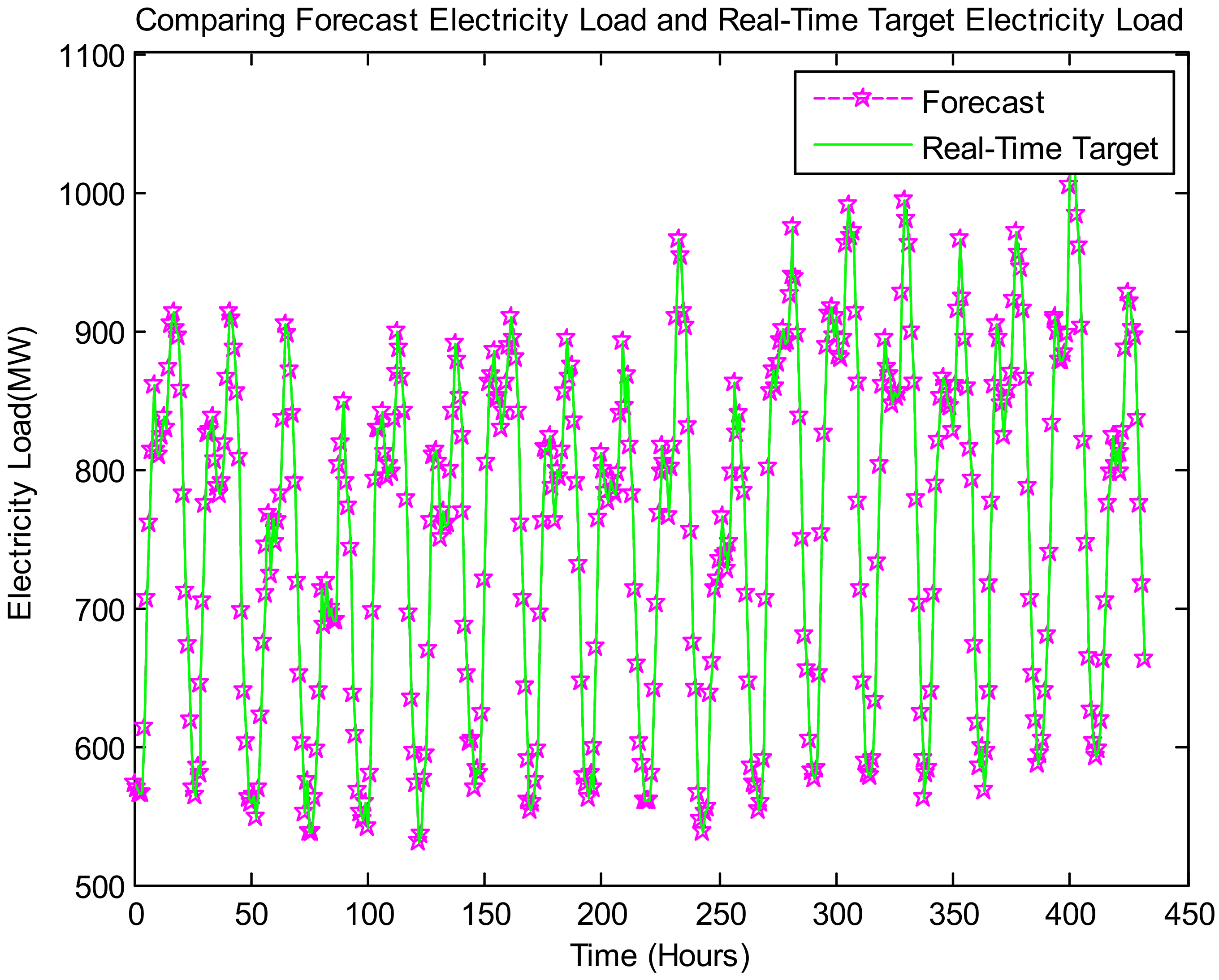
Figure 8 represents the proposed model-based output, namely, comparing the forecast electricity load with real-time target electricity load in the horizon of years ahead.
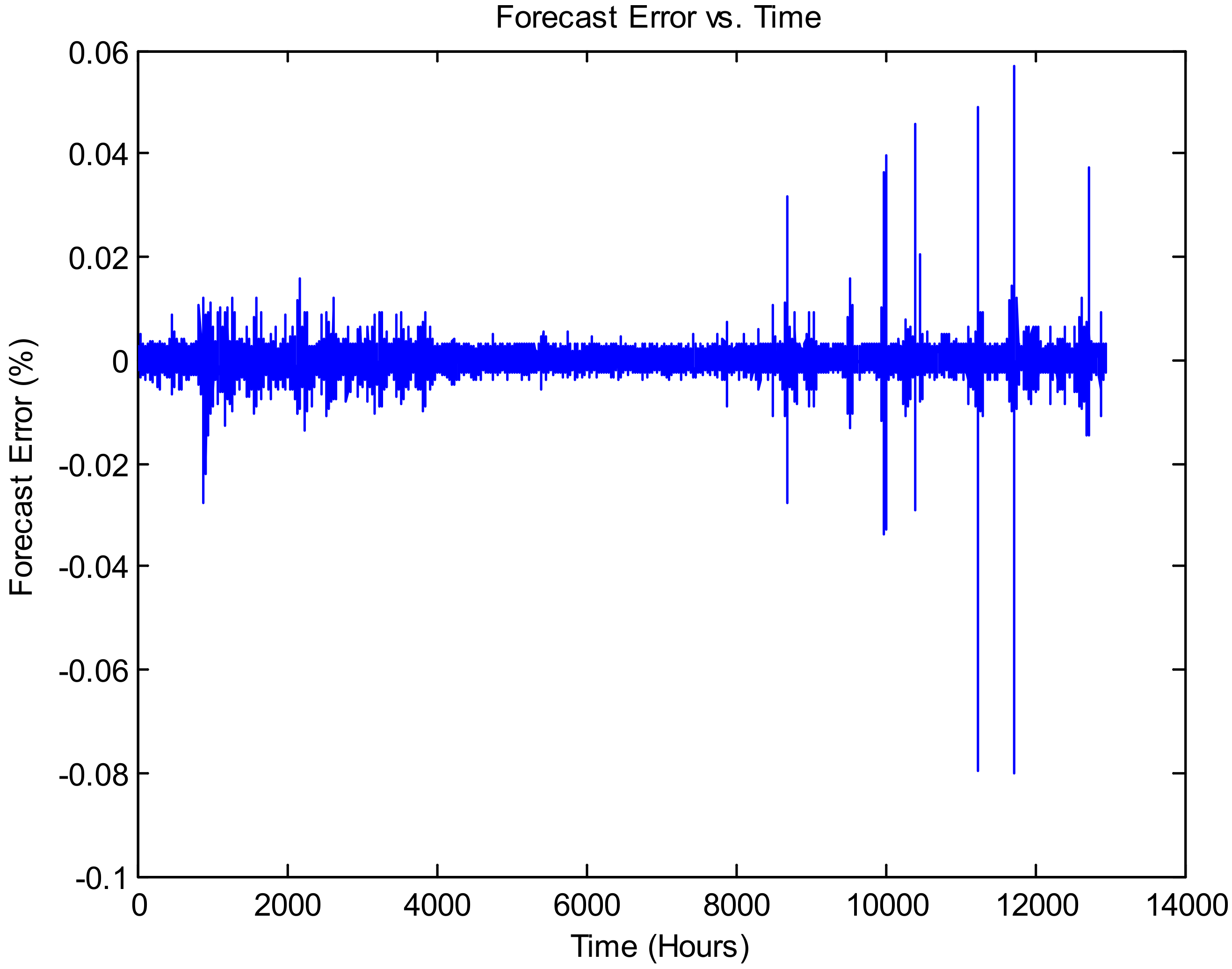
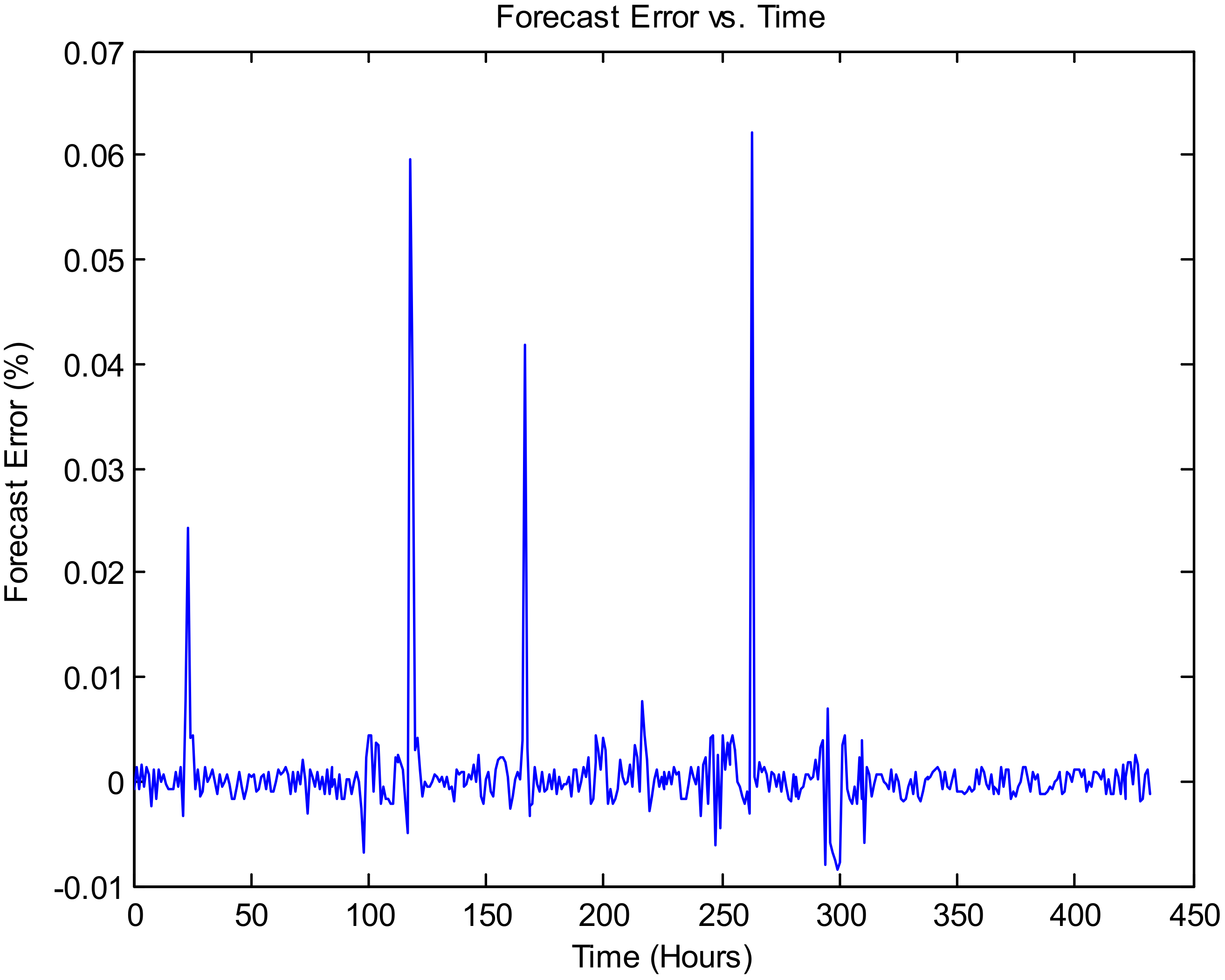
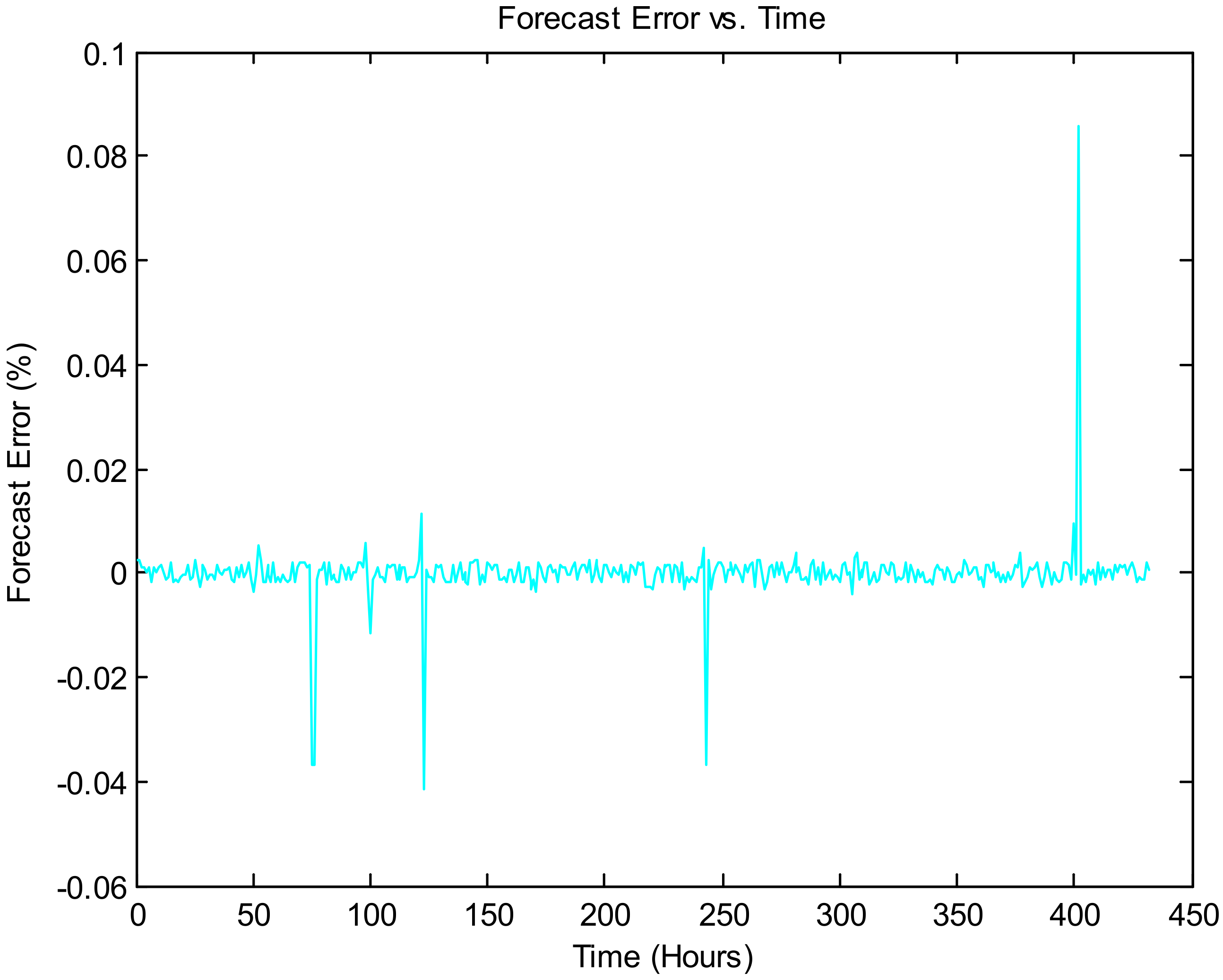
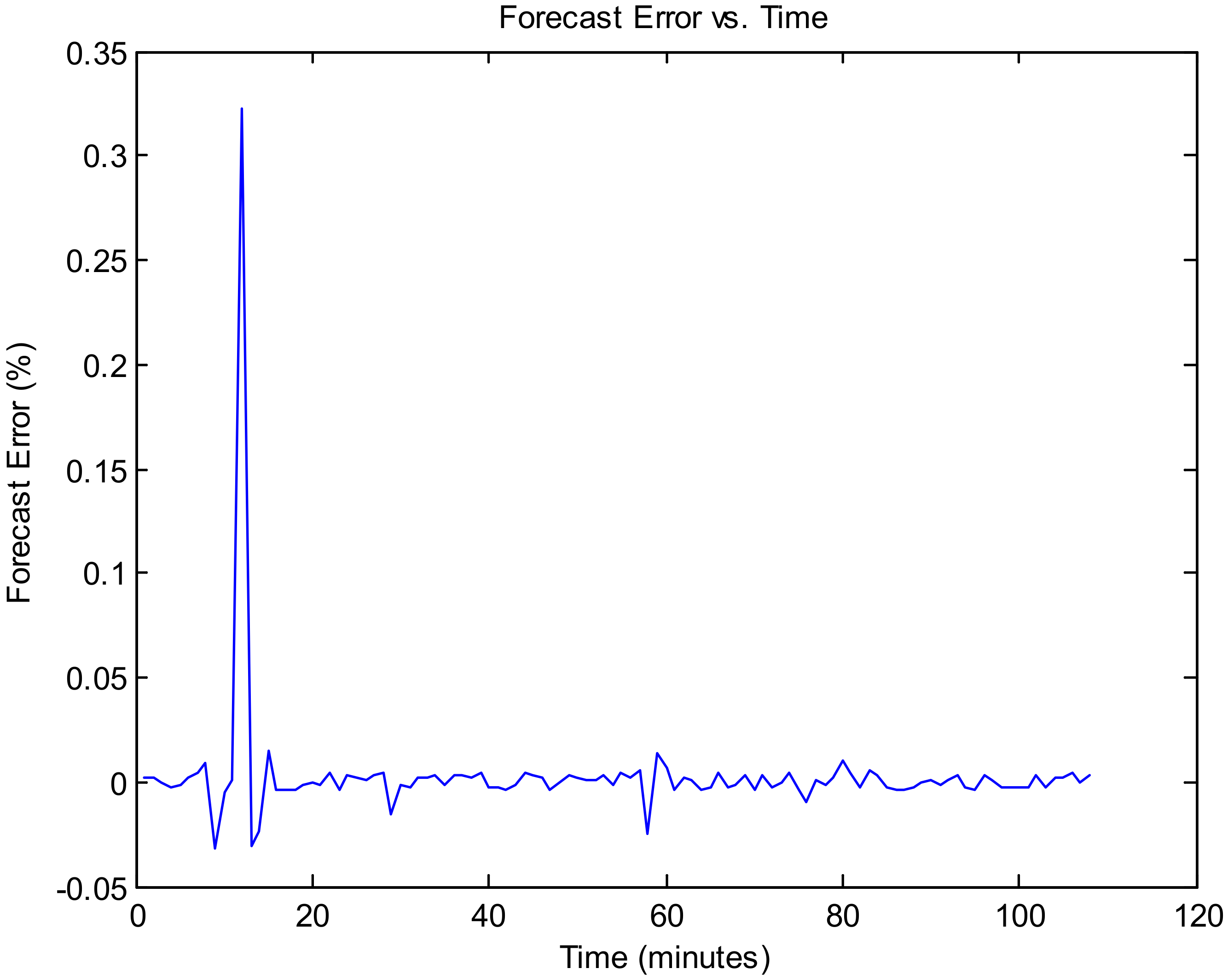
Figure 9 illustrates the forecasting error vs. time, and
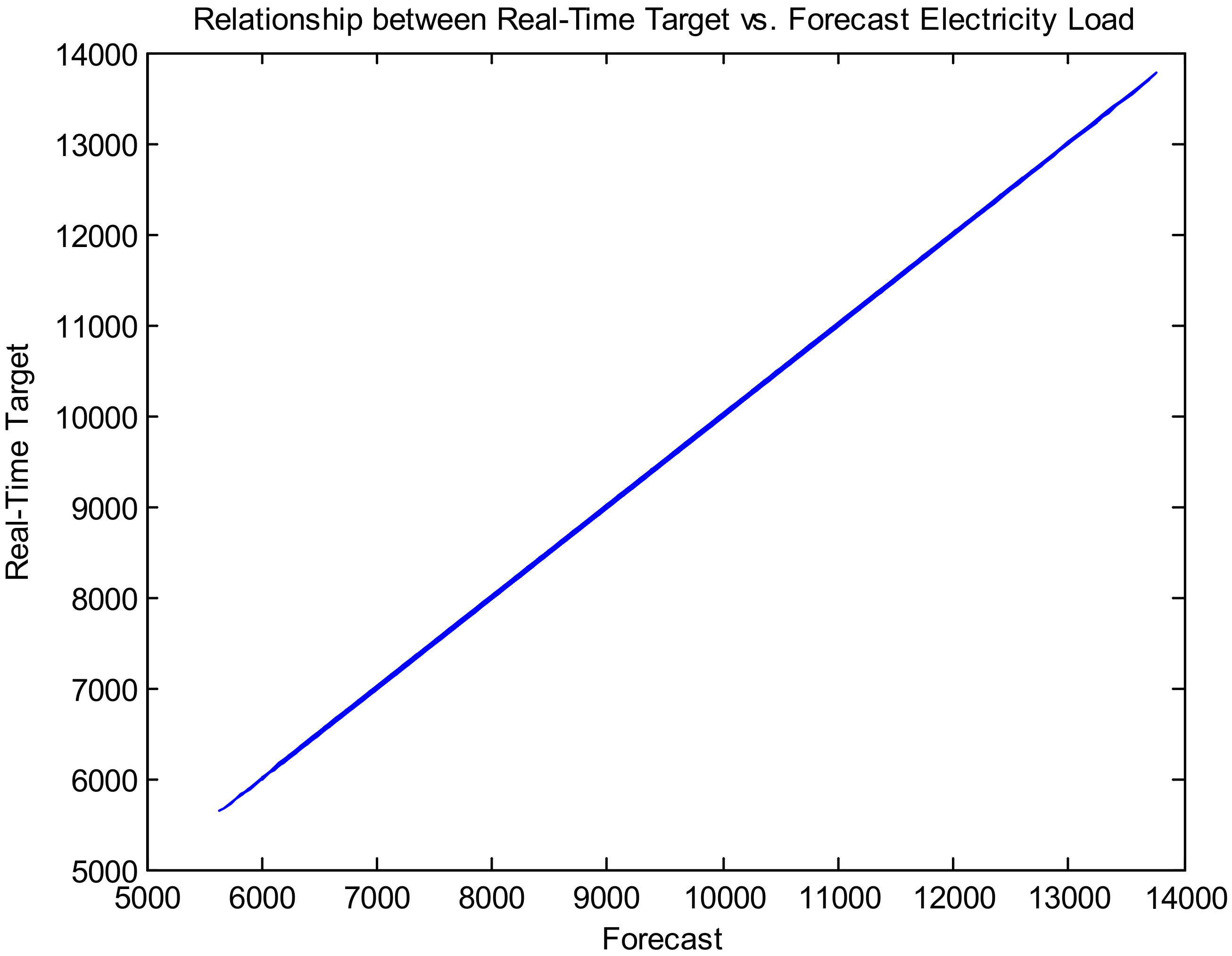
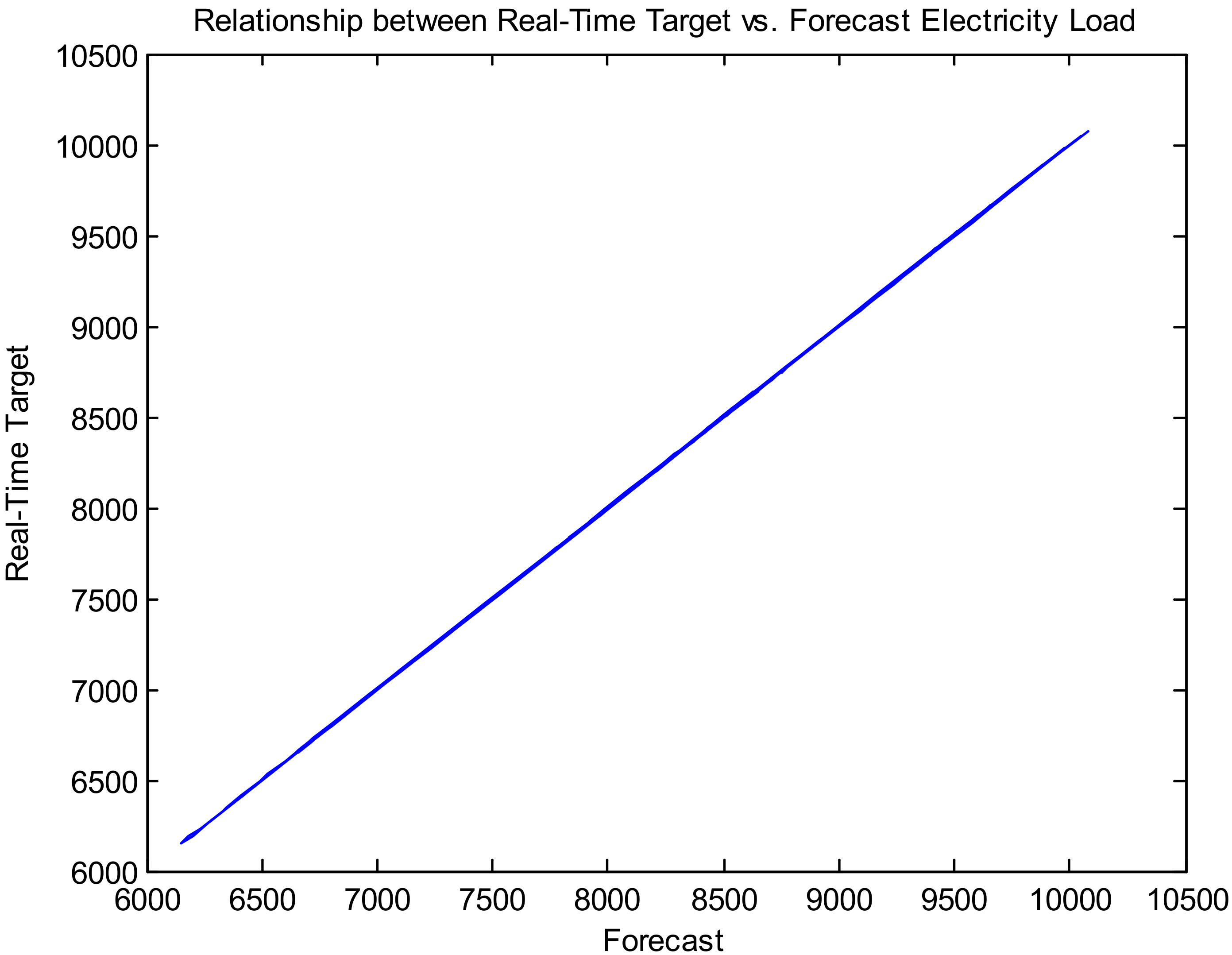
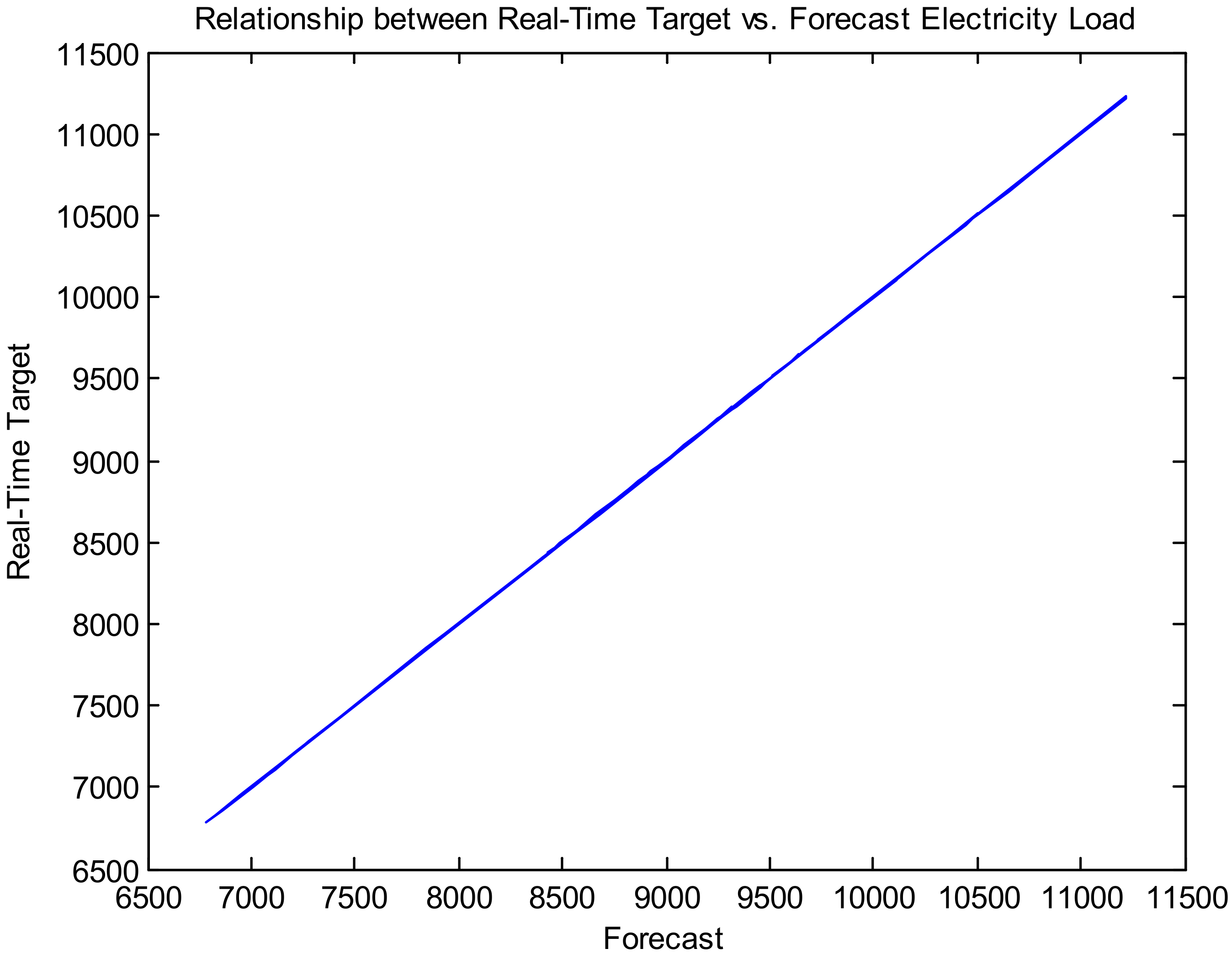
Figure 10 presents the relationship between real-time target and forecast electricity load for a long-term time horizon (dataset 1).
Figure 11,
Figure 12 and
Figure 13 show the results of long-term load forecasting concern on Dataset 2.
Figure 11 represents the proposed model-based output, namely, comparing the forecast electricity load with real-time target electricity load in the horizon of years ahead.
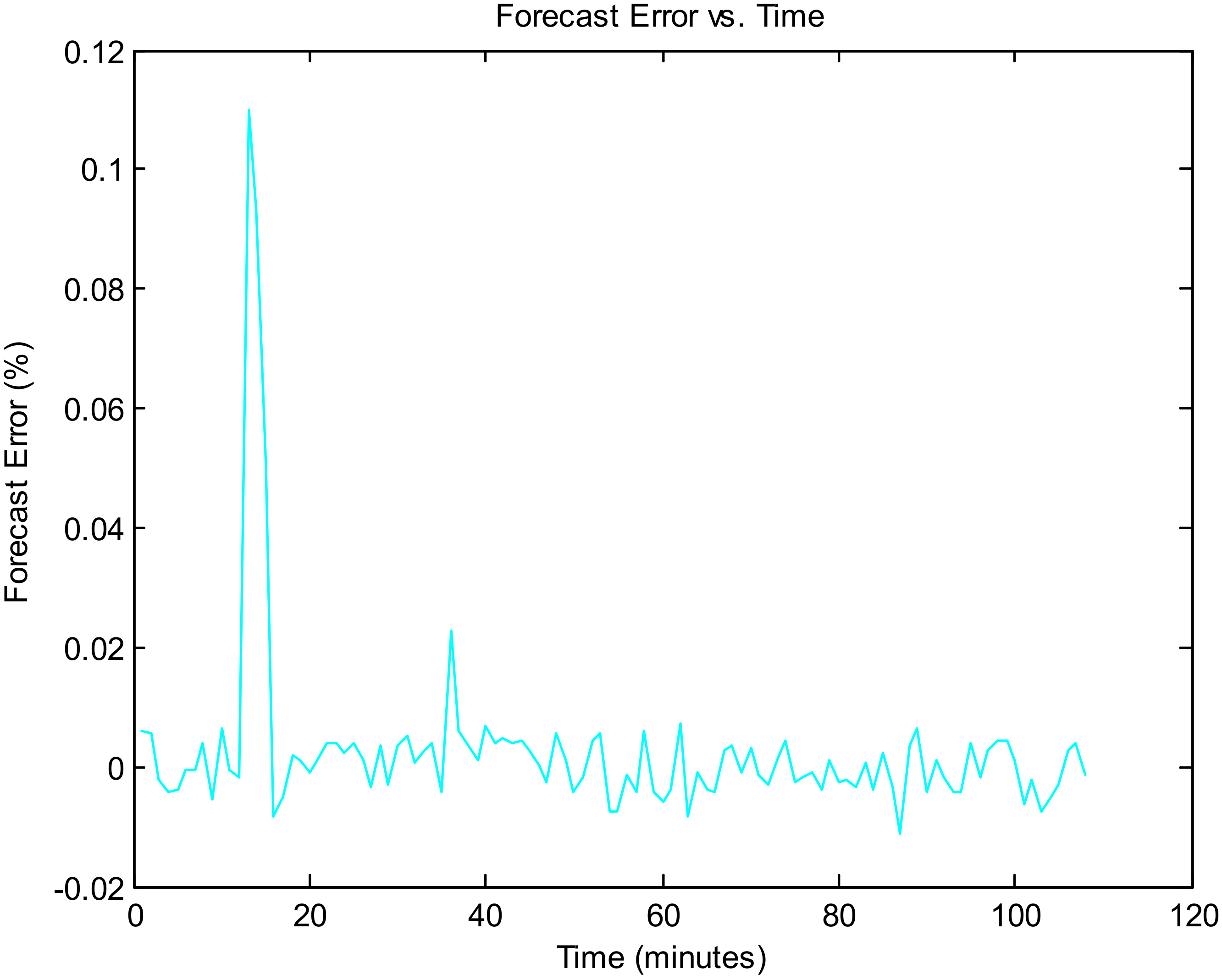
Figure 12 shows the forecasting error vs. time, and
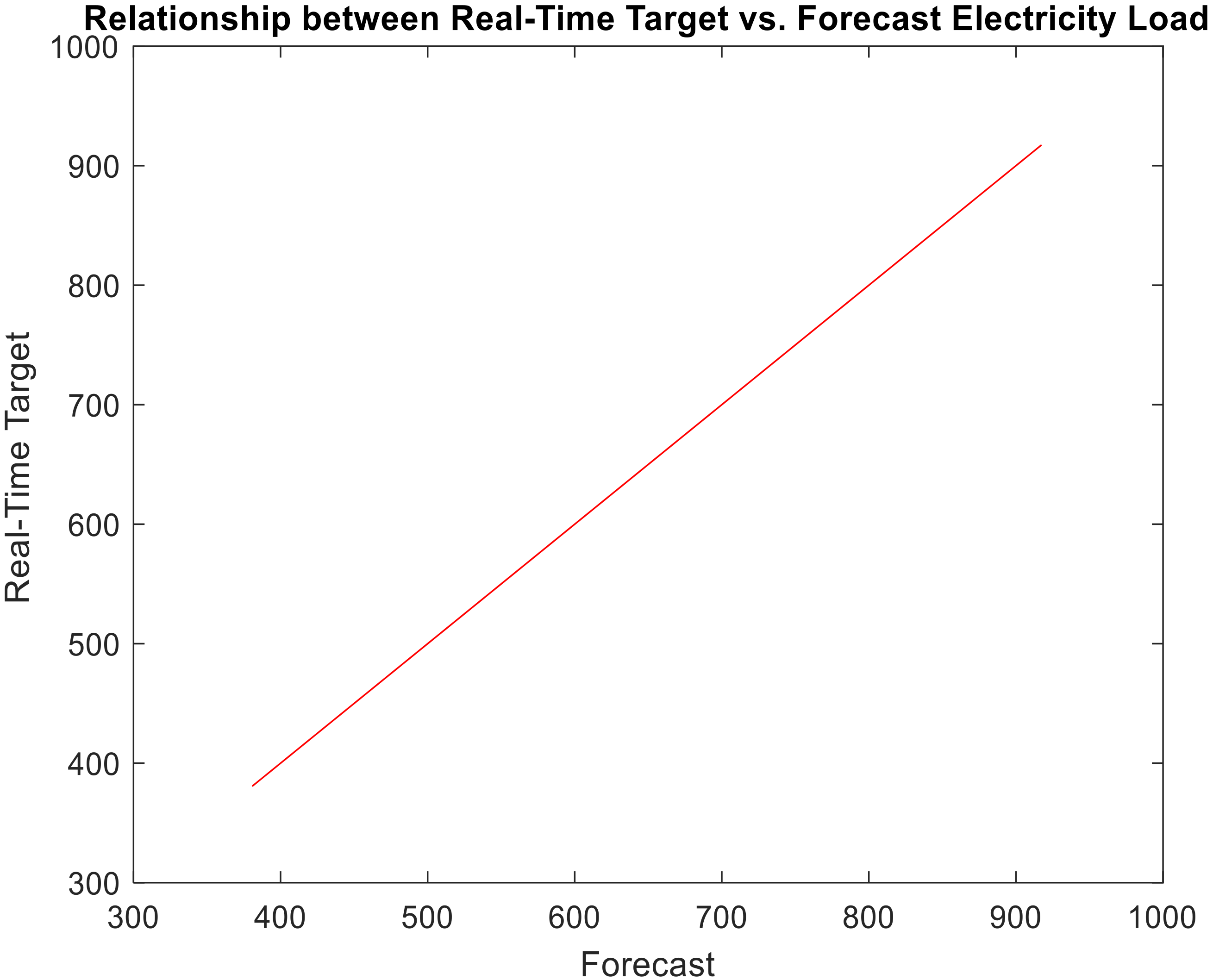
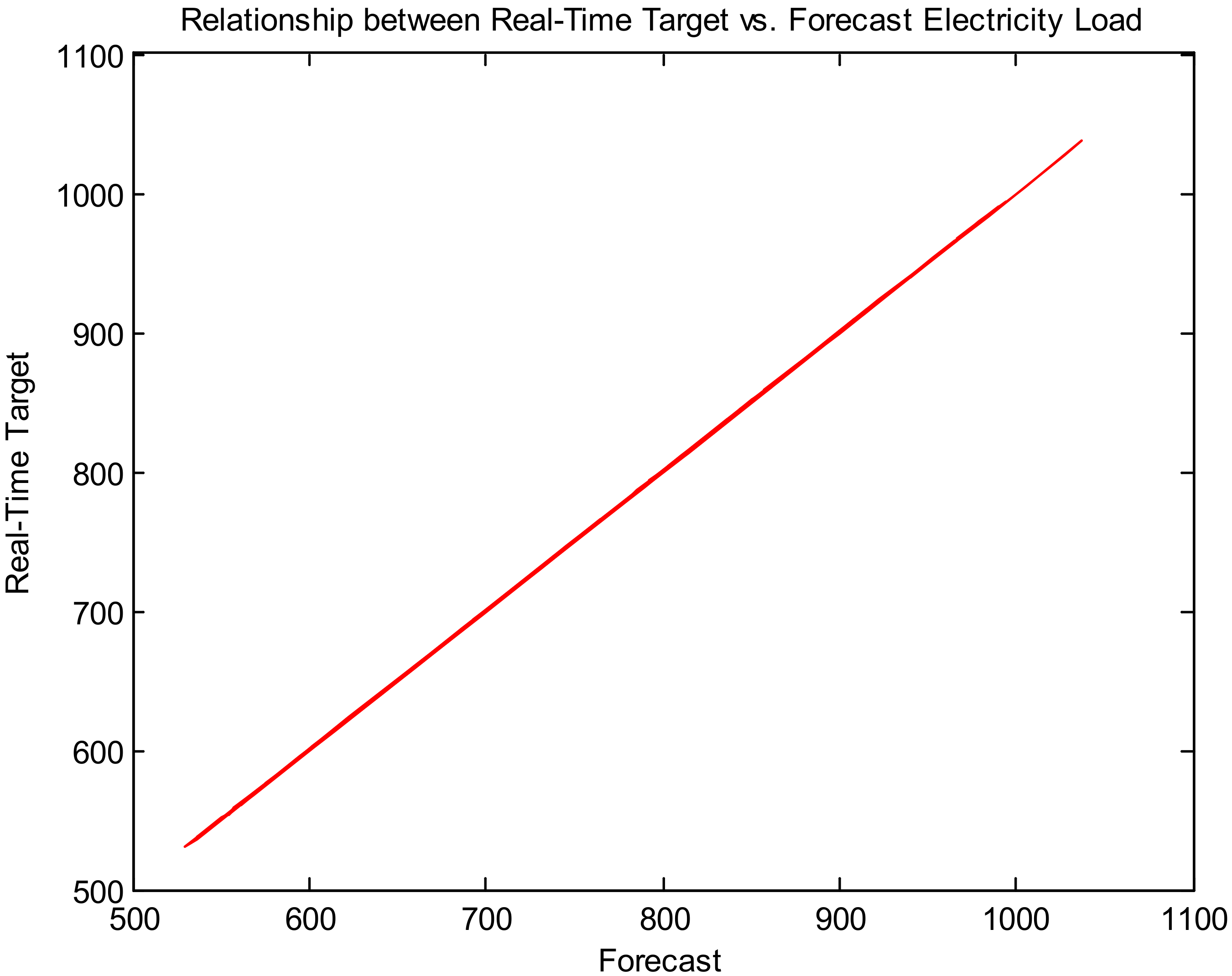
Figure 13 depicts the relationship between the real-time target and the forecast electricity load for a long-term time horizon (Dataset 2).
Similarly,
Figure 14,
Figure 15 and
Figure 16 show the results of medium-term load forecasting concern on Dataset 1.
Figure 14,
Figure 15 and
Figure 16 represent the proposed model-based output on Dataset 1, namely, comparing the forecast electricity load with real-time target electricity load in the horizon of 24 h ahead, forecasting error vs. time, and the relationship between real-time target and forecast electricity load for a medium-term time horizon, respectively (Dataset 1).
Figure 17,
Figure 18 and
Figure 19 show the results of medium-term load forecasting concern on Dataset 2.
Figure 17,
Figure 18 and
Figure 19 represent the proposed model-based output on Dataset 2, namely, comparing the forecast electricity load with real-time target electricity load in the horizon of 24 h ahead, forecasting error vs. time, and the relationship between real-time target and forecast electricity load for a medium-term time horizon, respectively (Dataset 2).
Figure 20,
Figure 21 and
Figure 22 show the results of short-term load forecasting concern on Dataset 1.
Figure 20,
Figure 21 and
Figure 22 represents the proposed model-based output on Dataset 1, namely, comparing the forecast electricity load with real-time target electricity load in the horizon of 6 h ahead, forecasting error vs. time, and the relationship between real-time target and forecast electricity load for a short-term time horizon (Dataset 1).
Figure 23,
Figure 24 and
Figure 25 show the results of short-term load forecasting concern on Dataset 2.
Figure 23,
Figure 24 and
Figure 25 represents the proposed model-based output on Dataset 2, namely, comparing the forecast electricity load with real-time target electricity load in the horizon of 6 h ahead, forecasting error vs. time, and the relationship between real-time target and forecast electricity load for a short-term time horizon (Dataset 2).
Figure 26,
Figure 27 and
Figure 28 show the results of very short-term load forecasting concern on dataset 1.
Figure 26,
Figure 27 and
Figure 28 represents the proposed model-based output on Dataset 1, namely, comparing the forecast electricity load with real-time target electricity load in the horizon of 30 min ahead, the forecasting error vs. time, and the relationship between real-time target and forecast electricity load for the very short-term time horizons, respectively (Dataset 1).
Figure 29,
Figure 30 and
Figure 31 show the results of very short-term load forecasting concern on Dataset 1.
Figure 29,
Figure 30 and
Figure 31 represent the proposed model-based output on Dataset 2, namely, comparing the forecast electricity load with real-time electricity load in the horizon of 30 min ahead, forecasting error vs. time, and the relationship between real-time target and forecast electricity load for the very short-term time horizons, respectively (Dataset 2).
Figure 8,
Figure 14,
Figure 20, and
Figure 26 show that the output results concerned to Dataset 1 (forecast electricity load) exactly match the target real-time electricity load for different forecasting horizons. Therefore, the forecasting errors are minimal, inferred from
Figure 9,
Figure 15,
Figure 21, and
Figure 27. The relationship between real-time target and forecast electricity load is linear, understood clearly from
Figure 10,
Figure 16,
Figure 22, and
Figure 28. Similarly,
Figure 11,
Figure 17,
Figure 23, and
Figure 29 show that the output results concerned to Dataset 2 (forecast electricity load) exactly match the target real-time electricity load for different forecasting horizons. Therefore, the forecasting errors are minimal, inferred from
Figure 12,
Figure 18,
Figure 24, and
Figure 30. The relationship between real-time target and forecast electricity load is linear, understood clearly from
Figure 13,
Figure 19,
Figure 25, and
Figure 31.
To better understand the proposed model’s effectiveness regarding different forecasting horizons, the graphical representation of the proposed model performance investigation is based on the different forecasting horizons depicted in
Figure 32 (Dataset 1) and
Figure 33 (Dataset 2).
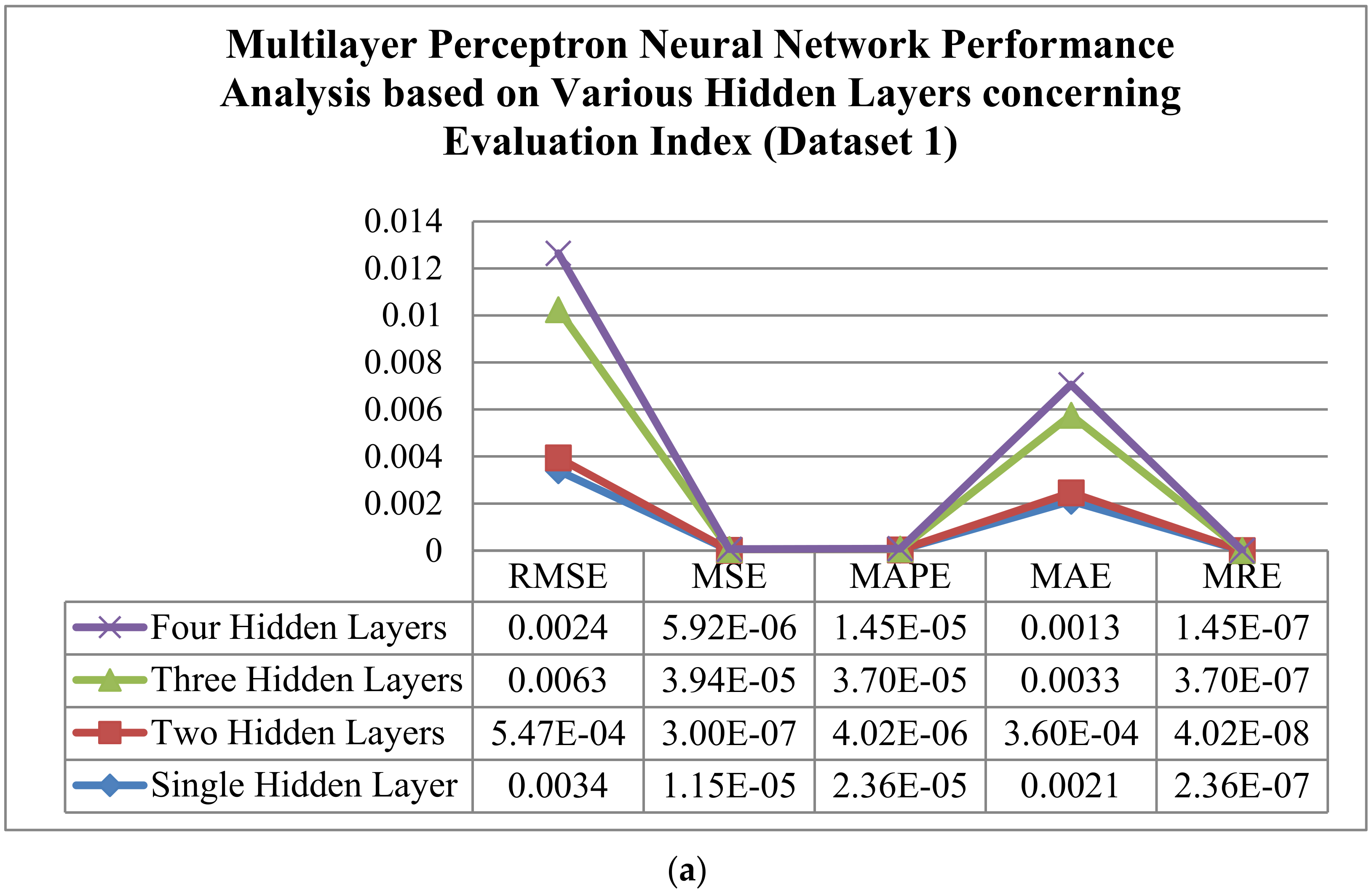
The authors carried out performance analysis with various hidden layers, namely, single hidden layer, two hidden layers, three hidden layers, and four hidden layers based on the obtained results are tabulated in
Table 9 and
Table 10, respectively, for Dataset 1 and Dataset 2. According to the universal approximation theorem [
28,
29], the multilayer perceptron neural network with two hidden layers can solve any problem. If the number of hidden layers is increased by more than two, it may cause an issue with respect to convergence and learning. From
Figure 34a,b and
Figure 35a,b, and
Table 9 and
Table 10, it is noticed that the results of the two hidden layer-based developed models perform well with improved accuracy.
To further analyze the performance, in addition to the above considered six inputs, the time-series data (holiday) was included as one of the proposed model’s inputs. The obtained results based on structure (1-17-1), one input layer with seven inputs, a single hidden layer with 17 hidden neurons, and one output layer for two datasets are tabulated in
Table 11. From
Table 11, it is noticed that the load forecasting model performance improved considering the time series as one of the inputs to the forecasting model. It perceives the importance of time series data on load forecasting.
The issues due to uncertainty in electricity load can be resolved by electricity load forecasting. Various electricity load forecasting models have endeavored during the past two decades, but a simple, faster, and highly accurate forecasting model is the thrust field in electricity load forecasting. Therefore, this paper proposed a multilayer perceptron neural network-based exact forecast for electricity forecasting required for the utility system’s effective operation.
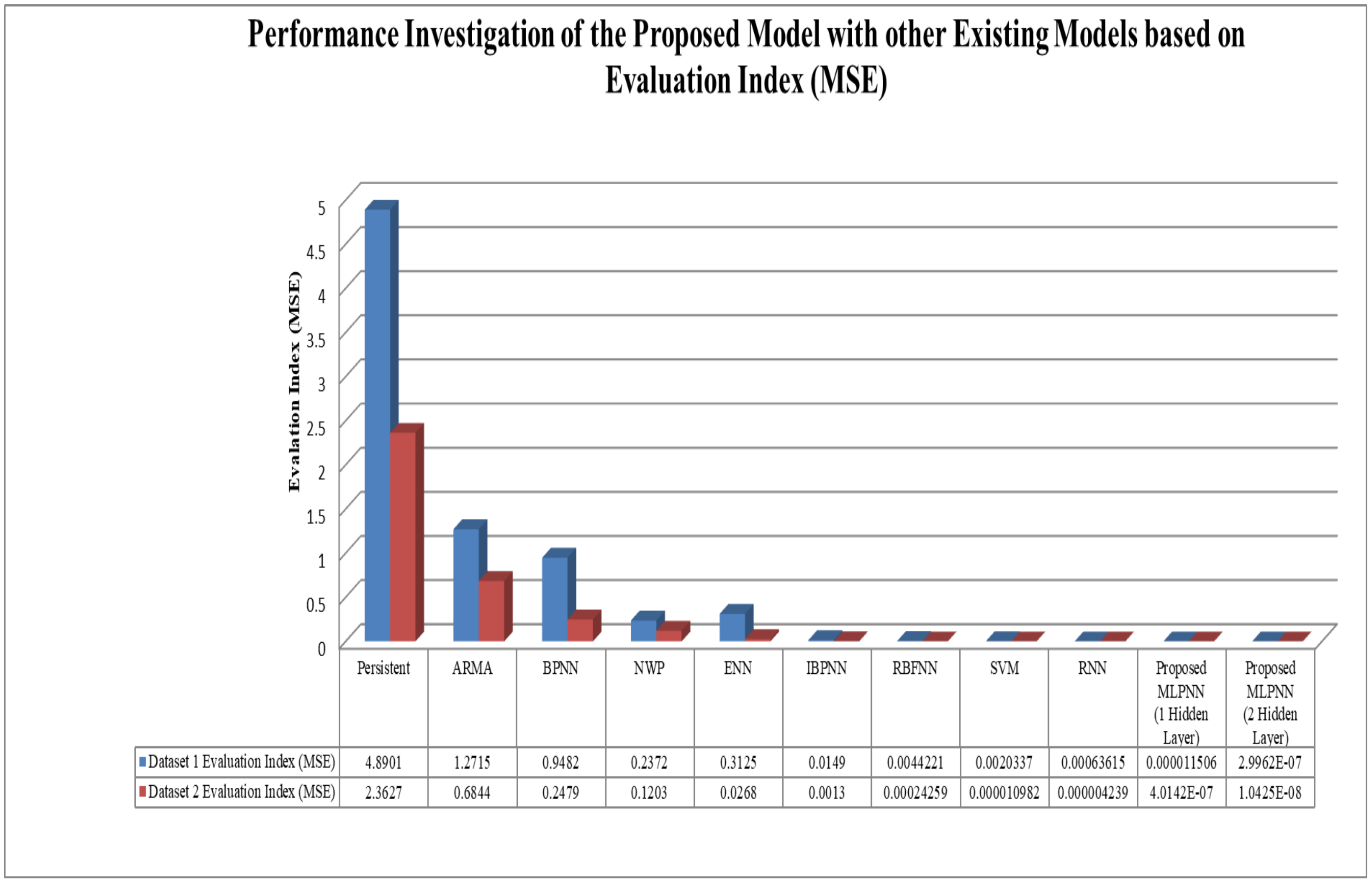
The proposed model’s performance is further investigated against other existing models that concern long-term electricity load forecasting. The corresponding outputs are based on the proposed model and other existing models reported in
Table 12. For comparative analysis, we use the existing model’s setting parameters as mentioned by the respective authors, and we performed an evaluation on the considered two datasets. The results were compared with previous models such as persistence, autoregression moving average, backpropagation neural network, numerical weather prediction, Elman neural network, improved back propagation neural network, radial basis function neural network, support vector machine, and recurrent neural network, comparative analysis proves the significance of the proposed model.
Table 12 infers that the proposed model-based results demonstrate superior performance and minimal evaluation index mean square error (MSE) of 1.1506 × 10
−05 for Dataset 1 and MSE of 4.0142 × 10
−07 for Dataset 2 with concern to the single hidden layer and MSE of 2.9962 × 10
−07 for Dataset 1, and MSE of 1.0425 × 10
−08 for Dataset 2 concern the two hidden-layers based proposed model than the considered existing models. For a better understanding, the graphical representation of the proposed model’s performance investigation with other existing models is shown in
Figure 36. The presented model-based forecasting simulation results indicate the superiority and outperforming capability that of the existing models.