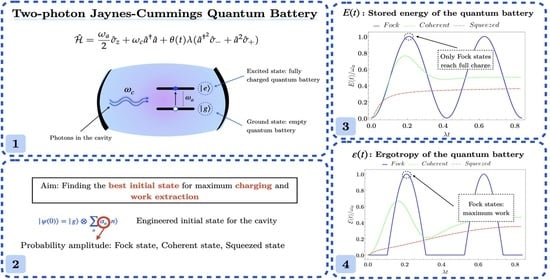
Characterization of a Two-Photon Quantum Battery: Initial Conditions, Stability and Work Extraction
Abstract
:1. Introduction
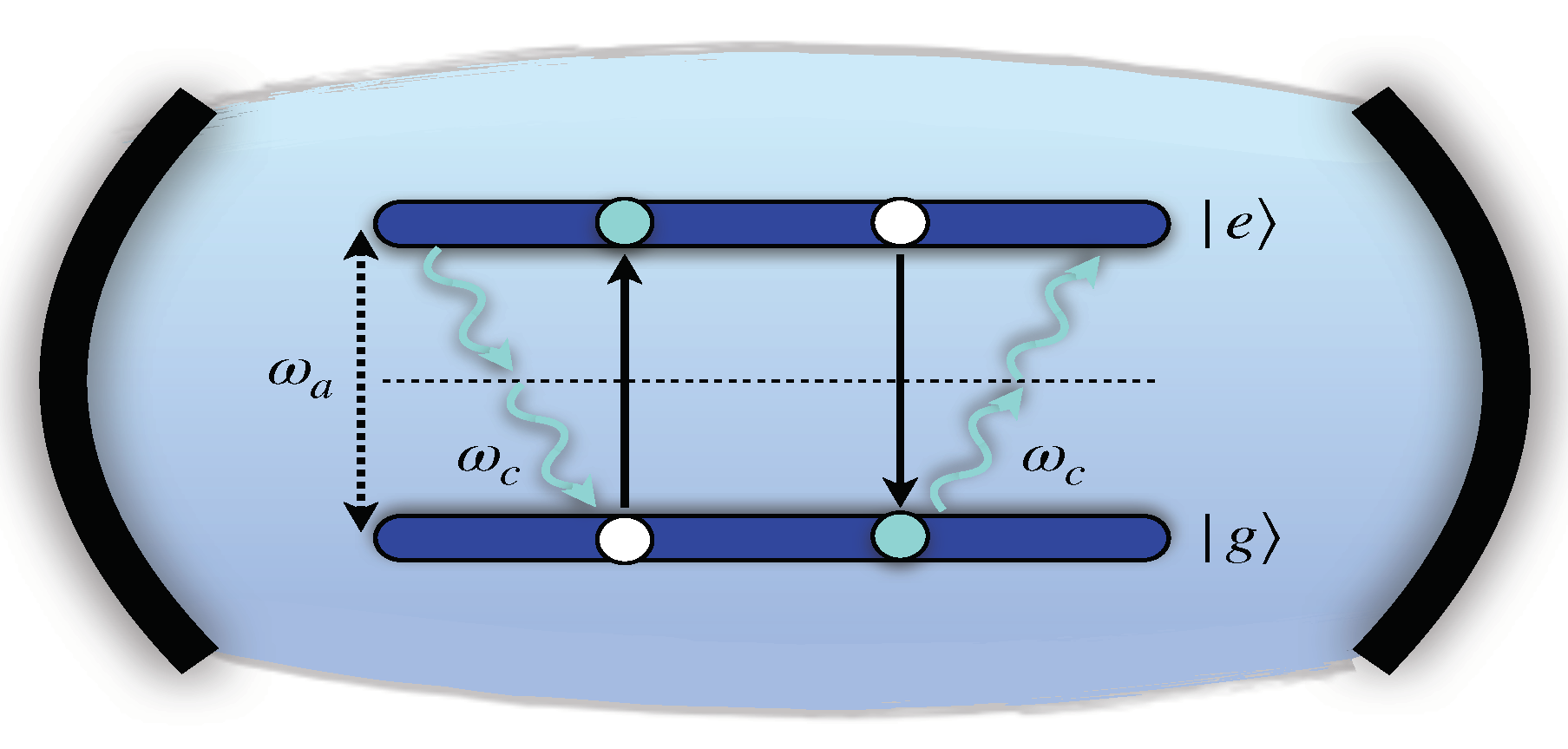
2. Model
3. Figures of Merit of the Quantum Battery
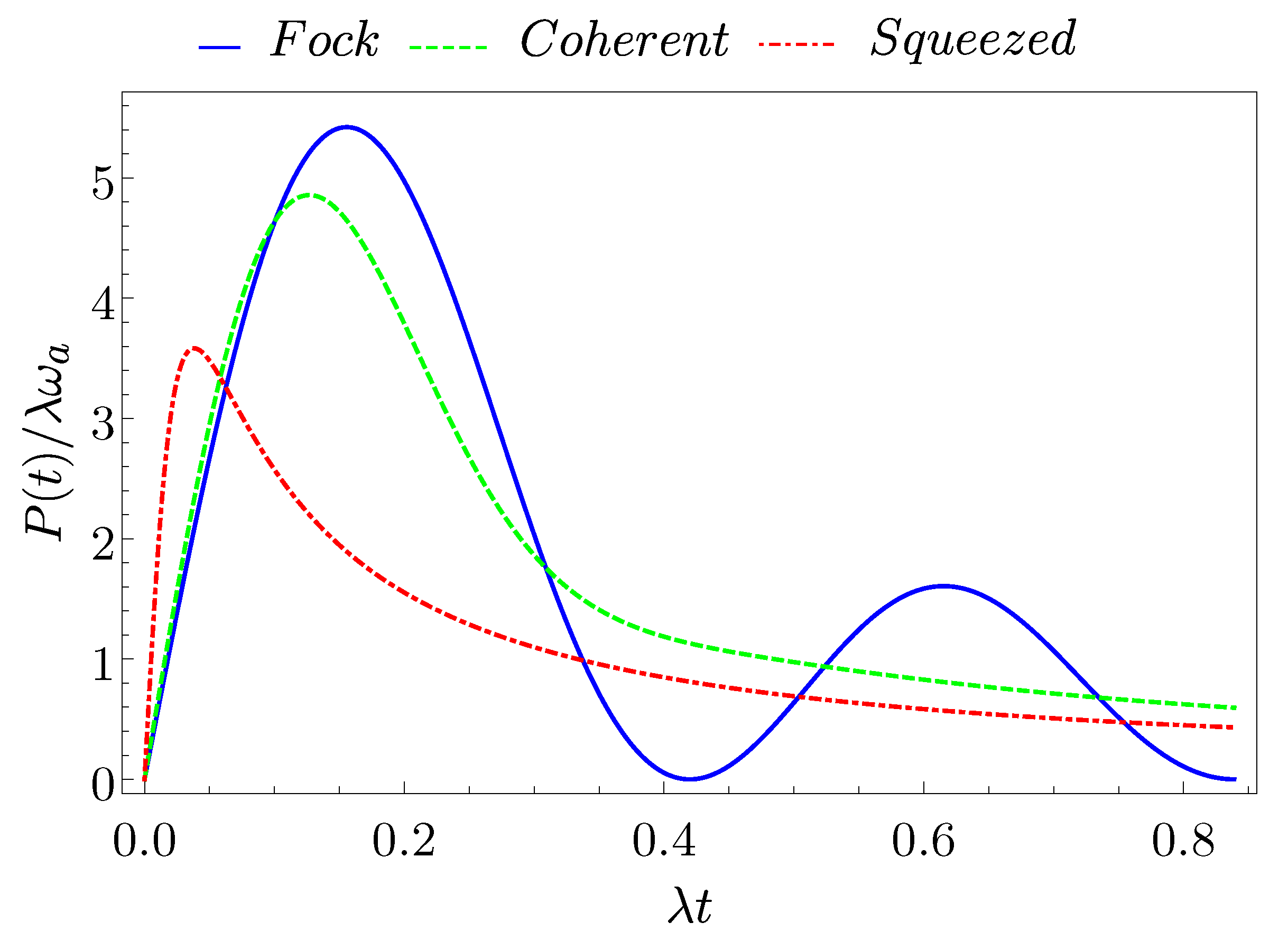
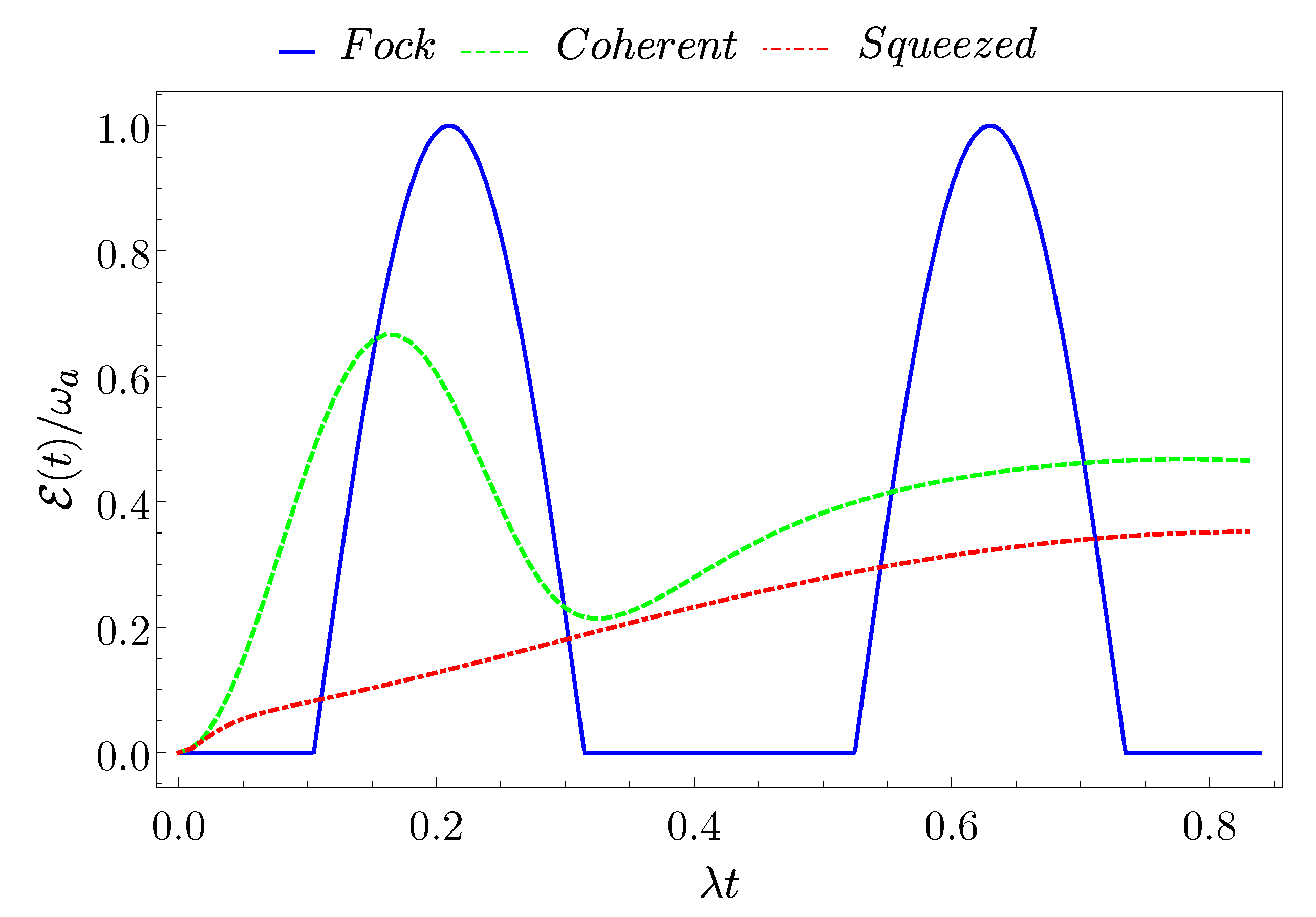
3.1. Stored Energy and Average Charging Power
3.2. Energy Fluctuations
3.3. Ergotropy
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| QB | Quantum Battery |
| TLS | Two-Level-System |
References
- Campisi, M.; Hänggi, P.; Talkner, P. Colloquium: Quantum fluctuation relations: Foundations and applications. Rev. Mod. Phys. 2011, 83, 771. [Google Scholar] [CrossRef] [Green Version]
- Levy, A.; Kosloff, R. Quantum Absorption Refrigerator. Phys. Rev. Lett. 2012, 108, 070604. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pekola, J. Towards quantum thermodynamics in electronic circuits. Nat. Phys. 2015, 11, 118. [Google Scholar] [CrossRef] [Green Version]
- Vinjanampathy, S.; Anders, J. Quantum thermodynamics. Contemp. Phys. 2016, 57, 545. [Google Scholar] [CrossRef] [Green Version]
- Benenti, G.; Casati, G.; Saito, K.; Whitney, R.S. Fundamental aspects of steady-state conversion of heat to work at the nanoscale. Phys. Rep. 2017, 694, 1. [Google Scholar] [CrossRef] [Green Version]
- Campisi, M.; Goold, J. Thermodynamics of quantum information scrambling. Phys. Rev. E 2017, 95, 062127. [Google Scholar] [CrossRef] [Green Version]
- Binder, F.; Correa, L.A.; Gogolin, C.; Anders, J.; Adesso, G. (Eds.) Thermodynamics in the Quantum Regime; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Carrega, M.; Sassetti, M.; Weiss, U. Optimal work-to-work conversion of a nonlinear quantum Brownian duet. Phys. Rev. A 2019, 99, 062111. [Google Scholar] [CrossRef] [Green Version]
- Porta, S.; Gambetta, F.M.; Traverso Ziani, N.; Kennes, D.M.; Sassetti, M.; Cavaliere, F. Nonmonotonic response and light-cone freezing in fermionic systems under quantum quenches from gapless to gapped or partially gapped states. Phys. Rev. B 2018, 97, 035433. [Google Scholar] [CrossRef] [Green Version]
- Alicki, R.; Fannes, M. Entanglement boost for extractable work from ensembles of quantum batteries. Phys. Rev. E 2013, 87, 042123. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharjee, S.; Dutta, A. Quantum thermal machines and batteries. arXiv 2020, arXiv:2008.07889. [Google Scholar]
- Hovhannisyan, K.V.; Perarnau-Llobet, M.; Huber, M.; Acin, A. Entanglement Generation is Not Necessary for Optimal Work Extraction. Phys. Rev. Lett. 2013, 111, 240401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Binder, F.C.; Vinjanampathy, S.; Modi, K.; Goold, J. Quantacell: Powerful charging of quantum batteries. New J. Phys. 2015, 17, 075015. [Google Scholar] [CrossRef] [Green Version]
- Moraes, L.F.C.; Saguia, A.; Santos, A.C.; Sarandy, M.S. Charging power and stability of always-on transitionless driven quantum batteries. arXiv 2020, arXiv:2012.05855. [Google Scholar]
- Santos, A.C. Quantum advantage of a two-level batteries in self-discharging process. Phys. Rev. E 2021, 103, 042118. [Google Scholar] [CrossRef]
- Bai, S.-Y.; An, J.-H. Floquet Engineering to Reactivate A Dissipative Quantum Battery. Phys. Rev. A 2020, 102, 060201(R). [Google Scholar] [CrossRef]
- Garcia-Pintos, L.P.; Hamma, A.; del Campo, A. Fluctuations in Extractable Work Bound the Charging Power of Quantum Batteries. Phys. Rev. Lett. 2020, 125, 040601. [Google Scholar] [CrossRef]
- Mitchison, M.T.; Goold, J.; Prior, J. Charging a quantum battery with linear feedback control. arXiv 2020, arXiv:2012.00350. [Google Scholar]
- Caravelli, F.; Yan, B.; García-Pintos, L.P.; Hamma, A. Energy storage and coherence in closed and open quantum batteries. arXiv 2020, arXiv:2012.15026. [Google Scholar]
- Peng, L.; He, W.-B.; Chesi, S.; Lin, H.-Q.; Guan, X.-W. Lower and upper bounds of quantum battery power in multiple central spin systems. arXiv 2021, arXiv:2103.07828. [Google Scholar]
- Liu, J.; Segal, D. Boosting quantum battery performance by structure engineering. arXiv 2021, arXiv:2104.06522. [Google Scholar]
- Hu, H.; Qi, S.; Jing, J. Fast and stable charging via shortcut to adiabaticity. arXiv 2021, arXiv:2104.12143. [Google Scholar]
- Cirac, J.I.; Zoller, P. Quantum Computations with Cold Trapped Ions. Phys. Rev. Lett. 1995, 74, 4091. [Google Scholar] [CrossRef] [PubMed]
- Bruzewicz, C.D.; Chiaverini, J.; McConnell, R.; Sage, J.M. Trapped-Ion Quantum Computing: Progress and Challenges. Appl. Phys. Rev. 2019, 6, 021314. [Google Scholar] [CrossRef] [Green Version]
- Georgescu, I. Trapped ion quantum computing turns 25. Nat. Rev. 2020, 2, 278. [Google Scholar] [CrossRef]
- Devoret, M.H.; Schoelkopf, R.J. Superconducting Circuits for Quantum Information: An Outlook. Science 2013, 339, 1169. [Google Scholar] [CrossRef] [Green Version]
- Singha, A.; Gibertini, M.; Karmakar, B.; Yuan, S.; Polini, M.; Vignale, G.; Katsnelson, M.I.; Pinczuk, A.; Pfeiffer, L.N.; West, K.W.; et al. Two-dimensional Mott-Hubbard electrons in an artificial honeycomb lattice. Science 2011, 332, 1176. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.-Y.; Yang, T.-R.; Fu, L.; Wang, X. Powerful harmonic charging in a quantum battery. Phys. Rev. E 2019, 99, 052106. [Google Scholar] [CrossRef] [Green Version]
- Crescente, A.; Carrega, M.; Sassetti, M.; Ferraro, D. Charging and energy fluctuations of a driven quantum battery. New J. Phys. 2020, 22, 063057. [Google Scholar] [CrossRef]
- Chen, J.; Zhan, L.; Shao, L.; Zhang, X.; Zhang, Y.-Y.; Wang, X. Charging Quantum Batteries with a General Harmonic Driving Field. Ann. Physik 2020, 532, 1900487. [Google Scholar] [CrossRef]
- Yang, T.-R.; Zhang, Y.-Y.; Dong, H.; Fu, L.; Wang, X. Optimal building block of multipartite quantum battery. arXiv 2020, arXiv:2010.09970. [Google Scholar]
- Traverso, Z.N.; Cavaliere, F.; Sassetti, M. Theory of the STM detection of Wigner molecules in spin-incoherent CNTs. Europhys. Lett. 2013, 102, 47006. [Google Scholar] [CrossRef]
- Le, T.P.; Levinsen, J.; Modi, K.; Parish, M.; Pollock, F.A. Spin-chain model of a many-body quantum battery. Phys. Rev. A 2018, 97, 022106. [Google Scholar] [CrossRef] [Green Version]
- Rosa, D.; Rossini, D.; Andolina, G.M.; Polini, M.; Carrega, M. Ultra stable charging of fast-scrambling SYK quantum batteries. J. High Energ. Phys. 2020, 67, 2020. [Google Scholar] [CrossRef]
- Rossini, D.; Andolina, G.M.; Rosa, D.; Carrega, M.; Polini, M. Quantum advantage in the charging process of Sachdev-Ye-Kitaev batteries. Phys. Rev. Lett. 2020, 125, 236402. [Google Scholar] [CrossRef]
- Ghosh, S.; De, S.A. Dimensional enhancements in quantum battery with imperfections. arXiv 2021, arXiv:2104.06899. [Google Scholar]
- Haroche, S.; Raimond, J.-M. Exploring the Quantum. Atoms, Cavities and Photons; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Schoelkopf, R.J.; Girvin, S.M. Wiring up quantum systems. Nature (London) 2008, 451, 664. [Google Scholar] [CrossRef]
- Ferraro, D.; Campisi, M.; Andolina, G.M.; Pellegrini, V.; Polini, M. High-Power Collective Charging of a Solid-State Quantum Battery. Phys. Rev. Lett. 2018, 120, 117702. [Google Scholar] [CrossRef] [Green Version]
- Andolina, G.M.; Keck, M.; Mari, A.; Campisi, M.; Giovannetti, V.; Polini, M. Extractable work, the role of correlations, and asymptotic freedom in quantum batteries. Phys. Rev. Lett. 2019, 122, 047702. [Google Scholar] [CrossRef] [Green Version]
- Andolina, G.M.; Keck, M.; Mari, A.; Giovannetti, V.; Polini, M. Quantum versus classical many-body batteries. Phys. Rev. B 2019, 99, 205437. [Google Scholar] [CrossRef] [Green Version]
- Ferraro, D.; Andolina, G.M.; Campisi, M.; Pellegrini, V.; Polini, M. Quantum supercapacitors. Phys. Rev. B 2019, 100, 075433. [Google Scholar] [CrossRef] [Green Version]
- Quach, J.Q.; McGhee, K.E.; Ganzer, L.; Rouse, D.M.; Lovett, B.W.; Gauger, E.M.; Keeling, J.; Cerullo, G.; Lidzey, D.G.; Virgili, T. An organic quantum battery. arXiv 2020, arXiv:2012.06026. [Google Scholar]
- Felicetti, S.; Padernales, J.S.; Egusquiza, I.L.; Romero, G.; Lamata, L.; Braak, D.; Solano, E. Spectral collapse via two-phonon interactions in trapped ions. Phys. Rev. A 2015, 92, 033817. [Google Scholar] [CrossRef] [Green Version]
- Felicetti, S.; Rossatto, D.Z.; Rico, E.; Solano, E.; Forn-Diaz, P. Two-photon quantum Rabi model with superconducting circuits. Phys. Rev. A 2018, 97, 013851. [Google Scholar] [CrossRef] [Green Version]
- Emary, C.; Bishop, R.F. Bogoliubov transformations and exact isolated solutions for simple nonadiabatic Hamiltonians. J. Math. Phys. (NY) 2002, 43, 3916. [Google Scholar] [CrossRef] [Green Version]
- Dolya, S.N. Quadratic Lie algebras and quasi-exact solvability of the two-photon Rabi Hamiltonian. J. Math. Phys. 2009, 50, 033512. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.-H.; Wang, C.; He, S.; Liu, T.; Wang, K.-L. Exact solvability of the quantum Rabi model using Bogoliubov operators. Phys. Rev. A 2012, 86, 023822. [Google Scholar] [CrossRef] [Green Version]
- Peng, J.; Zheng, C.; Guo, G.; Guo, X.; Zhang, X.; Deng, C.; Ju, G.; Ren, Z.; Lamata, L.; Solano, E. Dark-like states for the multi-qubit and multi-photon Rabi models. J. Phys. A Math. Theor. 2017, 50, 174003. [Google Scholar] [CrossRef] [Green Version]
- Garbe, L.; Egusquiza, I.L.; Solano, E.; Ciuti, C.; Coudreau, T.; Milman, P.; Felicetti, S. Superradiant phase transition in the ultrastrong-coupling regime of the two-photon Dicke model. Phys. Rev. A 2017, 95, 053854. [Google Scholar] [CrossRef] [Green Version]
- Garbe, L.; Peregrine, W.; Minganti, F.; Shammah, N.; Felicetti, S.; Nori, F. Dissipation-induced bistability in the two-photon Dicke model. Sci. Rep. 2020, 10, 13408. [Google Scholar] [CrossRef]
- Crescente, A.; Carrega, M.; Sassetti, M.; Ferraro, D. Ultrafast charging in a two-photon Dicke quantum battery. Phys. Rev. B 2020, 102, 245407. [Google Scholar] [CrossRef]
- Fink, J.M.; Bianchetti, R.; Baur, M.; Goppl, M.; Steffen, L.; Filipp, S.; Leek, P.J.; Blais, A.; Wallraff, A. Dressed Collective Qubit States and the Tavis-Cummings Model in Circuit QED. Phys. Rev. Lett. 2009, 103, 083601. [Google Scholar] [CrossRef] [Green Version]
- Andolina, G.M.; Farina, D.; Mari, A.; Pellegrini, V.; Giovannetti, V.; Polini, M. Charger-mediated energy transfer in exactly solvable models for quantum batteries. Phys. Rev. B 2018, 98, 205423. [Google Scholar] [CrossRef] [Green Version]
- Friis, N.; Huber, M. Precision and Work Fluctuations in Gaussian Battery Charging. Quantum 2018, 2, 61. [Google Scholar] [CrossRef] [Green Version]
- Caravelli, F.; Coulter-De Wit, G.; Garcia-Pintos, L.P.; Hamma, A. Random Quantum Batteries. Phys. Rev. Res. 2020, 2, 023095. [Google Scholar] [CrossRef]
- Allahverdyan, A.E.; Balian, R.; Nieuwenhuizen, T.M. Maximal work extraction from finite quantum systems. Europhys. Lett. 2004, 67, 565. [Google Scholar] [CrossRef] [Green Version]
- Jaynes, E.T.; Cummings, F.W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 1. [Google Scholar] [CrossRef] [Green Version]
- Bartzis, V.; Nayak, N. Two-photon Jaynes-Cummings model. J. Opt. Soc. Am. B 1991, 8, 8. [Google Scholar] [CrossRef]
- Schleich, W.P. Quantum Optics in Phase Space; Wiley: Berlin, Germany, 2001. [Google Scholar]
- Paladino, E.; Sassetti, M.; Falci, G.; Weiss, U. Characterization of coherent impurity effects in solid-state qubits. Phys. Rev. B 2008, 77, 041303(R). [Google Scholar] [CrossRef] [Green Version]
- Wendin, G. Quantum information processing with superconducting circuits: A review. Rep. Prog. Phys. 2017, 80, 106001. [Google Scholar] [CrossRef] [Green Version]
- Carrega, M.; Crescente, A.; Ferraro, D.; Sassetti, M. Dissipative dynamics of an open quantum battery. New J. Phys. 2020, 22, 083085. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Information. In 10th Anniversary Edition; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Grifoni, M.; Hänggi, P. Driven quantum tunneling. Phys. Rep. 1998, 304, 229–354. [Google Scholar] [CrossRef]
- Campaioli, F.; Pollock, F.A.; Binder, F.C.; Celeri, L.; Goold, J.; Vinjanampathy, S.; Modi, K. Enhancing the charging power of quantum batteries. Phys. Rev. Lett. 2017, 118, 150601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Francica, G.; Binder, F.C.; Guarnieri, G.; Mitchison, M.T.; Goold, J.; Plastina, F. Quantum Coherence and Ergotropy. Phys. Rev. Lett. 2020, 125, 180603. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delmonte, A.; Crescente, A.; Carrega, M.; Ferraro, D.; Sassetti, M. Characterization of a Two-Photon Quantum Battery: Initial Conditions, Stability and Work Extraction. Entropy 2021, 23, 612. https://0-doi-org.brum.beds.ac.uk/10.3390/e23050612
Delmonte A, Crescente A, Carrega M, Ferraro D, Sassetti M. Characterization of a Two-Photon Quantum Battery: Initial Conditions, Stability and Work Extraction. Entropy. 2021; 23(5):612. https://0-doi-org.brum.beds.ac.uk/10.3390/e23050612
Chicago/Turabian StyleDelmonte, Anna, Alba Crescente, Matteo Carrega, Dario Ferraro, and Maura Sassetti. 2021. "Characterization of a Two-Photon Quantum Battery: Initial Conditions, Stability and Work Extraction" Entropy 23, no. 5: 612. https://0-doi-org.brum.beds.ac.uk/10.3390/e23050612