A Multi-Objective Approach for Protein Structure Prediction Based on an Energy Model and Backbone Angle Preferences
Abstract
:1. Introduction
2. Results and Discussion
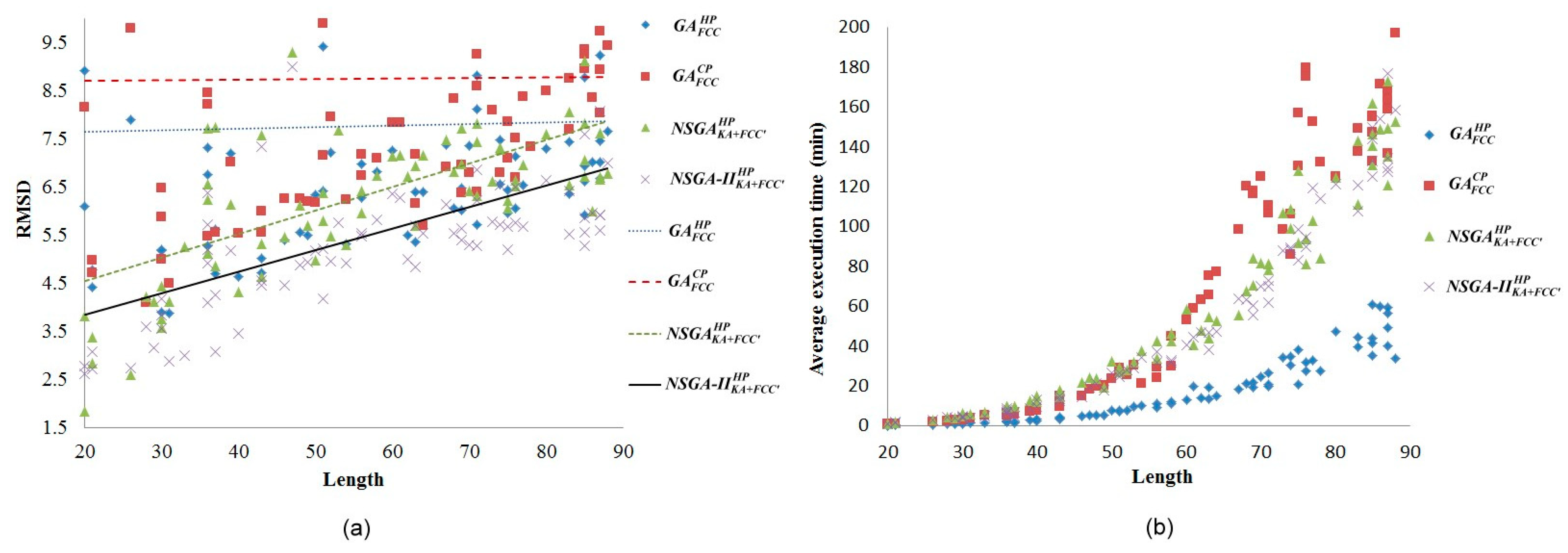
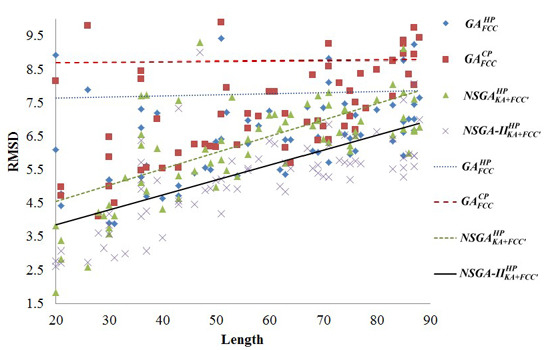
2.1. Comparisons with Visualization
| No. | PDB-ID | Native | |||
|---|---|---|---|---|---|
| 01 | 1EDN Len.21 |  |  |  |  |
| 02 | 1COI Len.29 |  |  |  |  |
| 03 | 1MRT Len.31 |  |  |  |  |
| 04 | 2ERL Len.40 |  |  |  |  |
| 05 | 1CRN Len.46 |  |  |  |  |
| 06 | 1RPO Len.61 |  |  |  |  |
2.2. Comparisons with Off-Lattice Models

3. Materials and Methods
3.1. Materials
3.1.1. 3D FCC Lattice

3.1.2. (κ, α)-Pair Angle Preferences

| α Angle | |||||||
|---|---|---|---|---|---|---|---|
| κ Angle | 60° | 80° | 180° | −130° | −110° | −10° | |
| 30° | 0 | 0 | 0 | 0 | 0 | 0 | |
| 40° | 0 | 0.05 | 0.01 | 0 | 0 | 0 | |
| 50° | 0.21 | 0.73 | 0.18 | 0.06 | 0 | 0.05 | |
| 60° | 1.24 | 1.5 | 0.34 | 0.49 | 0 | 0.38 | |
| 70° | 17.87 | 1.76 | 0.14 | 0.55 | 0 | 0.95 | |
| 80° | 11.08 | 0.59 | 0.21 | 0.51 | 0.02 | 1.65 | |
| 90° | 1.28 | 0.58 | 0.31 | 0.64 | 0.25 | 2.44 | |
| 100° | 0.87 | 0.68 | 0.39 | 0.98 | 0.56 | 2.98 | |
| 110° | 0.72 | 0.70 | 0.47 | 1.29 | 0.96 | 2.14 | |
| 120° | 0.28 | 0.56 | 0.57 | 1.22 | 1.78 | 1.04 | |
| 130° | 0.08 | 0.24 | 0.47 | 1.39 | 2.08 | 0.57 | |
| 140° | 0.04 | 0.10 | 0.40 | 1.99 | 2.03 | 0.43 | |
| 150° | 0.02 | 0.02 | 0.21 | 7.43 | 17.46 | 0.60 | |
3.1.3. Fitness Function
3.1.4. Root-Mean-Square-Deviation
3.2. Methods
3.2.1. Crossovers Operate
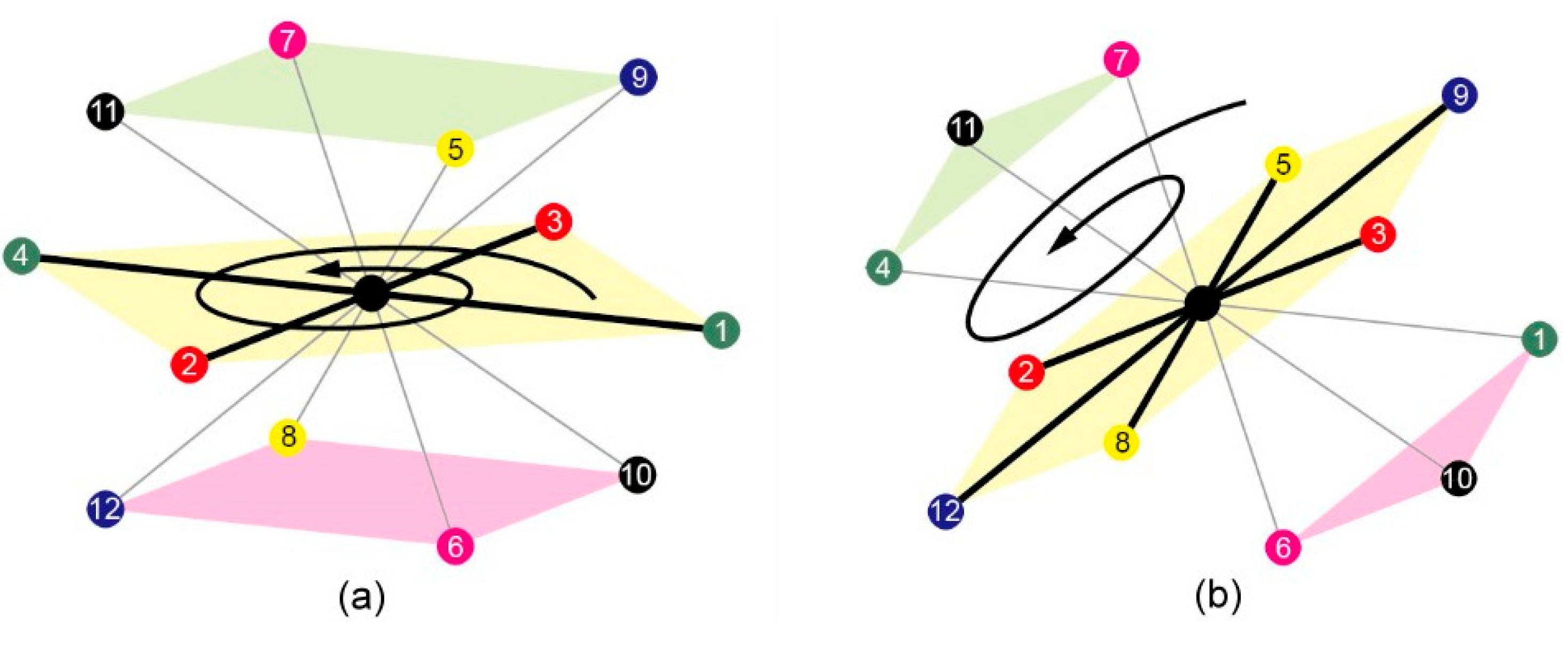
3.2.2. Local Search
3.2.3. Mutations Operate
3.2.4. Termination
3.2.5. Data Set
3.2.6. Experimental Parameters
| Operations/Parameters | Setting |
|---|---|
| Representation | 1–12 Represents 12 vertex coordinates |
| Population size | Equal to substring_length |
| Selection | Tournament selection |
| Crossover rate Pc | 0.85 |
| Mutation rate Pm | 1/(substring_length) |
| K size | 3 |
| Termination | Substring_length *2 generations |
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The protein data bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Dill, K.A.; MacCallum, J.L. The protein-folding problem, 50 years on. Science 2012, 338, 1042–1046. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Yang, X.; He, Z. Protein folding simulations of 2D HP model by the genetic algorithm based on optimal secondary structures. Comput. Biol. Chem. 2010, 34, 137–142. [Google Scholar] [CrossRef] [PubMed]
- Unger, R.; Moult, J. Genetic algorithms for protein folding simulations. J. Mol. Biol. 1993, 231, 75–81. [Google Scholar] [CrossRef] [PubMed]
- Lesh, N.; Mitzenmacher, M.; Whitesides, S. A complete and effective move set for simplified protein folding. In Proceedings of the Seventh Annual International Conference on Research in Computational Molecular Biology, Berlin, Germany, 10–13 April 2003; pp. 188–195.
- Su, S.-C.; Lin, C.-J.; Ting, C.-K. An effective hybrid of hill climbing and genetic algorithm for 2D triangular protein structure prediction. Proteome Sci. 2011, 9, S19. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.-J.; Su, S.-C. Protein 3 D HP model folding simulation using a hybrid of genetic algorithm and particle swarm optimization. Int. J. Fuzzy Syst. 2011, 13, 140–147. [Google Scholar]
- Hoque, M.T.; Chetty, M.; Lewis, A.; Sattar, A. Twin removal in genetic algorithms for protein structure prediction using low-resolution model. IEEE/ACM Trans. Comput. Biol. Bioinform. 2011, 8, 234–245. [Google Scholar] [CrossRef] [PubMed]
- Thachuk, C.; Shmygelska, A.; Hoos, H.H. A replica exchange Monte Carlo algorithm for protein folding in the HP model. BMC Bioinform. 2007, 8, 342. [Google Scholar] [CrossRef] [PubMed]
- Mann, M.; Will, S.; Backofen, R. CPSP-tools—Exact and complete algorithms for high-throughput 3D lattice protein studies. BMC Bioinform. 2008, 9, 230. [Google Scholar] [CrossRef] [PubMed]
- Mann, M.; Smith, C.; Rabbath, M.; Edwards, M.; Will, S.; Backofen, R. CPSP-web-tools: A server for 3D lattice protein studies. Bioinformatics 2009, 25, 676–677. [Google Scholar] [CrossRef] [PubMed]
- Ullah, A.D.; Steinhofel, K. A hybrid approach to protein folding problem integrating constraint programming with local search. BMC Bioinform. 2010, 11, S39. [Google Scholar] [CrossRef] [PubMed]
- Dotu, I.; Cebrian, M.; van Hentenryck, P.; Clote, P. On lattice protein structure prediction revisited. IEEE/ACM Trans. Comput. Biol. Bioinform. 2011, 8, 1620–1632. [Google Scholar] [CrossRef] [PubMed]
- Tsay, J.-J.; Su, S.-C. An effective evolutionary algorithm for protein folding on 3D FCC HP model by lattice rotation and generalized move sets. Proteome Sci. 2013, 11, S19. [Google Scholar] [CrossRef] [PubMed]
- Lau, K.; Dill, K. A Lattice statistical mechanics model of the conformation and sequence space of proteins. Macromolecules 1989, 22, 3986–3997. [Google Scholar] [CrossRef]
- Maňuch, J.; Gaur, D.R. Fitting protein chains to cubic lattice is NP-complete. J. Bioinform. Comput. Biol. 2008, 6, 93–106. [Google Scholar] [CrossRef] [PubMed]
- Mann, M.; Maticzka, D.; Saunders, R.; Backofen, R. Classifying proteinlike sequences in arbitrary lattice protein models using LatPack. HFSP J. 2008, 2, 396–404. [Google Scholar] [CrossRef] [PubMed]
- Ponty, Y.; Istrate, R.; Porcelli, E.; Clote, P. LocalMove: Computing on-lattice fits for biopolymers. Nucleic Acids Res. 2008, 36, W216–W222. [Google Scholar] [CrossRef] [PubMed]
- Mann, M.; Saunders, R.; Smith, C.; Backofen, R.; Deane, C.M. Producing high-accuracy lattice models from protein atomic coordinates including side chains. Adv. Bioinform. 2012, 2012, 6. [Google Scholar] [CrossRef] [PubMed]
- Bromberg, S.; Dill, K.A. Side-chain entropy and packing in proteins. Protein Sci. 1994, 3, 997–1009. [Google Scholar] [CrossRef] [PubMed]
- Anfinsen, C.B. Principles that govern the folding of protein chains. Science 1973, 181, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Berrera, M.; Molinari, H.; Fogolari, F. Amino acid empirical contact energy definitions for fold recognition in the space of contact maps. BMC Bioinform. 2003, 4, 8. [Google Scholar] [CrossRef] [Green Version]
- Miyazawa, S.; Jernigan, R.L. Estimation of effective interresidue contact energies from protein crystal structures: Quasi-chemical approximation. Macromolecules 1985, 18, 534–552. [Google Scholar] [CrossRef]
- Ramachandran, G.N.; Ramakrishnan, C.; Sasisekharan, V. Stereochemistry of polypeptide chain configurations. J. Mol. Biol. 1963, 7, 95–99. [Google Scholar] [CrossRef]
- Srinivas, N.; Deb, K. Muiltiobjective optimization using nondominated sorting in genetic algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. Evol. Comput. IEEE Trans. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Hart, W.E.; Istrail, S. Robust proofs of NP-hardness for protein folding: general lattices and energy potentials. J. Comput. Biol. 1997, 4, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Zhang, Y. Ab initio protein structure assembly using continuous structure fragments and optimized knowledge-based force field. Proteins 2012, 80, 1715–1735. [Google Scholar] [CrossRef] [PubMed]
- Olson, B.; Shehu, A. Multi-objective stochastic search for sampling local minima in the protein energy surface. In Proceedings of the International Conference on Bioinformatics, Computational Biology and Biomedical Informatics, Wshington, DC, USA, 22–25 September 2013; pp. 430–439.
- Olson, B.; Shehu, A. Multi-objective optimization techniques for conformational sampling in templatefree protein structure prediction. In Proceedings of the International Conference on Bioinformatics and Computational Biology, Las Vegas, NV, USA, 24–26 March 2014.
- Yang, J.-M.; Tung, C.-H. Protein structure database search and evolutionary classification. Nucleic Acids Res. 2006, 34, 3646–3659. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Dunbrack, R.L. PISCES: Recent improvements to a PDB sequence culling server. Nucleic Acids Res. 2005, 33, W94–W98. [Google Scholar] [CrossRef] [PubMed]
- Kabsch, W.; Sander, C. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 1983, 22, 2577–2637. [Google Scholar] [CrossRef] [PubMed]
- Maiorov, V.N.; Crippen, G.M. Significance of root-mean-square deviation in comparing three-dimensional structures of globular proteins. J. Mol. Biol. 1994, 235, 625–634. [Google Scholar] [CrossRef] [PubMed]
- Backofen, R.; Will, S.; Clote, P. Algorithmic approach to quantifying the hydrophobic force contribution in protein folding. Pac. Symp. Biocomput. 2000, 95–106. [Google Scholar]
- Cuff, J.A.; Barton, G.J. Evaluation and improvement of multiple sequence methods for protein secondary structure prediction. Proteins Struct. Funct. Bioinform. 1999, 34, 508–519. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsay, J.-J.; Su, S.-C.; Yu, C.-S. A Multi-Objective Approach for Protein Structure Prediction Based on an Energy Model and Backbone Angle Preferences. Int. J. Mol. Sci. 2015, 16, 15136-15149. https://0-doi-org.brum.beds.ac.uk/10.3390/ijms160715136
Tsay J-J, Su S-C, Yu C-S. A Multi-Objective Approach for Protein Structure Prediction Based on an Energy Model and Backbone Angle Preferences. International Journal of Molecular Sciences. 2015; 16(7):15136-15149. https://0-doi-org.brum.beds.ac.uk/10.3390/ijms160715136
Chicago/Turabian StyleTsay, Jyh-Jong, Shih-Chieh Su, and Chin-Sheng Yu. 2015. "A Multi-Objective Approach for Protein Structure Prediction Based on an Energy Model and Backbone Angle Preferences" International Journal of Molecular Sciences 16, no. 7: 15136-15149. https://0-doi-org.brum.beds.ac.uk/10.3390/ijms160715136