Spatial-Temporal Epidemiology of Tuberculosis in Mainland China: An Analysis Based on Bayesian Theory
Abstract
:1. Introduction
2. Methods
2.1. Data Sources
2.2. Statistical Methodology: Bayesian Methods and Negative Binomial Distribution
2.3. Model Selection
2.4. Statistical Analysis Software
3. Results
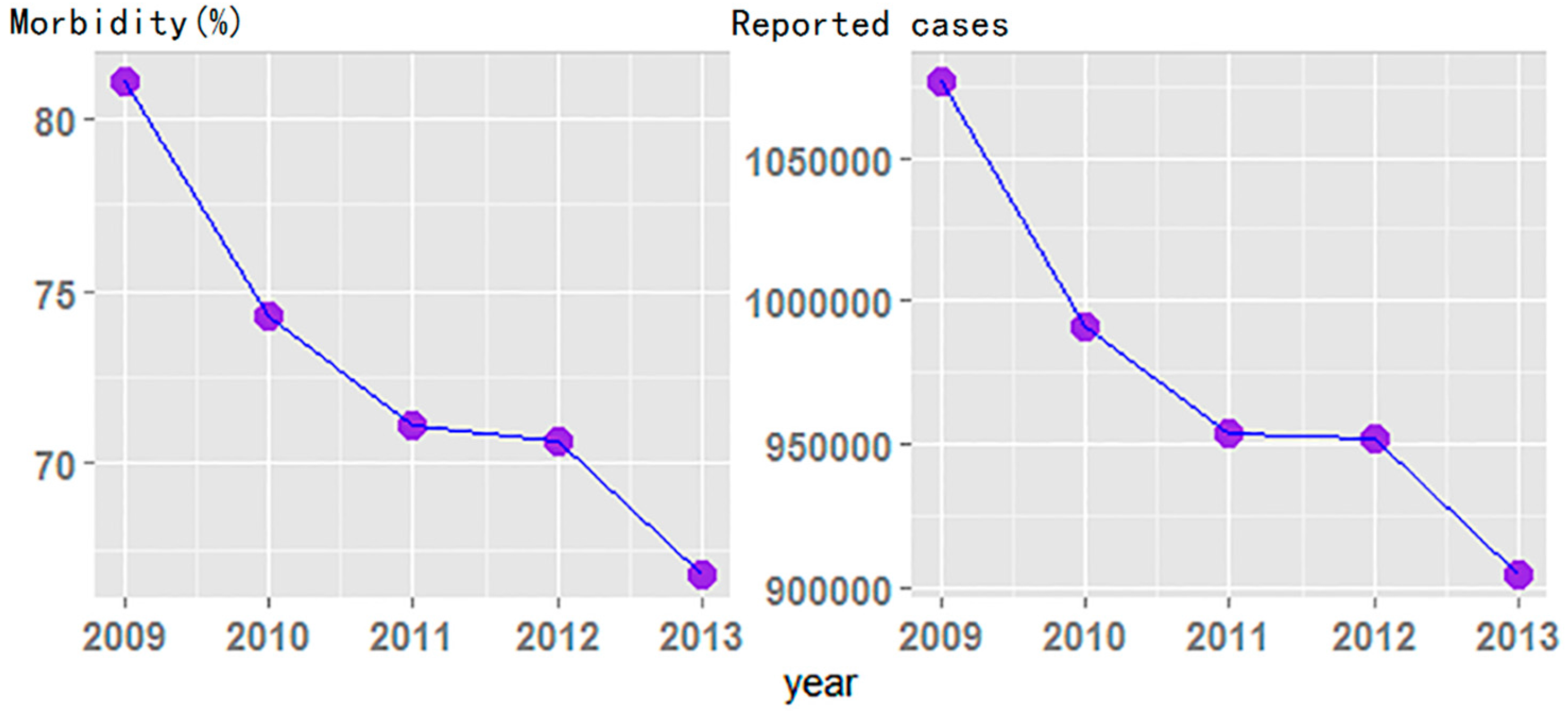
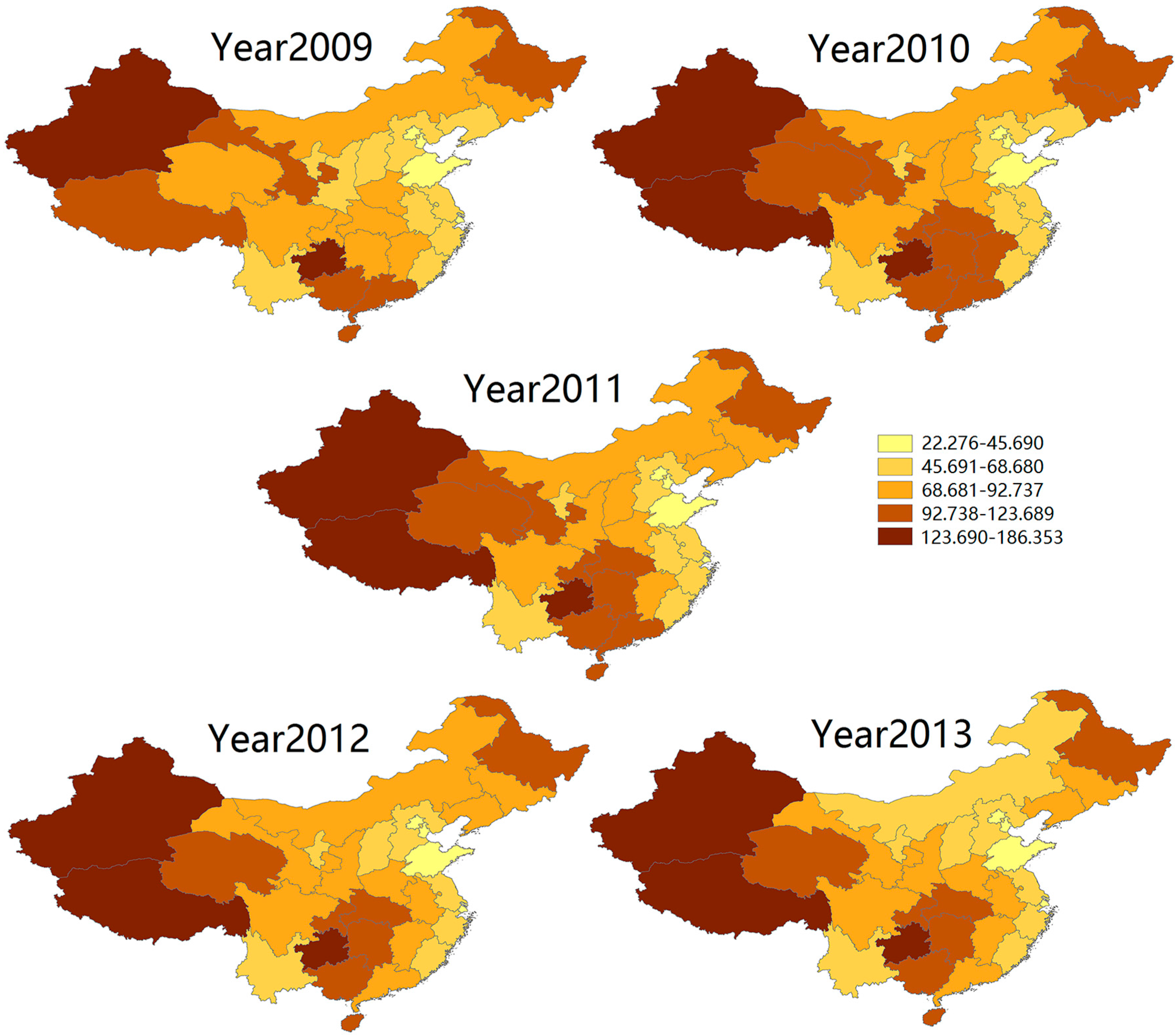
3.1. Descriptive Analysis
3.2. Exploration of Climate Factors
4. Discussion
5. Limitations and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, T.; Xue, F.; Chen, Y.; Ma, Y.; Liu, Y. The spatial epidemiology of tuberculosis in Linyi City, China, 2005–2010. BMC Public Health 2012, 12, 885. [Google Scholar] [CrossRef] [PubMed]
- Pan, H.Q.; Bele, S.; Feng, Y.; Qiu, S.S.; Lü, J.Q.; Tang, S.W.; Shen, H.B.; Wang, J.M.; Zhu, L.M. Analysis of the economic burden of diagnosis and treatment of tuberculosis patients in rural China. Int. J. Tuberc. Lung Dis. 2013, 17, 1575–1580. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Gong, J.; Zhou, J.; Zhao, Y.; Tan, J.; Ibrahim, A.N.; Zhou, Y. A spatial, social and environmental study of tuberculosis in China using statistical and GIS technology. Int. J. Environ. Res. Public Health 2015, 12, 1425–1448. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Jia, H.; Liu, F.; Pan, L.; Xing, A.; Gu, S.; Du, B.; Sun, Q.; Wei, R.; Zhang, Z. Prevalence and Risk Factors for Latent Tuberculosis Infection among Health Care Workers in China: A Cross-Sectional Study. PLoS ONE 2013, 8, e66412. [Google Scholar]
- Zhu, S.Y.; Hou, Y.C.; Shu, W.; Zhang, G.L.; Nie, S.F.; Chen, W.; Cheng, S.M.; Xu, Y.H. Study on the risk factors of tuberculosis in four cities and provinces in China. Zhonghua Liu Xing Bing Xue Za Zhi 2013, 34, 129–132. [Google Scholar] [PubMed]
- Pang, Y.; Song, Y.; Xia, H.; Zhou, Y.; Zhao, B.; Zhao, Y. Risk factors and clinical phenotypes of Beijing genotype strains in tuberculosis patients in China. BMC Infect. Dis. 2012, 12, 354. [Google Scholar] [CrossRef] [PubMed]
- Pan, H.; Dai, Y.; Tang, S.; Wang, J. Polymorphisms of NOD2 and the risk of tuberculosis: A validation study in the Chinese population. Int. J. Immunogenet. 2012, 39, 233–240. [Google Scholar]
- Valenca, M.S.; Scaini, J.L.; Abileira, F.S.; Gonçalves, C.V.; Von-Groll, A.; Silva, P.E. Prevalence of tuberculosis in prisons: Risk factors and molecular epidemiology. Int. J. Tuberc. Lung Dis. 2015, 19, 1182–1187. [Google Scholar]
- Dhanaraj, B.; Papanna, M.K.; Adinarayanan, S.; Vedachalam, C.; Sundaram, V.; Shanmugam, S.; Sekar, G.; Menon, P.A.; Wares, F.; Swaminathan, S. Prevalence and risk factors for adult pulmonary tuberculosis in a metropolitan city of South India. PLoS ONE 2015, 10, e124260. [Google Scholar]
- Wang, X.; Yang, Z.; Fu, Y.; Zhang, G.; Wang, X.; Zhang, Y.; Wang, X. Insight to the Epidemiology and Risk Factors of Extra pulmonary Tuberculosis in Tianjin, China during 2006–2011. PLoS ONE 2014, 9, e112213. [Google Scholar]
- Kirenga, B.J.; Ssengooba, W.; Muwonge, C.; Nakiyingi, L.; Kyaligonza, S.; Kasozi, S.; Mugabe, F.; Boeree, M.; Joloba, M.; Okwera, A. Tuberculosis risk factors among tuberculosis patients in Kampala, Uganda: Implications for tuberculosis control. BMC Public Health 2015, 15, 13. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Li, Y.; Li, X.; Zhang, W.; Pan, Z.; Wu, F.; Wang, C.; Chen, Z.; Jiang, T.; Xu, D. Association of the miR-146a, miR-149, miR-196a2 and miR-499 polymorphisms with susceptibility to pulmonary tuberculosis in the Chinese Uygur, Kazak and Southern Han populations. BMC Infect. Dis. 2015, 15, 41. [Google Scholar]
- Yang, J.; Chen, J.; Yue, J.; Liu, L.; Han, M.; Wang, H. Relationship between human LTA4H polymorphisms and extra-pulmonary tuberculosis in an ethnic Han Chinese population in Eastern China. Tuberculosis (Edinb.) 2014, 94, 657–663. [Google Scholar]
- Feng, Y.; Wang, F.; Pan, H.; Qiu, S.; Lü, J.; Wu, L.; Wang, J.; Lu, C. Obesity-associated gene FTO rs9939609 polymorphism in relation to the risk of tuberculosis. BMC Infect. Dis. 2014, 14, 592. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.Y.; Li, H.; Wang, Y.G.; Xu, C.Y.; Zhao, Y.L.; Ma, X.G.; Li, X.W.; Chen, H. Correlation analysis between single nucleotide polymorphisms of pulmonary surfactant protein A gene and pulmonary tuberculosis in the Han population in China. Int. J. Infect. Dis. 2014, 26, 31–36. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Zhao, Q.; Wu, L.; Wang, W.; Yuan, Z.; Xu, B. Prevalence of latent tuberculosis infection and its risk factors in schoolchildren and adolescents in Shanghai, China. Eur. J. Public Health 2013, 23, 1064–1069. [Google Scholar] [CrossRef] [PubMed]
- Zhao, P.; Li, X. J.; Zhang, S.F.; Wang, X.S.; Liu, C.Y. Social behaviour risk factors for drug resistant tuberculosis in mainland China: A meta-analysis. J. Int. Med. Res. 2012, 40, 436–445. [Google Scholar] [CrossRef] [PubMed]
- Nyasulu, P.; Mogoere, S.; Umanah, T.; Setswe, G. Determinants of Pulmonary Tuberculosis among Inmates at Mangaung Maximum Correctional Facility in Bloemfontein, South Africa. Tuberc. Res. Treat. 2015, 2015, 752709. [Google Scholar] [PubMed]
- Narula, P.; Sihota, P.; Azad, S.; Lio, P. Analyzing seasonality of tuberculosis across Indian states and union territories. J. Epidemiol. Glob. Health 2015, 5, 337–346. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.X.; Pang, C.K.; Liu, Y.; Sun, X.B.; Li, X.X.; Jiang, S.W.; Xue, F. Association between Multidrug-Resistant Tuberculosis and Risk Factors in China: Applying Partial Least Squares Path Modeling. PLoS ONE 2015, 10, e128298. [Google Scholar]
- Li, X.X.; Wang, L.X.; Zhang, J.; Liu, Y.X.; Zhang, H.; Jiang, S.W.; Chen, J.X.; Zhou, X.N. Exploration of ecological factors related to the spatial heterogeneity of tuberculosis prevalence in P. R. China. Glob. Health Action 2014, 7, 23620. [Google Scholar] [CrossRef] [PubMed]
- Lamichhane, A.P.; Warren, J.L.; Peterson, M.; Rummo, P.; Gordon-Larsen, P. Spatial-temporal modeling of neighborhood sociodemographic characteristics and food stores. Am. J. Epidemiol. 2015, 181, 137–150. [Google Scholar] [CrossRef] [PubMed]
- Naithani, K.J.; Baldwin, D.C.; Gaines, K.P.; Lin, H.; Eissenstat, D.M. Spatial distribution of tree species governs the spatio-temporal interaction of leaf area index and soil moisture across a forested landscape. PLoS ONE 2013, 8, e58704. [Google Scholar] [CrossRef] [PubMed]
- Bauer, C.; Wakefield, J.; Rue, H.; Self, S.; Feng, Z.; Wang, Y. Bayesian penalized spline models for the analysis of spatio-temporal count data. Stat. Med. 2015. [Google Scholar] [CrossRef]
- National Population and Health Science Data Sharing Platform [DB/OL]. Available online: http://www. phsciencedata.cn (accessed on 27 February 2016).
- China Meteorological Data Sharing Service System [DB/OL]. Available online: http://cdc.cma.gov.cn (accessed on 27 February 2016).
- Johnson, W.E.; Li, C.; Rabinovic, A. Adjusting batch effects in microarray expression data using empirical Bayes methods. Biostatistics 2007, 8, 118–127. [Google Scholar] [CrossRef] [PubMed]
- Leek, J.T.; Scharpf, R.B.; Bravo, H.C.; Simcha, D.; Langmead, B.; Johnson, WE.; Geman, D.; Baggerly, K.; Irizarry, R.A. Tackling the widespread and critical impact of batch effects in high-throughput data. Nat. Rev. Genet. 2010, 11, 733–739. [Google Scholar] [CrossRef] [PubMed]
- Loubet, P.; Mabileau, G.; Baysah, M.; Nuta, C.; Taylor, M.; Jusu, H.; Weeks, H.; Ingels, A.; Perennec-Olivier, M.; Chapplain, J.M. Likely effect of the 2014 Ebola epidemic on HIV care in Liberia. AIDS 2015, 29, 2347–2351. [Google Scholar] [CrossRef] [PubMed]
- Brousseau, N.; Green, H.K.; Andrews, N.; Pryse, R.; Baguelin, M.; Sunderland, A.; Ellis, J.; Pebody, R. Impact of influenza vaccination on respiratory illness rates in children attending private boarding schools in England, 2013–2014: A cohort study. Epidemiol. Infect. 2015, 143, 3405–3415. [Google Scholar] [CrossRef] [PubMed]
- Perez, V.; Mena, K.D.; Watson, H.N.; Prater, R.B.; McIntyre, J.L. Evaluation and quantitative microbial risk assessment of a unique antimicrobial agent for hospital surface treatment. Am. J. Infect. Control 2015, 43, 1201–1207. [Google Scholar] [CrossRef] [PubMed]
- Ypma, R.J.; Altes, H.K.; van Soolingen, D.; Wallinga, J.; van Ballegooijen, W.M. A sign of super spreading in tuberculosis: Highly skewed distribution of genotypic cluster sizes. Epidemiology 2013, 24, 395–400. [Google Scholar] [CrossRef] [PubMed]
- Freeman, R.; Charlett, A.; Hopkins, S.; O’Connell, A.M.; Andrews, N.; Freed, J.; Holmes, A.; Catchpole, M. Evaluation of a national microbiological surveillance system to inform automated outbreak detection. J. Infect. 2013, 67, 378–384. [Google Scholar] [CrossRef] [PubMed]
- Millar, R.B.; Mckechnie, S. A one-step-ahead pseudo-DIC for comparison of Bayesian state-space models. Biometrics 2014, 70, 972–980. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Ibrahim, J.G.; Chen, Q. Bayesian Case-deletion Model Complexity and Information Criterion. Stat. Interface 2014, 7, 531–542. [Google Scholar] [CrossRef] [PubMed]
- China Tuberculosis Control Collaboration. The effect of tuberculosis control in China. Lancet 2004, 364, 417–422. [Google Scholar]
- Vlad, I.T.; Juan, P.; Mateu, J. Bayesian spatio-temporal prediction of cancer dynamics. Comput. Math. Appl. 2015, 70, 857–868. [Google Scholar] [CrossRef]
- Mertz, D.F.; Löhnertz, W.; Nomade, S.; Pereira, A.; Prelevic, D.; Renne, P.R. Temporal–spatial evolution of low-SiO2 volcanism in the Pleistocene West Eifel volcanic field (West Germany) and relationship to upwelling asthenosphere. J. Geodyn. 2015, 88, 59–79. [Google Scholar] [CrossRef]
- Wong, N.S.; Lee, S.S. The spatio-temporal diffusion of Pandemic Influenza (H1N1) 2009 in Hong Kong. Procedia Environ. Sci. 2011, 3, 26–31. [Google Scholar] [CrossRef]
- Khaliq, A.; Batool, S.A.; Chaudhry, M.N. Seasonality and trend analysis of tuberculosis in Lahore, Pakistan from 2006 to 2013. J. Epidemiol. Glob. Health 2015, 5, 397–403. [Google Scholar] [CrossRef] [PubMed]
- Mabaera, B.; Naranbat, N.; Katamba, A.; Laticevschi, D.; Lauritsen, J.M.; Rieder, H.L. Seasonal variation among tuberculosis suspects in four countries. Int. Health 2009, 1, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Prudêncio, C.V.; Mantovani, H.C.; Cecon, P.R.; Prieto, M.; Vanetti, M.C.D. Temperature and pH influence the susceptibility of Salmonella Typhimurium to nisin combined with EDTA. Food Control 2016, 61, 248–253. [Google Scholar] [CrossRef]
- Keet, D.F.; Kriek, N.P.; Huchzermeyer, H.; Bengis, R.G. Advanced tuberculosis in an African buffalo (Syncerus caffer Sparrman). J. S. Afr. Vet. Assoc. 1994, 65, 79–83. [Google Scholar] [PubMed]
- Desalu, O.O. Seasonal variation in hospitalisation for respiratory diseases in the tropical rain forest of South Western Nigeria. Niger. Postgrad. Med. J. 2011, 18, 39–43. [Google Scholar] [PubMed]
- Knibbs, L.D.; Morawska, L.; Bell, S.C.; Grzybowski, P. Room ventilation and the risk of airborne infection transmission in 3 health care settings within a large teaching hospital. Am. J. Infect. Control. 2011, 39, 866–872. [Google Scholar] [CrossRef] [PubMed] [Green Version]
| Model | Estimated Relative Risk |
|---|---|
| UH | |
| UH + autoregressive time effect | |
| UH + time trend effect | |
| CH | |
| CH + UH | |
| CH + UH + temporal − spatial interaction |
| Variable | MEAN | SD | MC Error | θ (RR) | 95% CI |
|---|---|---|---|---|---|
| a0 | −0.29720 | 0.22050 | 0.00751 | 0.74289 | 0.40865–0.97988 |
| a1 | 0.16160 | 0.10180 | 0.00347 | 1.17538 | 0.99146–1.46507 |
| average temperature | 0.00324 | 0.00108 | 5.6890E-7 | 1.00324 | 1.00150–1.00550 |
| average rainfall | 0.01005 | 1.669E-5 | 8.2300E-7 | 1.01010 | 1.01007–1.01013 |
| average wind speed | −0.18010 | 0.00685 | 3.8360E-4 | 0.83518 | 0.93732–0.96138 |
| average humidity | −0.02535 | 0.01565 | 8.7610E-5 | 0.97496 | 0.97181–1.01386 |
| average air pressure | 0.01002 | 2.4150E-5 | 8.2430E-5 | 1.01007 | 1.01003–1.01011 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, K.; Yang, K.; Wang, C.; Guo, J.; Tao, L.; Liu, Q.; Gehendra, M.; Zhang, Y.; Guo, X. Spatial-Temporal Epidemiology of Tuberculosis in Mainland China: An Analysis Based on Bayesian Theory. Int. J. Environ. Res. Public Health 2016, 13, 469. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph13050469
Cao K, Yang K, Wang C, Guo J, Tao L, Liu Q, Gehendra M, Zhang Y, Guo X. Spatial-Temporal Epidemiology of Tuberculosis in Mainland China: An Analysis Based on Bayesian Theory. International Journal of Environmental Research and Public Health. 2016; 13(5):469. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph13050469
Chicago/Turabian StyleCao, Kai, Kun Yang, Chao Wang, Jin Guo, Lixin Tao, Qingrong Liu, Mahara Gehendra, Yingjie Zhang, and Xiuhua Guo. 2016. "Spatial-Temporal Epidemiology of Tuberculosis in Mainland China: An Analysis Based on Bayesian Theory" International Journal of Environmental Research and Public Health 13, no. 5: 469. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph13050469





