Multiobjective Cloud Particle Optimization Algorithm Based on Decomposition
Abstract
:1. Introduction
2. Related Backgrounds
2.1. Problem Definition
2.2. Multiobjective Evolutionary Algorithm Based on Decomposition
| Algorithm 1. The procedure of MOEA/D |
| Input: MOP, the multiobjective optimization problem; NP, population size; GEN, maximum generations; FES, the maximal number of function evaluations; NB, the number of weight vectors in the neighborhood of each weight vector; |
| Output: X, the non-dominated population; Approximation to the PF, {F(x1), … ,F(xN)} |
| 1: Randomly initial population Xn |
| 2: Compute the Euclidian distances between any two weight vectors and define neighborhood of each subproblem. For the ith subproblem, set B(i) = {i1,i2,…im}, where , , …, are the m closest weight vectors to |
| 3: Initialize z=(z1,…, zm)T by problem-specific method |
| 4: while t < FES do |
| 5: for i = 1:NP do |
| 6: Produce y by DE-mutation strategies |
| 7: polynomial mutation |
| 8: Evaluation y |
| 9: for each j = 1 to m do |
| 10: if zj > fj(y) then zj = fj(y) |
| 11: endfor |
| 12: for each j∈B(i) do |
| 13: if gte(y|,z) < gte(xj|,z)then |
| 14: xj = y and F(xj) = F(y) |
| 15: endif |
| 16: endfor |
| 17: endfor |
| 18: endwhile |
3. Frameworks of MOEA/D-CPDE
3.1. Cloud Generator
3.2. Cloud Particle Differential Evolution
3.3 Cloud Particle Mutation Operator
| Algorithm 2. The procedure of MOEA/D-CPDE. |
| Input: MOP, the multiobjective optimization problem; NP, population size; GEN, maximum generations; FES, the maximal number of function evaluations; NB, the number of weight vectors in the neighborhood of each weight vector; |
| Output: X, the non-dominated population; Approximation to the PF, {F(x1), … ,F(xN)} |
| 1: Generate initial population Xn by cloud generator |
| 2: Compute the Euclidian distances between any two weight vectors and define neighborhood of each subproblem. For the ith subproblem, set B(i)={i1,i2,…im}, where , , …, are the m closest weight vectors to . |
| 3: Initialize z = (z1,…, zm)T by problem-specific method |
| 4: while t < FES do |
| 5: for i = 1:NP do |
| 6: Exi = xi |
| 7: Eni = |Exi|/10 |
| 8: Hei = Eni/1000 |
| 9: generate c1 and c2 by cloud generator |
| 10: Produce yi by Cloud Particle Differential Evolution |
| 11: if rand ≥ 0.5 |
| 12: Cloud Particle Mutation Operator |
| 13: else |
| 14: polynomial mutation |
| 15: end |
| 16: Evaluation y |
| 17: for each j=1 to m do |
| 18: if zj > fj(y) then zj = fj(y) |
| 19: endfor |
| 20: for each j∈B(i) do |
| 21: if gte(y| ,z)<gte(xj| ,z)then |
| 22: xj = y and F(xj) = F(y) |
| 23: endif |
| 24: endfor |
| 25: endfor |
| 26: endwhile |
4. Experimental and Discussions
4.1. Parameter Settings
4.2. Performance Metrics
4.3. Experimental Results
| Function | Min | Mean | Std | Max | Algorithms |
|---|---|---|---|---|---|
| DEB | 0.005354 | 0.005355 | 4.7946e-7 | 0.005355 | MOEA/D |
| - | - | - | - | MOEA/D-DE+PSO | |
| 0.005354 | 0.005354 | 5.0741e-7 | 0.005355 | MOEA/D-CPDE | |
| ZDT1 | 0.003988 | 0.004054 | 5.1587e-5 | 0.004165 | MOEA/D |
| 0.004012 | 0.004142 | 7.1000e-5 | 0.004359 | MOEA/D-DE+PSO | |
| 0.003966 | 0.004036 | 4.7909e-5 | 0.004088 | MOEA/D-CPDE | |
| ZDT2 | 0.003799 | 0.003819 | 1.5762e-5 | 0.003864 | MOEA/D |
| 0.003811 | 0.003874 | 4.2400e-5 | 0.003992 | MOEA/D-DE+PSO | |
| 0.003784 | 0.003808 | 1.1640e-5 | 0.003831 | MOEA/D-CPDE | |
| ZDT3 | 0.007041 | 0.007084 | 3.4618e-5 | 0.007200 | MOEA/D |
| 0.008400 | 0.009025 | 5.9532e-4 | 0.012406 | MOEA/D-DE+PSO | |
| 0.007049 | 0.007081 | 2.8241e-5 | 0.007171 | MOEA/D-CPDE | |
| ZDT4 | 0.125709 | 0.195898 | 6.7636e-2 | 0.256064 | MOEA/D |
| 0.004141 | 0.007550 | 1.9710e-3 | 0.011584 | MOEA/D-DE+PSO | |
| 0.003953 | 0.003954 | 8.0301e-7 | 0.003956 | MOEA/D-CPDE | |
| ZDT6 | 0.008892 | 0.013408 | 3.6559e-3 | 0.017854 | MOEA/D |
| 0.006977 | 0.014575 | 4.0370e-3 | 0.022697 | MOEA/D-DE+PSO | |
| 0.005087 | 0.005970 | 6.5858e-4 | 0.006620 | MOEA/D-CPDE |



| Function | Min | Mean | Std | Max | Algorithms |
|---|---|---|---|---|---|
| UF1 | 0.004711 | 0.023042 | 0.053302 | 0.259563 | MOEA/D |
| 0.004466 | 0.028572 | 0.023609 | 0.071182 | MOEA/D-DE+PSO | |
| 0.004594 | 0.005203 | 0.000248 | 0.006144 | MOEA/D-CPDE | |
| UF2 | 0.009082 | 0.014285 | 0.007173 | 0.049397 | MOEA/D |
| 0.010218 | 0.011737 | 0.000756 | 0.013261 | MOEA/D-DE+PSO | |
| 0.008998 | 0.011877 | 0.001714 | 0.015334 | MOEA/D-CPDE | |
| UF3 | 0.016796 | 0.062967 | 0.028005 | 0.142894 | MOEA/D |
| 0.003940 | 0.006039 | 0.001826 | 0.010494 | MOEA/D-DE+PSO | |
| 0.008435 | 0.044706 | 0.029862 | 0.114730 | MOEA/D-CPDE | |
| UF4 | 0.061278 | 0.069968 | 0.006585 | 0.089038 | MOEA/D |
| 0.047843 | 0.054604 | 0.004053 | 0.071241 | MOEA/D-DE+PSO | |
| 0.043632 | 0.045344 | 0.001319 | 0.049677 | MOEA/D-CPDE | |
| UF5 | 0.208215 | 0.422297 | 0.128282 | 0.729846 | MOEA/D |
| 0.282111 | 0.490882 | 0.118561 | 0.708999 | MOEA/D-DE+PSO | |
| 0.115859 | 0.203445 | 0.045309 | 0.258254 | MOEA/D-CPDE | |
| UF6 | 0.162838 | 0.495739 | 0.199592 | 0.824257 | MOEA/D |
| 0.186140 | 0.243517 | 0.237355 | 0.674953 | MOEA/D-DE+PSO | |
| 0.073819 | 0.091573 | 0.030068 | 0.210588 | MOEA/D-CPDE | |
| UF7 | 0.005013 | 0.147765 | 0.219858 | 0.598471 | MOEA/D |
| 0.006726 | 0.243517 | 0.237355 | 0.674953 | MOEA/D-DE+PSO | |
| 0.005112 | 0.006067 | 0.000640 | 0.007461 | MOEA/D-CPDE | |
| UF8 | 0.090851 | 0.145518 | 0.031061 | 0.229571 | MOEA/D |
| 0.057600 | 0.078455 | 0.006532 | 0.101902 | MOEA/D-DE+PSO | |
| 0.112641 | 0.123347 | 0.006231 | 0.139016 | MOEA/D-CPDE | |
| UF9 | 0.087260 | 0.166323 | 0.033758 | 0.194023 | MOEA/D |
| 0.035499 | 0.071131 | 0.035008 | 0.149478 | MOEA/D-DE+PSO | |
| 0.074763 | 0.080028 | 0.002555 | 0.083058 | MOEA/D-CPDE | |
| UF10 | 0.231245 | 0.431299 | 0.084250 | 0.637907 | MOEA/D |
| 0.184050 | 0.187158 | 0.001552 | 0.190097 | MOEA/D-DE+PSO | |
| 0.369133 | 0.499921 | 0.078278 | 0.688156 | MOEA/D-CPDE |
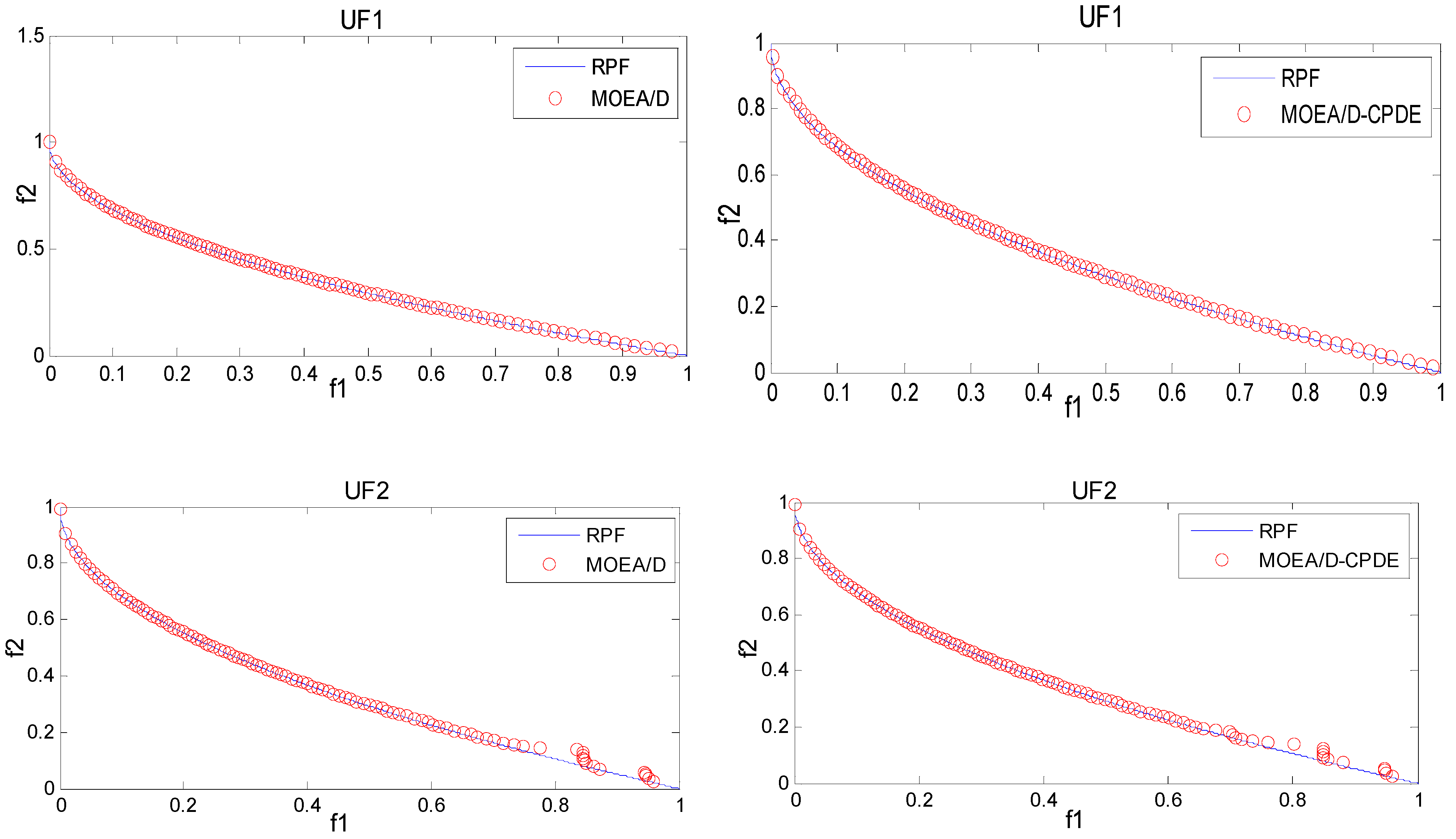



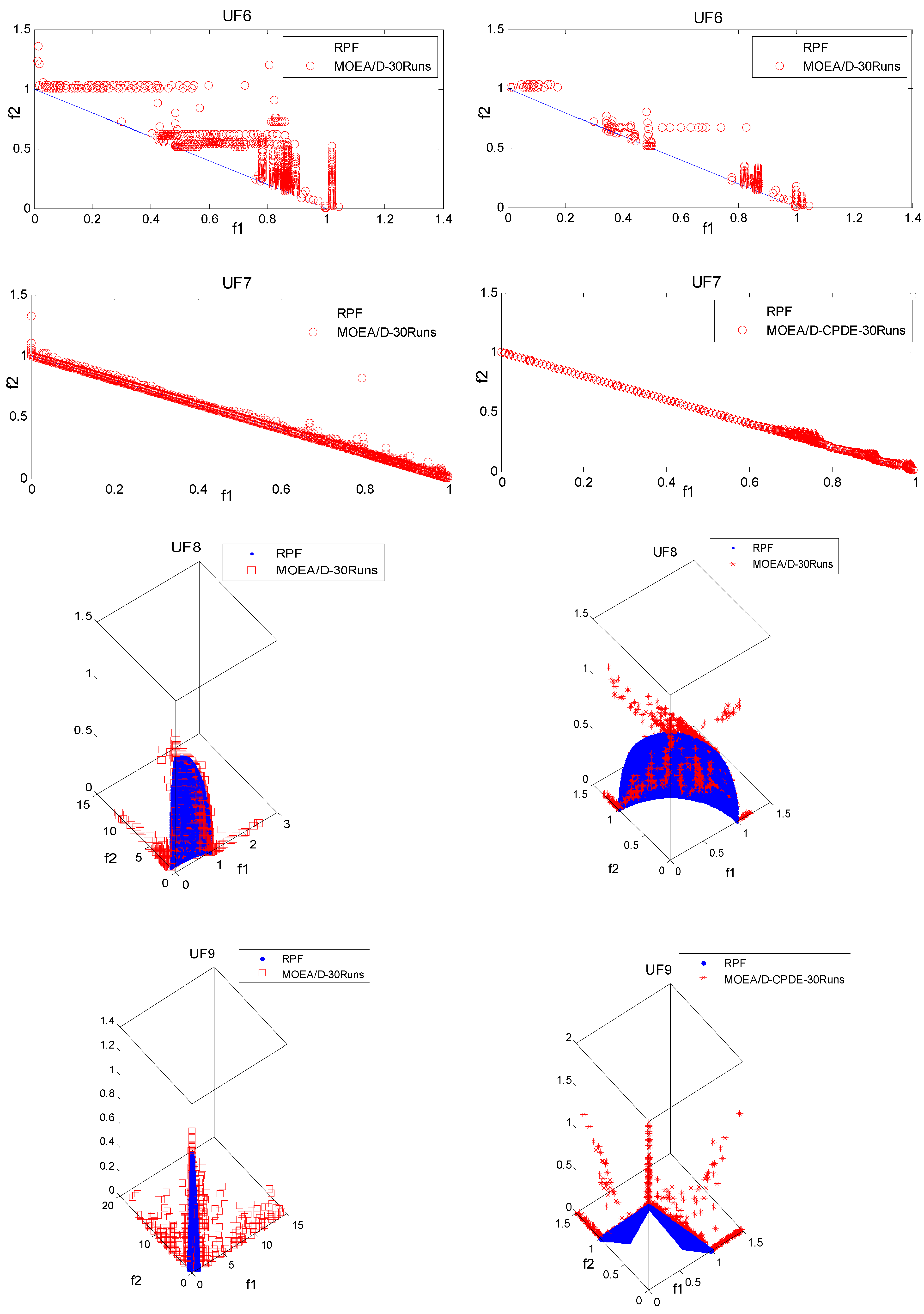

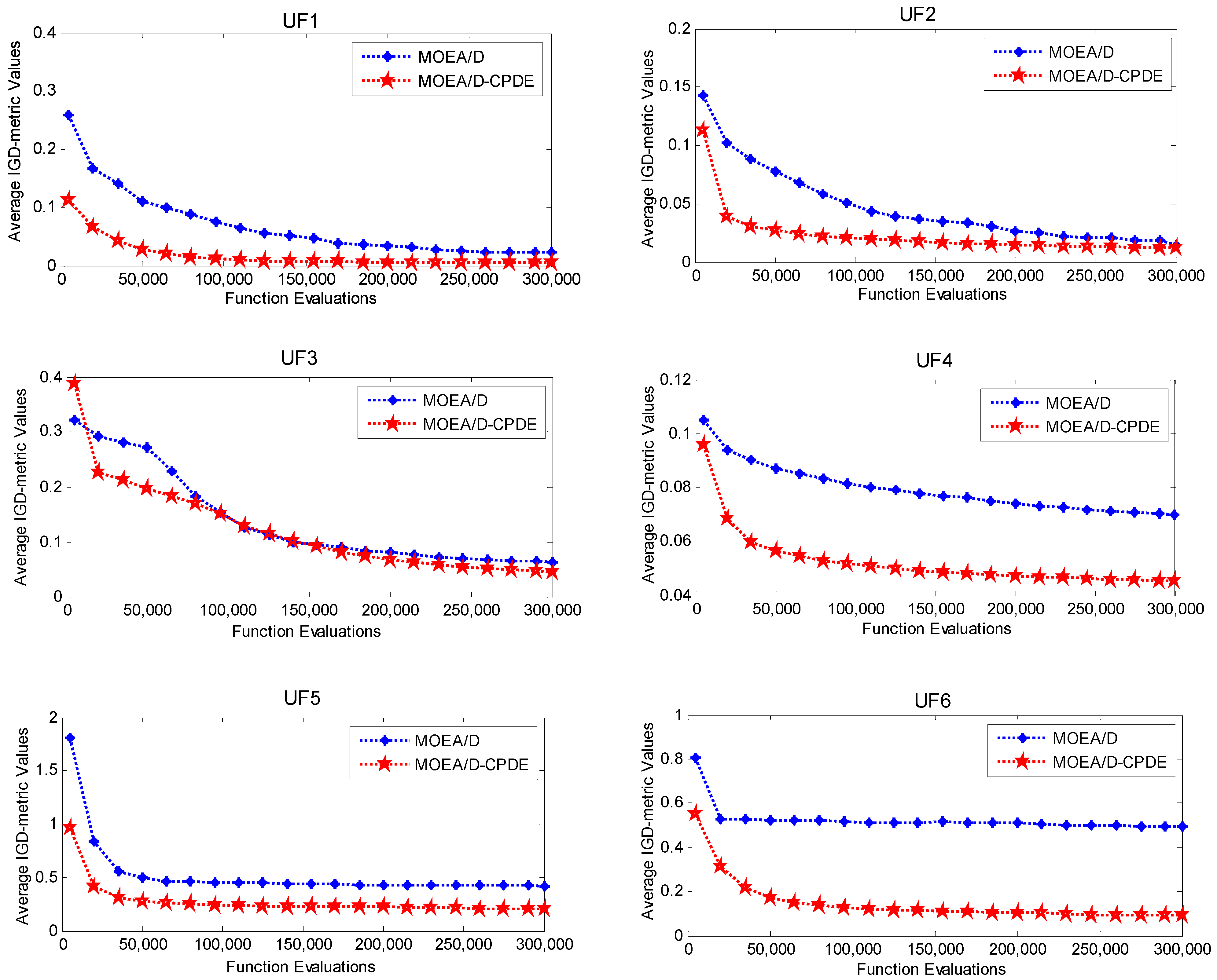

5. Conclusion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Coello, Coello, C.A.; Pulido, G.T.; Montes, E.M. Current and future research trends in evolutionary multiobjective optimization. From Industrial Applications to Academic Speculations. In Book Information Processing with Evolutionary Algorithms; Wu, X., Jain, L., Graña, M., Duro, R.J., d’Anjou, A., Wang, P.P., Eds.; Springer: London, UK, 2005; pp. 213–231. [Google Scholar] [CrossRef]
- Andersson, J. A survey of multiobjective optimization in engineering design. Tech. Rep. LiTH-IKP-R-1097; Department of Mechanical Engineering, Linköping University: Linköpings, Sweden, 2000. [Google Scholar]
- Marler, R.T.; Arora, J.S. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar]
- Lei, D. Multi-objective production scheduling: a survey. Int. J. Adv. Manuf. Technol. 2009, 43, 926–938. [Google Scholar] [CrossRef]
- Tapia, M.G.C.; Coello, Coello, C.A. Applications of multi-objective evolutionary algorithms in economics and finance: a survey. Evol. Comput. 2007, 532–539. [Google Scholar]
- Luna, F.; Durillo, J.J.; Nebro, A.J.; Alba, E. Evolutionary algorithms for solving the automatic cell planning problem: S survey. Eng. Optim. 2010, 42, 671–690. [Google Scholar] [CrossRef]
- Lust, T.; Teghem, J. The multiobjective traveling salesman problem: a survey and a new approach. In Advances in Multi-Objective Nature Inspired Computing; Coello Coello, C.A., Dhaenens, C., Eds.; Springer: Heidelberg, Berlin, Germany, 2010; Volume 272, pp. 119–141. [Google Scholar]
- Coello Coello, C.A.; Van Veldhuizen, D.A.; Lamont, G.B. Evolutionary Algorithms for Solving Multiobjective Problems; Springer US: New York, NY, USA, 2002. [Google Scholar]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II, IEEE. Tran. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Knowles, J.; Corne, D. Memetic algorithms for multiobjective optimiza-tion: issues, methods and prospects. In Recent Advances in Memetic Algorithms; Springer: Berlin Heidelberg, Germany, 2004; pp. 313–352. [Google Scholar]
- Suman, B.; Kumar, P. A survey of simulated annealing as a tool for single and multiobjective optimization. J. Oper. Res. Soc. 2006, 57, 1143–1160. [Google Scholar] [CrossRef]
- Reyes-Sierra, M.; Coello Coello, C.A. Multi-objective particle swarm optimiz-ers: a survey of the state-of-the-art. Int. J. Comput. Intell. Res. 2006, 2, 287–308. [Google Scholar]
- Gong, M.G.; Jiao, L.C.; Du, H.F.; Bo, L.F. Multiobjective immune algorithm with nondominated neighbor-based selection. Evol. Comput. 2008, 16, 225–255. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.F.; Zhou, A.M.; Jin, Y. RM-MEDA: a regularity model-based multi-objective estimation of distribution algorithm. IEEE Tran. Evol. Comput. 2008, 21, 41–63. [Google Scholar] [CrossRef]
- Largo, Á.R.; Zhang, Q.F. A.; Rodríguez, Miguel V. A multiobjective evolutionary algorithm based on decomposition with normal boundary intersection for traffic grooming in optical networks. Inform. Sci. 2014, 289, 91–116. [Google Scholar]
- Tadahiko, M.; Hisao, I.; Mitsuo, G. Specification of genetic search directions in cellular multi-objective genetic algorithms, Specification of Genetic Search Directions in Cellular Multi-objective Genetic Algorithms. In Evolutionary Multi-Criterion Optimization; Zitzler, E., Thiele, L., Deb, K., Coello Coello, C.A., Corne, D., Eds.; SpringerI: Berlin Heidelberg, Germany, EMO, 2001; Volume 1993, pp. 82–95. [Google Scholar]
- Zhang, Q.; Li, H. MOEA/D: a multiobjective evolutionary algorithm based on decomposition. IEEE Tran. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Palmers, P.; McConaghy, T.; Steyaert, M.; Gielen, G.G.E. Massively multi-topology sizing of analog integrated circuits. In Proceedings of Conference on Design, Automation and Test in Europe, Leuven, Belgium, 2009; pp. 706–711.
- Nebro, A.J.; Durillo, J.J. A study of the parallelization of the multi-objective metaheuristic MOEA/D. In Proceedings of 4th International Conference on Learning and Intelligent Optimization, LION 4, Venice, Italy, 18–22 January 2010; pp. 303–317.
- Mashwani, W.K.; Salhi, A. A decomposition-based hybrid multiobjective evolutionary algorithm with dynamic resource allocation. App. Soft Comput. 2012, 12, 2765–2780. [Google Scholar] [CrossRef]
- Tan, Y.Y.; Jiao, Y.C.; Li, H.; Wang, X.K. MOEA/D + uniform design: A new version of MOEA/D for optimization problems with many objectives. Comput. Oper. Res. 2013, 40, 1648–1660. [Google Scholar]
- Ma, X.L.; Liu, F.; Qi, Y.T.; Gong, M.G.; Yin, M.L.; Li, L.L.; Jiao, L.C.; Wu, J.S. MOEA/D with opposition-based learning for multiobjective optimization problem. Neurocomputing 2014, 146, 48–64. [Google Scholar] [CrossRef]
- Chang, P.C.; Chen, S.H.; Zhang, Q.; Lin, J.L. MOEA/D for flowshop scheduling problems. Evol. Comput. 2008, 2008, 1433–1438. [Google Scholar]
- Yuen, T.J.; Raml, R. Comparison of computational efficiency of MOEA/D and NSGA-II for passive vehicle suspension optimization. In Proceedings of 24th European Conference on Modelling and Simulation, Kuala Lumpur, Malaysia, ECMS, 2010; 2010; pp. 219–225. [Google Scholar]
- Konstantinidis, A.; Charalambous, C.; Zhou, A.; Zhang, Q. Multi-objective mobile agent-based sensor network routing using MOEA/D. Evol Comput. 2010, 1–8. [Google Scholar]
- Nicola, B.; Naujoks, B.; Emmerich, M. SMS-EMOA:Multiobjective selection based on dominated hypervolume. Eur. J. Oper. Res. 2007, 181, 1653–1669. [Google Scholar] [CrossRef]
- Johannes, B.; Eckart, Z. HypE: an algorithm for fast hypervolume-based many-objective optimization. Evol. Comput. 2010, 19, 45–76. [Google Scholar] [PubMed]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; Wiley: New York, NY, USA, 2001; p. 16. [Google Scholar]
- Li, D.Y. Uncertainty in Knowledge Representation. Eng. Sci. 2000, 2, 73–79. (in Chinese). [Google Scholar]
- Zitzler, E.; Deb, K.; Thiele, L. Comparsion of multiobjective evolutionary algorithms: emperical results. Evol. Comput. 2000, 8, 173–195. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Liu, W.; Li, H. The Performance of a new version of MOEA/D on CEC’09 unconstrained MOP Test Instances. In IEEE Congress On Evolutionary Computation (IEEE CEC 2009), Trondheim, Norway, May 18-21, 2009; pp. 203–208.
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.; Fonseca, V. Performance assessment of multiobjective optimizers: an analysis and review. IEEE Trans. Evol. Comput. 2003, 7, 117–132. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, A.; Zhao, S.; Suganthany, P.N.; Liu, W.; Tiwariz, S. Multiobjective optimization test instances for the CEC 2009 special session and competition. Technical. Report CES-487. 2009. Available online: http://dces.essex.ac.uk/staff/zhang/MOEAcompetition/cec09testproblem0904.pdf (accessd on 22 April 2015).
- Wali Khan, M.; Abdellah, S. Multiobjective memetic algorithm based on decomposition. App. Soft Comput. 2014, 21, 221–243. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Wang, L.; Jiang, Q.; Hei, X.; Wang, B. Multiobjective Cloud Particle Optimization Algorithm Based on Decomposition. Algorithms 2015, 8, 157-176. https://0-doi-org.brum.beds.ac.uk/10.3390/a8020157
Li W, Wang L, Jiang Q, Hei X, Wang B. Multiobjective Cloud Particle Optimization Algorithm Based on Decomposition. Algorithms. 2015; 8(2):157-176. https://0-doi-org.brum.beds.ac.uk/10.3390/a8020157
Chicago/Turabian StyleLi, Wei, Lei Wang, Qiaoyong Jiang, Xinhong Hei, and Bin Wang. 2015. "Multiobjective Cloud Particle Optimization Algorithm Based on Decomposition" Algorithms 8, no. 2: 157-176. https://0-doi-org.brum.beds.ac.uk/10.3390/a8020157





