1. Introduction
Infrared sensors have been employed in many applications such as military, industrial and civil fields. Moreover, the cost reduction is dramatic due to technological advancements. Thus, infrared sensors are expected to be employed in more fields. In fact, the infrared image reflects thermal radiation of the object in the scene which is not influenced by its surface features and illumination conditions. Specifically, much attention has been paid to long-wave infrared (LWIR) light in the range of 8–12 nm which can transmit in the conditions of smoke, fog, haze,
etc. [
1].
Target tracking is a key component in many vision-based tasks and many algorithms have been proposed. For an infrared image, its intensity denotes temperature and radiated heat; thus, very limited information can be employed to represent the target. Besides, infrared images are usually characterized by low signal to noise ratio (SNR), poor target visibility, and time-varying target appearances [
2]. All factors mentioned above make target tracking in infrared image still a challenging problem.
Sparse representation has drawn much attention in visual tracking. In L1 tracker [
3], the tracking problem is formulated to find a sparse representation of the target candidate using templates. A set of trivial templates is introduced to deal with occlusion, noise, and other challenging issues seamlessly. Similarity measurement is performed between each candidate and the target templates. Thus, hundreds of
norm minimization problems must be solved in each frame, which is equal to the number of target candidates. Finally, the target candidate with the smallest reconstruction error is treated as the optimal one.
In this paper, a parallel search strategy based on sparse representation is proposed to track target in infrared images. In the particle filter framework, all target candidates are treated as whole to compose an overcomplete dictionary. When the target templates are represented linearly with such a dictionary, the entries of the coefficient denote the weights of target candidates. Nonnegative sparse constraints are imposed to choose the efficient target states; thus, the efficient states with associate weights are selected simultaneously from all the particles. Finally, the optimal target state can be estimated by the weighted combination of such efficient states.
The rest of this paper is organized as follows.
Section 2 will review the related work about L1 tracker. In
Section 3, we propose a parallel search strategy based on sparse representation in the particle filter framework. Experimental results and analysis for infrared images are shown in
Section 4, and the conclusion is given in
Section 5.
2. Related Work
Target tracking is an important topic in computer vision which has been studied for decades. In fact, the existing methods can be divided in two categories: generative and discriminative [
4]. For generative methods, an appearance model is used to represent the target observation and tracking is formulated to search the similar area. One representative example is the subspace model which assumes that the target observations lie in a low dimensional manifold. For example, object appearance is represented with an eigenspace [
5], affine warps of learned linear subspaces [
6], incrementally learned low-dimensional subspace [
7], incremental tensor subspace [
8], online appearance model [
9],
etc.
Discriminative models treat tracking as a binary classification problem with the goal to separate target from background. A feature vector is constructed for each pixel of the reference image, then an adaptive ensemble of classifiers is trained to separate target pixels from background pixels [
10]. The TLD tracker [
11] uses P-N learning [
12] to exploit the data structures and get feedback about the performance of the classifier. It is shown to be reliable in long sequence tracking.
Sparse representation has been applied to tracking problem which shows excellent performance [
3]. In the particle filter framework, each target candidate is represented sparsely as a linear combination of target templates and trivial templates. Group sparsity is integrated and very high dimensional features are used for improving tracking robustness [
13]. To make full use of the sparse coefficients to discriminate between the target and the background, a robust tracking method is developed based on the structural local sparse appearance model [
14]. Besides, object tracking can be formulated as a multi-task sparse learning problem, and particles are modeled as linear combinations of dictionary templates which are updated dynamically to learn the representation of each particle [
15]. To exploit the relationship between particles which are represented as sparse linear combinations of dictionary templates, the tracking problem is casted as a low-rank matrix learning problem [
16].
The coefficient is obtained via solving either
or
norm minimization problem in these approaches. In [
3], the
norm minimization is solved based on interior point method [
17], which is very slow when solving large-scale
minimizations. A real-time tracker is proposed by adopting compressive sensing and a customized Orthogonal Matching Pursuit (OMP) algorithm to accelerate the tracking [
18]. A very fast numerical solver is developed to solve the
norm minimization problem with guaranteed quadratic convergence based on the accelerated proximal gradient approach [
19]. A tracking algorithm is developed with a static sparse dictionary and dynamic online updated basis distribution [
20].
3. Proposed Method
In a tracking system, when the target state is available in current frame, it is desired to locate it in subsequent frames. From the point of statistics, the tracking problem can be formulated to estimate the posteriori probability of target state.
3.1. Particle Filter
Particle filter is a recursive Bayesian filter by Monte Carlo (MC) simulations which generalize the traditional Kalman filter [
21]. It consists of two steps of prediction and update for estimating the posterior distribution of state. In particle filter framework, the posterior probability density function (PDF) is estimated with a set of samples with associated weights. If the number of samples is large enough, MC characterization estimates the true posterior pdf well to achieve the optimal Bayesian estimate. In most practical applications, the kinetic model of maneuvering target is nonlinear and pdf of target state is non-Gaussian. Particle filter can deal with it well because it can estimate the state pdf regardless of the underlying distribution.
Concretely, affine transform parameters are used as target state
at
t frame, and
denotes the available observations up to
frame. The predicting distribution given all available observations can be computed recursively as
After observation
is available at
t frame, the probability of target state is updated with the Bayesian principle
where
denotes the observation probability.
Then the posterior pdf is estimated by
N samples
with associated weights
. The samples are generated by sequential importance distribution
and weights are updated as
For bootstrap filter, and the weight has a simple form of .
However, the variance of the weights will increase over time thus most particles only have negligible weight after several iterations. In other words, most computational cost is spent on updating weights of those particles which are useless to estimate the posterior probability. To avoid such degeneracy phenomenon, resampling is performed according to weights and a set of new samples with equal weights are obtained in each frame. The number that appears in the new set is equal to .
3.2. Parallel Search Strategy
Given the target state in current frame, the goal of tracking is to locate it in the subsequent frames. In the particle filter framework, plenty of particles with associated weights are used to estimate the posterior pdf of target state. Generally speaking, the target candidates are compared to the templates in turn. For original L1 tracker, each candidate is represented sparsely in the linear space spanned by target templates and trivial templates. Then, target candidate with minimum reconstruction error in target template subspace is taken as the optimal estimation.
In such structure, plenty minimization must be solved in each frame which is equal to the number of particles; thus, it has to suffer heavy computational burden. Besides, it is not reliable to estimate the target state only with one state particle. In fact, target state is a continuous variable and it is more reliable to estimate it with more particles with associated weights. The weights can be obtained by the similarity measurement between candidates and templates. In fact, all target candidates can be divided into two categories. Those containing true target belong to the first category. By contraries, background is dominate in the second category. It is more reasonable to estimate the optimal target state only with the true candidates.
A parallel search strategy based on sparse representation is proposed to select efficient target candidates which are used to estimate the optimal target state. At the t frame, plenty of state particles are obtained by sampling, and the corresponding measurement are target candidates . In fact, the number of particles is much lager than that of target templates , which means .
Given that target templates and true candidates lie in the same linear subspace, each template can be represented as a linear combination of the true candidates. Sparse constraints on the coefficient guarantee that only true target candidates can be selected. In principle, the coefficients can be any real numbers without any restrictions; thus, candidates with reversed intensity patterns may be selected. It is necessary to impose nonnegative constraints on the coefficient to eliminate such false candidates; thus, the entries can reflect the associated weights of efficient target candidates. Then the optimal state can be estimated by the linear combination of such weighted states.
The above idea can be described as follows. For each target template
, all target candidates constitute an overcomplete dictionary
) then the weights of target candidates can be obtained simultaneously by solving
where
is the coefficient for the
ith target template. When the target template are used to search for efficient target states, their contribution are different. It can be measured with the reconstruction error; thus, the weights of target templates can be defined as
where
τ is used to control the shape of weight distribution. Then the coefficients of all target templates can be fused as
whose nonzero entries denote the associated weights of efficient state particles. The normalized weights of states are obtained by
where
. Due to the fact that the target state is a continuous vector, particles with associated weights are used to approximate the posterior pdf. The optimal state can be estimated as
3.3. Template Update
Intuitively, object appearance may remain unchanged only for a certain period of time; thus, fixed templates will not be available all the time. So they must be updated to deal with the appearance variation. However, error is inevitable to be introduced when templates are updated. If we update them too frequently, the tracker is easy to drift from the ground target due to accumulated error.
A method of updating templates dynamically is employed to alleviate the problem. This means that a target template is updated only when it is not similar to the tracking result . The similarity function is defined as , where θ is the angle between the two normalized vectors. A suitable threshold is selected to determine whether to update the target template. Once the maximal angle exceeds the threshold, this target template can be replaced by the optimal estimation to be updated. The whole algorithm is summarized in Algorithm 1.
| Algorithm 1 PS-L1 tracker |
Input:
current frame , sample set , target template ;
Output:
the optimal state , sample set , target template ;
1: for to the number of frames do
2: Draw the new samples from with respect to ;
3: for to the number of templates do
4: Each target template is represented sparsely with all the target candidates (4);
5: The reconstruction error is treated as the weight of each target template (5);
6: end for
7: The fused coefficient is obtained by (6) then normalized as (7);
8: The optimal state is estimated as (8);
9: Resample to obtain to avoid degeneracy phenomenon;
10: if then
11: Target template with maximal angle is replaced by the optimal estimation to be updated;
12: end if
13: end for |
4. Experiments
In our experiments, we compare the tracking results of PS-L1 tracker with L1 tracker and APG-L1 tracker, besides blue, red and green bounding boxes are used to denote them respectively. All algorithm are evaluated on the AMCOM FLIR dataset which comprises FLIR sequences in grayscale format ( pixels).
Algorithm parameters are set as follows.The template size is and variances of affine parameters are . Besides, 10 target templates are used and the number of state particles is 400. The angle threshold is 40 to determine whether to update a target template. Several numerical experiments are performed on the personal computer with 2.67GHz Inter(R) Core(TM) I3 CPU and 2GB memory. Besides, Windows 7 and MATLAB R2010a are installed. The minimization problem is solved by SPAMS software package for the PS-L1 tracker.
The first experiment is performed on the sequence of LW-16-08 and the results are shown in
Figure 1. The challenge of this sequence is the disturbance of similar target. A stationary target is at the center position whose size becomes larger with time, and another target with similar appearance moves to the existing one. Partial occlusion happens when they are close enough. The experimental results show that both L1 tracker and APG-L1 tracker fail after the two targets encounter though the latter can handle occlusion. The PS-L1 tracker also fails for a short time, it recovers soon to lock on the target during the rest frames of the sequence.
Figure 1.
Tracking results of three trackers for sequence LW-16-08.
Figure 1.
Tracking results of three trackers for sequence LW-16-08.
The second experiment is performed on the sequence of LW-17-20 and the results are shown in
Figure 2. The challenge of this sequence is the obvious variance of size and pose. A target moves along the road then turns right. It can be seen that both L1 tracker and APG-L1 tracker only lock on a little part of the target after its size becomes larger. For PS-L1 tracker, it can lock on the whole target though more background pixels are contained. The reason is that all the three trackers use the generative model thus various target appearance and background are hard to discriminate. In fact, holistic templates based on raw intensity values do not take large appearance variability into account which do not perform well in a situation of obvious variance of pose.
Figure 2.
Tracking results of three trackers for sequence LW-17-20.
Figure 2.
Tracking results of three trackers for sequence LW-17-20.
The third experiment is performed on the sequence of LW-19-NS and the results are shown in
Figure 3. The challenges of this sequence are occlusion and background clutter. Two targets move along the road. At first, occlusion happens due to vehicle exhaust; thus, only part of the first target is visible. All the three trackers perform well before the target turns right because sparse representation is insensitive to occlusion. Then the target appearance changes with time and the background clutter also causes disturbance. It can be seen that our tracker is more stable to lock on the target while the other two lose it.
Figure 3.
Tracking results of three trackers for sequence LW-19-NS.
Figure 3.
Tracking results of three trackers for sequence LW-19-NS.
The fourth experiment is performed on the sequence of LW-18-15 and the results are shown in
Figure 4. The challenge of this sequence is low contrast. A small target becomes close to the infrared sensor whose size becomes larger with time. The target is small and dark, and it is very hard to discriminate the target from background. At first, all the three trackers perform well because sparse representation can extract the principal features. Then the target appearance changes with time, the APG-L1 tracker even fails to track the target. Although the L1 tracker and PS-L1 tracker can lock on the target through the whole sequence, they do not perform well in estimation of target size. For the L1 tracker, many background pixels are included, and only a little part of target is locked for the PS-L1 tracker. Though all the three trackers are not very satisfying, the proposed method performs better than the others.
Figure 4.
Tracking results of three trackers for sequence LW-18-15.
Figure 4.
Tracking results of three trackers for sequence LW-18-15.
In fact, the measurement of state particle usually introduces larger error during a challenging situation, the PS-L1 tracker use efficient state particles with associated weights to estimate the target state which is more reliable and stable to alleviate the problem. That is the reason that the PS-L1 tracker performs better than the other two trackers.
Then the tracking results are quantitatively evaluated by two widely used criteria of position error(PosErr) and F-score. The former measures the distance by pixels between the ground truth target center and the tracking result center which is defined as
where
and
denote the central position of tracking and ground truth respectively. The F-score evaluates tracking results by taking both the recall and precision into account which is defined as
where TP, FP, and FN are the true positive, false positive, and false negative respectively. For an image, F-score can be calculated as
where
denotes the target region within tracking bounding and
denotes the object region obtained through ground truth. Besides, # denotes the number of pixels. The results of three trackers are shown in
Figure 5 and
Figure 6 and the numerical comparisons are shown in
Table 1 and
Table 2.
Figure 5.
Quantitative comparison of three trackers in terms of position errors (in pixel). (a) LW-16-08; (b) LW-17-20; (c) LW-19-NS; (d) LW-18-15.
Figure 5.
Quantitative comparison of three trackers in terms of position errors (in pixel). (a) LW-16-08; (b) LW-17-20; (c) LW-19-NS; (d) LW-18-15.
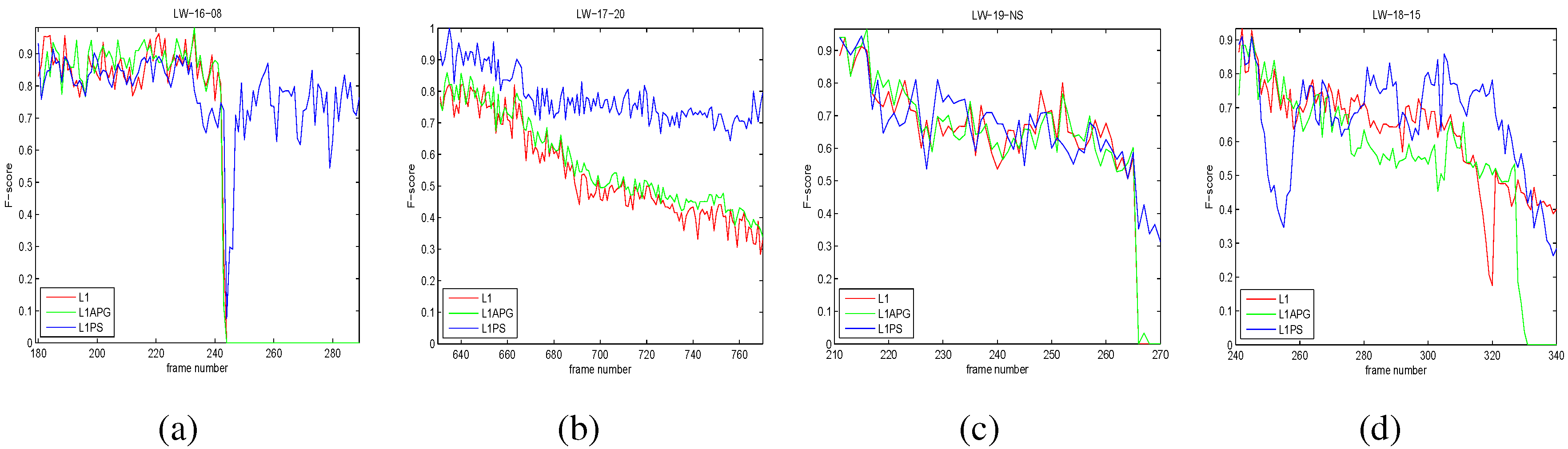
Figure 6.
Quantitative comparison of three trackers in terms of F-score. (a) LW-16-08; (b) LW-17-20; (c) LW-19-NS; (d) LW-18-15.
Figure 6.
Quantitative comparison of three trackers in terms of F-score. (a) LW-16-08; (b) LW-17-20; (c) LW-19-NS; (d) LW-18-15.
Table 1.
Numerical Comparison of Average of PosErr.
Table 1.
Numerical Comparison of Average of PosErr.
| | Methods | L1 | APG-L1 | PS-L1 |
|---|
| Sequence | |
|---|
| LW-16-08 | 17.77 | 20.54 | 3.24 |
| LW-17-20 | 8.44 | 8.33 | 5.83 |
| LW-19-NS | 5.85 | 5.50 | 4.45 |
| LW-18-15 | 4.78 | 14.06 | 4.30 |
Table 2.
Numerical Comparison of Average of F-score.
Table 2.
Numerical Comparison of Average of F-score.
| | Methods | L1 | APG-L1 | PS-L1 |
|---|
| Sequence | |
|---|
| LW-16-08 | 0.496 | 0.504 | 0.777 |
| LW-17-20 | 0.543 | 0.576 | 0.781 |
| LW-19-NS | 0.629 | 0.631 | 0.661 |
| LW-18-15 | 0.625 | 0.548 | 0.659 |
The computational cost of PS-L1 tracker is compared to that of L1 tracker and APG-L1 tracker on the four sequences, and the speed is measured in frame/s. The comparative result is shown in
Table 3. It shows that the advantage of proposed algorithm is obvious. The speed of PS-L1 tracker is about two times than the APG-L1 tracker, which is primarily achieved by the parallel strategy.
Table 3.
Comparison of Computational Cost by Frames/s.
Table 3.
Comparison of Computational Cost by Frames/s.
| | Methods | L1 | APG-L1 | PS-L1 |
|---|
| Sequence | |
|---|
| LW-16-08 | 0.90 | 14.54 | 30.23 |
| LW-17-20 | 1.32 | 16.99 | 31.89 |
| LW-19-NS | 0.77 | 17.91 | 30.26 |
| LW-18-15 | 0.88 | 16.29 | 27.12 |
In fact, the bottleneck of computation efficiency depends on solving norm minimization problem. Due to the parallel search strategy, efficient target states are selected simultaneously for each template. Thus only n norm minimization problems should be solved which is far less than the number of state particles N.