1. Introduction
A wireless sensor network (WSN) is a group of spatially-distributed autonomous sensors, which monitor physical or environmental conditions, such as temperature, humidity, speed, pressure,
etc., and then transmit the recorded data to a central computing unit for analysis. WSNs originate from military-oriented applications, such as battlefield surveillance and movement monitoring. Nowadays, WSNs have witnessed a rapid growth and have been implemented in a variety of promising applications, which can be classified as follows:
Military [
1]: battlefield surveillance; forces monitoring; battle damage assessment.
Health [
2,
3]: tracking and monitoring patients; telemonitoring of human physiological data.
Environment [
4,
5]: air pollution monitoring; water quality monitoring; forest fire detection.
Home [
6,
7]: home automation; home appliances management and monitoring.
Industry [
8]: machine health monitoring; waste monitoring; data logging.
Most of these applications require the clocks of network nodes to be synchronized, because performing a joint task requires all of the nodes to operate on a common time scale. For instance, data logging is a basic operation that collects, processes and transmits data and is used for temporal and spatial monitoring of a habitat. The advantage of data logging in WSNs over the conventional data logging lies in the property of real-time data being collected, which requires some or all nodes in the network to share a common time frame.
Each sensor in a WSN operates independently and has its own clock. Even if the clocks of sensors are initially tuned perfectly, due to the imperfections of the clock oscillator, they may drift away from the ideal time as time evolves [
9]. Hence, developing efficient clock synchronization protocols is critical in WSNs. In the literature, many clock synchronization algorithms rely on the clock information from the Global Positioning System (GPS). However, GPS is not ubiquitously available and requires a high-power receiver [
10]. This fact makes it impractical to implement GPS technology in the clock synchronization of WSNs, since WSNs generally consist of small sensors that have limited energy. Furthermore, sensors sometimes are positioned in an environment where the GPS signal is not available, as is the case with underwater or underground sensors for water quality monitoring. For clock synchronization applications in computer networks, the network time protocol (NTP) represents one of the oldest and standard Internet timing protocols in current use [
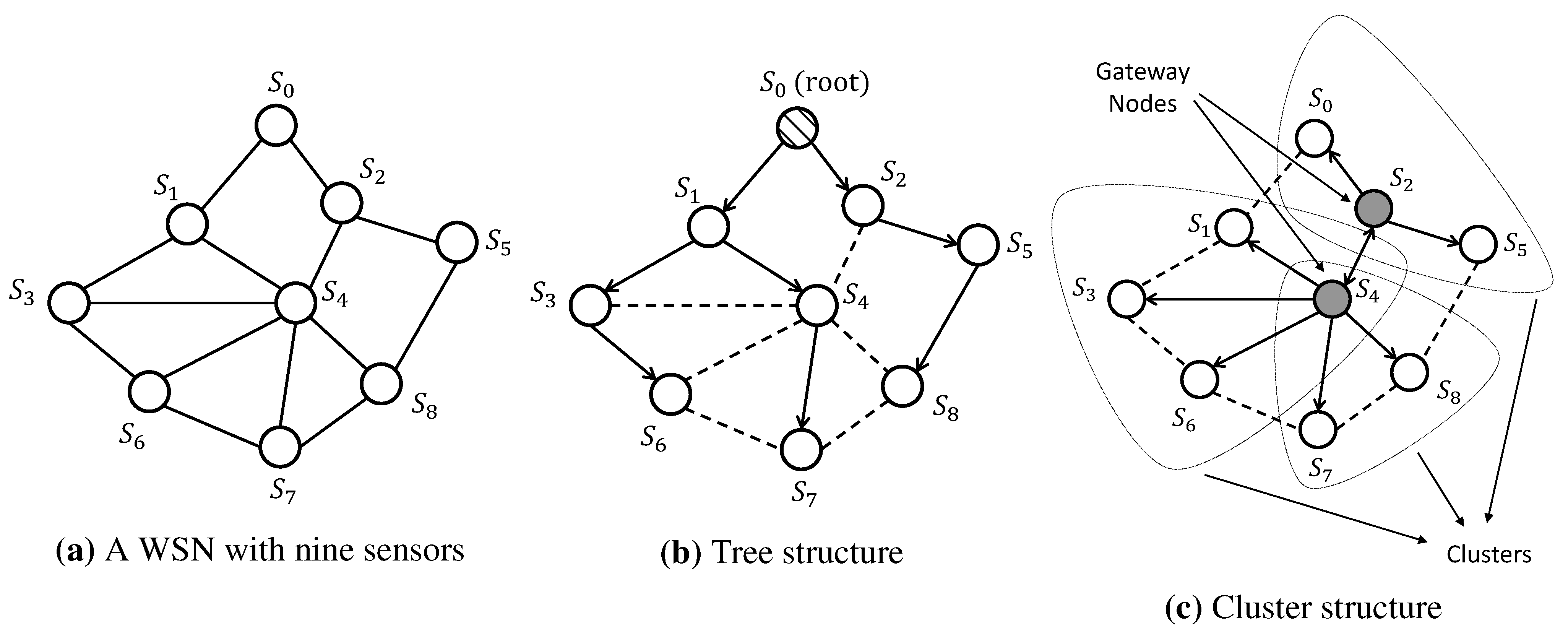
11]. However, NTP is still not suitable for WSNs, due to the lack of energy availability and unstable working environment in WSNs. Therefore, a variety of synchronization protocols have been particularly designed for WSNs. In general, these protocols perform clock synchronization via timing message exchanges among sensors. However, due to the power requirement for each individual sensor, sensors have a limited communication range, and they are not able to communicate with every other sensor. An example of a WSN with nine sensors is shown in
Figure 1a, where each circle denotes a sensor and each edge represents the communication link (if present) between the corresponding pair of sensors.
Figure 1.
Network topology for different synchronization approaches.
Figure 1.
Network topology for different synchronization approaches.
Traditional synchronization protocols for WSNs generally include two steps: first, the synchronization is conducted within a pair of neighboring nodes; second, a multi-hop structure is built, such that the synchronization can be extended into all of the nodes through a layer-by-layer synchronization. One natural approach to deal with the multi-hop structure of WSNs is to construct a tree-based network. Specifically, as illustrated in
Figure 1b, a sensor is selected as the reference node, then a spanning tree rooted at this node is built, and each sensor synchronizes with its parent pairwisely along the unique path from that sensor to the root. On the other hand, the cluster-based structure divides the network into several interconnected single-hop clusters, as graphically shown in
Figure 1c. In each cluster, a reference node is selected, and all of the other nodes are pairwisely synchronized by the reference node. The reference nodes of different clusters act as gateways to adjust the local clock of different clusters into one common time frame. In general, the core of these protocols is based on timing message exchanges between a pair of nodes, in which accurate and efficient pairwise clock synchronization algorithms play a key role. In the literature, some widely-used clock synchronization protocols, such as the timing-sync protocol for sensor networks (TPSN) [
12], the tiny/mini synchronization [
13], the light-weight time synchronization (LTS) [
14] and the flooding time synchronization protocol (FTSP) [
15], employ a two-way message exchange mechanism to adjust the clock between any two nodes.
However, the traditional synchronization protocols suffer from large overhead in building and maintaining the spanning-tree or cluster structure. In addition, some nodes act as a root (in the spanning-tree structure) or as a gateway (in the cluster structure), and the failure of such nodes may lead to the failure of a large number of nodes connecting to it. To tackle this problem, several algorithms based on a fully-distributed communication topology have been proposed. In such algorithms, there are no special nodes, such as roots and gateways, and thus, no structure needs to be built. With all of the nodes performing exactly the same algorithm and communicating with their neighboring nodes, these protocols are robust to the topology changes and failures of nodes.
In this paper, the latest algorithms in the realm of clock synchronization for WSNs are surveyed following a statistical signal processing viewpoint. Specifically, the rest of the paper is organized as follows.
Section 2 introduces the clock model and the two-way message exchange mechanism for pairwise clock synchronization. Based on the two-way message exchange mechanism, the state-of-the-art pairwise clock synchronization algorithms under Gaussian random delays are investigated in
Section 3.
Section 4 overviews the pairwise clock synchronization algorithms in the presence of exponential random delays.
Section 5 surveys the signal processing techniques employed in WSNs when the random delays are unknown. In
Section 6, synchronization algorithms that assume a fully-distributed operation are discussed. Finally,
Section 7 concludes the paper and provides some open research topics.
In the literature, surveys for clock synchronization in WSNs have been presented by [
9,
10,
16,
17]. The focus of [
10,
16] lies in the clock synchronization protocols that are applied in WSNs. The survey paper [
17] provides a technical overview of the history, recent advances and challenges in distributed clock synchronization for distributed wireless networks, while this article presents synchronization algorithms with emphasis on the mathematical and statistical techniques employed for clock synchronization parameters estimation. The work in [
9] surveys the latest advances in the clock synchronization of WSNs following a signal processing viewpoint. However, only pairwise synchronization methods are investigated in [
9], while our paper discusses both pairwise and fully-distributed synchronization algorithms.
3. Pairwise Clock Synchronization under Gaussian Delays
In general, probability density function (PDF) models have been employed for modeling the random portion of delays in WSNs. Examples of PDFs that have been adopted in the literature include exponential, Gaussian, Weibull and Gamma [
18,
19,
20,
21]. In this section, we use the Gaussian distribution to characterize the random delay in WSNs,
i.e.,
and
are Gaussian random variables with parameters
and
, respectively. The reasons for selecting the Gaussian distribution for modeling the random delays are as follows:
The central limit theorem (CLT) states that the PDF of the sum of a large number of independent and identically-distributed (i.i.d.) random variables is approximately normally distributed. Therefore, the Gaussian model is appropriate if the random delays are assumed to be the summation of multiple independent random variables.
Experimental results based on two Texas Instruments ez430-RF2500 evaluation boards were recorded in [
22] to demonstrate the fitness of the Gaussian distribution in modeling the random portion of delays in WSNs.
The most representative pairwise clock synchronization algorithms in the literature focused on developing maximum likelihood estimators (MLEs) for the clock offset and skew. The MLE is one of the most widely-used estimators in the area of parameter estimation, since it achieves asymptotically the Cramér–Rao lower bound (CRLB).
Based on the two-way message exchange model in Equation (4), where only the clock offset is considered, [
18] derived the MLE for clock offset by assuming a known fixed delay
d and symmetric random delays,
i.e.,
and
. In this framework, the likelihood function is expressed as:
The MLE of clock offset is derived by differentiating the log-likelihood function with respect to
θ and setting the corresponding derivative to zero, and it assumes the expression:
where
and
stand for the sample means of observations
and
, respectively. It can be verified that the estimator Equation (5) is unbiased and achieves the CRLB. The MLE estimator Equation (5) represents also the minimum variance unbiased estimator (MVUE).
Following the same assumptions,
i.e., a known fixed delay and symmetric random delays, the joint maximum likelihood estimates of the clock offset and skew were also proposed in [
18] based on the two-way message exchange model in Equation (2). Specifically, the likelihood function is first formulated as:
where
. Differentiating the log-likelihood function with respect to
θ leads to an equation of
θ in terms of
. In addition, differentiating the log-likelihood function with respect to
results in an equation of
in terms of
θ. The joint estimates of
θ and
, denoted as
and
, can be obtained by combining those two equations, and the MLE of
f is obtained as
, due to the invariance principle [
23].
However, in some practical cases, the value of the fixed delay
d is unknown and sometimes even represents a parameter that needs to be estimated, as is the case with the node localization application [
24]. Therefore, efficient algorithms for joint estimation of the clock offset, clock skew and fixed delay are of great interest. Based on the two-way message exchange mechanism in Equation (2), Leng
et al. [
24] extended the result in [
18] by assuming an unknown fixed delay
d. First, the signaling model Equation (2) is re-formulated in matrix form as:
where
,
and
with dimension
.
Since
and
are independent Gaussian random variables,
i.e.,
,
the log-likelihood function for
Φ and
d is expressed as:
For a fixed
d, the MLE of
Φ is given by:
Plugging Equation (6) into the log-likelihood function results in a compressed likelihood function with only one variable
d. The MLE of
d is derived by taking the derivative over the resulting log-likelihood function with respect to
d, and the MLE of
Φ is obtained by plugging the corresponding estimate of
d back into Equation (6). Finally, the MLEs of
θ and
f are obtained from the MLE of
Φ using the invariance principle [
23].
4. Pairwise Clock Synchronization under Exponential Delays
In the literature, the exponential distribution is also commonly exploited to represent the random portion of delays in WSNs. The reasons behind choosing the exponential distribution include:
For the point-to-point hypothetical reference connection (HRX) between two nodes, a single-server M/M/1queue can appropriately represent the aggregate link delay, where the random delays are modeled as independent exponential random variables [
25].
Experiment results were carried out in [
26,
27] to verify the appropriateness of choosing the exponential distribution to characterize the random delays in WSNs.
Among all distributions with a fixed mean in the support
, the exponential distribution achieves the maximum differential entropy, and thus, it is the least informative.
The most representative clock offset estimation methods for pairwise synchronization in the presence of exponential delays are the maximum likelihood estimator (MLE), the best linear unbiased estimator (BLUE) and the minimum variance unbiased estimator (MVUE), and they will be first reviewed in this section. The MLE for joint estimation of the clock offset and skew will be investigated later. Finally, an important statistical concept, referred to as the confidence interval for the clock offset, will be investigated.
4.1. Clock Offset Estimation under Exponential Delays
4.1.1. Maximum Likelihood Estimator
In the two-way message exchange mechanism Equation (4) where only clock offset exists, we assume that
and
are exponentially-distributed random variables with means
and
, respectively. Assuming a known fixed delay, Abdel-Ghaffar [
25] reported that the MLE of the clock offset does not exist when the exponential random delays are assumed to be known and symmetric,
i.e.,
, since the likelihood function does not admit a unique maximum. However, Jeske [
28] derived a closed-form solution for the MLE of clock offset by assuming an unknown fixed delay and an unknown mean for the exponential delay. In this way, a joint estimation of
and
λ can ensure a unique maximum of the likelihood function. Specifically, assuming symmetric exponential delays with a common mean
λ, the likelihood function for
is expressed as:
where
denotes the indicator function. Let the first order statistics
and
denote the minimum values of observations
and
, respectively. It can be shown that for fixed values of
d and
θ, the optimal value of
λ that maximizes the likelihood function is given by
. Therefore, the likelihood function Equation (7) can be simplified to:
It can be observed that the indicator function poses a high impact on the value of the likelihood function, and moreover, the indicator function depends on
and
. Hence, in order to maximize the likelihood function, different assumptions on
and
are discussed in [
28], e.g.,
,
and the region where
is illustrated separately for each assumption. The value of
θ that maximizes the likelihood function is found graphically from the corresponding support region. It is shown that all of the different assumptions on
and
lead to the same MLEs for the vector
:
Our primary interest is the MLE of the clock offset , but in the meantime, the MLEs for d and λ are also derived. It can be verified that is unbiased and has a variance . Interestingly, if d is unknown and the variable portions of delays are not symmetric, i.e., , the MLE of θ also admits the form . However, in this case, the MLE is biased.
Different from the graphical analysis used in [
28], [
29] analytically derived the MLE of clock offset under exponential delays using convex optimization tools. In particular, the system model in Equation (4) is re-written as:
where
and
. The goal is to determine the MLEs of
ξ and
ψ,
i.e.,
and
, such that the MLE of
θ can be obtained from:
based on the invariance principle [
23]. Towards this end, the density functions of
and
are expressed as:
The resulting MLE of
ξ can be formulated as a convex optimization problem:
and it follows that
The analysis of
ψ is analogous to the case of
ξ, and it yields that
Thus, the MLE of
θ follows from Equation (10) and admits the form:
which coincides with the result in Equation (8). The advantage of this analytical approach is that it provides a more general derivation of MLEs, which can by applied to obtain the MLEs for the delays under other types of distributions, which include Gaussian and log-normal as special cases [
29].
4.1.2. Best Linear Unbiased Estimator
In the statistical signal processing field, the minimum mean square error (MSE) is commonly selected as the criterion to measure the performance of estimators. The MSE of an estimator
is defined as:
where var
stands for the variance of
and bias
.
In general, the MVUE is referred to as the “optimal” estimator, since it minimizes the variance in the class of unbiased estimators. However, it frequently occurs that the MVUE is difficult or impossible to be derived or might not even exist [
23]. For such scenarios, a suboptimal estimator is required. A common approach is to constrain the estimator to be linear in terms of the observations and to find the linear estimator that is unbiased and achieves the minimum variance. Such an estimator is referred to as the BLUE. The BLUE of the clock offset under asymmetric exponential delays was first derived by Jeske and Sampath in [
30] using the order statistics of the observations
where
and
. Specifically, the BLUE is formulated as a linear combination of the order statistics:
The variance of estimator
T and the unbiasedness condition are further expressed in terms of
and
. Using Lagrange multipliers, it can be shown that the minimum of the variance subject to the unbiasedness condition is achieved when
with
and
for
. Thus, the BLUE of the clock offset admits the form:
On the other hand, the BLUE of the clock offset under symmetric exponential delays can also be derived following the aforementioned steps, and it is expressed as:
Using statistical signal processing techniques, [
31] later re-derived the joint BLUEs for the fixed delay, the clock offset and the mean of exponential delays under symmetric and asymmetric exponential delays, as shown in Equations (16) and (17), respectively.
These results were further used as a prerequisite to find the MVUE of the clock offset, a result that will be presented in the next sub-section.
4.1.3. Minimum Variance Unbiased Estimator
As discussed earlier, the MVUE is an unbiased estimator that exhibits lower variance than any other unbiased estimator. Finding the MVUE usually requires usage of the concept of sufficient statistics, the Neyman–Fisher factorization theorem and the Rao–Blackwell–Lehmann–Scheffe theorem [
23] (p. 101).
Let
Φ denote the parameters to be estimated and
z represent the set of the observations; then, the Neyman–Fisher factorization theorem states that if the likelihood function
can be factorized as:
where
g is a function depending on
z only through
and
h is a function depending on
z only, then
is a sufficient statistic for
Φ. In a two-way message exchange mechanism under symmetric exponential delays,
and
. The MVUE of
Φ was derived in [
31] by implementing the following procedure. Express first the likelihood function in terms of the unit step function
as follows:
and factorize Equation (18) as:
where:
In the above equations,
is independent of the unknown parameters
Φ and
are functions depending on the data only through
. Using the Neyman–Fisher factorization theorem, it turns out that
T is a sufficient statistic. Moreover, the Rao–Blackwell–Lehmann–Scheffe theorem (p. 109 in [
23]) claims that a sufficient statistic
T is complete if there is only one function
of
T that is unbiased, and this function leads to the MVUE,
i.e.,
. Therefore, the remaining task is to prove that
T is complete or, equivalently, that only one function of
T is unbiased, and to find that function.
The authors in [
31] employed a one-to-one transformation of
T, denoted as
. Then, it was shown that
is complete by assuming that there are two functions of
leading to unbiasedness,
i.e.,
, and then, proving that, actually,
. It turns out that
T is also complete, since the sufficient statistics are unique within one-to-one transformations [
23]. To this end, what remains to prove is to find an unbiased estimator for
Φ as a function of
T, which represents the MVUE according to the Rao–Blackwell–Lehmann–Scheffe theorem. It seems difficult to find three unbiased functions of
T for each of
and
λ just by inspection. However, it can be observed that the BLUE
in Equation (16) is a function of
T and is also unbiased. Therefore, it is concluded that the BLUE is also the MVUE:
Following an analogous approach, it was reported in [
31] that the MVUE of the clock offset is also equivalent to the BLUE in the presence of asymmetric exponential delays:
4.1.4. Comparison of Estimators
A comparison of MLE, BLUE and MVUE under both symmetric and asymmetric exponential delays is shown in
Table 1. The criteria adopted in
Table 1 include the estimator formula in terms of observations, bias, variance and MSE. It is observed that the BLUE and MVUE coincide in the presence of both symmetric and asymmetric distributions. Furthermore, all three estimators admit the same expression when the random delays are symmetrically exponential distributed. Under asymmetric exponential delays, albeit unbiased, the MLE can still outperform the MVUE when:
or equivalently:
It can be seen that the MLE achieves a better performance when the means of the exponential delays are close to each other. In this way, the right-hand side of Equation (20) resumes being a large number, and the inequality Equation (20) generally holds with a reasonable selection of N.
Table 1.
Comparison of estimators.
Table 1.
Comparison of estimators.
| Clock Offset | Symmetric Delays | Asymmetric Delays |
|---|
| Formula | Bias | Variance | MSE | Formula | Bias | Variance | MSE |
|---|
| MLE [28,29] | | 0 | | | | | | |
| BLUE [30,31] | | 0 | | | | 0 | | |
| MVUE [31] | | 0 | | | | 0 | | |
4.2. Joint Estimation of Clock Offset and Skew under Exponential Delays
In general, the clock synchronization in WSNs involves two steps. The first step assumes synchronizing the nodes by adjusting the clock phase offset (close offset), while the second step resumes correcting the clock frequency offset (clock skew). The clock skew correction plays a critical role in clock synchronization, especially for long-term synchronization, since it reduces the number of exchanged messages and, thus, brings down the energy consumption. Therefore, we discuss the joint estimation of clock offset and skew in this section.
In the literature, based on a two-way message exchange mechanism, the studies for joint estimation of clock offset and skew mainly concentrated on the development of MLEs, and there is no closed-form solution for the joint estimation of clock offset and skew under exponential delays. Roughly speaking, the algorithms for developing MLEs can be categorized into two types: in the first category, a suboptimal model is built by removing some nuisance parameters, and the corresponding MLEs are derived, while in the second category, the joint estimation is conducted directly.
4.2.1. Removing Nuisance Parameters
Based on the two-way message exchange mechanism in Equation (2) and assuming symmetric exponential delays, the likelihood function based on observations
and
is given by:
It is observed that the likelihood function Equation (21) assumes a complicated expression, and the MLEs might be difficult to derive. According to this observation, an algorithm for joint estimation of clock offset and skew, referred to as the ML-like estimator (MLL), was proposed in [
18] by using the first and last observations of timing message exchanges. Specifically, from the first equation in Equation (2), subtracting
from
yields:
Similarly, from the second equation in Equation (2), subtracting
from
leads to:
Such an approach helps to remove the explicit dependency on the nuisance parameters
λ,
d and
θ. In addition, an ML-like estimate
of the clock skew is derived using Equation (22) and (23). Finding an estimate of the clock offset is achieved by rewriting Equation (2) as:
where
and
. It can be seen that the above model shares the same form as the no-skew model in Equation (4). Therefore, an ML-like estimate of the clock offset is obtained
. The above algorithm for joint estimation of clock offset and skew is computationally simple, but it exhibits a suboptimal performance compared to the maximum likelihood estimator, since it exploits a reduced set of statistics. That is the reason why the above estimator is referred to as the ML-like estimator.
Another approach to remove the nuisance parameter was reported in [
32] by adding two equations in Equation (2). It follows that:
where the nuisance parameter
d is removed. Dividing the above expression by
f and defining
and
leads to a new model represented in matrix form as follows:
Assuming symmetric exponential delays, it is easy to verify that
follows a Laplace distribution with location parameter zero and scale parameter
. Thus, the log-likelihood function for model Equation (25) is expressed as:
Therefore, the MLEs of and can be found by maximizing Equation (26), and the corresponding estimators for θ and f are obtained using the relationships and .
4.2.2. Direct Joint Estimation of Clock Offset and Skew
Assuming symmetric exponential delays with a known mean
λ, [
33] addressed the problem of MLEs for clock offset and skew by optimizing over nonlinear constraints iteratively. In terms of the estimates
, four different cases were considered: (1)
d and
θ known,
f unknown; (2)
θ known,
d and
f unknown; (3)
d known,
θ and
f unknown; (4)
unknown. The ultimate goal is to jointly estimate
in the fourth case. However, similar to the derivation of the MLE in [
28] when no skew is considered, the MLEs are also determined by exploiting the boundary conditions of the support regions. For Cases 1 and 2, the support regions are 2D, and the discussion of these two cases gives an insight to further analyze Cases 3 and 4, where the support regions admit a 3D visualization.
Li and Jeske [
34] proposed a computationally-simpler algorithm to find the MLEs of clock offset and skew. Asymmetric exponential delays with unknown means were assumed in [
34], such that the estimation algorithm can be applied to a more general framework. In this case, the likelihood function resumes as:
Re-parameterizing in terms of
and
leads to:
To find the MLEs for likelihood function Equation (27), or equivalently Equation (28), the concept of profile likelihood function is employed in [
34], such that the MLEs can be alternatively found by maximizing the profile likelihoods. In particular, fixing
and
, the conditional MLEs of
and
are shown to be:
Plugging the above equations into Equation (28) yields the profile likelihood as a function of
and
, which is denoted as
. Following the same procedure with respect to
, the conditional MLEs for
and
are expressed as:
To this end, the original five-dimensional optimization problem Equation (27) is simplified to the maximization of a one-dimensional function
, whose solution represents the MLE for clock skew, and it is denoted as
. Additionally, the MLE for clock offset is obtained via:
since the corresponding estimates of
and
are
and
, respectively.
4.3. Confidence Interval for Clock Offset
From a statistical point of view, a confidence interval (CI) is used to describe the amount of uncertainty associated with a sample estimate of a parameter. More specifically, if a CI is constructed among a series of experiments, the proportion of such an interval that contains the true value of the parameter is given by the confidence level. Mathematically, suppose
X to be a random sample from a probability distribution with parameter
θ, a CI is an interval with endpoints
, such that the following property holds:
where
γ stands for the confidence level.
In terms of the confidence interval for clock offset under exponential delays, Li
et al. [
35] derived satisfactory CIs using an approximate pivotal quantity (APQ). By assuming asymmetric exponential delays, the authors in [
35] derived the relative likelihood function for
θ, say
, based on the likelihood function from model Equation (4). It was then shown that
is an asymptotic pivot in the sense that its limiting distribution does not depend on any unknown parameter. Thus, the asymptotic pivot property of
, as well as its easily invertible form lead to a way to obtain an asymptotic
CI for
θ as follows:
A generalized pivotal quantity (GPQ) was also employed in [
35] to propose a generalized confidence interval for
θ. Even though generalized confidence intervals generally do not have frequentist coverage probabilities that are exactly equal to the nominal value, the proposed GPQ actually leads to frequentist coverage probabilities that are very close to the nominal value. Furthermore, APQ and GPQ CIs under exponential delays were also extended in [
35] to any distribution within the one-parameter scale family.
Further discussions about CIs of clock offset were carried out in [
36,
37]. Specifically, under exponential network delays, [
36] explored sequential intervals with a preset width and proved that these CIs provide a satisfactory solution to minimize the number of samples. In this way, sequential CIs can be used to obtain the smallest sample size required to achieve a specified precision for the clock offset estimation. On the other hand, by considering the correlation between the uplink and downlink random delays, [
37] extended the CI procedure to bivariate models where the random delays are formulated as Freund and Marshall–Olkin bivariate exponential delays. In addition, the MLEs for clock offset under Freund and Marshall–Olkin models were also derived.
7. Conclusions and Open Problems
Wireless sensor networks can be applied to a variety of applications, and most of these applications require synchronization among the sensor nodes. Based on the two-way message exchange system model described in
Section 2.2, this paper surveyed the most representative pairwise and fully-distributed clock synchronization algorithms from a statistical signal processing viewpoint. The interested reader is referred to [
59,
60,
61,
62,
63] for references based on other system models. Specifically, similar to Equation (2), [
59] adopted a two-way message exchange mechanism where no random delay is considered and the fixed portion of delays is different for the uplink and downlink (
i.e., replace
d in Equation (2) by
and
). The main result is that while estimating the clock skew between two nodes is possible, it is impossible to determine the clock offset for pairwise synchronization, unless the delays in two-way message communication are symmetric,
i.e.,
. The same result was later extended in [
60] for the network case. Recently, timestamp-free synchronization algorithms were reported in [
61,
62] to avoid the overhead brought by timestamp exchanges. The approach employed in [
61] is based on conveying implicit timing information in the physical layer via the timing responses from the receiver to the transmitter. The work in [
62] avoids timestamp exchanges using the round-trip-time data, which can be measured by a time-to-digital converter in the master node. The clock parameters, such as the offset and skew, as well as the unknown range between the master and slave nodes were experimentally estimated and verified with an accuracy in the order of a nano-second. Without considering the random delays, a fully-distributed network-wide synchronization algorithm was presented in [
63] by assuming the constraint that the relative clock offsets in any network loop sum to zero. Recently, Jeske [
64] developed a statistical process control (SPC) algorithm that can be used in the context of the two-way message exchange mechanism to detect translations in the delay distribution.
In reflecting on the research problems which have been addressed, we have observed several open research topics that need further investigation. On the one hand, the algorithms presented in this article all assume a line-of-sight transmission. The fixed portion of delays
d herein is actually related to the propagation delay between the transmitter and the receiver nodes. It may occur that some obstacles exist in the signal path, and they might reflect or simply absorb the signal. In this case, the received signal strength and the propagation delay may be significantly affected, and thus, the mathematical system model proposed in this article might not be plausible. To our best knowledge, the clock synchronization problem under non-line-of-sight transmissions is still open. In addition, even though many references that exploit the statistical system model from
Section 2.2 have been reported in the literature, more convincing experimental results based on large-scale WSN testbeds are necessary for a more accurate clock synchronization system model. Other possible future research topics lie in the investigation of the convergence rate and computational complexity of the proposed distributed synchronization algorithms. Due to the limited energy of sensors in WSNs, designing new distributed synchronization schemes with reduced energy consumption, low implementation complexity and a fast convergence rate represents another fruitful research direction.