1. Introduction
In the context of wireless sensor networks (WSNs), the detection of unknown parameters by using a multitude of sensor nodes has been of significant interest over the past few decades (e.g., [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13] and the references therein). The widely-deployed sensors are designated to provide measurements of a given physical process (temperature, humidity,
etc.), as well as to detect specific events (mobile target, acoustic source,
etc.) over a region of interest. An important strategy has been followed in many studies, where a fusion center (FC) is employed to make a global decision based on original observations fromlocal sensors.
In practice, especially to meet bandwidth/energy constraints, there is a need to reduce the dimension of raw measurements from each sensor to the FC by using one-bit quantization [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11]. In [
4], a fixed quantization (FQ) approach was examined for distributed estimation of a mean parameter (
i.e., the mean of observations). It was shown that the optimum quantization threshold depends on the unknown parameter to be estimated and is thus practically infeasible. To overcome this difficulty, a distributed adaptive quantization (AQ) approach was proposed in [
5,
6], where the threshold is dynamically regulated from one sensor to another, in such a way that the threshold converges to the optimum threshold.In [
7], the design of the binary antisymmetric quantizer was studied by the minimization of the worst case of the Cramér–Rao bound (CRB). Using a generalized likelihood ratio test (GLRT) framework, joint estimation and detection of an unknown mean parameter based on one-bit quantization was considered in [
8]. A one-bit Rao detector was introduced as a computationally-efficient alternative to the GLRTin [
9]. Meanwhile, distributed estimation of both an unknown mean parameter and a scale parameter was considered in [
10], where sensors are divided into two groups, each using a different threshold to generate binary observations. In situations with less stringent bandwidth/power constraints, multi-bit quantization strategies can be employed with enhanced estimation performance [
11,
12,
13].
In this paper, we consider the problem of quantization for change detection using one-bit quantized observations collected by distributed sensors and forwarded to a FC through distortive binary symmetric channels (BSCs). The change detection problem involves an unknown change of the power, i.e., a scale parameter, of the observed signals. To deal with the unknown parameter, we employ the GLRT approach to develop a fusion rule for the FC to solve the change detection problem. We propose a one-bit quantizer based on an asymptotic analysis of the GLRT. Our analysis demonstrates that the optimum quantization thresholds for local sensors for GLRT fusion rule are identical and unrelated to the unknown scale parameter. However, the optimum quantization threshold is dependent on the cross-over error probability of the BSCs.
This paper is organized as follows. The problem is formulated in
Section 2. In
Section 3, the GLRT fusion rule is proposed. In
Section 4, we present an asymptotic analysis of the GLRT, which is used to design the one-bit GLRT quantizers. In
Section 5, the GLRT using unquantized observations in presented as a benchmark to the proposed quantization/detection schemes. Simulation results and comparisons are provided in
Section 6. Finally, concluding remarks are given in
Section 7.
2. Problem Formulation
We use a WSN with
N spatially-distributed sensor nodes to detect a random Gaussian signal with an unknown variance
. Each sensor collects an observation described as follows:
Specifically, are independent and identically distributed (i.i.d.) Gaussian random variables with zero mean and variance under hypothesis , , where it is assumed that the scale parameter is known, whereas is not. For the considered problem, the sensors are employed to monitor a sudden change of the signal power from a normal state with a known to an abnormal state with anunknown .
There are several applications to which our formulation is relevant. One notable example is spectrum sensing (SS), where the secondary user (SU) needs to reliably detect weak licenseduser (LU) signals of possibly unknown types over a targeted frequency band in order to opportunistically use under-utilized frequency bands [
14,
15]. In distributed SS scenarios, multiple SUs collaborate in detecting the presence/absence of the LU [
14]. The received signal at each SU is often modeled as a zero-mean Gaussian random variable with different variances under the null and alternative hypotheses, respectively (e.g., [
14,
15,
16]). We assume the sensors are in a small neighborhood, and each of them is exposed to the same phenomenon. For the aforementioned spectral sensing problems, this implies that the collaborating secondary users are relatively close to each other, compared with their distances to the licensed user (e.g., a TV tower). As a result, their received signals have similar power.
Due to limited bandwidth/power budgets in WSNs, we consider a case where all sensor nodes quantize their local observations into one-bit binary data before transmitting them to the FC. The quantized observations are transmitted to the FC through some noisy wireless links, and the FC forms a global decision. The problem of interest is to design the one-bit quantizer for the sensors and the fusion rule for the FC.
6. Simulation Results
In this section, we present computer simulation results to illustrate the performance of the proposed quantization scheme. Specifically, we use MATLAB to simulate distributed detection in a wireless sensor network with a parallel configuration, where N sensors make observations of a random Gaussian signal, and each sensor quantizes its observations into one bit of information, which is sent to the fusion center with a binary symmetric channel. The fusion center forms a global decision regarding the change of the scale parameter from to . Our simulation is carried out with the following setups: , , , .
Figure 2 plots the detection probabilities of the unquantized case and the one-bit GLRT detector with the optimum threshold
versus the number of sensors. In the figure, a solid line and a dashed line represent the theoretical asymptotic performance, while the plus marks and circle marks represent the performance of the Monte Carlo (MC) experiments obtained by averaging over
independents runs. It is observed that the theoretical asymptotic analysis provides a good approximation of the experimental performance with an increasing number of sensors. When the probability of false alarm (
) is reduced, more sensors are required for the simulation to match asymptotic analysis.
Figure 2.
Performance the proposed one-bit generalized likelihood ratio test (GLRT) detector with the optimum threshold and the unquantized detector, when PF A = 0.1 (a) and (b).
Figure 2.
Performance the proposed one-bit generalized likelihood ratio test (GLRT) detector with the optimum threshold and the unquantized detector, when PF A = 0.1 (a) and (b).
We provide simulation results to illustrate the performance of the GLRT used along with the proposed one-bit quantization scheme.
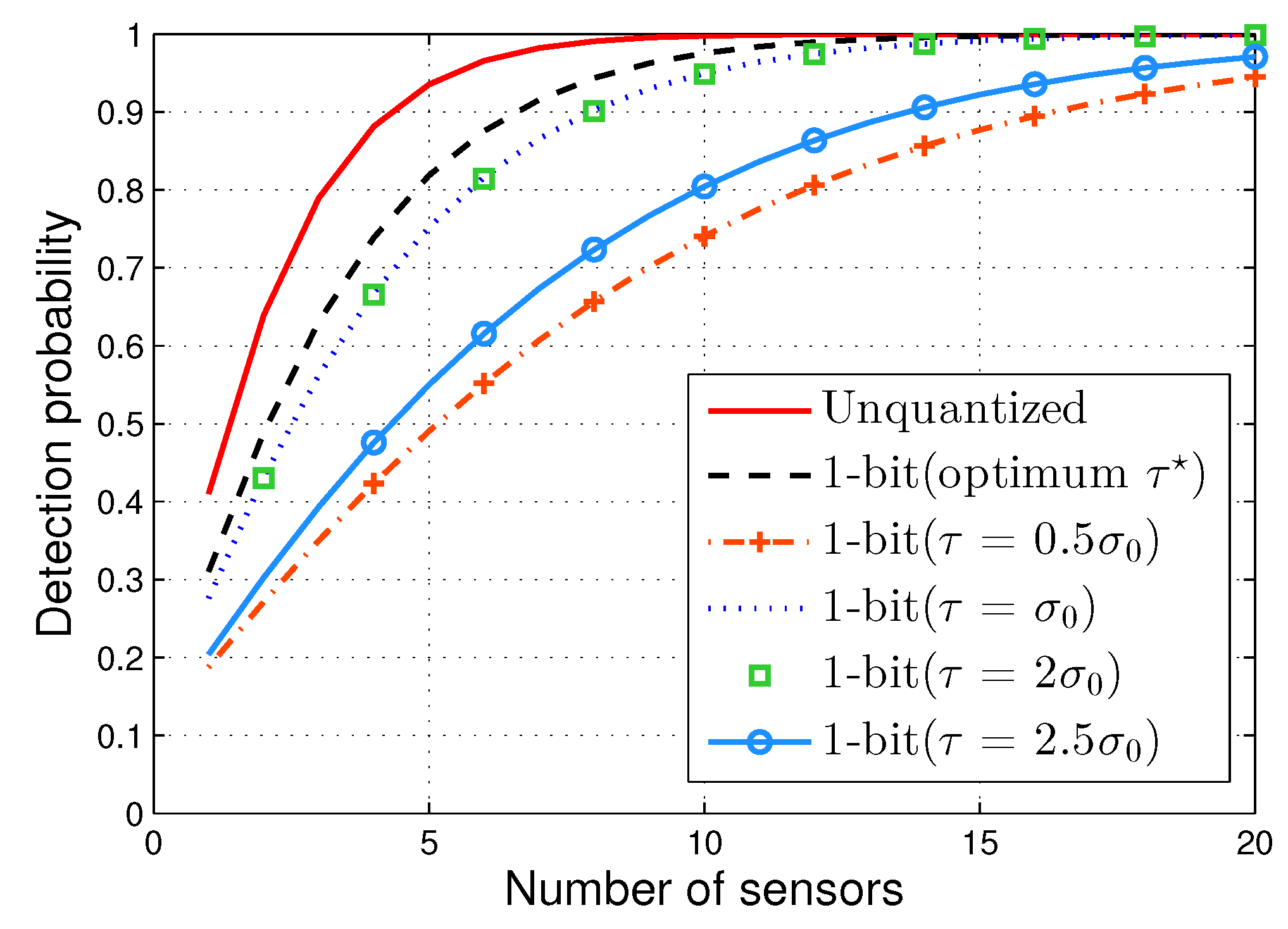
Figure 3 depicts the detection probabilities of the GLRT (assuming error-free transmission between the sensors and the FC)
versus the number of sensors. As a benchmark, the performance of the unquantized detector is also reported. In our simulation, for the proposed scheme, we consider three choices of the threshold, include two heuristic choices, including
and
, as well as the optimum threshold
selected from
Table 1. We assume that the standard deviation under
and
is
and
, respectively. In the figure, the performance of the Monte Carlo (MC) experiments is obtained by averaging over
independent runs. It is observed that the theoretical asymptotic analysis provides a good approximation of the experimental performance when the number of sensors is increasing. Meanwhile, the two heuristic thresholds lead to considerable performance loss.
Figure 3.
Performance the proposed one-bit GLRT detector with several choices of the threshold τ and the unquantized detector, when .
Figure 3.
Performance the proposed one-bit GLRT detector with several choices of the threshold τ and the unquantized detector, when .
Figure
Figure 4 plots the receiver operating characteristics (ROC) curves of the unquantized detector and the one-bit GLRT detector in BSC channels with several cross-over probabilities
. The unquantized case provides a reference on the optimal detection performance. It is seen that channel errors have a notable impact on the the one-bit detector.
Figure 4.
ROC curves of the proposed one-bit GLRT in BSC channels, when .
Figure 4.
ROC curves of the proposed one-bit GLRT in BSC channels, when .
As shown in (
13), the proposed quantization scheme requires knowledge of the crossover probability
, which needs to be estimated in practice. Let the estimated crossover probability be denoted by
. It is of interest to examine how sensitive the proposed quantization scheme is to a mismatch between
and
.
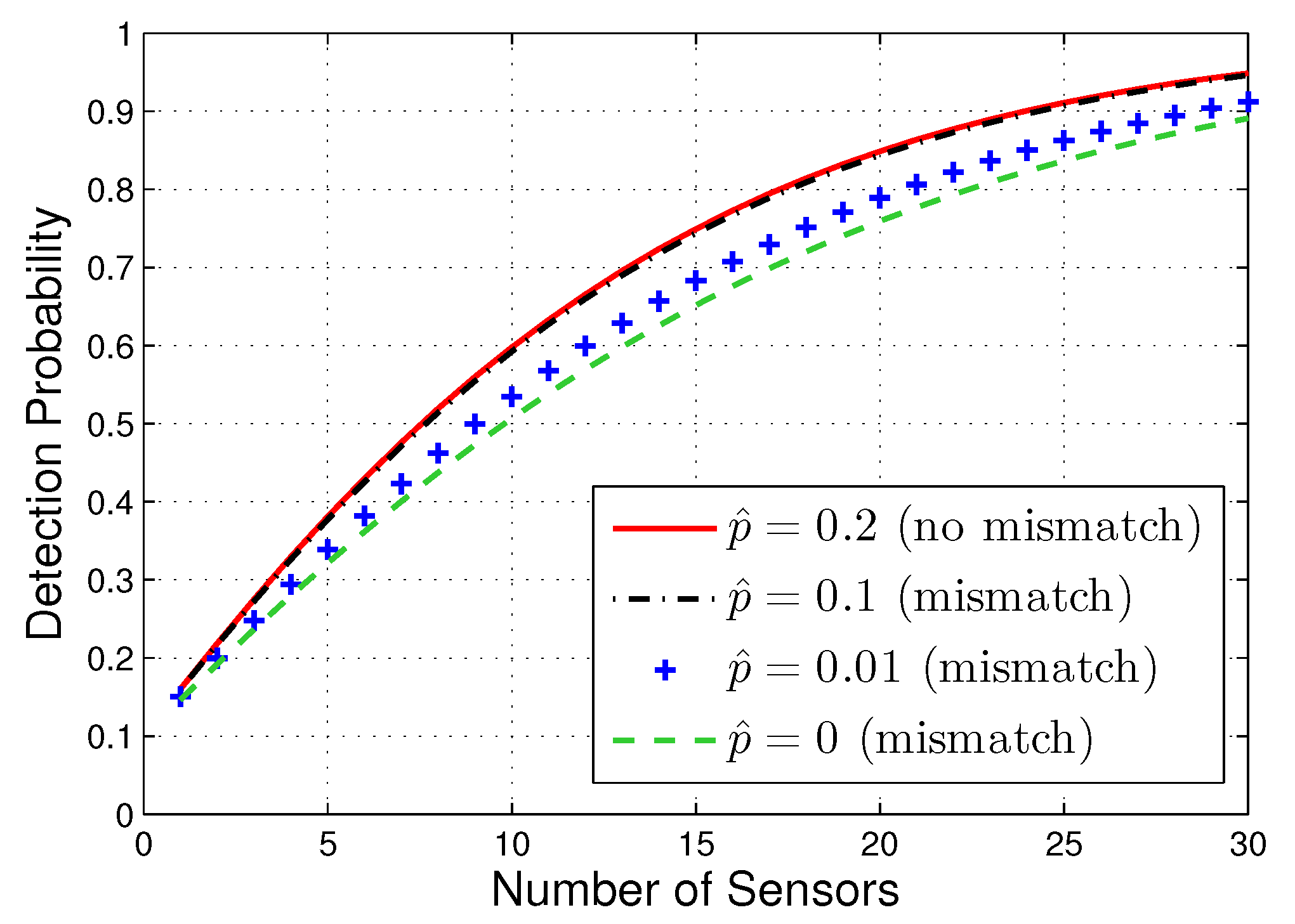
Figure 5 shows the detection probability curves as a function of the number of sensors for several estimated crossover probabilities
, where the actual crossover probability
is 0.2. It is seen from
Figure 5 that a slight mismatch (e.g.,
) leads to negligible performance loss. As expected, with notable estimation error in
(e.g.,
is away from
by an order of magnitude), the resulting performance loss is no longer negligible.
Figure 5.
Performance of the proposed one-bit GLRT with several estimated values of the crossover probability .
Figure 5.
Performance of the proposed one-bit GLRT with several estimated values of the crossover probability .