1. Introduction
In general, the roots of a nonlinear equation
cannot be expressed in a closed form and this problem is commonly carried out by applying iterative methods. So, starting from one or several initial approximations of a solution
of Equation (
1), a sequence
of approximations is constructed so that it converges to
. We can get the sequence
in different ways, depending on the iterative method that is applied. The best-known iterative scheme is Newton’s method,
Observe that we need the operator F to be differentiable Fréchet in order to apply Newton’s method.
Efficiency is generally the most important aspect to take into account when choosing an iterative method to approximate a solution of Equation (
1) (see [
1,
2,
3,
4]). The classic efficiency index, defined by Ostrowski in [
5], provides a balance between the order of convergence
ρ and the number of functional evaluations
d:
. However, it is interesting to note that if Equation (
1) represents a system of
n nonlinear equations, the computational cost of evaluating the operators
F and
is not similar, as it happens in the case of scalar equations. So, for one evaluation of
F,
n functional evaluations are required. Meanwhile, the evaluation of the associated jacobian matrix
requires
functional evaluations, so that the evaluations of
F and
cannot be considered in the same way. Therefore, this efficiency index must be modified to consider the number of functional evaluations in order for it to be a good efficiency measurement for an iterative process in the multivariate case.
Taking into account this extension of the efficiency index from the Chebyshev method with cubical convergence, Ezquerro and Hernández define in [
6] a family of multipoint iterative processes with cubical convergence under the usual conditions required of the operator
F. This family of iterative processes is given by
and has better index of efficiency than Newton’s method Equation (
2). In this paper, we focus our attention on the analysis of the local convergence of sequence Equation (
3) in Banach spaces under weak convergence conditions. In fact, we only consider conditions for the first derivative of the operator
F, as in the case of the Newton method [
7].
In any case, the efficiency index is not the only aspect to compare iterative processes. Another important aspect to take into account is the domain of accessibility associated to the iterative process, which is defined as the domain of starting points from which the iterative process converges to a solution of the equation. The location of starting approximations, from which the iterative methods converge to a solution of the equation, is a difficult problem to solve. This location is from the study of the convergence that is made of the iterative process. The analysis of the accessibility of an iterative process from the local study of the convergence is based on demanding conditions to the solution
, from certain conditions on the operator
F, and provide the so-called ball of convergence of the iterative process, that shows the accessibility to
from the initial approximation
belonging to the ball. This study requires conditions on the operator
F. As we indicate previously, family Equation (
3) has higher efficiency index than the Newton method, but it presents problems of accessibility to the solution
of Equation (
1) if we consider a semilocal study of the convergence (see [
6]).
The paper is organized as follows. In
Section 2, a local convergence result is provided. In
Section 3, from the previous local convergence result, we observe that the size of the ball of convergence of family Equation (
3) depends on the parameter
and, then, we do an optimization study. Moreover, we realize a comparative study from the point of view of the accessibility or, equivalently, from the ball of convergence with the Newton method. Finally, in the last section, a numerical test confirms the theoretical results obtained.
2. Local Convergence
As we indicated above, the local convergence results for iterative methods require conditions on the operator
F and the solution
of Equation (
1). Note that a local result provides what we call ball of convergence and denote by
. From the value
, the ball of convergence gives information about the accessibility of the solution
.
An interesting local result for Newton’s method Equation (
2) is given in [
7] by Dennis and Schnabel, where the following conditions are required:
Let
be a solution of Equation (
1) and exist
, so that
and the operator
exists with
,
, , for all .
Now, our aim is to establish the local convergence study for family Equation (
3), with cubical convergence (see [
6]), from conditions
and
. So, we obtain a local convergence result in the same initial conditions that for the Newton method, which is a second order method.
Firstly, we provide two technical lemmas, where we obtain some results about the operator
F and the sequences
,
and
, which define family Equation (
3).
Lemma 1. Let us suppose that conditions –
are satisfied. Let us assume that exists S, a positive real number, with .
If ,
then, for all ,
the operator exists and Proof. Taking into account the Banach lemma on invertible operators and conditions –, the proof follows. □
Lemma 2. Fixed ,
we assume that and there exists .
Then, we obtain the following decompositions Proof. From the Taylor series of
,
and
are easily obtained. Now, by considering iterative scheme Equation (
3), it follows
:
□
Now, we are able to obtain a result of local convergence to family Equation (
3).
Theorem 1. Let be a nonlinear continuously differentiable operator on a non-empty open convex domain Ω
of a Banach space X with values in a Banach space Y. Suppose that conditions and are satisfied. Then, fixed ,
there exists ,
such that the sequence ,
given by the iterative process of family Equation (3), corresponding to the value of p prefixed, is well-defined and converges to a solution of the equation ,
from every point .
Proof. Firstly, fixed
, we define two auxiliary scalar functions:
with
and
, which are strictly increasing in
.
Secondly, let
, where
and
is the positive real root of the equation
. As
, with
and
, then by Lemma 1 the operator
exists and is such that
So,
is well-defined and, from Lemma 2
, we obtain
where
.
As , then . On the other hand, taking into account that and , it follows that and then . Therefore .
Moreover,
is well-defined and
, since, from item
of Lemma 2, it follows
as a consequence of
.
Furthermore,
is well-defined and, from item
of Lemma 2, we obtain that
, since
Now, as and , it follows that and then . Therefore .
Following now an inductive procedure on
, we have:
Therefore, , for all , and consequently . □
As we have just seen in the previous result, the equation determines the value of which allows us to obtain the radius of the ball of convergence.
Concerning the uniqueness of the solution , we have the following result.
Theorem 2. Under the conditions ,
the limit point is the only solution of Equation (1) in .
Proof. Let
be such that
. If
is invertible, it follows that
, since
. By the Banach lemma, we have that
J is invertible, since
The proof is complete. □
3. On the Accessibility
A procedure to determine the accessibility of an iterative process to
is to estimate the ball of convergence of the method from a local convergence result. In this way, from the local convergence result obtained in the previous section, we study the accessibility of family Equation (
3). To start the comparative study of accessibility of the different iterative processes of family Equation (
3), we can see in
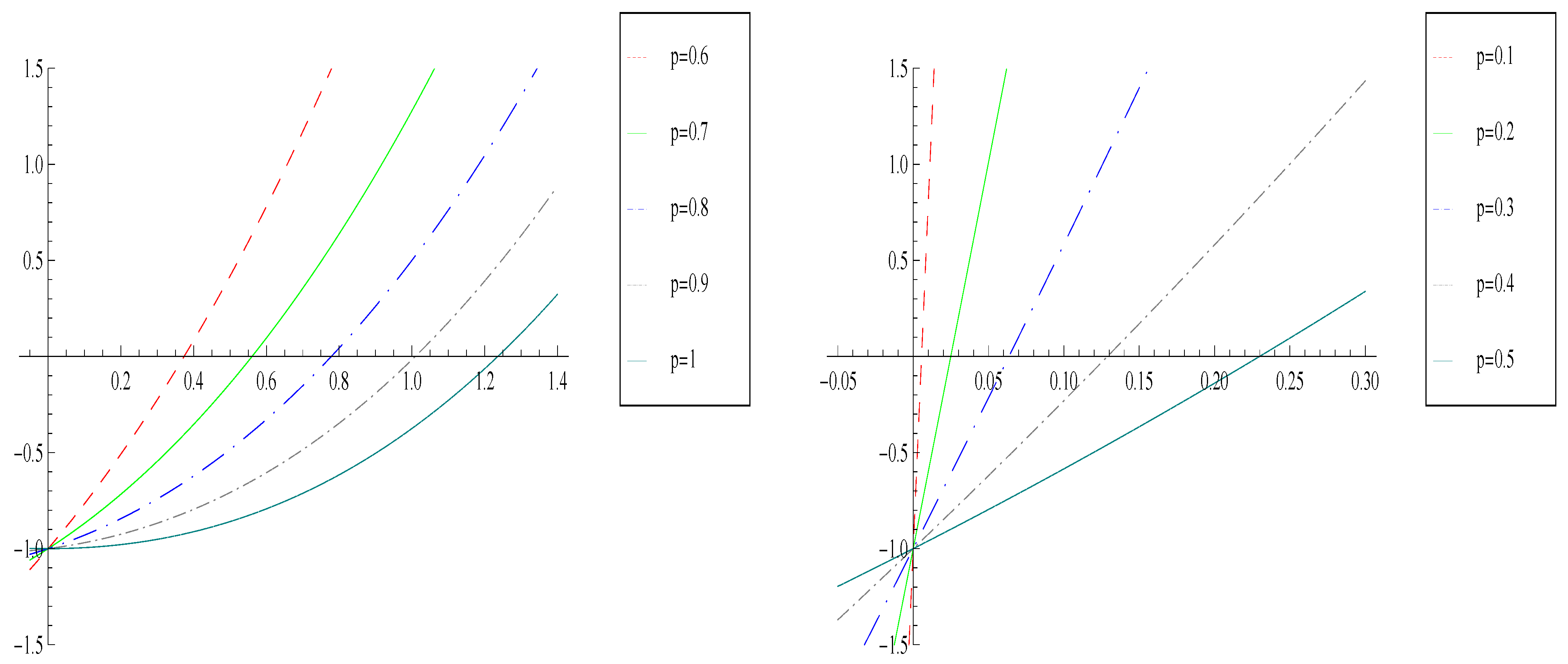
Figure 1 that the function
is strictly increasing on
, tends to infinite and
. Therefore, for each fixed
p, there is a positive real root
of the equation
. In addition, as we can see in
Table 1, the value of this root can be increased by increasing the value of
p. So, we can conclude that the accessibility of the iterative processes of family Equation (
3) increase by increasing the value of
p.
Figure 1.
Graph of the function g(t)-1 for different values of p.
Figure 1.
Graph of the function g(t)-1 for different values of p.
On the other hand, we want to compare the accessibility of the iterative processes of family Equation (
3) with that of the Newton method. For this, we consider the result of convergence obtained by Dennis and Schnabel in [
7]. They prove that under conditions
and
, for any starting point belonging to
, where
and
, the Newton method is convergent. As the radii of the balls of convergence of family Equation (
3) and the Newton method are given under conditions
and
, it is clear that the radius of the ball of convergence of the Newton method is larger than that of family Equation (
3), for
, while for
, the iterative processes of family Equation (
3) have improved accessibility to the Newton method, coinciding both for
(see
Table 1). Therefore, we have obtained, for
, iterative processes with better accessibility and efficiency than the Newton method.
Table 1.
Positive real roots of the equation
and the values of
R for different values of
p in Equation (
3).
Table 1.
Positive real roots of the equation and the values of R for different values of p in Equation (3).
| p | | R |
|---|
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
4. Application
Next, we illustrate the previous result with the following example given in [
7]. We choose the max-norm.
Let be defined as . It is obvious that is a solution of the system.
From
F, we have
and
is the identity matrix
. So,
and
. On the other hand, there exists
, such that
, and it is easy to prove that
in
. Therefore,
and Newton’s method is convergent from any starting point belonging to
. However, from Theorem 1 and once fixed
in family Equation (
3), this iterative process is convergent from any starting point belonging to
.