Faster Force-Directed Graph Drawing with the Well-Separated Pair Decomposition †
Abstract
:1. Introduction
1.1. Previous Work
1.2. Our Contribution
2. Algorithm
2.1. Constructing a WSPD
2.2. The Force-Directed Algorithm
| Algorithm 1: WSPD-Based Force Computation for a Graph . |
 |
2.3. Running Time
2.4. Implementation
2.5. Improvements
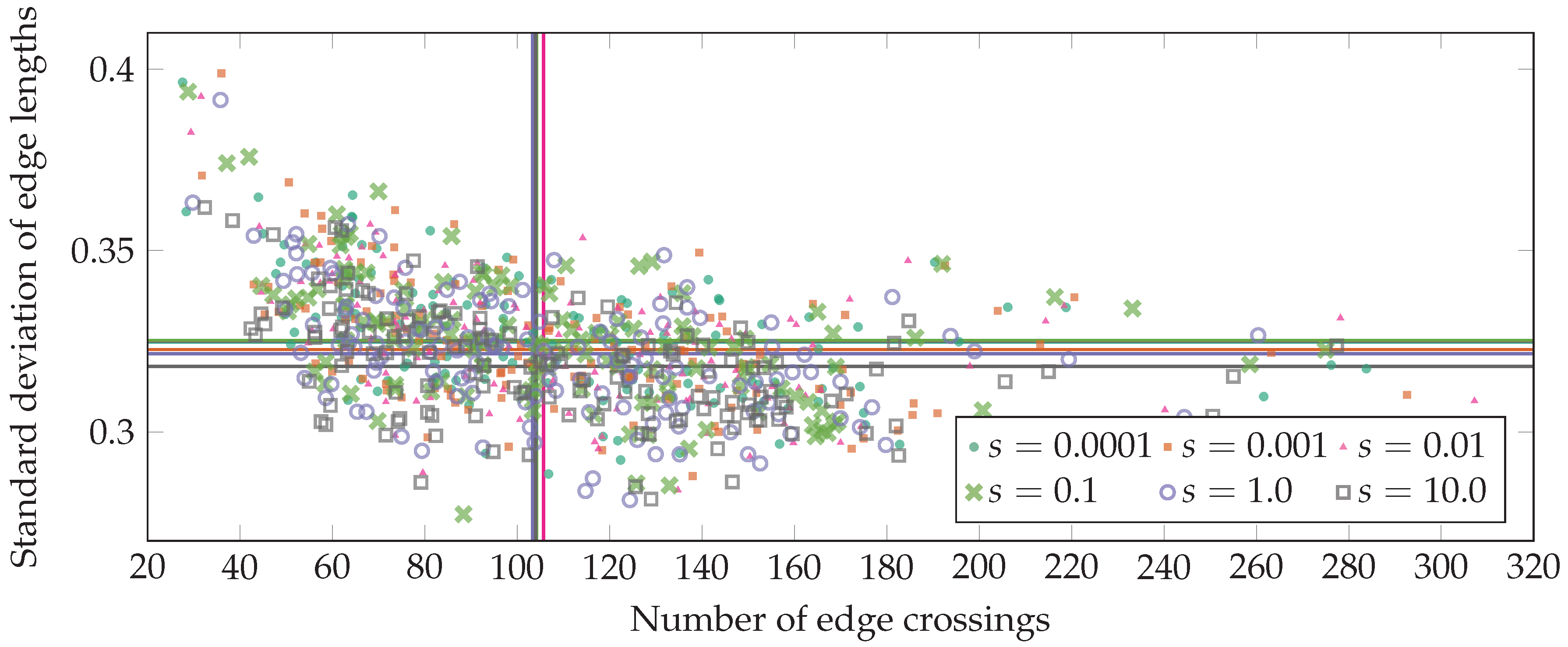
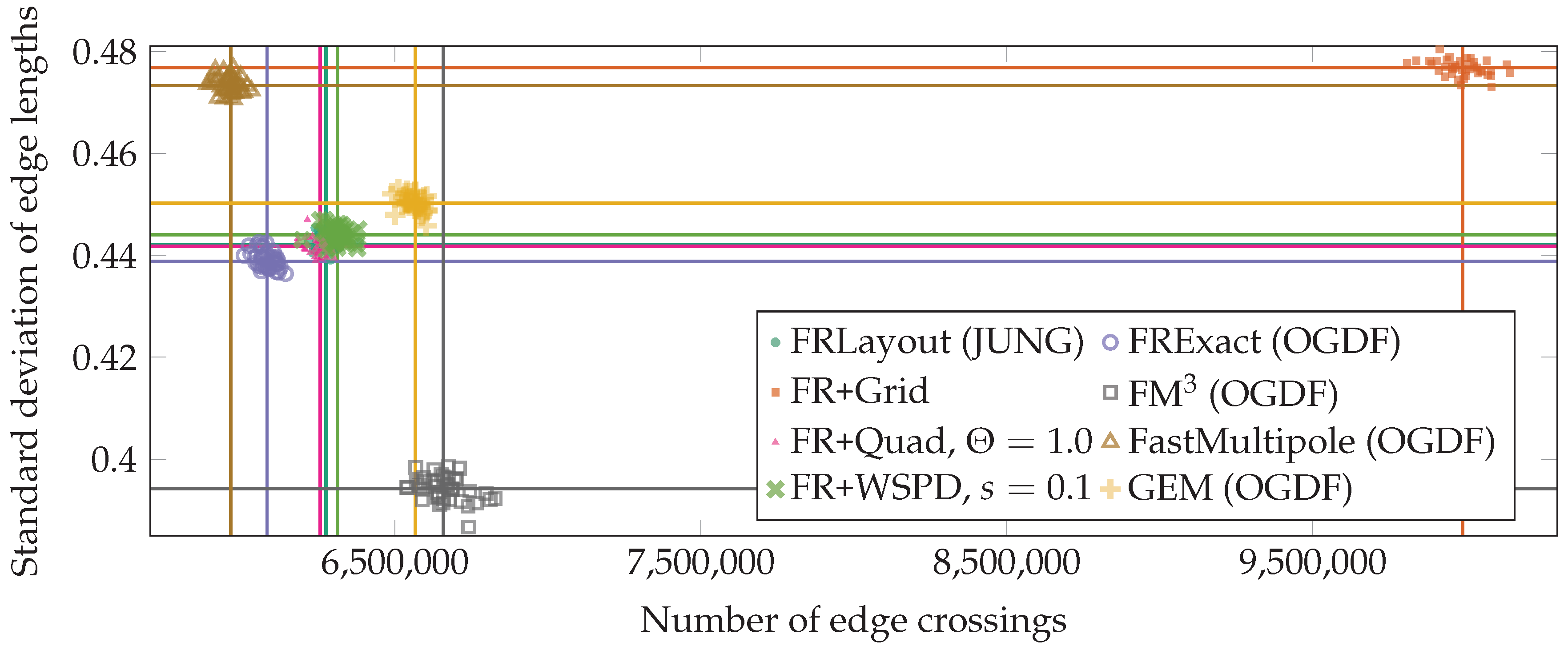
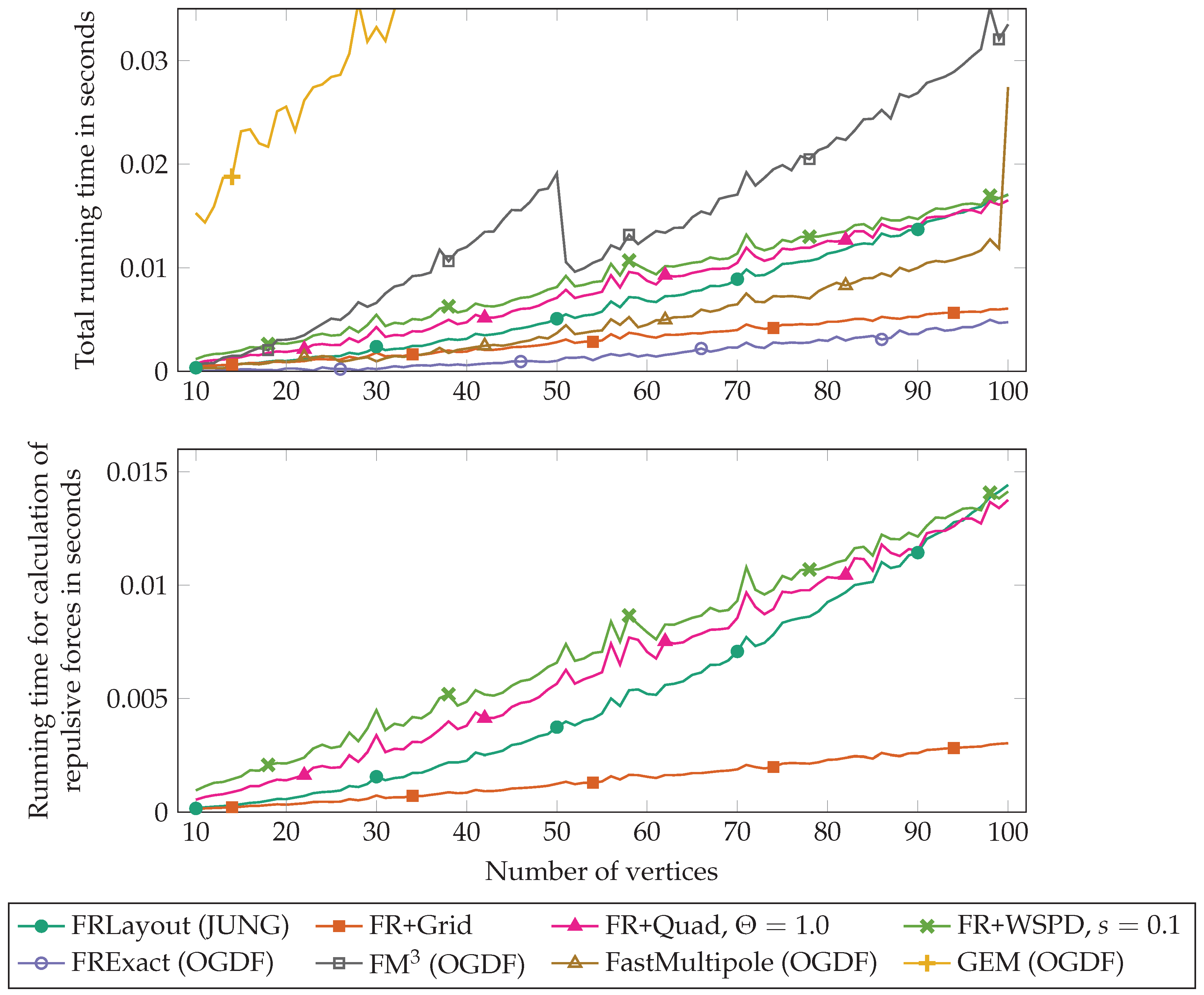
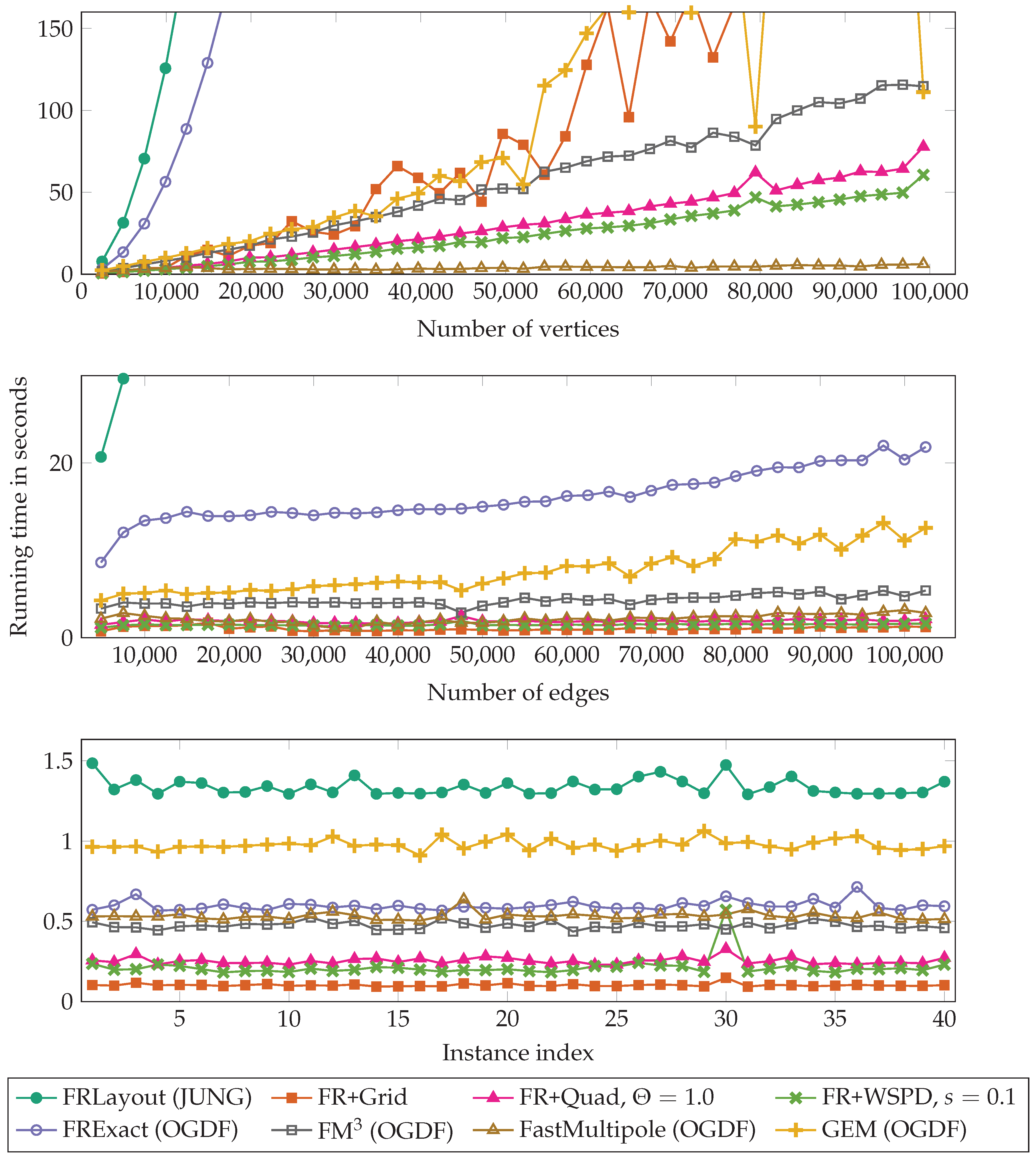
3. Experimental Comparison
- (H1)
- The quality of the drawings produced by FR+WSPD is comparable to that of FRLayout.
- (H2)
- On sufficiently large graphs, FR+WSPD is faster than FRLayout.
3.1. Experimental Setup
- (DS1)
- Rome: The Rome graph collection [23] contains 11,528 undirected connected graphs with 10–100 vertices each.
- (DS2)
- North: The North graphs [24], a subset of the AT&T graph collection, contain 1277 directed connected graphs with 10–100 vertices each. We only consider the underlying undirected graphs.
- (DS3)
- Rand-IncVtc-LoDens: A set of 40 random graphs that we generated using the class EppsteinPowerLawGenerator [25] in JUNG, which yields graphs whose structure is similar to web graphs. We generated instances with 2500, , 100,000 vertices and approximately 2.5-times as many edges. We considered only the largest connected component of each generated graph, which contains most of the original vertices.
- (DS4)
- Rand-5000Vtc-IncDens: A set of 40 random graphs generated as (DS3). We fixed the number of vertices to 5000 and generated approximately -times as many edges to be able to test graphs with different densities. We considered only the largest connected component of each generated graph. This affected only the graphs with less than 25,000 edges.
- (DS5)
- Rand-1000Vtc-HiDens: A set of 40 random graphs generated as (DS3). We fixed the number of vertices to 1000 and the number of edges to approximately . Each of these graphs is connected.
- (DS6)
- Hachul: The set of artificial graphs generated by Hachul and Jünger [22]. We use a subset of 45 graphs containing up to 10,000 vertices and up to 22,402 edges for our experiments. Some of these graphs are not connected.
3.2. Results of Comparison
4. Conclusions and Perspectives
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Eades, P. A heuristics for graph drawing. Congr. Numerantium 1984, 42, 146–160. [Google Scholar]
- Fruchterman, T.M.J.; Reingold, E.M. Graph drawing by force-directed placement. Softw. Pract. Exp. 1991, 21, 1129–1164. [Google Scholar] [CrossRef]
- Fink, M.; Haverkort, H.; Nöllenburg, M.; Roberts, M.; Schuhmann, J.; Wolff, A. Drawing Metro Maps Using Bézier Curves. In Graph Drawing; Springer: Heidelberg, Germany, 2013; pp. 463–474. [Google Scholar]
- Barnes, J.; Hut, P. A hierarchical O(N log N) force-calculation algorithm. Nature 1986, 324, 446–449. [Google Scholar] [CrossRef]
- Walshaw, C. A Multilevel Algorithm for Force-Directed Graph-Drawing. J. Graph Algorithms Appl. 2003, 7, 253–285. [Google Scholar] [CrossRef]
- Hachul, S.; Jünger, M. Drawing large graphs with a potential-field-based multilevel algorithm. In Graph Drawing; Springer: Heidelberg, Germany, 2005; pp. 285–295. [Google Scholar]
- Greengard, L.; Rokhlin, V. A fast algorithm for particle simulations. J. Comput. Phys. 1987, 73, 325–348. [Google Scholar] [CrossRef]
- Hachul, S. A Potential-Field-Based Multilevel Algorithm for Drawing Large Graphs. Ph.D. Thesis, Universität zu Köln, Cologne, Germany, 2005. [Google Scholar]
- Godiyal, A.; Hoberock, J.; Garland, M.; Hart, J.C. Rapid Multipole Graph Drawing on the GPU. In Graph Drawing; Springer: Heidelberg, Germany, 2009; pp. 90–101. [Google Scholar]
- Bartel, G.; Gutwenger, C.; Klein, K.; Mutzel, P. An Experimental Evaluation of Multilevel Layout Methods. In Graph Drawing; Springer: Heidelberg, Germany, 2011; pp. 80–91. [Google Scholar]
- Brandenburg, F.J.; Himsolt, M.; Rohrer, C. An experimental comparison of force-directed and randomized graph drawing algorithms. In Graph Drawing; Springer: Heidelberg, Germany, 1996; pp. 76–87. [Google Scholar]
- Frick, A.; Ludwig, A.; Mehldau, H. A fast adaptive layout algorithm for undirected graphs. In Graph Drawing; Springer: Heidelberg, Germany, 1995; pp. 388–403. [Google Scholar]
- Callahan, P.B.; Kosaraju, S.R. A decomposition of multidimensional point sets with applications to k-nearest-neighbors and n-body potential fields. J. ACM 1995, 42, 67–90. [Google Scholar] [CrossRef]
- Gronemann, M. Engineering the Fast-Multipole-Multilevel Method for Multicore and SIMD Architectures. Master’s Thesis, Technical University of Dortmund, Germany, 2009. [Google Scholar]
- Huang, W.; Eades, P.; Hong, S.H.; Lin, C.C. Improving multiple aesthetics produces better graph drawings. J. Vis. Lang. Comput. 2013, 24, 262–272. [Google Scholar] [CrossRef]
- Lin, C.C.; Yen, H.C. A new force-directed graph drawing method based on edge–edge repulsion. J. Vis. Lang. Comput. 2012, 23, 29–42. [Google Scholar] [CrossRef]
- Hu, Y. Efficient, High-Quality Force-Directed Graph Drawing. Math. J. 2006, 10, 37–71. [Google Scholar]
- O’Madadhain, J.; Fisher, D.; White, S. Java Universal Network/Graph Framework (JUNG). Available online: http://jung.sourceforge.net (accessed on 2 September 2015).
- Chimani, M.; Gutwenger, C.; Jünger, M.; Klau, G.W.; Klein, K.; Mutzel, P. The Open Graph Drawing Framework (OGDF). In Handbook of Graph Drawing and Visualization; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Lipp, F.; Wolff, A.; Zink, J. Faster Force-Directed Graph Drawing with the Well-Separated Pair Decomposition. Available online: http://www1.pub.informatik.uni-wuerzburg.de/pub/data/frwspd/ (accessed on 27 July 2016).
- Narasimhan, G.; Smid, M. Geometric Spanner Networks; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Hachul, S.; Jünger, M. Large-Graph Layout Algorithms at Work: An Experimental Study. J. Graph Algorithms Appl. 2007, 11, 345–369. [Google Scholar] [CrossRef]
- Rome Graphs. Available online: http://graphdrawing.org/data.html (accessed on 2 September 2015).
- North, S. North Graphs. Available online: http://graphdrawing.org/data.html (accessed on 7 December 2015).
- Eppstein, D.; Wang, J.Y. A steady state model for graph power laws. In Proceedings of the 2nd International Workshop on Web Dynamics, Honolulu, HI, USA, 7 May 2002.
- Rumsey, D.J. Statistics II for Dummies; Wiley Publishing: Indianapolis, IN, USA, 2009. [Google Scholar]







© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lipp, F.; Wolff, A.; Zink, J. Faster Force-Directed Graph Drawing with the Well-Separated Pair Decomposition. Algorithms 2016, 9, 53. https://0-doi-org.brum.beds.ac.uk/10.3390/a9030053
Lipp F, Wolff A, Zink J. Faster Force-Directed Graph Drawing with the Well-Separated Pair Decomposition. Algorithms. 2016; 9(3):53. https://0-doi-org.brum.beds.ac.uk/10.3390/a9030053
Chicago/Turabian StyleLipp, Fabian, Alexander Wolff, and Johannes Zink. 2016. "Faster Force-Directed Graph Drawing with the Well-Separated Pair Decomposition" Algorithms 9, no. 3: 53. https://0-doi-org.brum.beds.ac.uk/10.3390/a9030053






