Author Contributions
Conceptualization, B.R., M.K. and D.H.; methodology, B.R. and M.K.; software, B.R.; validation, B.R.; formal analysis, B.R.; investigation, B.R.; resources, M.K., A.A. and X.X.; writing—original draft preparation, B.R.; writing—review and editing, M.K. and D.H; visualization, B.R.; supervision, M.K.
Figure 1.
South Dakota State University (SDSU) identified standard region of interest (ROI) and optimal region of Pseudo-Invariant Calibration Site (PICS); (a) Egypt 1 (27.41°N, 26.38°); (b) Libya 1(24.70°N, 13.49°E); (c) Niger 1(9.36°N, 20.41°E); (d) Niger 2(10.44°N, 20.8°E); (e) Sudan 1 (21.40°N, 27.70°E).
Figure 1.
South Dakota State University (SDSU) identified standard region of interest (ROI) and optimal region of Pseudo-Invariant Calibration Site (PICS); (a) Egypt 1 (27.41°N, 26.38°); (b) Libya 1(24.70°N, 13.49°E); (c) Niger 1(9.36°N, 20.41°E); (d) Niger 2(10.44°N, 20.8°E); (e) Sudan 1 (21.40°N, 27.70°E).
Figure 2.
Simple Linear bidirectional reflectance distribution function (BRDF) correction model of Egypt 1 based on solar zenith angle.
Figure 2.
Simple Linear bidirectional reflectance distribution function (BRDF) correction model of Egypt 1 based on solar zenith angle.
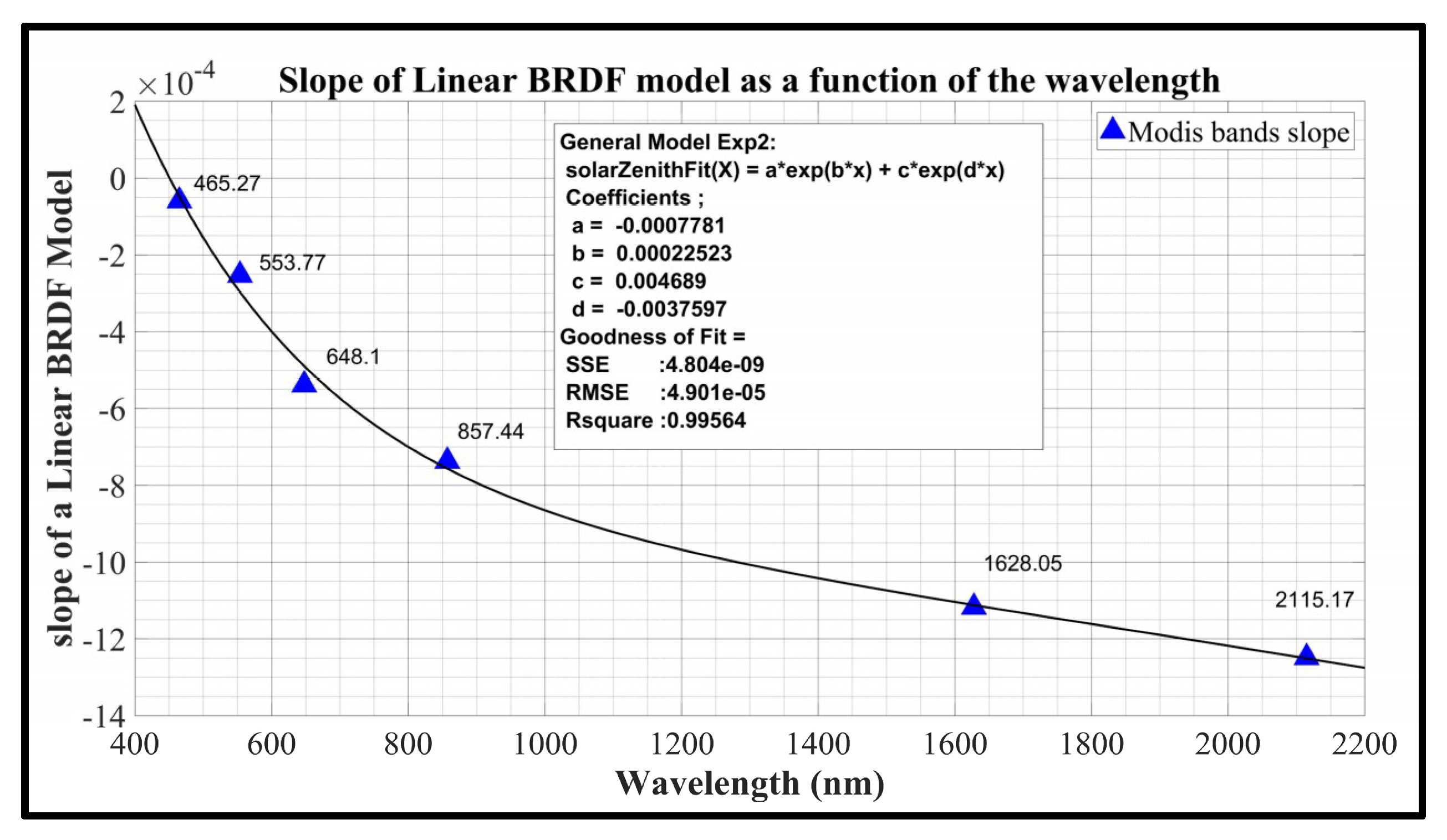
Figure 3.
MODIS Solar Zenith Angle Slope Prediction Model as a function of wavelength.
Figure 3.
MODIS Solar Zenith Angle Slope Prediction Model as a function of wavelength.
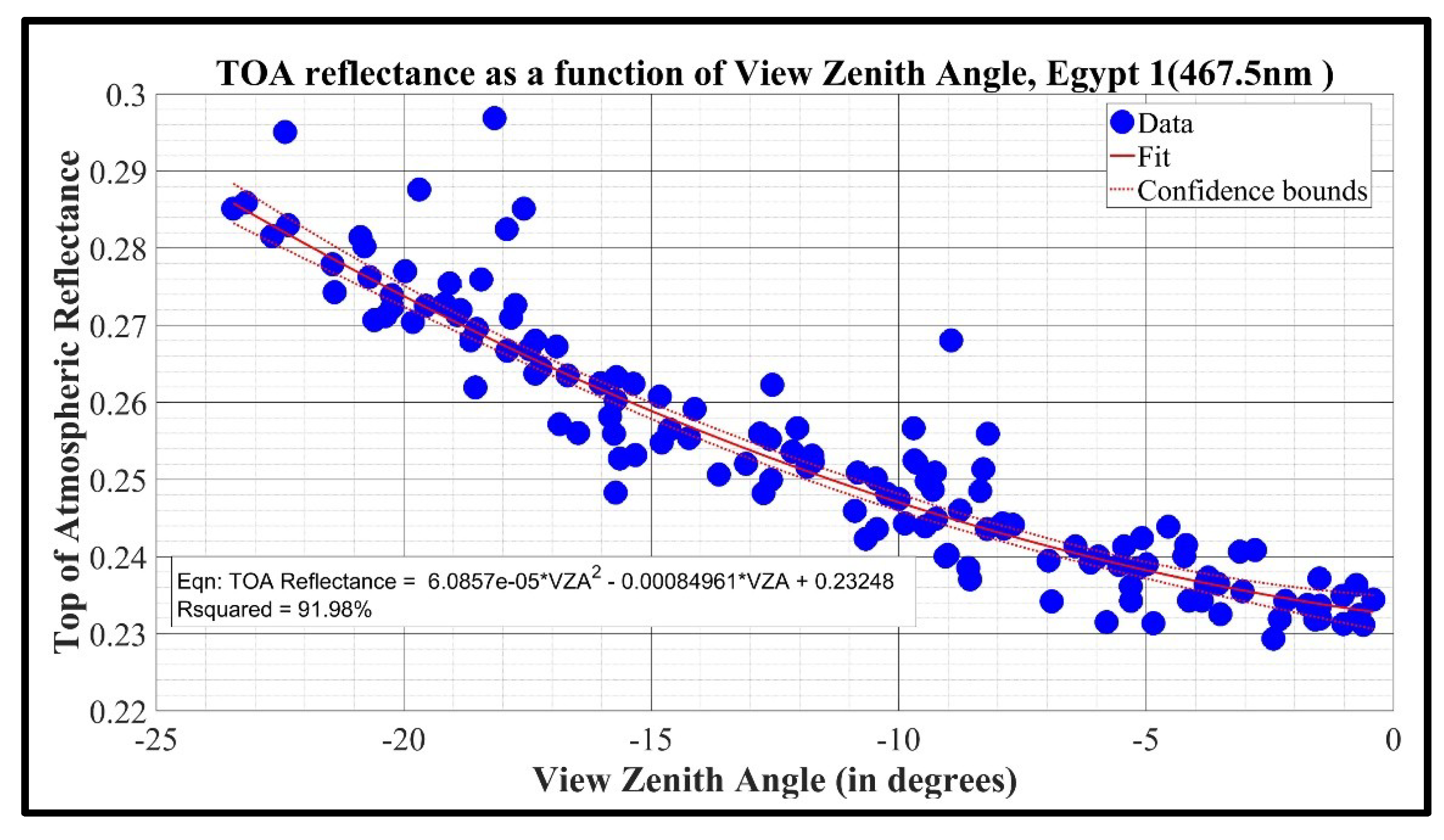
Figure 4.
Quadratic BRDF correction Model of Egypt 1 based on view zenith angle.
Figure 4.
Quadratic BRDF correction Model of Egypt 1 based on view zenith angle.
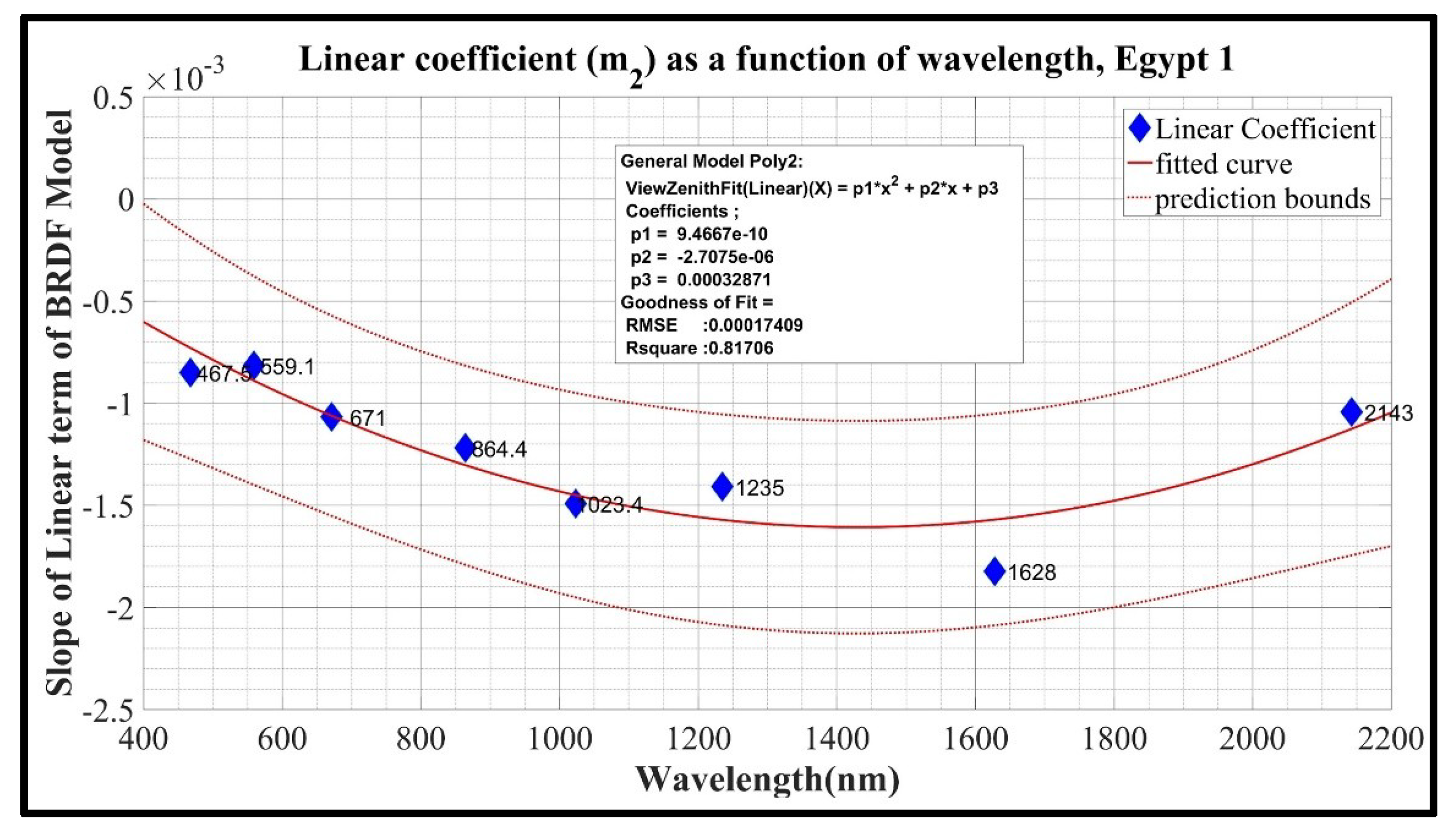
Figure 5.
Quadratic model fit on linear coefficient as a function of wavelength for Egypt 1.
Figure 5.
Quadratic model fit on linear coefficient as a function of wavelength for Egypt 1.
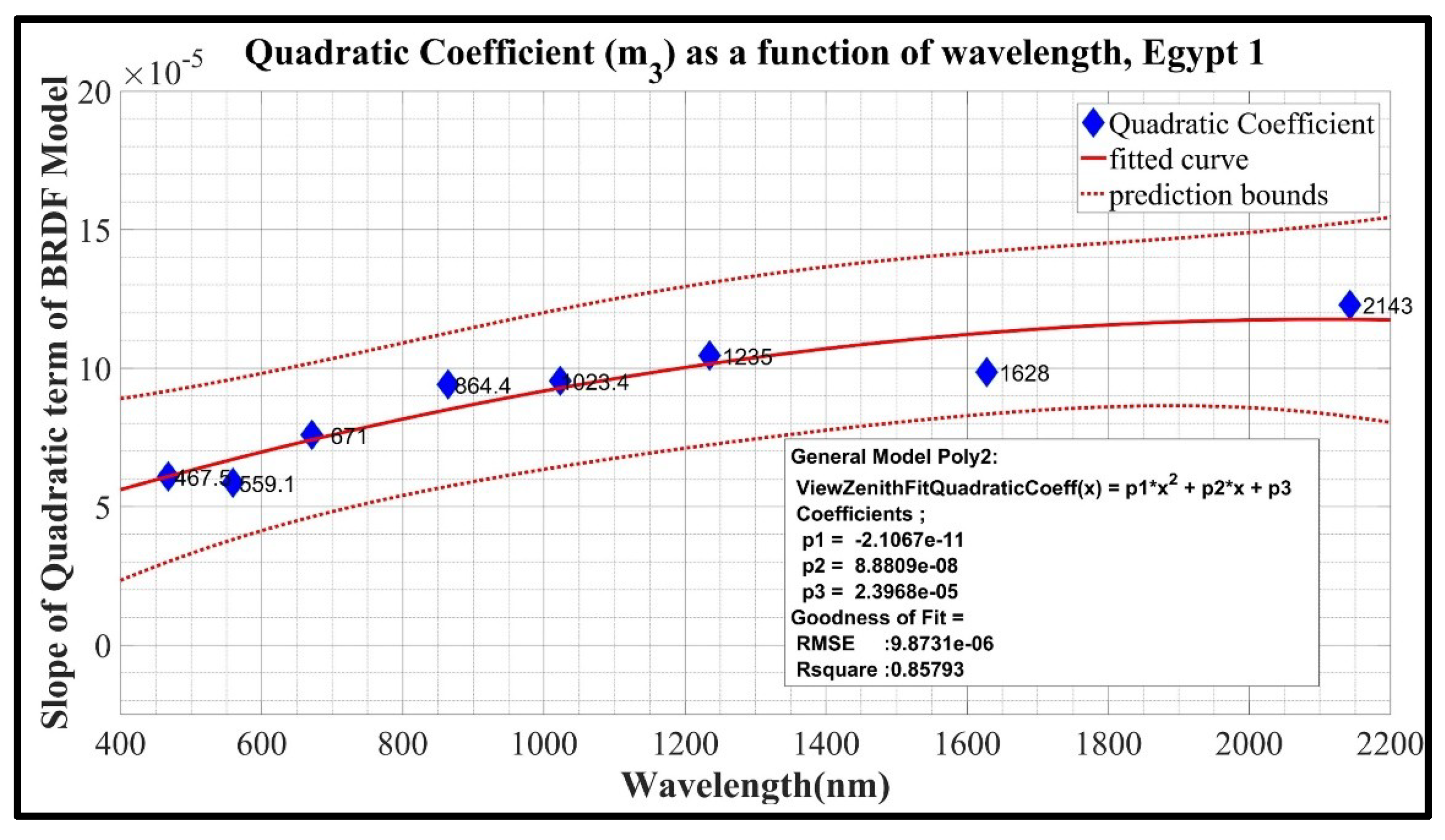
Figure 6.
Quadratic model fit on quadratic coefficient as a function of wavelength for Egypt 1.
Figure 6.
Quadratic model fit on quadratic coefficient as a function of wavelength for Egypt 1.
Figure 7.
Terra MODIS observation of Egypt 1(magenta circle) NIR band and model prediction (black circle).
Figure 7.
Terra MODIS observation of Egypt 1(magenta circle) NIR band and model prediction (black circle).
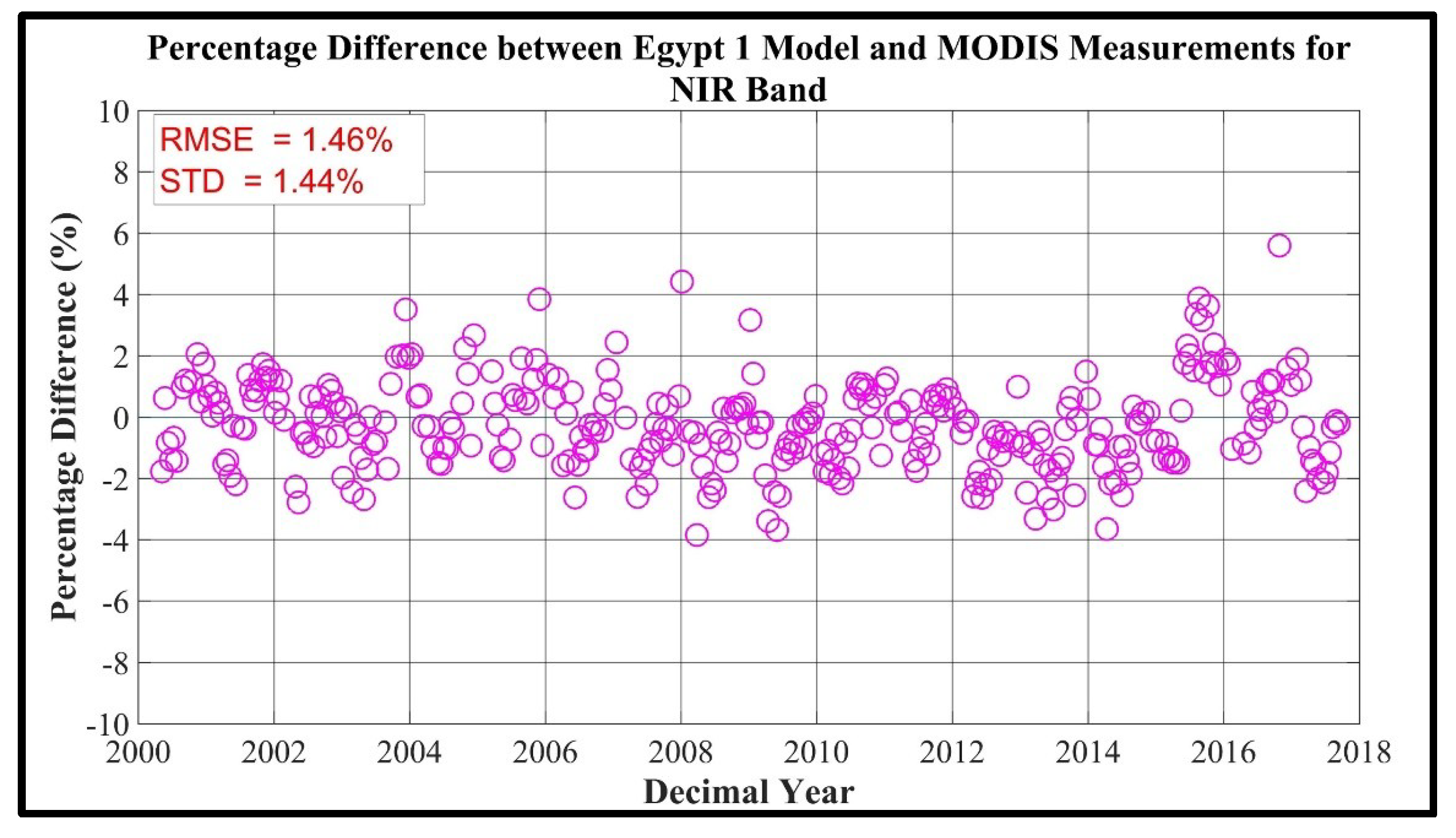
Figure 8.
Comparison between Egypt 1 Model and MODIS Measurement (band 2).
Figure 8.
Comparison between Egypt 1 Model and MODIS Measurement (band 2).
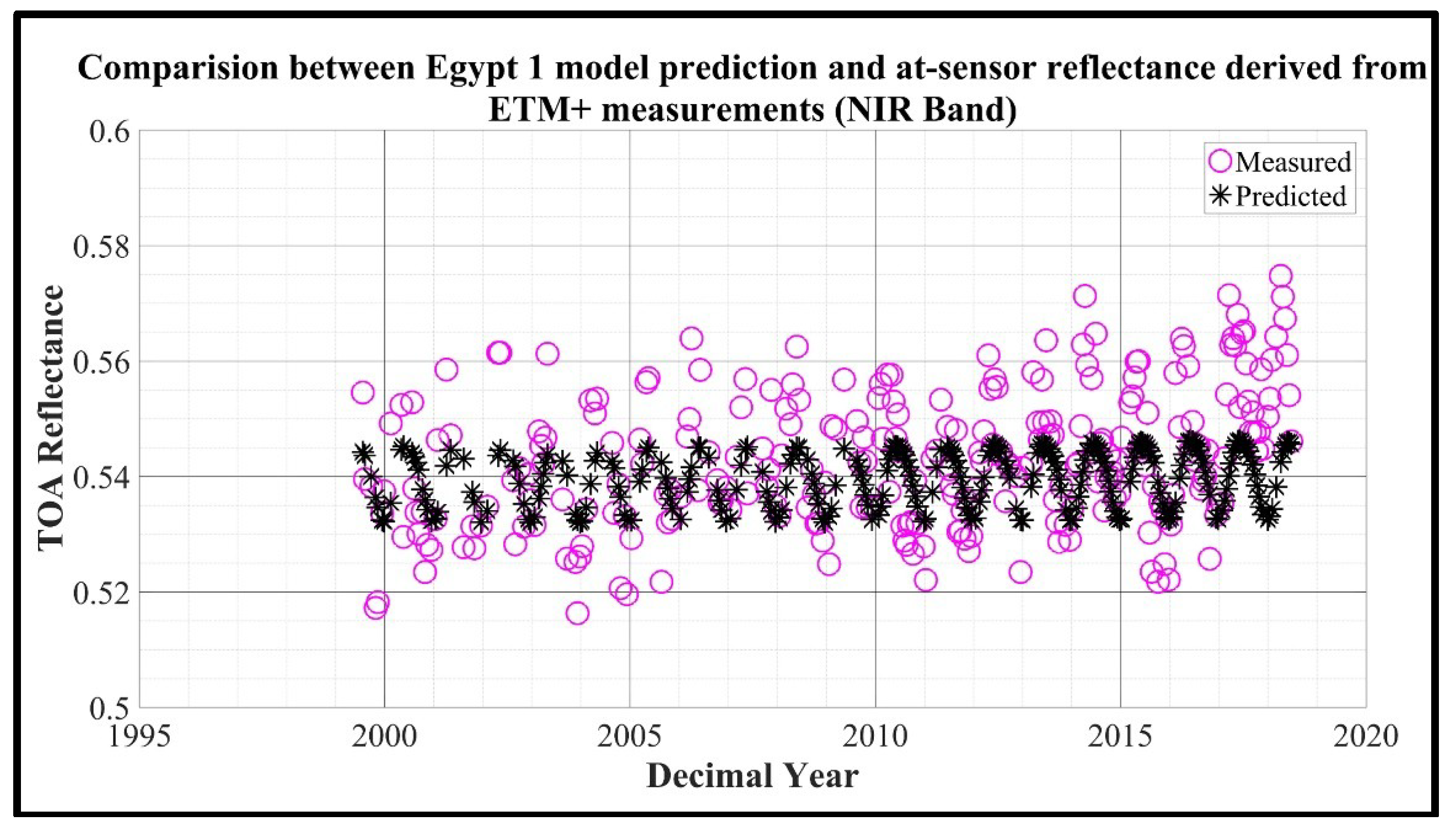
Figure 9.
L7 ETM+ observations of Egypt 1(circle) and model prediction (asterisk).
Figure 9.
L7 ETM+ observations of Egypt 1(circle) and model prediction (asterisk).
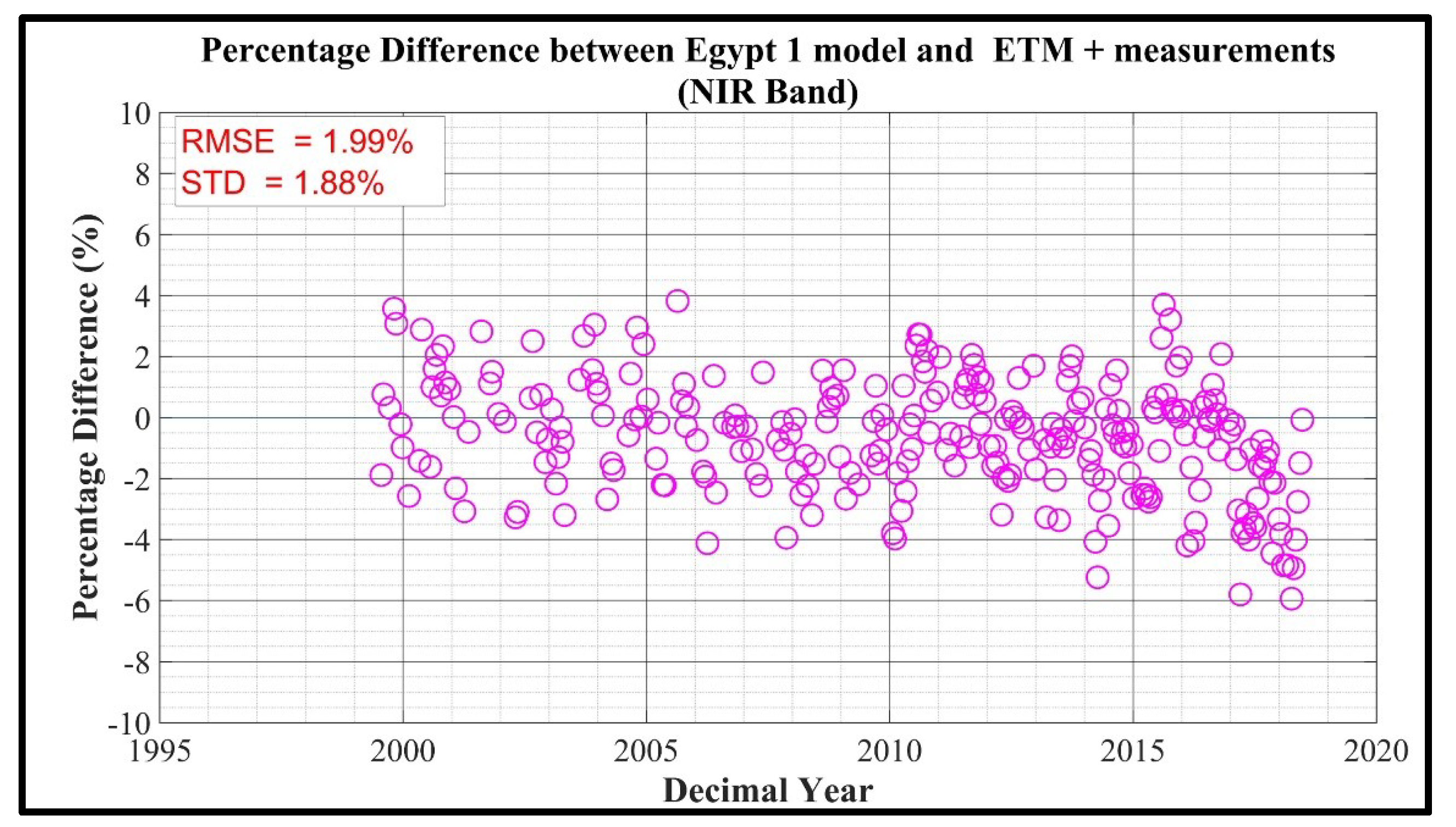
Figure 10.
Percentage difference between L7 ETM+ observations and model predictions.
Figure 10.
Percentage difference between L7 ETM+ observations and model predictions.
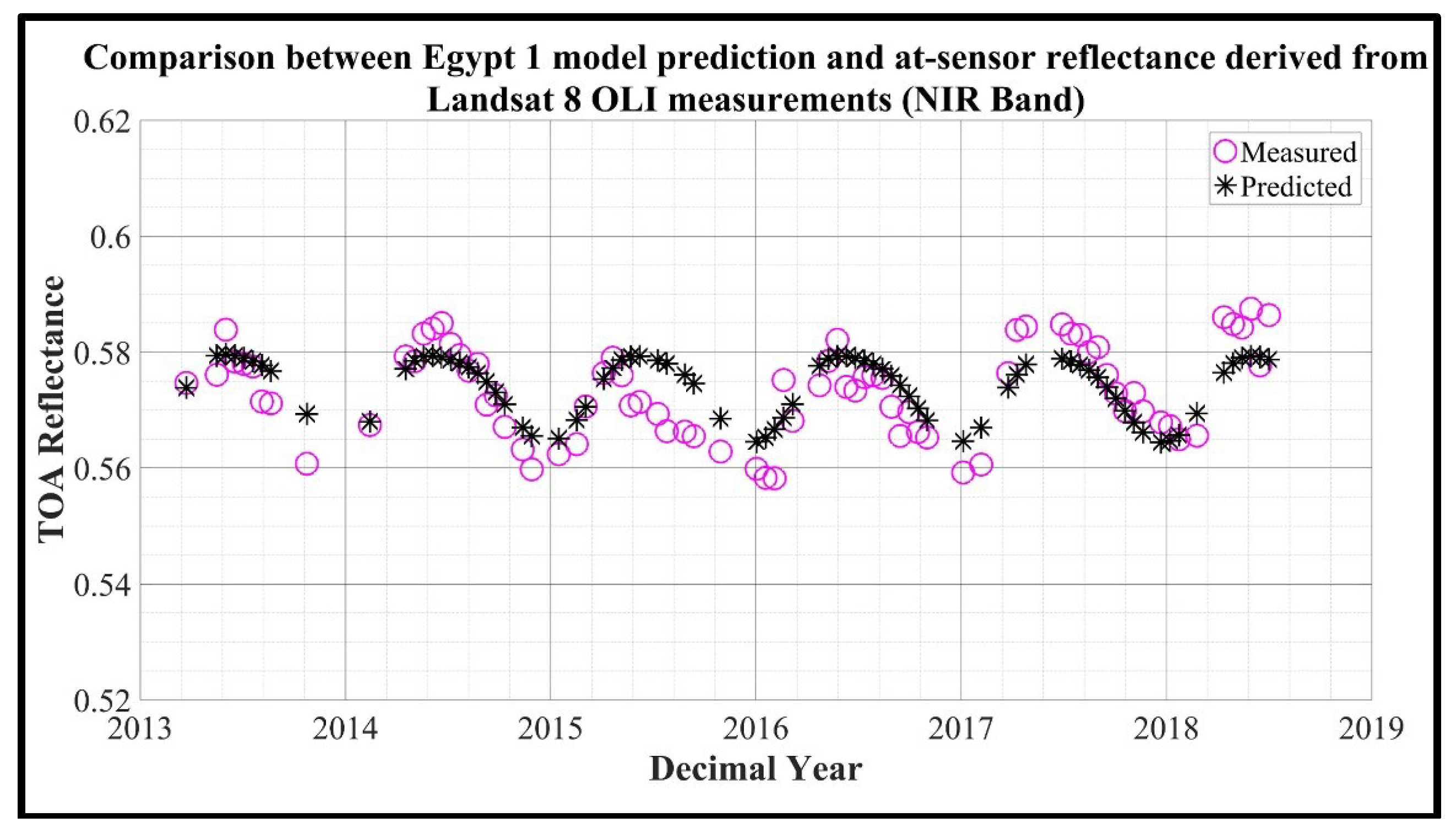
Figure 11.
L8 OLI observations of Egypt 1(circle) and model prediction (asterisk).
Figure 11.
L8 OLI observations of Egypt 1(circle) and model prediction (asterisk).
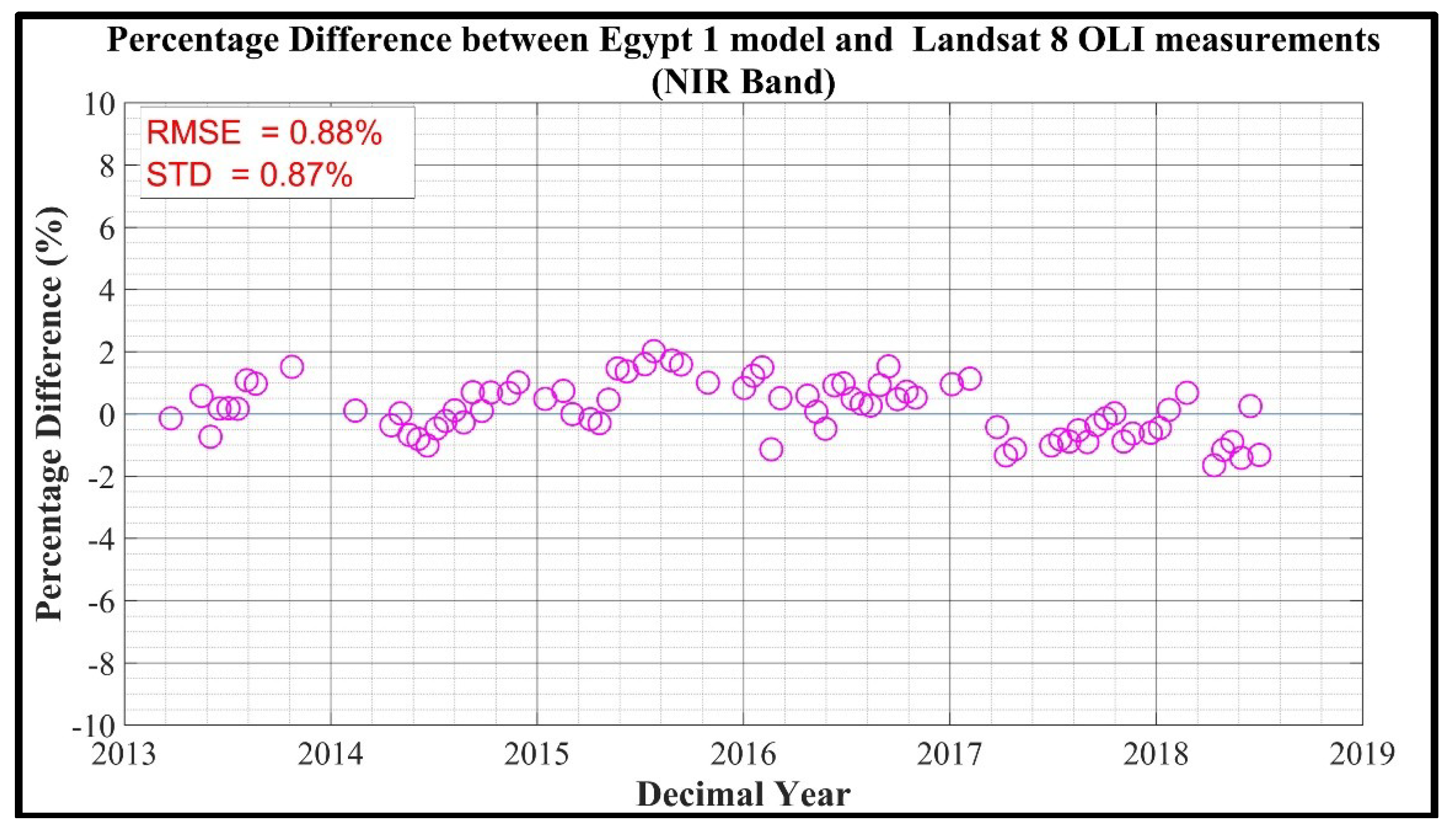
Figure 12.
Percentage difference between L8 OLI observations and model predictions.
Figure 12.
Percentage difference between L8 OLI observations and model predictions.
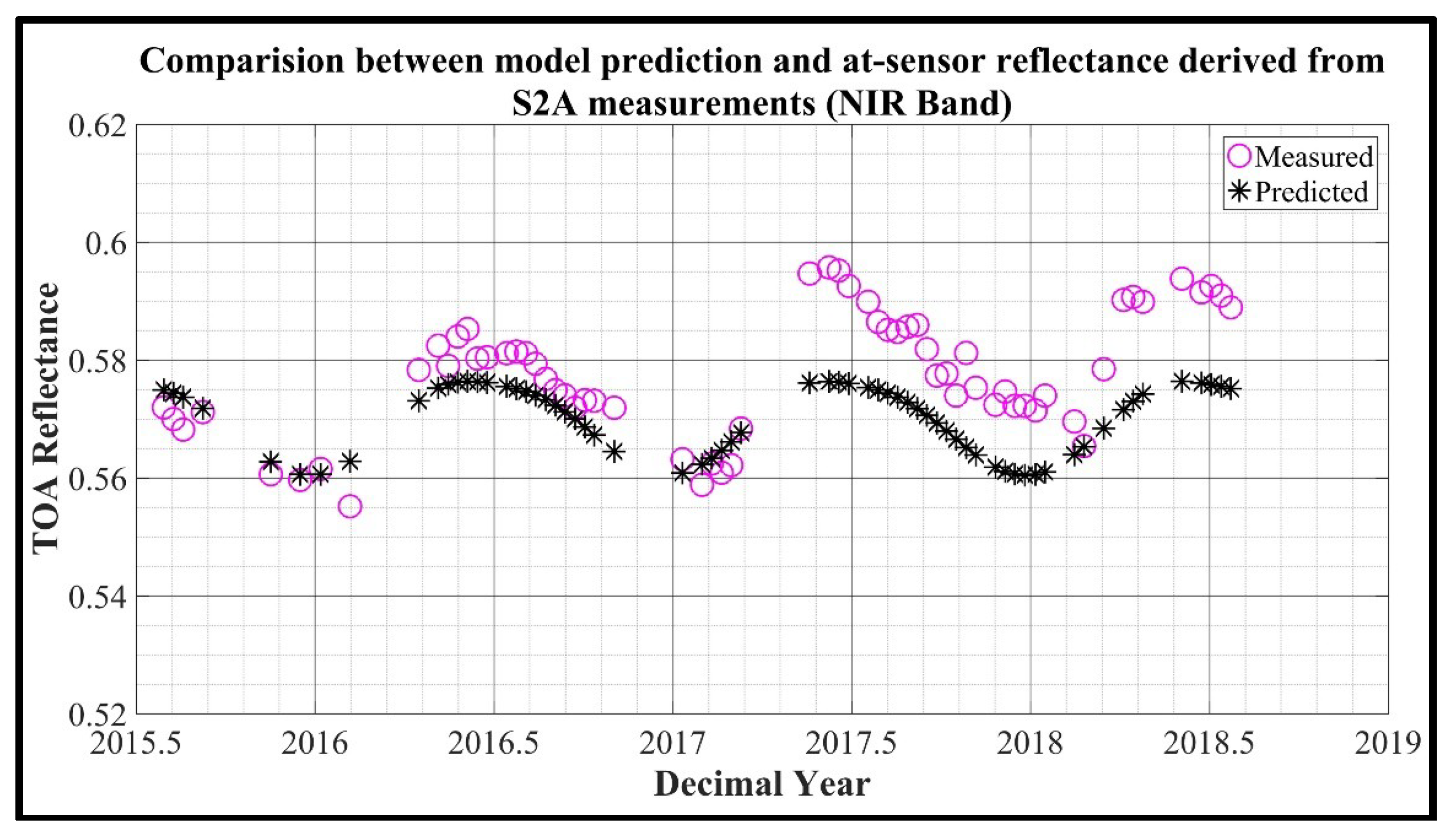
Figure 13.
S2A MSI observation of Egypt 1(circle) and model prediction (asterisk).
Figure 13.
S2A MSI observation of Egypt 1(circle) and model prediction (asterisk).
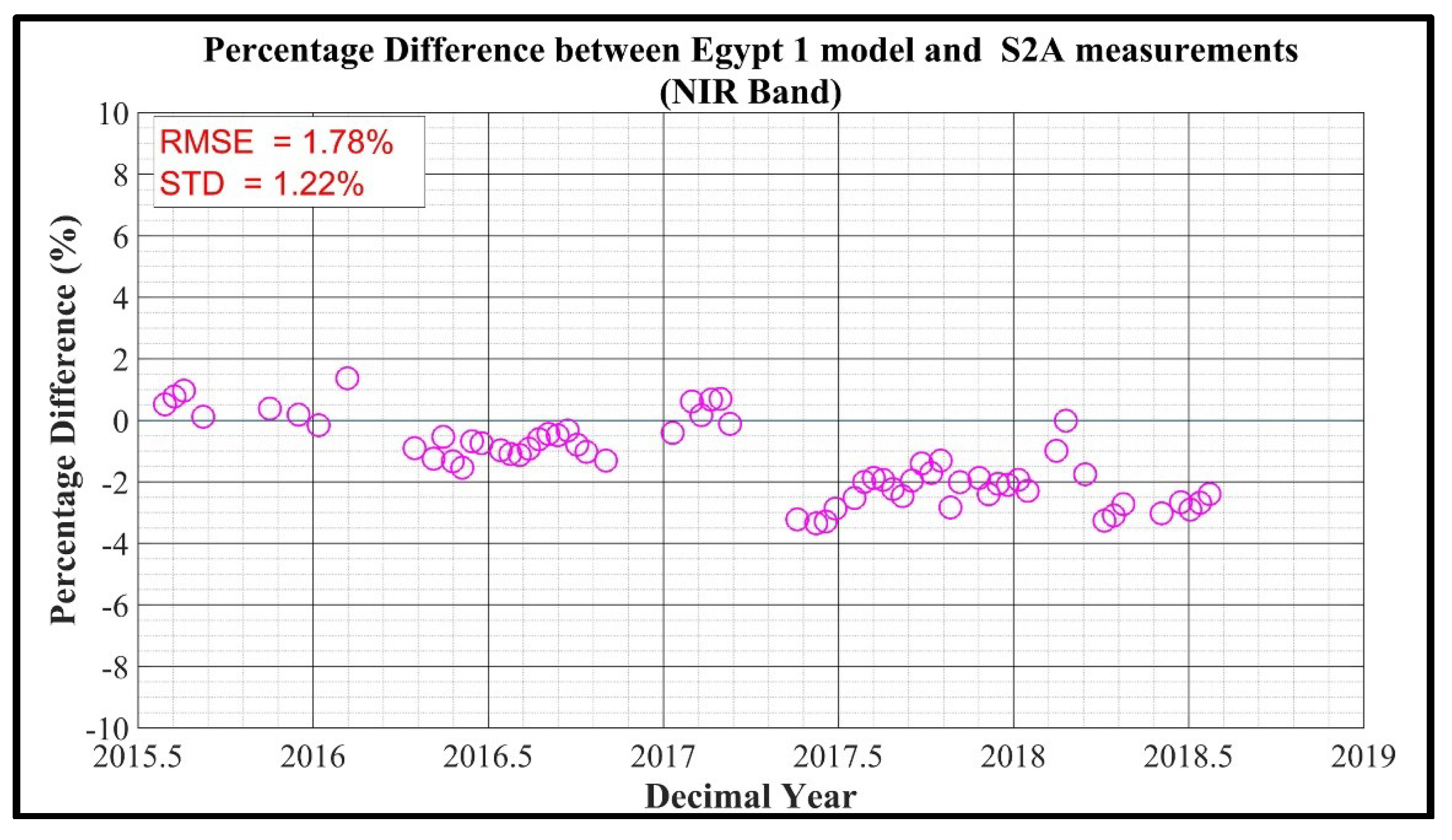
Figure 14.
Percentage Difference between S2A MSI measurements and model predictions.
Figure 14.
Percentage Difference between S2A MSI measurements and model predictions.
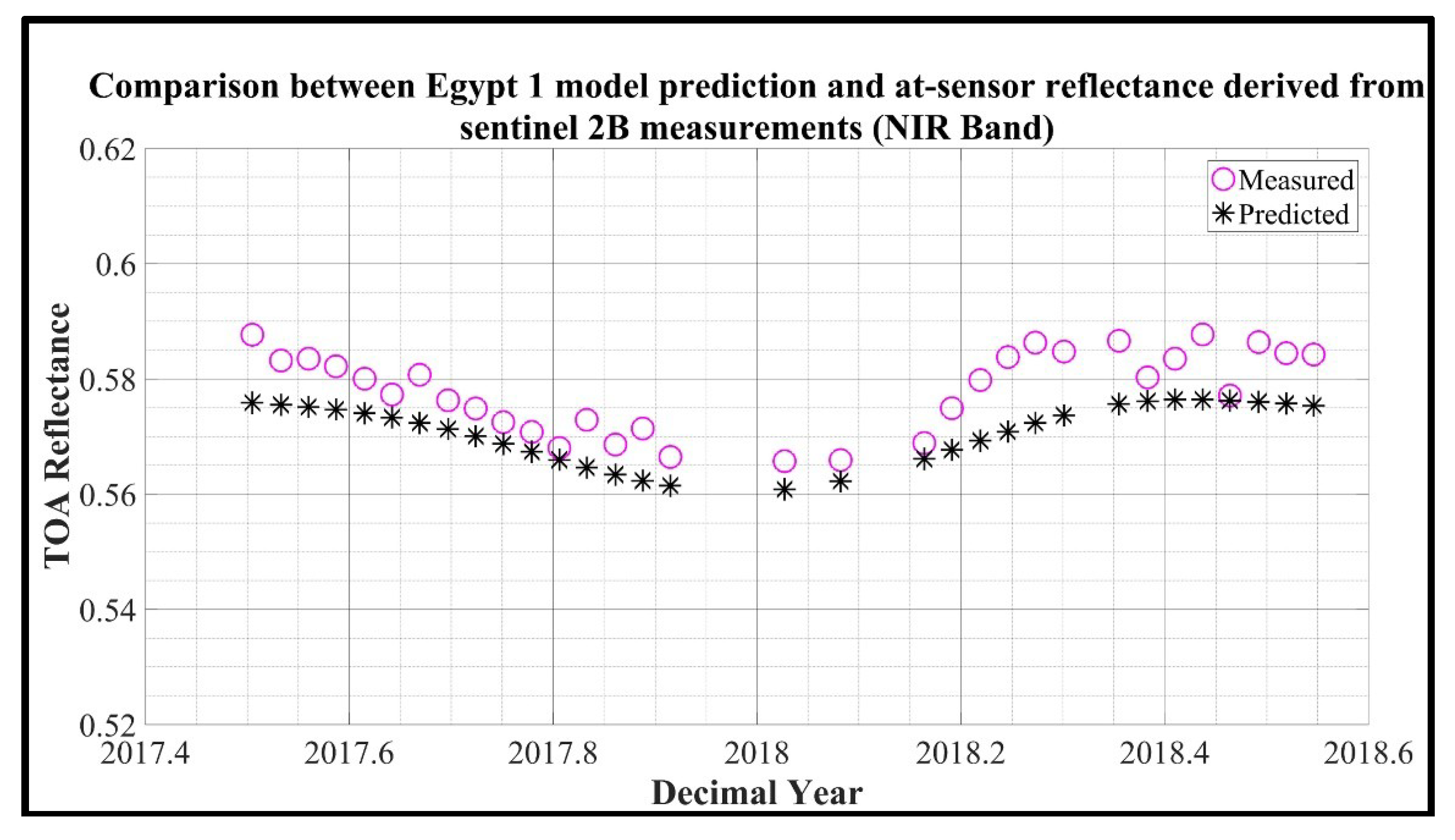
Figure 15.
S2B MSI observation of Egypt 1(circle) and model prediction (asterisk).
Figure 15.
S2B MSI observation of Egypt 1(circle) and model prediction (asterisk).
Figure 16.
Percentage Difference between S2B MSI measurements and model predictions.
Figure 16.
Percentage Difference between S2B MSI measurements and model predictions.
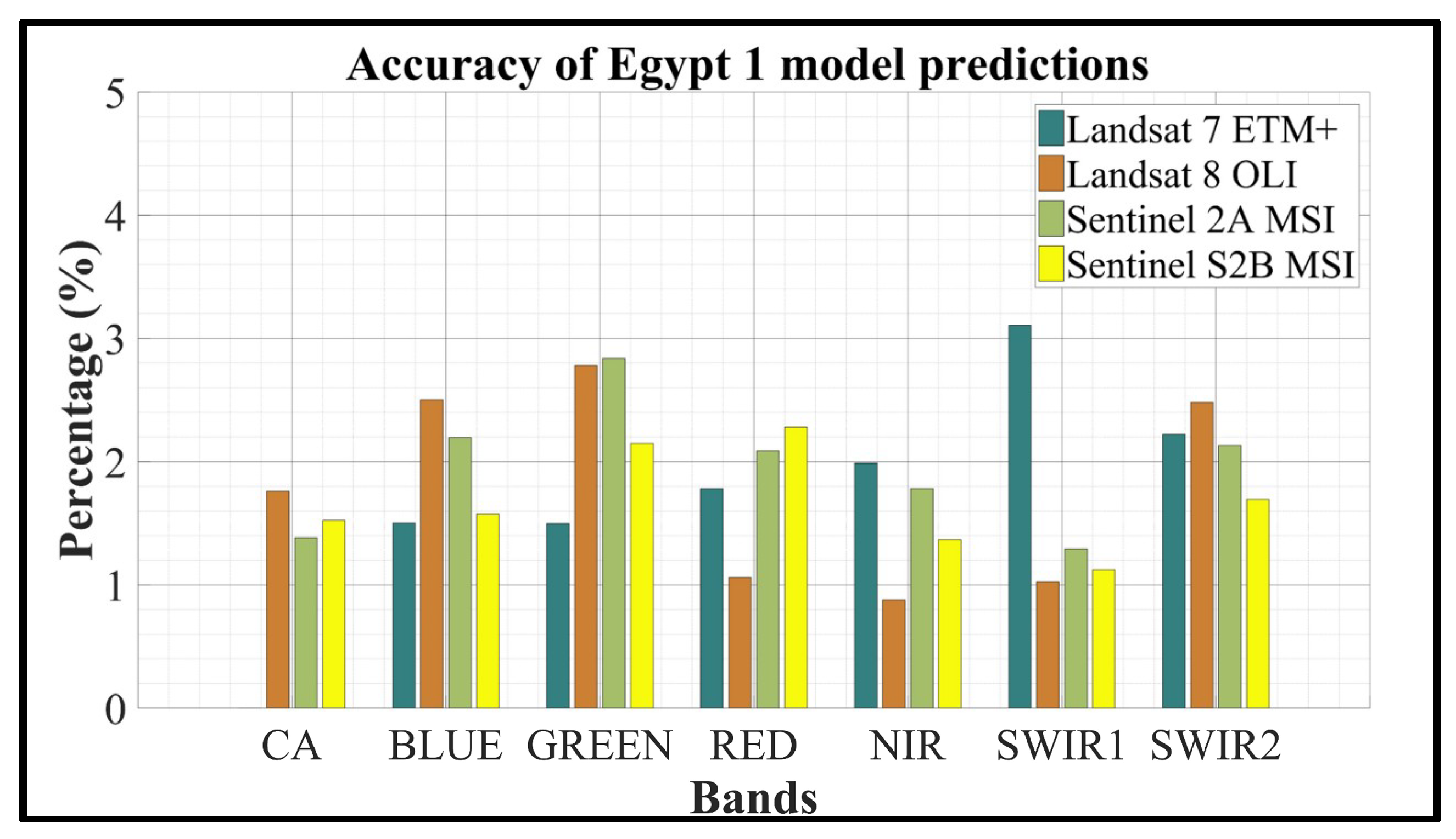
Figure 17.
Estimate of accuracy between sensor observation and Egypt1 model prediction.
Figure 17.
Estimate of accuracy between sensor observation and Egypt1 model prediction.
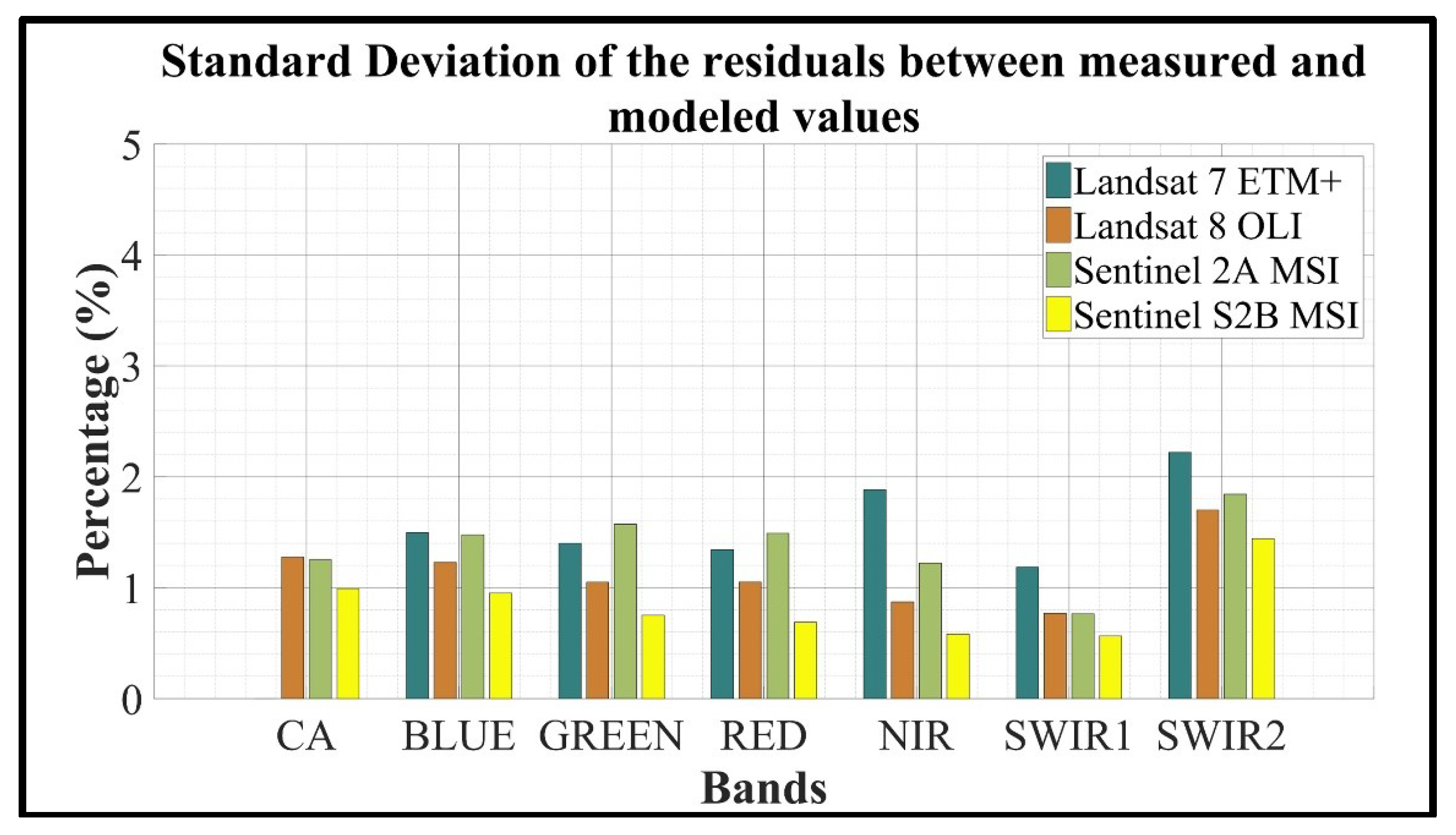
Figure 18.
Estimate of precision of the Egypt 1 model for the selected sensor.
Figure 18.
Estimate of precision of the Egypt 1 model for the selected sensor.
Table 1.
Fixed optimal region ROI latitude and longitude coordinates.
Table 1.
Fixed optimal region ROI latitude and longitude coordinates.
| PICS | WRS-2 Path/Row | Upper Left Latitude | Upper Left Longitude | Lower Right Latitude | Lower Right Longitude |
|---|
| Egypt 1 | 179/41 | 27.68° | 26.26° | 27.16° | 26.50° |
| Libya 1 | 187/43 | 24.86° | 13.32° | 24.56° | 13.67° |
| Niger 1 | 189/46 | 20.54° | 9.20° | 20.28° | 9.53° |
| Niger 2 | 188/45 | 21.48° | 10.39° | 21.25° | 10.71° |
| Sudan1 | 177/45 | 21.76° | 27.60° | 21.41° | 27.81° |
Table 2.
Hyperspectral model of BRDF slope and intercept as functions of solar zenith angle.
Table 2.
Hyperspectral model of BRDF slope and intercept as functions of solar zenith angle.
| PICS | Number of Scenes | Solar Zenith Angle Variation (degree) | Slope Model Fit | Intercept Model Fit |
|---|
| Egypt 1 | 330 | 13–53 | Two-piece Exponential | Two-piece Exponential |
| Libya 1 | 347 | 13–51 | Quadratic | Two-piece Exponential |
| Niger 1 | 318 | 15–46 | Cubic | Two-piece Exponential |
| Niger 2 | 269 | 14–49 | Cubic | Two-piece Exponential |
| Sudan 1 | 258 | 13–50 | Two-piece Exponential | Two-piece Exponential |
Table 3.
Summary of line fit for calculated slope of first order and second term as a function of wavelength for five PICS.
Table 3.
Summary of line fit for calculated slope of first order and second term as a function of wavelength for five PICS.
| Sites | Number of Scenes | Model Fit for First order Term (m1) | Model Fit for Second order Term (m2) |
|---|
| Egypt 1 | 135 | Quadratic | Quadratic |
| Libya 1 | 73 | Cubic | Cubic |
| Niger 1 | 30 | Cubic | Cubic |
| Niger 2 | 5 | Cubic | Cubic |
| Sudan 1 | 112 | Cubic | Cubic |
Table 4.
Mean k-scale Factors derived from MODIS/Hyperion near coincident pairs.
Table 4.
Mean k-scale Factors derived from MODIS/Hyperion near coincident pairs.
| Bands/PICS | Egypt 1 | Libya 1 | Niger 1 | Niger 2 | Sudan 1 |
|---|
| Blue (465.27 nm) | 1.016 ± 0.03 | 0.989 ± 0.03 | 1.007 ± 0.02 | 0.995 ± 0.08 | 0.987 ± 0.03 |
| Green (553.77 nm) | 1.050 ± 0.03 | 1.024 ± 0.03 | 1.062 ± 0.01 | 1.023 ± 0.03 | 1.011 ± 0.04 |
Red
(648.1 nm) | 1.029 ± 0.02 | 1.000 ± 0.02 | 1.025 ± 0.01 | 1.023 ± 0.00 | 0.982 ± 0.03 |
| NIR (857.44 nm) | 1.013 ± 0.02 | 0.988 ± 0.01 | 0.999 ± 0.03 | 1.007 ± 0.01 | 0.963 ± 0.03 |
| SWIR-1 (1628.05 nm) | 0.978 ± 0.01 | 0.948 ± 0.01 | 0.949 ± 0.01 | 0.950 ± 0.03 | 0.935 ± 0.02 |
| SWIR-2 (2115.12 nm) | 0.925 ± 0.01 | 0.902 ± 0.02 | 0.918 ± 0.01 | 0.924 ± 0.07 | 0.890 ± 0.03 |
Table 5.
Accuracy between model predictions and Terra MODIS observations.
Table 5.
Accuracy between model predictions and Terra MODIS observations.
| Bands/PICS. | Egypt 1 (%) | Libya 1 (%) | Niger 1 (%) | Niger 2 (%) | Sudan 1 (%) |
|---|
| Blue | 2.64 | 3.13 | 2.38 | 2.74 | 2.09 |
| Green | 1.66 | 1.9 | 2.33 | 1.74 | 2.45 |
| Red | 1.68 | 2.44 | 2.94 | 1.83 | 1.66 |
| NIR | 1.58 | 2.23 | 2.79 | 2.20 | 1.63 |
| SWIR-1 | 2.04 | 2.93 | 1.26 | 5.25 | 1.55 |
| SWIR-2 | 2.89 | 2.56 | 2.38 | 7.87 | 1.97 |
Table 6.
Random uncertainties between model predictions and Terra MODIS observations.
Table 6.
Random uncertainties between model predictions and Terra MODIS observations.
| Bands/PICS | Egypt 1 (%) | Libya 1 (%) | Niger 1 (%) | Niger 2 (%) | Sudan 1 (%) |
|---|
| Blue | 1.40 | 2.69 | 2.38 | 2.65 | 1.56 |
| Green | 1.48 | 1.59 | 1.12 | 1.73 | 1.12 |
| Red | 1.61 | 0.90 | 0.96 | 1.50 | 1.20 |
| NIR | 1.45 | 0.95 | 1.21 | 1.53 | 1.25 |
| SWIR-1 | 0.98 | 1.17 | 1.19 | 0.94 | 0.88 |
| SWIR-2 | 2.11 | 2.09 | 2.02 | 2.25 | 1.75 |
Table 7.
Accuracy between measured and Libya 1 simulated values.
Table 7.
Accuracy between measured and Libya 1 simulated values.
| Sensors | CA | Blue | Green | Red | NIR | SWIR-1 | SWIR-2 |
|---|
| L7 ETM + (%) | NA | 3.77 | 2.96 | 1.03 | 2.93 | 0.95 | 2.82 |
| L8 OLI (%) | 2.23 | 2.53 | 1.13 | 2.12 | 1.51 | 1.00 | 1.25 |
| S2A MSI (%) | 1.47 | 1.48 | 1.55 | 2.42 | 1.46 | 0.57 | 1.66 |
| S2B MSI (%) | 1.37 | 1.95 | 1.89 | 2.18 | 0.97 | 1.21 | 1.54 |
Table 8.
Libya 1 random error (precision) between measured and simulated values.
Table 8.
Libya 1 random error (precision) between measured and simulated values.
| Sensors | CA | Blue | Green | Red | NIR | SWIR-1 | SWIR-2 |
|---|
| L7 ETM + (%) | NA | 1.90 | 1.15 | 0.54 | 1.33 | 0.89 | 1.35 |
| L8 OLI (%) | 1.76 | 1.76 | 1.08 | 0.60 | 0.53 | 0.83 | 1.12 |
| S2A MSI (%) | 1.45 | 1.37 | 0.92 | 0.37 | 0.28 | 0.46 | 1.62 |
| S2B MSI (%) | 1.40 | 1.50 | 1.02 | 0.44 | 0.29 | 0.60 | 0.82 |
Table 9.
Accuracy between measured and Sudan 1 simulated values.
Table 9.
Accuracy between measured and Sudan 1 simulated values.
| Sensors | CA | Blue | Green | Red | NIR | SWIR-1 | SWIR-2 |
|---|
| L7 ETM + (%) | NA | 2.85 | 2.14 | 2.13 | 1.98 | 3.77 | 2.04 |
| L8 OLI (%) | 2.21 | 1.51 | 1.25 | 1.33 | 1.02 | 1.16 | 2.17 |
| S2A MSI (%) | 1.52 | 2.67 | 1.86 | 0.92 | 0.69 | 0.56 | 2.18 |
| S2B MSI (%) | 1.96 | 3.00 | 2.44 | 0.82 | 1.17 | 0.87 | 1.61 |
Table 10.
Sudan 1 random error (precision) between measured and simulated values.
Table 10.
Sudan 1 random error (precision) between measured and simulated values.
| Sensors | CA | Blue | Green | Red | NIR | SWIR-1 | SWIR-2 |
|---|
| L7 ETM + (%) | NA | 1.72 | 1.21 | 1.18 | 1.81 | 1.11 | 2.04 |
| L8 OLI (%) | 1.47 | 1.45 | 1.25 | 1.31 | 1.02 | 1.17 | 2.14 |
| S2A MSI (%) | 1.34 | 1.19 | 0.80 | 0.87 | 0.66 | 0.50 | 1.97 |
| S2B MSI (%) | 1.34 | 1.19 | 0.80 | 0.87 | 0.66 | 0.50 | 1.97 |
Table 11.
Accuracy between measured and Niger 1 simulated values.
Table 11.
Accuracy between measured and Niger 1 simulated values.
| Sensors | CA | Blue | Green | Red | NIR | SWIR-1 | SWIR-2 |
|---|
| L7 ETM + (%) | NA | 1.90 | 0.99 | 0.76 | 1.98 | 1.31 | 1.79 |
| L8 OLI (%) | 1.70 | 4.67 | 5.13 | 1.97 | 0.50 | 1.28 | 1.72 |
| S2A MSI (%) | 2.50 | 4.63 | 5.66 | 1.18 | 0.53 | 0.76 | 2.27 |
| S2B MSI (%) | 1.37 | 5.06 | 6.77 | 2.55 | 1.20 | 1.45 | 2.66 |
Table 12.
Niger 1 random error (precision) between measured and simulated values.
Table 12.
Niger 1 random error (precision) between measured and simulated values.
| Sensors | CA | Blue | Green | Red | NIR | SWIR-1 | SWIR-2 |
|---|
| L7 ETM + (%) | NA | 1.80 | 0.82 | 0.56 | 1.28 | 1.12 | 1.64 |
| L8 OLI (%) | 1.67 | 1.56 | 0.75 | 0.58 | 0.43 | 0.87 | 1.70 |
| S2A MSI (%) | 1.49 | 1.25 | 0.61 | 0.55 | 0.43 | 0.69 | 1.63 |
| S2B MSI (%) | 0.28 | 0.29 | 0.43 | 0.65 | 0.59 | 0.92 | 1.60 |
Table 13.
Accuracy between measured and Niger 2 simulated values.
Table 13.
Accuracy between measured and Niger 2 simulated values.
| Sensors | CA | Blue | Green | Red | NIR | SWIR-1 | SWIR-2 |
|---|
| L7 ETM + (%) | NA | 4.25 | 4.55 | 2.57 | 3.97 | 1.57 | 7.58 |
| L8 OLI (%) | 2.19 | 1.25 | 1.38 | 1.82 | 2.09 | 2.53 | 3.71 |
| S2A MSI (%) | 6.69 | 3.81 | 3.41 | 4.57 | 4.34 | 3.35 | 6.54 |
| S2B MSI (%) | 3.60 | 2.57 | 1.11 | 3.81 | 3.40 | 3.30 | 7.79 |
Table 14.
Niger 2 random error (precision) between measured and simulated values.
Table 14.
Niger 2 random error (precision) between measured and simulated values.
| Sensors | CA | Blue | Green | Red | NIR | SWIR-1 | SWIR-2 |
|---|
| L7 ETM + (%) | NA | 1.67 | 1.35 | 1.45 | 2.06 | 1.54 | 2.49 |
| L8 OLI (%) | 0.51 | 0.54 | 0.41 | 0.53 | 0.65 | 0.80 | 1.21 |
| S2A MSI (%) | 3.83 | 3.83 | 2.43 | 1.78 | 1.60 | 1.23 | 2.37 |
| S2B MSI (%) | 1.39 | 1.41 | 1.06 | 1.09 | 1.08 | 1.08 | 2.14 |
Table 15.
Absolute calibration model parameter uncertainties.
Table 15.
Absolute calibration model parameter uncertainties.
| Uncertainty Source | Uncertainty (%) | Remarks |
|---|
| k-scale factor | 0.1%–8.7% | All bands and all five PICS |
| Hyperion spectra | 1.3%– 4.8% | All bands and all five PICS |
| SZA [20°–60°] | 0.1% | All bands and all five PICS |
| VZA [± 200 of nadir] | 0.5% | All bands and all five PICS |
Table 16.
Total uncertainties for each PICS absolute calibration model.
Table 16.
Total uncertainties for each PICS absolute calibration model.
| Bands | Egypt 1 | Libya 1 | Niger 1 | Niger 2 | Sudan 1 |
|---|
| CA (%) | 3.86 | 3.88 | 5.63 | 9.08 | 5.55 |
| Blue (%) | 3.82 | 4.02 | 5.49 | 9.35 | 4.98 |
| Green (%) | 3.62 | 2.73 | 5.03 | 4.08 | 4.88 |
| Red (%) | 2.91 | 1.07 | 3.99 | 1.88 | 4.08 |
| NIR (%) | 2.60 | 1.55 | 3.81 | 1.74 | 3.69 |
| SWIR-1 (%) | 1.85 | 1.35 | 4.06 | 3.39 | 2.85 |
| SWIR-2 (%) | 2.71 | 3.72 | 5.78 | 7.50 | 4.00 |