1. Introduction
Deep space exploration is the focus of space activities around the world, which aims to explore the mysteries of the universe, search for extraterrestrial life and acquire new knowledge [
1,
2,
3]. Planetary science plays an increasingly important role in the high-quality and sustainable development of deep space exploration [
4,
5]. Asteroids, as a kind of special celestial body revolving around the sun, are of great scientific significance for human beings in studying the origin and evolution of the solar system, exploring the mineral resources and protecting the safety of the earth due to their large number, different individual characteristics and special orbits [
6,
7,
8]. Studies have shown that the thermal radiation from asteroids mainly depends on its size, shape, albedo, thermal inertia and roughness of the surface [
9,
10]. The asteroids with different types (such as the S-type, V-type, etc.) in different regions (such as the Jupiter trojans, Hungarian group, etc.) show different spectral characteristics, which establishes the foundations for identifying different kinds of asteroids via remote spectral observation [
11,
12]. For example, the near-infrared data can reveal the diagnostic compositional information, and the salient features at 1 and 2 μm bands can be used to indicate the existence or absence of olivine and pyroxene [
12]. The astronomers have developed many remote observation methods for asteroids, such as spectral and polychromatic photometry, infrared and radio radiation methods [
13,
14,
15,
16]. Thus, a large volume of asteroid visible and near-infrared spectral data has been collected with the development of space and ground-based telescope observation technologies, which induced great progress in the field of asteroid taxonomy through their spectral characteristics [
17,
18,
19,
20].
The Eight-Color Asteroid Survey (ECAS) is the most remarkable ground-based asteroid observation survey, which gathered the spectrophotometric observations of about 600 large asteroids [
14]. However, very few small main-belt asteroids have been observed due to their faintness. With the appearance of charge-coupled device (CCD), it has been possible to study the large-scale spectral data of small main-belt asteroids with a diameter less than 1 km [
21]. The first phase of the Small Main belt Asteroid Spectroscopic Survey (SMASSI) was implemented from 1991 to 1993 at the Michigan-Dartmouth-MIT Observatory [
15,
20]. The main objective of SMASSI was to measure the spectral properties for small and medium-sized asteroids, and it primarily focuses on the objects in the inner main belt aiming to study the correlations between meteorites and asteroids. Based on the survey, abundant spectral measurements for 316 different asteroids have been collected. In view of the successes of SMASSI, the second phase of the Small Main-belt Asteroid Spectroscopic Survey (SMASSII) mainly focused on gathering an even larger and internally consistent asteroid dataset with spectral observations and reductions, which were carried out as consistently as possible [
20]. Thus, SMASSII has provided a new basis for studying the composition and structure of the asteroid belt [
9].
For asteroid taxonomy, Tholen et al. applied the minimal tree method by a combination with the principal component analysis (PCA) method in order to classify nearly 600 asteroid spectra from the ECAS [
14]. For more comprehensive and accurate classification of asteroids, DeMeo et al. developed an extended taxonomy to characterize visible and near -infrared wavelength spectra [
20]. The asteroid spectral data used for the taxonomy are based on the reflectance spectral characteristics measured in the wavelength range from 0.45 to 2.45 μm with 379–688 bands. In summary, the dataset was comprised of 371 objects with both visible and near-infrared data. SMASSII dataset provided the most visible wavelength spectra, and the near-infrared spectral measurements from 0.8 to 2.5 μm were obtained by using SpeX, the low-resolution to medium-resolution near-infrared spectrograph and imager at the 3-m NASA IRTF in Mauna Kea, Hawaii [
20]. A detailed description for the dataset is illustrated in
Table 1. Based on the dataset, DeMeo et al. have presented the taxonomy, as well as the method and rationale, for the class definitions of different kinds of asteroids. Specifically, three main complexes, i.e., S-complex, C-complex and X-complex, were defined based on some empirical spectral characteristics/features, such as the spectral curve slope, absorption bands and so on.
Nevertheless, the question of how to automatically discover the key category-related spectral characteristics/features for different kinds of asteroids remains an open problem [
9,
22,
23]. Meanwhile, owing to the noise of observation systems and the ever-changing external conditions, the observed spectral data usually contain noise and distortions, which will cause spectrum mixture due to the random perturbation of electronic observation devices. As a result, the observed asteroid spectra data often show indivisible pattern characteristics [
24,
25]. Furthermore, the observed spectral data always have wide bands, such as the visible and near-infrared bands. Thus, the reflectance at one wavelength is usually correlated with the reflectance of the adjacent wavelengths [
26]. Accordingly, the adjacent spectral bands are usually redundant, and some bands may not contain discriminant information for asteroid classification. Moreover, the abundant spectral information will result in high data dimensionality containing useless or even harmful information and bring about the “curse of dimensionality” problem, i.e., under a fixed and limited number of training samples, the classification accuracy of spectral data might decrease when the dimensionality of spectral feature increases [
27]. Therefore, it is necessary to develop effective low-dimensional asteroid spectral feature learning methods and find the latent key discriminative knowledge for different kinds of asteroids, which will be very beneficial for the precise classification of asteroids.
Machine learning techniques have developed rapidly in recent years for spectral data processing and applications, such as the classification and target detection [
28,
29,
30,
31,
32,
33,
34,
35]. For example, the classic PCA has been applied to extract meaningful features from the observed spectral data without using the prior label information. PCA is also useful for asteroid and meteorite spectra analysis due to the fact that many of the variables, i.e., the reflectance at different wavelengths, are highly correlated [
15,
20,
36]. Linear discriminant analysis (LDA) can make full use of the label priors by concurrently minimizing the within-class scatter and maximizing the between-class scatter in a dimension-reduced subspace [
37]. In addition to the above statistics-based methods, some geometry theory-based methods have also been proposed for the problem of data dimensionality reduction. For example, the locality preserving projections (LPP) assume that neighboring samples are likely to share similar labels, and the affinity relationships among samples should be preserved in subspace learning/dimension reduction [
38]. Locality preserving discriminant projections (LPDP) have also been developed with locality and Fisher criterions, which can be seen as a combination of LDA and LPP [
39,
40].
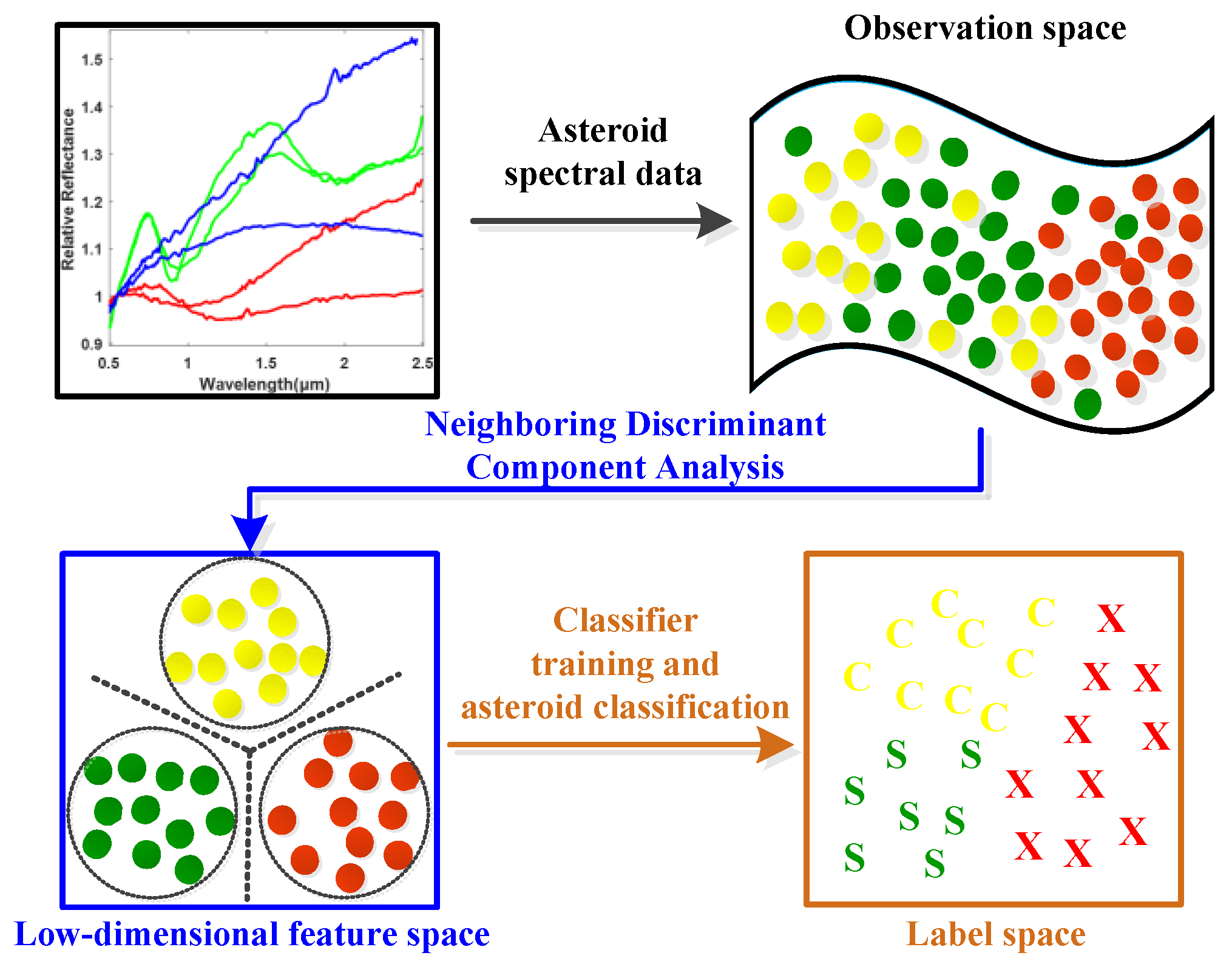
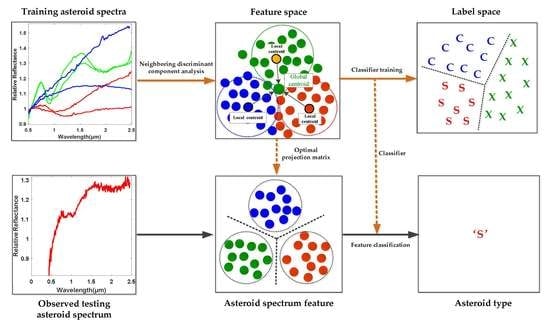
In order to define the class boundaries for asteroid classification, traditional methods always empirically determine the spectral features by relying on the presence or absence of specific features, such as the spectral curve slope, absorption wavelengths and so on, which might be intricate and less reliable. Based on the well labeled asteroid spectral dataset described in
Table 1 the main objective of this paper is to study the pattern characteristics of different categories of asteroids from the perspective of data-driven machine learning technique and to develop efficient asteroid spectral feature learning and classification method in a supervised fashion, as shown in
Figure 1. In order to be specific, it is assumed that not only the specified absorption bands, such as the 1 μm and 2 μm bands but also all the spectral wavelengths might carry some useful diagnostic information for asteroid category identification and will contribute to the accurate classification of different kinds of asteroids. As a result, the spectral data spanning across the visible to near-infrared wavelengths, i.e., from 0.45 to 2.45 μm, are treated as a whole in order to automatically discover the key category-related discriminative information for efficient asteroid spectral feature learning and classification by using supervised data-driven machine learning methodology. The novelties and contributions of this paper are summarized as below.
- (1)
Instead of empirically determining the spectral features via the presence or absence of specific spectral features to define asteroid class boundaries for classification, this paper presents a novel supervised Neighboring Discriminant Components Analysis (NDCA) model for discriminative asteroid spectral feature learning by simultaneously maximizing the neighboring between-class scatter and data variances, minimizing the neighboring within-class scatter to alleviate the overfitting problem caused by outliers and enhancing the discrimination and generalization ability of the model.
- (2)
With the neighboring discrimination learning strategy, the proposed NDCA model has stronger robustness to abnormal samples and outliers, and the generalization performance can thus be improved. In addition, the NDCA model transforms the data from the observation space into a more separable subspace, and the key category-related knowledge can be well discovered and preserved for different classes of asteroids with neighboring structure preservation and label prior guidance.
- (3)
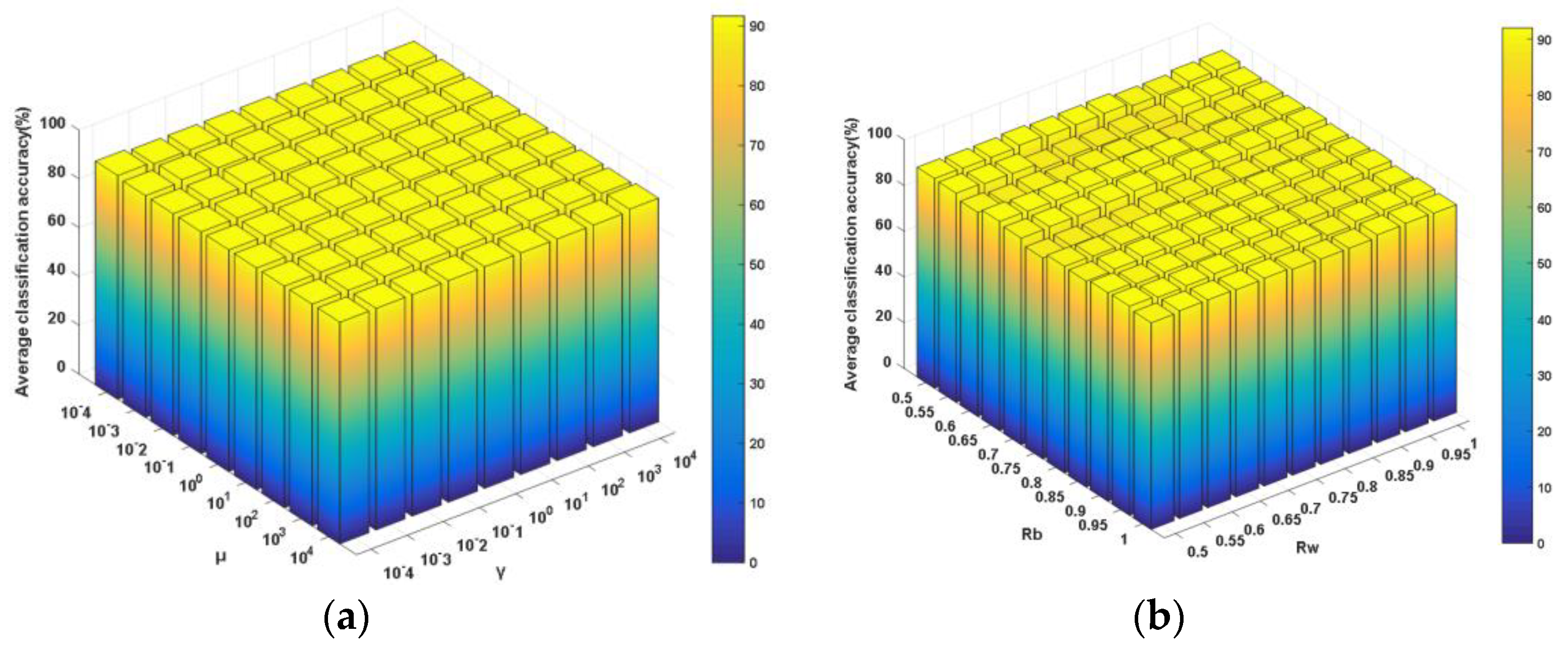
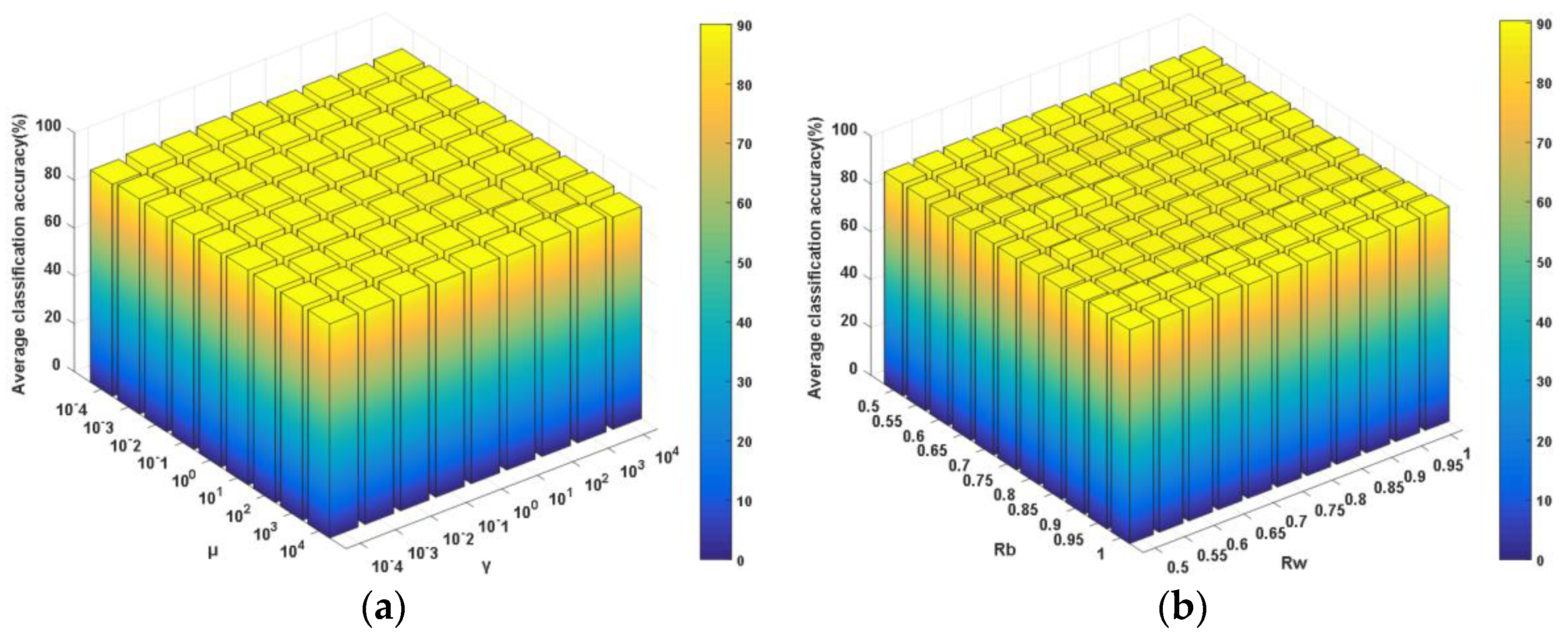
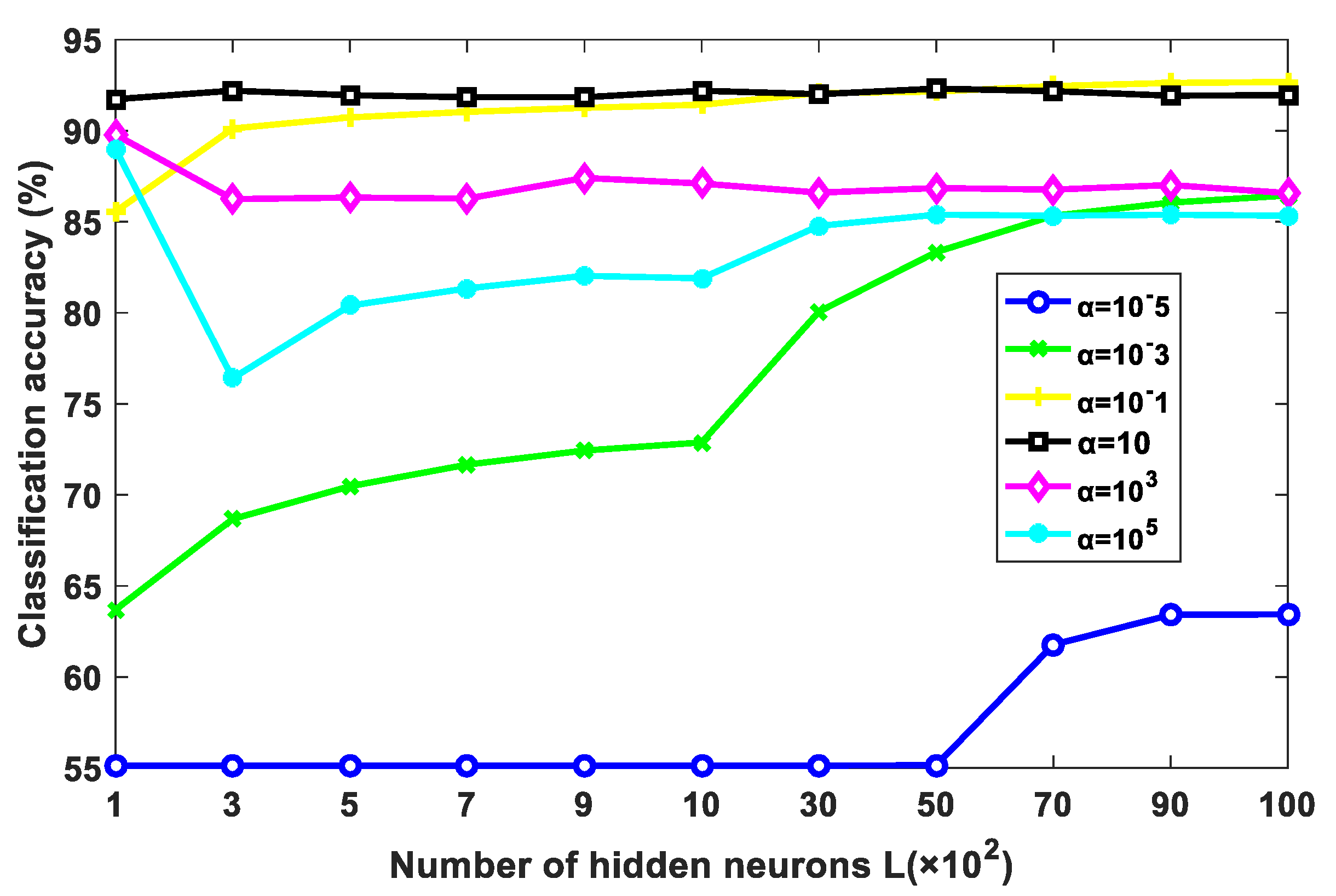
The performance of the proposed NDCA model is verified on real-world asteroid dataset covering the spectral wavelengths from 0.45 to 2.45 μm by combining with different baseline classifier models, including the nearest neighbor (NN), support vector machine (SVM) and extreme learning machine (ELM). In particular, the best result is achieved by ELM, with a classification accuracy of about 95.19%.
The reminder of this paper is structured as follows.
Section 2 introduces related works on subspace learning/dimension reduction and machine learning classifier models. The proposed NDCA model is meticulously introduced in
Section 3.
Section 4 contains the experimental results and discussions. The final conclusion is given in
Section 5.
3. The Proposed Neighboring Discriminant Component Analysis Model: Formulation and Optimization
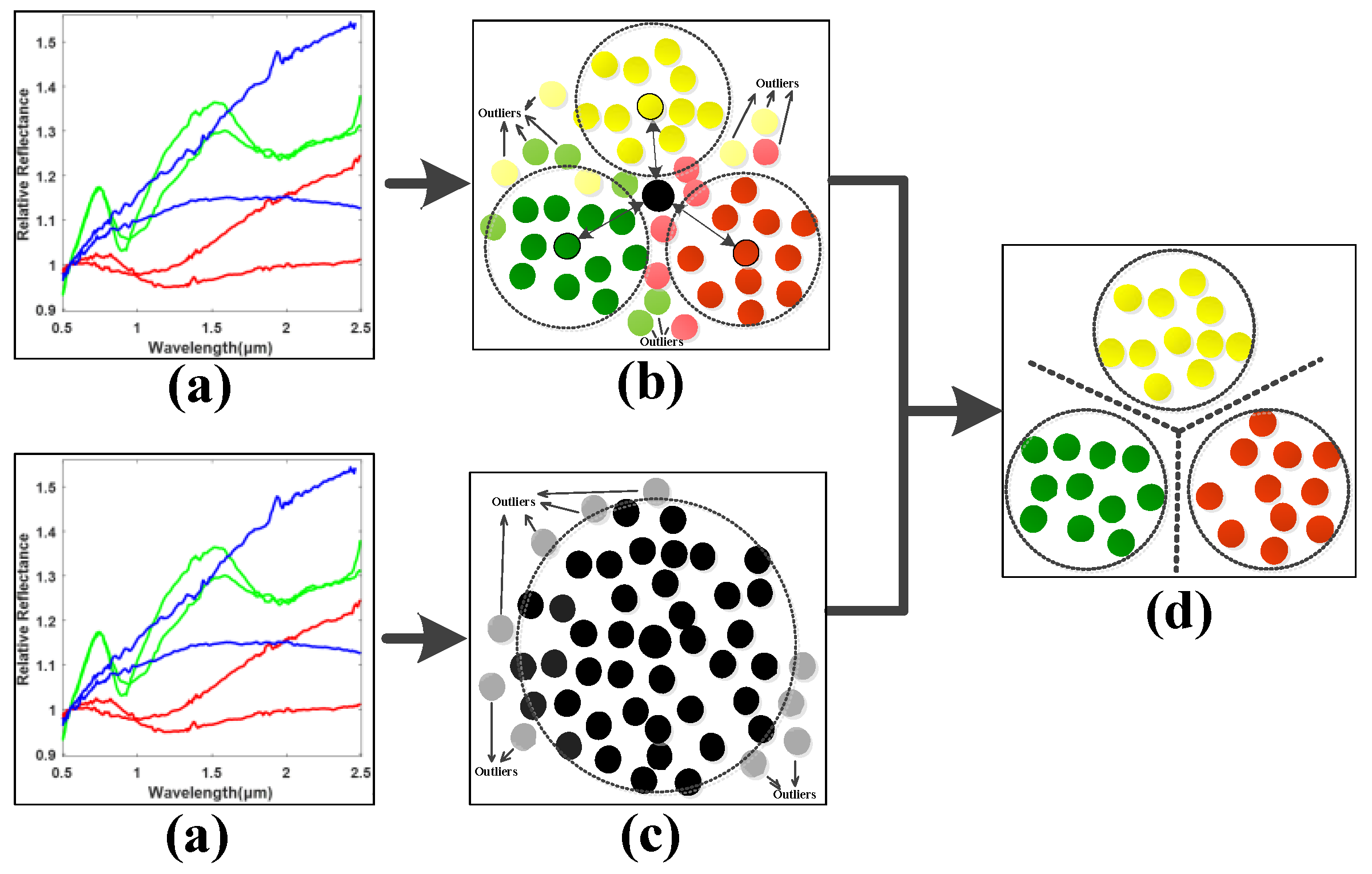
The remote observed asteroid spectral data usually contain noise and outliers, which will mix different categories of asteroids and make them inseparable. In addition, learning with outliers will easily cause overfitting problem, which will decrease the generalization ability of machine learning models for testing samples. Thus, the key problem is to distinguish the outliers and to select the most valuable samples for the learning of low-dimensional feature subspace and preserve the key discriminative data knowledge for different classes of asteroids.
To this end, the idea of neighboring learning is introduced to find a neighboring group of valuable samples from all the training samples as well as the samples in each class, and the outliers and noised samples are excluded in dimension reduction learning in order to enhance the generalization ability of the model. As shown in
Figure 2, the normalized asteroid spectral data are firstly inputted as in (a). Secondly, (b) finds the neighboring samples in each asteroid class in order to characterize the neighboring within-class and between-class properties of data. Meanwhile, the neighboring samples from all the samples for neighboring principal components were found to preserve the most valuable data information as in (c). With the basic principles of (b) and (c), a clearer class boundary can be found to alleviate the overfitting problem caused by the outliers and noised samples and enhance the neighboring and discriminative information of data for efficient spectral feature learning shown in (d). In order to achieve this goal, the neighboring between-class and within-class scatter matrices need to be calculated in order to characterize the neighboring discriminative properties of the observed asteroid spectra.
Neighboring between-class scatter matrix
computation: Firstly, calculate the global centroid
for all the samples in training dataset
and find
Nb =
Rb ·
N neighboring samples to
by using between-class neighboring ratio
Rb (0 <
Rb < 1). Thus,
Nb = [
Nb1,
Nb2, …,
Nbc, …,
NbC] global neighboring samples
can be obtained with
Nbc as the number of the neighboring samples in the
c-th class for computing the neighboring between-class scatter matrix. Secondly, compute the local centroid
for the
c-th class, and
is the
j-th sample in the
c-th class of the neighboring samples
. Finally, the neighboring between-class scatter matrix is calculated as follows.
At the same time, the
global neighboring samples are used to calculate the covariance matrix as below.
Neighboring within-class scatter matrix
computation: Firstly, calculate the basic local centroid
for each class of samples, where
is the
i-th sample in the
c-th class of
, and then find the samples group containing
Nwc =
Rw ·
Nc neighboring samples to
by using within-class neighboring ratio
Rw (0 <
Rw < 1) in the
i-th class. Secondly, refine the local centroid of each class using the samples in the obtained neighboring group of samples
. Finally, compute the neighboring within-class scatter matrix as follows:
where
is the refined centroid of each class based on the neighboring sample groups
, and
is the
i-th samples of
c-th class samples in the neighboring group. By comprehensively consider Equations (10)–(12) in a dimension-reduced subspace, the following optimization problem is formulated.
The details for deriving Equation (13) based on Equations (10)–(12) are shown in
Appendix A. In Equation (13),
γ and
μ are the tradeoff parameters for balancing the corresponding components in the objective function, from which one can observe that, in the subspace formed by
P, the goals of neighboring between-class scatter maximization, within-class scatter minimization and neighboring principal components preservation can be simultaneously achieved. Accordingly, the side effects of outliers and noised samples will be suppressed to the largest extent. As a result, the global and local neighboring discriminative structures and principal components will be enhanced and preserved by using the neighboring learning mechanism. Furthermore, optimization problem (13) can be transformed into the following one by introducing an equality constraint [
49]:
where
is a constant used to ensure a unique solution for model (13). The objective function for model (14) can be formulated as the following unconstrained one by introducing the Lagrange multiplier
λ.
Then, the partial derivative of the objective function (15) with respect to
P is calculated and set as zero, resulting in the following equations:
where the projection matrix
can be acquired, which is composed of the eigenvectors corresponding to the first
d largest eigenvalues λ
1, λ
2 …, λ
d of the eigenvalue decomposition problem as described below.
Once the above optimal projection matrix is calculated, the training data are projected into the subspace using in order to acquire the low-dimensional discriminative feature of the observed spectral data. Afterwards, a classifier model is trained using the dimension-reduced training data. For testing, an asteroid spectral sample with unknown label is firstly transformed into the subspace by using the optimal projection matrix P and then classified by the trained classifier model.