Self-Enforcing Price Leadership
Abstract
:1. Introduction
2. Model
Monopolistic Profits
3. Price Leadership
- I.
- At any period , the informed firm sets a price equal to if the state is and equal to if the state is ;
- U.
- the uninformed firm starts by setting the price at and after that always sets a price that matches the informed firm’s previous price, that is, .
3.1. Payoffs from Price Leadership
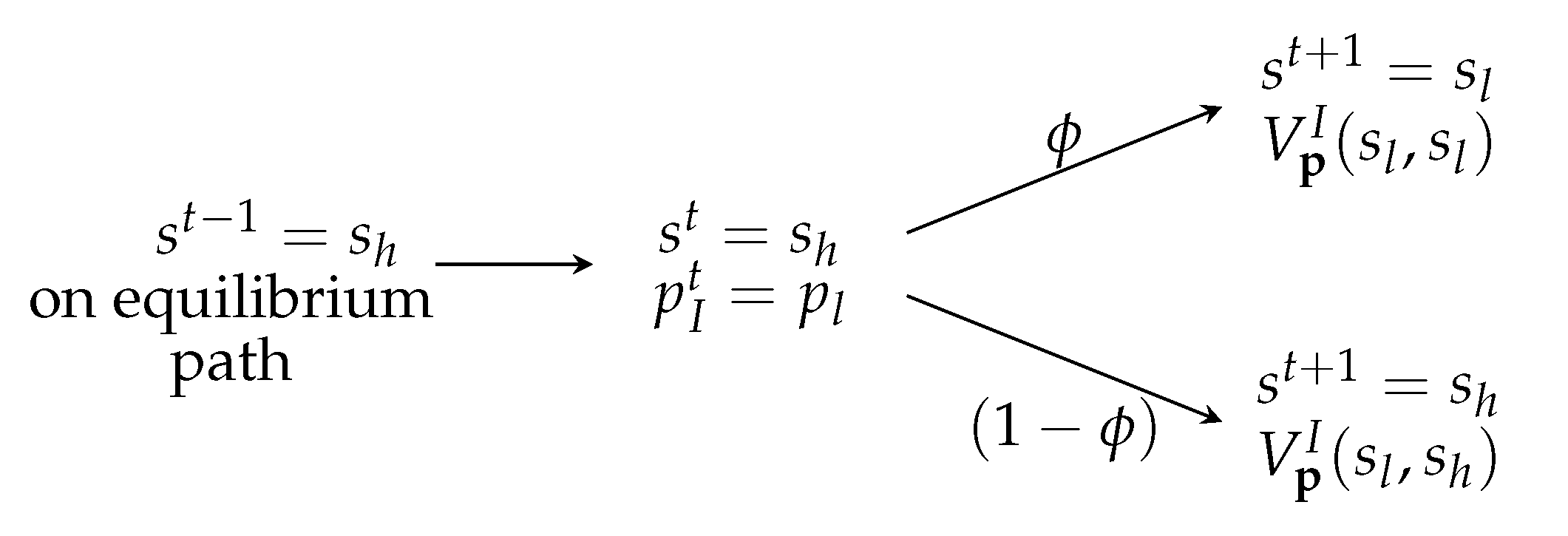
- If the informed firm’s previous price was , the uninformed is setting the price today. Furthermore, it must be the case that the market size was in the previous period so the state today is with probability and with probability . If the current state is again, both firms set a price and split the market today and the uninformed firm derives a continuation value of . On the other hand, if the current state is , the informed firm sets a price and the uninformed gets the whole market today at a price and a continuation value of . That is,
- If the informed firm’s previous price was , the expected discounted payoff for the uninformed firm is given by
- When both the previous and the current states are low, the informed firm knows that the uninformed is going to set a price equal to because the previous state (and the informed firm previous price) was low. Hence, because the state today is also , the informed firm also sets a price equal to and both firms equally split the market today. The next state is with probability in which case the continuation value of firm I is . With probability , the next state is in which case the informed gets a continuation payoff of . Then,
- When the previous state was low and the current state is high, the expected discounted payoff for the informed firm is
- When the previous state was high and the current state is low, the expected discounted payoff for the informed firm is
- When both the previous and the current states are high, the expected discounted payoff for the informed firm is
3.2. Price Leadership as an Equilibrium
3.2.1. Price Leadership Equilibrium with Monopolistic Prices
- When is low, the monopolistic price for the low state, , is low relative to and that makes the option of deviating to set less desirable.
- When is low, the demand is persistent, the market size is likely to stay high in the next period and deviating would lead to a low price by the uninformed firm.
- Exists a , such that for any , price leadership with monopolistic profits is a PBE.
- The ex-ante expected joint profits go to the monopolistic profits as ϕ goes to 0.
3.2.2. Price Leadership When Monopolistic Prices Are Not Sustainable
4. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Potentially Profitable Deviations from Price Leadership
- If the informed firm previous price was , the uninformed firm believes that the previous market size was and that the current state is with probability and with probability . Then, the uninformed firm can deviate by:
- -
- Charging a slightly lower price than . In that case, the uninformed firm gets the whole market and believes that with probability its stage payoff will be arbitrarily close to and with probability its stage payoff will be arbitrarily close to . This deviation triggers a Nash reversal. This type of deviation is not profitable if:
- -
- Charging a slightly lower price than (and above ). In that case, the uninformed firm sells only if the current state is , a scenario the uninformed firm believes to occur with probability and will lead to a stage payoff of . Again, this deviation triggers a Nash reversal and is not profitable as long as,
- Similarly, if the informed firm previous price was , the uninformed firm believes that the current state is with probability and with probability and can deviate by:
- -
- Charging a slightly lower price than . This type of deviation is not profitable as long as,
- -
- Charging a slightly lower price than . This type of deviation is not profitable if:
- When the demand goes from to : Because firms are following the price leadership profile, the informed firm previous price was implying that the uninformed firm current price is also . In this case, the only potentially profitable deviation is for the informed firm is to charge a price slightly below , a scenario in which the informed firm gets a stage payoff arbitrarily close to .This type of deviation is not profitable if:
- When the demand goes from to : The informed firm knows that the the uninformed is setting a price equal to so the only potentially profitable deviation is for the informed firm is to charge a price slightly below and get a stage payoff close to . This type of deviation is not profitable if:
- When the demand goes from to : In that case, the informed firm is obtaining the whole monopolistic profits in that period so there is no potential profitable deviation.
- When the demand goes from to : In that case, the uninformed sets a current price of because the informed previous price was . Then, there are two potential profitable deviations for the informed firm:
- -
- It can charge a price slightly below (and above ) and get a stage payoff close to . Such a deviation is not profitable as long as:
- -
- It can deviate by pretending the state is by charging a price as in Figure 1. The informed firm gets the whole market deriving a stage payoff of . The uninformed firm does not make a sale and therefore is not able to distinguish whether the market size was low or there was a deviation. Therefore, the next period the uninformed firm will set a price equal to . Furthermore, next period market size is with probability and the informed firm will face an identical problem as the case in which market size went from to . Similarly, next period market size is with probability and the informed firm will face an identical problem to the case in which the market size went from to . Consequently, if price leadership with monopolistic prices is an equilibrium, it must be the case that:
Appendix B. Proofs
| 1 | The model introduces information asymmetries into a two-firm and two-state version of Kandori [8]. |
| 2 | If the uninformed firm was unable to infer the state with certainty in any prior period, then the beliefs are derived in a similar manner from the initial distribution and the transition matrix. |
| 3 | See [1], on p. 446. |
| 4 | The described setting is a special case of Obara and Zincenko [13]. They consider a Bertrand oligopoly with complete information in which firms can have different discount factors. |
| 5 | See Section 6.7.1 in [15] for an example. |
References
- Stigler, G.J. The Kinky Oligopoly Demand Curve and Rigid Prices. J. Political Econ. 1947, 55, 432–449. [Google Scholar] [CrossRef]
- Markham, J.W. Nature and Significance of Price Leadership. Am. Econ. Rev. 1951, 41, 891–905. [Google Scholar]
- Rotemberg, J.J.; Saloner, G. Collusive Price Leadership; MIT Sloan Working Paper 2003-88; MIT Alfred P. Sloan School of Management: Cambridge, MA, USA, 1988. [Google Scholar]
- Cooper, D.J. Barometric price leadership. Int. J. Ind. Organ. 1997, 15, 301–325. [Google Scholar] [CrossRef]
- Rotemberg, J.J.; Saloner, G. Collusive Price Leadership. J. Ind. Econ. 1990, 39, 93–111. [Google Scholar] [CrossRef]
- Seaton, J.S.; Waterson, M. Identifying and characterising price leadership in British supermarkets. Int. J. Ind. Organ. 2013, 31, 392–403. [Google Scholar] [CrossRef] [Green Version]
- Escobar, J.F.; Llanes, G. Cooperation dynamics in repeated games of adverse selection. J. Econ. Theory 2018, 176, 408–443. [Google Scholar] [CrossRef]
- Kandori, M. Correlated Demand Shocks and Price Wars During Booms. Rev. Econ. Stud. 1991, 58, 171–180. [Google Scholar] [CrossRef]
- Deneckere, R.J.; Kovenock, D. Price Leadership. Rev. Econ. Stud. 1992, 59, 143–162. [Google Scholar] [CrossRef]
- Yano, M.; Komatsubara, T. Endogenous price leadership and technological differences. Int. J. Econ. Theory 2006, 2, 365–383. [Google Scholar] [CrossRef]
- Mouraviev, I.; Rey, P. Collusion and leadership. Int. J. Ind. Organ. 2011, 29, 705–717. [Google Scholar] [CrossRef]
- Yano, M.; Komatsubara, T. Price Competition or Tacit Collusion; KIER Discussion Paper 807; Kyoto University: Kyoto, Japan, 2012. [Google Scholar]
- Obara, I.; Zincenko, F. Collusion and heterogeneity of firms. RAND J. Econ. 2017, 48, 230–249. [Google Scholar] [CrossRef]
- Marshall, R.C.; Marx, L.M.; Raiff, M.E. Cartel price announcements: The vitamins industry. Int. J. Ind. Organ. 2008, 26, 762–802. [Google Scholar] [CrossRef]
- Tirole, J. The Theory of Industrial Organization; MIT Press: Cambridge, MA, USA, 1988. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gudino, G. Self-Enforcing Price Leadership. Games 2021, 12, 59. https://0-doi-org.brum.beds.ac.uk/10.3390/g12030059
Gudino G. Self-Enforcing Price Leadership. Games. 2021; 12(3):59. https://0-doi-org.brum.beds.ac.uk/10.3390/g12030059
Chicago/Turabian StyleGudino, Gustavo. 2021. "Self-Enforcing Price Leadership" Games 12, no. 3: 59. https://0-doi-org.brum.beds.ac.uk/10.3390/g12030059





