Surface Topography Measurement of Mirror-Finished Surfaces Using Fringe-Patterned Illumination
Abstract
:1. Introduction
2. Materials and Methods
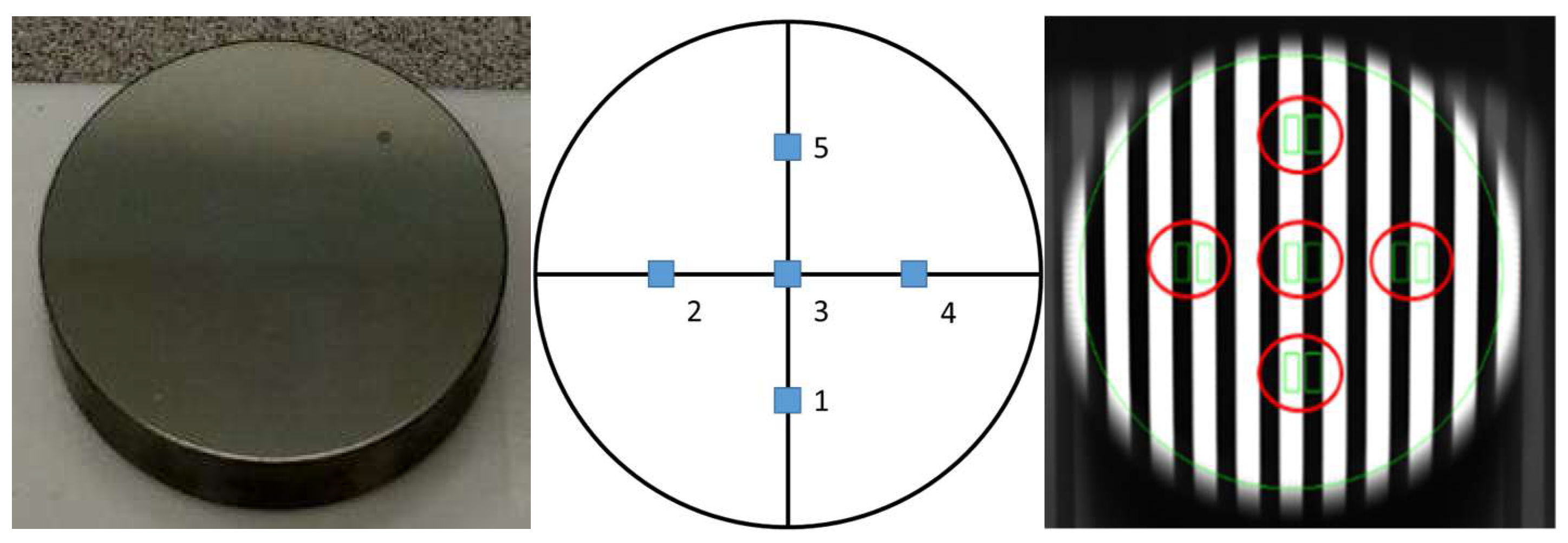
2.1. Test Coupons
2.2. Coherence Scanning Interferometer
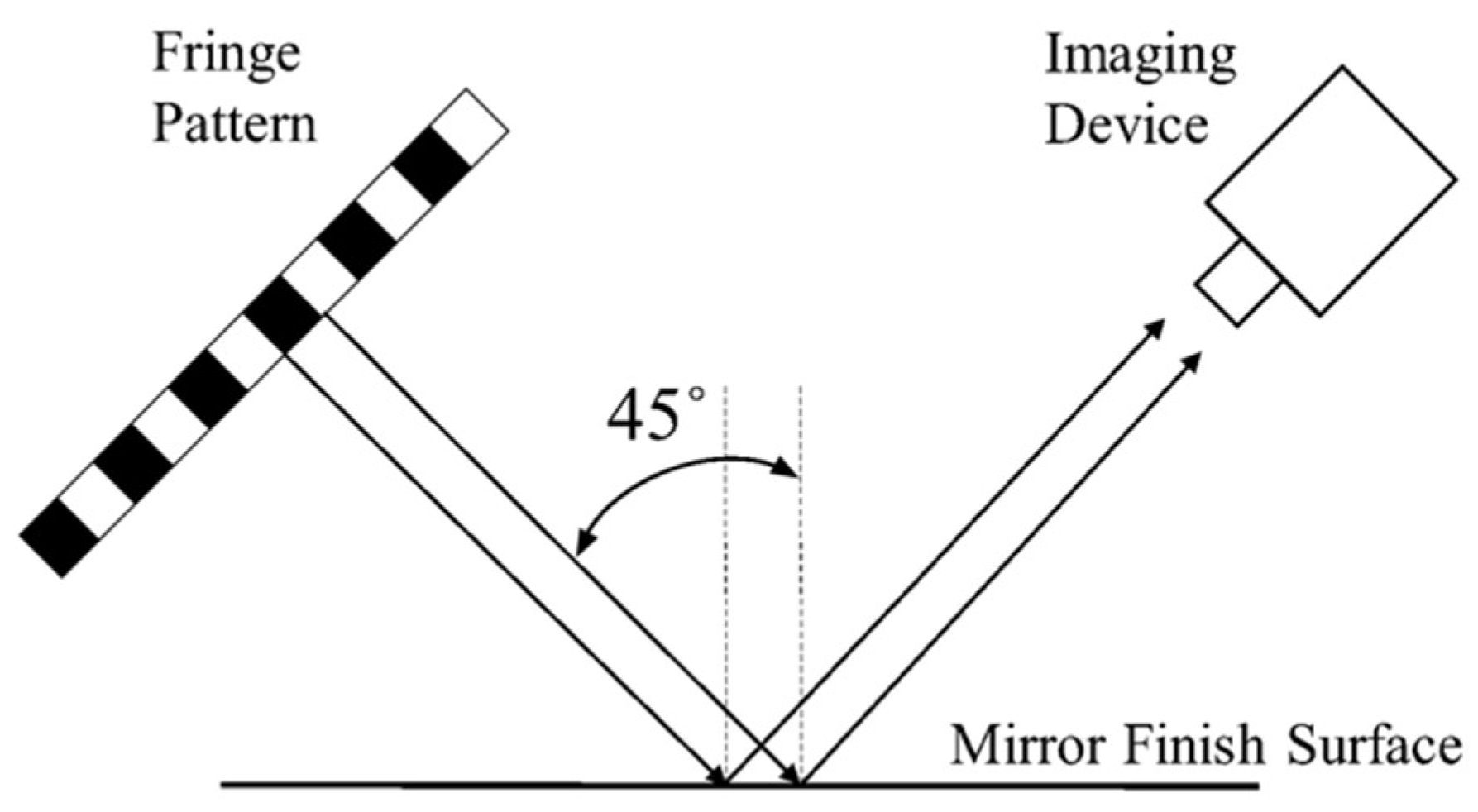
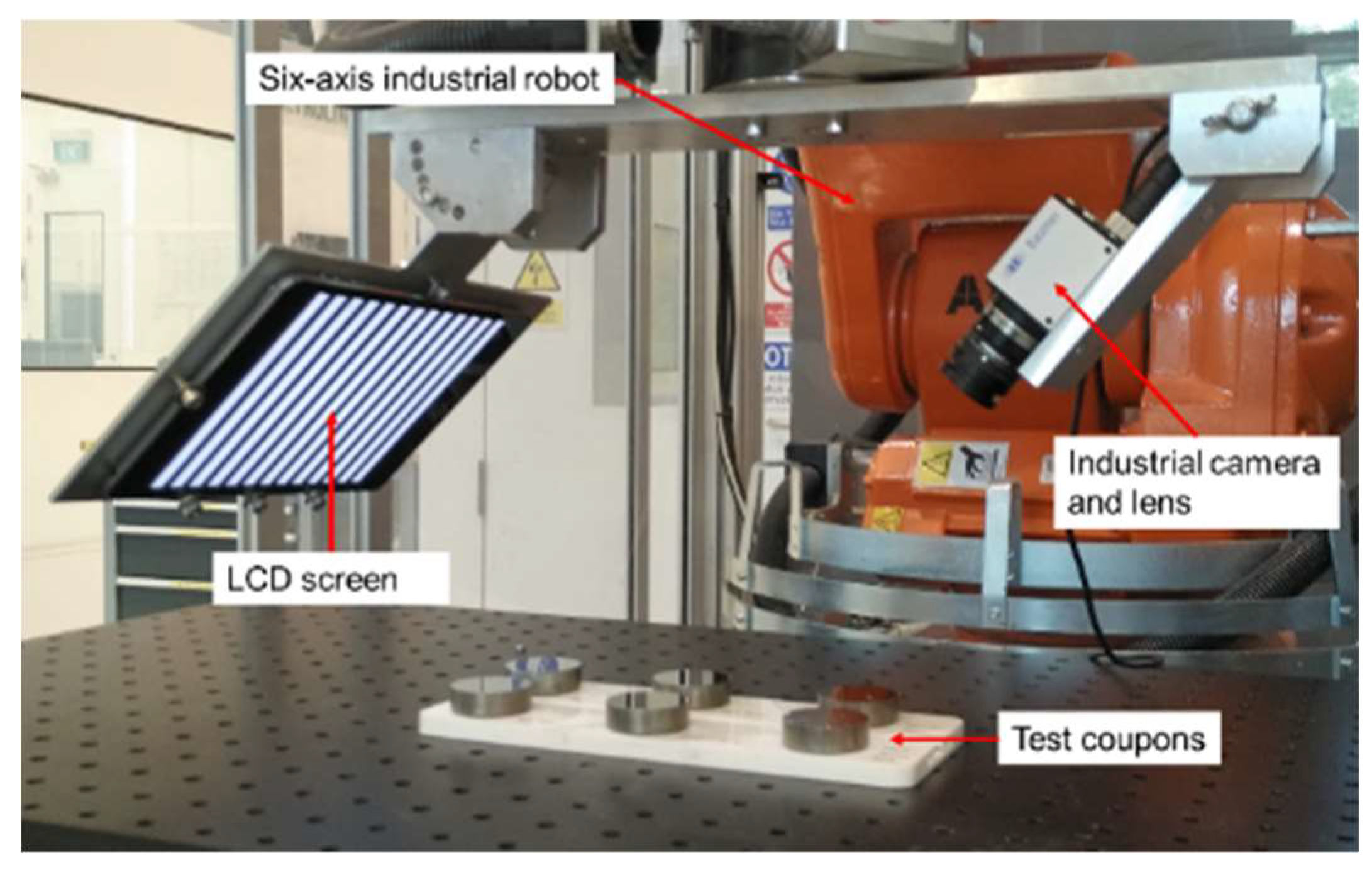
2.3. Mirror-Finished Surface Measurement System
2.3.1. Modelling and Software Development
- Create the region of interest on the acquired image.
- Extract the intensity plane of the image to get the grayscale image.
- Dilate the grayscale image to increase contrast and sharpness.
- Use a median filter to remove the background noises.
- Locate the measurement areas and calculate the average intensity of the black and white fringes.
- Calculate the contrast and surface roughness based on the proposed empirical equations.
- Display the contrast and roughness-measurement results in the inspection front window.
2.3.2. Inspection System Setup
3. Results and Discussion
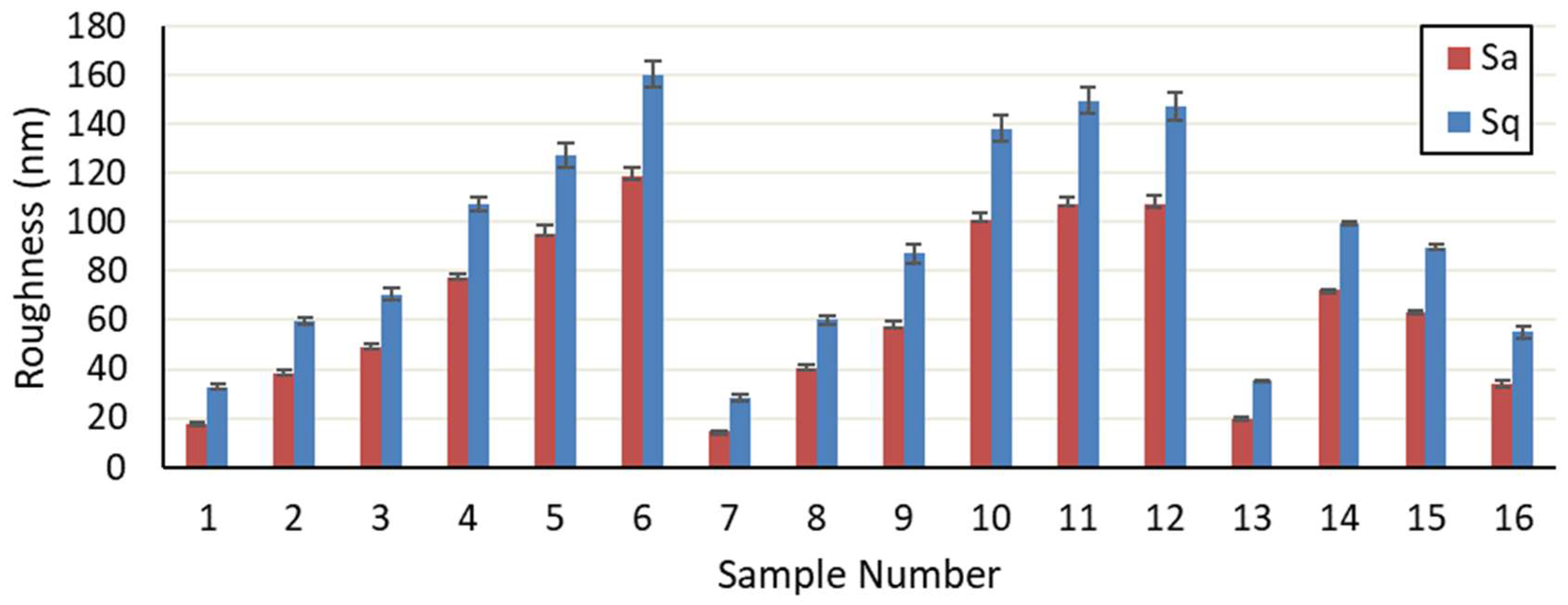
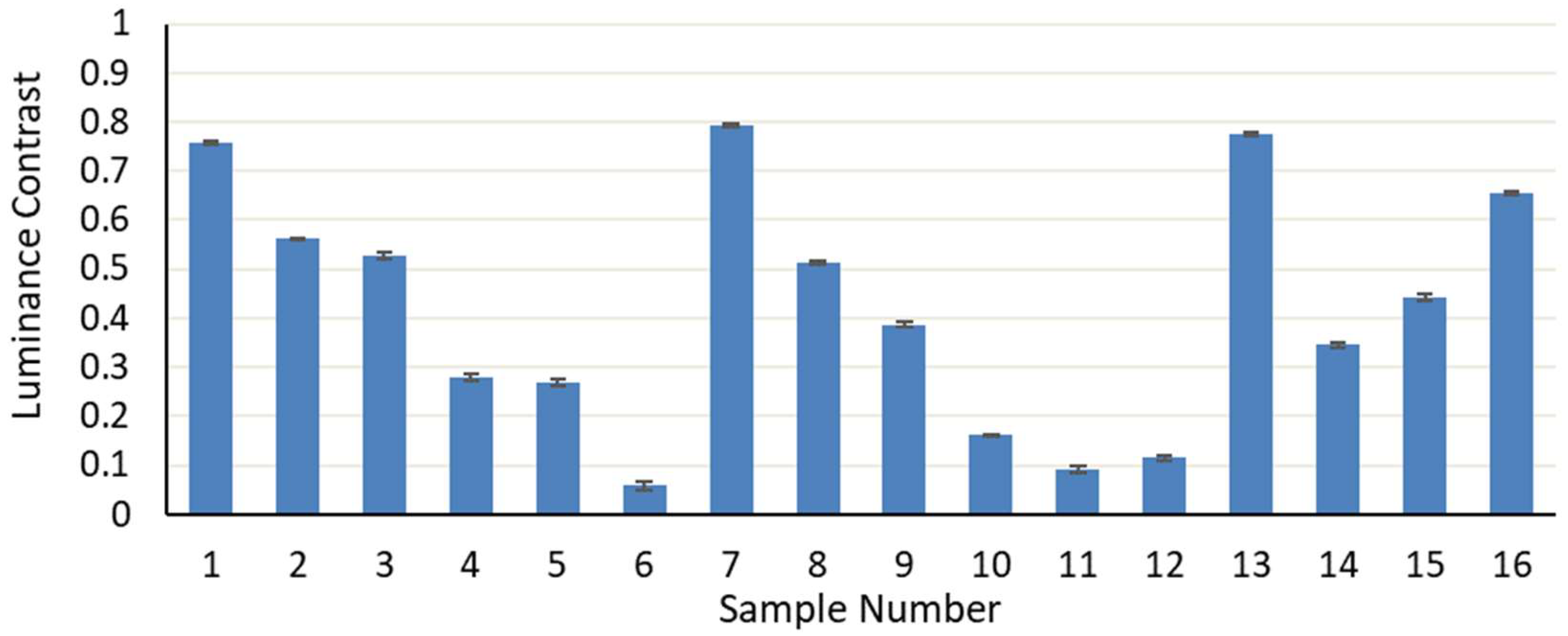
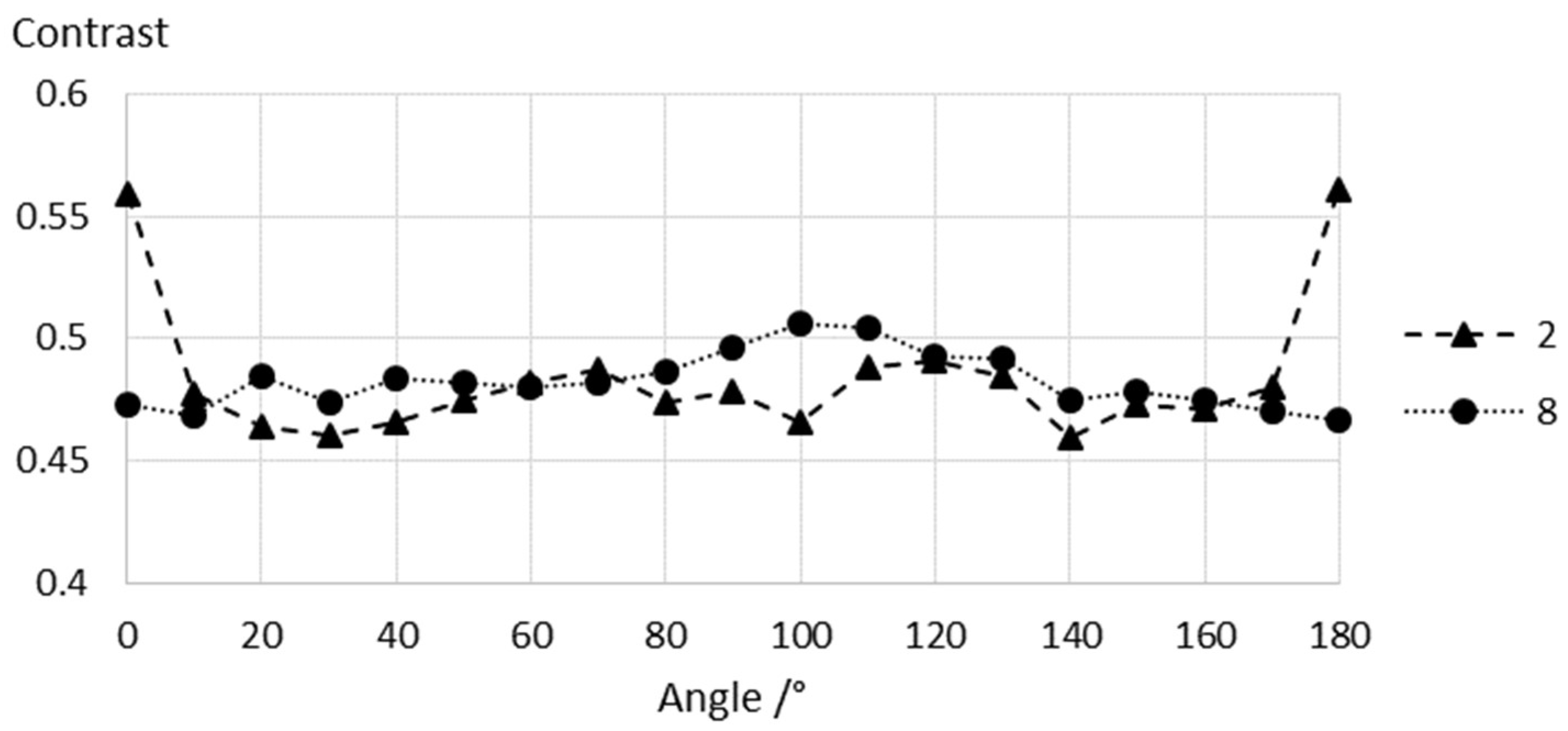
3.1. Luminance Contrast Measurement
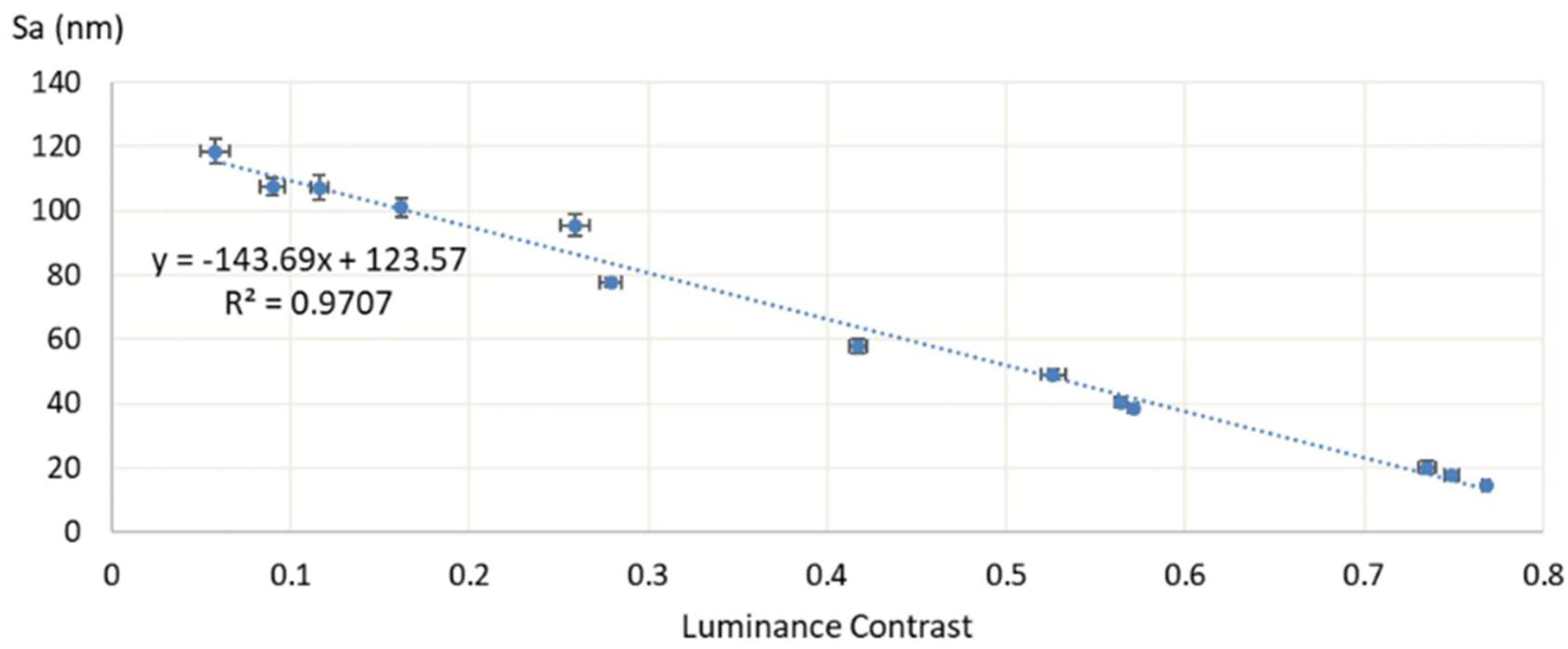
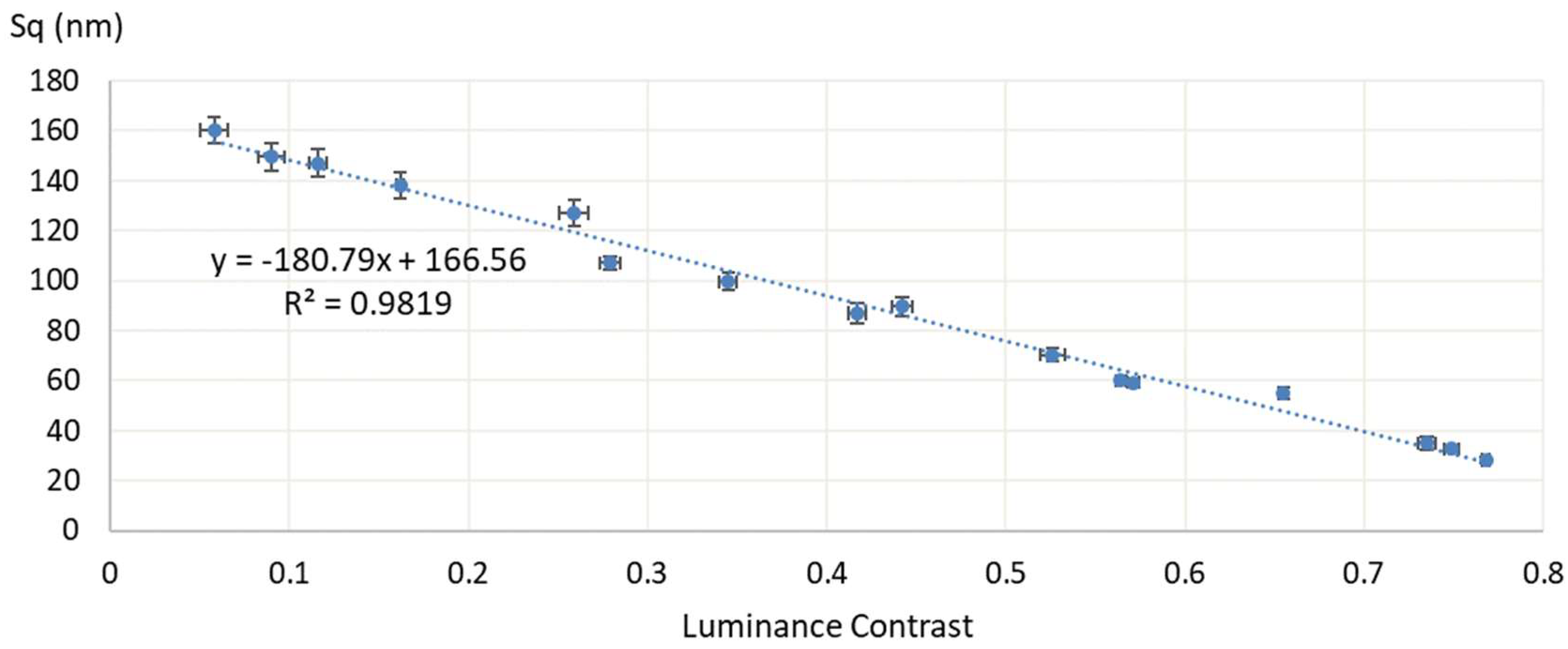
3.2. Surface Uniformity Measurement
4. Conclusions and Future Study
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- ASTM. A480/A480M 14b: Standard Specification for General Requirements for Flat-Rolled Stainless and Heat- Resisting Steel Plate, Sheet, and Strip; ASTM International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- Bogue, R. Finishing robots: A review of technologies and applications. Ind. Robot Int. J. 2009, 36, 6–12. [Google Scholar] [CrossRef]
- Brinksmeier, E.; Riemer, O.; Gessenharter, A.; Autschbach, L. Polishing of Structured Molds. CIRP Ann. Manuf. Technol. 2004, 53, 247–250. [Google Scholar] [CrossRef]
- Kanda, T.; Mitsuhashi, M.; Ueda, T.; Toyohara, A.; Yamamoto, K. New mirror-finish surface-grinding technology for the fabrication of optical device endfaces. In Proceedings of the International Conference on Optical Fabrication and Testing, Tokyo, Japan, 2 August 1995; Kasai, T., Ed.; International Society for Optics and Photonics: San Diego, CA, USA, 1995; Volume 2576, pp. 84–91. [Google Scholar]
- Ando, M.; Negishi, M.; Takimoto, M.; Deguchi, A.; Nakamura, N. Super-smooth polishing on aspherical surfaces. Nanotechnology 1995, 6, 111–120. [Google Scholar] [CrossRef]
- Tay, C.; Wang, S.; Quan, C.; Ng, B.; Chan, K. Surface roughness investigation of semi-conductor wafers. Opt. Laser Technol. 2004, 36, 535–539. [Google Scholar] [CrossRef]
- Tournier, C.; Iabassene, C.; Guiot, A.; Quinsat, Y.; Of, G. Grinding of medical implants in cobalt-chromium alloy. In Proceedings of the 1st International Conference on Design and Processes for Medical Devices, Brescia, Italy, 2–4 May 2012; pp. 95–98. [Google Scholar]
- Zantye, P.B.; Kumar, A.; Sikder, A.K. Chemical mechanical planarization for microelectronics applications. Mater. Sci. Eng. R Rep. 2004, 45, 89–220. [Google Scholar] [CrossRef]
- Pollicove, H.M.; Fess, E.M.; Schoen, J.M. Deterministic manufacturing processes for precision optical surfaces. In Proceedings of the Window and Dome Technologies VIII, Orlando, FL, USA, 21–25 April 2003; Tustison, R.W., Ed.; International Society for Optics and Photonics: San Diego, CA, USA, 2003; p. 90. [Google Scholar]
- Zhong, Z.W. Recent Advances in Polishing of Advanced Materials. Mater. Manuf. Process. 2008, 23, 449–456. [Google Scholar] [CrossRef]
- Kanaoka, M.; Takino, H.; Nomura, K.; Mori, Y.; Mimura, H.; Yamauchi, K. Removal properties of low-thermal-expansion materials with rotating-sphere elastic emission machining. Sci. Technol. Adv. Mater. 2007, 8, 170–172. [Google Scholar] [CrossRef]
- Han, X.; Gan, Y.X. Analysis the complex interaction among flexible nanoparticles and materials surface in the mechanical polishing process. Appl. Surf. Sci. 2011, 257, 3363–3373. [Google Scholar] [CrossRef]
- British Standards Institution. BS 1449-2 Steel Plate, Sheet and Strip. Specification for Stainless and Heat-Resisting Steel Plate, Sheet and Strip; British Standards Institution: London, UK, 1983. [Google Scholar]
- Golkar, E.; Prabuwono, A.; Patel, A. Real-Time Curvature Defect Detection on Outer Surfaces Using Best-Fit Polynomial Interpolation. Sensors 2012, 12, 14774–14791. [Google Scholar] [CrossRef]
- Fu, S.; Cheng, F.; Tjahjowidodo, T.; Zhou, Y.; Butler, D. A Non-Contact Measuring System for In-Situ Surface Characterization Based on Laser Confocal Microscopy. Sensors 2018, 18, 2657. [Google Scholar] [CrossRef] [Green Version]
- Xue, S.; Chen, S.; Fan, Z.; Zhai, D. Adaptive wavefront interferometry for unknown free-form surfaces. Opt. Express 2018, 26, 21910–21928. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Zhang, G. A review of interferometry for geometric measurement. Meas. Sci. Technol. 2018, 29, 102001. [Google Scholar] [CrossRef]
- El-Hayek, N.; Anwer, N.; Nouira, H.; Gibaru, O.; Damak, M.; Bourdet, P. 3D Measurement and Characterization of Ultra-precision Aspheric Surfaces. Procedia CIRP 2015, 27, 41–46. [Google Scholar] [CrossRef] [Green Version]
- Fuh, Y.K.; Wang, C.H. Adaptive Optics Integrated Surface Roughness Measurement of Sputtered PT Film on Silicon Substrate. Microw. Opt. Technol. Lett. 2013, 55, 2055–2059. [Google Scholar] [CrossRef]
- Joenathan, C.; Sirohi, R.S.; Bernal, A. Advances in Speckle Metrology. In The Optics Encyclopedia: Basic Foundations and Practical Applications; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2015; pp. 1–99. ISBN 9783527600441. [Google Scholar]
- Fuh, Y.-K.; Fan, J.R.; Huang, C.Y.; Jang, S.C. In-process surface roughness measurement of bulk metallic glass using an adaptive optics system for aberration correction. Measurement 2013, 46, 4200–4205. [Google Scholar] [CrossRef]
- Sugino, T.; Tashiro, Y.; Yamane, Y. Gloss Evaluation of Hairline-Finished Metal Surface Using Patterned Area Illumination Method: Relationship between Gloss Evaluation and Surface Roughness for the Estimation of Surface Roughness. Key Eng. Mater. 2017, 749, 251–256. [Google Scholar] [CrossRef]
- Fu, S.; Cheng, F.; Tjahjowidodo, T. Surface Texture Evaluation on Mirror Finish Surface Using Patterned Area Illumination Method. In Lecture Notes in Mechanical Engineering; Itoh, S., Shukla, S., Eds.; Springer: Singapore, 2020; pp. 155–162. [Google Scholar]
- British Standards Institution. BS EN ISO 25178-604-2013 Coherence Scanning Interferometry; British Standards Institution: London, UK, 2013. [Google Scholar]
- Vorburger, T.V.; Rhee, H.G.; Renegar, T.B.; Song, J.F.; Zheng, A. Comparison of optical and stylus methods for measurement of surface texture. Int. J. Adv. Manuf. Technol. 2007, 33, 110–118. [Google Scholar] [CrossRef]
- Lehmann, P.; Tereschenko, S.; Xie, W. Fundamental aspects of resolution and precision in vertical scanning white-light interferometry. Surf. Topogr. Metrol. Prop. 2016, 4, 024004. [Google Scholar] [CrossRef] [Green Version]
- De Groot, P. Coherence Scanning Interferometry. In Optical Measurement of Surface Topography; Springer: Berlin/Heidelberg, Germany, 2011; pp. 187–208. [Google Scholar]
- Leach, R.; Leigh Brown, X.J.; Blunt, R.; Mike Conroy, D.M. Guide for the Measurement of Smooth Surface Topography Using Coherence Scanning Interferometry; National Physical Laboratory: London, UK, 2008. [Google Scholar]
- British Standards Institution. BS EN ISO 25178-2 Terms, Definitions and Surface Texture Parameters; British Standards Institution: London, UK, 2012. [Google Scholar]
- Leach, R. Characterisation of Areal Surface Texture; Springer: Berlin, Germany, 2013; ISBN 978-3-642-36457-0. [Google Scholar]
- Pelli, D.G.; Bex, P. Measuring contrast sensitivity. Vis. Res. 2013, 90, 10–14. [Google Scholar] [CrossRef] [Green Version]
- Cowan, W.B.; MacIntyre, B. A practical approach to calculating luminance contrast on a CRT. ACM Trans. Graph. 1992, 11, 336–347. [Google Scholar]
- Kukkonen, H.; Rovamo, J.; Tiippana, K.; Näsänen, R. Michelson contrast, RMS contrast and energy of various spatial stimuli at threshold. Vis. Res. 1993, 33, 1431–1436. [Google Scholar] [CrossRef]


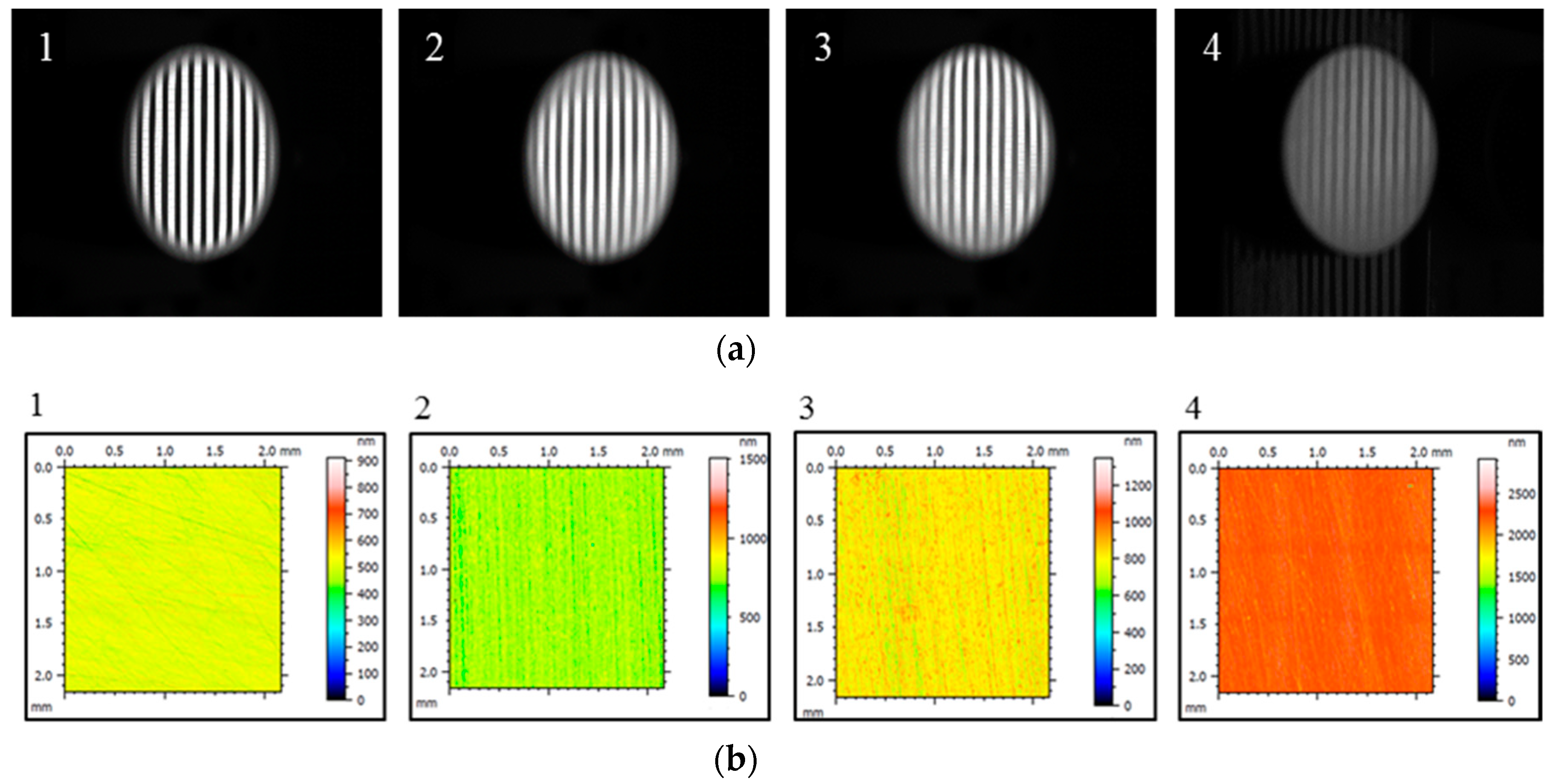


| Coupon No. | Sa (nm) | Sq (nm) | Str |
|---|---|---|---|
| Coupon 2 | 38.6 ± 1.0 | 59.4 ± 1.5 | 0.072 ± 0.006 |
| Coupon 8 | 40.4 ± 1.4 | 60.1 ± 1.8 | 0.426 ± 0.013 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, S.; Cheng, F.; Tjahjowidodo, T. Surface Topography Measurement of Mirror-Finished Surfaces Using Fringe-Patterned Illumination. Metals 2020, 10, 69. https://0-doi-org.brum.beds.ac.uk/10.3390/met10010069
Fu S, Cheng F, Tjahjowidodo T. Surface Topography Measurement of Mirror-Finished Surfaces Using Fringe-Patterned Illumination. Metals. 2020; 10(1):69. https://0-doi-org.brum.beds.ac.uk/10.3390/met10010069
Chicago/Turabian StyleFu, Shaowei, Fang Cheng, and Tegoeh Tjahjowidodo. 2020. "Surface Topography Measurement of Mirror-Finished Surfaces Using Fringe-Patterned Illumination" Metals 10, no. 1: 69. https://0-doi-org.brum.beds.ac.uk/10.3390/met10010069





