Generation and Propagation of a Hermite-Gaussian Correlated Schell-Model LG0l Beam
Abstract
:1. Introduction
2. Propagation Equation of a HGCSMLG0l Beam
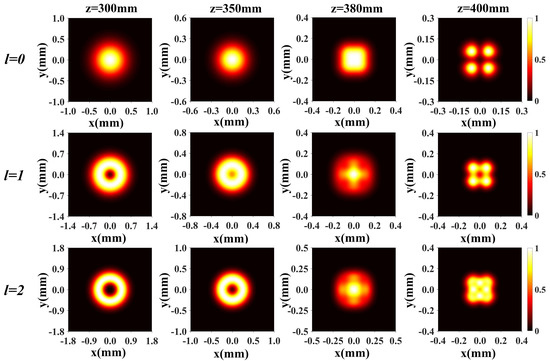
3. Theoretical Analysis the Propagation of an HGCSMLG0l Beam
4. Experimental Verification
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Soskin, M.S.; Vasnetsov, M.V. Singular optics. In Progress in Optics; Wolf, E., Ed.; Elsevier: Amsterdam, The Netherlands, 2001; Volume 42, pp. 219–276. ISBN 978-0-444-50908-6. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics; Cambridge University Press: Cambridge, UK, 1999; ISBN 978-0-521-64222-4. [Google Scholar]
- Nye, J.F.; Berry, M.V. Dislocations in wave trains. Proc. R. Soc. Lond. A 1974, 336, 1605. [Google Scholar] [CrossRef]
- Gahagan, K.T.; Swartzlander, G.A. Optical vortex trapping of particles. Opt. Lett. 1996, 21, 827–829. [Google Scholar] [CrossRef] [PubMed]
- Gibson, G.; Courtial, J.; Padgett, M.; Vasnetsov, M.; Pas’ko, V.; Barnett, S.; Franke-Arnold, S. Free-space information transfer using light beams carrying orbital angular momentum. Opt. Express 2004, 12, 5448–5456. [Google Scholar] [CrossRef] [PubMed]
- Lavery, M.P.J.; Speirits, F.C.; Barnett, S.M.; Padgett, M.J. Detection of a spinning object using light’s orbital angular momentum. Science 2013, 341, 537–540. [Google Scholar] [CrossRef] [PubMed]
- Vaziri, A.; Pan, J.W.; Jennewein, T.; Weihs, G.; Zeilinger, A. Concentration of higher dimensional entanglement: Qutrits of photon orbital angular momentum. Phys. Rev. Lett. 2003, 91, 227902. [Google Scholar] [CrossRef] [PubMed]
- Flossmann, F.; Schwarz, U.T.; Maier, M. Propagation dynamics of optical vortices in Laguerre–Gaussian beams. Opt. Commun. 2005, 250, 218–230. [Google Scholar] [CrossRef]
- Orlov, S.; Regelskis, K.; Smilgevičius, V.; Stabinis, A. Propagation of Bessel beams carrying optical vortices. Opt. Commun. 2002, 209, 155–165. [Google Scholar] [CrossRef]
- Yang, Y.; Dong, Y.; Zhao, C.; Cai, Y. Generation and propagation of an anomalous vortex beam. Opt. Lett. 2013, 38, 5418–5421. [Google Scholar] [CrossRef] [PubMed]
- Vaity, P.; Rusch, L. Perfect vortex beam: Fourier transformation of a Bessel beam. Opt. Lett. 2015, 40, 597–600. [Google Scholar] [CrossRef]
- Berkhout, G.C.G.; Beijersbergen, M.W. Method for probing the orbital angular momentum of optical vortices in electromagnetic waves from astronomical objects. Phys. Rev. Lett. 2008, 101, 100801. [Google Scholar] [CrossRef] [PubMed]
- Sztul, H.I.; Alfano, R.R. Double-slit interference with Laguerre-Gaussian beams. Opt. Lett. 2006, 31, 999–1001. [Google Scholar] [CrossRef] [PubMed]
- de Araujo, L.E.E.; Anderson, M.E. Measuring vortex charge with a triangular aperture. Opt. Lett. 2011, 36, 787–789. [Google Scholar] [CrossRef] [PubMed]
- Vinu, R.V.; Singh, R.K. Determining helicity and topological structure of coherent vortex beam from laser speckle. Appl. Phys. Lett. 2016, 109, 111108. [Google Scholar] [CrossRef]
- Prabhakar, S.; Kumar, A.; Banerji, J.; Singh, R.P. Revealing the order of a vortex through its intensity record. Opt. Lett. 2011, 36, 4398–4400. [Google Scholar] [CrossRef] [PubMed]
- Zhao, P.; Li, S.; Feng, X.; Cui, K.; Liu, F.; Zhang, W.; Huang, Y. Measuring the complex orbital angular momentum spectrum of light with a mode-matching method. Opt. Lett. 2017, 42, 1080–1083. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Chen, Y.; Yu, J.; Liu, X.; Liu, L. Generation of Partially Coherent Beams. Prog. Opt. 2017, 62, 157–223. [Google Scholar] [CrossRef]
- Wang, F.; Liu, X.; Yuan, Y.; Cai, Y. Experimental generation of partially coherent beams with different complex degrees of coherence. Opt. Lett. 2013, 38, 1814–1816. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Chen, Y.; Wang, F. Generation and propagation of partially coherent beams with nonconventional correlation functions: A review [Invited]. J. Opt. Soc. Am. A 2014, 31, 2083–2096. [Google Scholar] [CrossRef] [PubMed]
- Kato, Y.; Mima, K.; Miyanaga, N.; Arinaga, S.; Kitagawa, Y.; Nakatsuka, M.; Yamanaka, C. Random phasing of high-power lasers for uniform target acceleration and plasma-instability suppression. Phys. Rev. Lett. 1984, 53, 1057–1060. [Google Scholar] [CrossRef]
- Ricklin, J.C.; Davidson, F.M. Atmospheric turbulence effects on a partially coherent Gaussian beam: Implications for free-space laser communication. J. Opt. Soc. Am. A 2002, 19, 1794–1802. [Google Scholar] [CrossRef]
- Wang, F.; Liu, X.; Cai, Y. Propagation of partially coherent beam in turbulent atmosphere: A review (Invited review). Prog. Electromagn. Res. 2015, 150, 123–143. [Google Scholar] [CrossRef]
- Cai, Y.; Zhu, S.Y. Ghost imaging with incoherent and partially coherent light radiation. Phys. Rev. E 2005, 71, 056607. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Wang, F.; Zhang, M.; Cai, Y. Effects of atmospheric turbulence on lensless ghost imaging with partially coherent light. Appl. Sci. 2018, 8, 1479. [Google Scholar] [CrossRef]
- Zhao, C.; Cai, Y. Trapping two types of particles using a focused partially coherent elegant Laguerre-Gaussian beam. Opt. Lett. 2011, 36, 2251–2253. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Zhu, S.; Cai, Y. Experimental study of the focusing properties of a Gaussian Schell-model vortex beam. Opt. Lett. 2011, 36, 3281–3283. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Shen, Y.; Liu, L.; Wang, F.; Cai, Y. Experimental demonstration of vortex phase-induced reduction in scintillation of a partially coherent beam. Opt. Lett. 2013, 38, 5323–5326. [Google Scholar] [CrossRef]
- Wu, G.; Dai, W.; Tang, H.; Guo, H. Beam wander of random electromagnetic Gaussian-shell model vortex beams propagating through a Kolmogorov turbulence. Opt. Commun. 2015, 336, 55–58. [Google Scholar] [CrossRef]
- Li, J.; Lü, B. Propagation of Gaussian Schell-model vortex beams through atmospheric turbulence and evolution of coherent vortices. J. Opt. A 2009, 11, 045710. [Google Scholar] [CrossRef]
- Liu, X.; Peng, X.; Liu, L.; Wu, G.; Zhao, C.; Wang, F.; Cai, Y. Self-reconstruction of the degree of coherence of a partially coherent vortex beam obstructed by an opaque obstacle. Appl. Phys. Lett. 2017, 110, 181104. [Google Scholar] [CrossRef]
- Liang, C.; Wang, F.; Liu, X.; Cai, Y.; Korotkova, O. Experimental generation of cosine Gaussian correlated Schell-model beams with rectangular symmetry. Opt. Lett. 2014, 39, 769–772. [Google Scholar] [CrossRef]
- Chen, Y.; Cai, Y. Generation of a controllable optical cage by focusing a Laguerre–Gaussian correlated Schell-model beam. Opt. Lett. 2014, 39, 2549–2552. [Google Scholar] [CrossRef] [PubMed]
- Lajunen, H.; Saastamoinen, T. Propagation characteristics of partially coherent beams with spatially varying correlations. Opt. Lett. 2011, 36, 4104–4106. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Cai, Y.; Gbur, G. Rectangular Hermite non-uniformly correlated beams and its propagation properties. Opt. Express 2018, 26, 27894–27906. [Google Scholar] [CrossRef] [PubMed]
- Liang, C.; Zhu, X.; Mi, C.; Peng, X.; Wang, F.; Cai, Y.; Ponomarenko, S.A. High-quality partially coherent Bessel beam array generation. Opt. Lett. 2018, 43, 3188–3191. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Gu, J.; Wang, F.; Cai, Y. Self-splitting properties of a Hermite-Gaussian correlated Schell-model beam. Phys. Rev. A 2015, 91, 013823. [Google Scholar] [CrossRef]
- Ma, L.; Ponomarenko, S.A. Free-space propagation of optical coherence lattices and periodicity reciprocity. Opt. Express 2015, 23, 1848–1856. [Google Scholar] [CrossRef]
- Liu, X.; Liu, L.; Wang, F.; Cai, Y. Generation of a flexible far-field anomalous hollow beam spot through superposition of two partially coherent sources with different degrees of coherence. Opt. Commun. 2018, 428, 69–76. [Google Scholar] [CrossRef]
- Gori, F.; Santarsiero, M. Devising genuine spatial correlation functions. Opt. Lett. 2007, 32, 3531–3533. [Google Scholar] [CrossRef]
- Gori, F.; Sanchez, V.R.; Santarsiero, M.; Shirai, T. On genuine cross-spectral density matrices. J. Opt. A Pure Appl. Opt. 2009, 11, 085706. [Google Scholar] [CrossRef]
- Yuan, Y.; Liu, X.; Wang, F.; Chen, Y.; Cai, Y.; Qu, J.; Eyyuboglu, H.T. Scintillation index of a multi-Gaussian Schell-model beam in turbulent atmosphere. Opt. Commun. 2013, 305, 57–65. [Google Scholar] [CrossRef]
- Gu, Y.; Gbur, G. Scintillation of nonuniformly correlated beams in atmospheric turbulence. Opt. Lett. 2013, 38, 1395–1397. [Google Scholar] [CrossRef] [PubMed]
- Liang, C.; Wu, G.; Wang, F.; Li, W.; Cai, Y.; Ponomarenko, S.A. Overcoming the classical Rayleigh diffraction limit by controlling two-point correlations of partially coherent light sources. Opt. Express 2017, 25, 28352–28362. [Google Scholar] [CrossRef]
- Wang, F.; Cai, Y.; Korotkova, O. Partially coherent standard and elegant Laguerre-Gaussian beams of all orders. Opt. Express 2009, 17, 22366–22379. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Wang, F.; Dong, Y.; Han, Y.; Cai, Y. Effect of spatial coherence on determining the topological charge of a vortex beam. Appl. Phys. Lett. 2012, 101, 261104. [Google Scholar] [CrossRef]
- Shao, Y.; Lu, X.; Konijnenberg, S.; Zhao, C.; Cai, Y.; Urbach, H.P. Spatial coherence measurement and partially coherent diffractive imaging using self-referencing holography. Opt. Express 2018, 26, 4479–4490. [Google Scholar] [CrossRef] [PubMed] [Green Version]













© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, X.; Lu, X.; Liu, X.; Zhao, C.; Lin, R.; Liu, L.; Cai, Y. Generation and Propagation of a Hermite-Gaussian Correlated Schell-Model LG0l Beam. Appl. Sci. 2019, 9, 610. https://0-doi-org.brum.beds.ac.uk/10.3390/app9030610
Peng X, Lu X, Liu X, Zhao C, Lin R, Liu L, Cai Y. Generation and Propagation of a Hermite-Gaussian Correlated Schell-Model LG0l Beam. Applied Sciences. 2019; 9(3):610. https://0-doi-org.brum.beds.ac.uk/10.3390/app9030610
Chicago/Turabian StylePeng, Xiaofeng, Xingyuan Lu, Xianlong Liu, Chenliang Zhao, Rong Lin, Lin Liu, and Yangjian Cai. 2019. "Generation and Propagation of a Hermite-Gaussian Correlated Schell-Model LG0l Beam" Applied Sciences 9, no. 3: 610. https://0-doi-org.brum.beds.ac.uk/10.3390/app9030610