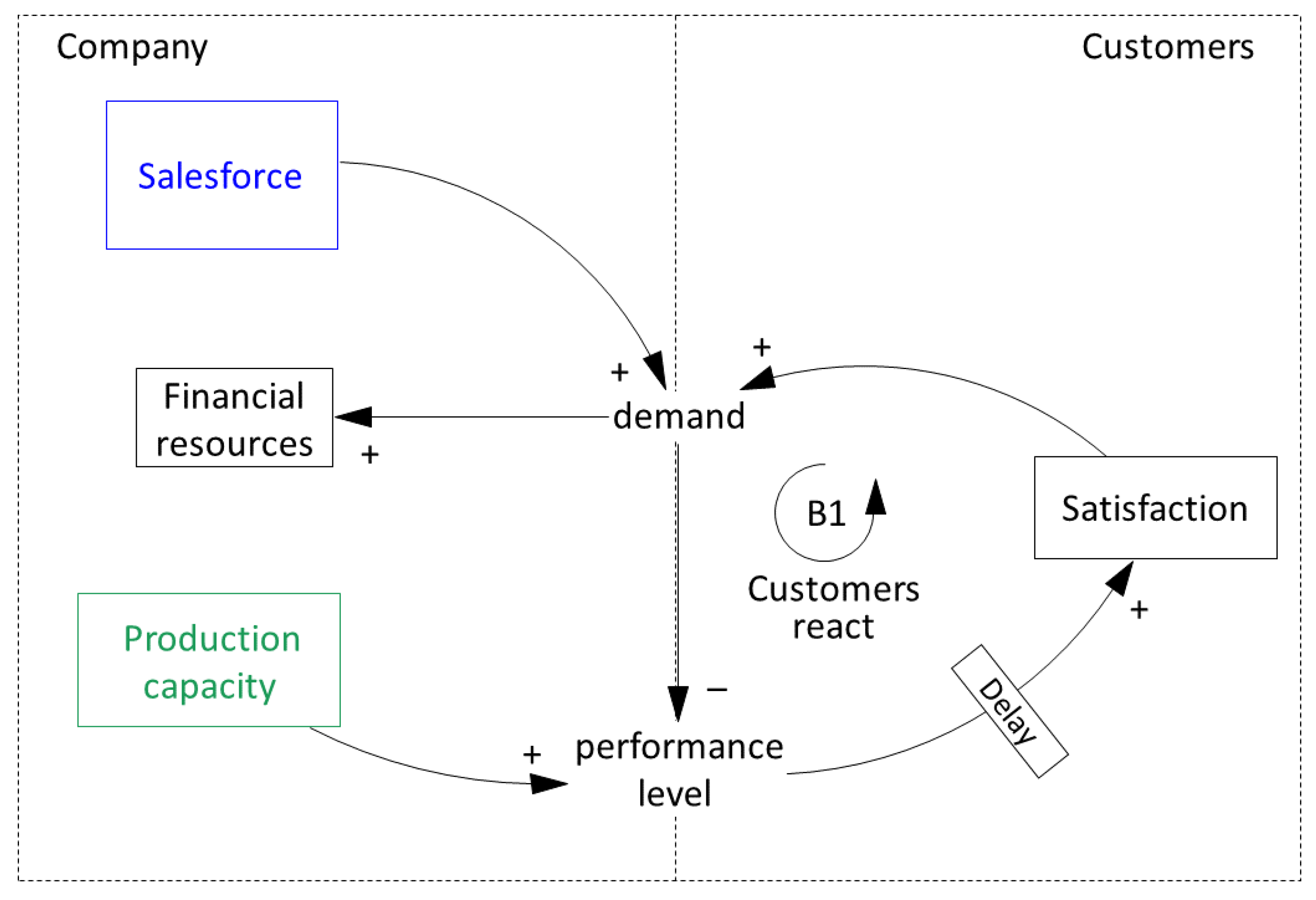
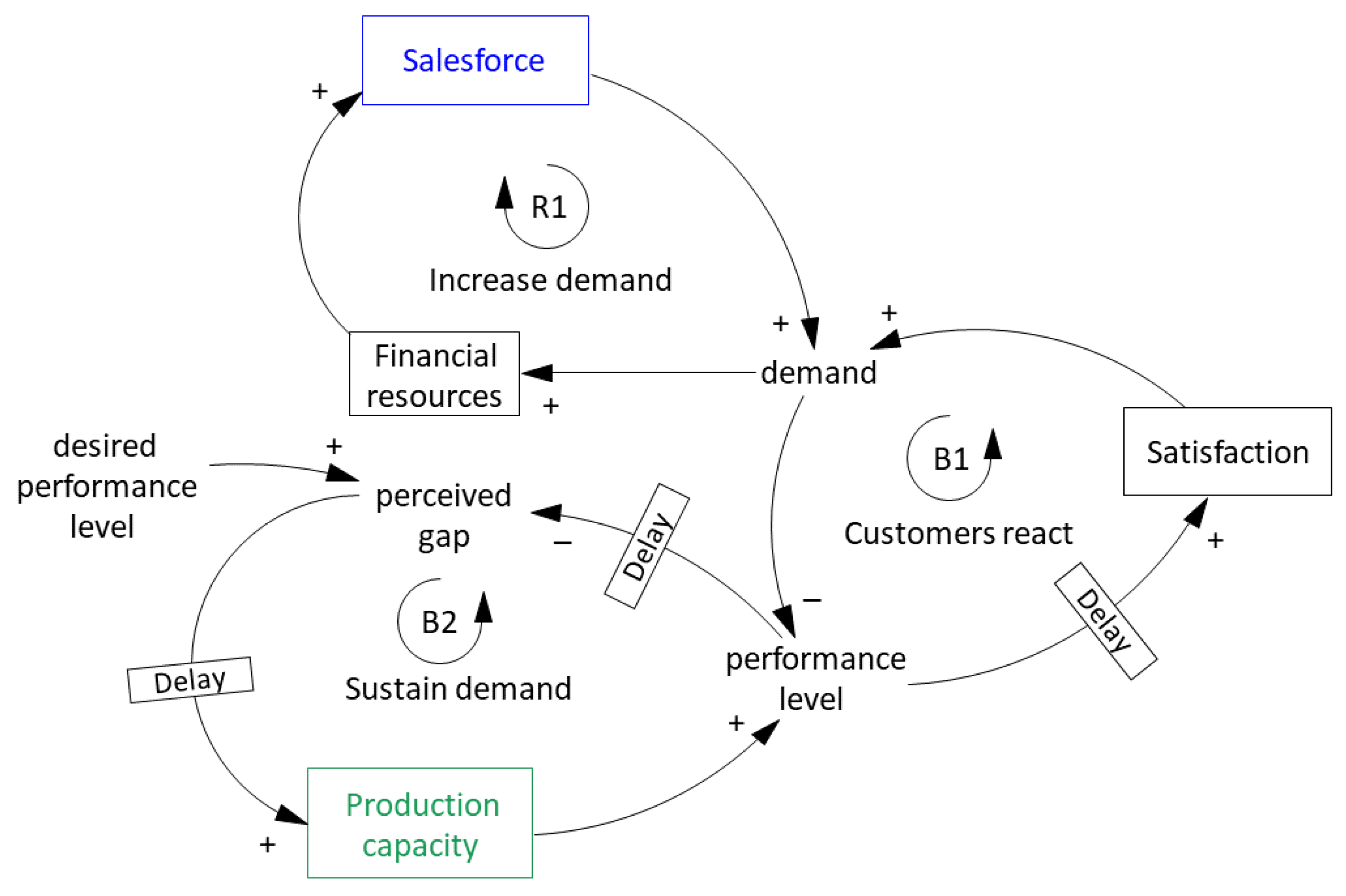
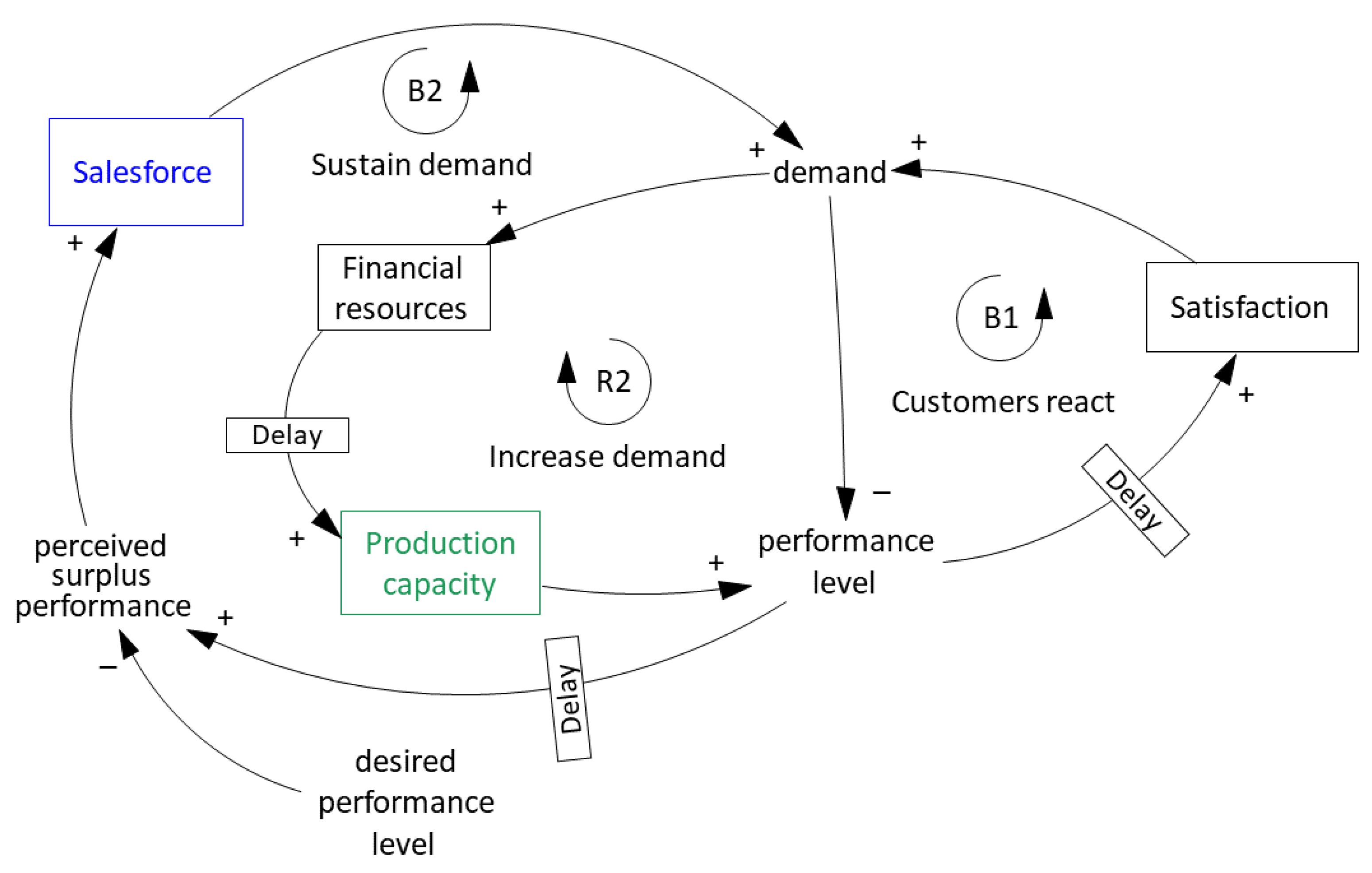
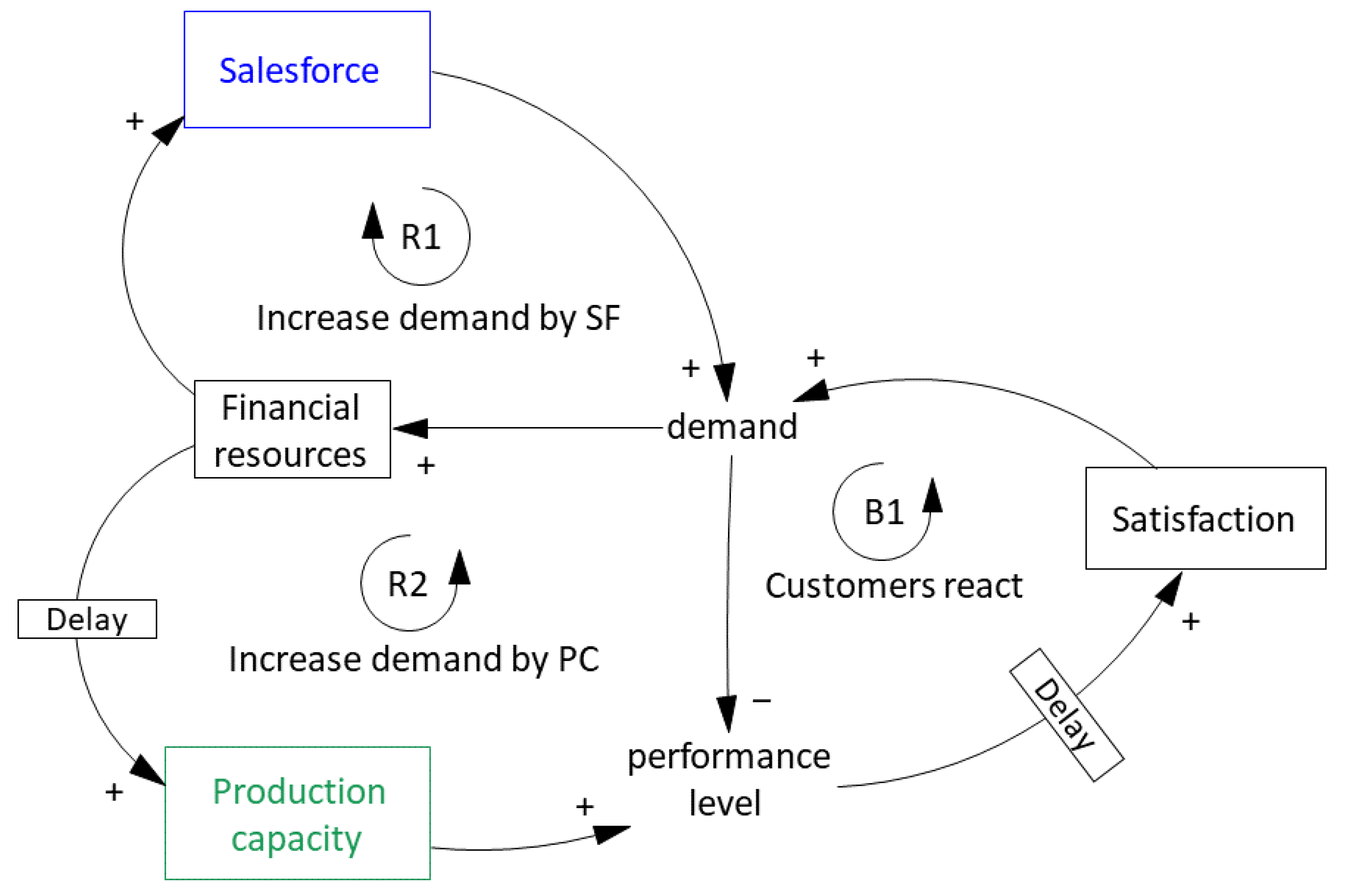
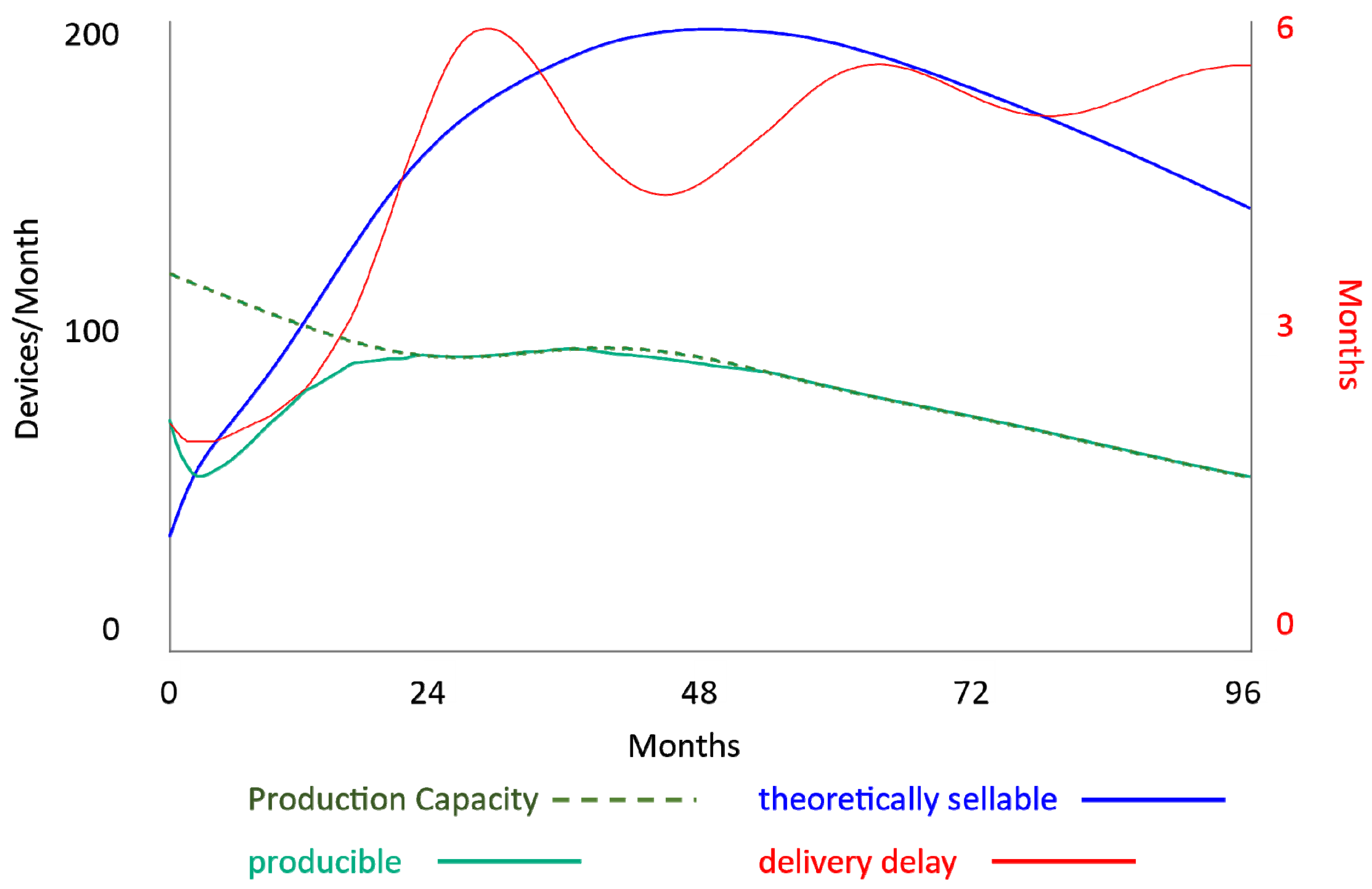
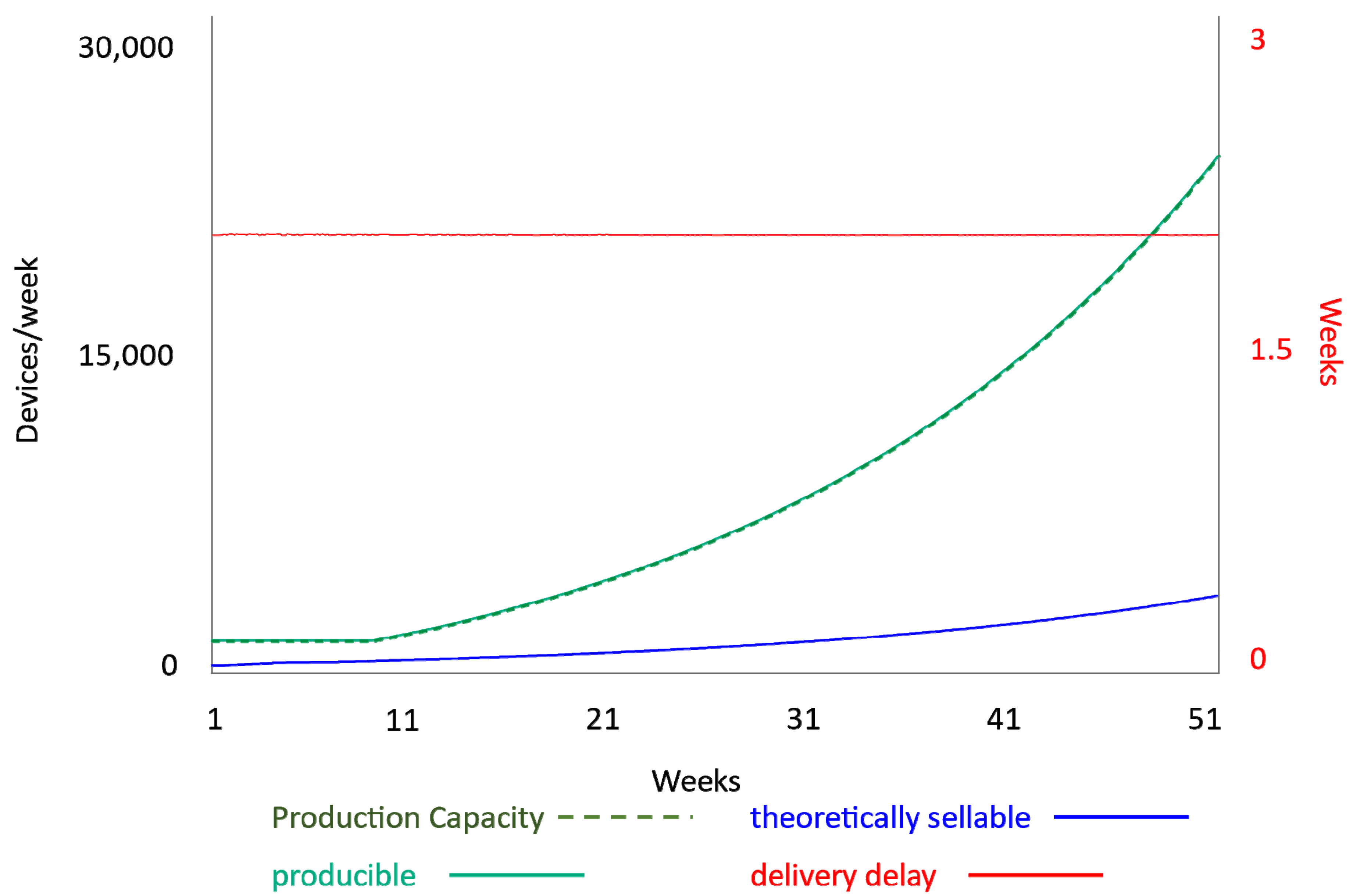
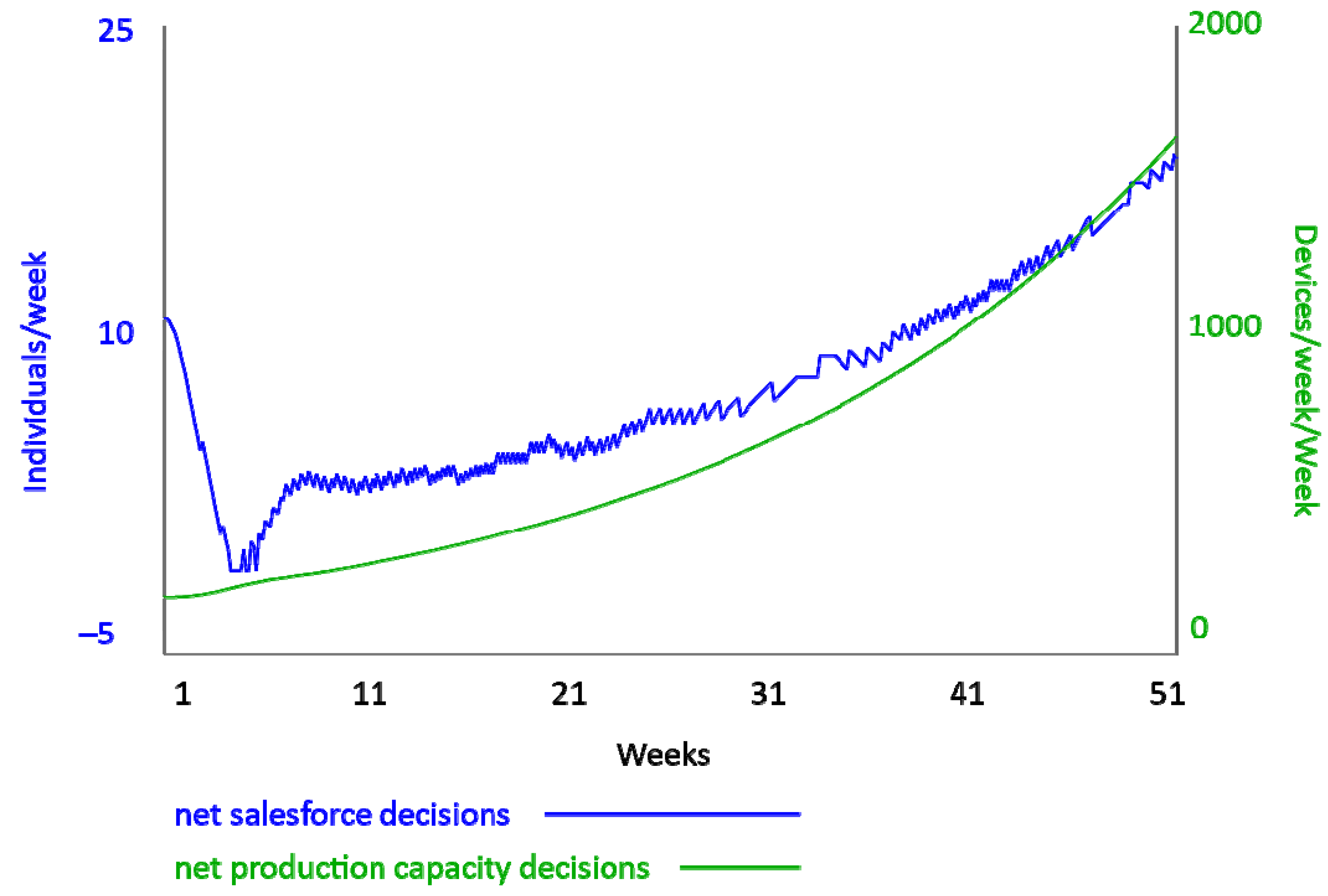
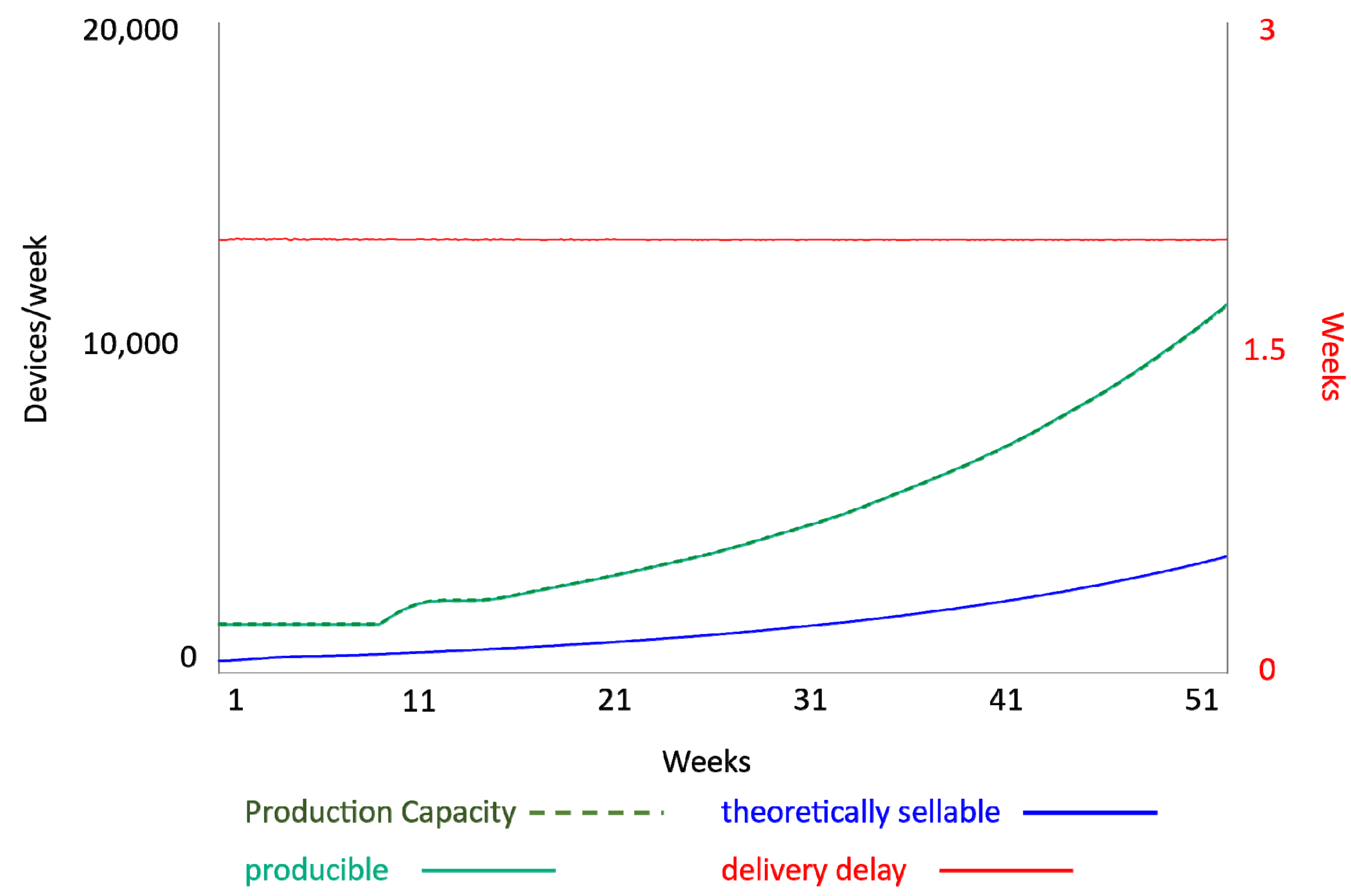
Appendix C.1.2. Production Capacity
Capacity_in_preparation(t) = Capacity_in_preparation(t − dt) + (additional_production_capacity − going_into_service) * dt.
INIT Capacity_in_preparation = 0.
UNITS: Device/Weeks.
DEF: Capacity units being prepared currently.
USED BY: Production_Capacity_considered.
INFLOW: additional_production_capacity = additional_production_capacity_Participant * (autopilot_switch = 0) + capacity_adjustment_by_P1 * (autopilot_switch * Policy = 1) + capacity_adjustment_by_P2 * (autopilot_switch * Policy = 2) + capacity_adjustment_by_P3 * (autopilot_switch * Policy = 3).
UNITS: Device/Weeks/Weeks.
DEF: Additional Capacity units whose preparation is decided per week. If autopilot is off, then the box/slider put a fraction of the investment indicated by effort. If the autopilot is on, then the Policy controls the decision: (1) P1 and P2: investment indicated by effort; (3): P3, additional production capacity P3.
USED BY: going_into_service, Accounting, net_production_capacity_decisions, Accounting.investment_costs, Capacity_in_preparation.
OUTFLOW: going_into_service = DELAY(additional_production_capacity; capacity_installment_delay; 0).
UNITS: Device/Weeks/Weeks.
DEF: Capacity units going on-line per week.
USED BY: Capacity_in_preparation, Production_Capacity.
Production_Capacity(t) = Production_Capacity(t − dt) + (going_into_service − capacity_sold_off) * dt.
INIT Production_Capacity = PC_init.
UNITS: Device/Weeks.
DEF: Weekly number of watches that can be produced at full capacity utilization
USED BY: producible, Potentials, Production_Capacity_considered, Accounting, CUF_indicated, delivery_delay_min, Potentials.PPC_5, Potentials.PPC_6, Potentials.PPC_7, Potentials.PPC_10, Potentials.PPC_12, Potentials.PPC_14, Potentials.PPC_15, Potentials.PPC_18, Potentials.PPC_21, Accounting.capacity_maintenance_costs.
INFLOW: going_into_service = DELAY (additional_production_capacity; capacity_installment_delay; 0).
UNITS: Device/Weeks/Weeks.
DEF: Capacity units going on-line per week.
USED BY: Capacity_in_preparation, Production_Capacity.
OUTFLOW: capacity_sold_off = −disinvestment.
UNITS: Device/Weeks/Weeks.
DEF: Capacity units sold off per week.
USED BY: net_production_capacity_decisions, Production_Capacity.
Appendix C.1.4. Intermediate Variables
Additional_production_capacity_Participant = IF (Capacity_adjustment_box = 0) THEN (investment_indicated_by_effort * Capacity_adjustment_slider) ELSE (investment_indicated_by_effort * Capacity_adjustment_box)
UNITS: Device/Weeks/Weeks.
DEF: Additional production capacity according to a player.
USED BY: additional_production_capacity.
Additional_salesforce_for_excess_producibility = theoretic_excess_productibility/(0.9 * salesman_productivity_max)
UNITS: Individual.
DEF: Number of additional salespeople that would be needed to sell those watches that can be produced but not sold by the current workforce.
USED BY: recruitment_by_policy, Salesforce_fractional_effort_from_Capacity
additional_SF_monthly_salary_costs = payable_additional_salesforce * salesperson_monthly_salary.
UNITS: Euros/Month.
DEF: Money implied by salaries of the additional salespeople.
autopilot_switch = 1.
UNITS: unitless.
DEF: if set to 1, the model policies regulate the decisins; if set to 0, users take the decisions.
USED BY: deliveries_limit, additional_production_capacity, to_recruit
capacity_adjustment_indicated_by_effort = Capacity_indicated_by_effort-Production_Capacity_considered.
UNITS: Device/Weeks.
DEF: Theoretically indicated additional production capacity units according to the “stress” reasoning. This is the stock’s value, so it cannot directly be used in a flow.
USED BY: investment_indicated_by_effort, disinvestment_indicated_by_effort
Capacity_fractional_effort = (desirable_deliveries/theoretically_productible)/2.
UNITS: unitless.
USED BY: Capacity_indicated_by_effort.
Capacity_adjustment_box = 1.
UNITS: unitless.
DEF: Value of the edit box in the user interface.
USED BY: additional_production_capacity_Participant, disinvestment
Capacity_adjustment_slider = 0.
UNITS: unitless.
DEF: Value of the slider in the user interface.
USED BY: additional_production_capacity_Participant, disinvestment.
Capacity_indicated_by_effort = Production_Capacity_considered * (proactiveness + Capacity_fractional_effort).
UNITS: Device/Weeks.
USED BY: capacity_adjustment_indicated_by_effort.
capacity_installment_delay = 8
UNITS: Weeks.
USED BY: going_into_service.
Capacity_Utilization_Fraction = Shifts_per_week/Shifts_per_week_max.
UNITS: unitless.
USED BY: producible, theoretically_productible.
Days_per_week = 7.
UNITS: days/week.
USED BY: Shifts_per_week.
delay_perceived = 1.
UNITS: unitless.
DEF: Allows to simulate according to if the decision-maker takes the capacity installment delay into account (=1, default) or not (=0: like in the literature).
USED BY: Production_Capacity_considered.
delay_perception_time = 6.
UNITS: Weeks.
USED BY: delivery_delay_perceived.
deliveries_limit = INT (deliveries_max/(1 + autopilot_switch))
UNITS: Device/Weeks.
USED BY: deliveries.
delivery_delay_perceived = SMTH1 (delivery_delay_real; delay_perception_time; delivery_delay_real).
UNITS: Weeks.
DEF: The clients’ expectation regarding the delivery delay, which adjusts progressively to the actual delivery delay.
USED BY: effect_of_delivery_delay_on_demand.
delivery_delay_real = SAFEDIV(Backlog; deliveries).
UNITS: Weeks.
DEF: Actual number of weeks it takes between order and delivery.
USED BY: delivery_delay_perceived, reported_delivery_delay disinvestment = IF (Capacity_adjustment_box = 0) THEN (disinvestment_indicated_by_effort * Capacity_adjustment_slider) ELSE (disinvestment_indicated_by_effort * Capacity_adjustment_box).
UNITS: Device/Weeks/Weeks.
USED BY: capacity_sold_off.
Disinvestment_indicated_by_effort = MIN(0; capacity_adjustment_indicated_by_effort)/time_unit.
UNITS: Device/Weeks/Weeks.
DEF: Theoretically indicated excess production capacity units according to the “stress” reasoning. Adjusted to time units to fit as flow variable.
USED BY: disinvestment.
effect_of_delivery_delay_on_demand = GRAPH(delivery_delay_perceived).
| Input | Output |
| 0 | 1.000 |
| 1 | 0.970 |
| 2 | 0.900 |
| 3 | 0.730 |
| 4 | 0.530 |
| 5 | 0.380 |
| 6 | 0.250 |
| 7 | 0.150 |
| 8 | 0.080 |
| 9 | 0.030 |
| 10 | 0.020 |
UNITS: unitless.
DEF: Effect of the expectation regarding the delivery delay on the willingness to buy.
USED BY: orders.
expected_sales_revenues = SMTH1(sales_revenues; revenue_averaging_time; sales_revenues).
UNITS: Euros/Weeks.
DEF: The expected sales revenues are a moving average of the past weeks.
USED BY: payable_salesforce, budget_for_salesforce_costs.
firing_delay = 1.
UNITS: Weeks.
DEF: Time it takes to implement layoff decisions.
USED BY: laid_off.
hiring_delay = 1 + relative_SF_gap * (hiring_delay_max-hiring_delay_min)
UNITS: Weeks.
DEF: Time it takes to find and recruit the number of additional salespeople sought for. Depends on the relationship of the number of searched salespeople to the current salesforce.
USED BY: recruited.
hiring_delay_max = 4.
UNITS: Weeks.
DEF: Longest possible time to find and recruit additional salespeople.
USED BY: hiring_delay.
hiring_delay_min = 1.
UNITS: Weeks.
DEF: Shortest possible time to find and recruit additional salespeople.
USED BY: hiring_delay.
Investment_indicated_by_effort = MAX(capacity_adjustment_indicated_by_effort; 0)/time_unit.
UNITS: Device/Weeks/Weeks.
DEF: Theoretically indicated additional production capacity units according to the “stress” reasoning. Adjusted to time units to fit as flow variable.
USED BY: additional_production_capacity_Participant, capacity_adjustment_by_P1, capacity_adjustment_by_P2, additional_capacity_investment_costs.
Sales_force_box = 1.
UNITS: unitless.
DEF: Value of the edit box in the user interface.
USED BY: now_hiring_C, now_firing_C.
Sales_force_slider = 0
UNITS: unitless.
DEF: Value of the slider in the user interface.
USED BY: now_hiring_E, now_firing_E.
recruitment_by_policy = IF(Policy = 2) THEN(additional_salesforce_for_excess_producibility) ELSE(payable_additional_salesforce).
UNITS: Individual.
DEF: Weekly number of salespeople to be searched and recruited according to one pf the policies implemented in the model. If it is policy P2, then hiring is driven by the additional salesforce for excess producibility, otherwise it is driven by payable additional salesforce.
USED BY: to_recruit.
Now_firing = IF(now_firing_C=0) THEN(now_firing_E) ELSE(now_firing_C)
UNITS: Individual.
USED BY: laid_off.
Now_firing_C = INT(Sales_force_box * MIN(0; payable_additional_salesforce)).
UNITS: Individual.
USED BY: now_firing.
Now_firing_E = INT(Sales_force_slider * MIN(0; payable_additional_salesforce)).
UNITS: Individual.
USED BY: now_firing.
Now_hiring = IF(now_hiring_C = 0) THEN(now_hiring_E) ELSE(now_hiring_C).
UNITS: Individual.
DEF: Weekly number of salespeople to be searched and recruited according to a player.
USED BY: to_recruit.
Now_hiring_C = INT(Sales_force_box * MAX(payable_additional_salesforce; 0))
UNITS: Individual.
DEF: Weekly number of salespeople to be searched and recruited according to a player if the user interface has an edit box as control.
USED BY: now_hiring.
Now_hiring_E = INT(Sales_force_slider * MAX(payable_additional_salesforce; 0))
UNITS: Individual.
DEF: Weekly number of salespeople to be searched and recruited according to a player if the user interface has a slider as control.
USED BY: now_hiring.
Payable_additional_salesforce = payable_salesforce-Sales_Force.
UNITS: Individual.
DEF: Number of additional salespeoplpe which can be paid, accounting for the currently searched salespeople (to avoid oscillations).
USED BY: recruitment_by_policy, now_hiring_E, now_hiring_C, now_firing_C, now_firing_E, additional_SF_monthly_salary_costs, sales_force_growth_rate, Salesforce_fractional_effort_from_budget.
payable_salesforce = INT((revenue_fraction_for_salesforce_salaries * expected_sales_revenues)/(salesperson_monthly_salary/weeks_per_month))
UNITS: Individual.
DEF: Payable number pf salespeople according to the salaries and the expected sales revenues, assuming a stable fraction.
USED BY: payable_additional_salesforce, Potentials, Potentials.payable_sales
PC_init = 1512.
UNITS: Device/Weeks.
DEF: 1512.
proactiveness = 1.
UNITS: unitless.
DEF: Used to determine capacity indicated by effort, which can be in a reactive mode to replicate results from Forrester and from Morecroft, or in a proactive mode to drive, for instance, the weightlifter.
USED BY: Capacity_indicated_by_effort.
producible = INT(Capacity_Utilization_Fraction * Production_Capacity).
UNITS: Device/Weeks.
USED BY: deliveries.
Production_Capacity_considered = delay_perceived * Capacity_in_preparation+Production_Capacity.
UNITS: Device/Weeks.
USED BY: theoretically_productible, Capacity_indicated_by_effort, capacity_adjustment_indicated_by_effort, capacity_adjustment_by_P3, Capacity_indicated_by_delay_gap, capacity_adjustment_indicated_by_delay_gap.
relative_SF_gap = Searching/Sales_Force.
UNITS: unitless.
DEF: The relationship of the number of searched salespeople to the current salesforce.
USED BY: hiring_delay.
revenue_averaging_time = 3.
UNITS: Weeks.
DEF: Number of weeks in the moving average for sales values expected.
USED BY: expected_sales_revenues.
revenue_fraction_for_salesforce_salaries = 0.25.
UNITS: unitless.
DEF: Percentage of the expected sales revenues which can be used for paying salesforce salaries. In the original mode = 0.1. Under the price and salary assumptions of the revised model, it has to be at least 19.5% (initialization equilibrium). If = 25%, the default situation generates the possibility to pay 51 salespeople, therefore there is space to hire additional salesforce.
USED BY: payable_salesforce, budget_for_salesforce_costs.
Sales_revenues = deliveries * unit_sales_price.
UNITS: Euros/Weeks.
DEF: Amount received for the watches delivered weekly.
USED BY: expected_sales_revenues, Accounting, Accounting.total_revenues.
Salesman_productivity_max = 10.
UNITS: Device/Weeks/Individual.
DEF: Highest theoretical number of weekly new orders one salesperson can achieve.
USED BY: orders, minimum_delivery_to_pay_current_salesforce, expected_sales, salesforce_costs_per_watch, theoretically_sellable, additional_salesforce_for_excess_producibility.
Salesperson_monthly_salary = 3000.
UNITS: Euros/Month/Individual.
DEF: Monthly salary for each of the salespeople.
USED BY: payable_salesforce, Accounting, additional_SF_monthly_salary_costs, salesforce_costs_per_watch, Accounting.salesforce_costs.
Shifts_per_day = 3.
UNITS: shifts/days.
USED BY: Shifts_per_week.
Shifts_per_week = Days_per_week * Shifts_per_day.
UNITS: shifts/week.
USED BY: Capacity_Utilization_Fraction, Accounting, Accounting.extra_shifts_multiplier.
Shifts_per_week_max = 21.
UNITS: shifts/week.
USED BY: Capacity_Utilization_Fraction.
theoretic_excess_productibility = MAX(theoretically_productible-theoretically_sellable; 0).
UNITS: Device/Weeks.
DEF: Weekly number of producible watches that would not be sold with the current salesforce.
USED BY: additional_salesforce_for_excess_producibility.
Theoretically_productible = Capacity_Utilization_Fraction * Production_Capacity_considered
UNITS: Device/Weeks.
DEF: Weekly number of producible watches according to the considered production capacity and the capacity utilization fraction.
USED BY: Capacity_fractional_effort, theoretic_excess_productibility
theoretically_sellable = Sales_Force * 0.9 * salesman_productivity_max
UNITS: Device/Weeks.
DEF: Weekly number of new orders which the salesforce could achieve at the maximum productivity.
USED BY: theoretic_excess_productibility.
unit_sales_price = 431.
UNITS: Euros/Device.
DEF: Amount paid by clients per watch.
USED BY: sales_revenues.
weeks_per_month = 4.
UNITS: Weeks/Month.
DEF: Each month is assumed to last exactly 4 weeks.
USED BY: payable_salesforce, Accounting, salesforce_costs_per_watch, Accounting.salesforce_costs.