Assessment of Segmentation Parameters for Object-Based Land Cover Classification Using Color-Infrared Imagery
Abstract
:1. Introduction
2. Study Area and Data Pre-Processing
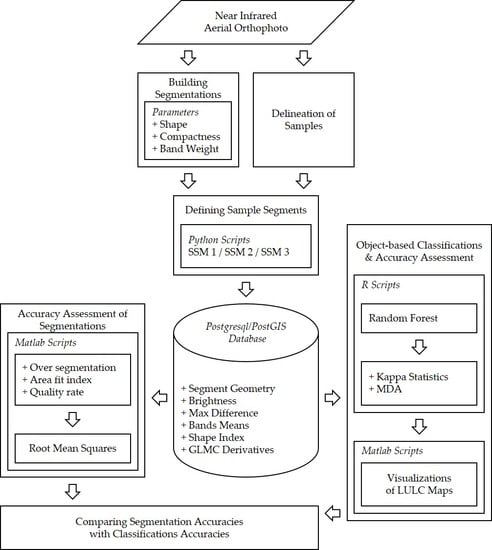
3. Methodology
- Oversegmentation assessment was proposed by Reference [23] and applied in References [48,49]. Oversegmentation of a single sample can be defined as subtracting the division of the total intersecting area of the sample and segments from one (Equation (5)). The overall oversegmentation of the segmentation can be calculated using the means of all (Equation (6)). and have a range between 0 and 1, with 0 as a perfect match.
- Area fit index assessment was proposed by Reference [50] and applied in References [23,51,52]. The area fit index of a single sample can be defined as dividing the sum of the subtracted segments from the sample area by the sample area (Equation (7)). The overall oversegmentation of the segmentation can be calculated by the means of all (Equation (8)). and have a range between 0 and 1, with 0 as a perfect match.
- Quality rate assessment was proposed by Reference [53] and applied in References [48,54,55]. The quality rate of a single sample can be defined as dividing the total intersecting area of the sample and the segments by the union area of the sample and the segments (Equation (9)). The overall over segmentation of the segmentation can be calculated by the means of all (Equation (10)). and have a range between 0 and 1, with 1 as a perfect match.
- Randomly select m variable subsets from M where m < M.
- Calculate the best split point among the m feature for node d.
- Divide the node into two nodes using the best split.
- Repeat the first three steps until a certain number of nodes has been reached.
- Repeat the first four steps to build the forest N times.
- Predict new observations with a majority vote.
4. Results and Discussion
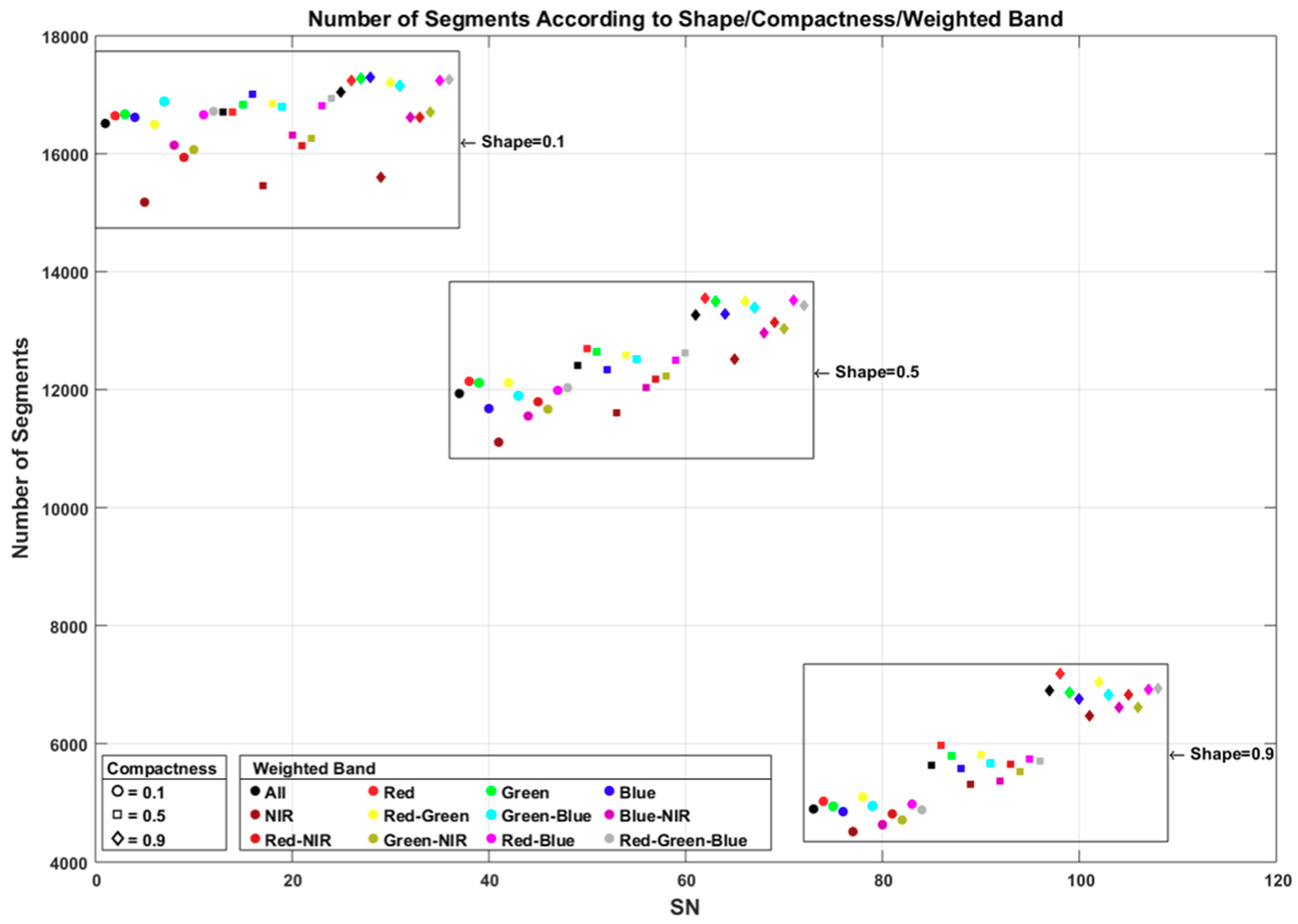
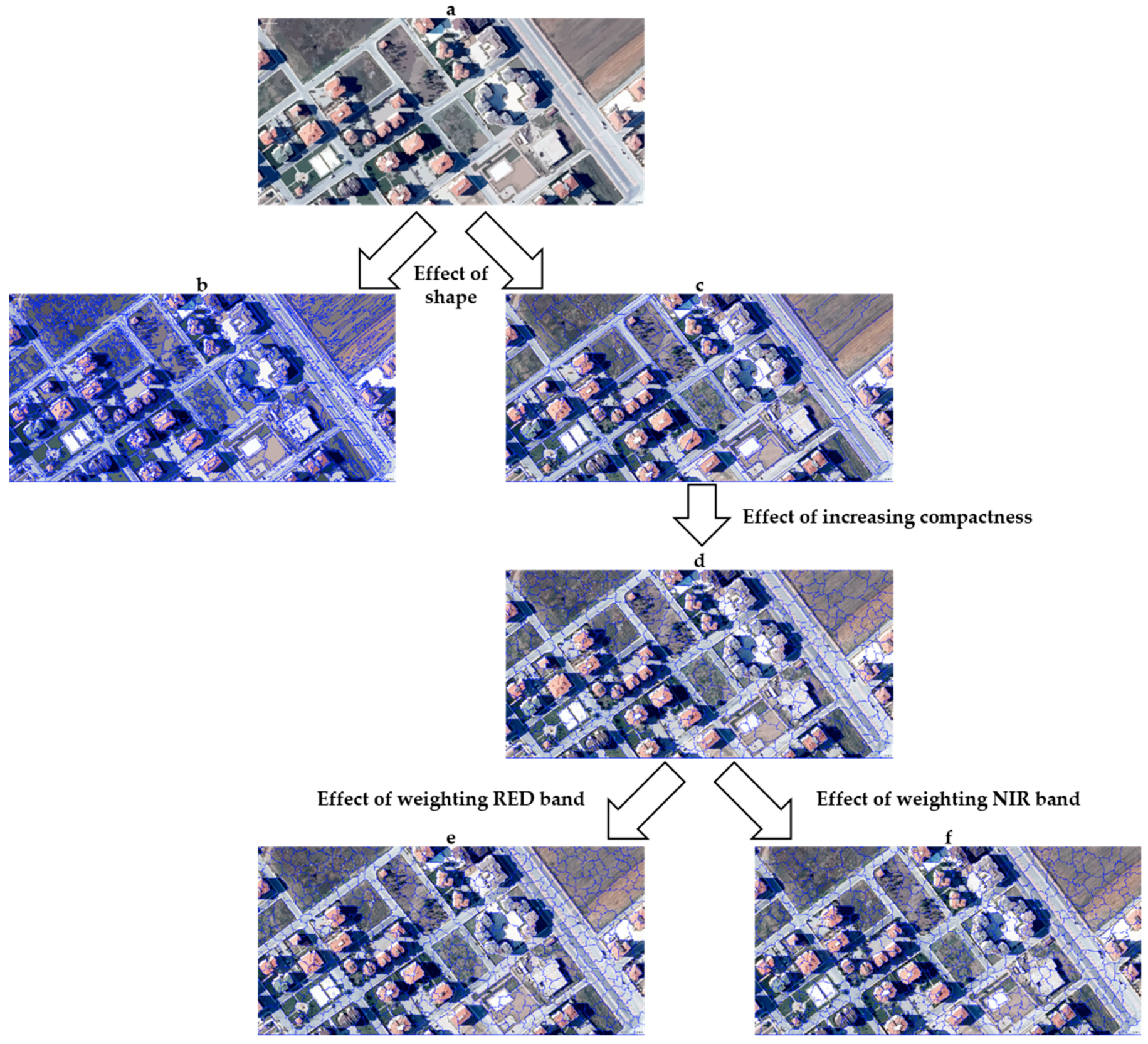
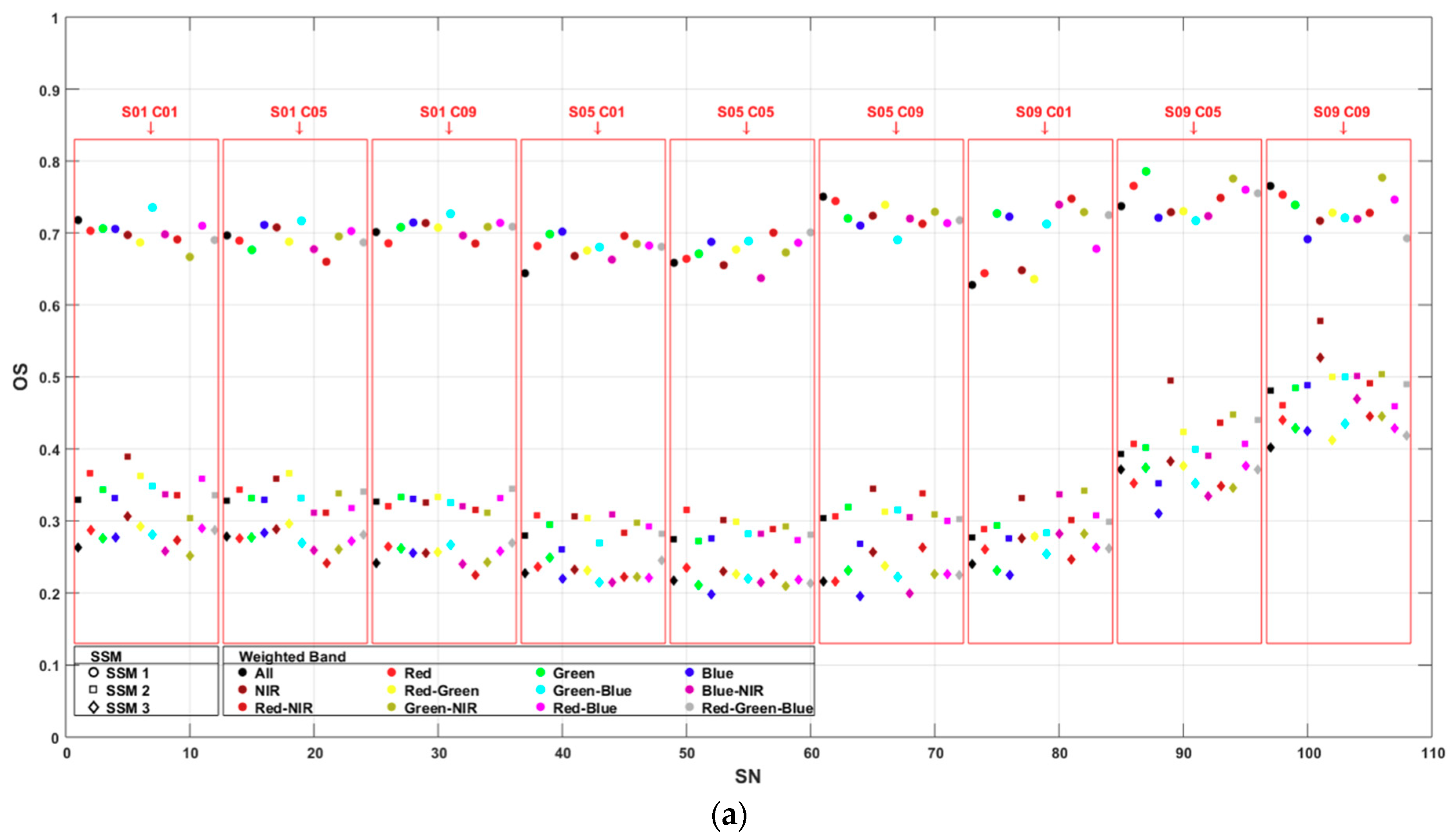
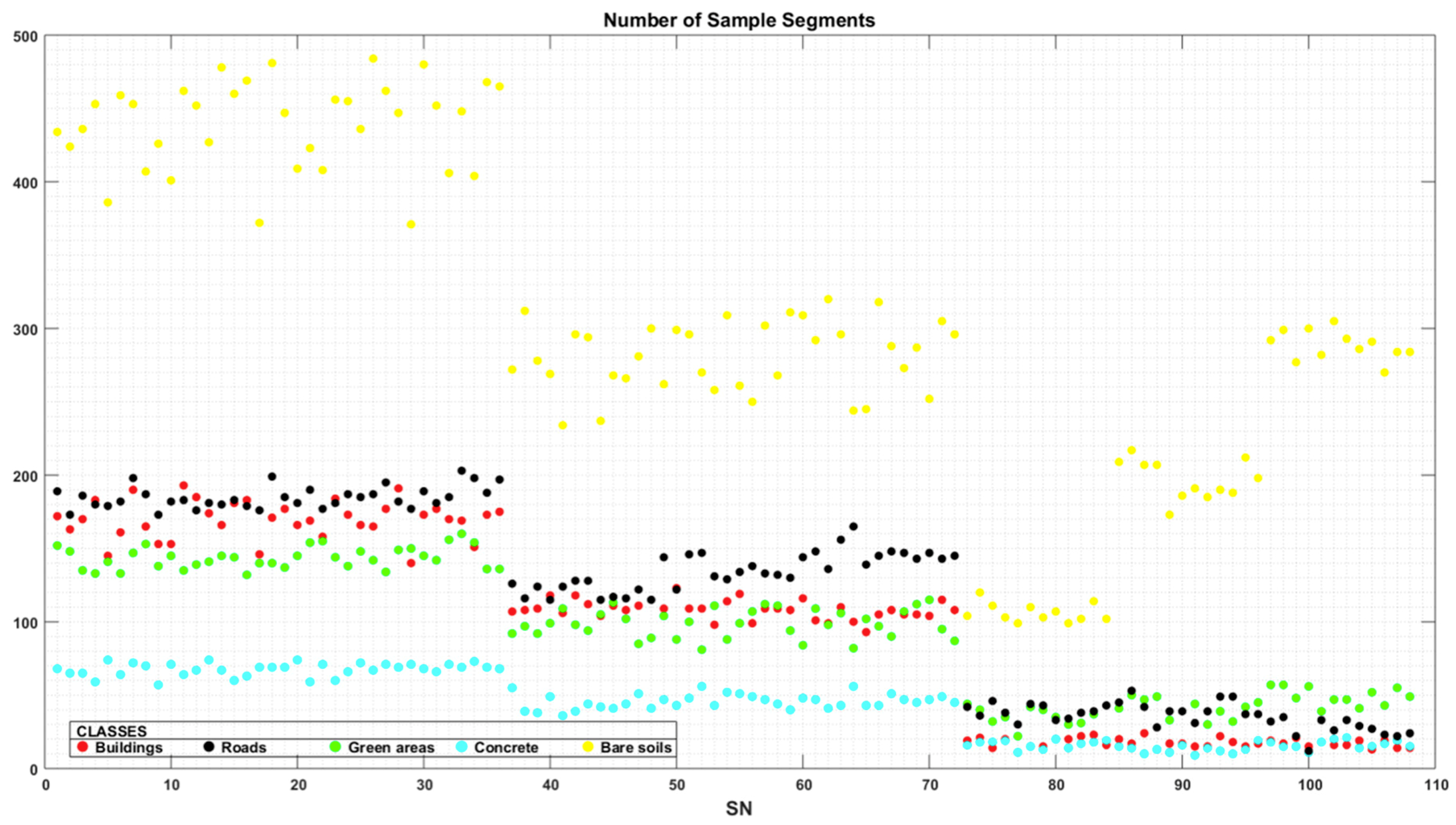
4.1. Segmentation Accuracy
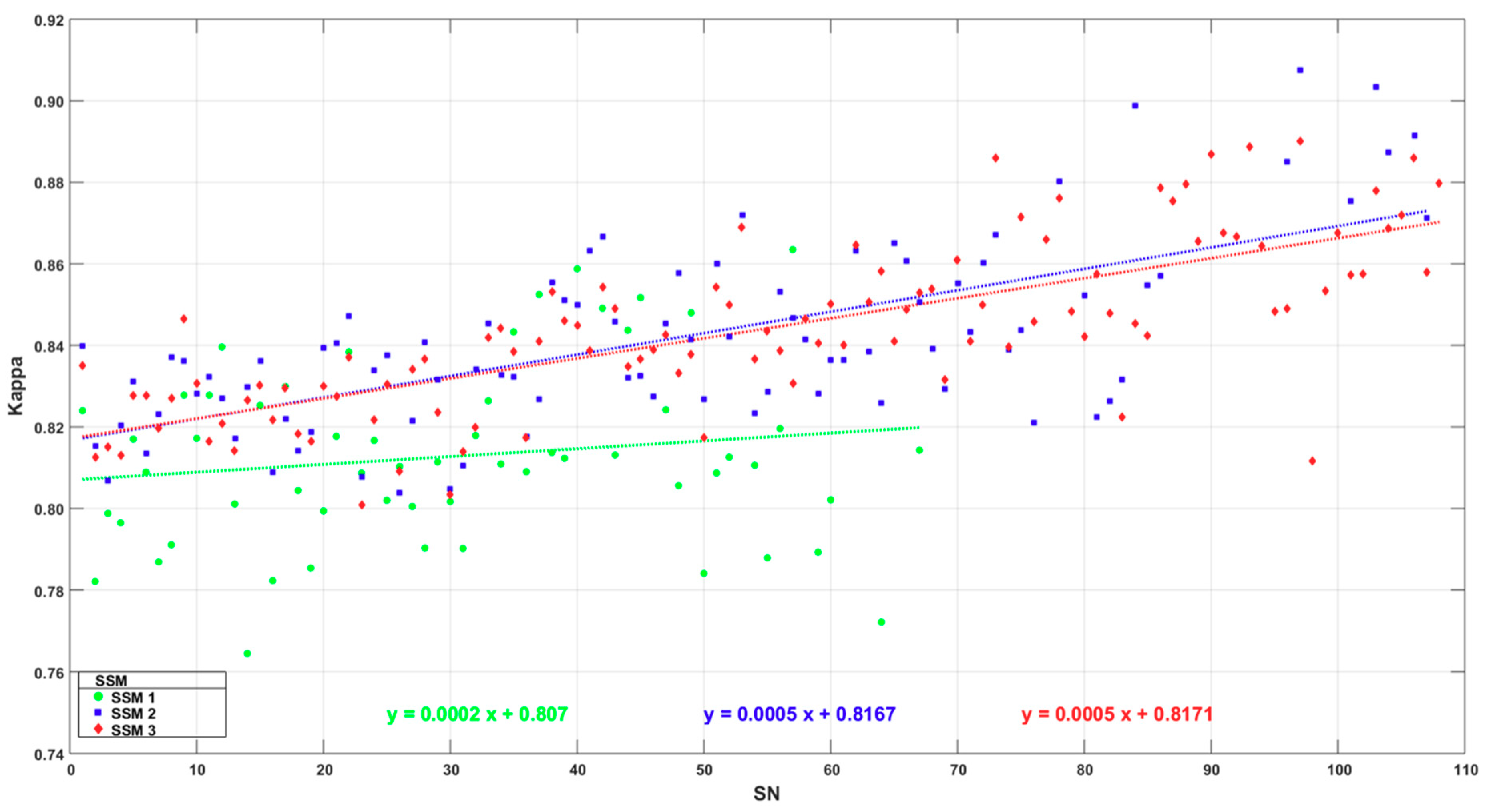
4.2. Classification Accuracy
4.3. Variable Importance
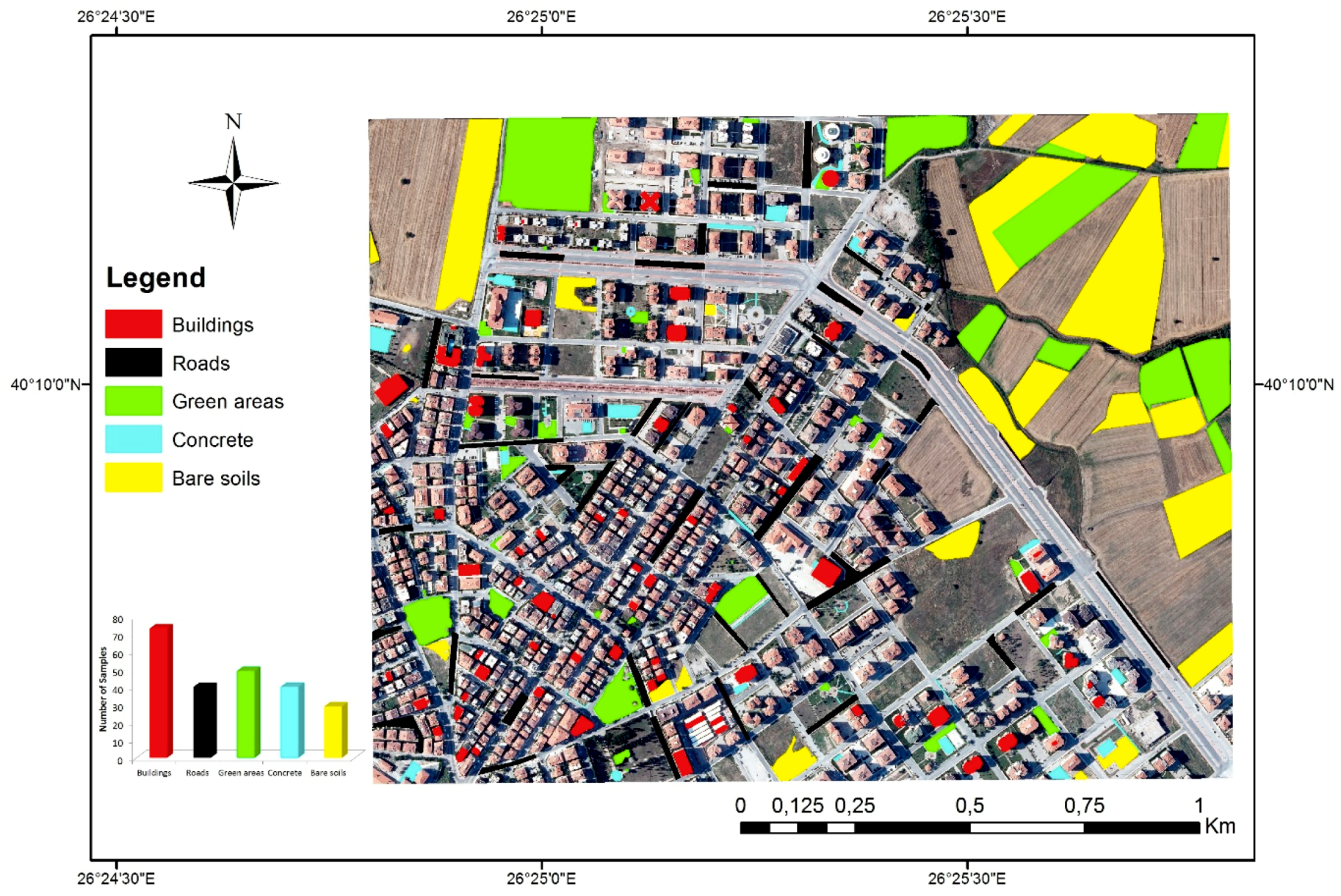
4.4. Classification Results
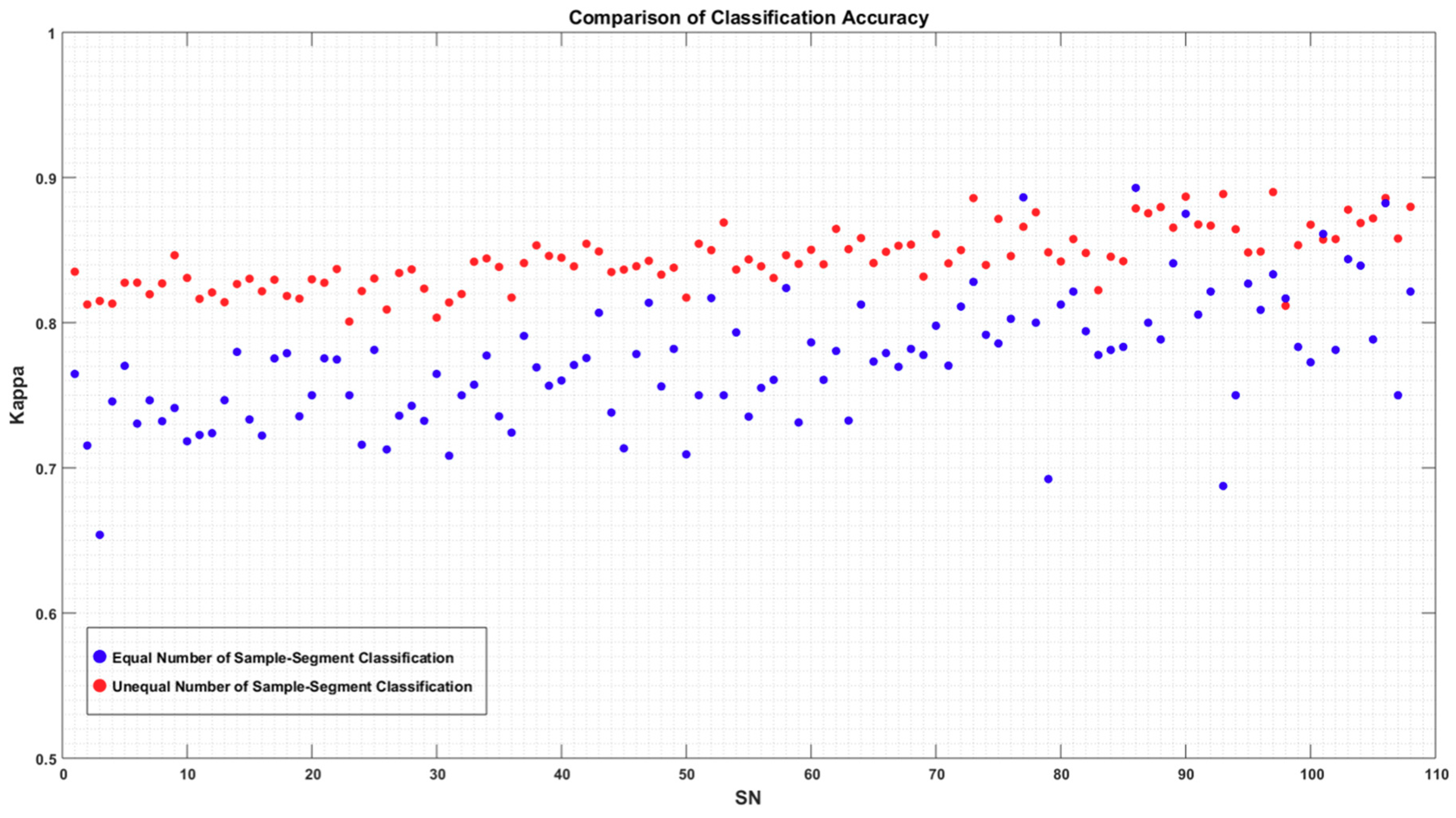
4.5. Comparison between Segmentation and Classification Accuracies
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Saadat, H.; Adamowski, J.; Bonnel, R.; Shafiri, F.; Namdar, M.; Ale-Ebrahim, S. Land use land cover classification over a large area in Iran based on single date analysis of satellite imagery. ISPRS J. Photogramm. 2011, 66, 608–619. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Jebuv, M.N. A comparative assessment between object and pixel-based classification approaches for land use/land cover mapping using SPOT 5 imagery. Geocarto Int. 2013, 29, 351–369. [Google Scholar] [CrossRef]
- Roelfsema, C.M.; Lyons, M.; Kovacs, E.M.; Maxwell, P.; Saunders, M.I.; Samper-Villarreal, J.; Phinn, S.R. Multi-temporal mapping of seagrass cover, species and biomass: A semi-automated object based image analysis approach. Remote Sens. Environ. 2014, 150, 172–187. [Google Scholar] [CrossRef]
- Mafanya, M.; Tsele, P.; Botai, J.; Manyama, P.; Swart, B.; Monate, T. Evaluating pixel and object based image classification techniques for mapping plant invasions from UAV derived aerial imagery: Harrisia pomanensis as a case study. ISPRS J. Photogramm. 2017, 129, 1–11. [Google Scholar] [CrossRef]
- Torres-Sánchez, J.; López-Granados, F.; Peña, J.M. An automatic object-based method for optimal thresholding in UAV images: Application for vegetation detection in herbaceous crops. Comput. Electron. Agric. 2015, 114, 43–52. [Google Scholar] [CrossRef] [Green Version]
- de Alwis Pitts, D.A.; So, E. Enhanced change detection index for disaster response, recovery assessment and monitoring of accessibility and open spaces (camp sites). Int. J. Appl. Earth Obs. 2017, 57, 49–60. [Google Scholar] [CrossRef]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- Ma, L.; Li, M.; Ma, X.; Cheng, L.; Du, P.; Liu, Y. A review of supervised object-based land-cover image classification. ISPRS J. Photogramm. 2017, 130, 277–293. [Google Scholar] [CrossRef]
- Baatz, M.; Schäpe, A. Multiresolution segmentation: An optimization approach for high quality multi-scale image segmentation. In Angewandte Geographische Informations-Verarbeitung XII; Strobl, J., Blaschke, T., Griesbner, G., Eds.; Wichmann Verlag: Karlsruhe, Germany, 2000; pp. 12–23. [Google Scholar]
- Benz, U.C.; Hofmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS J. Photogramm. 2004, 58, 239–258. [Google Scholar] [CrossRef] [Green Version]
- Commaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. 2002, 24, 603–619. [Google Scholar] [CrossRef]
- Michel, J.; Youssefi, D.; Grizonnet, M. Stable mean-shift algorithm and its application to the segmentation of arbitrarily large remote sensing images. IEEE Trans. Pattern Anal. 2015, 53, 952–964. [Google Scholar] [CrossRef]
- Jin, X. Segmentation-Based Image Processing System. U.S. Patent 8,260,048, 14 November 2007. [Google Scholar]
- Roerdink, J.B.; Meijster, A. The watershed transform: Definitions, algorithms, and parallelization strategies. Fund. Inform. 2000, 41, 187–228. [Google Scholar] [CrossRef]
- Alshehhi, R.; Marpu, P.R. Hierarchical graph-based segmentation for extracting road networks from high-resolution satellite images. ISPRS J. Photogramm. 2017, 126, 245–260. [Google Scholar] [CrossRef]
- Esch, T.; Thiel, M.; Bock, M.; Roth, A.; Dech, S. Improvement of image segmentation accuracy based on multiscale optimization procedure. IEEE Geosci. Remote Sens. 2008, 5, 463–467. [Google Scholar] [CrossRef]
- Yang, J.; Li, P.; He, Y. A multi-band approach to unsupervised scale parameter selection for multi-scale image segmentation. ISPRS J. Photogramm. 2014, 94, 13–24. [Google Scholar] [CrossRef]
- Drăguţ, L.; Csillik, O.; Eisank, C.; Tiede, D. Automated parameterisation for multi-scale image segmentation on multiple layers. ISPRS J. Photogramm. 2014, 88, 119–127. [Google Scholar] [CrossRef] [PubMed]
- Anders, N.S.; Seijmonsbergen, A.C.; Bouten, W. Segmentation optimization and stratified object-based analysis for semi-automated geomorphological mapping. Remote Sens. Environ. 2011, 115, 2976–2985. [Google Scholar] [CrossRef]
- Belgiu, M.; Drǎguţ, L. Comparing supervised and unsupervised multiresolution segmentation approaches for extracting buildings from very high resolution imagery. ISPRS J. Photogramm. 2014, 96, 67–75. [Google Scholar] [CrossRef] [PubMed]
- Momeni, R.; Aplin, P.; Boyd, D.S. Mapping complex urban land cover from spaceborne imagery: The influence of spatial resolution, spectral band set and classification approach. Remote Sens. 2016, 8, 88. [Google Scholar] [CrossRef]
- Costa, H.; Foody, G.M.; Boyd, D.S. Supervised methods of image segmentation accuracy assessment in land cover mapping. Remote Sens. Environ. 2018, 205, 338–351. [Google Scholar] [CrossRef]
- Clinton, N.; Holt, A.; Scarborough, J.; Yan, L.I.; Gong, P. Accuracy assessment measures for object-based image segmentation goodness. Photogramm. Eng. Remote Sens. 2010, 76, 289–299. [Google Scholar] [CrossRef]
- Zhang, X.; Feng, X.; Xiao, P.; He, G.; Zhu, L. Segmentation quality evaluation using region-based precision and recall measures for remote sensing images. ISPRS J. Photogramm. 2015, 102, 73–84. [Google Scholar] [CrossRef]
- Yang, J.; He, Y.; Caspersen, J.; Jones, T. A discrepancy measure for segmentation evaluation from the perspective of object recognition. ISPRS J. Photogramm. 2015, 101, 186–192. [Google Scholar] [CrossRef]
- Su, T.; Zhang, S. Local and global evaluation for remote sensing image segmentation. ISPRS J. Photogramm. 2017, 130, 256–276. [Google Scholar] [CrossRef]
- Lindquist, E.J.; D’Annunzio, R. Assessing global forest land-use change by object-based image analysis. Remote Sens. 2016, 8, 678. [Google Scholar] [CrossRef]
- Zou, X.; Zhao, G.; Li, J.; Yang, Y.; Fang, Y. Object Based Image Analysis Combining High Spatial Resolution Imagery and Laser Point Clouds for Urban Land Cover. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, XXIII ISPRS Congress, Prague, Czech Republic, 12–19 July 2016; Volume XLI-B3, pp. 733–739. [Google Scholar]
- Goodin, D.G.; Anibas, K.L.; Bezymennyi, M. Mapping land cover and land use from object-based classification: An example from a complex agricultural landscape. Int. J. Remote Sens. 2015, 36, 4702–4723. [Google Scholar] [CrossRef]
- Cleve, C.; Kelly, M.; Kearns, F.R.; Moritz, M. Classification of the wildland—Urban interface: A comparison of pixel- and object-based classifications using high-resolution aerial photography. Comput. Environ. Urban 2008, 32, 317–326. [Google Scholar] [CrossRef]
- Kettig, R.L.; Landgrabe, D.A. Classification of multispectral image data by extraction and classification of homogenous objects. IEEE Trans. Geosci. Remote 1976, 14, 19–26. [Google Scholar] [CrossRef]
- Jensen, J.R.; Cowen, D.C. Remote sensing of urban suburban infrastructure and socio-economic attributes. Photogramm. Eng. Remote Sens. 1999, 65, 611–622. [Google Scholar] [CrossRef]
- Bauer, T.; Steinnocher, K. Per-parcel land use classification in urban areas using a rule-based technique. GeoBIT 2001, 6, 12–17. [Google Scholar]
- Benediktsson, J.A.; Pesaresi, M.; Arnason, K. Classification and feature extraction for remote sensing images from urban areas base on morphological transformations. IEEE Trans. Geosci. Remote 2003, 41, 1940–1949. [Google Scholar] [CrossRef]
- Ehlers, M.; Gahler, M.; Janowski, R. Automated analysis of ultra high resolution remote sensing data for biotope type mapping: New possibilities and challenges. ISPRS J. Photogramm. 2003, 57, 315–326. [Google Scholar] [CrossRef]
- Herold, M.; Gardner, M.E.; Roberts, D.A. Spectral resolution requirements for mapping urban areas. IEEE Trans. Geosci. Remote 2003, 41, 1907–1919. [Google Scholar] [CrossRef]
- Myint, S.W.; Gober, P.; Brazel, A.; Grossman-Clarke, S.; Weng, Q. Per-pixel vs. object-based of urban land cover extraction using high resolution imagery. Remote Sens. Environ. 2011, 115, 1145–1161. [Google Scholar] [CrossRef]
- Georganos, S.; Grippa, T.; Lennert, M.; Vanhuysse, S.; Johnson, B.; Wolff, E. Scale Matters: Spatially Partitioned Unsupervised Segmentation Parameter Optimization for Large and Heterogeneous Satellite Images. Remote Sens. 2018, 10, 1440. [Google Scholar] [CrossRef]
- Duro, D.C.; Franklin, S.E.; Dube, M.G. A comparison of pixel-based and object-based image analysis with selected machine learning algorithms for the classification of agricultural landscapes using SPOT-5 HRG imagery. Remote Sens. Environ. 2012, 118, 259–272. [Google Scholar] [CrossRef]
- Hussain, M.; Chen, D.; Cheng, A.; Wei, H.; Stanley, D. Change detection from remotely sensed images: From pixel-based to object-based approaches. ISPRS J. Photogramm. 2013, 80, 91–106. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Lein, J.K. Object-based analysis. In Environmental Sensing: Analytical Techniques for Earth Observation; Springer: London, UK, 2012; pp. 259–278. [Google Scholar]
- Congalton, R. Accuracy and error analysis of global and local maps: Lessons learned and future considerations. In Remote Sensing of Global Croplands for Food Security; CRC Press: Boca Raton, FL, USA, 2009; pp. 441–458. [Google Scholar]
- Jensen, J.R. Digital Image Processing: A Remote Sensing Perspective; Prentice Hall: Upper Saddle River, NJ, USA, 2004; pp. 316–317. [Google Scholar]
- Breiman and Cutler’s Random Forests for Classification and Regression. Available online: https://cran.r-project.org/web/packages/randomForest/randomForest.pdf (accessed on 17 September 2018).
- Drǎguţ, L.; Tiede, D.; Levick, S.R. ESP: A tool to estimate scale parameter for multiresolution image segmentation of remotely sensed data. Int. J. Geogr. Inf. Sci. 2010, 24, 859–871. [Google Scholar] [CrossRef]
- Zhang, Y.J. A survey on evaluation methods for image segmentation. Pattern Recogn. 1996, 29, 1335–1346. [Google Scholar] [CrossRef]
- Liu, Y.; Bian, L.; Meng, Y.; Wang, H.; Zhang, S.; Yang, Y.; Shao, X.; Wang, B. Discrepancy measures for selecting optimal combination of parameter values in object-based image analysis. ISPRS J. Photogramm. 2012, 68, 144–156. [Google Scholar] [CrossRef]
- Johnson, B.A.; Tateishi, R.; Hoan, N.T. Satellite image pansharpening using a hybrid approach for object-based image analysis. ISPRS Int. J. Geo-Inf. 2012, 1, 228–241. [Google Scholar] [CrossRef]
- Lucieer, A.; Stein, A. Existential uncertainty of spatial objects segmented from satellite sensor imagery. IEEE Trans. Geosci. Remote 2002, 40, 2518–2521. [Google Scholar] [CrossRef]
- Neubert, M.; Herold, H.; Meinel, G. Assessing image segmentation quality-concepts, methods and application. In Object-Based Image Analysis; Blaschke, T., Lang, S., Hay, G.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 769–784. [Google Scholar]
- Bar Massada, A.; Kent, R.; Blank, L.; Perevolotsky, A.; Hadar, L.; Carmel, Y. Automated segmentation of vegetation structure units in a Mediterranean landscape. Int. J. Remote Sens. 2012, 33, 346–364. [Google Scholar] [CrossRef]
- Winter, S. Location similarity of regions. ISPRS J. Photogramm. 2000, 55, 189–200. [Google Scholar] [CrossRef]
- Weidner, U. Contribution to the assessment of segmentation quality for remote sensing applications. In Proceedings of the International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume XXXVII-B7, XXI ISPRS Congress, Beijing, China, 3–11 July 2008. [Google Scholar]
- Whiteside, T.G.; Maier, S.W.; Boggs, G.S. Site-specific area-based validation of classified objects. In Proceedings of the 4th GEOBIA, Rio de Janeiro, Brazil, 7–9 May 2012. [Google Scholar]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Li, M.; Ma, L.; Blaschke, T.; Cheng, L.; Tiede, D. A systematic comparison of different object-based classification techniques using high spatial resolution imagery in agricultural environments. Int. J. Appl. Earth Obs. 2016, 49, 87–98. [Google Scholar] [CrossRef]
- Ma, L.; Fu, T.; Blaschke, T.; Li, M.; Tiede, D.; Zhou, Z.; Ma, X.; Chen, D. Evaluation of feature selection methods for object-based land cover mapping of unmanned aerial vehicle imagery using random forest and support vector machine classifiers. ISPRS Int. J. Geo-Inf. 2017, 6, 51. [Google Scholar] [CrossRef]
- Stehman, S.V. Selecting and interpreting measures of thematic classification accuracy. Remote Sens. Environ. 1997, 62, 77–89. [Google Scholar] [CrossRef]
- Bylander, T. Estimating generalization error on two-class data sets using out-of-bag estimates. Mach. Learn. 2002, 48, 287–297. [Google Scholar] [CrossRef]
- Archer, K.J.; Kimes, R.V. Empirical characterization of random forest variable importance measures. Comput. Stat. Data Anal. 2008, 52, 2249–2260. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Strobl, C.; Hothorn, T.; Zeileis, A. Party on! A new, conditional variable-importance measure for Random Forests available in the party package. R J. 2009, 1–2, 14–17. [Google Scholar]












| Microsoft UltraCam Eagle Digital Aerial Camera | |
|---|---|
| Image size | 20010 × 13080 pixels |
| Physical pixel size | 5.2 μm |
| Focal length | 80 mm |
| Spectral bands | PAN + R, G, B, NIR |
| Image Features | |
|---|---|
| Accuracy | ±2 m (Horizontal) |
| Datum Coordinate System | WGS84 (World Geodetic System 1984) UTM (Universal Transverse Mercator) Projection |
| Spatial Resolution | 30 cm |
| Spectral bands | RGB + NIR |
| File Format | GeoTIFF |
| Compression Format | ECW (Enhanced Compressed Wavelet) |
| S0.1 | S0.5 | S0.9 | WB | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C0.1 | C0.5 | C0.9 | C0.1 | C0.5 | C0.9 | C0.1 | C0.5 | C0.9 | R | G | B | NIR | |
| Segment No. | 1 | 13 | 25 | 37 | 49 | 61 | 73 | 85 | 97 | ✓ | ✓ | ✓ | ✓ |
| 2 | 14 | 26 | 38 | 50 | 62 | 74 | 86 | 98 | ✓ | ||||
| 3 | 15 | 27 | 39 | 51 | 63 | 75 | 87 | 99 | ✓ | ||||
| 4 | 16 | 28 | 40 | 52 | 64 | 76 | 88 | 100 | ✓ | ||||
| 5 | 17 | 29 | 41 | 53 | 65 | 77 | 89 | 101 | ✓ | ||||
| 6 | 18 | 30 | 42 | 54 | 66 | 78 | 90 | 102 | ✓ | ✓ | |||
| 7 | 19 | 31 | 43 | 55 | 67 | 79 | 91 | 103 | ✓ | ✓ | |||
| 8 | 20 | 32 | 44 | 56 | 68 | 80 | 92 | 104 | ✓ | ✓ | |||
| 9 | 21 | 33 | 45 | 57 | 69 | 81 | 93 | 105 | ✓ | ✓ | |||
| 10 | 22 | 34 | 46 | 58 | 70 | 82 | 94 | 106 | ✓ | ✓ | |||
| 11 | 23 | 35 | 47 | 59 | 71 | 83 | 95 | 107 | ✓ | ✓ | |||
| 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | ✓ | ✓ | ✓ | ||
| SSM | Total Area () of Training Segments for any Class | Condition Based on Sample Area () and Segment Area () |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 |
| No | Name | Explanation |
|---|---|---|
| 1 | Brightness | Brightness defines the sum of the mean intensities of all object layers. |
| 2 | Maximum difference | Maximum difference defines the absolute difference of the minimum and maximum object mean intensities. |
| 3, 4, 5, 6 | RMean, GMean, BMean, NIRMean | The mean features represent the mean intensities of red, green, blue, and NIR layer pixels forming the image object. |
| 7 | Shape index | The shape index describes the smoothness of an image object border. |
| 8, 9, 10, 11, 12, 13, 14 | GLCMHom, GLCMCon, GLCMDis, GLCMEnt, GLCMMean, GLCMStd, GLCMCor | Homogeneity, contrast, dissimilarity, entropy, mean, standard deviation, and correlation are derivatives of GLCM that quantify surface texture. |
| SSM 1 | SSM 2 | SSM 3 | Total | |
|---|---|---|---|---|
| Number of accomplished classifications | 58 | 91 | 108 | 257 |
| Number of unaccomplished classifications | 50 | 17 | 0 | 67 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akcay, O.; Avsar, E.O.; Inalpulat, M.; Genc, L.; Cam, A. Assessment of Segmentation Parameters for Object-Based Land Cover Classification Using Color-Infrared Imagery. ISPRS Int. J. Geo-Inf. 2018, 7, 424. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi7110424
Akcay O, Avsar EO, Inalpulat M, Genc L, Cam A. Assessment of Segmentation Parameters for Object-Based Land Cover Classification Using Color-Infrared Imagery. ISPRS International Journal of Geo-Information. 2018; 7(11):424. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi7110424
Chicago/Turabian StyleAkcay, Ozgun, Emin Ozgur Avsar, Melis Inalpulat, Levent Genc, and Ahmet Cam. 2018. "Assessment of Segmentation Parameters for Object-Based Land Cover Classification Using Color-Infrared Imagery" ISPRS International Journal of Geo-Information 7, no. 11: 424. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi7110424