Hierarchical Behavior Model for Multi-Agent System with Evasion Capabilities and Dynamic Memory

Abstract

The behavior of an agent may be simple or complex depending on its role. Behavioral simulation using agents can have multiple approaches that have different advantages and disadvantages. By combining different behaviors in a hierarchical model, situational inefficiencies can be compensated. This paper proposes a behavioral hierarchy model that combines different mechanisms in behavior plans. The study simulates the social behavior in an office environment during an emergency using collision avoidance, negotiation, conflict solution, and path-planning mechanisms in the same multi-agent model to find their effects and the efficiency of the combinational setups. Independent agents were designed to have memory expansion, pathfinding, and searching capabilities, and the ability to exchange information among themselves and perform evasive actions to find a way out of congestion and conflict. The designed model allows us to modify the behavioral hierarchy and action order of agents during evacuation scenarios. Moreover, each agent behavior can be enabled or disabled separately. The effects of these capabilities on escape performance were measured in terms of time required for evacuation and evacuation ratio. Test results prove that all mechanisms in the proposed model have characteristics that fit each other well in situations where different hierarchies are needed. Dynamic memory management (DMM), together with a hierarchical behavior plan, achieved a performance improvement of 23.14% in escape time without providing agents with any initial environmental information.

1. Introduction

Most multi-agent applications and studies aim to replicate specific human behaviors such as herding [1], negotiation [2], and cooperation [3]. Humans are complex organisms with a dynamic behavior and inference structure that can change in case planned actions do not give the anticipated results. It is quite difficult to create an agent model that will infer and decide at the human level. However, it is possible to provide predefined actions to the agent within a certain hierarchy and thus obtain an agent model that can make decisions dynamically. Providing an agent with the ability to consider different actions increases its overall capability, but it is quite a difficult task to implement human behaviors for all possible situations. A goal-driven approach that defines behaviors for specific cases may contribute to the solution of this problem. For instance, Greco et al. [4] proposed an agent-based methodology for seismic vulnerability assessment. Cao et al. [5] studied the problem of a leader following the consensus and proposed a leader switching procedure. Su et al. [6] proposed consensus protocols with connected and jointly connected switching networks. Mendoza-Silva et al. [7] modeled agents as drivers to develop a smart parking system. Eivazy and Malek [8] offered an agent-based solution for flood management. Several simulations with multiple agents were performed for emergency evacuations [9,10,11,12,13,14,15,16].

Emergency evacuation (also known as emergency egress) is a problem that requires determining the safest plan or approach for evacuating in an emergency. Safely evacuating masses of people from a place when danger is occurring is a difficult task. The evacuation problem has two main analytic dimensions: the physical environment and the behaviors of people who require egress. The emergency evacuation problem has a complex nature in a crowded environment, particularly due to the behavior of people under stress. This situation may become even more complicated depending on the physical structure of the environment. Emergency evacuation studies have been simulated for environments such as ships [17], stadiums [18], airports [19], public transport terminals [20], and foundation pits [21].

As a workspace, an office environment is usually designed for a large group of people to work in a considerably small space. Such a crowded workspace may raise serious safety concerns, which could cause delays or unforeseen consequences during an emergency.

The evacuation process usually has a time constraint, hence requires fast decision-making and traversing mechanisms due to the imminent danger in the environment. The estimated routes of some agents may intersect with others and thus create bottlenecks, collisions, and conflicts depending on the crowd. These cases require solution mechanisms. Different methodologies have been offered for this task by various studies. Niyomubyeyi et al. [22] compared metaheuristic approaches to the evacuation problem. Musharraf et al. [23] used lecture-based training to develop a decision tree for evacuating agents. Golas et al. [24] proposed a method for long-range collision avoidance using a multi-agent system with local collision avoidance mechanisms and global path planning. Berg et al. [25] precomputed a path to foresee collisions and used velocity changes to avoid them. Foudil et al. [26] suggested actions such as changing directions, moving forward or backward, and waiting to avoid collision. Wu et al. [27] emphasized the relationship between commuting and traffic congestion and proposed a speed management model for agents to decrease the congestion ratio. Since there are multiple agents in the same environment, interactions between agents can also be used to solve conflicts. Sycara [28] suggested using negotiation to solve noncooperative multi-agent conflicts. Mechanisms involving the transfer of environmental information have also been used [29]. Zhao et al. [30] defined static information depository points in their work and proved that agents improved their evacuation performance when using the proposed tools. Choi et al. [31] defined different types of agents representing impairments and disabilities, which are responsive to different kinds of markers.

Most evacuation scenarios are stressful because they are the result of apparent or possibly dangerous situations. Therefore, the psychological aspects of the problem should also be considered. Dosey and Meisels [32] stated that humans tend to create buffer zones to serve as protection from perceived threats. These buffer zones expand under stress conditions. Sommer et al. [33] pointed out that violation of personal space may result in higher levels of stress and agitation. Different mechanisms [34] for maintaining personal space have been simulated using multi-agent models. Amaoka et al. [35] built a personal space simulation while handling the spacing of agents depending on their relationship, which can be on the friend, business, or stranger level. A Geographic Information System (GIS)-based work [36] limited occupation of grid cells to a certain number to maintain personal space between agents during earthquake/tsunami evacuation. The grid–graph approach allows representation of spatial data and objects as grids [37] and is used in many egress models [38]. This approach is proven to be useful for creating an analytical model [39,40] and is especially applicable to indoor environments [41]. The grid–graph approach also provides scalability [42] and ease of optimization [43].

The concept of agents capable of changing their behavior, role, or approach has been handled in several studies [44,45,46]. Pires et al. [44] developed a hybrid decision system in which agents can change roles or goals according to the situation. Al-Yaseen et al. [45] offered an adaptive behavior model in which agents change their behavior according to instant observations or inputs. Adaptation can also be achieved by using machine learning or neural networks [46]. Studies on emergency egress mostly focus on physical environmental conditions, with an assumption that either agents have prior information about the environment or information is provided to them during evacuation. Besides, they mostly focus on a single behavior model rather than combining behavioral characteristics of agents. Simulations with some missing attributes may not represent real-world situations. Therefore, models with combined behaviors that have more attributes are needed to reflect real-world cases more accurately.

This paper offers a parametric agent model that simulates memorization and social behavior in an office environment during an emergency using collision avoidance, negotiation, conflict solution, and path-planning mechanisms. In the model, multiple evasion and conflict solution mechanisms were defined as elements of a decision tree (a hierarchical model) to eliminate their characteristic disadvantages. The memory management algorithm was developed to mimic the “memorization by exploration” behavior of humans providing a solution to the problem that arises due to the absence of prior spatial information. The proposed multi-agent model enables us to measure and tune the performance using parametric controls. These controls provide a calibration mechanism so that the model can adapt to different environments. To find the effects of agents on each other and the efficiency of the parametric setups, observations via simulations were carried out using the proposed model. These setups were tested to observe the success of the parameter sets that provide optimally designed behavior models for safe evacuation.

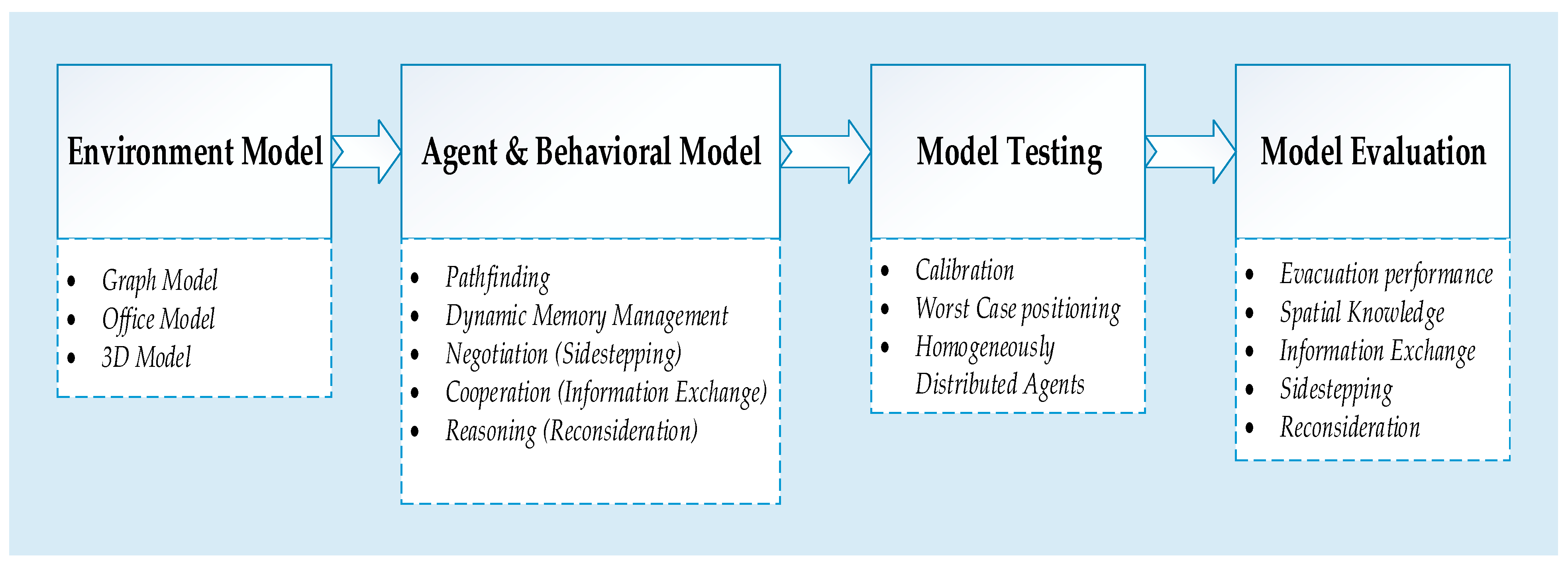
2. Materials and Methods

The overall process diagram of the hierarchical behavior model of the study is shown in Figure 1. The environment model was developed at the initial stage of the study. At this stage, a graph model was created by placing an office layout on this model. Later, the 3D model of the simulation environment was developed. In the second stage, the agent behavior model to be run on the designed graph model was developed. In the model, negotiation, cooperation, and reasoning mechanisms were programmed with dynamic memory management (DMM) for agents. At the same time, the pathfinding algorithm that the agents would use on the move was programmed. The simulation environment was developed in the Unity3D environment with C# programming language. In the third stage, the model was tested with the simulation environment. In the simulation environment, agent behaviors were tested taking into account their initial physical position (e.g., worst case and homogeneously distributed case scenarios) by parametric calibration. In the fourth stage of the study, the model was evaluated. At this stage, the evacuation performance of the agents was evaluated concerning their spatial knowledge and the use of behavioral hierarchy states including information exchange, sidestepping, and reconsideration mechanisms.

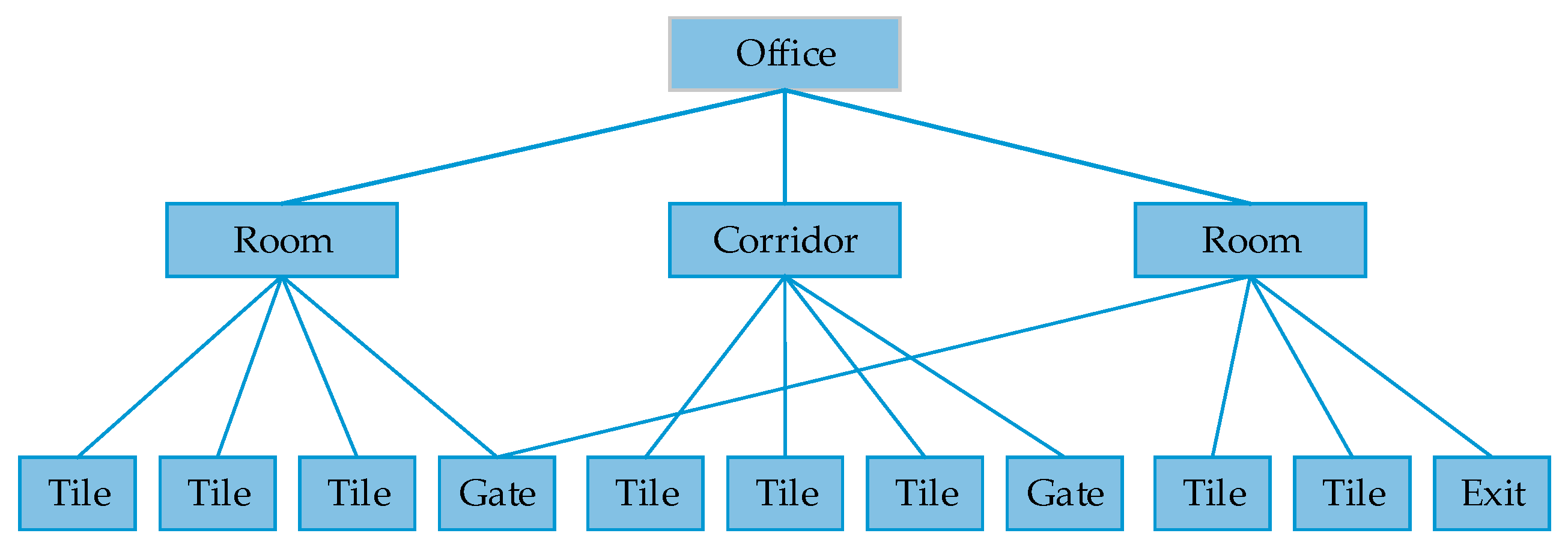
2.1. Environment Model

The ability to grow in size or complexity and find an optimal solution for the model to be developed and ease of implementation are among the criteria used in the environment model. Grid–graph applications provide scalability and ease of optimization. Micro or small-scale grid–graph models can be extended to macro- or large-scale space models. Therefore, the grid–graph model is preferred, as in [23,24] for simulating the environment model.

An office layout usually has a symmetrical geometric design and is easy to implement on a grid–graph. Components used in office design are implemented in a hierarchy. Rooms and corridors are subgroups of the complete graph representing the office. Figure 2 shows the hierarchy of entities in an office.

The environment model for the simulation has layouts consisting of the floor, rooms, entrances, gates, corridors, and exit points. The floor is the base of the graph. For simplicity, the office floor consists of 64 tiles in the form of an 8 × 8 grid with equal size, which is 5 × 5 units. Each node (regular nodes, gates, or exits) belongs to either a room or a corridor. Since gates consist of at least two nodes and serve as passages between rooms or corridors, they can belong to more than one entity. In the model, the office area is divided into tiles, and each tile represents a node of the graph. All tiles are connected by edges (Figure 3).

In the model, walls are located on the borders of tiles and prevent agents from passing over them. Blocks are implemented by removing the edges in the block area connecting the tiles. Rooms are enclosed areas surrounded by walls. All rooms have at least one opening, representing the door. Entrances are modeled basically as edges that connect room nodes to the whole graph. Some rooms can have more than one entrance. Entrances are designed to be wide enough to let a single agent out or in at a time. Gates are modeled by pairs of nodes connected by the entrance edge. Figure 4a shows the nodes of gates and an entrance represented by an edge. Exits are modeled as single tiles and marked as exits, while corridors are modeled as connected nodes of lines. Each node is connected with edges. In the graph, weights of the edges are defined by the distance of points they connect. Weights of edges represent the unit length, which is a measure of agents’ movement between nodes. All edges are assumed to be linear. Therefore, the weights are equal to the Euclidean distance of two endpoints of the edges. Diagonal edge weights are greater than orthogonal ones (Figure 4b).

2.2. Agent Model

The individuals simulated in this work were programmed as autonomous agents. Once the simulation started, the main goal of all agents was “to reach the exit node at once.” Agents used the A* search algorithm [47] to find their targets.

The A* algorithm is a well-known heuristic search algorithm. It provides the convenience of solving multidimensional problems with the help of a predictive heuristic function. In its most basic form, the cost of optimal path f(n) is

$$f\left(n\right)=g\left(n\right)+h\left(n\right),$$

(1)

where (n) is the next node on the path, and g(n) is the actual cost of an optimal path from the starting point to node n. The heuristic function h(n) is the cost estimate of an optimal path from node n to a preferred goal node of n. The algorithm has a fairly simple structure. It follows a path of the lowest known cost, keeping a sorted priority queue of alternate path segments along the way. The A* algorithm selects the lowest-cost node, the node with the lowest f(n) value, as the starting node and keeps following the path with the lowest known cost until it reaches the target node. If the cost of a path segment at any node is higher than the other, it chooses the lower-cost one as an alternate path. This process continues until the goal is reached. The pseudo-code of A* algorithm is given in Appendix A (

Table A1. Pseudo-code for A* search algorithm.

Algorithm:Pseudo-code for A* Pathfinding

openList: stores pending unevaluated nodes in form of a list

closedList: stores visited nodes

w: weight function; consists of weights of connecting edges

g: cost function of the node from the start

h: heuristic function

currentNode = node_start

g(node_start) = 0; f(node_start)=h(node_start)

openList.Add(node_start)

While(openList is not empty)

If(currentNode = goal) break;

For each agent in currentNode.agent

If agent is not in (openList or closedList)

openList.add(agent)

agent.Predecessor = currentNode;

if(g(agent) > g(Predecessor) + w(Predecessor,agent))

g(agent) = g(Predecessor) + w(Predecessor,agent)

For each node n in openList

Select n with min(g(n) + h(n))

closedList.Add(currentNode);

openList.Delete(currentNode);

currentNode = n;

).

There are two heuristic functions commonly used in geographic information systems (GIS) to calculate the distance between two points, Manhattan and Euclidean distances. Compared to Manhattan, Euclidean distance always guarantees the shortest distance between two points if the distance between the two points is not remote. Euclidean distance was chosen as the heuristic function in the agent model.

The heuristic function (h) is evaluated in 3-dimensional space as the Euclidean distance to the target that can be calculated using distance vector ($\partial x,\partial y,\partial z$) as in Equation (2):

$$h=\sqrt{{\left(\partial x\right)}^2+{\left(\partial y\right)}^2+{\left(\partial z\right)}^2}.$$

(2)

The heuristic function has another critical use other than effecting path cost calculations during A* search. Agents make their decisions on the next targets entirely depending on the heuristic function values where multiple target options are available. This design choice aims to mimic the loss of planning ability under stress.

In the model, an agent was allowed to occupy only one tile (node) at a time due to the personal space constraints to mimic the loss of planning ability under stress. All agents were programmed to have the same movement speed, 4 units/s. This provides the agility to traverse a nondiagonal edge in 1.25 s. Revisiting Figure 4b, this also implies that an agent can change its node diagonally in 1.25√2 s.

Agents can distinguish gates and exits from other tiles. At the start, all agents check their spatial map memory for any exit positions. If they find one or more exits, they determine the nearest exit as a target. Otherwise, they search for known gates and select the nearest unexplored gate as the target. As the office gets crowded, agents may block each other. This blocking may occur in two forms, congestion and conflict. Figure 5 shows the nature of congestion and conflict.

When agents start to move to reach a certain target (e.g., exit, gate) at the same time, this mass movement might create congestion. In case of congestion, agents may have to wait until it is removed. A crowd-threshold parameter was defined for the situation to be perceived by the agent as congestion. When an agent stops, it starts to count obstructing agents. If there are more obstructing agents than a predefined crowd-threshold value, agents perceive it as congestion and set a crowd flag. Since multiple agents search the same map, their lower-cost paths may intersect at some nodes. Let A and B be adjacent nodes that are connected with an edge and agents 1 and 2 are on these nodes. When agents 1 and 2 try to move to nodes A and B, as seen in Figure 5b, a conflict occurs and is detected by the first agent that checks if its target node is occupied. Once a conflict is detected, agents set a conflict flag and stop their movement.

The most important difference between congestion and conflict is that congestion is usually a temporary setback while a conflict is permanent if no precaution is taken or alternate plan is defined. The agent’s movement, interaction, conflict, and congestion solution abilities are controlled with four parameters: spatial knowledge, information exchange, sidestepping, and reconsideration.

2.3. Behavioral Model

The proposed behavioral model to be used by agents has a hierarchical structure that consists of DMM, negotiation, cooperation, and reasoning actions. The behavior model combines different mechanisms hierarchically. In the model, each mechanism can be controlled parametrically. These mechanisms are presented under three subsections: dynamic memory with spatial knowledge, evasion mechanisms, and behavioral action hierarchy.

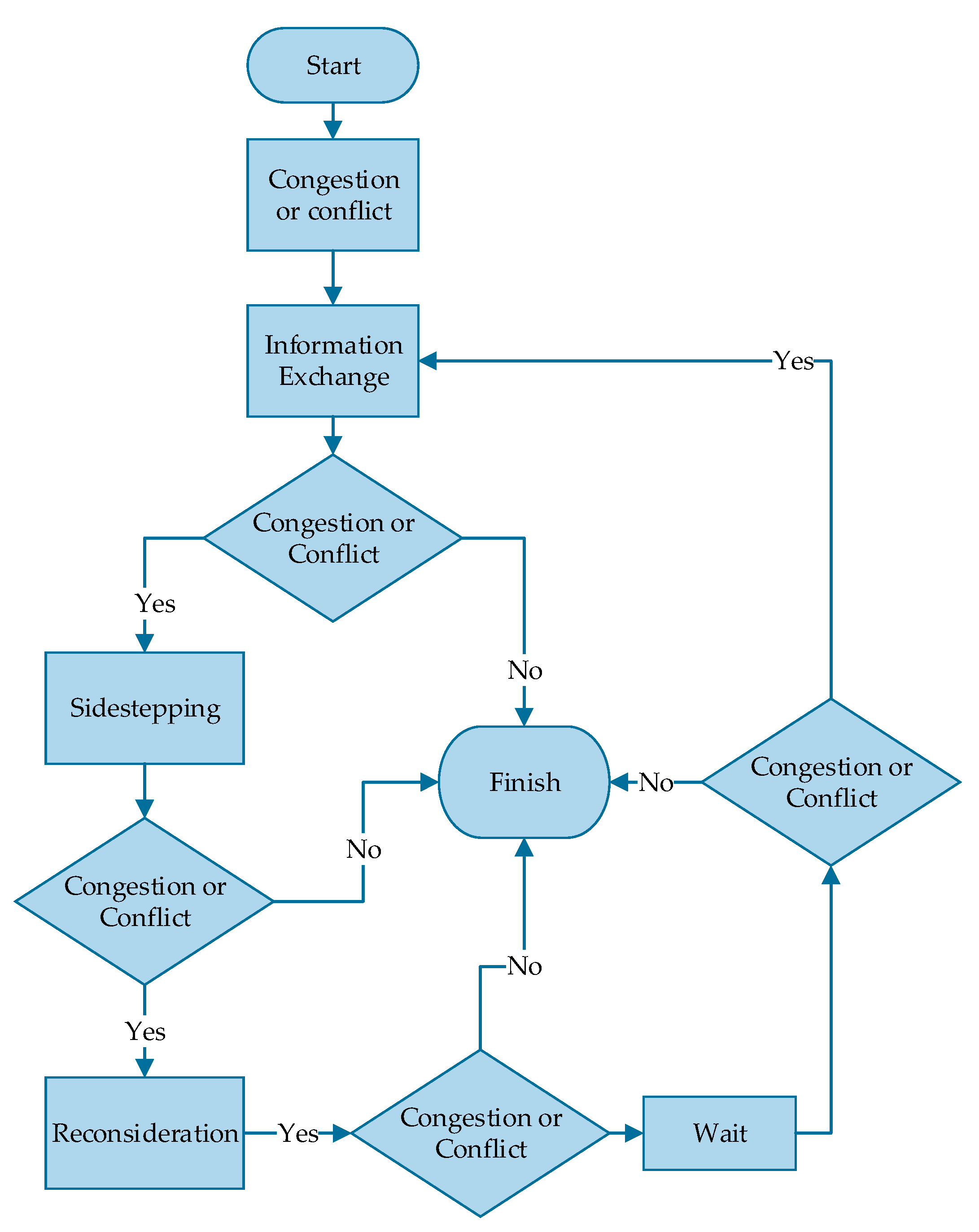
2.3.1. Dynamic Memory Management

Dynamic memory management (DMM) is controlled by the binary spatial knowledge parameter. Spatial knowledge sets the initial state of the agents’ knowledge of the office layout. If the spatial knowledge parameter is false, agents start their search without any initial spatial knowledge (empty memory) and tend to use their memorization ability as they explore the map.

Exploring and memorization are built on a simple dynamic memory expansion mechanism. Figure 6 shows the memory expansion process during exploration. Similar to humans, agents are designed to be able to perceive the room they are in. So, when an agent is in a room, it can gain information on all nodes of the room. When a node is in sight of an agent, it is immediately added to that agent’s memory. The agent expands its spatial knowledge on the map by memorizing the room once it reaches the gate of an unexplored room. If the spatial knowledge parameter is set to true, every agent starts the simulation knowing every room, gate, and exit in the office. Therefore, all agents directly select the nearest exit as their target.

2.3.2. Evasion Mechanisms

Three evasion mechanisms were defined for the model: information exchange, sidestepping, and reconsideration.

Information exchange is a simple agent cooperation mechanism to handle conflict or congestion. In case of conflict or congestion, if information exchange is allowed and spatial knowledge is false, agents that are on adjacent nodes may communicate to share their spatial knowledge on the map. During the information exchange, both sides check whether one of them has information on the grid that is unknown by the other. When one has new information, it is added to the other agents’ spatial map memory. Room and corridor layouts are the smallest office elements during memory expansion and thus are considered as the smallest piece of exchangeable information.

When a conflict occurs, the agent detecting the conflict (agent 1) sends a signal to the other agent (agent 2) to confirm the conflict and demands to know its current target node ($t_2$). If agent 1 has information about the target of agent 2 in its memory ($M_1$), it starts an information exchange procedure and shares its information with agent 2. Then the exchange procedure updates the memory collection of agent 2 as in Equation (3). After the exchange, agent 1 checks if agent 2 has changed its target. Using newly gained information, agent 2 may change its destination path to solve the conflict. Otherwise, agent 2 follows the same procedure to inform agent 1.

$$t_2\in M_1⟹M_2=M_{2}U\left(M_1-M_2\right)$$

(3)

Sidestepping is a negotiation mechanism that is effective for conflicts. However, it is not effective in resolving congestion. The sidestepping procedure starts according to the behavior plan. The procedure consists of four steps:

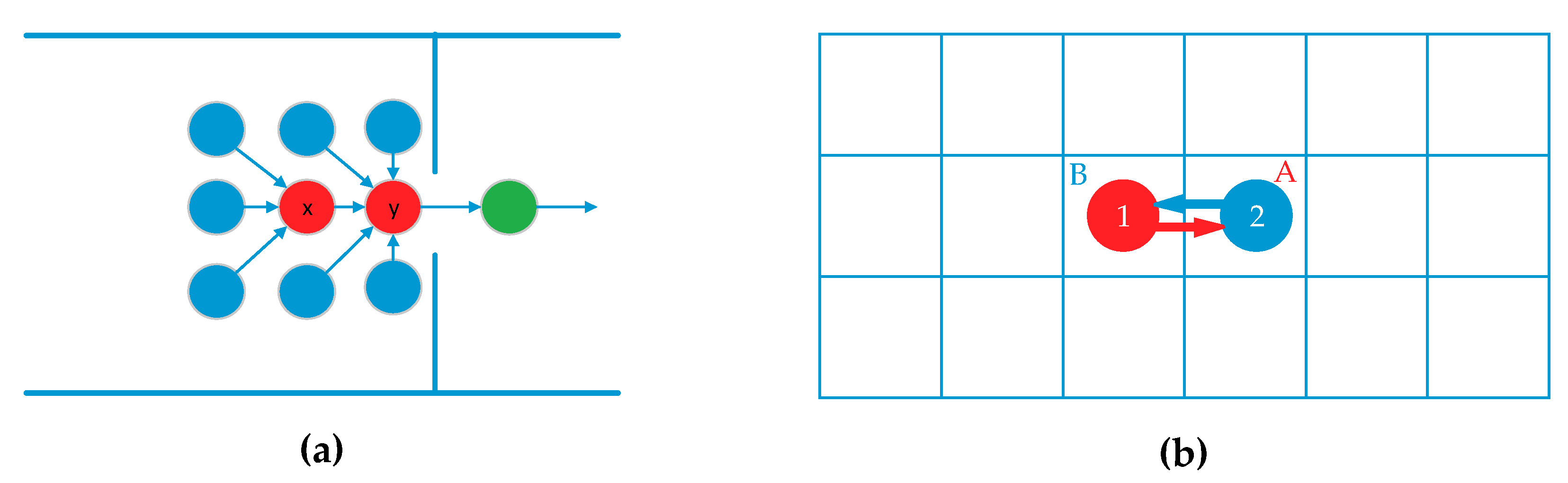
• To detect the conflict, the agent first searches adjacent nodes in order of increasing heuristic value to find an unoccupied tile.
• If there is an unoccupied slot, it sets the slot as its temporary target. With this move, the conflict condition no longer exists and can be considered as solved.
• If the first agent cannot find an unoccupied slot, this means it is surrounded. In this case, the agent raises a crowd flag and the other agent starts the same scan.
• If the second agent finds an unoccupied slot, it sets the slot as its new target. If not, both agents are surrounded and they have to wait until there is an opening or the next action in the plan is triggered.

Reconsideration is a simple agent reasoning mechanism where multiple goals are evaluated depending on the surrounding agents’ situation. If reconsideration of a path is allowed, when an agent’s path is blocked by more agents than the crowd-threshold limit, it temporarily stops moving, sets its crowd flag, and starts to wait. The waiting time is defined by the time-to-wait parameter. When a crowd flag is set, it checks whether the current situation is a deadlock or a temporary setback caused by relatively small congestion.

In decision-making, reconsideration of a path is closely related to the time-to-wait and crowd-threshold parameters. As the crowd-threshold value declines, agents tend to raise the crowd flag more often. On the other hand, if time-to-wait is set to higher values, it is more likely that the number of activated reconsideration procedures will be decreased due to the increased possibility that the congestion will be resolved. If the path is still crowded and blocked after a certain amount of time, the agent starts the reconsideration procedure. Pseudo-code for triggering the reconsideration procedure is given in Appendix A (

Table A2. Pseudo-code for triggering reconsideration procedure.

Algorithm:Pseudo-code for triggering reconsideration procedure
	If path is blocked
	wait = true;
	While (wait)
	If path is blocked
	time_waited++;
	Else time_waited = 0 and wait = false
	If time_waited ≥ time_to_wait
	Reconsideration();
	End While

).

When reconsideration is triggered, the agent checks the occupation status of eight nodes (Oadj) neighboring the current node. Then, it considers that the crowd is likely to move to the same target and keep the congestion status and calculates crowd coefficient ($C{C}_t$) as in Equation (4) by counting the occupied nodes. Pseudo-code for the crowd-coefficient calculation is given in Appendix A (

Table A3. Pseudo-code for triggering reconsideration procedure.

Algorithm:Pseudo-code for crowd-coefficient calculation
	for each adjacent node n
	if (n is occupied)
	seed++
	for(i = current_step to path_length)
	if (path[i + 1] is occupied)
	coefficient + = seed

).

$$C{C}_t={\displaystyle \sum }_{k=1}^{8}Oad{j}_{k }$$

(4)

The agent then re-evaluates the cost of the target ($C_t$) as in Equation (5) by modifying the heuristic value ($h_t$). The heuristic value is modified simply by multiplying it with the crowd-coefficient for the target.

$$C_t=h_t .C{C}_t$$

(5)

After the temporary cost is calculated for the target, the agent starts searching for its new target for the updated situation. The decision of the alternate target is made by comparing the heuristic values ($h_t$) and target (T) with minimum cost.

$$T=\left\{T_i|C_{T_i}=min\left(C_{i,n}\right)\right\}$$

(6)

Since the crowd coefficient is always greater than 1, modifying the heuristic value of the current target raises its cost. In this case, the current target is not expected to be re-selected. However, if the agent is marginally closer to this target than the other possible ones, its cost still may be the lowest. As a result, the agent may insist on its current decision. Once the new target is selected by the reconsideration process, modifications of heuristic values will be rolled back and the new path will be constructed using the A* algorithm.

2.3.3. Behavioral Hierarchy Plan

Agents are designed to execute one action at a time, which yields a conflict/congestion solution plan. Behavior plans define the hierarchy of solution mechanisms and agents’ decision flows. The conflict resolution mechanisms are triggered in order according to the order of the selected behavior plan. A procedure or action can be used only if the previous ones fail to resolve the conflict or congestion. If all actions in the plan fail, the agent waits and starts its behavior plan again in the next time step. Six behavior plans (I-S-R, I-R-S, S-I-R, S-R-I, R-I-S, and R-S-I) can be created with the three conflict–congestion resolution actions. A flowchart of the I-S-R plan is shown in Figure 7. The plan executes information exchange, sidestepping, and reconsideration procedures sequentially.

2.4. Testing the Model

To test the proposed approach, a simulation environment of a 3D office model was designed and programmed. The designed office consists of 4 rooms connected by 2 corridors and has 2 exits. Sixteen agents representing office workers were placed on different starting positions. Agent programs were designed to run as independent threads. Meanwhile, all agents were programmed to have the same size, speed, and behavior plans and to be controlled by Boolean flags that enable or disable their information exchange, memory expansion, sidestepping, and reconsideration abilities. A timer is programmed to start with the initiation of the simulation and end when all agents in the office reach one of the exits.

Agent behaviors were simulated concerning their initial physical positions and spatial knowledge to test the model. However, there is an initial positioning problem of agent replacement on the office layout when the numbers of agents and tiles are considered. The number of possible initial positions of the agents can be calculated as in Equation (7):

$$C_r^n=\frac{n!}{r!\left(n-r\right)!} ,$$

(7)

where n is the number of tiles representing agents’ personal space and r is the number of agents. The simulation environment has 64 tiles and 16 agents; 2 of the 64 tiles represent exits, and 62 tiles can be used to define an initial position (personal space) for each agent. In this case, Equation (8) results in approximately 2.73 × 10¹⁴ combinations of where agents can be located initially:

$$C_r^n=\frac{62!}{16!\left(62-16\right)!} .$$

(8)

It should also be noted that each combination has 28 scenarios. Therefore, the problem becomes a positioning problem for the simulations.

One of the approaches to solve this problem is to start the simulation with randomly located agents. However, this approach may not be realistic or represent a real case. Thus, for the simulation, we chose 2 realistic physical positioning scenarios for the agents: the worst case and a homogeneously distributed case, as shown in Figure 8. In the worst case (Figure 8a), all agents were initially positioned in 2 rooms farthest from the exit. It can be considered as an analogy of the situation that there were 2 parallel meetings or events in these rooms just before an emergency evacuation. This layout also enabled us to evaluate the evacuation performance when the agents behave under stress. In the homogeneously distributed agent case (Figure 8b), all agents were positioned as they would be in their usual positions in the office.

During the simulation, we also took into consideration the following situations related to sidestepping, reconsideration, and information exchange mechanisms along with the agents’ initial locations:

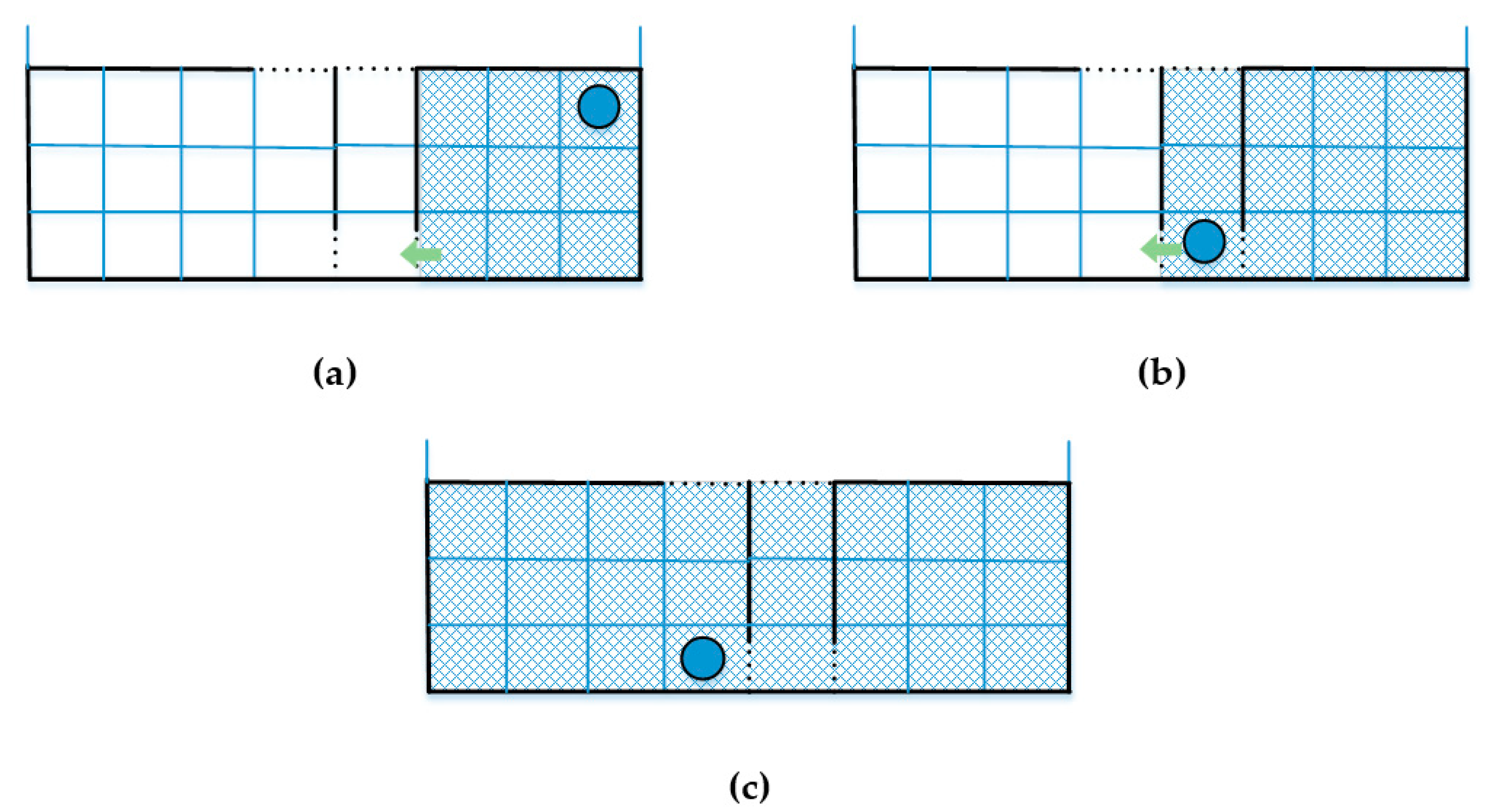
• To observe the effect of the sidestepping mechanism, there should be empty nodes around the agents to lead to the area in which they conflict.
• The reconsideration mechanism evaluates alternative routes in case of congestion. When multiple agents are placed in a room with a single door, congestion will naturally occur at the door. In this case, the effects of this mechanism cannot be observed since agents cannot find an alternative exit by running the reconsideration procedure.
• The spatial information in their memory is usually almost the same when all agents start in nearby locations. In this case, the impact of the information exchange mechanism tends to decrease.

If the agents are placed where the office doors are located, they will proceed directly to the exit without the need for an evasion mechanism. In this case, meaningful data may not be obtained from the simulation. Color coding was assigned to the agents for each procedure to visually monitor their movements and active procedures during the simulation (Figure 9).

3. Results and Discussion

Simulations were performed to evaluate (i) the effect of spatial knowledge on evacuation performance for both cases depicted in Figure 8; (ii) calibration of the reconsideration mechanism along with (i) for each case to evaluate evacuation performance; and (iii) hierarchical behavior model performance for both cases with 28 possible behavior plans.

3.1. Effect of Spatial Knowledge

Having information on the map layout is the most effective boost in the model. Since the goal is to reach the exits, knowing their locations contributes significantly to the agents’ performance. All parameters contributing to agent behavior were set to false to evaluate only the effect of spatial knowledge on escape performance. Then, the simulation was run with a different number of agents having spatial information for both cases.

Table 1. Effect of spatial knowledge on evacuation performance.

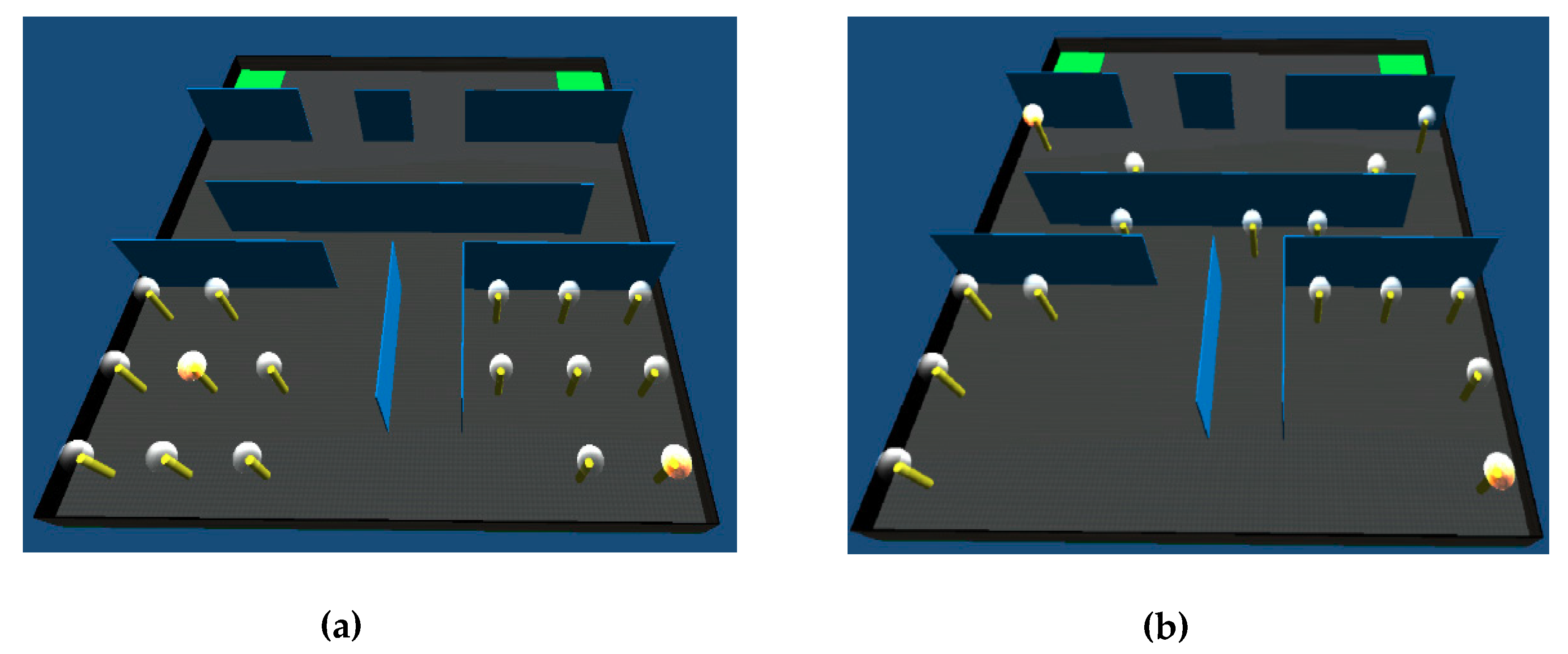
No. of Agents with Spatial Knowledge	No. of Agents Evacuated (case 1/case 2)	Evacuation of All Agents (case 1/case 2)	Avg. Escape Time (s) (case 1/case 2)
0	2/7	Fail/Fail	-/-
1	2/8	Fail/Fail	-/-
2	2/9	Fail/Fail	-/-
3	3/9	Fail/Fail	-/-
4	3/12	Fail/Fail	-/-
5	4/12	Fail/Fail	-/-
6	5/12	Fail/Fail	-/-
7	6/13	Fail/Fail	-/-
8	6/13	Fail/Fail	-/-
9	7/13	Fail/Fail	-/-
10	7/13	Fail/Fail	-/-
11	8/16	Fail/Succeed	-/32.99
12	8/16	Fail/Succeed	-/33.02
13	9/16	Fail/Succeed	-/30.24
14	11/16	Fail/Succeed	-/30.24
15	16/16	Succeed/Succeed	38.07/30.24
16	16/16	Succeed/Succeed	35.39/28.50

Case 1: worst-case layout of agents; case 2: homogeneously distributed agents (normal layout).

shows the effect of spatial knowledge on evacuation performance. In a successful evacuation scenario, it is intended that all agents escape in the shortest possible time interval. Therefore, in the study, average escape time was measured only if all agents arrived at the exit.

As shown in Table 1, successful evacuation with an average escape time of 38.07 s was observed for case 1 when at least 15 of 16 agents had spatial knowledge. Similarly, for case 2, successful evacuation with an average escape time of 32.99 s was observed when 11 of 16 agents had spatial knowledge. When all or at least 15 of 16 agents had spatial knowledge on the map, successful evacuation with different average escape times was observed for both cases. The average escape time, as expected, was higher in case 1, which represents the worst-case situation, compared to case 2.

The results in Table 1 show that when all agents were informed about the layout, the problem took a straightforward form and agents evacuated the office in the shortest time interval. In this case, performance was not affected by any other parameters, because when agents are set to reach the same target, the model will not generate any conflict or congestion. Therefore, solving mechanisms for conflict and congestion will not be needed. Thus, the smallest successful average escape time can be interpreted as an optimal value for the model.

3.2. Calibration of Reconsideration Mechanism

As discussed in Section 2 on evasion mechanisms, the reconsideration procedure is triggered when a congestion state is detected. The count of the procedure run by the agents gives an idea about the size of the congestion. Activation of the reconsideration procedure is solely related to time-to-wait and crowd-threshold parameters. The crowd-threshold parameter defines how an agent perceives whether it is a crowd, and the time-to-wait parameter tells an agent how long it is supposed to wait before continuing its movement in case a conflict/congestion is detected. It was expected that during the simulation a higher crowd-threshold value would lower the reconsideration procedure triggered by agents. Similarly, it was expected that as the time-to-wait increased, the reconsideration procedure would be triggered because the possibility of resolving congestion increases since agents wait longer before searching for an alternate path.

The reconsideration mechanism can be calibrated and optimized by tuning the parameters. In optimization, time-to-wait and crowd-threshold parameters were tuned by considering the office layout. To adjust the optimal time-to-wait and crowd-threshold values for the reconsideration procedure, tests were performed while spatial knowledge, sidestepping, and information exchange were disabled. The average time for all agents to escape was used as the performance criterion of the model. Then the evacuation performance was analyzed as time-to-wait and crowd-threshold parameters changed until optimal values were obtained. The effects of the two parameters on reconsideration performance are given in

Table 2. Effects of time-to-wait and crowd-threshold parameters on reconsideration performance.

Time-to-Wait (s)	Crowd-Threshold
	1		2		3
	Case 1	Case 2	Case 1	Case 2	Case 1	Case 2
0	43.86	38.49	45.45	37.46	43.36	35.68
0.2	42.20	38.82	47.22	43.62	42.65	39.12
0.4	46.85	36.37	43.25	33.57	44.40	38.03
0.6	43.33	37.73	49.75	35.85	46.16	36.47
0.8	50.84	38.11	50.25	35.41	46.82	38.71
1	46.65	37.15	44.45	37.45	48.55	38.95
1.2	50.77	38.72	51.10	39.23	49.37	40.17
1.4	50.43	38.53	49.95	40.83	50.20	41.03
1.6	50.69	42.01	50.49	40.71	50.58	42.01
1.8	56.12	40.37	53.94	40.79	54.90	41.03
2	59.61	42.11	61.09	42.25	58.67	42.61
2.2	64.91	44.42	60.79	44.43	57.04	45.02
2.4	67.00	45.62	64.40	44.49	55.43	46.02
2.6	67.34	46.81	71.21	43.07	55.45	46.91
2.8	71.63	48.03	63.52	48.04	55.53	48.70
3	74.08	50.76	73.61	50.65	55.57	51.76

Case 1: worst-case layout of agents; case 2: homogeneously distributed agents (normal layout).

.

As shown in Table 2, the optimal combination of values for reconsideration guaranteeing the shortest evacuation time was observed in case 1 when time-to-wait and crowd-threshold were 0.2 s and 1, respectively, and in case 2 when time-to-wait and crowd-threshold were 0.4 s and 2, respectively.

The relation between the number of reconsideration procedures triggered during evacuation and the time-to-wait parameter for the worst-case scenario is given in

Table 3. Relation between number of reconsideration procedures triggered during evacuation and time-to-wait parameter for worst-case scenario.

Time-to- Wait (s)	Crowd-Threshold
	1	2	3	1	2	3
	Spatial Knowledge True			Spatial Knowledge False
0	3685	3396	1172	2425	2058	1165
0.2	475	451	153	452	417	242
0.4	222	214	76	252	224	146
0.6	132	124	46	167	139	96
0.8	87	85	32	146	145	95
1	72	65	24	107	106	71
1.2	45	42	15	88	85	70
1.4	33	29	10	75	73	70
1.6	25	24	8	73	66	36
1.8	19	18	8	47	46	36
2	17	15	7	46	41	30
2.2	14	12	7	35	33	29
2.4	8	8	4	33	32	20
2.6	7	7	2	33	31	15
2.8	5	4	2	19	16	14
3	4	4	2	12	10	6

. As seen in Table 3, when the spatial knowledge parameter was set to true, all agents immediately determined the lowest-cost path to the exit and started to move. In the worst-case scenario, since most agents were in the same room, they may have chosen the same lowest-cost path as others. In this case, when time-to-wait was small, agents frequently showed a tendency to search for an alternate lowest-cost path. As time-to wait increased, agents followed their lowest-cost path with less frequent searches for an alternate lowest-cost path. Similar behavior of agents was observed when the spatial knowledge parameter was set to false.

On the other hand, it should be noted that if crowd-threshold is set to a value higher than 3, congestion may occur with fewer agents than the specified value. Consequently, the reconsideration procedure might not be triggered properly and successful evacuation is not guaranteed.

3.3. Test Results

The simulation was run using all possible parameter settings with all agents using all possible behavior plans. The simulation runs in real time and agents have their own unique and dynamic perceptions. Thus, the simulation can be considered to have a non-deterministic structure and this may have a slight effect on model performance. Tests were repeated several times for each behavior plan and escape times were recorded during the tests to obtain the average escape time.

Table 4. Test results.

Test No.	Behavior Plan	Spatial Knowledge	S	I	R	Escape Ratio		Avg. Escape Time (s)
						Case 1	Case 2	Case 1	Case 2
0	-	T	F	F	F	1	1	35.39	28.50
1	-	F	F	F	F	0.125	0.5	Fail	Fail
2	-	F	F	F	T	1	1	42.20	33.57
3	-	F	F	T	F	0.125	0.5	Fail	Unstable
4	-	F	T	F	F	1	1	52.65	40.01
5	I-S-R	F	F	T	T	1	1	41.55	34.42
6	I-S-R	F	T	F	T	1	1	45.49	39.32
7	I-S-R	F	T	T	F	1	1	46.17	30.75
8	I-S-R	F	T	T	T	1	1	43.71	35.09
9	S-I-R	F	F	T	T	1	1	41.55	34.42
10	S-I-R	F	T	F	T	1	1	45.49	39.32
11	S-I-R	F	T	T	F	1	1	48.97	32.45
12	S-I-R	F	T	T	T	1	1	41.57	36.59
13	R-S-I	F	F	T	T	1	1	43.03	35.11
14	R-S-I	F	T	F	T	1	1	43.98	34.57
15	R-S-I	F	T	T	F	1	1	48.97	32.45
16	R-S-I	F	T	T	T	1	1	43.14	35.49
17	R-I-S	F	F	T	T	1	1	43.03	35.11
18	R-I-S	F	T	F	T	1	1	43.98	34.57
19	R-I-S	F	T	T	F	1	1	46.17	30.75
20	R-I-S	F	T	T	T	1	1	42.22	35.22
21	I-R-S	F	F	T	T	1	1	41.55	34.42
22	I-R-S	F	T	F	T	1	1	43.98	34.57
23	I-R-S	F	T	T	F	1	1	46.17	30.75
24	I-R-S	F	T	T	T	1	1	41.48	34.78
25	S-R-I	F	F	T	T	1	1	43.03	35.11
26	S-R-I	F	T	F	T	1	1	45.49	39.32
27	S-R-I	F	T	T	F	1	1	48.97	32.45
28	S-R-I	F	T	T	T	1	1	44.91	36.1

Case 1: worst-case layout of agents; case 2: homogeneously distributed agents (normal layout). I, information exchange; R, reconsideration; S, sidestepping.

gives the test results for 29 scenarios for both cases; 24 of the 29 scenarios correspond to 6 behavior plans. In Table 4, T and F stand for true and false, respectively. Test 0 was derived from Table 1, representing the data for both cases with the shortest evacuation times. In test 1, all parameters were set to false, representing the condition in which agents did not have spatial knowledge and the behavior plan was not defined. Tests 2–4 show the average escape results when only one mechanism was active.

More than one mechanism is required to create a hierarchical plan. Therefore, the results of the first five tests should be interpreted independent of the plan. The evacuation process failed when none of the mechanisms were activated. In tests 1 and 3, 14 of 16 agents for case 1 and half the agents for case 2 could not reach any of the exits because of conflicts, thus evacuation failed. Test 3 shows that information exchange alone is not always enough for a solution. However, when information exchange was combined with one or more additional conflict solution mechanisms, as in tests 5, 7, and 8, the model was stable and always found a solution. In tests 2 and 4, the reconsideration mechanism alone achieved successful evacuation for both cases with better performance compared to sidestepping.

The corresponding behavior plans of 24 of 29 scenarios are summarized as 12 hierarchy plans in

Table 5. Summary of test results with hierarchy plans.

Hierarchy Plan	Tests	Avg. Escape Time (s)
		Case 1	Case 2
I-R	5, 9, 21	41.55	34.42
R-I	13, 17, 25	43.03	35.11
R-S	14, 18, 22	43.98	34.57
S-R	6, 10, 26	45.49	39.32
I-S	7, 19, 23	46.17	30.75
S-I	11, 15, 27	48.97	36.59
I-R-S	24	41.48	34.78
S-I-R	12	41.57	36.59
R-I-S	20	42.22	35.22
R-S-I	16	43.14	35.49
I-S-R	8	43.71	35.09
S-R-I	28	44.91	36.10

.

Table 5 shows double and triple combinations of behavior actions in a hierarchy plan. The evacuation performance of binary combinations in a plan can be compared to evaluate the effect of the order of actions in a hierarchy, e.g., I-R vs. R-I, and the use of actions with other alternatives such as I-R vs. I-S. Then, the effect of each action on the evacuation performance of the hierarchy plan with triple combinations can be evaluated.

For the worst-case layout (case 1), tests 5, 9, and 21 with the I-R plan resulted in the best stable evacuation performance among binary combinations of actions. On the other hand, the I-S plan (tests 7, 19, 23) generated the best stable evacuation performance for case 2. Tests 13, 17, and 25 and tests 5, 9, and 21 demonstrated that if the hierarchy was changed from R-I to I-R, evacuation performance improved for both cases. Similar results were observed in both cases for hierarchy changes of S-I (tests 11, 15, 27) to I-S (tests 7, 19, 23) and S-R (tests 6, 10, 26) to R-S (tests 14, 18, 22). When the stable evacuation performance for binary combinations was sorted in a descending manner, Equation (9) for case 1 and Equation (10) for case 2 were obtained:

$$\mathrm{I}-\mathrm{R}<\mathrm{R}-\mathrm{I}<\mathrm{R}-\mathrm{S}<\mathrm{S}-\mathrm{R}<\mathrm{I}-\mathrm{S}<\mathrm{S}-\mathrm{I},$$

(9)

$$\mathrm{I}-\mathrm{S}<\mathrm{I}-\mathrm{R}<\mathrm{R}-\mathrm{S}<\mathrm{R}-\mathrm{I}<\mathrm{S}-\mathrm{I}<\mathrm{S}-\mathrm{R}.$$

(10)

A comparison of Equations (9) and (10) suggests that designating information exchange as the first action improves the evacuation performance by shortening the average escape time. In other words, information exchange can be considered as the fastest conflict/congestion solution mechanism only when combined with other mechanisms. However, it is the only mechanism that does not guarantee a stable solution when used alone. Similarly, a comparison of Equations (9) and (10) implies that the second most effective mechanism is reconsideration if time-to-wait and crowd-threshold parameters are optimized. Therefore, the hierarchy can be sorted as information exchange–reconsideration–sidestepping (I-R-S), where information exchange has the highest rank in the plan. Test 24 in Table 5 confirms that the I-R-S plan achieved the best performance for both cases compared to other triple combinations of behavior actions in a hierarchy plan.

The nature of emergency egress problems can differ in many ways. There are a few emergency evacuation studies in the literature that could be considered as related to our approach.

Table 6. Comparison of proposed model performance improvement.

Model	Simulated Environment	Spatial Knowledge/Situational Awareness	Improvement (%)
Obstacle control [11]	Single room	Yes	10.4
Parametric [12]	High-rise building	Yes	24
GAM [13]	Vertical ship lift	Yes	28.5
Management Optimization [14]	Building	Yes	25,2
	Roads	Yes	12
Planned evacuation [15]	Santai County (China)	Yes	31
PSEP [16]	Multi-exit building	Yes	30
HBP	Office environment (multi-exit)	Yes	32.78
		No	23.14

GAM, guided evacuation agent model; PSEP, positioned and staged evacuation planning; HBP, hierarchical behavior plan (proposed in this paper).

summarizes a comparison of our study with others in terms of evacuation performance. The existing studies use either spatial knowledge or situational awareness or both as parameters to inform agents in their models. Situational awareness informs agents as to the locations of danger areas and exits and thus can be interpreted as similar to spatial knowledge in our study.

A simple approach [11] splitting the flow by using obstacles in front of exits to control congestion formation managed to decrease evacuation time by up to 10.4%. An evacuation model that was built for high-rise buildings [12] achieved 24% performance improvement when agents were provided with situational awareness. The guided evacuation agent model (GAM) [13] resulted in a 28.5% improvement in evacuation time when crew member agents were used as guides to direct other agents according to optimal evacuation plans. The simulations provided in [14] highlighted that management optimization is a key factor in evacuation performance. Evacuation time from the building was improved up to 25.2% when items on evacuation paths were removed with management optimization. In research based on a time-extended network model for evacuation with optimization [15], the planned evacuation model achieved up to 31% faster evacuations. The partitioned and staged evacuation planning (PSEP) algorithm for multi-exit evacuation [16], which requires evacuation planning to be divided and processed in smaller groups to reduce the complexity of the problem, had similar efficiency with reduced computational cost compared to the model in [15].

As shown in Table 6, studies have mostly focused on physical environmental conditions, while this paper focuses on simulating the social hierarchical behavior of agents in emergencies with both supervised (with spatial knowledge) and unsupervised (without spatial information) conditions. The hierarchical behavior planning (HBP) model proposed in this paper achieved a performance enhancement of 23.14% when spatial knowledge was not available to agents. When agents were supplied with spatial knowledge, as in the other studies in Table 6, the proposed model demonstrated up to a 32.78% improvement in evacuation performance in the simulated environment.

4. Conclusions

In this paper, a hierarchical behavior model for a multi-agent system with evasion capabilities and dynamic memory simulating the social behavior in an office environment during an emergency was presented. Collision avoidance, negotiation, conflict solution, and path-planning mechanisms were used to simulate the behaviors of agents.

The test results prove that the mechanisms in the proposed model have different characteristics that fit each other well in situations where different hierarchies are needed. Each mechanism contributes at a different level to evacuation performance. The ranks defining priorities within the hierarchy can be sorted as information exchange–reconsideration–sidestepping, where information exchange is ranked highest in the plan. Information exchange contributed the most to conflict/congestion prevention, reconsideration the most to conflict/congestion resolution, and sidestepping to evacuation performance, with its conflict resolution property. The degree of contribution depended on the involvement of either one or both mechanisms. It provided the least contribution when the I-R-S hierarchy was applied. The contribution of behaviors was also heavily dependent on environmental circumstances. Mechanisms used in the hierarchical model are loosely coupled and can easily be modified or completely changed. Thus, the proposed mechanism calibration methods enhance the model’s ability to adapt to different situations.

The DMM algorithm in the model provides a solution to the problem of the unavailability of prior spatial knowledge, which most evacuation approaches need. The DDM algorithm explores the map by coordinating with the information exchange mechanism. DMM with a hierarchical behavior plan achieved a performance improvement of 23.14% in escape time without providing agents with any initial environmental information.

Although the proposed model was tested on a grid–graph structure, it is applicable and adaptable to any graph-based environment structure. In this case, it should be noted that the pathfinding algorithm and heuristic function may require customization. The simulation results reveal that the proposed model successfully demonstrates the social behavior of agents. Therefore, the model may be used to support emergency evacuation planners, providing simulations with different hierarchical social behaviors of agents. Our further studies will focus on advancing and adapting the hierarchical behavior models to different environments and scenarios, such as cooperative search and rescue in disaster situations.