1. Introduction
In recent years, natural hazards have occurred quite frequently [
1]. Landslides, which threaten human life and property, are considered as one of the most detrimental geological disasters that frequently occur in the mountainous area [
2,
3]. Landslides are defined as the downslope mass-displacement of earth, debris, and rock, because of gravity impact [
4,
5]. It has proven that landslides have an important role in the environmental, social, economic, and cultural sustainability of human beings [
6]. Landslides occur in different sizes and shapes and are triggered by diverse factors such as earthquakes, rainfall, volcanic eruptions, and slope erosion [
7]. It is predicted that the occurrence of landslides will increase in the future because of various factors, such as infrastructure development, population growth, and mistreatment of natural resources [
1,
8]. Landslides can be considered as a natural phenomenon that is often triggered by the impact of human undertakings [
9]. The scientific community has significantly seen an upturn in the novel approaches being considered for the assessment of landslides due to the alarming increase of landslides across the globe [
10]. It is vital to study the region’s susceptibility to landslides to understand the impact of various factors influencing the occurrences of landslides. Landslide susceptibility mapping (LSM) is the quantification of the likelihood of incidences of landslides depending on the impact of the various conditioning factors in the given region [
11]. The LSM is pivotal in managing the landslides and there are diverse approaches used for deriving landslide susceptibility maps [
7,
12]. LSM mainly wishes to measure, map, and eventually comprehend the spatial distribution of the occurrences of landslides in the future [
13]. There has been very little research on landslide susceptibility done at the national scale, rather focusing more on the regional scale [
14].The LSM can help authorities and decision makers to plan effective management strategies for landslide prevention and mitigation [
15,
16].
Geographic information systems (GIS) have been proven to be a robust tool for studying various natural hazards, including landslides, such as preparation of inventory data, landslide susceptibility mapping, and landslide detection [
17,
18,
19]. Remote sensing (RS) have also contributed to augmented assistance in mitigating and planning of natural hazards [
20]. Multi-criteria decision making (MCDM) is a broadly accepted approach that has been applied in a wide range of issues in diverse fields, which also includes studies on LSM. The integration of GIS and the MCDM approach allows for converting spatial as well as non-spatial data into meaningful information. Analytical hierarchical process (AHP) assessment is a multi-criteria expert-based approach that is widely used in susceptibility mapping [
21,
22]. However, the AHP approach has some gaps and limitations, such as ignoring the interrelations among the different causes at different levels, low performance in the case of 5 × 5 or larger Pairwise Comparisons, and the eigenvector optimality problem [
23]. Some of the limitations and inabilities of the application of the AHP in the spatial decision support systems are described by [
24,
25,
26,
27,
28]. The Fuzzy set theory, mimicking human judgment, has been designed to reduce inconsistency and uncertainty in decisions as well as overcoming the limitations of AHP [
29]. In this regard, several fuzzy-based methods have been introduced and implemented in different fields in recent years; the successful application of the Fuzzy Analytical hierarchical process (FAHP) method in LSM can be an example.
The best-worst multi-criteria decision-making method (BWM) is one of the latest MCDM models created by Rezaei in 2015 [
30]. It seeks to overcome the inconsistency derived from pairwise comparisons by minimizing the pairwise comparisons as well as obtaining the weights of criteria and alternatives with respect to different criteria [
31]. Even though the BWM uses a 1–9 scale to perform the pairwise comparisons, like AHP, it only executes the preference of the best and the worst criteria over all the other criteria that are completely different from AHP. Because the secondary comparisons are not executed in this method, it is much more comfortable, more precise, and has lesser redundancy. However, expert knowledge and judgment, which usually hold some drawbacks, such as ambiguity and uncertainty into the model, play an important role in the BWM method. Therefore, employing a fuzzy set theory, which may be more in line with real-world situations and can achieve better results, is considered an efficient solution. However, expert knowledge and judgment, which usually hold some drawbacks, such as ambiguity and uncertainty into the model, play an important role in the BWM method [
27]. Therefore, employing a fuzzy set theory, which might be more in line with real-world situations and can achieve better results, is considered to be an efficient solution [
23].
In an alpine and mountainous country, like Austria, mass movements or landslides are a prevalent natural hazard [
32]. Several studies were carried out assessing land susceptibility map at national scales worldwide, mostly focusing on fewer conditioning factors and statistical approaches [
9,
33,
34,
35,
36,
37]. For example, while applying seven factors and hybrid methods, Suh and others (2011) generated a national-scale assessment of landslide susceptibility of rock-cut slopes along expressways in Korea [
35]. Trigila and others (2013) used different models (logistic regression, discriminant analysis, and Bayesian tree random forest) to produce an LSM in Italy [
34]. In 2011, an LSM for Romania was obtained using seven main factors and landslide susceptibility index by Balteanu and others. In the case of Austria, there are two studies that have been carried out for entire Austria [
38,
39]; however, there remain some challenges in terms of susceptibility mapping and the approaches used [
40]. This paper aims to investigate the application of fuzzy best-worst multi-criteria decision-making (FBWM) for generating an LSM at a national scale that has not yet been carried out to date, to our best knowledge. This study is quite relevant to the present scenario, where there have been heavy landslides in Austria causing several mortalities and major economic losses. This study also investigates the role of employing a few numbers of pairwise comparisons on LSM by comparing FBWM and FAHP.
3. Methods
The methodology of present research contains three stages, as follows: (1) Deterring the criteria affecting LSM and submitting them to experts for initial ranking and identifying the best criterion and the worst criterion (see
Section 2.2.2). (2) Implementing the FBWM and FAHP to generate LSM. (3) Validation FBWM and FAHP using the Receiver operating characteristic curve (ROC) and area under the curve (AUC). (4) Comparison of generated landslide susceptibility maps.
3.1. Fuzzy Best–Worst Method
The Best–Worst Method (BWM) was suggested by Rezaei [
30], where he demonstrated that the MCDM problems might be resolved by pairwise comparisons having a very low number [
56]. In the proposed method, the user selects the most important criterion and the least important criterion from all of the criterions available and the best or the most important criterion is then compared with all other criteria and assigned a number in the range between 1 to 9, where 1 represents that the criterion is as important as the best or most important criterion, and 9 represents that the best criterion is nine times more important than the worst criterion [
57]. Likewise, the comparison is done for the least or the worst important criterion, with all the other criteria. These numbers or values are then used for an optimization process [
58]. The objective of this optimization process is to gain the maximum degree of consistency via minimizing the maximum difference between the best-criterion-to-any-criterion comparison value and the ratio of the weights of the best criterion and that criterion. It also targets minimizing the maximum difference between the any-criterion-to-worst-criterion comparison value and the ratio of the weights of that particular criterion and the worst criterion. This optimization is done by some more value constraints, such as the maximum possible value of the sum of the weights.
Generating LSM in Austria, we applied FBWM that contains six main steps in order to determine the weights of the criteria, as follows:
Phase 1. Generate the decision criteria system. As the values of decision criteria have an impact on the performances of different alternatives, generating the decision criteria system, which involves a set of decision criteria, is considered a vital step for realistically performing the assessment on alternatives.
Phase 2. Defining the best criterion (the most important) and the worst criterion (the least important). In this step, based on experts’ opinions, the best criterion and the worst criterion should be identified.
Phase 3. Determining the fuzzy preference of the best criterion against all other criteria. In this section, applying the linguistic terms of experts that are listed in
Table 2, the fuzzy preference of the best criterion against all the other criteria can be identified. Subsequently, based on the transformation rules that are shown in
Table 1, the acquired fuzzy preferences are transformed to TFNs. The achieved fuzzy best criterion -to-others vector is:
where
symbolizes the fuzzy best criterion -to-others vector and
symbolizes the fuzzy preference of the most important criterion
over criterion
j, j = 1, 2, ···,
n.Phase 4. Determining the fuzzy preference of the worst criterion against all other criteria. In this step, imitating the previous step, the fuzzy preference of the worst criterion against all the other criteria is identified. The achieved fuzzy worst criterion-to-others vector is:
where
symbolizes the fuzzy worst criterion-to-others vector and
symbolizes the fuzzy preference of the least important criterion
i over criterion
,
i = 1, 2, ···,
n.Phase 5. Defining the ideal fuzzy weights. The ideal fuzzy weights for each criterion
can be reached when for each fuzzy pair
and
. To obtain these conditions, the maximum absolute gaps
and
for all
j should be minimized (see Equation (3)). Transforming the crisp value of fuzzy weight
is another section that should be done in this phase; in this study, the graded mean integration representation was used to this end (see Equation (4)).
Phase 6. Analyzing the consistency ratio (CR). CR is considered to be a vital indicator to assess the consistency ratio of pairwise comparisons. A fuzzy comparison can be counted as fully consistent when
, where
,
are the fuzzy preference of the best criterion against the worst criterion, the fuzzy preference of the best criterion against the criterion
j, and the fuzzy preference of the criterion
j against the worst criterion, respectively. In general, the CR can be calculated for FBWM, as follows:
where
.
The maximum possible
can be reached, which is implemented as the consistency index (CI) for fuzzy BWM, by solving Equation (5) for dissimilar
. When considering different linguistic terms of expert’s opinions, the obtained CI for FBWM is listed in
Table 3.
3.2. Fuzzy Analytical Hierarchical Process (FAHP)
Fuzzy analytical hierarchical process has been widely used in recent years in order to deal with uncertainty and fuzziness in the multi criteria decision making. The approach of FAHP entails utilization of scientific approach where the weights are derived through fuzzy pair wise comparisons matrices [
59]. There are various approaches of FAHP used by researchers for diverse applications transportation [
60]. A novel approach of synthetic extent standards for handling FAHP through pairwise comparison was proposed [
61]. For this study, a method for synthesized multi-index analysis using FAHP analysis to define index weight was used. An eight-step procedure describing FAHP is provided in
Figure 2, whilst a detailed description of the methodology is presented in
Figure 3.
By using the fuzzy sets theory, it is possible to consider more than one susceptible class while using the concept of partial membership. Based on this perspective, the spatial variability was analyzed using the fuzzy membership functions. The practice of fuzzy sets theory in landslide assessment has been considered to improve the resulting susceptibility mapping. Consequently, all of the landslide initiating factors were harmonized in range of 0 (low susceptible) to 1 (high susceptible).
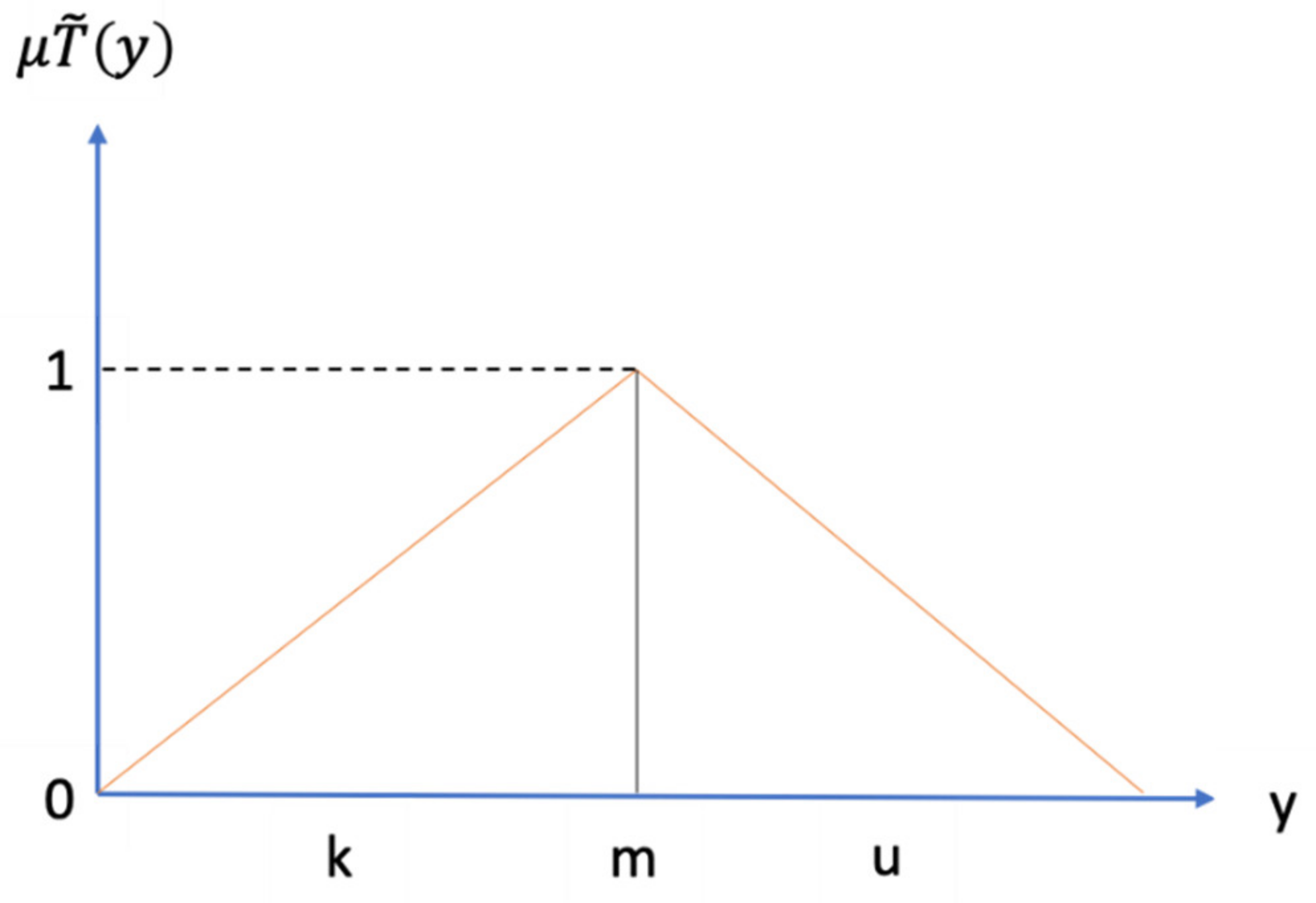
A fuzzy number
on
to be a triangular fuzzy number if its membership function
is equal to the following formula (6):
From formula (1),
and
mean the lower and upper bounds of the fuzzy number
and
is the modal value for
. The triangular fuzzy number can be denoted by
. The operational laws of triangular fuzzy number
and
are displayed as following Equations (7)–(11). Addition of the fuzzy number
A triangular fuzzy set was utilized for transforming the linguistic variables to the quantitative values for this study, as shown n
Figure 2.
Multiplication of the fuzzy number
Subtraction of the fuzzy number
Division of a fuzzy number
Reciprocal of the fuzzy number
For this study, we used the triangular fuzzy numbers scale which is a computational technique was used.
Table 4 shows the triangular fuzzy numbers scale [
62].
The engaged pairwise comparison matrices are crafted based on the hierarchical structure. Pairwise comparisons are crafted by assigning linguistic terms to equate which criteria are the more important than the other with respect to the main one, as
the bigger matrix (
) in the study, as presented below in Equation (12):
where
where a
is fuzzy comparison value of dimension
to criterion
j.
The fuzzy geometric mean was used for aggregating the fuzzy weights as shown in Equations (13)–(14).
is a geometric mean of fuzzy comparison value of criterion to each criterion and is the fuzzy weight of the th criterion that can be designated by a triangular fuzzy number, . The stand for the lower, middle, and upper values of the fuzzy weight of the th dimension.
3.3. Receiver Operating Characteristics (ROC)
Validation is a key aspect of any analysis that enables insights into the accuracy of the models used for the study [
5,
63]. The relationship between the inventory data and the resulting LSM is very important for predicting the effectiveness of the model. The accuracy of the model indicates whether the model has correctly predicted the areas susceptible to landslides.
The receiver operating characteristics (ROC) curve was used for validating the resulting landslide susceptibility maps while using the validation data. The ROC approach allows for a comparison between the true positive rate and the false positive rate in the resulting landslide susceptibility maps [
64,
65]. ROC curves were calculated for all landslide susceptibility maps. Pixels that are correctly identified (high susceptibility) and thus match the landslide reference data are the true positive rates, while the incorrectly labeled pixels are the FPRs. ROC curves are generated by plotting the true positive rates versus the false positive rates. The area under the curve (AUC) is the degree that specifies the accuracy of the resulting landslide susceptibility maps. The AUC indicates the probability that more pixels were correctly labeled than incorrectly labeled. Greater AUC values indicate a higher accuracy and lower AUC values indicate lower accuracy of the susceptibility map. If the AUC values are close to unity, then this indicates a significant susceptibility map. A value of 0.5 shows an insignificant map, because it means that the map was generated by coincidence [
66].
5. Conclusions
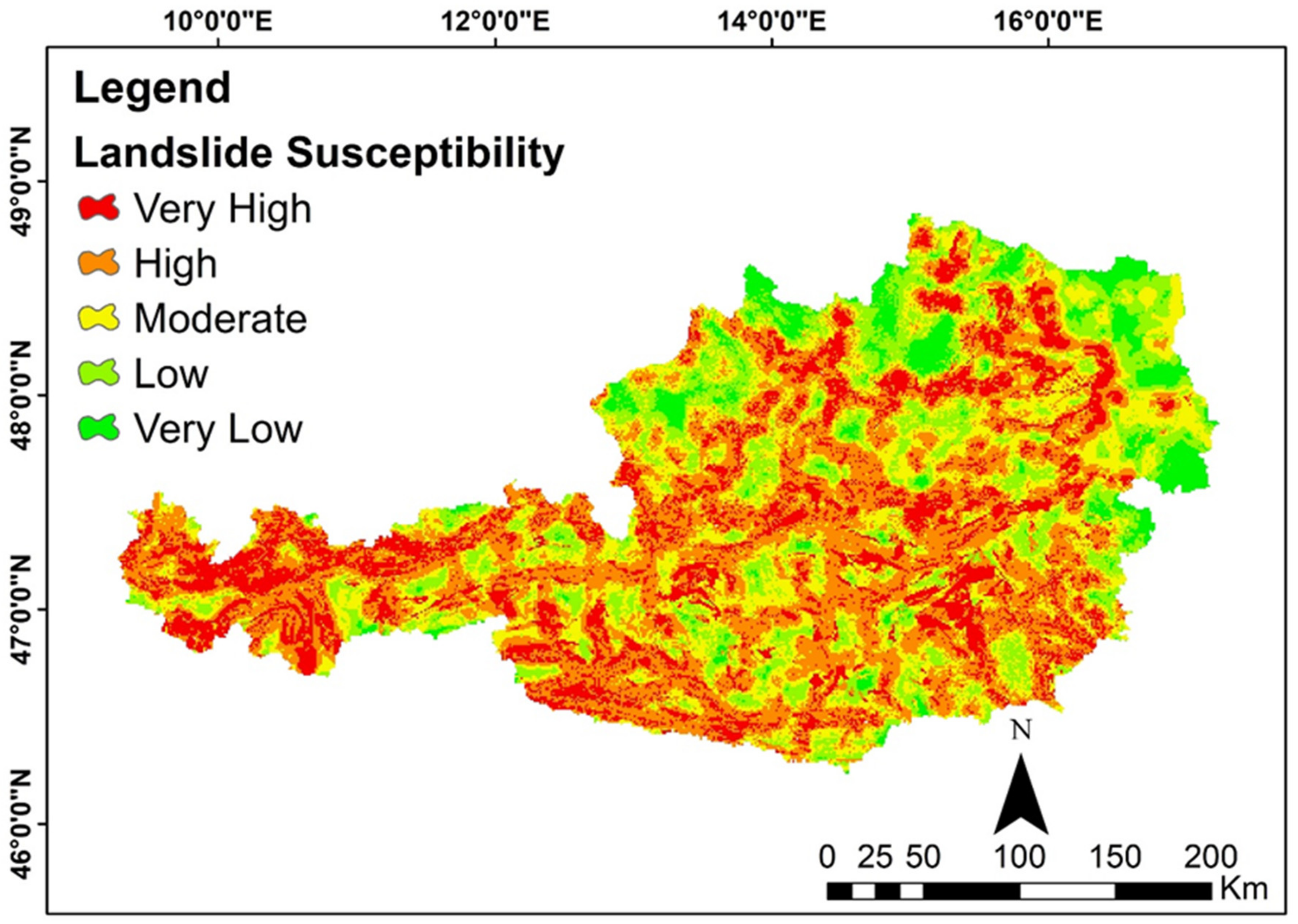
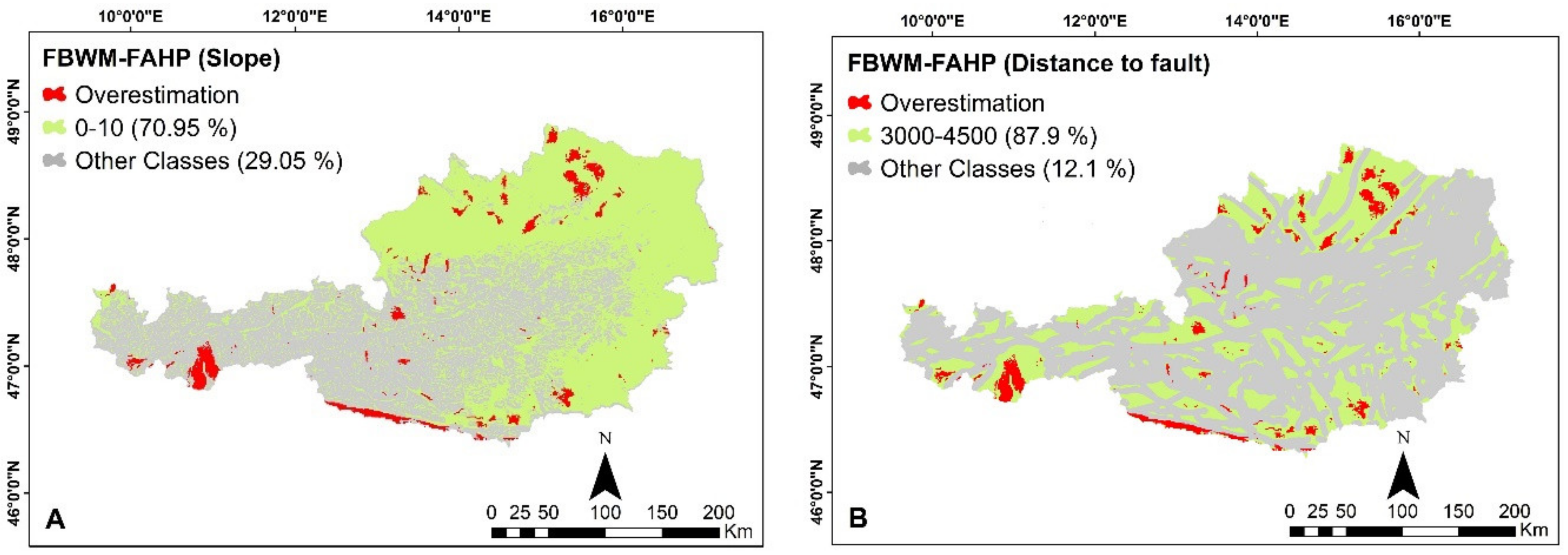
The mapping of landslide susceptible areas is for identifying areas that are prone or susceptible to future occurrences of landslides. LSM is a crucial step in the analysis of risk assessments of landslides. So far, there are very few detailed studies on landslide susceptibility mapping at a national scale in Austria. FAHP was developed for solving hierarchical problems in handling the uncertainty and vagueness that are involved in the pairwise comparison process, whereas the FBWM is an extension of classical set theory that can solve the practical problems in an uncertain environment. By comparing the approaches along with the susceptibility maps, we can concur the by the accuracy of the models regarding the suitable approach for national level landslide susceptibility mapping. For this study, we produced LSM for entire Austria based on FBWM, which is a novel approach for landslide susceptibility and also compared the results with the FAHP approach. The results clearly show that the accuracy of the FBWM approach is higher than the FAHP approach in both success rate and prediction rate curves. The AUC of the SR for the FAHP was 90% when compared to higher SR for the FBWM at 93%. Whereas, the AUC of PR for FAHP was 84% as compared to 89% for fuzzy BWM. The FBWM is a vector-based technique that needs lesser pairwise comparisons when compared to the matrix based FAHP approach. Another advantage of FBWM is that the final weights derived show higher CR when compared to MCDM approaches that do not get higher CRs.
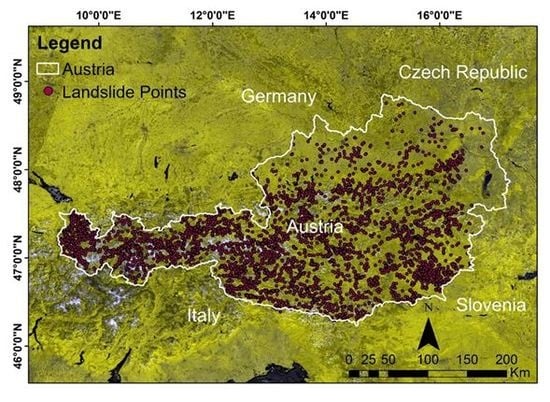
For this study, we used the landslide inventory that was obtained from the Geological Survey of Austria that might not be yet complete and for future studies, we would like to carry out assessments with a more comprehensive landslide inventory dataset, ideally as polygons rather than points. A complementary study could be carried out based on the polygon-based landslide inventory dataset to check and compare the accuracy of the methodology and the effect of the input inventory data. This study can be further investigated with other methodologies, like machine learning and deep learning, to observe the impact of various approaches on the inventory data as well as checking the robustness of methods for this region. The resulting susceptibility map at the national scale for Austria can help planners and policymakers to better manage and plan risk mitigation measures. The resulting LSM maps can be quite useful to allocate adequate resources in regions that are more impacted by landslides.