1. Introduction
Raman spectroscopy is a powerful and extremely useful technique to characterize any kind of graphene related system, since it is possible to obtain information about disorder effects, including pontual defects and the atomic structure of the edges [
1,
2], the stacking order and the orientation between different layers, like the number of graphene layers stacked in a Bernal configutation [
3,
4], strain effects [
5,
6], charge transfer [
7,
8,
9], and many other properties. Additionally, when the energy of the exciting laser can be tuned, it is also possible to obtain further information about the electronic structure and the dispersion of phonons near the Dirac point [
10].
In monolayer graphene, only one optical mode is active in the first order Raman scattering, which gives rise to the so-called G band that appears around 1580 cm
. Other Raman bands are also observed in monolayer graphene due to the double-resonance (DR) mechanism, which is used to interpret two distinct kinds of phenomena, the defect induced processes which involve just one phonon but with momentum conserved by a defect: like the defect induced D (
cm
), D
(
cm
) and D
(
cm
) bands, as well as processes involving two phonons with opposite momenta, like the combination D + D
band (
cm
) and the overtone 2D band (
cm
). The Raman peaks related to the DR mechanism have the remarkable property of being dispersive with the excitation energy. The position, intensity, and width of these bands can be well reproduced using the fourth order perturbation theory [
11], where all possible phonons, obtained from fully ab initio calculations based on density-functional theory (DFT) corrected with GW, are considered and the electronic structure is treated within a tight-binding approach in which the parameters are fitted to reproduce DFT + GW calculations.
Since its discovery, graphene materials have attracted a lot of attention because of their potential use in technological applications, mostly in electronics [
12]. In particular, when a graphene layer is deposited on top or, alternatively, covered by another periodic two-dimensional crystalline structure, which can be another single layer graphene (SLG), hexagonal boron nitride (h-BN), or any kind of transition-metal dichalcogenide (TMD) layer, like WSe
or MoS
, the static interlayer potential gives rise to Moiré patterns which correspond to a superstructure that depends on the twist angle due to misalignment between layers and/or the ratio between the lattice parameters of the two crystalline layers. In graphene, Moiré patterns can be directly observed by scanning tunneling and electron microscopy techniques, and the relationship between Moiré pattern arrangement and electronic properties has been extensively studied [
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29].
Recently, the appearance of strong correlated phases in twisted bilayer graphene (TBG) was reported by Cao et al. [
30,
31], caused by a flattening of the electronic bands in the vicinity of the Fermi energy that only occurs when the twist angle is close to 1.1
, the so-called magic angle. In momentum space, the Dirac cones of each layer in TBG are rotated by the twist angle, which controls the intersect of the energy bands. When the energy scale of the intersection is comparable to the interlayer coupling energy, flat bands with energy width of only a few meV are induced by hybridization. In this regime, the electron–electron interactions can dominate the many body interactions and give rise to correlated phenomena like superconductivity.
In general, the Moiré pattern interlayer interaction depends strongly on the angle between adjacent layers, and the dependence of the electronic properties with the twist angle can be useful in applications such as ultra-sensitive strain sensors and ultra-thin capacitors [
13]. In this way, systematic studies of misoriented graphene layers are quite interesting, and Raman spectroscopy plays an important role on its characterization, considering that several previous works in the literature show that the Moiré patterns can activate new Raman peaks in the spectra. The Raman mechanism involves both the electron and phonon properties that are essential for describing the physical properties and technological applications of the system.
The additional possibility of controlling the twisting angle
in TBG opens a fascinating route to build novel tunable quantum devices. For example, the interaction between electrons of different layers (interlayer el-ph processes) generates van Hove singularities (vHs) in the density of electronic states, whose energies are
dependent [
15,
16,
17]. On the other hand, electron–phonon coupling is a fundamental interaction that affects a broad range of phenomena in condensed matter physics such as electron mobility and thermal conductivity, and in atomically thin heterostructures, the interaction can involve electrons in the same layer(intralayer el-ph interaction) or in adjacent layers (interlayer el-ph interaction). The interlayer el-ph interaction can be observed in different kinds of layers as in the WSe
/h-BN heterostructures [
32], while the intralayer process was also observed in the Raman spectra of gr/h-BN samples. It allows the experimental determination of the mismatch angle between the crystallographic axes of graphene and h-BN even when lattice parameters of these structures do not match. In this case, the el-ph process occurs in a graphene monolayer and the h-BN surface imposes a periodic potential needed for the momentum conservation in the resonant Raman process. This effect is expected to be sensitive to the strength of the interaction between monolayer graphene and any other single layer or crystalline surface.
In this article, we review the main important feature in the spectra and the ability of Raman spectroscopy to probe and distinguish the two kinds of interlayer and intralayer el-ph interactions in TBG and graphene heterostructures. First, we introduce the basic physics of Raman spectroscopy in graphene, and discuss the effects of a different scattering mechanism. Then, we will present some recent results from Raman spectroscopy in different samples of TBG and gr/h-BN, with a previously determined mismatch twisting angle
, for different excitation photon energy. It will be shown that prominent new peaks are observed in the Raman spectra of TBG samples and that the origin of these peaks is related to phonons within the interior of the Brillouin zone (BZ) of graphene that are folded to the center of the reduced Moiré pattern BZ and the frequencies of these phonons depend on the twisting angle
[
14,
19,
20,
21,
33,
34,
35]. Finally, we will propose some directions where the Raman spectroscopy could be applied to better understand and appoint some open questions for both an experimental and theoretical point of view.
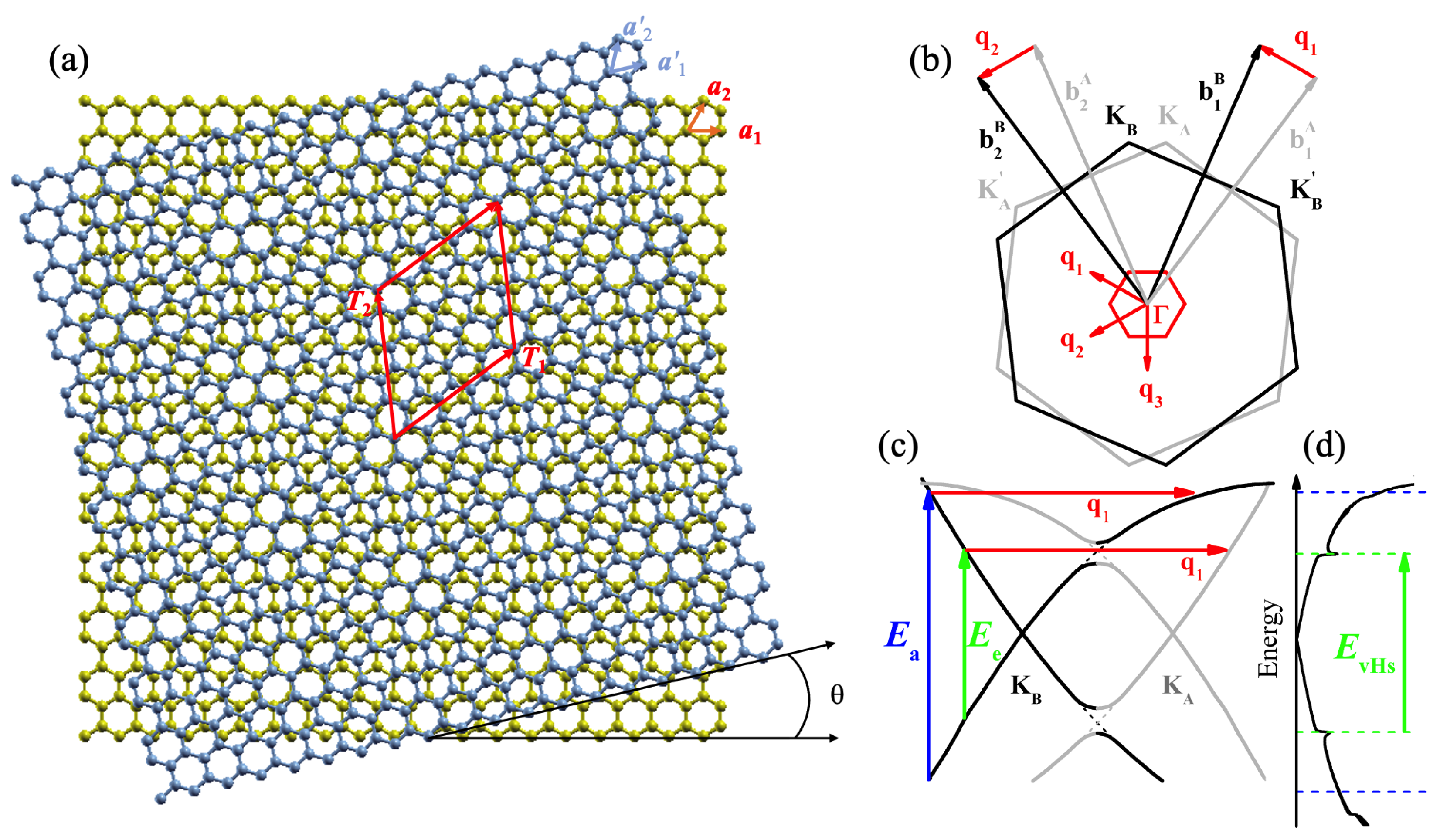
2. Background Theory
The periodic structure of a bilayer graphene twisted by a angle
can be built introducing a twisting vector
with respect to the first layer of a bilayer graphene lattice (golden layer in
Figure 1a), where
n and
m are integers (
) without any integer common divisor greater than 1, while
and
are the lattice vectors for the first graphene layer, with
Å being the lattice constant of graphene. Assuming, for simplicity, that the two layers have the same origin, for a commensurate unit cell, and
n and
m represent the minimal number of steps in each lattice direction until the top and bottom atoms meet again. It means that there is another vector
(not shown in
Figure 1a) given by a different pair of integers with respect to the lattice vectors
and
of the second layer, which are rotated by
with respect to the first layer. Both vectors,
and
, must have the same size and, after some algebra [
16], it can be shown that
The commensurate unit cell is then constructed by the superlattice vectors
and
, where the last vector is simply the former one rotated by
and can be given, in terms of
n and
m, by
. For all TBG structures, including commensurate or incommensurate structures, we can also observe a quasi-periodic pattern, known as Moiré pattern, whose size is less than or equal to the unit cell defined by
, since the unit cell of the Moiré pattern is not strictly periodic but only quasi-periodic [
18]. The size or lattice constant of the Moiré unit cell is given by [
36]
Notice that the size of the Moiré unit cell depends only on the twisting angle
. In fact, the size
of the Moiré unit cell is
smaller than the superlattice unit cell size, that is,
. Therefore,
=
only for the family
= 1. For example, the superlattice unit cell and Moiré unit cell for the
TBG structure belongs to the
family, and the size of the Moiré cell is one half of the superlattice size [
23]. The number
N of carbon atoms in the superlattice unit cell of TBG is given by
By the above expression, we get that
, which means that commensurate structures can only be generated when the twisted angle
provides an integer value of
N. In this way,
(
and
) corresponds to AB stacked bilayer graphene (Bernal) with four atoms in the unit cell and
(
) represents the graphene AA stacked with twelve atoms in the cell, which is three times larger than in the conventional unit cell. In
Figure 1a, we show an example of a commensurate unit cell with
carbon atoms, twisting vector
, and twisted angle
.
In the momentum space, we can define two reciprocal lattice vectors
and
of TBG in terms of the graphene reciprocal vectors
and
. They are simply given by
for
where
is a rotation matrix for an angle
around the perpendicular axis of the TBG surface.
Figure 1b shows the hexagonal Brillouin zones of two graphene layers A and B twisted by
= 13.2
and represented, respectively, by the grey and black hexagons. The vectors
,
and
correspond to the unit vectors of the Moiré reciprocal lattice. The reduced BZ of the Moiré superlattice is shown by the small red hexagon in the center of
Figure 1b, and it can be understood by considering the rotated monolayers BZ, since, in TBG, they can be superimposed with a relative rotation. The line
connecting the two original
K points from each layer,
and
, forms one edge of the Moiré BZ, and the
point folds back to the origin.
The electronic band structure of a single graphene layer near the Fermi level consists of a Dirac-cone-like structure at the Brillouin zone edge (
K point). When two single layers of graphene are combined with no rotation between them (
), the Dirac cones from the two layers are placed exactly on top of each other in reciprocal space. Therefore, when
, the Dirac cones of the two graphene layers are now separated in reciprocal space by
, but the two Dirac cones are still overlapping in a small region between the cones. The interaction between the Dirac cones of the two graphene layers is particularly strong in the overlap region, and it opens a hybridization small gap and leads to van Hove singularities (vHs) in the density of states (DOS) of the TBG which depends on the angle
. It is important to mention that a relative displacement between graphene layers does not affect considerably the energy bands and the optical spectra for both commensurate or incommensurate supercells, except for
= 0 [
17]. In this way, it is entirely possible to study electronic phenomena as a function of
, in the theoretical point of view, considering only rotations between two graphene BZ.
Figure 1c shows the energy versus momentum diagram for TBG with
= 13.2
. The grey (black) curves represent the Dirac cone of layer A (layer B) from
Figure 1b.
Figure 1d shows the DOS of the 13.2
TBG, as well as the optical transition between vHs in the valence and conduction bands.
Since the positions of the singularities in the DOS of the TBG are
dependent, one can use Raman spectroscopy to study selectively certain regions of their electronic spectra, controlling the energy of the incoming excitation photon. Raman spectroscopy is an experimental technique commonly used to characterize carbon-based materials, and it provides a wide amount of information about the electronic and vibrational properties. Without disorder, the two most prominent Raman bands in the spectra of graphene-based systems are the G and the 2D peaks. The mechanism behind of the G band is simpler than the 2D, since it involves creation of just one phonon at the Brillouin zone center per each scattered photon (momentum conservation requires that the created phonon must have zero momentum because the momenta of the incoming and the scattering photons are negligible). On the other hand, the 2D band involves emissions of two phonons with opposite momenta per each scattered photon. In TBG, the intensity of the Raman G peak is also dependent on the twisted angle
with a huge intensity increase (
) when the incoming photon energy is comparable to the separation between the vHs, while Raman 2D peak intensity, position, and width present a much more complicated
dependence [
37].
The full theoretical description of the Raman bands will always involve a computation of the electron–phonon and the electron–photon matrix elements, which control the selection rules and the relative intensities between different bands. However, a lot of information can be extracted from a complex graphene-based system since the electron and phonon properties in the single layer graphene are well known.
3. Raman Signature in Twisted Graphene Layers
In 2010, Gupta et al. [
33] reported the presence of a non dispersive new peak around 1380 cm
in the Raman spectra of a graphene system with a monolayer folded back upon itself. They interpreted the result considering that the static interlayer perturbation between layers activates a finite wavevector that conserves momentum with a phonon through the double-resonant Raman (DRR) scattering. Several peaks were also reported later by Righi et al. [
14], and the authors showed that these extra peaks are associated with phonon modes from the interior of the graphene BZ that are folded to the center of the reduced BZ and become Raman-active by the neighbor graphene layers twisted between each other. They also showed that each family of peaks, observed by many other authors, can be associated with Moiré patterns with specific rotational angles
[
14,
19,
20,
21,
33,
34,
35]. In a paper in 2011, Carozo et al. [
34] attributed the new peaks in the vicinity of the G band position to the intervalley and intravalley DRR processes, and they estimated the resonance energies as a function of
for these two processes. The valleys considered in this work belong to the same graphene layer and, therefore, both cases correspond to an intralayer electron–phonon scattering process.
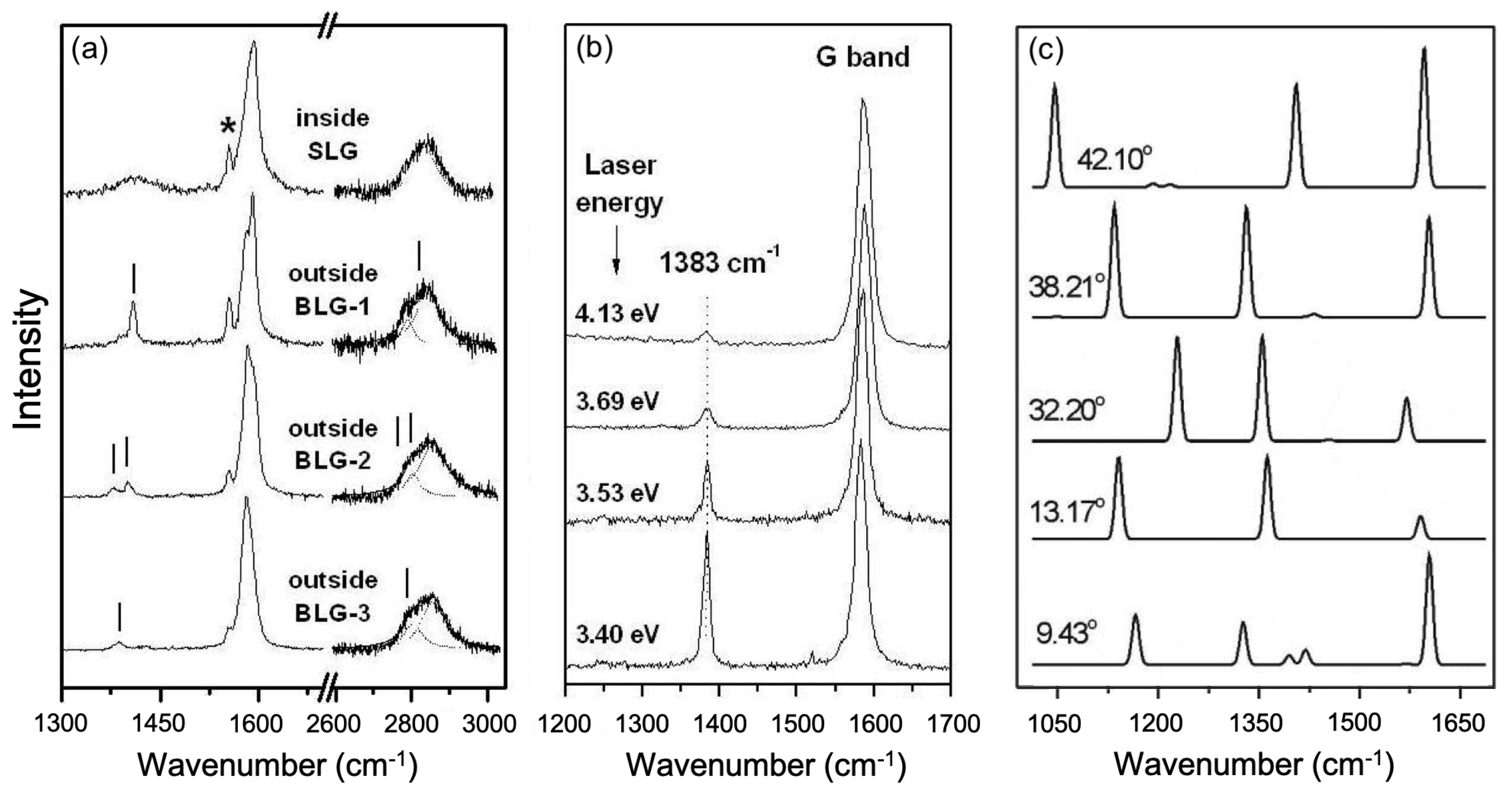
Figure 2a shows the Raman spectra obtained by Righi et al. [
14] in four different regions of the sample, grown by chemical vapor deposition (CVD) on a copper-foil enclosure at a high temperature, inside and outside the Cu enclosure. The top spectrum of
Figure 2a was recorded in a region inside the enclosure that contains domains of single layer graphene (SLG), and shows the D, G, and the 2D bands (the D band is dispersive and appears around 1420 cm
using the 3.82 eV laser line) [
1,
10]. The three other spectra in
Figure 2a were obtained in three different regions of the film grown on the outside of the Cu enclosure, with a high density of bilayer graphene (BLG) domains. Notice that, in addition to the G band, these three spectra also exhibit a number of sharp extra around 1400 cm
(the absence of the D band can be ascribed to the high crystalline quality of the sample in these three regions).
The authors interpreted the origin of the new Raman peaks showed in
Figure 2a as a consequence of a periodical perturbation
originated from the twisted-double-layer Moiré pattern. The perturbation allows for elastic scattering from electron states
to
, described by matrix elements
. This leads to a double resonance (DR) Raman scattering process, similar to those of the D and
bands, where the electron is (i) optically excited, (ii) inelastically scattered by a phonon of wavevector
, (iii) back-scattered by the elastic scattering process with wavevector
, and (iv) radiatively de-excited. In the cases of the D and D
bands, the local perturbation
, which is due to defects, leads to non-null values of
in a continuum range of
[
1]. In contrast, the periodic Moiré perturbation
leads to allowed scattering (non-null
) only for a discrete set of
, where
is the magnitude of the reciprocal lattice unit vectors of the Moiré pattern. This process can therefore be described as an umklapp DR process for the Moiré lattice. From momentum conservation, we have
, and therefore the only relevant phonon scattering events in such umklapp-Moiré double resonance process are those for phonons with wavevectors
.
The similarity between the physical processes (elastic scattering, double resonance) involved in the D band and those of the umklapp-Moiré peaks suggests that they should occur at similar wavenumber ranges, for a given laser photon energy.
Figure 2a shows the Raman spectra of monolayer graphene in a region of the sample with defects, where the broad D band can be observed centered around 1420 cm
. Notice that the frequencies of sharp peaks of the umklapp-Moiré spectra overlap with the broader D band shown in the top of
Figure 2a. The main difference is that umklapp-Moiré peaks are much narrower than the D band, and they are not dispersive, as can be seen in
Figure 2b, where the Raman spectrum were taken in the same spot of the sample using different laser energies (3.40, 3.53, 3.69, and 4.13 eV). The frequency of the peak at 1383 cm
does not depend on the laser energy, but its intensity changes, as expected for a U-DR process. In this type of process, each phonon with allowed wavevector
will achieve resonance at a specific laser energy, and, for the analyzed sample, the resonance condition for the peak at 1383 cm
has not yet been achieved at 3.40 eV, and it should occur at lower laser energies.
In order to check the laser energy dependence of the extra peaks, Righi et al. [
19] measured the same region of the TBG using different laser lines in the range of 2.54–4.14 eV.
Figure 3a shows the Raman spectra in the 1200–1700 cm
range, obtained with many different laser lines, where one can observe the peak around 1380 cm
associated with the TBG. Notice, in
Figure 3a, that the position of the extra peak does not depend significantly on the laser energy
, whereas its intensity is strongly dependent on
, with the maximum intensity occurring around 3.04 eV. The authors interpreted the resonance behavior of the extra peaks in the framework of the double resonance process involving the wavevectors of the Moiré superlattice for the momentum conservation, as described before. They simulated the umklapp double-resonance (U-DR) Raman spectrum
, for two different twisting angles (7.34
and 13.17
), and for different incident laser energies, following the methodology described in Ref. [
14], but assuming that the TBG is a monolayer of graphene interacting with a network of defects corresponding to the Moiré lattice vectors.
Figure 3d shows the Raman excitation profile (REP) of the intensity of the extra peak around 1380 cm
, normalized by the intensity of the G-band. The black squares correspond to the experimental results presented in
Figure 3a and the open and black circles correspond to the simulated spectra for the two different twisting angles shown, respectively, in
Figure 3b,c for three different laser energies close to the resonance. As one can see, there is a nice qualitative agreement between experimental and simulated results, showing that the extras peaks are indeed due to U-DR processes.
It was shown that there is a simple physical interpretation that explains both the origin and the position of the laser energy resonance, as well as the width of the REP, which is very large in comparison with the small widths of the Raman peaks. From momentum conservation, the only relevant phonon scattering events in such U-DR process are those for phonons with wavevector with the same magnitude as the Moiré reciproal lattice . As a consequence, instead of a wide and dispersive Raman resonance as observed for the D band, the umklapp Moiré resonances is characterized by several sharp, non-dispersive resonances peaks found in the same spectral region as that of the D and D bands.
Assuming that the periodic perturbative potential of the Moiré lattice can be approximated by a periodic array of localized perturbations that leads to the D band, the umklapp Moiré resonances become, essentially, a “filtered” D band. That is, each resonance is placed at the energy of a phonon with wavevectors
, with its intensity given by the intensity of the D band at that same energy. Therefore, within this approximation, the analysis of the laser energy dependence of the intensity of a given Moiré resonance peak at phonon frequency
, given by
, can be mapped into the laser energy dependence of the intensity
of the D band at the same frequency
. It was also proposed in Ref. [
19] that the peak width
in the REP of the
for a given
is proportional to the width
of the D band, which is consistent with the experimental results.
The spectra computed for several possible twist angles between graphene layers using the model described in Refs. [
14,
19] are shown in
Figure 2c. For all angles, the simulated Raman peaks group at three distinct wavenumber regions. The first and second groups, respectively in the ranges 1050–1250 cm
and 1325–1450 cm
, show stronger dispersions with respect to twist angles, and come from the longitudinal acoustic (LA) and in-plane transversal optical (TO) branches, respectively. The third group, near 1600 cm
and associated with the in-plane longitudinal optical (LO) phonon branch, is almost dispersionless with respect to twist angle.
This theoretical model presents qualitative agreement between the simulated and observed spectra. However, the intensity of the simulated Raman bands is not well reproduced since the selection rules and the matrix elements are not taken into account for the calculation of these bands [
14]. This issue can be partially overcome assuming that the intensity of the extra peak can be mapped into the laser energy dependence of the D band intensity at the same frequency [
19]. Anyway, the qualitative agreement between the observed and simulated spectra provides a support for the interpretation that the families of Raman peaks are associated with Moiré patterns of graphene layers twisted with different angles. In a sample of two graphene layers presenting domains misoriented between each other, the maps of the Moiré peaks can give a direct image of these domains.
5. Intralayer and Interlayer Electron–Phonon Processes
In 2013, Carozo et al. [
35] and Wang et al. [
21] reported measurements of TBG samples with intermediate twisting angles (13
–16
) using different laser lines. In both works, the appearance of new peaks in the range 1380–1450 cm
was observed to occur in the same spectra where the G band was enhanced. This resonance behavior could not be explained by the predictions of the process involving the periodic potential of the Moiré cell [
34], and revealed that a different electron–phonon process involving phonons with momentum
might exist. In 2018, Eliel et al. [
38] have shown that the new phonons observed in the previous works by Carozo et al. [
35] and Wang et al. [
21] are activated by the interlayer electron–phonon scattering processes.
The extra peaks below and above the G band position used to be called in the literature as the R and R
peaks [
34,
35]. However, since they can be activated either by the intralayer or the interlayer electron–phonon scattering process, a physical meaningful notation was proposed by Eliel et al. [
38]. They proposed to call these peaks as A
, where A = T or L refers to the branch (TO or LO) of the unfolded phonon and
refers to the electron–phonon scattering mechanism (
= a or e for intralayer and interlayer processes, respectively).
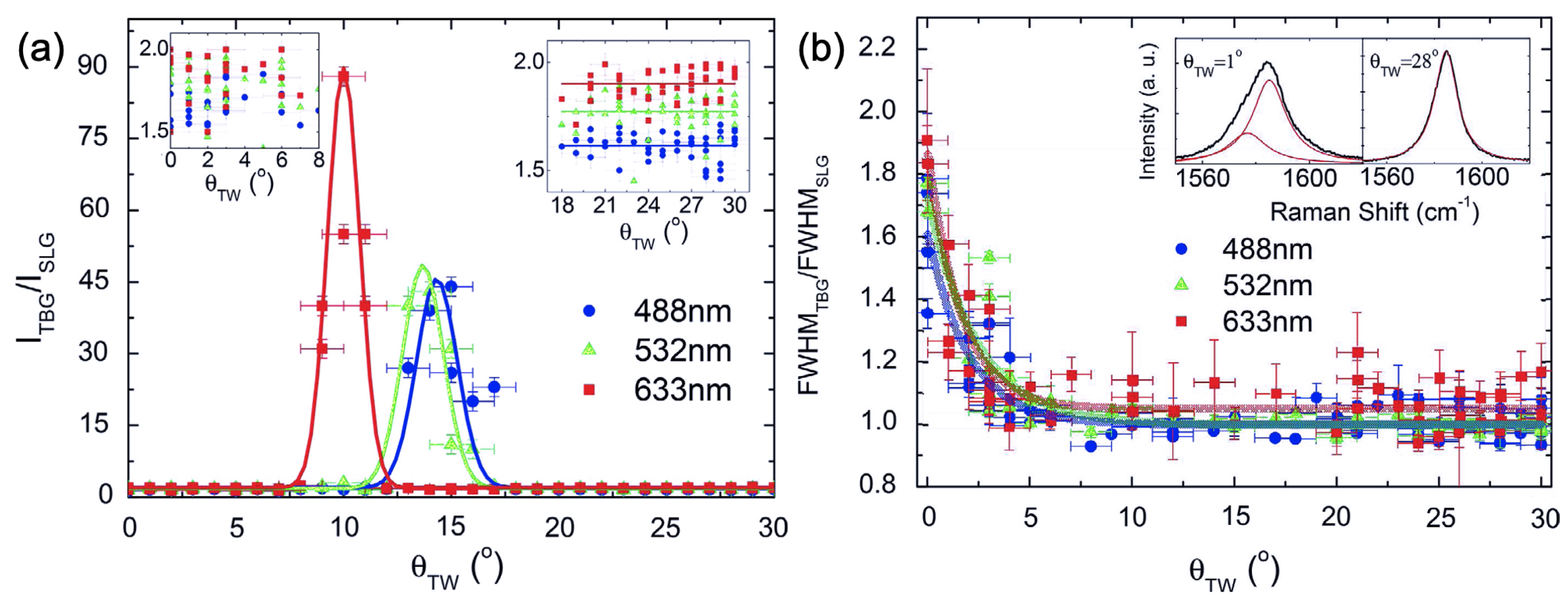
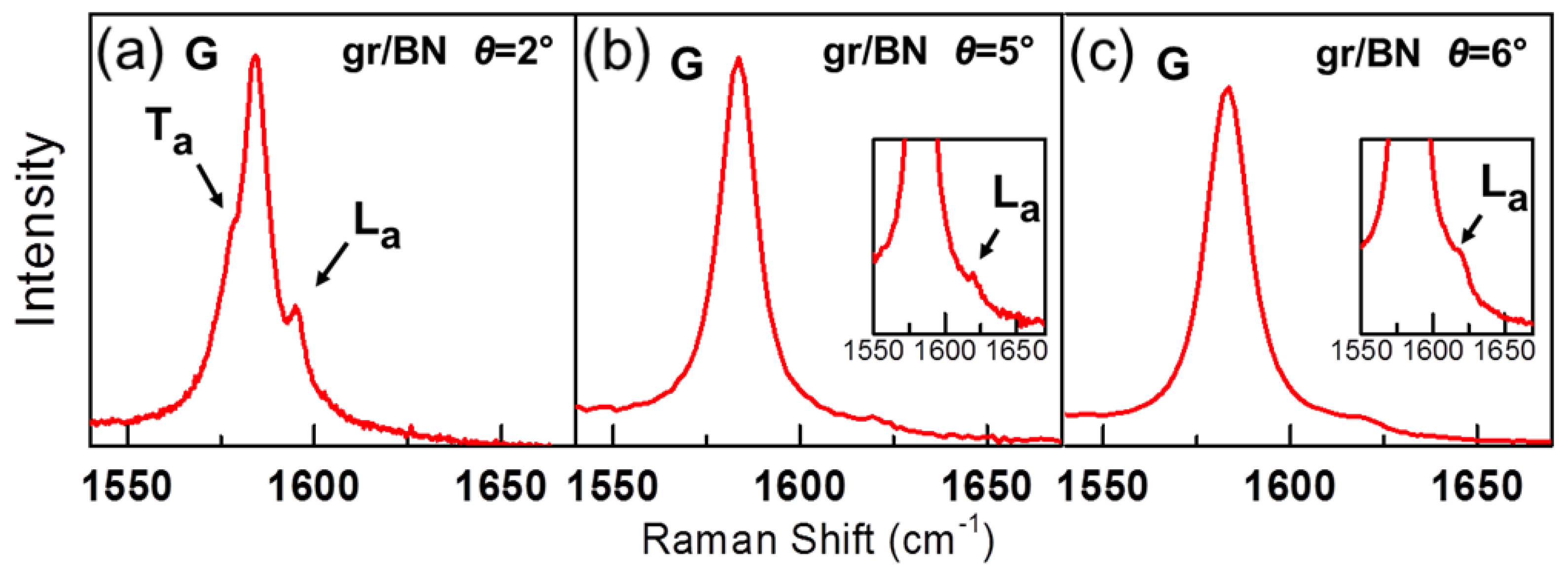
Figure 5a,b show clearly that the extra peaks apart from the G band might be called L
and T
, respectively. These figures show the Raman spectra for two TBG samples with
= 6
and 13
, recorded with the 2.18 eV and 2.41 eV laser lines, respectively. The vertical scale,
, corresponds to the ratio of the peak intensities in TBG and single-layer graphene (SLG). The ratio
= 1.8 for the G band intensity (around 1580 cm
) of the
= 6
sample shown in
Figure 5a corresponds to the observed value far from resonances [
23]. However, for the
= 13
sample shown in
Figure 5b, the G band ratio
is more than 50. This huge increase of the G band intensity has already been observed in previous Raman studies of TBGs [
23,
24,
25,
37] and explained by the resonance of the incident photons with the optical transition between van Hove singularities (vHs) in a density of electronics states of a TBG.
Multiple-excitation Raman measurements using many different laser lines in the visible range were reported in Ref. [
38], and the results were used to obtain an accurate Raman excitation profile (REP) of Raman peaks in samples with small and intermediate twisting angles. It was observed that the G band ratio
of the
= 6
sample does not depend on the photon energy and is always around 1.8, an expected value far from resonance conditions [
23]. On the other hand, the L
peak exhibits a resonance behavior and reaches the maximum intensity for photon energies around 2.2 eV, where it becomes as intense as the G band in SLG. However, for the
= 13
sample, both the G band and the T
peak exhibit a resonance behavior and are enhanced in the same excitation energy range.
Figure 5c,d show the the intensity of each peak as a function of the photon energy of the G, L
and T
peaks, that is, the Raman excitation profile (REP), for the
= 6
and
= 13
samples, respectively.
Figure 5c shows that the REP of the L
peak exhibits maximum enhancement at approximately 2.2 eV and has a width around 0.7 eV. This value of width agrees with the result in a previous UV Raman study of TBGs [
19]. In the case of the
= 13
sample shown in
Figure 5d, the G band and the T
peak exhibit very similar REPs, except for the fact that the intensity of the extra peak was multiplied by ≈ 100 for comparison. The data in
Figure 5d were fitted by the expression of the Raman-cross section based on the third-order perturbation model [
35], where the fitting parameters are the energies of the optical transitions between vHs,
, and the width
of the REP. The values of the parameters that fit the experimental data in
Figure 5d are
= 2.37 eV and
= 0.25 eV. Notice that this value of
agrees with the width of the peaks in the optical absorption spectra of TBGs [
26]. Several other samples with low (4
–6
) and intermediate (12
–16
) twisting angles were also investigated by the authors using multiple excitation Raman measurements. The dependence on the values of
and
for the G band on the twisting angle
is shown in Ref. [
27].
6. Electronic Transitions in TBG
The difference between the intralayer and interlayer processes can be understood by a theoretical simulation, where, in the first case, the excited electronic state from one layer is scattered by phonon with momentum to another excited state in the same layer (intralayer process), whereas, in the other case, the excited electron is scattered to an excited state of the other layer (interlayer process). These mechanisms give rise to resonances at different energies.
The intralayer and interlayer processes in TBG are represented by the energy dispersion curves shown in
Figure 6a,b for
= 13.2
. In the intralayer process in
Figure 6a, an incident photon with energy
(represented by the vertical dashed arrows) creates an electron–hole pair, and a phonon with momentum
(represented by the horizontal red arrow) scatters the excited electron near the K point to another state in the same K point Dirac cone (−) or to the other Dirac cone (+). The symbols − and + thus design the intravalley and intervalley processes, respectively. For simplicity, it was not plotted in these figures the change in energy between the two states since the phonon energy is much smaller than the energy of visible photons. In the interlayer process represented in
Figure 6b, an incident photon with energy
creates one electron–hole pair, but now the electron from one layer is scattered to a state of the other layer by a phonon with momentum
. In both cases, the electron is then scattered back elastically to the first excited state by the Moiré potential with wave vector
, for electron–hole recombination and emission of the scattered photon. Notice that, for both processes, in the limit of small and large twisting angles, the low energy transitions
involve states near the K point of graphene (intravalley process), whereas the high energy transitions
involve states near the M point (intervalley process).
Figure 6c illustrates the interlayer process in the graphene reciprocal space. The dark and light green curves correspond to the equi-energy curves
around the Dirac points K
and K
, respectively. An excited electron with momentum
ℏk from the Dirac cone of one layer (dark green curve) is scattered by a phonon with momentum
(red arrows) to a state with momentum
in the Dirac cone of the other layer (light green curve). The lowest possible value of
occurs when the equi-energies curves of the two layers tangentiate, as shown in
Figure 6c. In this situation, the anti-crossing between states of the Dirac cones gives rise to van Hove singularities (vHs) in the density of states (DOS), shown in
Figure 1d. For photons with energies below
, the difference
is always smaller than
and the interlayer condition cannot be satisfied. Therefore, the minimum energy for the interlayer scattering process,
, corresponds to the energy separation
between the vHs in the valence and conduction bands of a TBG.
The intralayer el-ph scattering process is schematically represented in
Figure 6d. Now, the light and dark blue curves around K
and K
, from different layers, respectively, correspond to the curves of constant energy
. In this case, the excited states with momenta
and
belong to the Dirac cones of the same layer (dark or light blue curves). The intralayer process is similar to the double-resonance Raman mechanism that gives rise to the disorder-induced D and D
bands in the Raman spectrum of graphene [
1]. For the disorder-induced bands, the electron is scattered back to the initial excited state by a defect, whereas, in the case of TBG, the back-scattering is provided by a periodic potential of the Moiré pattern. This double resonance (DR) Raman process, where momentum conservation is provided by a vector
of the Moiré lattice, has been called the U-DR process [
14] previously.
The discussion of the two processes above were made in the extended BZ scheme, where the activated phonons have finite
. In the reduced BZ scheme, they are folded to the center of the reduced BZ and have zero momenta. The first-order Raman process can be accomplished in this scheme since the two excited states
k and
in the extended BZ in
Figure 6c are folded to the same point in the reduced BZ, which are represented by the green dots in
Figure 6e. They are located at the saddle point in the electronic structure of TBG, near the M point in the reduced BZ that gives rise to a van Hove singularity (vHs). The intralayer process can be also represented in the reduced BZ scheme.
Figure 6f shows that the two excited states
k and
in the extended BZ in
Figure 6d are folded to the blue dots within the reduced BZ. Differently from the case of the interlayer process that occurs near the M point of the reduced BZ, the intralayer process occur for states at general positions within the interior of the reduced BZ.
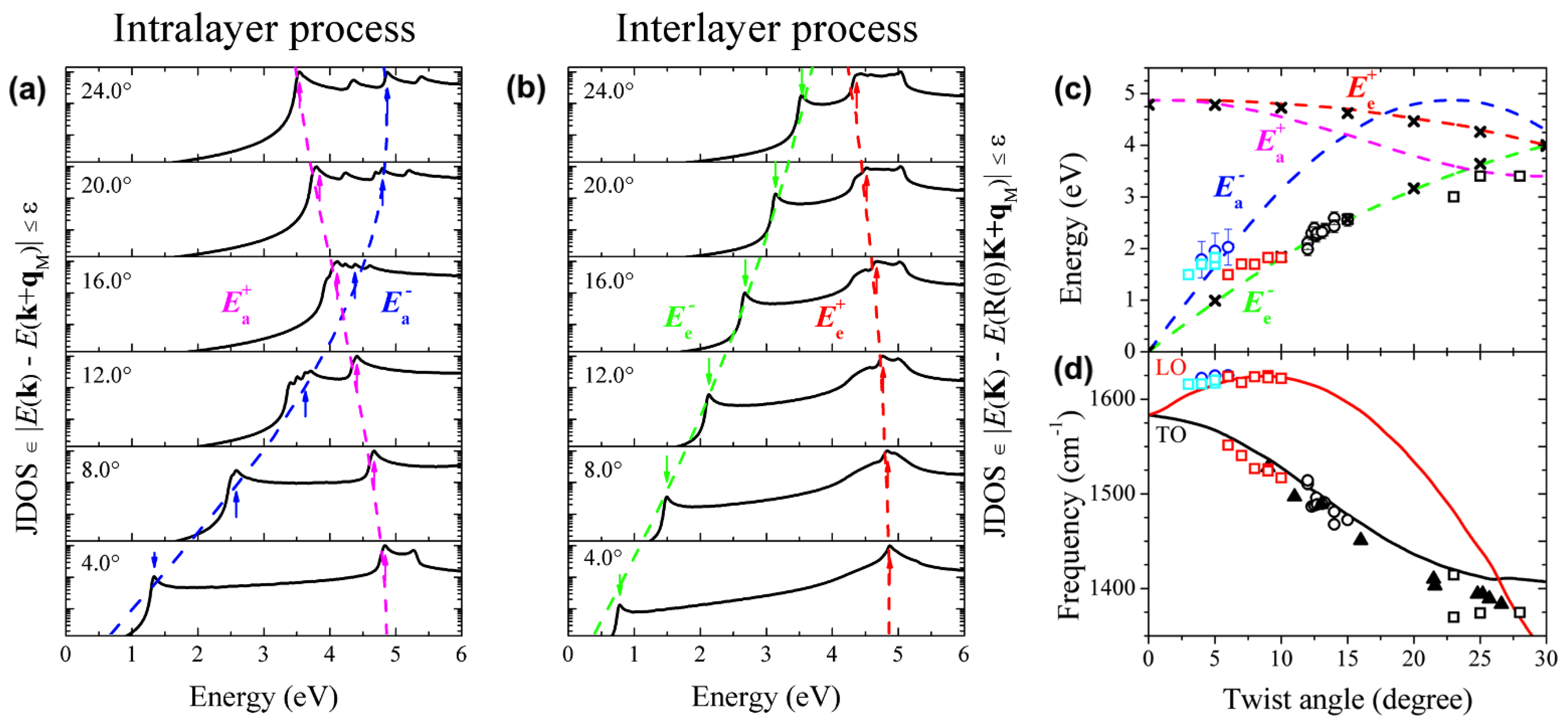
The resonance energies
and
can be calculated by the restricted density of joint electronic states that satisfy the intralayer and interlayer conditions. For the calculation, the graphene BZ was divided in a
k-points grid and, for each twisted angle
, the number of joint electronic states that satisfy the restriction
is stored, where the superscript
symbolizes the valence or the conduction bands and
eV is an arbitrary tolerance. The electronic structures were obtained by folding the SLG calculation based on a fifth neighbors tight-binding approach, following the procedure given in Ref. [
11], in which the parameters are fitted to reproduce density functional theory (DFT) calculations with many-body corrections. For the intralayer case, we have that
because the two electronic states,
and
, are connected by
while, for the interlayer process,
, being
the rotation matrix that takes the Dirac cone of one layer into the Dirac cone of the other layer. Considering these two conditions in the model, momentum conservation is always achieved by a given pair of states
and
, as long as the density of
k-points considered in the calculation is large enough that the energy difference between the states becomes less than the value of
, as shown in
Figure 6c,d, where the small circles in the equi-energy edges represent the tolerance.
Figure 7a,b show the calculated joint density of states (JDOS) that satisfy the intralayer and interlayer resonance conditions, respectively. The results were smoothed by Lorentzian functions with
eV of FWHM and normalized by the maximum intensity for best visualization of the peaks. In both cases, some peaks are observed in the restricted JDOS, and their energies depend on the twisting angle
. The position of the low energy peaks increases, whereas the position of the high energy peaks decreases with increasing values of
. These two maximums are associated with electronic transitions close to K and M points of the graphene, and will be called
and
. For the intralayer process, the positions of
and
are indicated by the blue and purple arrows in
Figure 7a, respectively, and the positions of
and
for the interlayer process are marked in
Figure 7b by the green and red arrows. Notice in
Figure 7b that
corresponds in fact to the onset for the interlayer process, which occurs when the Dirac cones touch each other as shown in
Figure 6c, giving rise to vHs in the valence and conduction bands with energy separation
. The values of
and
correspond in fact to the energies of the optical absorption peaks observed in TBG [
26].
Figure 7c shows the calculated values of
,
,
and
as a function of the twisting angle
represented by the dashed blue, green, pink, and red curves, respectively. The experimental values of the resonance energies obtained from the analysis of the REPs of the extra Raman peaks are also plotted in
Figure 7c. The blue open circles in
Figure 7c represent the resonance energies of the peaks in the range 1600–1620 cm
that are observed in samples with small angles (4
to 6
). They nicely agree with the calculated
versus
results represented by the dashed blue curve. The values of the resonance energies obtained from the REPs of the extra peaks in the range 1450–1550 cm
for samples with intermediate twisting angles (12
–16
) are plotted as full and open black circles in
Figure 7c. These points are close to the dashed green curve that represents
as a function of
. The black symbols × in
Figure 7c represent the experimental values of optical transition energies
measured directly by optical conductivity [
26]. It is interesting to note that, despite the fact that the model does not consider electronic coupling between the layers that opens a mini-gap which split the valence and the conduction bands in TBG, the agreement between the minimum possible value
shown in
Figure 7b and the experimental values of the optical transitions [
26] is remarkable. It means that the allowed transitions do not depend on the size of the minigap and, therefore, the folding approach is supposed to give good results concerning the Raman processes investigated [
26].
The red and black curves in
Figure 7d display, respectively, the calculated frequencies of LO and TO phonons with momenta
as a function of
. The phonon structures were also obtained by folding the SLG calculation results where the phonon dispersion was obtained from many-body corrected DFT calculations. The many-body corrections change the phonon slope of the highest optical branch near K (with respect to DFT), reproducing the Kohn anomaly and providing a much better agreement with inelastic X-ray scattering measurements for graphite [
39]. These curves accurately describe the D band of graphene when a red shift of 40 cm
is applied for phonons close to the K point. However, in order to reproduce the phonons close to the graphene G band, a constant blue shifted of 20 cm
is applied to all frequencies. Even though the calculations were done only by folding the SLG results, the physics of the intralayer and interlayer processes in TBG is nicely captured, since the weak van der Waals interactions between layers in TBG do not significantly alter the frequencies of the optical phonon branches [
28].
The frequencies of the extra peaks of samples with small (intermediate) values of
are plotted as open blue (black) circles in
Figure 7d. By comparing the experimental with the calculated results of the resonance energies and phonon frequencies shown in
Figure 7c,d, one can conclude that, using visible photons, the Raman peaks below the G band come from TO phonons and are activated by the interlayer process, whereas the peaks above the G band come from the LO phonon branch and are activated by the intralayer process.
In principle, the intralayer and interlayer el-ph processes can also activate TO and LO phonons, respectively, and give rise to T
and L
peaks for samples with intermediate angles. However, T
and L
were not observed by the authors in the multiple excitation experiments using visible photons. The lack of observation of L
can be due to the huge enhancement of the G band. Since the position of the L
peak is very close to the G band position in samples with intermediate twisting angles, it is possibly masked by the G band enhancement. For samples with
around 10
and measured using the 1.96 eV laser line, Campos-Delgado et al. [
20] reported the observation of a peak at 1622 cm
that might be assigned to the L
. The absence of T
can be ascribed to the very weak cross-section of TO phonons activated by the intralayer process. Electron–phonon matrix elements’ calculations would be necessary to better clarify this issue.
7. Raman Spectra of TBG Using Infrared and Ultraviolet Photons
The calculated results presented in
Figure 7c show that, for TBG samples with small twisting angles, both the intralayer and the interlayer processes are expected to be observed using excitation energies below ∼2 eV. This prediction was indeed observed in several Raman results performed in many different samples with
in the range 2
–9
, using near infrared (IR) laser lines. It was observed that the LO phonon is activated by the intralayer el-ph process, but, for very small angles, the L
peak is much stronger than the G band, suggesting that the electron–phonon coupling for this phonon branch increases with decreasing
, when the wave vector
tends to the center of the BZ. In general, a huge enhancement of the Raman intensity is observed in this regime, and only in the tails of the G band is it possible to observe the two extra peaks below and above the G band that are assigned, respectively, as the T
and L
peaks. The L
peak, due to the activation of a LO phonon by the interlayer el-ph process, is not usually seen in the visible range, and it can also be explained by the increase of electron–phonon coupling for the LO phonons when
tends to zero.
The theoretical predictions in
Figure 7c for samples with large twisting angles
(between 20
and 30
) show that extra peaks are expected to appear in the UV Raman spectra (for excitation energies above 3 eV).
Figure 7d shows that the activated phonons are close to the K point of the single-layer graphene, and come from both the TO and LO branches, with frequencies in the range 1350–1420 cm
. The non-dispersive extra peaks observed in the pioneer Raman study of Gupta et al. [
33] lays in this frequency range, and they were enhanced in the UV Raman spectrum (
= 3.41 eV). These extra peaks were also studied by Righi et al. [
14,
19] in the UV Raman spectra of TBGs, but the twisting angles
could not be determined in this work. In both studies [
14,
33], the appearance of new peaks was not accompanied by the enhancement of the G band, as expected for an intralayer el-ph process. In contrast, the UV data of Wang et al. [
21] in TBG samples with large values of
show the activation of new peaks in spectra where the G band also exhibits an enhancement of 5 to 20 times, thus indicating an interlayer electron–phonon scattering. These peaks observed in the UV Raman spectra are represented by the black open squares in
Figure 7c,d, respectively.
Notice in
Figure 7c that, for large twisting angles, both the intralayer (
) and interlayer (
) resonances occur in the same energy range (3–4 eV). In principle, these two processes can be distinguished by observing the enhancement of the G band of TBG, which is a signature of the interlayer process.
Although the folding method provides a good description of the phonon frequencies and of the electronic transitions of TBG, the theoretical model proposed above does not provide the intensities of Raman peaks. For that, one needs to consider the values of the matrix elements for the electron–phonon and electron–photon interactions. The computation of these matrix elements could clarify, through the intensity, the origin of the peaks for large twisted angles, since the T and L peaks are very close to each other in this regime