Resolving Energy Losses Caused by End-Users in Electrical Grid Systems
Abstract
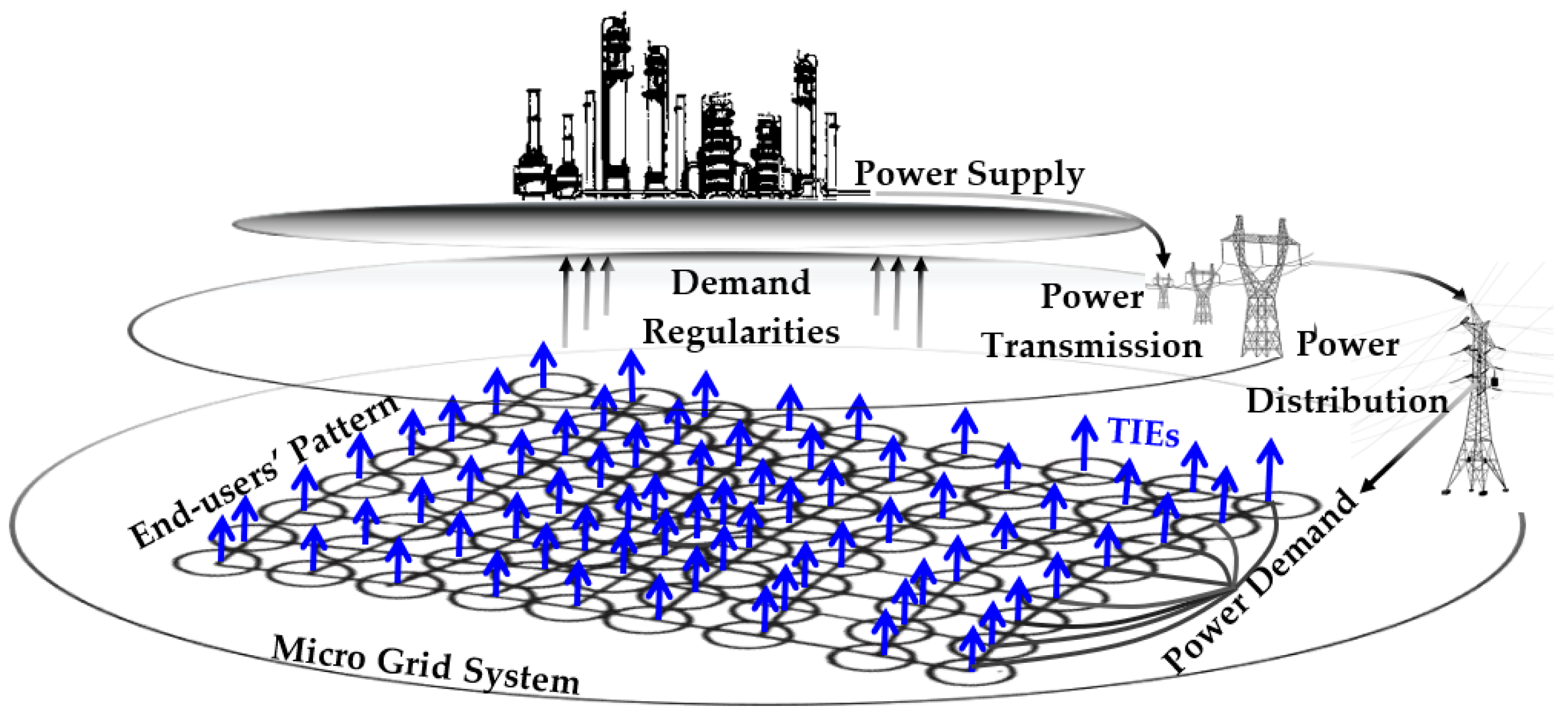
:1. Introduction
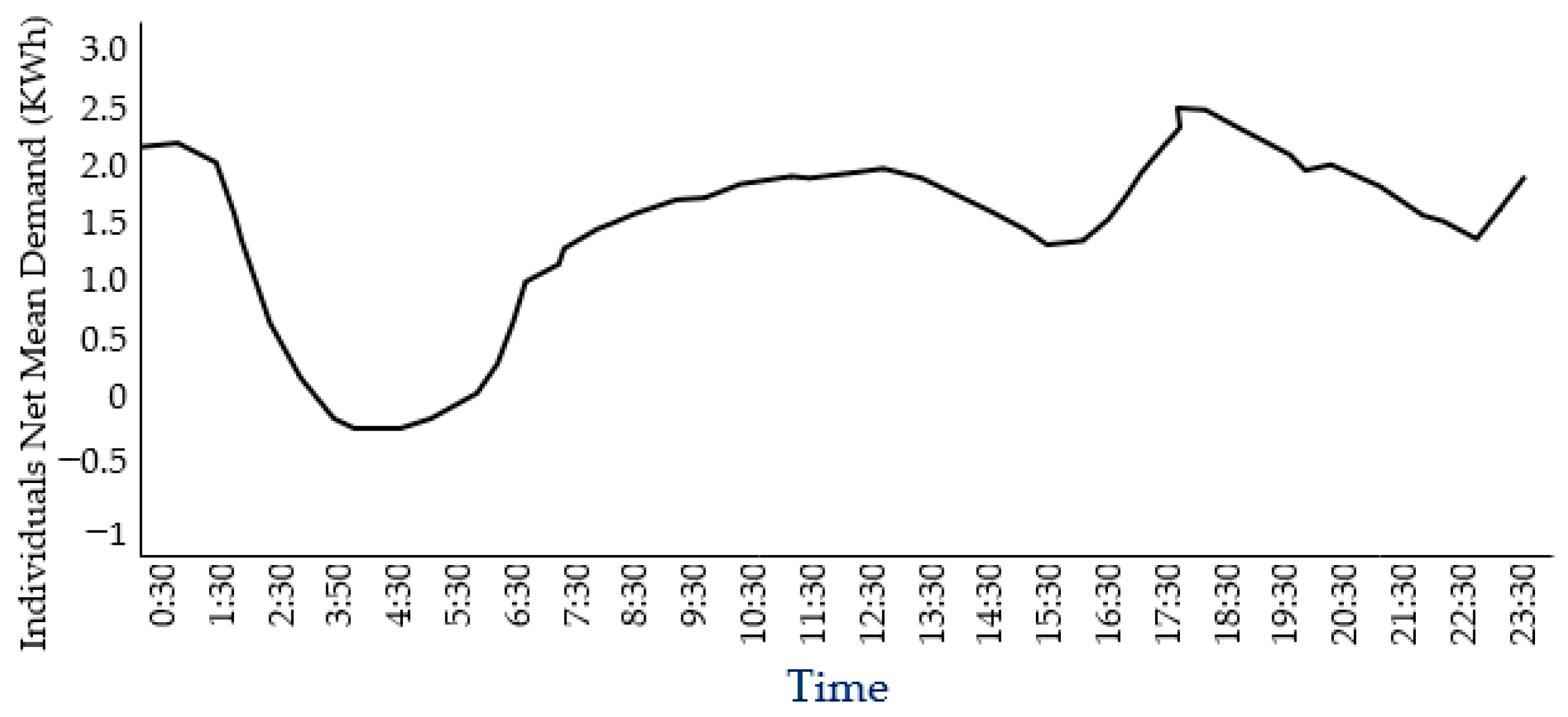
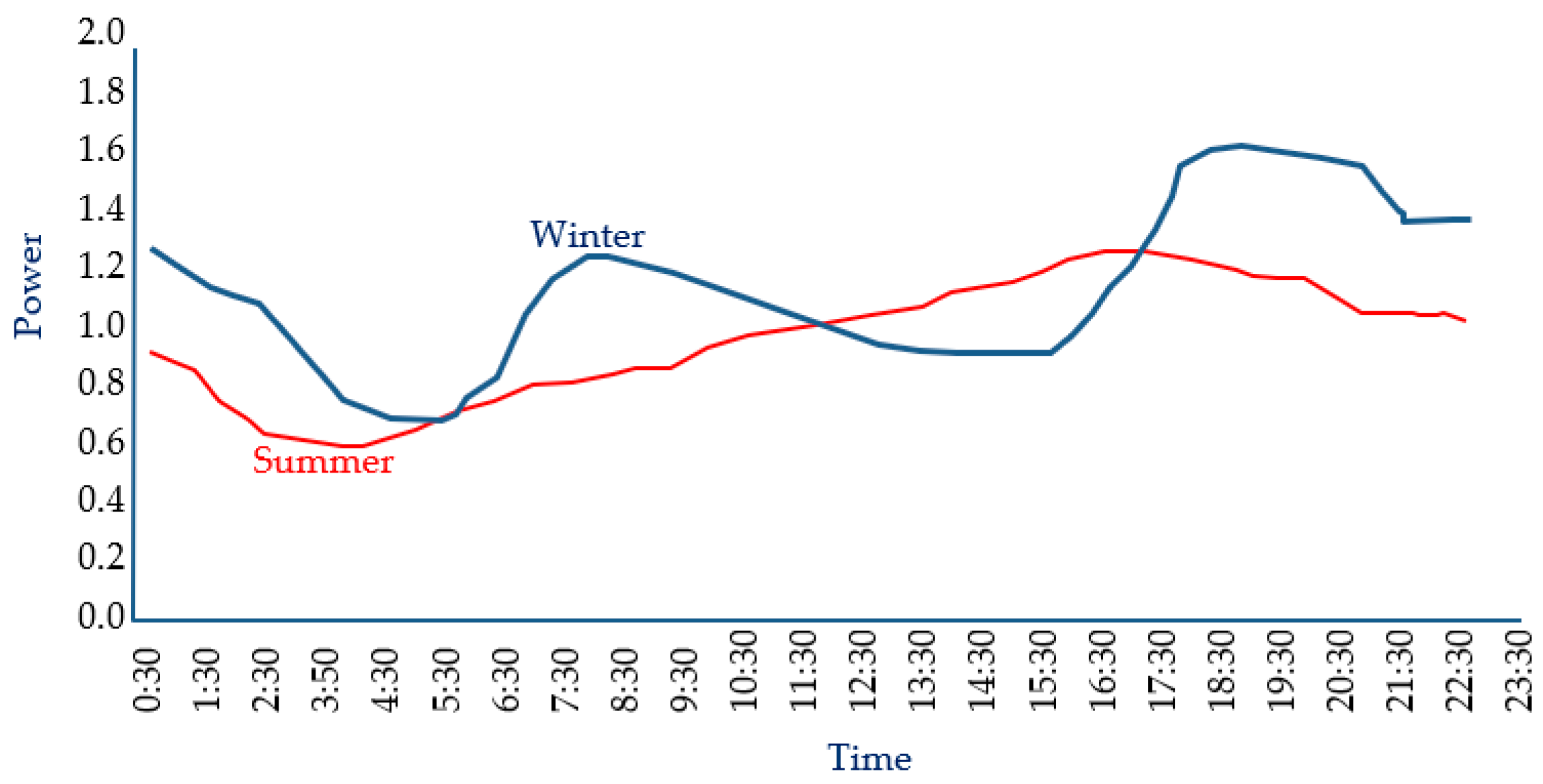
2. Review Actual Demand Data
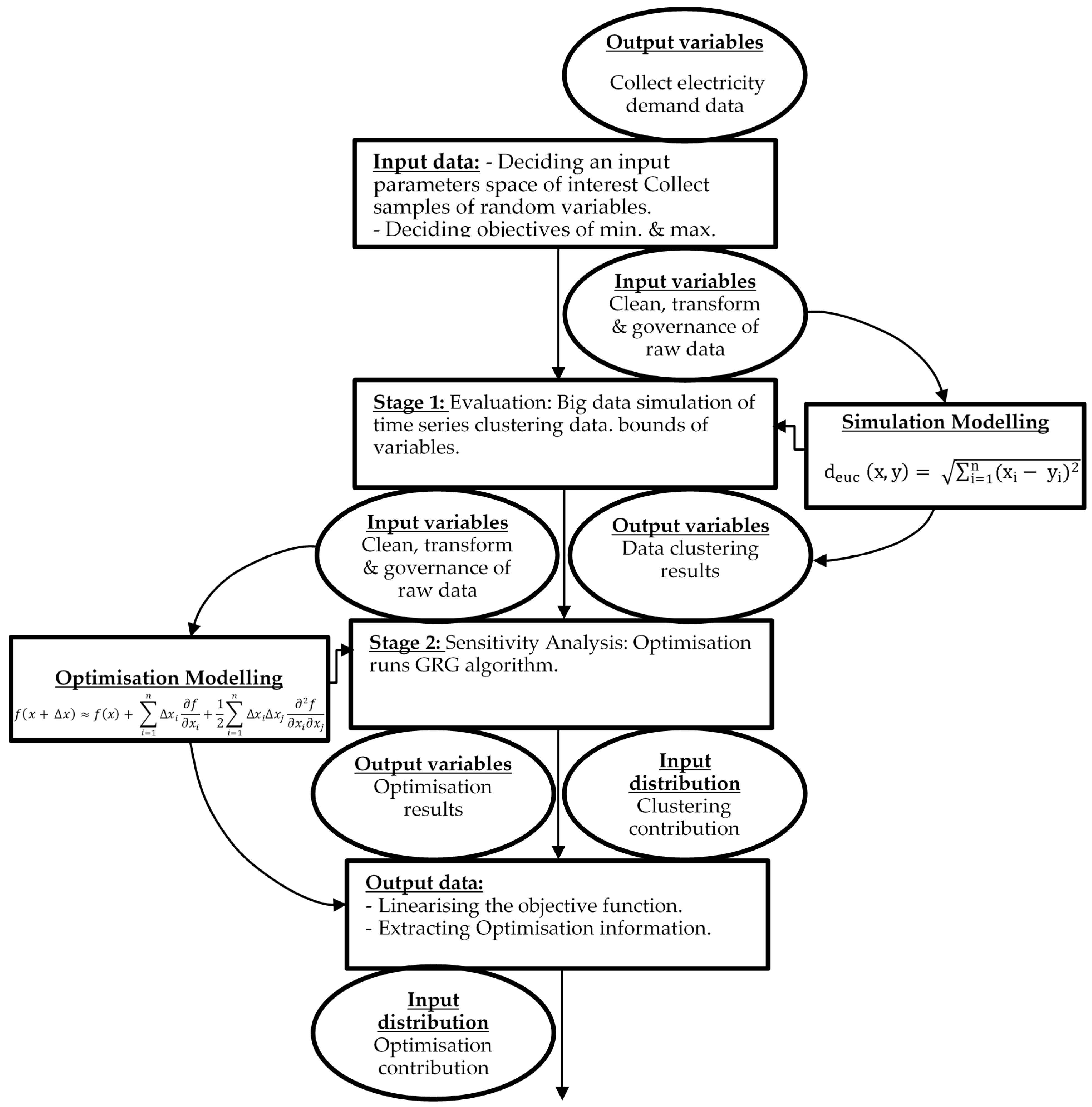
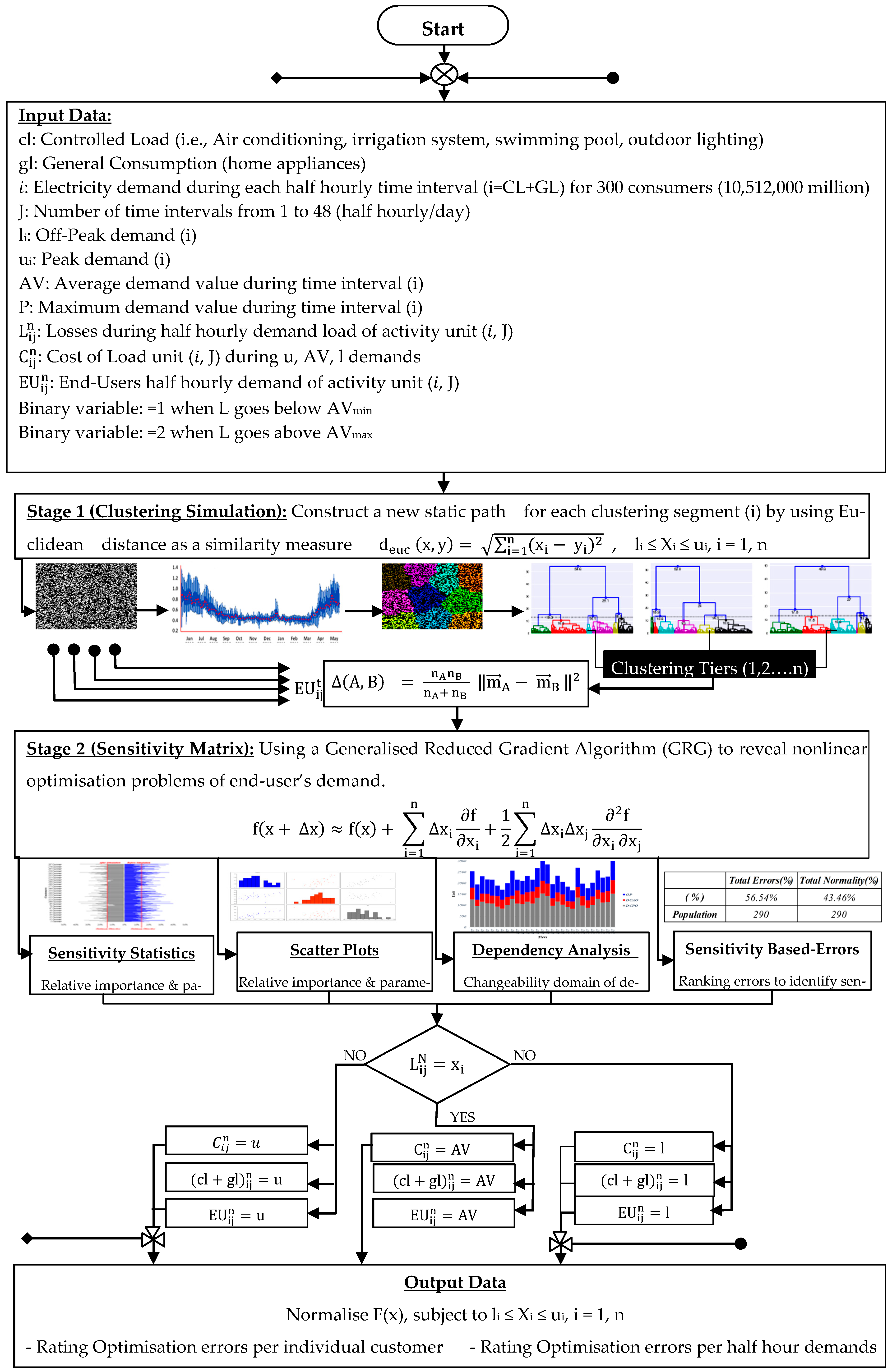
3. Methods
4. Power Laws (PLs)
5. Results and Discussion
6. Need for Future Research
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gigerenzer, G.; Selten, R. Bounded Rationality: The Adaptive Toolbox; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Colson, C.; Nehrir, M. A review of challenges to real-time power management of microgrids. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–8. [Google Scholar] [CrossRef]
- The Australian Academy of Technological Sciences and Engineering (ATSE). The Hidden Costs of Electricity: Externalities of Power Generation in Australia; Parkville: Victoria, Australia, 2009; pp. 1–88. Available online: https://www.applied.org.au/ (accessed on 10 September 2020).
- Fan, Z.; Kulkarni, P.; Gormus, S.; Efthymiou, C.; Kalogridis, G.; Sooriyabandara, M.; Zhu, Z.; Lambotharan, S.; Chin, W.H. Smart grid communications: Overview of research challenges, solutions, and standardisation activities. IEEE Commun. Surv. Tutor. 2013, 15, 21–38. [Google Scholar] [CrossRef] [Green Version]
- Su, W.; Wang, J. Energy management systems in microgrid operations. Electr. J. 2012, 25, 45–60. [Google Scholar] [CrossRef]
- Grid Australia. National Electricity Rules: Distribution Losses in Expenditure Forecasts. 2012. Available online: http://www.aemc.gov.au/getattachment/fc5d7ca3-b07c-405e-84c4-f72bf9b37010/Grid-Australia.aspx (accessed on 15 March 2019).
- Noor, S.; Yang, W.; Guo, M.; van Dam, K.H.; Wang, X. Energy demand side management within micro-grid networks enhanced by blockchain. Appl. Energy 2018, 228, 1385–1398. [Google Scholar] [CrossRef]
- Wu, D.; Radhakrishnan, N.; Huang, S. A hierarchical charging control of plug-in electric vehicles with simple flexibility model. Appl. Energy 2019, 253, 113490. [Google Scholar] [CrossRef]
- Zhang, T.; Pota, H.; Chu, C.-C.; Gadh, R. Real-time renewable energy incentive system for electric vehicles using prioritisation and cryptocurrency. Appl. Energy 2018, 226, 582–594. [Google Scholar] [CrossRef]
- Uhl-Bien, M.; Marion, R. Complexity leadership. In Part 1—Conceptual Foundations; Leadership Horizons Series; Information Age Pub (IAP): Charlotte, NC, USA, 2008; Available online: http://search.ebscohost.com.ezproxy.laureate.net.au/login.aspx?direct=true&db=nlebk&AN=469811&site=ehost-live (accessed on 13 August 2020).
- Steel, M. Self-sustaining autocatalytic networks within open-ended reaction systems. J. Math. Chem. 2015, 53, 1687–1701. [Google Scholar] [CrossRef]
- Liu, J.; Xiao, Y.; Gao, J. Accountability in smart grids. In Proceedings of the 2011 IEEE Consumer Communications and Networking Conference (CCNC), Las Vegas, NV, USA, 9–12 January 2011; pp. 1166–1170. [Google Scholar]
- Yilmaz, S.; Chambers, J.; Patel, M. Comparison of clustering approaches for domestic electricity load profile characterisation—Implications for demand side management. Energy 2019, 180, 665–677. [Google Scholar] [CrossRef]
- Soldatos, P.G. The long-run marginal cost of electricity in rural regions. Energy Econ. 1991, 13, 187–198. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, B.; Jiang, Y.; Bie, P.; Li, H. Chance-constrained stochastic congestion management of power systems considering uncertainty of wind power and demand side response. Int. J. Electr. Power Energy Syst. 2019, 107, 703–714. [Google Scholar] [CrossRef]
- Wolisz, H.; Schütz, T.; Blanke, T.; Hagenkamp, M.; Kohrn, M.; Wesseling, M.; Müller, D. Cost optimal sizing of smart buildings’ energy system components considering changing end-consumer electricity markets. Energy 2017, 137, 715–728. [Google Scholar] [CrossRef]
- Ferreira, L.N.; Zhao, L. A time series clustering technique based on community detection in networks. Procedia Comput. Sci. 2015, 53, 183–190. [Google Scholar] [CrossRef] [Green Version]
- Buza, K.; Nanopoulos, A.; Schmidt-Thieme, L. Time-Series Classification Based on Individualised Error Prediction. In Proceedings of the 2010 13th IEEE International Conference on Computational Science and Engineering, Hong Kong, China, 11–13 December 2010; pp. 48–54. [Google Scholar]
- Lund, H.; Arler, F.; Østergaard, P.A.; Hvelplund, F.K.; Connolly, D.; Mathiesen, B.V.; Karnøe, P. Simulation versus optimisation: Theoretical positions in energy system modelling. Energies 2017, 10, 840. [Google Scholar] [CrossRef]
- Balankin, A.S.; Matamoros, O.M.; Galvez, E.M.; Perez, A. A Crossover from Antipersistent to Persistent Behavior in Time Series Possessing the Generalyzed Dynamic Scaling Law 69. 2004. Available online: https://www.adelaide.edu.au/library/ (accessed on 14 August 2020).
- Wang, X.; Keogh, E.J.; Lonardi, S.; Shelton, C. Data Mining Techniques on Historical Image Databases. 2010. Available online: https://www.adelaide.edu.au/library/ (accessed on 23 July 2020).
- Batista, G.; Keogh, E.; Tataw, A.; Souza, P. CID: An efficient complexity-invariant distance for time series. Data Min. Knowl. Discov. 2014, 28, 634–669. [Google Scholar] [CrossRef]
- Ferreira, L.N.; Zhao, L. Time series clustering via community detection in networks. Inf. Sci. 2016, 326, 227–242. [Google Scholar] [CrossRef] [Green Version]
- McBurney, P.W.; Jiang, S.; Kessentini, M.; Kraft, N.A.; Armaly, A.; Mkaouer, M.W.; McMillan, C. Towards Prioritising Documentation Effort. IEEE Trans. Softw. Eng. 2018, 44, 897–913. [Google Scholar] [CrossRef]
- Spendler, L.I. Data mining and management (Ser. Computer science, technology and applications). Nova Science. 2010. Available online: https://lesa.on.worldcat.org/oclc/753956716 (accessed on 29 July 2020).
- Kuc-Czarnecka, M. Sensitivity analysis as a tool to optimise Human Development Index. Equilibrium 2019, 14, 425–440. [Google Scholar] [CrossRef] [Green Version]
- Ruda, M.M.; Thompson, D.W. Comparison of primal and dual solution methods for the chemical equilibrium problem using GRG and sensitivity analysis. Can. J. Chem. Eng. 1985, 63, 113–121. [Google Scholar] [CrossRef]
- Pirnia, M.; Cañizares, C.A.; Bhattacharya, K. Revisiting the power flow problem based on a mixed complementarity formulation approach. IET Gener. Transm. Distrib. 2013, 7, 1194–1201. [Google Scholar] [CrossRef]
- Proietto, R.R.; Arnone, D.; Bertoncini, M.; Rossi, A.; La Cascia, D.; Miceli, R. Mixed heuristic-non linear optimisation of energy management for hydrogen storage-based multi carrier hubs. In Proceedings of the IEEE International Energy Conference (ENERGYCON), Cavtat, Croatia, 13–16 May 2014; pp. 1019–1026. [Google Scholar] [CrossRef]
- Pal, P.; Bhunia, A.; Goyal, S. On optimal partially integrated production and marketing policy with variable demand under flexibility and reliability considerations via Genetic Algorithm. Appl. Math. Comput. 2007, 188, 525–537. [Google Scholar] [CrossRef]
- Li, M.; Vo, Q.B.; Kowalczyk, R. A Pareto-efficient and fair mediation approach to multilateral negotiation. Multiagent Grid Syst. 2014, 10, 1–22. [Google Scholar] [CrossRef]
- Prieto, F.; Sarabia, J.M. A generalisation of the power law distribution with nonlinear exponent. Commun. Nonlinear Sci. Numer. Simul. 2017, 42, 215–228. [Google Scholar] [CrossRef] [Green Version]
- Nicolson, M.L.; Fell, M.J.; Huebner, G.M. Consumer demand for time of use electricity tariffs: A systematised review of the empirical evidence. Renew. Sustain. Energy Rev. 2018, 97, 276–289. [Google Scholar] [CrossRef]
- Xu, Z.; Le, J.-L. On power-law tail distribution of strength statistics of brittle and quasibrittle structures. Eng. Fract. Mech. 2018, 197, 80–91. [Google Scholar] [CrossRef]
- Elhabyan, R.; Shi, W.; St-Hilaire, M. A Pareto optimisation-based approach to clustering and routing in Wireless Sensor Networks. J. Netw. Comput. Appl. 2018, 114, 57–69. [Google Scholar] [CrossRef]
- Hambuckers, J.; Groll, A.; Kneib, T. Understanding the economic determinants of the severity of operational losses: A regularised generalised Pareto regression approach. J. Appl. Econ. 2018, 33, 898–935. [Google Scholar] [CrossRef] [Green Version]
- García-León, A.A.; Dauzère-Pérès, S.; Mati, Y. An efficient pareto approach for solving the multi-objective flexible job-shop scheduling problem with regular criteria. Comput. Oper. Res. 2019, 108, 187–200. [Google Scholar] [CrossRef]
- Ihtisham, S.; Khalil, A.; Manzoor, S.; Khan, S.A.; Ali, A.; Ribeiro, H.V. Alpha-power pareto distribution: Its properties and applications. PLoS ONE 2019, 14. [Google Scholar] [CrossRef]
- Meng, Q.; Khoo, H.L. A Pareto-optimization approach for a fair ramp metering. Transp. Res. Part. C Emerg. Technol. 2010, 18, 489–506. [Google Scholar] [CrossRef]
- Lejaeghere, K.; Cottenier, S.; Van Speybroeck, V. Ranking the stars: A refined pareto approach to computational materials design. Phys. Rev. Lett. 2013, 111, 1–5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McIntyre, A.R.; Heywood, M.I. Classification as clustering: A pareto cooperative-competitive GP approach. Evol. Comput. 2011, 19, 137–166. [Google Scholar] [CrossRef]
- Ravalico, J.K.; Maier, H.R.; Dandy, G.C. Sensitivity analysis for decision-making using the MORE method—A Pareto approach. Reliab. Eng. Syst. Saf. 2009, 94, 1229–1237. [Google Scholar] [CrossRef]
- Andriani, P.; Mckelvey, B. Managing in a pareto world calls for new thinking. M@n@Gement 2011, 14, 89. [Google Scholar] [CrossRef]
- Pan, X. Calculation of sampling size for non-zero tolerance level. Glob. Ecol. Conserv. 2020, 22, e00982. [Google Scholar] [CrossRef]
- Australian Energy Market Operator. 2020 Electricity Price & Demand. 2021. Available online: https://www.aemo.com.au/ (accessed on 10 January 2021).
- Australian Bureau of Statistics. Sample Size Calculator. 2021. Available online: https://www.abs.gov.au/websitedbs/d3310114.nsf/home/sample+size+calculator (accessed on 10 January 2021).
- Urken, A.B.; Schuck, T.M. Designing evolvable systems in a framework of robust, resilient and sustainable engineering analysis. Adv. Eng. Inform. 2012, 26, 553–562. [Google Scholar] [CrossRef]
- Ratanamahatana, C.A.; Keogh, E. Everything you know about Dynamic Time Warping is Wrong. 2004. Available online: http://wearables.cc.gatech.edu/paper_of_week/DTW_myths.pdf (accessed on 19 July 2020).
- Independent Pricing and Regulatory Tribunal—IPART. Long Run Marginal Cost of Electricity. 2021. Available online: https://www.ipart.nsw.gov.au/Home (accessed on 20 January 2021).









| Metrics | Formula | Parameters |
|---|---|---|
| Pareto | F(x) = 1 – (k/x) β | X: random variable |
| distribution | K: lower bound of data β: scale parameter shape index data slop |
| Metrics | Formula | Parameters | Confidence Level | Population | Sample Size |
|---|---|---|---|---|---|
| Determine Sample Size | Z: Index value of Confidence Level P: Percentage picking a choice expressed as a decimal. C: Confidence interval expressed as decimal | 99% | 2,471,221 | 218 (Residential houses needed for analysis) |
| Time Int. | Max | Min | Mean | Median | 10% Conf | 90% Conf | ui | Avi | li | ui (%) | Avi (%) | li (%) | EUij | (∑li+ui) | (AVi) | (∑li+AVi+ui) | FALSE(%) | TRUE(%) | Total Events(%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0:30 | 5.94 | 0.00 | 0.47 | 0.17 | 0.71 | 0.08 | 26,156 | 7587 | 72,025 | 24.73% | 7.17% | 68.10% | 100.00% | 98,181 | 7588 | 105,769 | 92.83% | 7.17% | 100.00% |
| 1:00 | 5.87 | 0.00 | 0.46 | 0.16 | 0.69 | 0.07 | 25,185 | 6529 | 74,054 | 23.81% | 6.17% | 70.02% | 100.00% | 99,239 | 6530 | 105,769 | 93.83% | 6.17% | 100.00% |
| 1:30 | 5.58 | 0.00 | 0.43 | 0.15 | 0.68 | 0.07 | 23,311 | 5713 | 76,744 | 22.04% | 5.40% | 72.56% | 100.00% | 100,055 | 5714 | 105,769 | 94.60% | 5.40% | 100.00% |
| 2:00 | 5.32 | 0.00 | 0.35 | 0.14 | 0.66 | 0.07 | 19,367 | 5622 | 80,779 | 18.31% | 5.32% | 76.37% | 100.00% | 100,146 | 5623 | 105,769 | 94.68% | 5.32% | 100.00% |
| 2:30 | 4.63 | 0.00 | 0.29 | 0.14 | 0.60 | 0.07 | 15,914 | 5357 | 84,497 | 15.05% | 5.06% | 79.89% | 100.00% | 100,411 | 5358 | 105,769 | 94.93% | 5.07% | 100.00% |
| 3:00 | 4.27 | 0.00 | 0.24 | 0.13 | 0.66 | 0.07 | 13,137 | 5176 | 87,455 | 12.42% | 4.89% | 82.69% | 100.00% | 100,592 | 5177 | 105,769 | 95.11% | 4.89% | 100.00% |
| 3:30 | 4.27 | 0.00 | 0.22 | 0.13 | 0.59 | 0.07 | 11,958 | 5038 | 88,772 | 11.31% | 4.76% | 83.93% | 100.00% | 100,730 | 5039 | 105,769 | 95.24% | 4.76% | 100.00% |
| 4:00 | 4.25 | 0.00 | 0.21 | 0.13 | 0.65 | 0.07 | 11,483 | 5065 | 89,220 | 10.86% | 4.79% | 84.35% | 100.00% | 100,703 | 5066 | 105,769 | 95.21% | 4.79% | 100.00% |
| 4:30 | 4.31 | 0.00 | 0.21 | 0.13 | 0.61 | 0.07 | 11,151 | 5676 | 88,941 | 10.54% | 5.37% | 84.09% | 100.00% | 100,092 | 5677 | 105,769 | 94.63% | 5.37% | 100.00% |
| 5:00 | 4.32 | 0.00 | 0.21 | 0.13 | 0.25 | 0.37 | 11,579 | 5816 | 88,373 | 10.95% | 5.50% | 83.55% | 100.00% | 99,952 | 5817 | 105,769 | 94.50% | 5.50% | 100.00% |
| 5:30 | 4.16 | 0.00 | 0.23 | 0.13 | 0.09 | 0.21 | 12,766 | 6469 | 86,533 | 12.07% | 6.12% | 81.81% | 100.00% | 99,299 | 6470 | 105,769 | 93.88% | 6.12% | 100.00% |
| 6:00 | 4.22 | 0.00 | 0.25 | 0.14 | 0.04 | 0.49 | 14,253 | 7419 | 84,096 | 13.48% | 7.01% | 79.51% | 100.00% | 98,349 | 7420 | 105,769 | 92.98% | 7.02% | 100.00% |
| 6:30 | 4.85 | 0.00 | 0.29 | 0.15 | 0.09 | 0.21 | 17,072 | 9750 | 78,946 | 16.14% | 9.22% | 74.64% | 100.00% | 96,018 | 9751 | 105,769 | 90.78% | 9.22% | 100.00% |
| 7:00 | 5.32 | 0.00 | 0.35 | 0.18 | 0.06 | 0.27 | 21,781 | 11,701 | 72,286 | 20.59% | 11.06% | 68.34% | 100.00% | 94,067 | 11,702 | 105,769 | 88.94% | 11.06% | 100.00% |
| 7:30 | 5.23 | 0.00 | 0.36 | 0.20 | 0.09 | 0.44 | 22,875 | 14,146 | 68,747 | 21.63% | 13.37% | 65.00% | 100.00% | 91,622 | 14,147 | 105,769 | 86.62% | 13.38% | 100.00% |
| 8:00 | 5.51 | 0.00 | 0.37 | 0.22 | 0.06 | 0.84 | 23,928 | 15,086 | 66,754 | 22.62% | 14.26% | 63.11% | 100.00% | 90,682 | 15,087 | 105,769 | 85.74% | 14.26% | 100.00% |
| 8:30 | 4.90 | 0.00 | 0.36 | 0.22 | 0.08 | 0.23 | 22,959 | 15,604 | 67,205 | 21.71% | 14.75% | 63.54% | 100.00% | 90,164 | 15,605 | 105,769 | 85.25% | 14.75% | 100.00% |
| 9:00 | 5.55 | 0.00 | 0.35 | 0.21 | 0.13 | 0.11 | 22,648 | 14,507 | 68,613 | 21.41% | 13.72% | 64.87% | 100.00% | 91,261 | 14,508 | 105,769 | 86.28% | 13.72% | 100.00% |
| 9:30 | 6.59 | 0.00 | 0.34 | 0.20 | 0.35 | 0.07 | 21,719 | 13,657 | 70,392 | 20.53% | 12.91% | 66.55% | 100.00% | 92,111 | 13,658 | 105,769 | 87.09% | 12.91% | 100.00% |
| 10:00 | 5.25 | 0.00 | 0.33 | 0.19 | 0.16 | 0.08 | 20,725 | 13,086 | 71,957 | 19.59% | 12.37% | 68.03% | 100.00% | 92,682 | 13,087 | 105,769 | 87.63% | 12.37% | 100.00% |
| 10:30 | 5.56 | 0.00 | 0.32 | 0.19 | 0.05 | 0.07 | 20,003 | 12,608 | 73,157 | 18.91% | 11.92% | 69.17% | 100.00% | 93,160 | 12,609 | 105,769 | 88.08% | 11.92% | 100.00% |
| 11:00 | 4.49 | 0.00 | 0.31 | 0.19 | 0.10 | 0.07 | 19,596 | 12,282 | 73,890 | 18.53% | 11.61% | 69.86% | 100.00% | 93,486 | 12,283 | 105,769 | 88.39% | 11.61% | 100.00% |
| 11:30 | 4.76 | 0.00 | 0.31 | 0.19 | 0.06 | 0.07 | 19,445 | 11,988 | 74,335 | 18.38% | 11.33% | 70.28% | 100.00% | 93,780 | 11,989 | 105,769 | 88.66% | 11.34% | 100.00% |
| 12:00 | 5.74 | 0.00 | 0.31 | 0.19 | 0.09 | 0.07 | 19,646 | 12,367 | 73,755 | 18.57% | 11.69% | 69.73% | 100.00% | 93,401 | 12,368 | 105,769 | 88.31% | 11.69% | 100.00% |
| 12:30 | 5.89 | 0.00 | 0.31 | 0.19 | 0.08 | 0.07 | 19,550 | 13,255 | 72,963 | 18.48% | 12.53% | 68.98% | 100.00% | 92,513 | 13,256 | 105,769 | 87.47% | 12.53% | 100.00% |
| 13:00 | 6.22 | 0.00 | 0.31 | 0.19 | 0.06 | 0.07 | 19,149 | 13,466 | 73,153 | 18.10% | 12.73% | 69.16% | 100.00% | 92,302 | 13,467 | 105,769 | 87.27% | 12.73% | 100.00% |
| 13:30 | 4.73 | 0.00 | 0.31 | 0.19 | 0.08 | 0.16 | 18,839 | 13,546 | 73,383 | 17.81% | 12.81% | 69.38% | 100.00% | 92,222 | 13,547 | 105,769 | 87.19% | 12.81% | 100.00% |
| 14:00 | 5.10 | 0.00 | 0.31 | 0.19 | 0.08 | 0.11 | 18,052 | 13,234 | 74,482 | 17.07% | 12.51% | 70.42% | 100.00% | 92,534 | 13,235 | 105,769 | 87.49% | 12.51% | 100.00% |
| 14:30 | 5.63 | 0.00 | 0.30 | 0.19 | 0.34 | 0.08 | 16,950 | 13,363 | 75,455 | 16.03% | 12.63% | 71.34% | 100.00% | 92,405 | 13,364 | 105,769 | 87.36% | 12.64% | 100.00% |
| 15:00 | 5.85 | 0.00 | 0.30 | 0.19 | 0.10 | 0.07 | 16,657 | 13,332 | 75,779 | 15.75% | 12.60% | 71.65% | 100.00% | 92,436 | 13,333 | 105,769 | 87.39% | 12.61% | 100.00% |
| 15:30 | 6.31 | 0.00 | 0.31 | 0.19 | 0.79 | 0.11 | 17,235 | 13,763 | 74,770 | 16.30% | 13.01% | 70.69% | 100.00% | 92,005 | 13,764 | 105,769 | 86.99% | 13.01% | 100.00% |
| 16:00 | 5.80 | 0.00 | 0.32 | 0.20 | 0.34 | 0.25 | 18,416 | 14,555 | 72,797 | 17.41% | 13.76% | 68.83% | 100.00% | 91,213 | 14,556 | 105,769 | 86.24% | 13.76% | 100.00% |
| 16:30 | 6.30 | 0.00 | 0.34 | 0.22 | 0.20 | 0.14 | 20,672 | 15,539 | 69,557 | 19.54% | 14.69% | 65.76% | 100.00% | 90,229 | 15,540 | 105,769 | 85.31% | 14.69% | 100.00% |
| 17:00 | 5.93 | 0.00 | 0.38 | 0.24 | 0.15 | 0.11 | 24,898 | 16,429 | 64,441 | 23.54% | 15.53% | 60.93% | 100.00% | 89,339 | 16,430 | 105,769 | 84.47% | 15.53% | 100.00% |
| 17:30 | 5.40 | 0.00 | 0.45 | 0.28 | 0.19 | 0.11 | 31,454 | 17,200 | 57,114 | 29.74% | 16.26% | 54.00% | 100.00% | 88,568 | 17,201 | 105,769 | 83.74% | 16.26% | 100.00% |
| 18:00 | 5.44 | 0.00 | 0.51 | 0.32 | 0.13 | 0.11 | 37,801 | 18,445 | 49,522 | 35.74% | 17.44% | 46.82% | 100.00% | 87,323 | 18,446 | 105,769 | 82.56% | 17.44% | 100.00% |
| 18:30 | 6.57 | 0.00 | 0.53 | 0.35 | 0.69 | 0.11 | 40,813 | 19,556 | 45,399 | 38.59% | 18.49% | 42.92% | 100.00% | 86,212 | 19,557 | 105,769 | 81.51% | 18.49% | 100.00% |
| 19:00 | 6.34 | 0.00 | 0.53 | 0.36 | 0.15 | 0.11 | 40,767 | 20,896 | 44,105 | 38.54% | 19.76% | 41.70% | 100.00% | 84,872 | 20,897 | 105,769 | 80.24% | 19.76% | 100.00% |
| 19:30 | 6.31 | 0.00 | 0.51 | 0.35 | 0.19 | 0.69 | 39,170 | 22,385 | 44,213 | 37.03% | 21.16% | 41.80% | 100.00% | 83,383 | 22,386 | 105,769 | 78.84% | 21.16% | 100.00% |
| 20:00 | 6.07 | 0.00 | 0.50 | 0.35 | 0.13 | 0.98 | 38,192 | 23,334 | 44,242 | 36.11% | 22.06% | 41.83% | 100.00% | 82,434 | 23,335 | 105,769 | 77.94% | 22.06% | 100.00% |
| 20:30 | 5.69 | 0.00 | 0.50 | 0.35 | 0.15 | 0.50 | 38,403 | 23,804 | 43,561 | 36.31% | 22.51% | 41.19% | 100.00% | 81,964 | 23,805 | 105,769 | 77.49% | 22.51% | 100.00% |
| 21:00 | 5.59 | 0.00 | 0.48 | 0.34 | 0.31 | 0.40 | 36,352 | 24,129 | 45,287 | 34.37% | 22.81% | 42.82% | 100.00% | 81,639 | 24,130 | 105,769 | 77.19% | 22.81% | 100.00% |
| 21:30 | 5.46 | 0.00 | 0.45 | 0.32 | 0.33 | 0.39 | 33,508 | 23,530 | 48,730 | 31.68% | 22.25% | 46.07% | 100.00% | 82,238 | 23,531 | 105,769 | 77.75% | 22.25% | 100.00% |
| 22:00 | 6.52 | 0.00 | 0.44 | 0.30 | 0.19 | 0.38 | 31,186 | 21,054 | 53,528 | 29.49% | 19.91% | 50.61% | 100.00% | 84,714 | 21,055 | 105,769 | 80.09% | 19.91% | 100.00% |
| 22:30 | 6.34 | 0.00 | 0.44 | 0.27 | 0.69 | 0.26 | 30,254 | 17,857 | 57,657 | 28.60% | 16.88% | 54.51% | 100.00% | 87,911 | 17,858 | 105,769 | 83.12% | 16.88% | 100.00% |
| 23:00 | 6.54 | 0.00 | 0.42 | 0.23 | 0.54 | 0.06 | 27,480 | 14,707 | 63,581 | 25.98% | 13.90% | 60.11% | 100.00% | 91,061 | 14,708 | 105,769 | 86.09% | 13.91% | 100.00% |
| 23:30 | 6.41 | 0.00 | 0.43 | 0.21 | 0.89 | 0.08 | 26,744 | 12,120 | 66,904 | 25.29% | 11.46% | 63.26% | 100.00% | 93,648 | 12,121 | 105,769 | 88.54% | 11.46% | 100.00% |
| 0:00 | 5.59 | 0.00 | 0.46 | 0.19 | 1.19 | 0.07 | 26,608 | 9727 | 69,433 | 25.16% | 9.20% | 65.65% | 100.00% | 96,041 | 9728 | 105,769 | 90.80% | 9.20% | 100.00% |
| Population-Id | Demand Unit | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| (l + u)-False | AV-True | l-False | u-False | AV-True | Under-Demand | Over-Demand | Optimum | ||
| 1 Tier | 44 | 4 | 23 | 0 | 25 | −0.4792 | 0.0000 | 0.5208 | 0.4792 |
| 2 Tier | 43 | 5 | 32 | 15 | 1 | −0.6667 | 0.3125 | 0.0208 | 0.9792 |
| 3 Tier | 44 | 4 | 23 | 5 | 20 | −0.4792 | 0.1042 | 0.4167 | 0.5833 |
| 4 Tier | 43 | 5 | 12 | 0 | 36 | −0.2500 | 0.0000 | 0.7500 | 0.2500 |
| 5 Tier | 46 | 4 | 31 | 8 | 9 | −0.6458 | 0.1667 | 0.1875 | 0.8125 |
| 6 Tier | 41 | 7 | 4 | 0 | 44 | −0.0833 | 0.0000 | 0.9167 | 0.0833 |
| 7 Tier | 40 | 8 | 3 | 0 | 45 | −0.0625 | 0.0000 | 0.9375 | 0.0625 |
| 8 Tier | 42 | 6 | 6 | 0 | 42 | −0.1250 | 0.0000 | 0.8750 | 0.1250 |
| 9 Tier | 43 | 5 | 0 | 0 | 48 | 0.0000 | 0.0000 | 1.0000 | 0.0000 |
| 10 Tier | 40 | 8 | 7 | 1 | 40 | −0.1458 | 0.0208 | 0.8333 | 0.1667 |
| 11 Tier | 41 | 7 | 12 | 5 | 31 | −0.2500 | 0.1042 | 0.6458 | 0.3542 |
| 12 Tier | 43 | 5 | 22 | 0 | 26 | −0.4583 | 0.0000 | 0.5417 | 0.4583 |
| 13 Tier | 41 | 7 | 4 | 3 | 41 | −0.0833 | 0.0625 | 0.8542 | 0.1458 |
| 14 Tier | 42 | 6 | 8 | 0 | 40 | −0.1667 | 0.0000 | 0.8333 | 0.1667 |
| 15 Tier | 44 | 4 | 9 | 0 | 39 | −0.1875 | 0.0000 | 0.8125 | 0.1875 |
| 16 Tier | 43 | 5 | 13 | 0 | 35 | −0.2708 | 0.0000 | 0.7292 | 0.2708 |
| 17 Tier | 44 | 4 | 27 | 0 | 21 | −0.5625 | 0.0000 | 0.4375 | 0.5625 |
| 18 Tier | 43 | 5 | 40 | 8 | 0 | −0.8333 | 0.1667 | 0.0000 | 1.0000 |
| 19 Tier | 42 | 6 | 13 | 4 | 31 | −0.2708 | 0.0833 | 0.6458 | 0.3542 |
| 20 Tier | 43 | 5 | 19 | 29 | 0 | −0.3958 | 0.6042 | 0.0000 | 1.0000 |
| 21 Tier | 43 | 5 | 0 | 0 | 48 | 0.0000 | 0.0000 | 1.0000 | 0.0000 |
| 22 Tier | 44 | 4 | 24 | 10 | 14 | −0.5000 | 0.2083 | 0.2917 | 0.7083 |
| 23 Tier | 43 | 5 | 11 | 0 | 37 | −0.2292 | 0.0000 | 0.7708 | 0.2292 |
| 24 Tier | 44 | 4 | 25 | 0 | 23 | −0.5208 | 0.0000 | 0.4792 | 0.5208 |
| 25 Tier | 41 | 7 | 1 | 0 | 47 | −0.0208 | 0.0000 | 0.9792 | 0.0208 |
| 26 Tier | 45 | 3 | 32 | 0 | 16 | −0.6667 | 0.0000 | 0.3333 | 0.6667 |
| 27 Tier | 44 | 4 | 17 | 0 | 31 | −0.3542 | 0.0000 | 0.6458 | 0.3542 |
| 28 Tier | 44 | 4 | 7 | 1 | 40 | −0.1458 | 0.0208 | 0.8333 | 0.1667 |
| 29 Tier | 43 | 5 | 8 | 1 | 39 | −0.1667 | 0.0208 | 0.8125 | 0.1875 |
| Percentile Demand Rate | False-Demand (%) | True-Demand (%) |
|---|---|---|
| Optimisation (%) | 56.54% | 43.46% |
| Simulation (%) | 89.30% | 10.70% |
| Total Population | 290 | 290 |
| Optimal Capacity Factor for Generators Associated with Entry Cost $/MWh. | |||
|---|---|---|---|
| Load Factor (CF) | 100% | 55% | 14% |
| Thermal Coal-CP | $36.2 MWh | Higher than $55.9 MWh | Higher than $109.0 MWh |
| CCGT | Higher than $36.2 MWh | $55.9MWh | Higher than $109.0 MWh |
| OCGT | Higher than $36.2 MWh | Higher than $55.9 MWh | $109.0MWh |
| Demand Cost Benefit(₵) | |||||
|---|---|---|---|---|---|
| Tiers | Simulation Modelling | Optimisation Modelling | |||
| DCBO(₵) | Losses(%) | DCAO(₵) | Gains (%) | OG(₵) | |
| 1T | 1268.37 | 0.4149 | 526.24 | 0.5851 | 742.13 |
| 2T | 970.15 | 0.2900 | 281.34 | 0.7100 | 688.81 |
| 3T | 1156.29 | 0.3191 | 368.98 | 0.6809 | 787.31 |
| 4T | 1083.83 | 0.3968 | 430.07 | 0.6032 | 653.75 |
| 5T | 1077.13 | 0.3266 | 351.78 | 0.6734 | 725.34 |
| 6T | 943.93 | 0.4854 | 458.20 | 0.5146 | 485.74 |
| 7T | 852.32 | 0.4690 | 399.71 | 0.5310 | 452.60 |
| 8T | 999.49 | 0.3761 | 375.89 | 0.6239 | 623.60 |
| 9T | 1282.73 | 0.1167 | 149.64 | 0.8833 | 1133.09 |
| 10T | 1079.53 | 0.5443 | 587.59 | 0.4557 | 491.94 |
| 11T | 1049.83 | 0.4137 | 434.35 | 0.5863 | 615.47 |
| 12T | 1160.90 | 0.3669 | 425.88 | 0.6331 | 735.02 |
| 13T | 1079.98 | 0.5001 | 540.06 | 0.4999 | 539.92 |
| 14T | 1340.14 | 0.3676 | 492.64 | 0.6324 | 847.50 |
| 15T | 1532.55 | 0.3711 | 568.79 | 0.6289 | 963.76 |
| 16T | 1424.33 | 0.3902 | 555.81 | 0.6098 | 868.52 |
| 17T | 977.42 | 0.3381 | 330.47 | 0.6619 | 646.95 |
| 18T | 1164.67 | 0.3529 | 410.99 | 0.6471 | 753.68 |
| 19T | 1026.28 | 0.4496 | 461.42 | 0.5504 | 564.86 |
| 20T | 918.47 | 0.2900 | 266.36 | 0.7100 | 652.12 |
| 21T | 838.67 | 0.3905 | 327.53 | 0.6095 | 511.14 |
| 22T | 1348.01 | 0.3541 | 477.39 | 0.6459 | 870.63 |
| 23T | 987.16 | 0.4173 | 411.93 | 0.5827 | 575.23 |
| 24T | 883.66 | 0.3835 | 338.86 | 0.6165 | 544.80 |
| 25T | 1005.46 | 0.3900 | 392.13 | 0.6100 | 613.33 |
| 26T | 1287.68 | 0.3151 | 405.78 | 0.6849 | 881.90 |
| 27T | 1122.55 | 0.4017 | 450.95 | 0.5983 | 671.60 |
| 28T | 1147.01 | 0.4270 | 489.80 | 0.5730 | 657.20 |
| 29T | 1523.30 | 0.3974 | 605.33 | 0.6026 | 917.97 |
| Energy Losses | Cost of Losses (¢) | Cost of Gains (¢) | Impact (%) | |
|---|---|---|---|---|
| Simulation | DCBO | (32,531.83) | −(100%) | |
| Optimisation | DCAO | (12,315.92) | −(37.86%) | |
| OG | 20,215.90 | +(62.14%) | ||
| Population-id | Electricity Supply (KWh) (GC + CL) | Constraints (End-Users Demand) | Expected Power Constraints at Homes | |||
|---|---|---|---|---|---|---|
| Fault 1 | Fault 2 | |||||
| Available Stock | Optimisation Results | Under Demand | Over Demand | GG2 | GG1 | |
| 1TIER | 175.61 | 183.59 | −7.98 | 0.00 | 1 | 2 |
| 2TIER | 163.84 | 181.67 | −44.61 | 26.78 | 2 | 2 |
| 3TIER | 147.95 | 158.14 | −12.12 | 1.93 | 2 | 2 |
| 4TIER | 167.00 | 176.27 | −9.27 | 0.00 | 1 | 2 |
| 5TIER | 134.00 | 152.08 | −20.33 | 2.25 | 2 | 2 |
| 6TIER | 221.62 | 222.96 | −1.34 | 0.00 | 1 | 2 |
| 7TIER | 193.55 | 194.43 | −0.88 | 0.00 | 1 | 2 |
| 8TIER | 174.27 | 177.06 | −2.79 | 0.00 | 1 | 2 |
| 9TIER | 154.14 | 154.14 | 0.00 | 0.00 | 1 | 1 |
| 10TIER | 211.7 | 215.94 | −4.24 | 0.00 | 1 | 2 |
| 11TIER | 175.33 | 178.44 | −9.09 | 5.98 | 1 | 2 |
| 12TIER | 147.18 | 163.18 | −16.00 | 0.00 | 1 | 2 |
| 13TIER | 210.15 | 210.82 | −0.67 | 0.00 | 1 | 2 |
| 14TIER | 172.79 | 174.00 | −1.21 | 0.00 | 1 | 2 |
| 15TIER | 171.62 | 177.50 | −5.88 | 0.00 | 1 | 2 |
| 16TIER | 177.61 | 184.74 | −7.13 | 0.00 | 1 | 2 |
| 17TIER | 140.74 | 157.99 | −17.25 | 0.00 | 1 | 2 |
| 18TIER | 140.74 | 158.11 | −26.12 | 8.75 | 2 | 2 |
| 19TIER | 185.23 | 188.98 | −4.96 | 1.21 | 2 | 2 |
| 20TIER | 166.33 | 139.20 | −7.54 | 34.67 | 2 | 2 |
| 21TIER | 166.71 | 166.71 | 0.00 | 0.00 | 1 | 1 |
| 22TIER | 157.00 | 169.41 | −15.09 | 2.68 | 2 | 2 |
| 23TIER | 170.03 | 177.38 | −7.35 | 0.00 | 1 | 2 |
| 24TIER | 155.34 | 165.00 | −9.66 | 0.00 | 1 | 2 |
| 25TIER | 234.99 | 234.99 | 0.00 | 0.00 | 1 | 1 |
| 26TIER | 130.53 | 149.24 | −18.71 | 0.00 | 1 | 2 |
| 27TIER | 168.53 | 177.18 | −8.65 | 0.00 | 1 | 2 |
| 28TIER | 189.57 | 192.28 | −2.71 | 0.00 | 1 | 2 |
| 29TIER | 179.23 | 185.73 | −6.50 | 0.00 | 1 | 2 |
| Capacity | Impact Factor | Expected Power Sources | |
|---|---|---|---|
| Under Demand Constraints | 268.08 | 89.65% | GG1 |
| Over Demand Constraints | 84.25 | 24.13% | GG2 |
| Total Available Stock | 4983.33 | 89.65% | (GC+CL) |
| Total Optimisation Results | 5167.16 | 100.00% | Mix |
| Z-Test: One Sample | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | x14 | x15 | x16 | x17 | x18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 0.357 | 0.357 | 0.357 | 0.357 | 0.357 | 0.357 | 0.357 | 0.357 | 0.357 | 0.357 | 0.357 | 0.357 | 0.357 | 0.357 | 0.357 | 0.357 | 0.357 | 0.357 |
| Known Variance | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 |
| Observations | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 |
| Hypothesized Mean | 0.29 | 0.30 | 0.31 | 0.32 | 0.33 | 0.34 | 0.35 | 0.36 | 0.37 | 0.38 | 0.39 | 0.40 | 0.41 | 0.42 | 0.43 | 0.44 | 0.45 | 0.46 |
| z | 5.03 | 4.284 | 3.539 | 2.794 | 2.048 | 1.303 | 0.558 | −0.19 | −0.93 | −1.68 | −2.42 | −3.17 | −3.91 | −4.66 | −5.4 | −6.15 | −6.89 | −7.64 |
| P(Z ≤ z) two-tail | 5 × 10−7 | 2 × 10−5 | 4 × 10−4 | 0.005 | 0.041 | 0.193 | 0.577 | 0.851 | 0.351 | 0.093 | 0.015 | 0.002 | 9 × 10−5 | 3 × 10−6 | 7 × 10−8 | 8 × 10−10 | 5 × 10−12 | 2 × 10−14 |
| z Critical two-tail | 2.576 | 2.576 | 2.576 | 2.576 | 2.576 | 2.576 | 2.576 | 2.576 | 2.576 | 2.576 | 2.576 | 2.576 | 2.576 | 2.576 | 2.576 | 2.576 | 2.576 | 2.576 |
| p-value | <0.001 | <0.001 | <0.001 | <0.001 | >0.001 | >0.001 | >0.001 | >0.001 | >0.001 | >0.001 | >0.001 | >0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaghwan, A.; Gunawan, I. Resolving Energy Losses Caused by End-Users in Electrical Grid Systems. Designs 2021, 5, 23. https://0-doi-org.brum.beds.ac.uk/10.3390/designs5010023
Zaghwan A, Gunawan I. Resolving Energy Losses Caused by End-Users in Electrical Grid Systems. Designs. 2021; 5(1):23. https://0-doi-org.brum.beds.ac.uk/10.3390/designs5010023
Chicago/Turabian StyleZaghwan, Ashraf, and Indra Gunawan. 2021. "Resolving Energy Losses Caused by End-Users in Electrical Grid Systems" Designs 5, no. 1: 23. https://0-doi-org.brum.beds.ac.uk/10.3390/designs5010023





