1. Introduction
Neutron scattering facilities such as the European Spallation Source (ESS) currently under construction in Lund, Sweden, and the world-leading Institut Laue Langevin (ILL) in Grenoble, France, rely increasingly upon beam simulations to steer the evolution of the design of their instruments. The credibility of instrument conceptual design is now largely driven by Monte-Carlo simulation in preference to the more traditional approach of using analytical derivations. Such a change already happened in other fields—such as high energy and nuclear physics—due to the increased complexity of the respective scientific problems. Indeed, part of the reason in neutron scattering is likely to be the use of more complex instrument geometries, as will be touched upon in later sections of this paper.
There exist several software packages for building Monte-Carlo simulations of neutron beams, the most popular being McSTAS [
1], SimRes [
2], and VitESS [
3]. McSTAS has the widest user base, and requires the user to write a modified version of C. VitESS has a design philosophy around GUI-based, modular, pre-compiled code running sequentially via pipes. SimRes allows easy switching between bi-directional simulation options, either forwards or the adjoint Monte-Carlo method in reverse.
Neutron guide simulations can be a very time consuming activity. A large fraction of the computing resource allocation at ESS was not just for neutronics jobs but also McStas simulations of guides.
In this paper, a new software methodology and tool for the design of neutron guides is described, called “Sandman”. It is currently available on GitHub [
4], and offers significant computing speed improvements over the existing codes. It is written in C++, and is provided as a library. Instrument descriptions are written as a single instance of a class, and then a sequence of geometrical functions from that class. This is compiled and linked to the library.
There are three significant differences between Sandman and existing codes, though naturally each of these have a solid grounding in computational physics.
Firstly, Sandman works directly on 2-D phase space maps, called acceptance diagrams (see, for example, Reference [
5]). These are maps of beam divergence angle
and position
y that are transmitted by each component. By manipulating these maps, one can accurately define the transmission region of the beam from one optical module to the next. The principle was computationally automated for monochromatic beams in a previous technique called neutron acceptance diagram shading (NADS) [
6]. It provided a significant performance gain for the simulation of high resolution instruments, which would normally take several hours on large computing clusters using 3D Monte-Carlo approaches.
The main drawback with acceptance diagram shading is that it is monochromatic. A poly-chromatic neutron beam, such as produced by spallation sources, requires multiple passes or an assumed wavelength integral range that is small (≲15%). For example, a mechanical velocity selector, monochromator, or narrow bandwidth chopper instrument would require normalisation simply by multiplying by the width of the wavelength band. This approximation breaks down for poly-chromatic beams.
The solution for wide bandwidth poly-chromatic simulations is to marry the acceptance diagram shading technique with a Monte-Carlo sampling approach. It is important to note that this results in quite a different code compared to existing 3D Monte-Carlo approaches. The acceptance diagram shading method is two dimensional, and intrinsically faster than 3D ray tracing for an identical optical system. As will be shown later in this article, there is no planar intersection to solve. The fundamental requirement in the 2D method is that the horizontal and vertical phase space maps are independent, as one obtains from neutron guides with quadrilateral cross sections. Octagonal neutron guides or those with mirrors that are similarly inclined in a diagonal sense, so as to mix the horizontal and vertical phase space, cannot be modelled at present using NADS or Sandman, though the use case for such guides is quite narrow. Until this phase space mixing is implemented, second order effects such as rotational misalignment or multiple scattering cannot be done internally and would rely on external software.
The second major feature of the code is the adjoint method, reverse tracing, which is a long-time optional feature of SimRes [
2]. Adjoint Monte-Carlo was formulated at an early stage in computer simulations, as a variance reduction method to deal with neutron and photon shielding issues [
7], and has been demonstrated in high energy physics [
8]. It also has precedence in computer graphics ray tracing for decades, enabling CGI effects in movies, interactive 3D simulations and computer games. One would not trace photons from a light source in all possible directions and hope that the ray eventually intersects the camera location. Similarly, in the design of a neutron optical system, it will be shown in
Section 2.1 why one should start at the sample end of the guide. Sandman is written in such a way to
only compute the adjoint physical model. The adjoint method can be more problematic, particularly in the case of shielding and high energy work where particle interactions and secondary particles are created. However, in the current application of simple, non-interacting particle beams, these additional complications are not present.
Thirdly, Sandman is not designed to run on the CPU, like traditional software, nor is it a hybrid code that detects available hardware and deploys itself to the most efficient devices. Instead, it is written purely for the graphics card (GPU) using the Cuda API. This paper represents a second (and successful!) attempt to produce pure GPU neutron beam simulations. The first attempt failed in 2008–2010, in the sense that the CPU code was still faster, for a number of reasons. Cuda was a very new API at the time, and the development was in very early stages. The GPU memory transfer bottleneck, and the available memory, were major code design issues: one had to prepare the memory, process the data, and receive the output data quicker than simply doing the computation on the CPU. The direct computational treatment of acceptance diagrams was also a fairly new idea. The developments that enabled a successful project this time, starting in 2018, are a combination of easy access to good pseudo-random number generators on the GPU; an increasingly large memory bandwidth driven by the hardware needs of the 3D game industry; multiple GB of GPU memory being available; and mature, parallel methods to reduce large arrays of data.
The speed of this code brings great utility. Sandman offers a neutron guide designer the possibility of simulating a neutron guide with performance matching that of many real-world instruments in real-time, namely ∼ neutrons per second on the sample. From the perspective of the guide designer, running a white beam simulation is essentially instantaneous.
2. Description of the Method
2.1. Reverse Tracing
Sandman is an adjoint method, modelling the neutron beam in reverse, starting at the sample end of the guide. To see why this is effective, one must first consider the neutron transport system as a black box with a transmission efficiency T in the forwards direction, and in the reverse direction.
The probability that a neutron trajectory passes successfully from the source to the sample is a conditional probability , where is the probability that the neutron emerges from the system and reaches the sample, and is the probability that a neutron successfully enters the guide system from the moderator. Thus we see that T, the forwards transmission efficiency, is the conditional probability that a neutron hits the sample, assuming it enters the guide.
Existing Monte-Carlo codes generate trajectories already by pre-selecting the edges of phase space so that the generated trajectories have
. The problem is that, as the resolution of the instrumentation increases,
T becomes increasingly small. Neutron fluxes at the guide entrance could be
–
n/cm
/s, decreasing to on-sample fluxes of
n/cm
/s. Calculating
T in the optimisation of a high-resolution small angle scattering instrument requires many CPU-hours of computing time [
6].
Now, if we consider the adjoint problem, in reverse —this is the conditional probability that the neutron trajectory intersects the moderator, assuming that the trajectory intersects the sample position. If we only generate neutron trajectories at the sample such that , then accurately simulating by computing backwards is significantly faster than the equivalent simulation of T by computing forwards.
To see why this is so, we must only consider Bayes’ theorem:
Or equivalently, . The moderator illumination is designed to be as efficient as possible, that is, maximising , whereas the instrument Q resolution is inversely proportional to terms depending on , so . T also depends on the beam conditioning in general, which prepares the divergence and wavelength ranges to a minimum tolerable value that define the Q (=) and E resolution, so . T is often very small, typically with x in the range 3–6, and is therefore very close to 1. Hence, there is a difference that is several orders of magnitude between and T in computing time. All that remains afterwards is to multiply by the moderator brightness, as usual, and normalise the initial phase space to the much smaller area and solid angle factors of the sample to guide exit rather than the moderator-guide entrance phase space as one would for T. It is a useful exercise for the reader to verify for themselves that the two calculation directions produce an identical numerical result for the instrument performance, but it is an intuitive result. After all, the classical geometrical equations for non-interacting particles are independent on the direction of time.
2.2. Neutron Trajectory Calculation Method
2.2.1. GPU Software Development
Graphics accelerator cards were originally designed to accelerate matrix calculations for 3D computer graphics in games. In the mid-2000s, scientists realised that these computing devices could be tapped for general purpose computing. In response, NVIDIA—a major manufacturer of these cards—created a C++ API that facilitated this use case, called Cuda. This had an order of magnitude impact on computational sciences, and was revolutionary.
Cuda can be used in a very low-level way, giving access to precisely how computations are performed. At the time of writing, the creators have provided a vast online library [
9] of online material to get started. Cuda allows many thousands of parallel threads to run whilst working on a task. The threads are broken up into
warps of 32 threads each, and each warp is placed in a queue to run on one of many “Streaming Multiprocessors” (SMs). Whilst all of these threads can be thought of as being evaluated independently during the computation, one must bear in mind that within a warp, all conditional branches are evaluated by all threads. The threads that fail the conditional do not skip over the code block and continue to the next instruction, instead they step through to keep all threads synchronised within the warp. This means that careless branching can cause significant performance penalties.
Whilst Cuda allows for a concept called “unified memory”, meaning that the graphics card software automatically manages whether data is stored in system memory or GPU memory, and transfers backwards and forwards as needed, there can be a performance hit for this developer convenience. Sandman does not use unified memory. It allocates memory on the GPU, generates all the random numbers in place, and only transfers data from the GPU to system RAM after the simulation is complete and the individual trajectories have been fully reduced. The performance impact of this choice has not been experimentally tested, but it would be expected to be small given the efficient organisation of the Sandman code. Nonetheless, there is a (subjective) clarity argument for having well-defined memory allocation, transfer, and clean-up steps that the author prefers, and some other developers prefer a single allocation statement for the compiler and drivers to resolve.
Cuda contains a number of utility functions that are very helpful for this kind of work. Good pseudo-random number generators are available with cuRAND. In particular, the Mersenne Twister is easily accessed by passing CURAND_RNG_PSEUDO_MTGP32 to the function curandCreateGenerator().
Atomic functions allow the user to perform computations and guarantee that another thread will not interfere with the result. atomicAdd(addr,b) is called frequently in Sandman to reduce the final histograms. The value stored at addr is added to b and the result is written back to the address addr.
One final, noteworthy point for GPU software development is the precision of the floating point mathematics. Moving from single precision to double precision floating point decreases the performance by a factor of 2–3 on high end, modern GPUs, and more than a factor of ten for older GPUs. For this reason, Sandman is compiled using single precision floating point and uses fused multiply-add extensively, according to NVIDIA’s guidelines [
10]. As will be clear later in the paper, there is no observable impact on accuracy compared to other codes that use double precision, which may help other development teams evaluate their requirements and code efficiency.
2.2.2. Beam Geometry and Propagation
The initial phase space volume is calculated from the same double triangle method as for standard computational acceptance diagrams [
6], except that the trajectory “source” phase space is computed at the sample end with the guide exit geometry. The algorithm for triangle point picking is used to generate the initial phase space samples [
11].
Beam propagation through a spatial distance
d along the beam axis is, in the small-angle approximation, a simple shear operation of every point in
phase space, with the updated position values
given by:
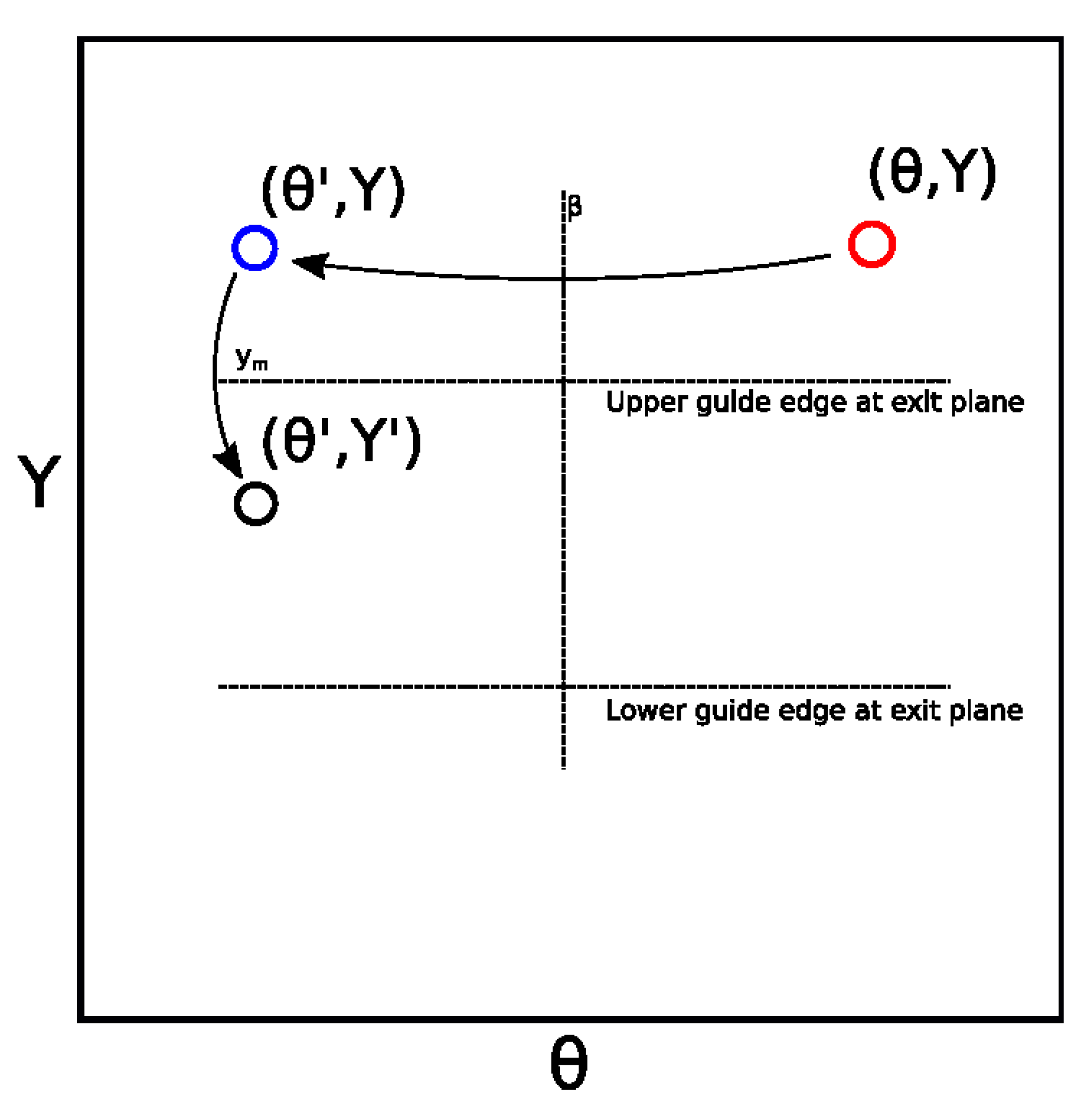
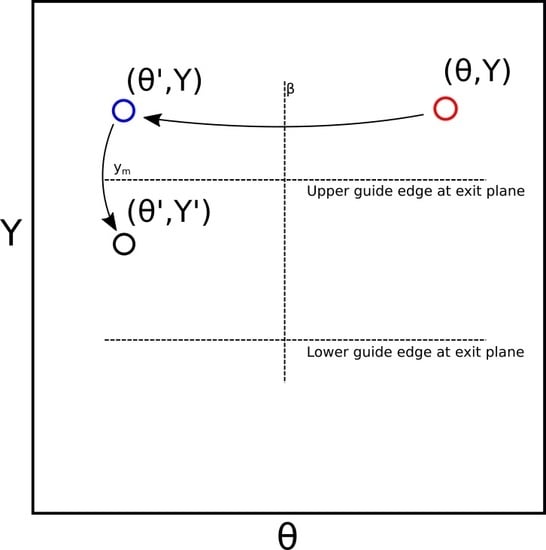
Reflection in a supermirror is a three stage process. Before one deals with the mirror itself, the prerequisite is to transport the beam to the end of the distance
d corresponding to the length of the supermirror as described in Equation (
3). If the spatial component
y of the particle is skewed to a point beyond the position
of the mirror surface in question, then we know that this particle intersected the mirror somewhere.
This is perhaps the most useful distinction between acceptance diagram work and conventional ray tracing, and a contributing factor to the speed of the technique. One does not care
where the reflection happened—it could be anywhere at all along the length of the mirror—only
if it happened. The mirror does not have to be parallel to the beam axis, one assumes the general case that is inclined at a grazing angle
relative to the reference axis of the beam (with
being the parallel case). If the reflection occurred, then the point in phase space is transformed according to these three steps:
where
is the new divergence coordinate of the trajectory relative to the straight beam axis,
is the new spatial coordinate, and
is the new statistical weight of the trajectory. The
and
calculations are visualised in
Figure 1.
Equation (
6) contains the function
, which is the supermirror reflectivity at a wavelength
and a grazing angle
, empirically given by:
where the wavelength- and
m-dependent critical angle
is given relative to that of total external reflection from atomically smooth nickel with natural isotopic abundances (
) by:
when the units for
are Ångstroms, and for
are degrees.
A neutron guide of arbitrary shape is constructed by breaking the system into sections. The beam is first propagated to the exit of the section according to Equation (
3), and then for both opposite faces of the guide mirror one performs the application of Equations (
4)–(
6) in a
while() loop until no more point transformations occur. This is done twice in total, once for each acceptance diagram, that is, once in the horizontal plane and once in the vertical plane, in order to model the beam in its entirety.
These equations are fast and simple to deploy. They are prime candidates for fused multiply-add functions (FMA), which are implemented in the GPU hardware and are enabled by default as a compiler optimisation option. An astute reader will note that a
while() loop involves branching. According to the basic Cuda introduction, this could slow down the warp dramatically. In practice, however, it is found that particles requiring reflection operations are not isolated cases, and running the reflection steps across the whole warp does not have a measurable impact on the speed, compared to isolating the individual particles requiring reflections. The same result was found for polygons in the original acceptance diagram code [
6].
An aperture component can be modelled by setting the statistical weight of the trajectory to zero for trajectories where the position of the neutron y lies beyond the edge of the aperture. This is done by multiplication with a Heaviside function.
A change in axis origin, such as might happen when a guide splits into multiple channels, is modelled by a translation in the
y axis by the required amount:
where
s is the transverse distance between the centre of the two guide pieces at the join.
Similarly, a rotation of the beam axis—as happens for each section of a curved guide—is modelled by a translation in the
axis according to
where
is the angle of rotation. Curved guides can then be modelled by repeatedly simulating a straight guide section of the appropriate length (typically 0.5–1 m) using Equations (
3)–(
6), followed by a rotation with Equation (
10), for as many sections as are needed for the curve.
Converging and diverging guides, following elliptic or parabolic shapes, are modelled in a similar way, except that the guides have different entrance and exit widths/heights given by the conic section equations, and no rotation stage.
The final important geometry type is a multi-channel bender. To avoid the use of conditionals, and to allow transporting the neutrons through an accurate simulation of several individual channels, the first step is to divide the phase space into channels and identify which channel the neutron trajectory intersects. Then, for each trajectory, one stores the channel number at the entrance plane. One then shifts the trajectory spatially, so that all trajectories are simulated entering the same bender channel. Optionally, an aperture frame can be modelled that is narrower than the channel width by the channel wafer thickness, to simulate the phase space losses on the front face of the wafers. The neutrons are then transported down a single, narrow channel using the curved guide function described above. Then, at the exit plane, the lateral trajectory shift is applied in reverse so that the trajectories emerge from the correct physical location as though there were multiple channels.
2.2.3. Monitoring and Merging Phase Space
Simulating the trajectories according to the previous two sections will create two matrices in computer memory of 3 columns each, with one matrix representing the horizontal transport efficiency and the other representing the vertical transport efficiency. Beam monitors create a snapshot of the phase space, which are finalised with the statistical weights w at the end of the simulation.
To arrive at a computation of the neutron flux at the sample position, one must merge these two phase spaces and normalise the data to the solid angle illumination of the sample geometry and source brightness of the moderator.
Just as for acceptance diagrams, the moderator brightness is given by:
and we separate the integral of the brightness into two parts, one for each plane, in the small angle approximation, so that
where
and
are the width and height of the sample, and
and
are the width and height of the guide exit, separated from the sample by a distance
D.
The flux is given by
with the guide system reverse transmission
being exactly as discussed in
Section 2.1. Now we can see why the reverse tracing method works:
The phase spaces are merged by calculating a total weight , where and are the independently calculated weights of the horizontal and vertical planes respectively. is then simply the sum of divided by the array size. The current is computed from the flux by trivially integrating over the wavelength.
It might be possible, in some future research, to “bootstrap” the computation by exploiting the independence of the horizontal and vertical planes still further. This could be achieved by repeatedly offsetting the and array indices before multiplication, thus artificially expanding the number of 3D samples. However, since the code is already very fast there was no material benefit to exploring this curious idea, and one could easily stumble into a statistical minefield without exercising caution.