Phase Stress Measurement of Centrifugally Cast Duplex Stainless Steel by Neutron Diffraction
Abstract
:1. Introduction
2. Material and Methods
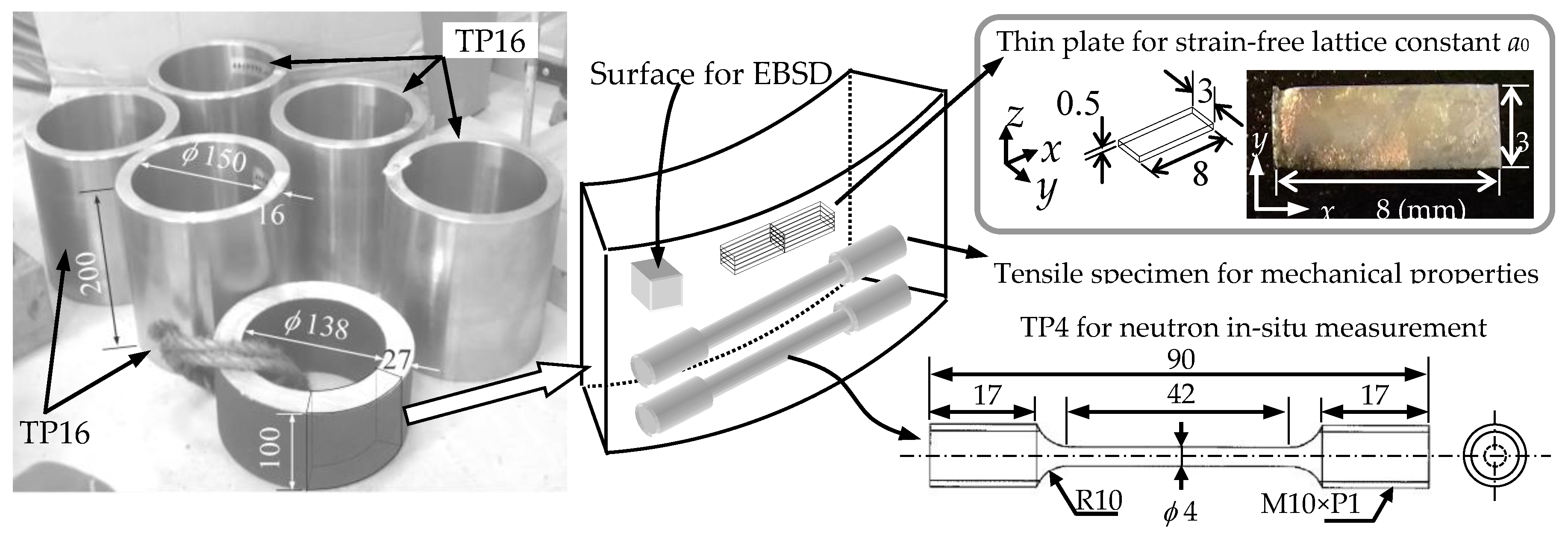
2.1. Material and Specimen
2.2. Triaxial Stress Evaluation
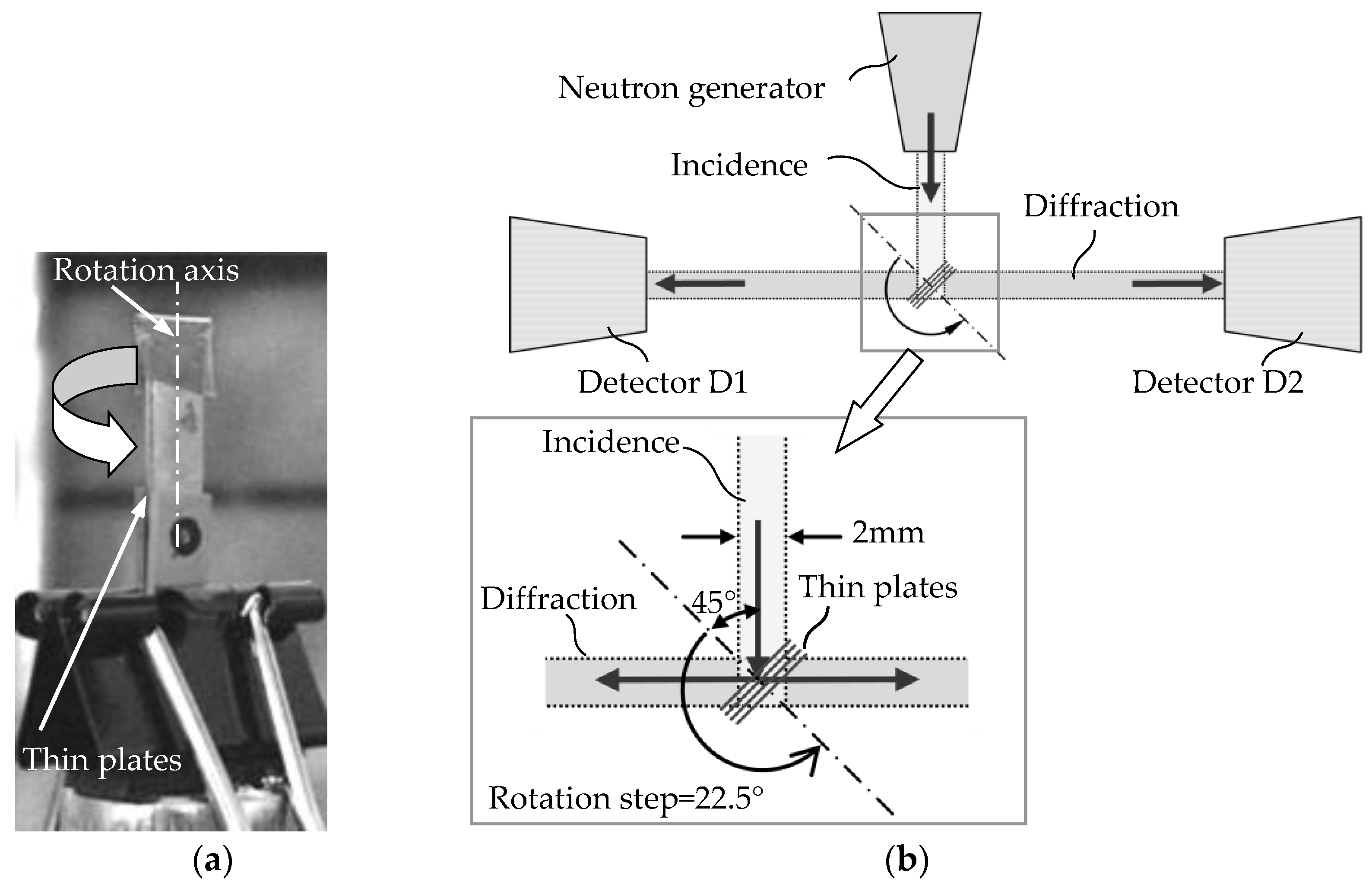
2.3. Preparation of Strain-Free Specimen
2.4. Measurement Conditions of Neutron Diffraction
2.4.1. Strain-Free Specimen
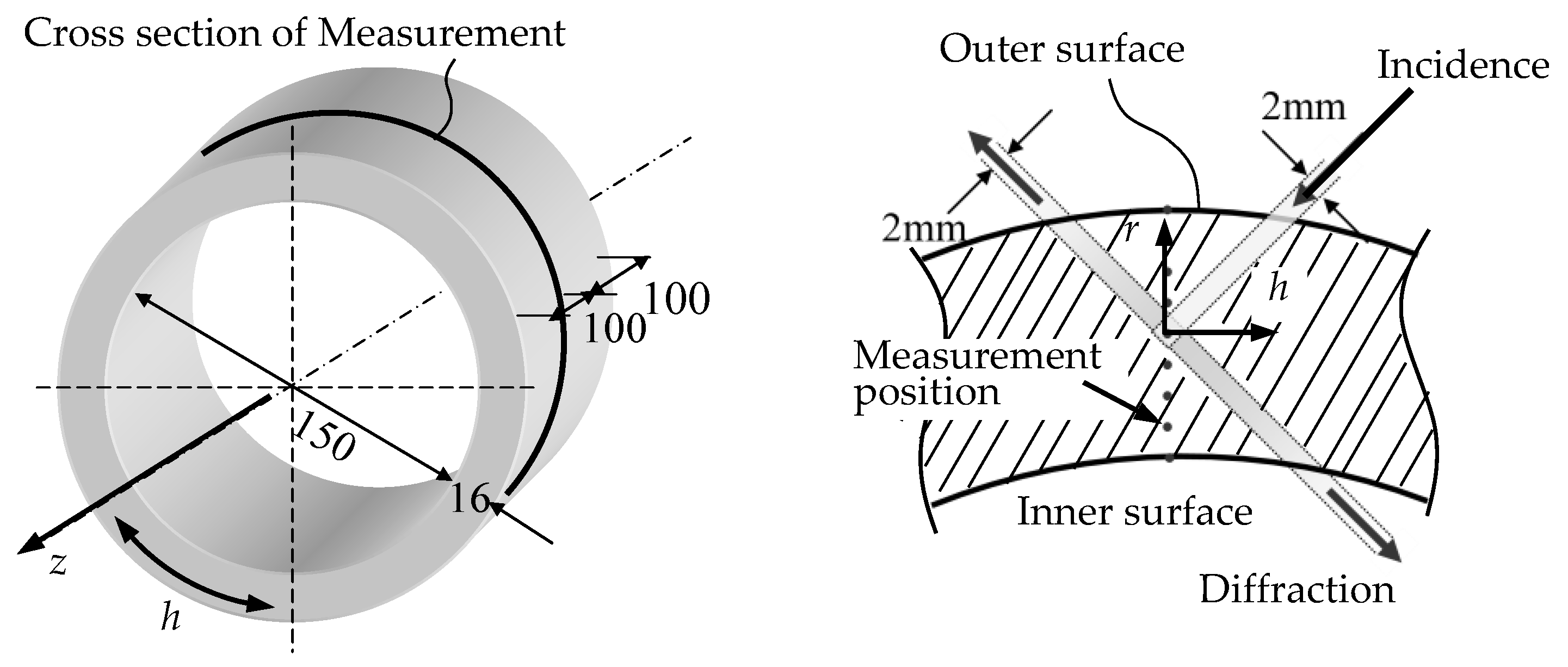
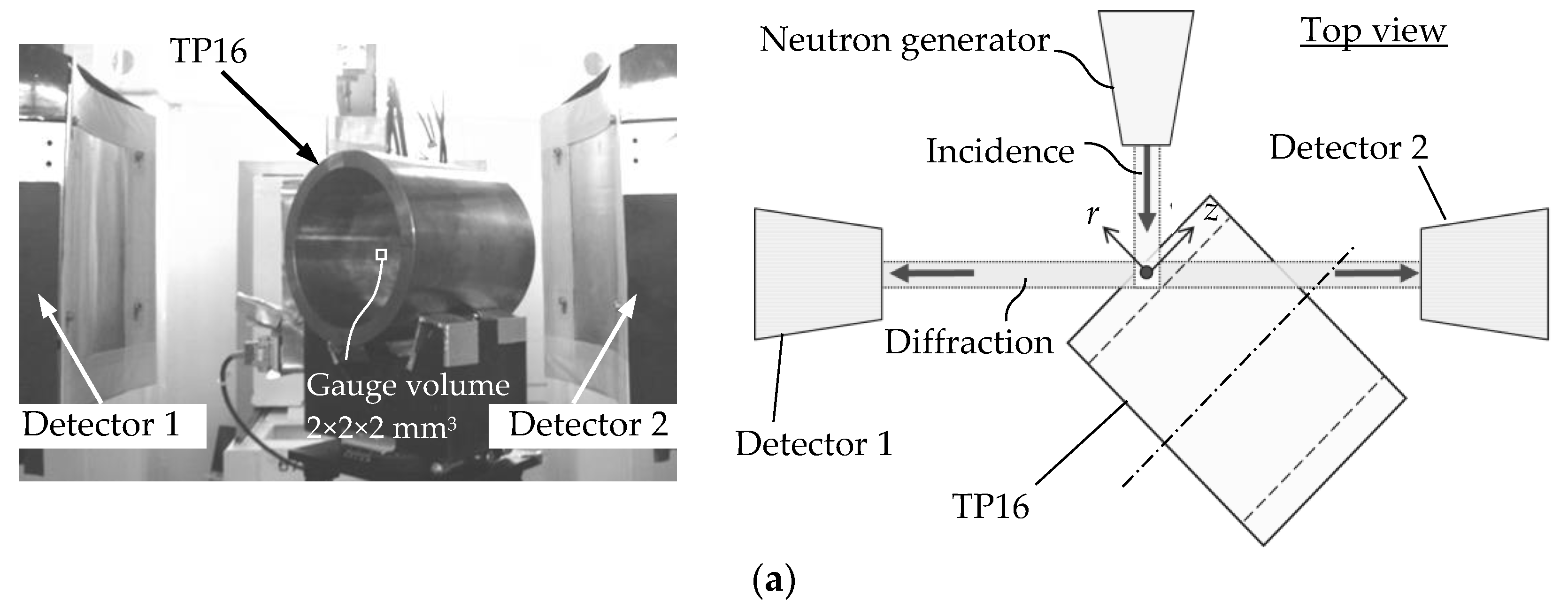
2.4.2. Hollow Cylinder
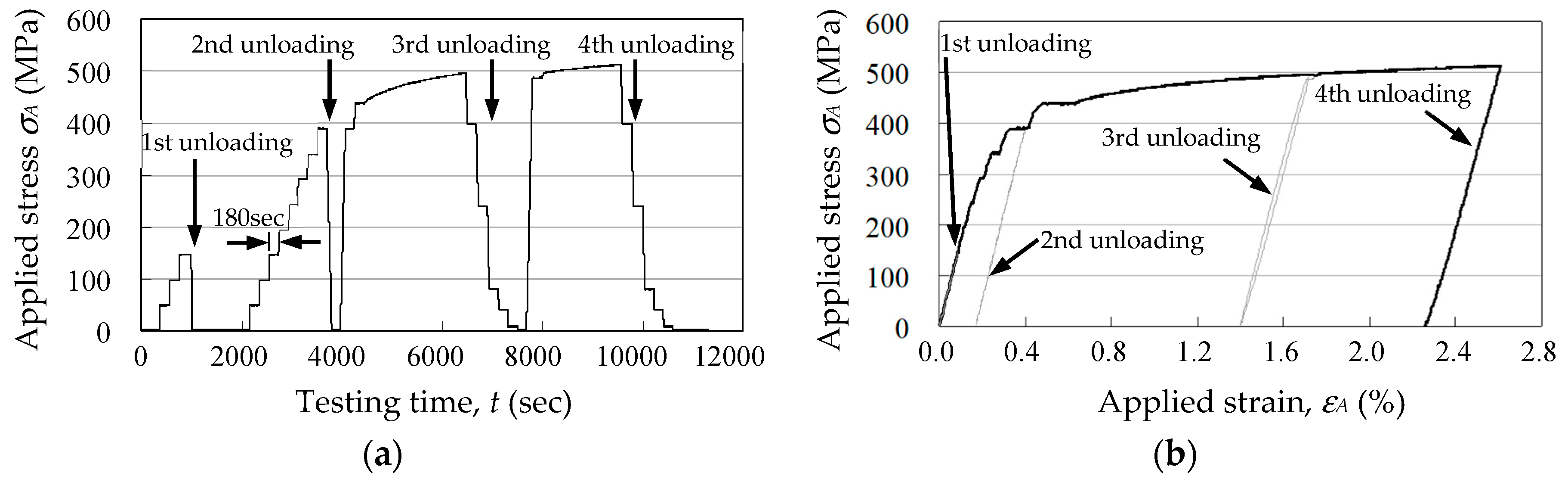
2.4.3. In-Situ Measurement of Lattice Strain during Tensile Test
3. Results
3.1. Lattice Constant of Strain-Free Specimen
3.2. Residual Stress of Hollow Cylinder
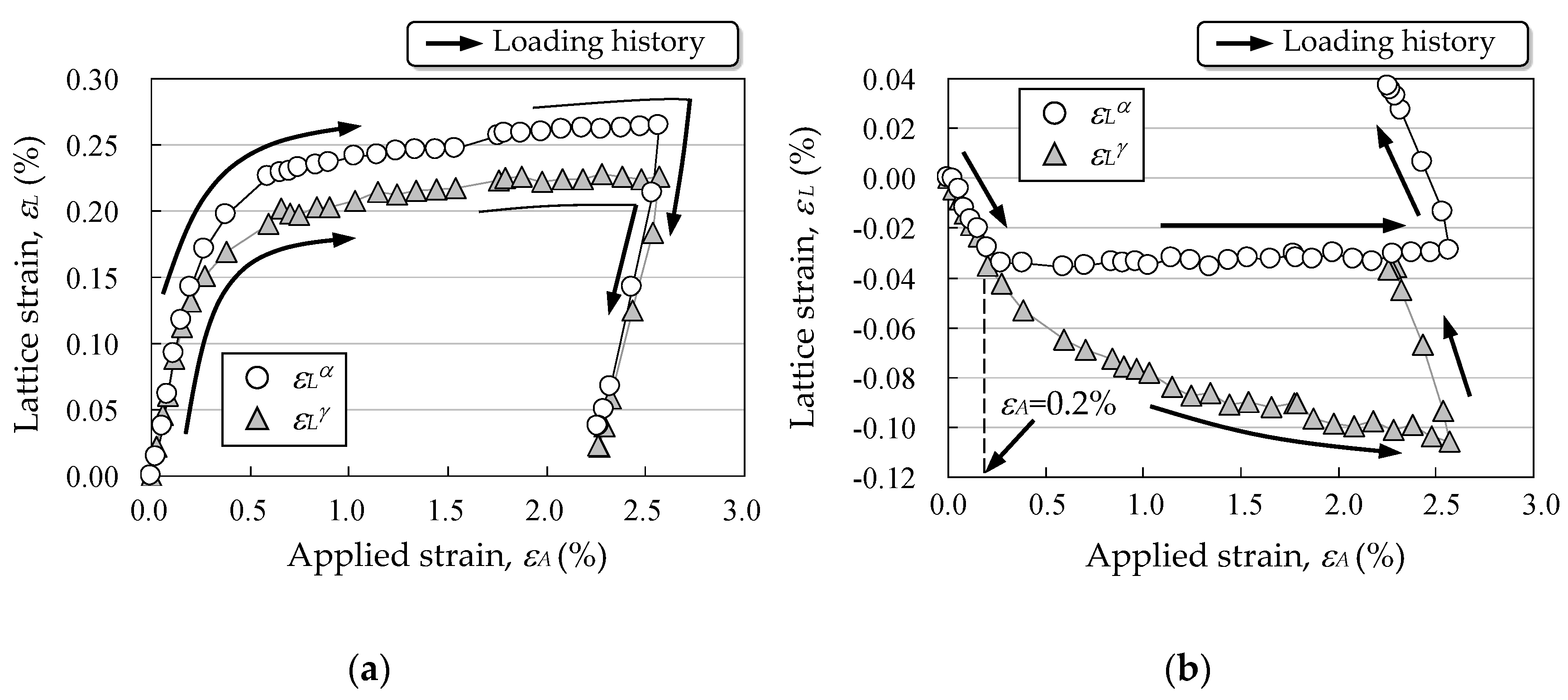
3.3. In-Situ Measurement of Lattice Strain during Tensile Test
4. Discussion
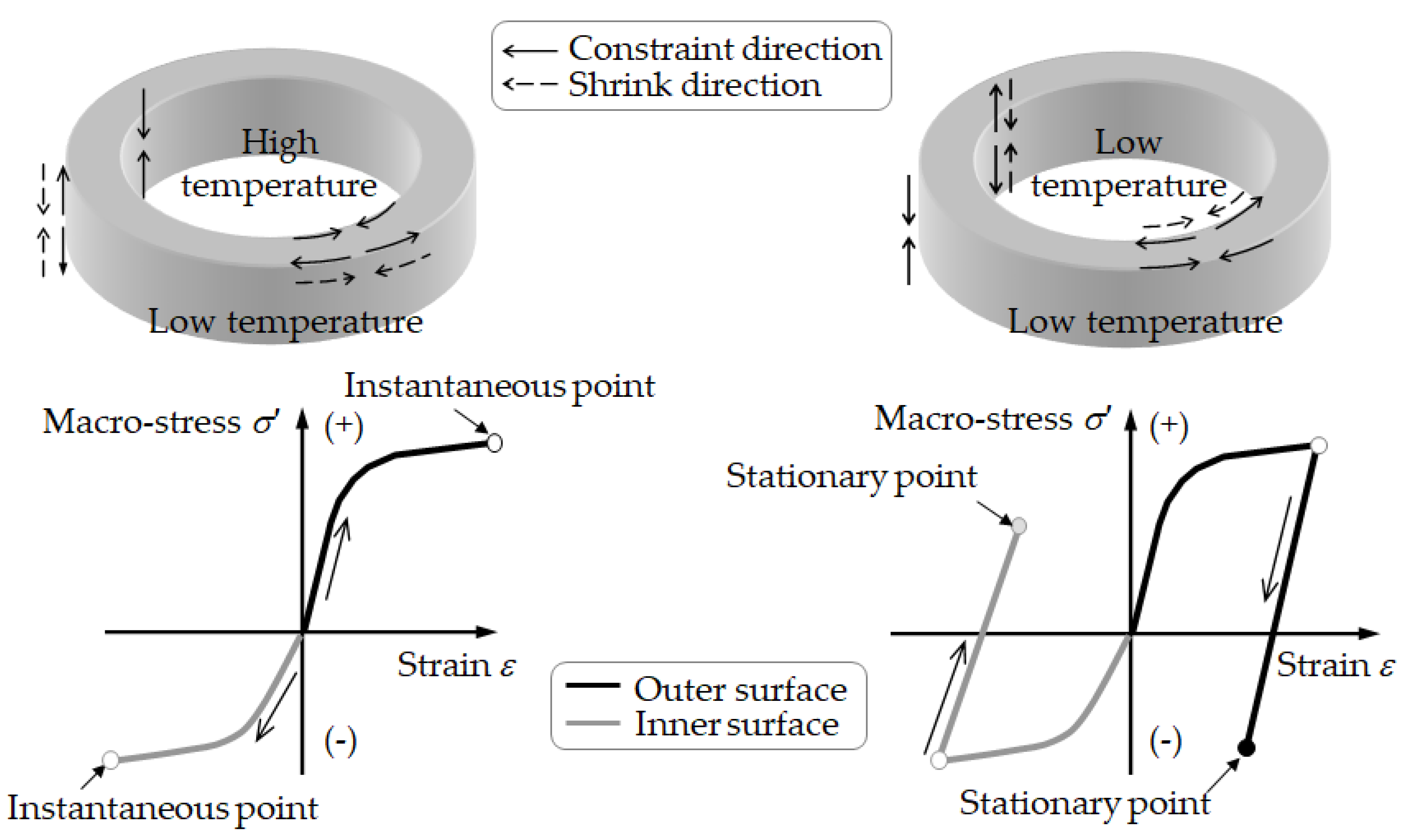
4.1. Mechanism of Micro-Stress Formation
4.2. Phase Stress Evolution under Tensile Loading
5. Conclusions
- (1)
- Strain-free lattice constants of both phases were measured from the thin plates fabricated by electropolishing, based on which the measurement of triaxial phase stress was successfully conducted by neutron diffraction.
- (2)
- The triaxial phase stress distribution along the thickness direction shows that, in general, the phase stress of γ phase is in tension and higher than that of α phase.
- (3)
- The mechanism of macro-stress formation in the hollow cylinder is explainable when considering the thermal shrinkage behavior during the cooling process of water quench after solution heat treatment.
- (4)
- The magnitude relationship and even the tension or compression status of α phase and γ phase might reverse after plastic deformation, which could occur during the material process, such as plastic working. These characteristics should be taken into consideration when evaluating the material properties of DSS that are easily affected by residual stress, such as fatigue strength and stress corrosion cracking resistance.
Funding
Acknowledgments
Conflicts of Interest
References
- Silberschmidt, V.V.; Werner, E.A.; Messner, C. Thermal loading of duplex steels. J. Eng. Mater. Technol. 2003, 125, 56–64. [Google Scholar] [CrossRef]
- Siegmund, T.; Werner, E.; Fischer, F.D. The Irreversible deformation of a duplex stainless steel under thermal cycling. Mater. Sci. Eng. A 1993, 169, 125–134. [Google Scholar] [CrossRef]
- Siegmund, T.; Werner, E.; Fischer, F.D. On the thermomechanical deformation behavior of duplex-type materials. J. Mech. Phys. Solids 1995, 43, 495–532. [Google Scholar] [CrossRef]
- Lodini, A.; Fitzpatrick, M.E. Analysis of Residual Stress by Diffraction Using Neutron and Synchrotron Radiation; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Hutchings, M.T.; Krawitz, A.D. Measurement of Residual and Applied Stress Using Neutron Diffraction; Kluwer Academic Publisher: Dordrecht, The Netherlands, 1992. [Google Scholar]
- Albertini, G.; Peng, R.L.; Manescu, A.; Ponzetti, A. Neutron diffraction measurement of residual stress in a centrifugal bowl of duplex steel. J. Neutron Res. 2001, 9, 305–312. [Google Scholar] [CrossRef]
- Harjo, S.; Tomota, Y.; Ono, M. Measurements of thermal residual elastic strain in ferrite-austenite Fe-Cr-Ni alloys by neutron and X-ray diffractions. Acta Mater. 1999, 47, 353–362. [Google Scholar] [CrossRef]
- Harjo, S.; Tomota, Y.; Torii, S.; Kamiyama, T. Residual thermal phase stresses in α-γ Fe-Cr-Ni alloys measured by a neutron diffraction time-of-flight methods. Mater. Trans. 2002, 43, 1696–1702. [Google Scholar] [CrossRef]
- Harjo, S.; Tomota, Y.; Lukáš, P.; Neov, D.; Vrána, M.; Mikula, P.; Ono, M. In situ neutron diffraction study of α–γ Fe–Cr–Ni alloys under tensile deformation. Acta Mater. 2001, 49, 2471–2479. [Google Scholar] [CrossRef]
- Johansson, J.; Odén, M.; Zeng, X.-H. Evolution of the residual stress state in a duplex stainless steel during loading. Acta Mater. 1999, 47, 2669–2684. [Google Scholar] [CrossRef]
- Daymond, M.R.; Priesmeyer, H.G.; Korsunsky, A.M. Elastoplastic deformation of two phase steels studied by neutron diffraction and self-consistent modelling. In Recent Advances in Experimental Mechanics; Gdoutos, E.E., Ed.; Springer: New York, NY, USA, 2002; pp. 495–506. [Google Scholar]
- Tanaka, K.; Suzuki, K.; Akiniwa, Y. Evaluation of Residual Stress by X-ray Diffraction-Fundamentals and Applications; Yokendo Ltd.: Tokyo, Japan, 2006. [Google Scholar]
- Wang, Y. Residual stress measurement of centrifugally cast duplex stainless steel by neutron diffraction. J. Soc. Mater. Sci. Jpn. 2014, 63, 789–796. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y. A study on phase stress of centrifugally cast duplex stainless steel by neutron diffraction. Hamon Jpn. Soc. Neutron Sci. 2014, 24, 28–33. [Google Scholar] [CrossRef]
- Young, R.A. The Rietveld Method; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Sasaki, T.; Lin, Z.; Hirose, Y. X-ray measurement of macro- and microstresses using imaging plate and its application to ferritic and austenitic dual phase stainless steel. Trans. JSME (A) 1996, 62, 2741–2749. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, H.; Akita, K. Discussion on accuracy of weld residual stress measurement by neutron diffraction. Influence of strain free reference. J. Soc. Mater. Sci. Jpn. 2012, 61, 604–611. [Google Scholar] [CrossRef]
- Santisteban, J.R.; Steuwer, A.; Edwards, L.; Withers, P.J.; Fitzpatrick, M.E. Mapping of unstressed lattice parameters using pulsed neutron transmission diffraction. J. Appl. Crystallogr. 2002, 35, 497–504. [Google Scholar] [CrossRef]
- Withers, P.J.; Preuss, M.; Steuwer, A.; Pang, J.W.L. Methods for obtaining the strain-free lattice parameter when using diffraction to determine residual stress. J. Appl. Crystallogr. 2007, 40, 891–904. [Google Scholar] [CrossRef]
- Tomota, Y.; Harjo, S.; Tokumura, K.; Sato, H.; Ono, M. Measurements of phase stresses in a commercial dual phase stainless steel by using neutron and X-ray diffractions. Netsu Shori 1998, 38, 174–179. [Google Scholar]
- Suzuki, H.; Akita, K. Residual stress measurement of large scaled welded pipe using neutron diffraction method. Effect of SCC crack propagation and repair weld on residual stress distribution. Q. J. Jpn. Weld. Soc. 2011, 29, 294–304. [Google Scholar] [CrossRef] [Green Version]
- Oishi, R.; Yonemura, M.; Nishimaki, Y.; Torii, S.; Hoshikawa, A.; Ishigaki, T.; Morishima, T.; Mori, K.; Kamiyama, T. Rietveld analysis software for J-PARC. Nucl. Instrum. Methods Phys. Res. 2009, 600, 94–96. [Google Scholar] [CrossRef]
- Oishi-Tomiyasu, R.; Yonemura, M.; Morishima, T.; Hoshikawa, A.; Torii, S.; Ishigaki, T.; Kamiyama, T. Application of matrix decomposition algorithms for singular matrices to the Pawley method in Z-rietveld. J. Appl. Crystallogr. 2012, 45, 299–308. [Google Scholar] [CrossRef]
- JSMS Committee on X-ray Study of Mechanical Behavior of Materials. Standard Method for X-ray Stress Measurement; The Society of Materials Science: Kyoto, Japan, 2002. [Google Scholar]
- Chen, L.; Ling, Y.; Kang, X.; Xia, L.; Li, D. Numerical simulation of stress and deformation for a duplex stainless steel impeller during casting and heat treatment processes. J. Mater. Sci. Technol. 2008, 24, 364–368. [Google Scholar]







| Specification | C | Si | Mn | P | S | Ni | Cr | Mo | N | Fe |
|---|---|---|---|---|---|---|---|---|---|---|
| <0.06 | <1.00 | <1.00 | <0.040 | <0.040 | 4.0–6.0 | 24.0–27.0 | 1.75–2.50 | 0.15–0.25 | Bal. | |
| Inspection certificate | 0.02 | 0.41 | 0.64 | 0.016 | 0.002 | 4.8 | 24.7 | 1.86 | 0.19 | - |
| Young’s Modulus E′ (GPa) | Poisson’s Ratio ν′ | Proof Stress σ0.2% (MPa) | Ultimate Strength σB (MPa) | Elongation (%) |
|---|---|---|---|---|
| 197 | 0.29 | 485 | 687 | 39 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y. Phase Stress Measurement of Centrifugally Cast Duplex Stainless Steel by Neutron Diffraction. Quantum Beam Sci. 2020, 4, 28. https://0-doi-org.brum.beds.ac.uk/10.3390/qubs4030028
Wang Y. Phase Stress Measurement of Centrifugally Cast Duplex Stainless Steel by Neutron Diffraction. Quantum Beam Science. 2020; 4(3):28. https://0-doi-org.brum.beds.ac.uk/10.3390/qubs4030028
Chicago/Turabian StyleWang, Yun. 2020. "Phase Stress Measurement of Centrifugally Cast Duplex Stainless Steel by Neutron Diffraction" Quantum Beam Science 4, no. 3: 28. https://0-doi-org.brum.beds.ac.uk/10.3390/qubs4030028




