Nonlinear Analysis of a Steel Frame Structure Exposed to Post-Earthquake Fire
Abstract
:1. Introduction
2. State of the Art
3. Basis of the Analysis
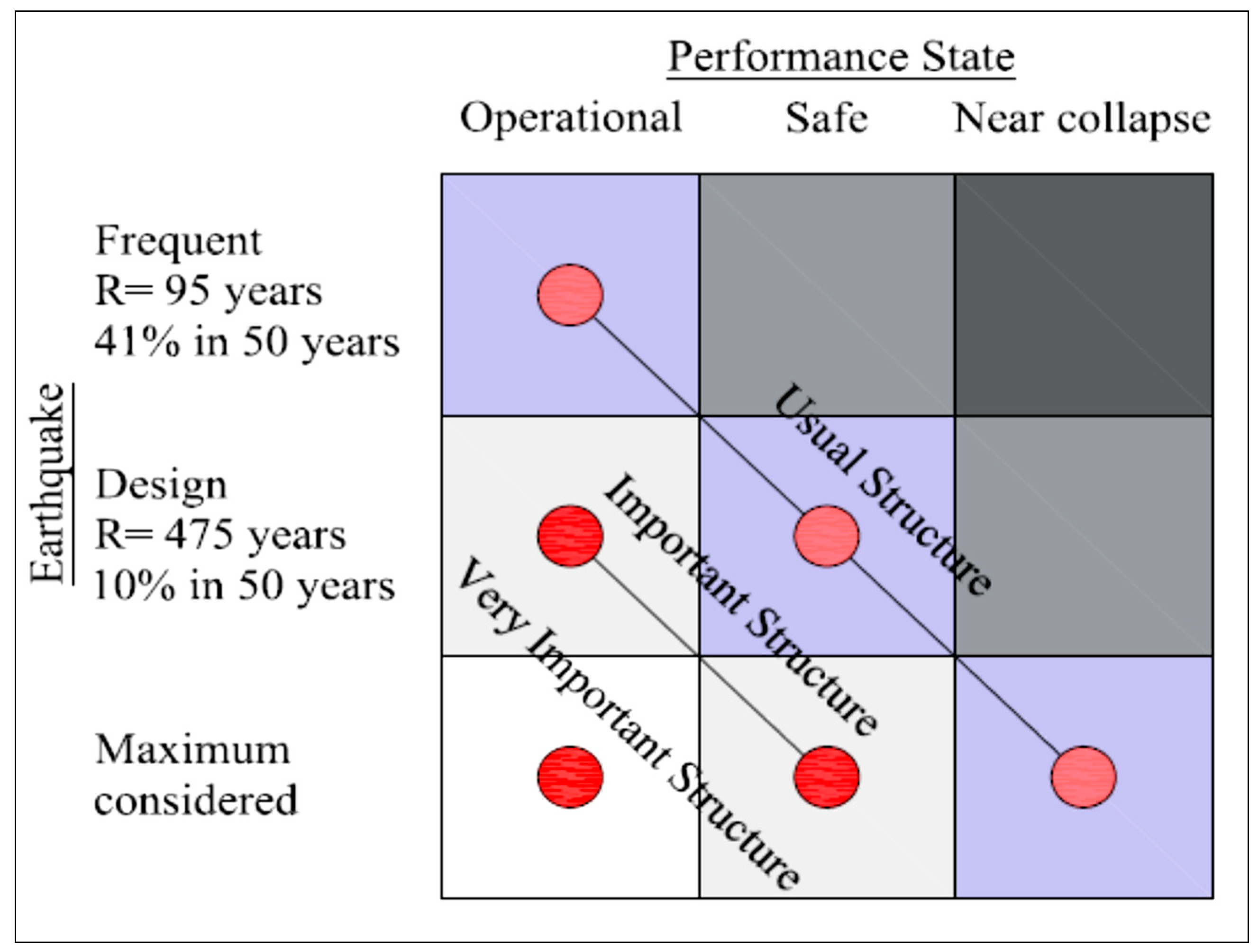
3.1. Seismic Analysis for PEF
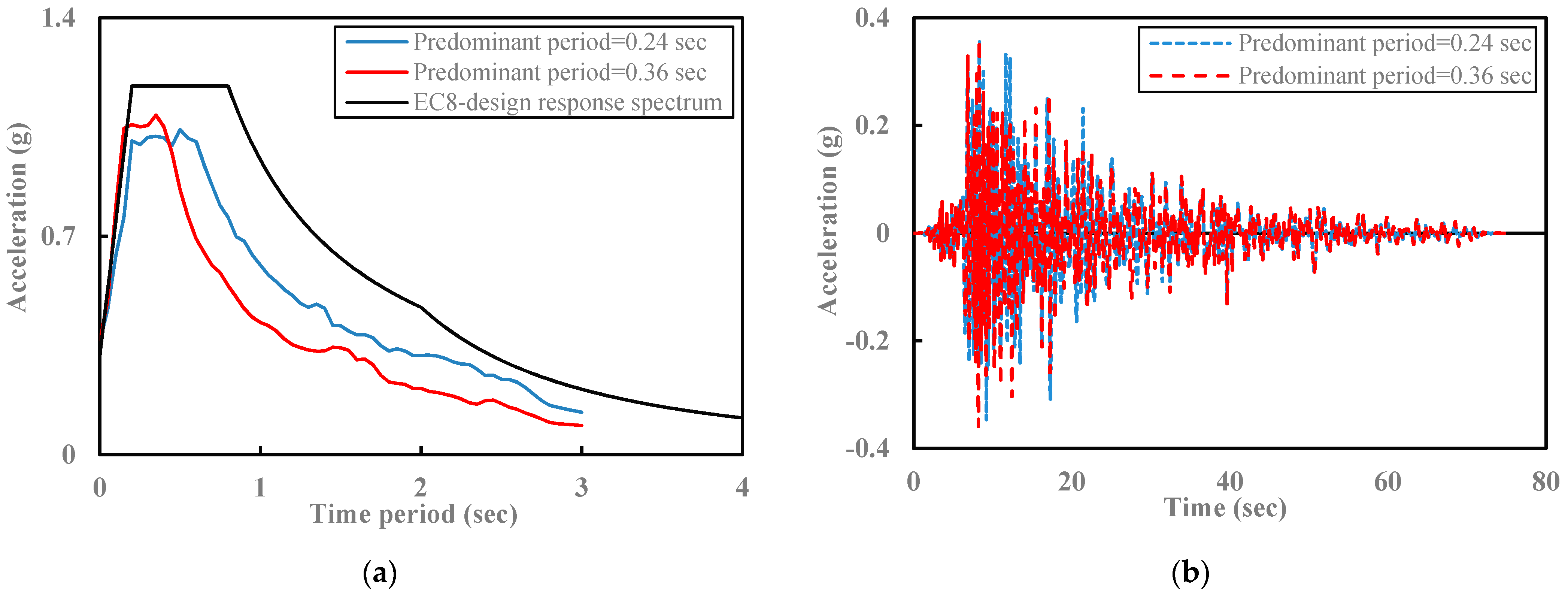
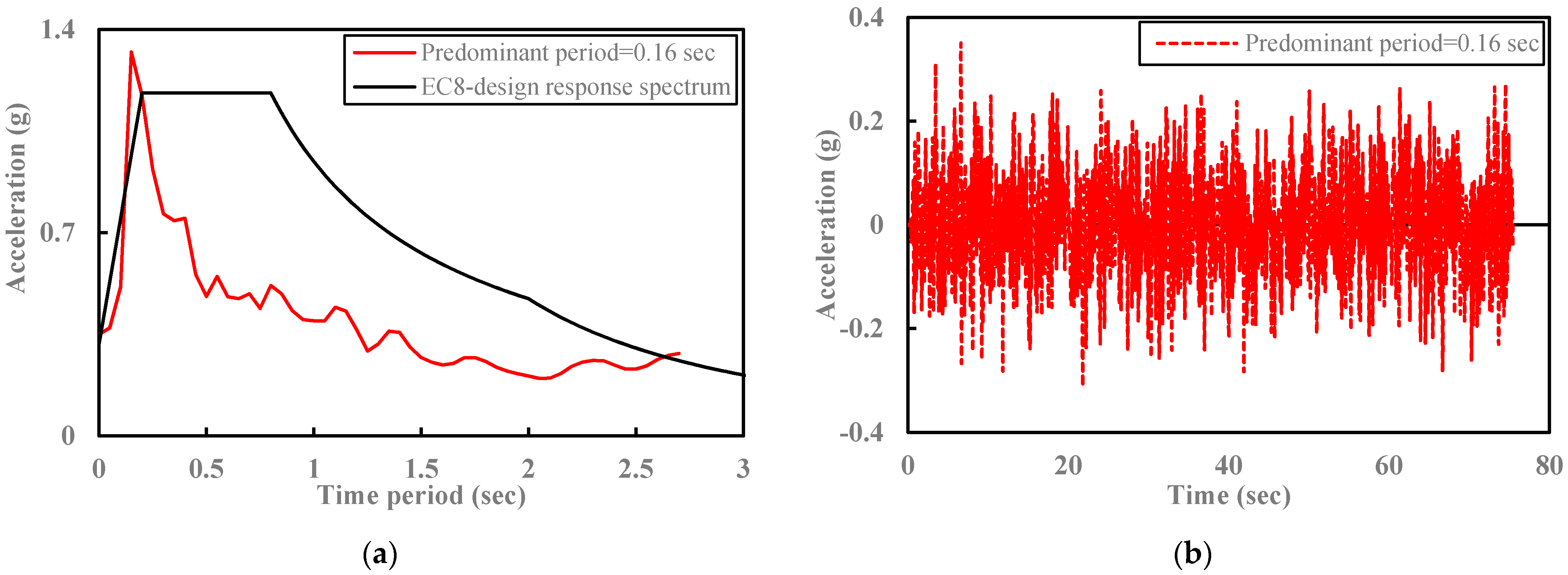
3.2. Input Data
3.3. Thermal Stress Analysis in PEF Analysis
4. Development of the Numerical Model
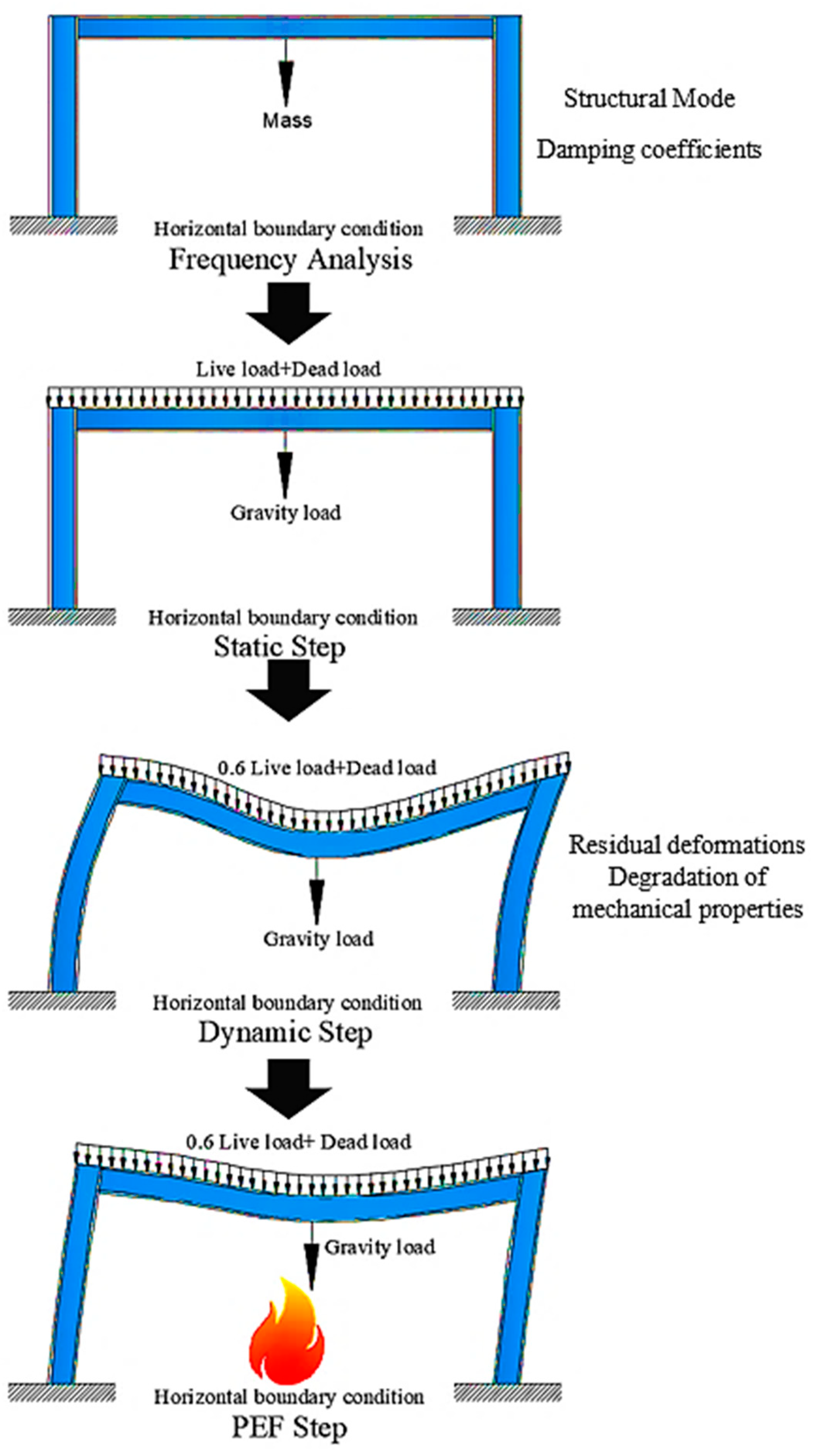
4.1. General
4.2. Elements, Meshing and Boundary Conditions
4.3. Loading and Solution Procedure
5. Results and Analysis
5.1. Frequency Analysis
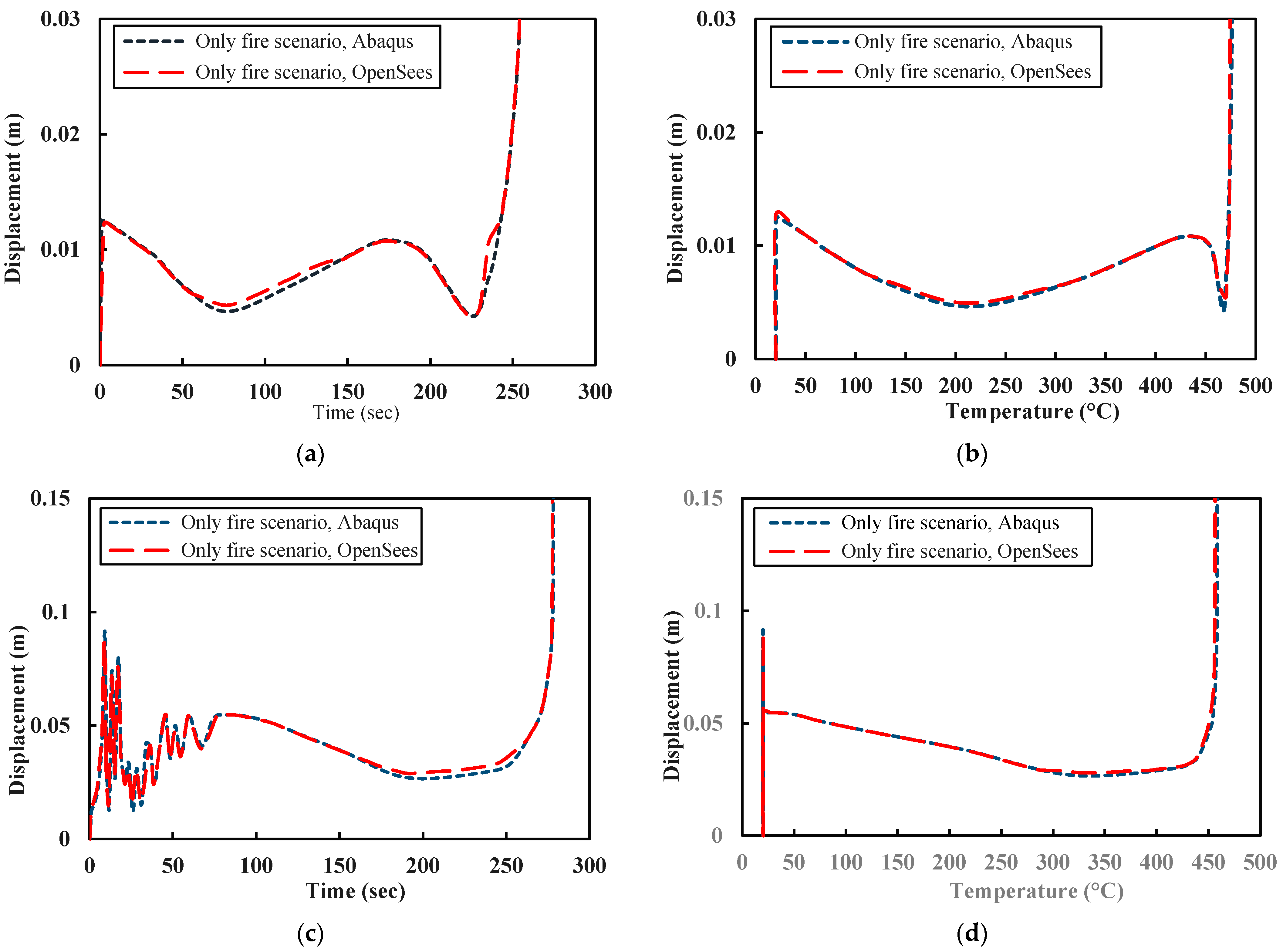
5.2. Validation Study
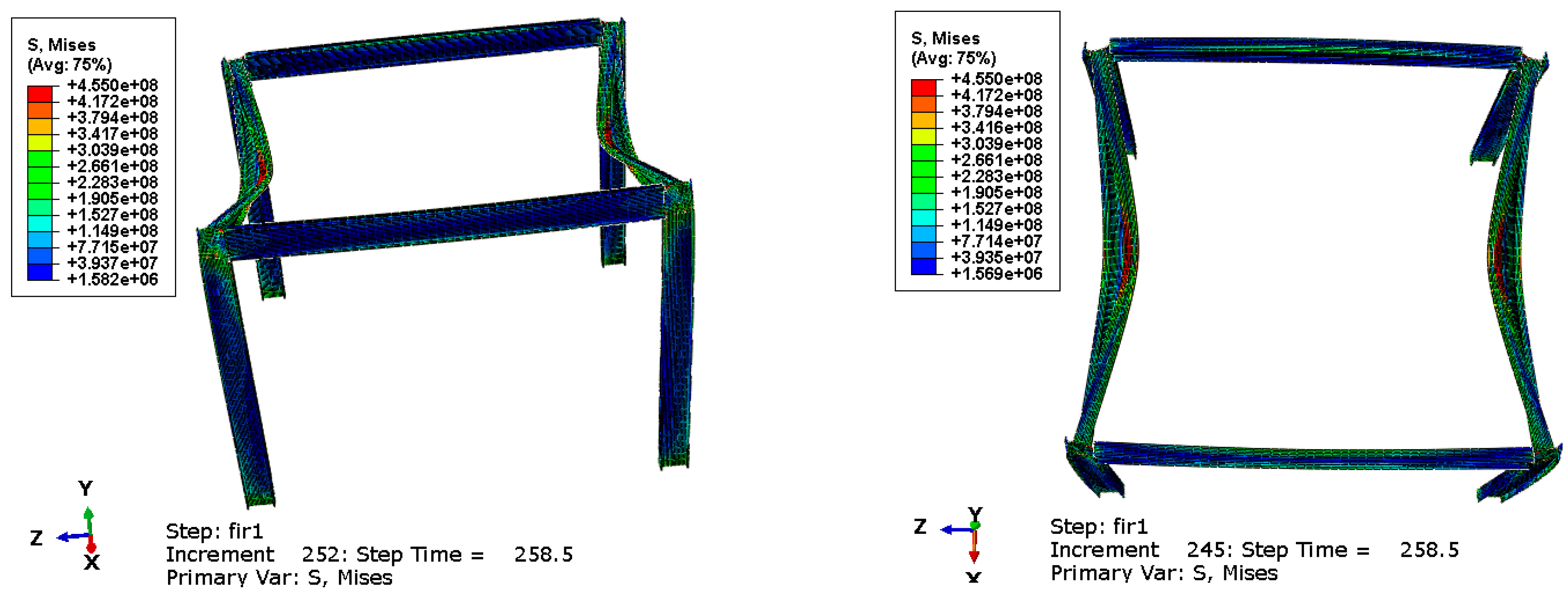
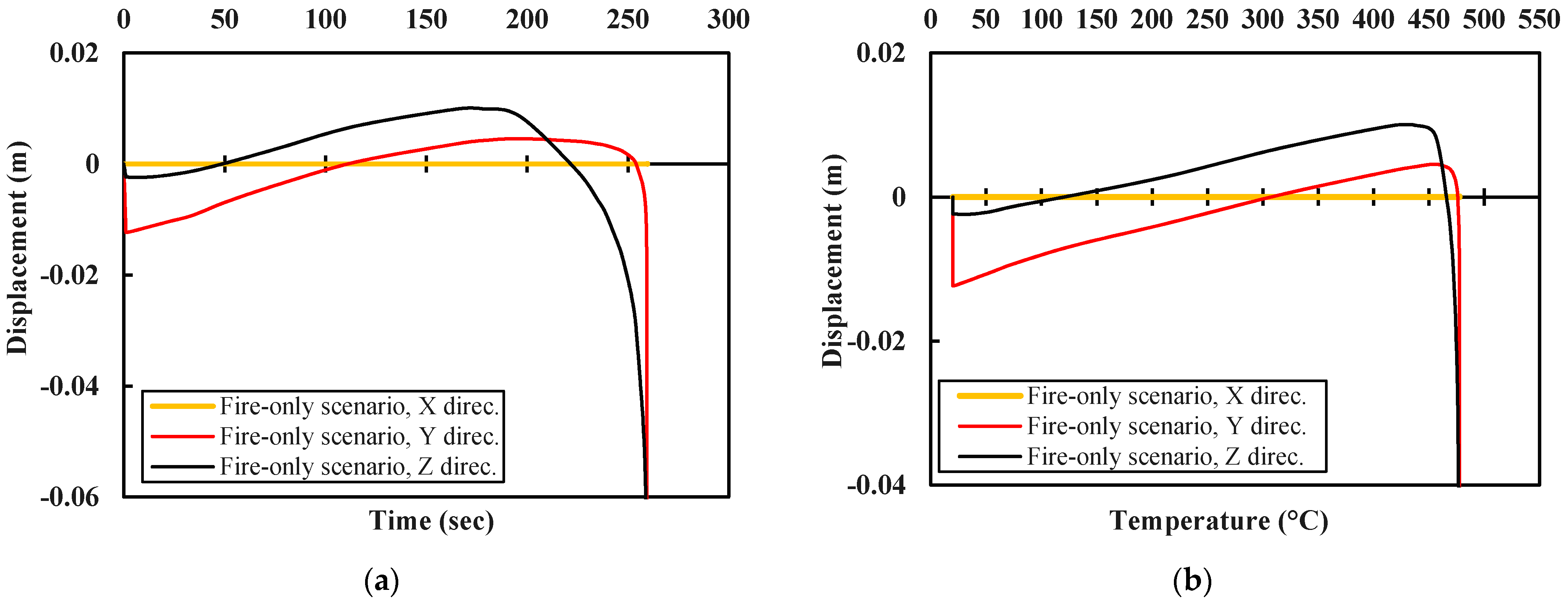
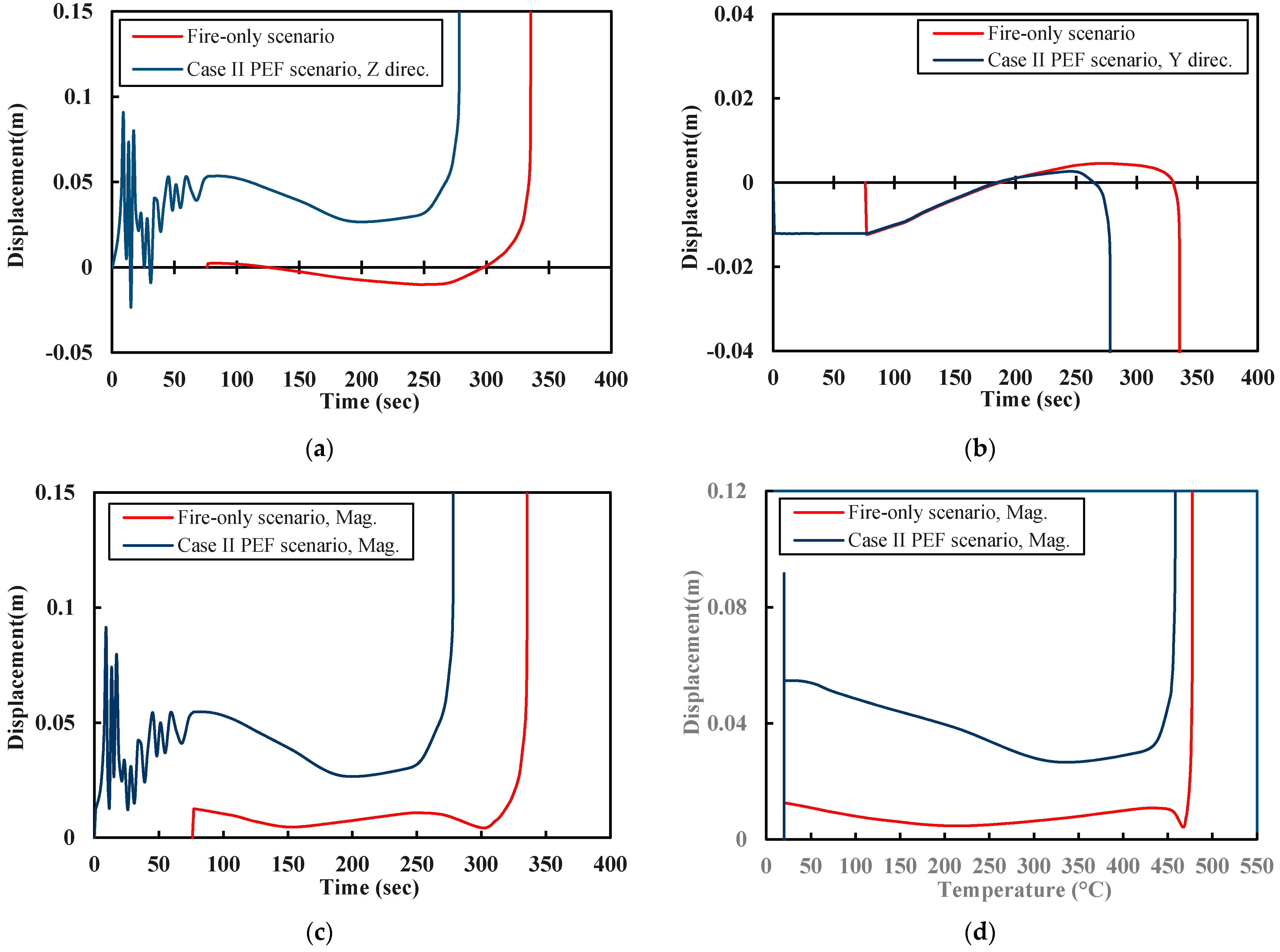
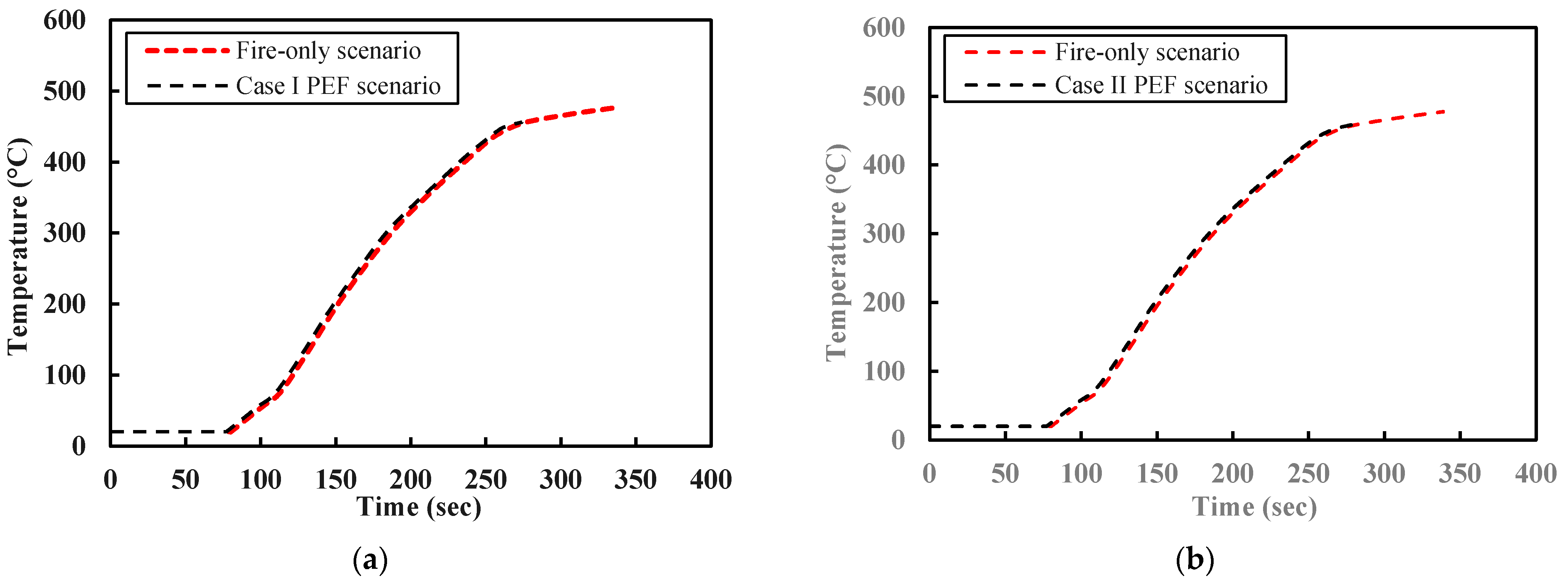
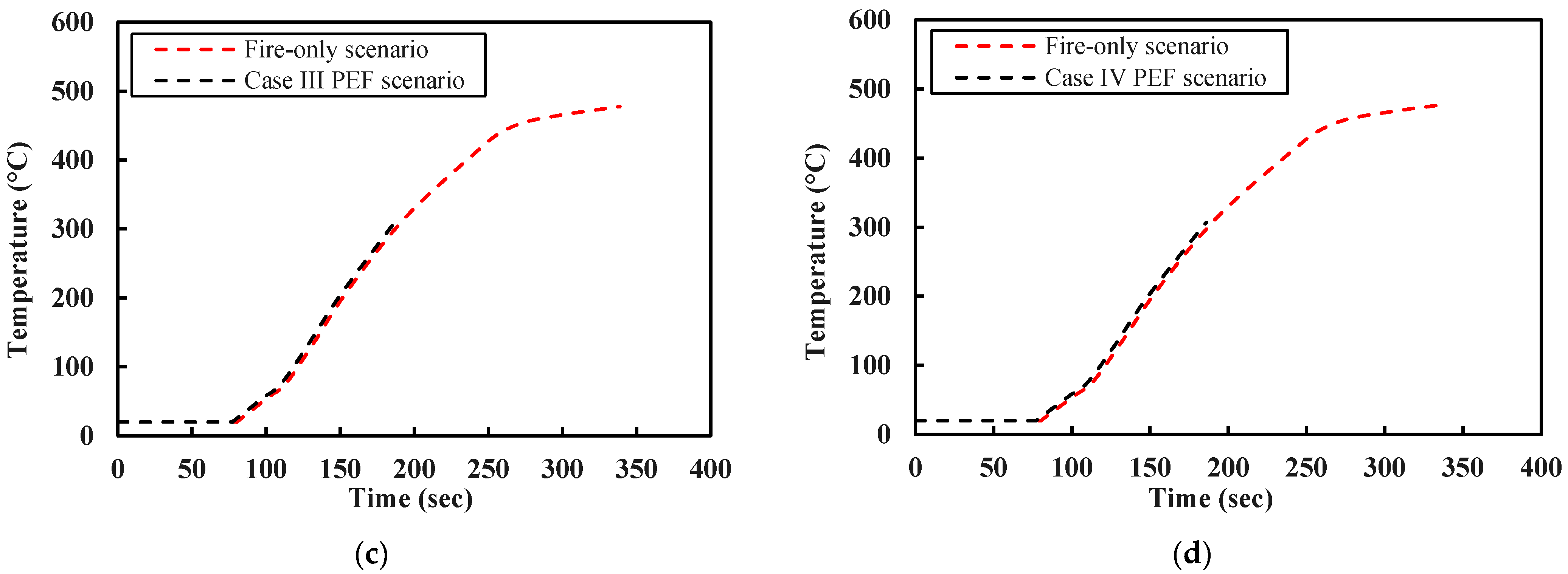
5.3. Post-Earthquake Fire
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chicchi, R.; Varma, A.H. Research review: Post-earthquake fire assessment of steel buildings in the United States. Adv. Struct. Eng. 2018, 21, 138–154. [Google Scholar] [CrossRef]
- Li, G.Q.; Zhang, C.; Jiang, J. A review on fire safety engineering: Key issues for high-rise buildings. Int. J. High-Rise Build. 2018, 7, 265–285. [Google Scholar] [CrossRef]
- Yassin, H.; Iqbal, F.; Bagchi, A.; Kodur, V.K.R. Assessment of Post-Earthquake Fire Performance of Steel-Frame Buildings. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Ronagh, H.R.; Behnam, B. Investigating the Effect of Prior Damage on the Post-Earthquake Fire Resistance of Reinforced Concrete Portal Frames. Int. J. Concr. Struct. Mater. 2012, 6, 209–220. [Google Scholar] [CrossRef] [Green Version]
- Kamath, P.; Sharma, U.K.; Kumar, V.; Bhargava, P.; Usmani, A.; Singh, B.; Singh, Y.; Torero, J.; Gillie, M.; Pankaj, P. Full-scale fire test on an earthquake-damaged reinforced concrete frame. Fire Saf. J. 2015, 73, 1–19. [Google Scholar] [CrossRef] [Green Version]
- British Standards Institution. Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings Eurocode; National Standards Authority of Ireland: Dublin, Ireland, 2004; Volume BS EN 1998, p. 231. [Google Scholar]
- British Standards Institution. Eurocode 3: Design of Steel Structures—Part 1–2: General Rules—Structural Fire Design; European Committee for Standardization: Brussels, Belgium, 1993; Volume BS EN, p. 227. [Google Scholar]
- Douglas, J.; Gkimprixis, A. Using targeted risk in seismic design codes: A summary of the state of the art and outstanding issues. In Proceedings of the 6th National Conference on Earthquake Engineering and 2nd National Conference on Earthquake Engineering and Seismology, Bucharest, Romania, 14–17 June 2017. [Google Scholar]
- Solomos, G.; Pinto, A.; Dimova, S. A Review of the seismic Hazard Zonation in National Building Codes in the Context of Eurocode 8. JRC Sci. Tech. Rep. 2008. Available online: https://publications.jrc.ec.europa.eu/repository/handle/JRC48352 (accessed on 1 July 2021).
- Smith, M. ABAQUS/Standard User’s Manual; Version 2018; Dassault Systèmes Simulia Corp: Providence, RI, USA, 2018; p. 1146. [Google Scholar]
- Kobes, M.; Helsloot, I.; de Vries, B.; Post, J.G. Building safety and human behaviour in fire: A literature review. Fire Saf. J. 2010, 45, 1–11. [Google Scholar] [CrossRef]
- Della Corte, G.; Landolfo, R.; Mazzolani, F.M. Post-earthquake fire resistance of moment resisting steel frames. Fire Saf. J. 2003, 38, 593–612. [Google Scholar] [CrossRef]
- Ali, H.M.; Senseny, P.E.; Alpert, R.L. Lateral displacement and collapse of single-story steel frames in uncontrolled fires. Eng. Struct. 2004, 26, 593–607. [Google Scholar] [CrossRef]
- Mousavi, S.; Bagchi, A.; Kodur, V.K.R. Review of post-earthquake fire hazard to building structures. Can. J. Civ. Eng. 2008, 698, 689–698. [Google Scholar] [CrossRef]
- Zaharia, R.; Pintea, D. Fire after Earthquake Analysis of Steel Moment Resisting Frames. Int. J. Steel Struct. 2009, 9, 275–284. [Google Scholar] [CrossRef]
- Ghoreishi, M.; Bagchi, A.; Sultan, M.A. Estimating the response of structural systems to fire exposure: State-of-the-art review. In Proceedings of the Fire and Materials 2009, 11th International Conference, San Francisco, CA, USA, 26–28 January 2009; pp. 475–483. [Google Scholar]
- Memari, M.; Mahmoud, H.; Ellingwood, B. Post-earthquake fire performance of moment resisting frames with reduced beam section connections. J. Constr. Steel Res. 2014, 103, 215–229. [Google Scholar] [CrossRef]
- Zhou, M.; Jiang, L.; Chen, S.; Cardoso, R.P.R.; Usmani, A. Remaining fire resistance of steel frames following a moderate earthquake—A case study. J. Constr. Steel Res. 2020, 164, 105754. [Google Scholar] [CrossRef]
- Jelinek, T.; Zania, V.; Giuliani, L. Post-earthquake fire resistance of steel buildings. J. Constr. Steel Res. 2017, 138, 774–782. [Google Scholar] [CrossRef] [Green Version]
- Alasiri, M.R.; Chicchi, R.; Varma, A.H. Post-earthquake fire behavior and performance-based fire design of steel moment frame buildings. J. Constr. Steel Res. 2021, 177, 106442. [Google Scholar] [CrossRef]
- Fajfar, P. Structural Analysis in Earthquake Engineering—A Breakthrough of Simplified Non-Linear Methods. In Proceedings of the 12th European Conference on Earthquake Engineering, London, UK, 9–13 September 2002; p. 843. [Google Scholar]
- Suwondo, R.; Gillie, M.; Cunningham, L.; Bailey, C. Effect of earthquake damage on the behaviour of composite steel frames in fire. Adv. Struct. Eng. 2018, 21, 2589–2604. [Google Scholar] [CrossRef] [Green Version]
- Behnam, B.; Abolghasemi, S. Post-earthquake Fire Performance of a Generic Fireproofed Steel Moment Resisting Structure. J. Earthq. Eng. 2019, 25, 1–26. [Google Scholar] [CrossRef]
- British Standards Institution. Eurocode2: Design of Concrete Structures: Part 1–1: General Rules and Rules for Buildings; Committee for Standardization: Brussels, Belgium, 2004; Volume BS EN 1991-1-1, p. 240. [Google Scholar]
- SeismoSoft. Manual and Program Description of the Program SeismoStruct. Available online: http://www.seismosoft.com (accessed on 20 May 2020).
- U.S. Geological Survey. PEER Ground Motion Database. Pacific Earthquake Engineering Research Centre. 2018. Available online: https://ngawest2.berkeley.edu/ (accessed on 12 March 2020).
- Mondal, D.R. High Risk of Post-Earthquake Fire Hazard in Dhaka, Bangladesh. Fire 2019, 2, 24. [Google Scholar] [CrossRef] [Green Version]
- Fischer, E.C.; Maddalozzo, W. Post-Earthquake Fire Performance of Industrial Facilities PEER Transportation Systems Research Program. Available online: https://peer.berkeley.edu/sites/default/files/walker_maddalozzo_peer2020_poster.pdf (accessed on 1 July 2021).
- ISO 834-10. In Fire Resistance Tests—Elements of Building Construction—Part 10: Specific Requirements to Determine the Contribution of Applied Fire Protection Materials to Structural Steel Elements; International Organization for Standardization: Geneva, Switzerland, 2014.
- British Standards Institution. Eurocode: Basis of Structural Design; Committee for Standardization: Brussels, Belgium, 2011; Volume BS EN 1990:2002+A1, p. 112. [Google Scholar]
- British Standards Institution. Eurocode 1: Actions on Structures Part 1–6: General Actions during Execution; Committee for Standardization: Brussels, Belgium, 2011; Volume BS EN 1991-1, p. 31. [Google Scholar]
- Carrera, E.; Fazzolari, A.F.; Cinefra, M. Chapter 9—Static Response of Uncoupled Thermoelastic Problems; Academic Press: Oxford, UK, 2017; pp. 311–326. Available online: https://0-www-sciencedirect-com.brum.beds.ac.uk/science/article/pii/B9780124200661000124 (accessed on 10 July 2020).
- Khose, V.N.; Singh, Y.; Lang, D.H. A comparative study of design base shear for RC buildings in selected seismic design codes. Earthq. Spectra 2012, 28, 1047–1070. [Google Scholar] [CrossRef]
- Crowley, H.; Pinho, R. Revisiting Eurocode 8 formulae for periods of vibration and their employment in linear seismic analysis. Earthq. Eng. Struct. Dyn. 2010, 39, 223–235. [Google Scholar] [CrossRef] [Green Version]
- Zembaty, Z.; Kokot, S.; Kuś, J. Mitigating Rockburst Effects for Civil Engineering Infrastructure and Buildings. In Rockburst: Mechanisms, Monitoring, Warning, and Mitigation; Elsevier: Amsterdam, The Netherlands, 2018; pp. 541–548. [Google Scholar]
- McKenna, F.T. Object-Oriented Finite Element Programming: Frameworks for Analysis, Algorithms and Parallel Computing; University of California: Berkeley, CA, USA, 1997. [Google Scholar]
- Usmani, A.; Zhang, J.; Jiang, J.; Jiang, Y.; May, I. Using OpenSees for structures in fire. J. Struct. Fire Eng. 2010, 3, 919–926. [Google Scholar] [CrossRef] [Green Version]

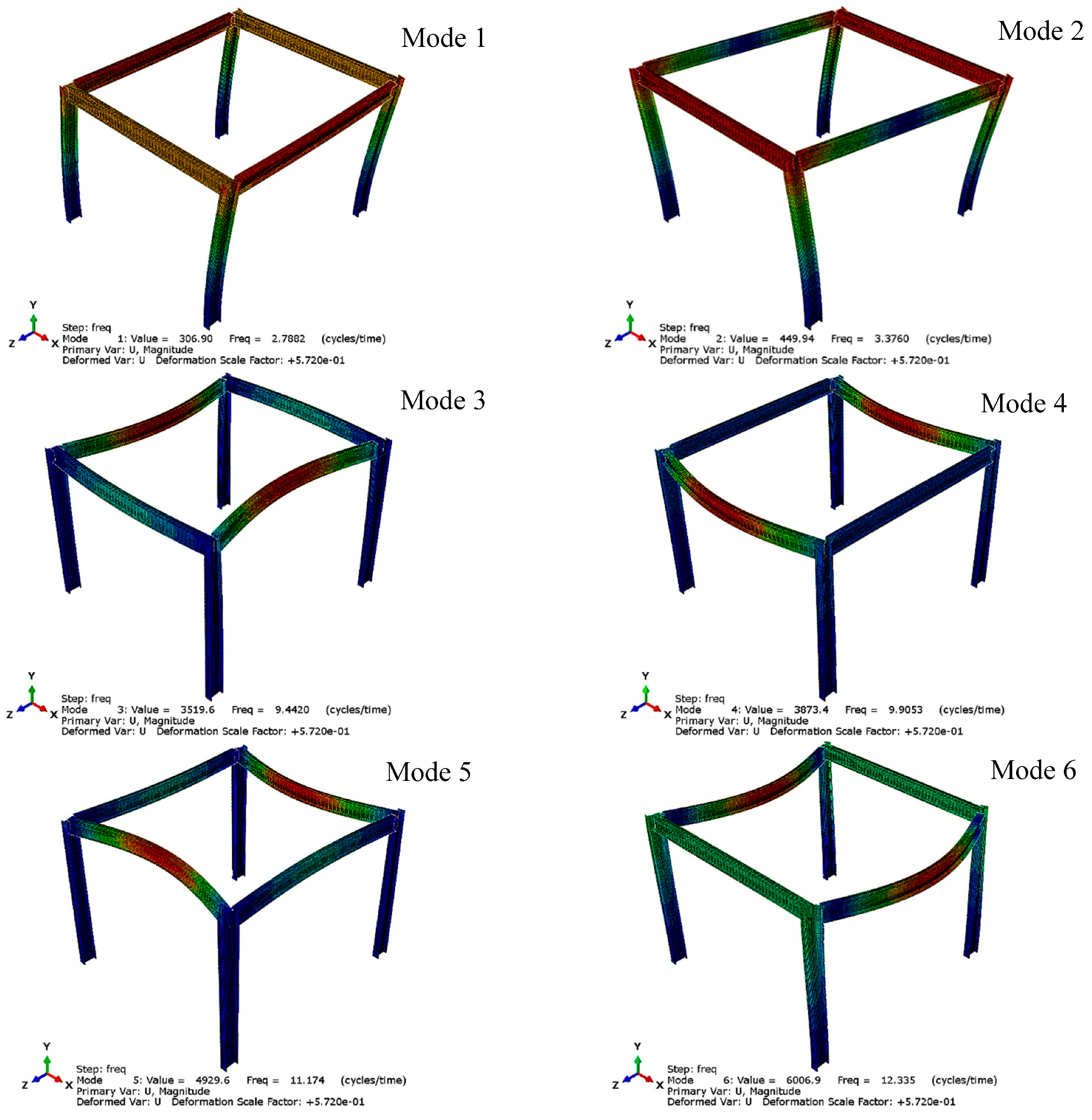













| Model | Natural Vibration Period (sec), T | Damping Coefficients | |||||||
|---|---|---|---|---|---|---|---|---|---|
| FE Model | Code | ||||||||
| Modes | EN 1998-1 | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||||
| Value | 0.36 | 0.296 | 0.106 | 0.101 | 0.09 | 0.081 | 0.16 | 0.959 | 0.0026 |
| Case No. | Type of Analysis | Type of Excitation | Failure | Time Failure, Compared to Fire-Only Results | Type of Failure | |
|---|---|---|---|---|---|---|
| Time (sec) | Tem. (°C) | |||||
| Fire-Only | Fire-Only | No excitation | 336 | 480 | - | Local/Symmetrical |
| Case I | PEF | Unidirectional | 272 | 455 | −19% | Local/Asymmetrical |
| Case II | PEF | Unidirectional | 277 | 455 | −18% | Local/Asymmetrical |
| Case III | PEF | Bidirectional | 185 | 306 | −45% | Global/Asymmetrical |
| Case IV | PEF | Bidirectional | 185 | 306 | −45% | Global/Asymmetrical |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alisawi, A.T.; Collins, P.E.F.; Cashell, K.A. Nonlinear Analysis of a Steel Frame Structure Exposed to Post-Earthquake Fire. Fire 2021, 4, 73. https://0-doi-org.brum.beds.ac.uk/10.3390/fire4040073
Alisawi AT, Collins PEF, Cashell KA. Nonlinear Analysis of a Steel Frame Structure Exposed to Post-Earthquake Fire. Fire. 2021; 4(4):73. https://0-doi-org.brum.beds.ac.uk/10.3390/fire4040073
Chicago/Turabian StyleAlisawi, Alaa T., Philip E. F. Collins, and Katherine A. Cashell. 2021. "Nonlinear Analysis of a Steel Frame Structure Exposed to Post-Earthquake Fire" Fire 4, no. 4: 73. https://0-doi-org.brum.beds.ac.uk/10.3390/fire4040073






