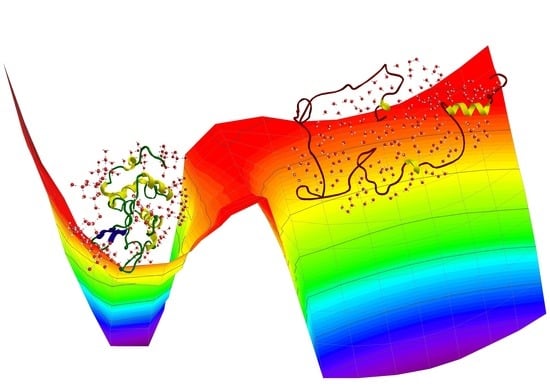
The Role of Hydrogen Bonding in the Folding/Unfolding Process of Hydrated Lysozyme: A Review of Recent NMR and FTIR Results
Abstract
:1. Introduction
2. Results and Discussion
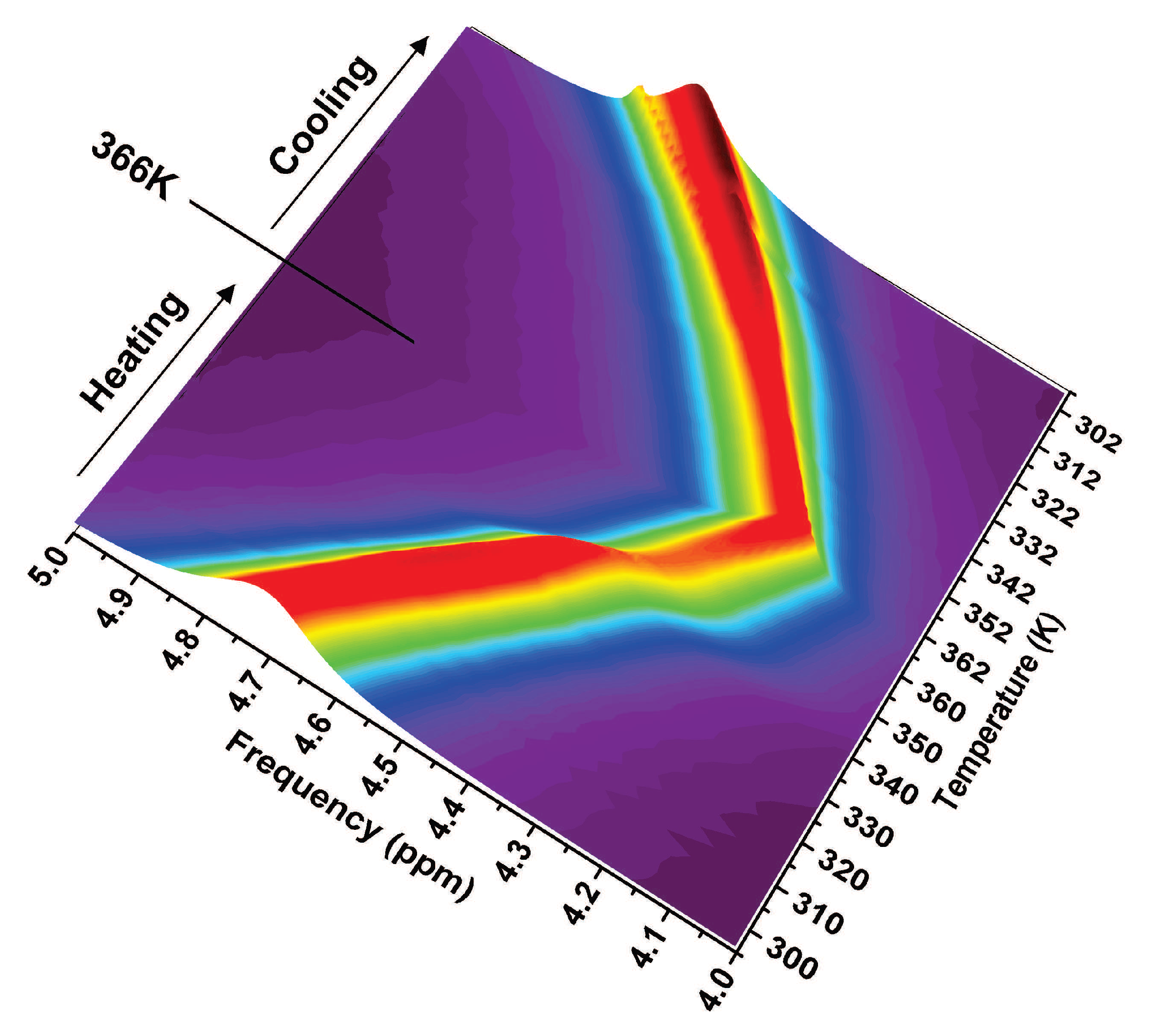
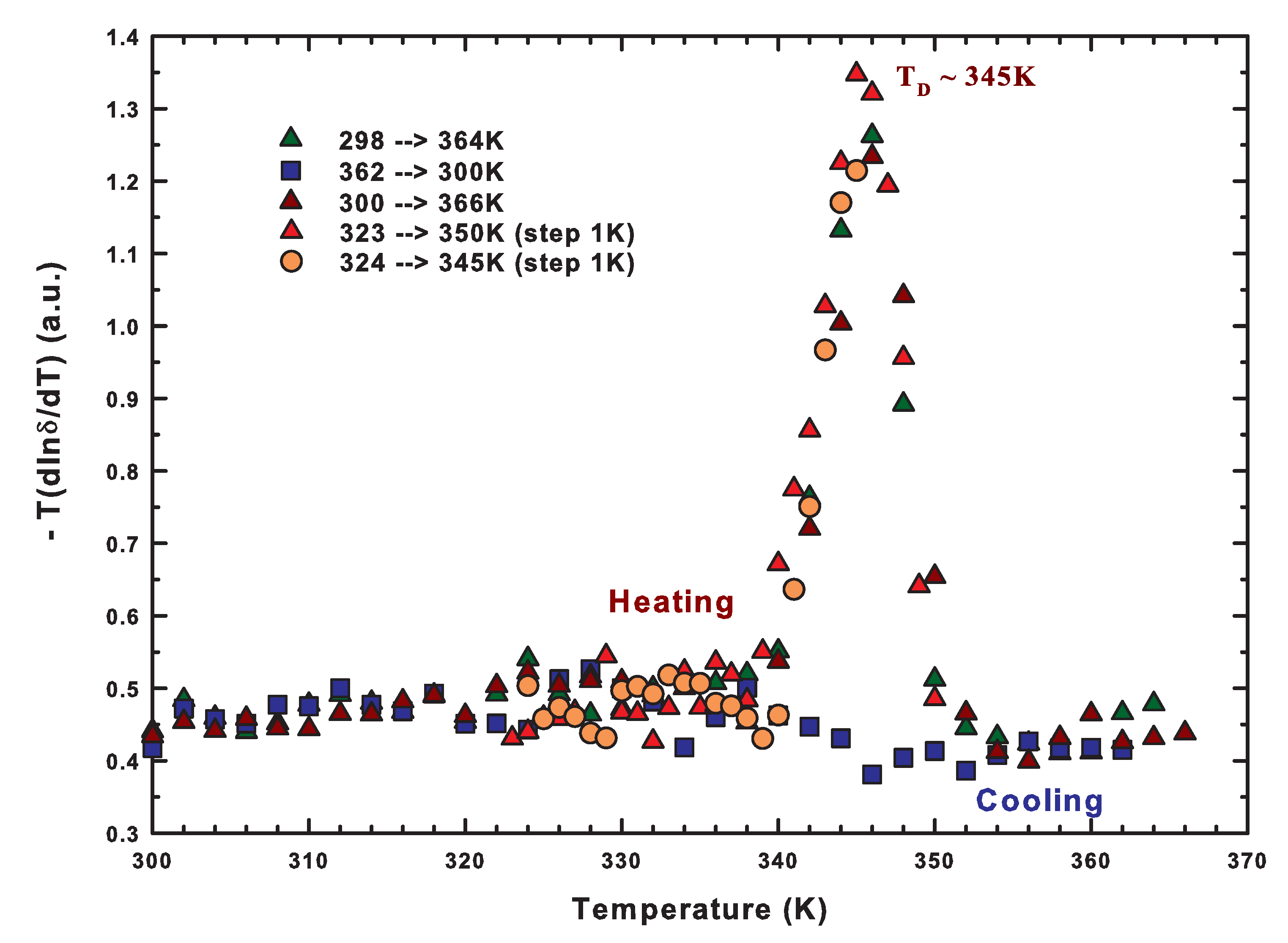
2.1. Specific Heat and Self-Diffusion of Hydrated Lysozyme
2.2. The Role of Water: NMR Results
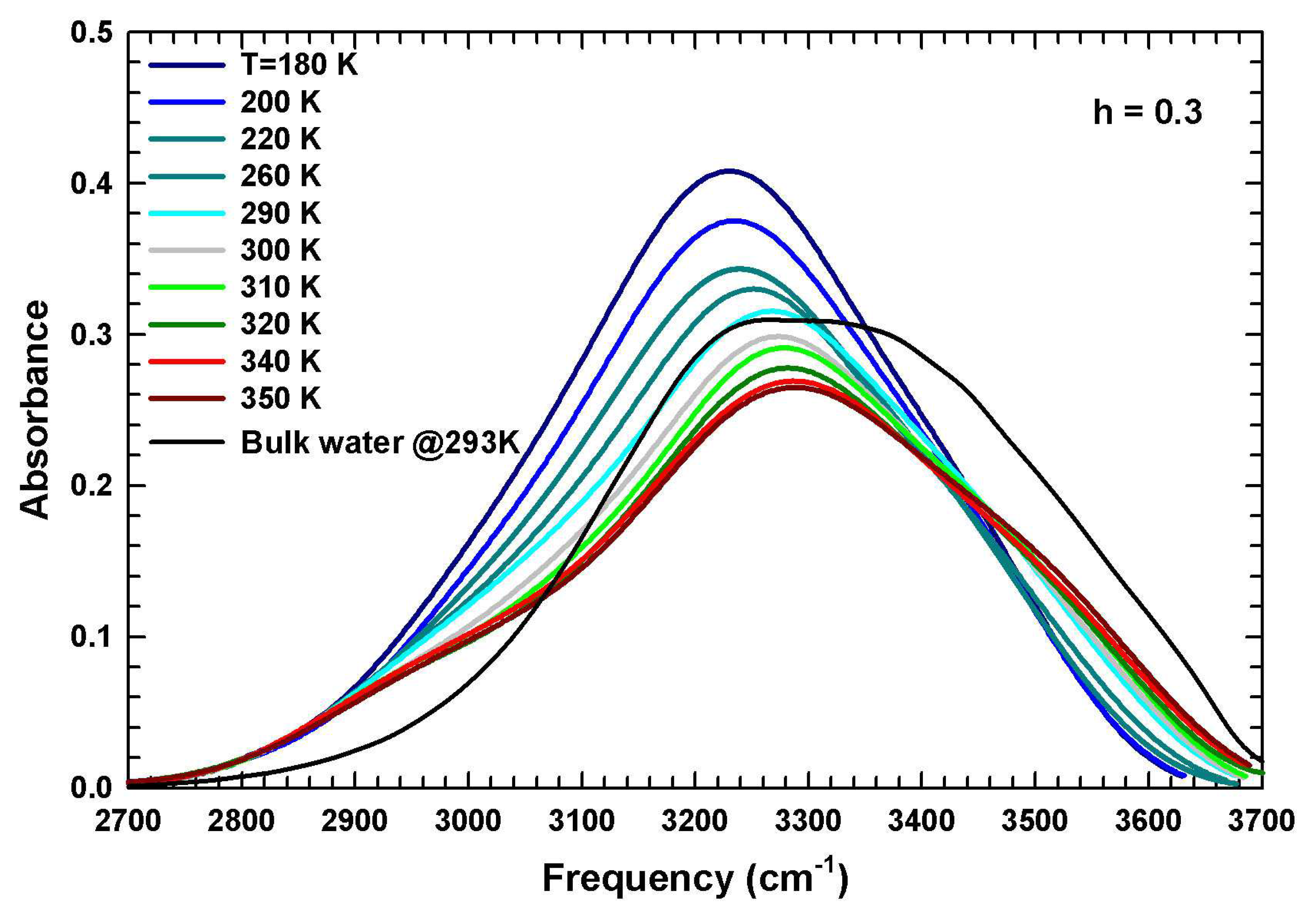
2.3. The Role of Water: FTIR Results
2.4. The Lysozyme Moieties: FTIR Results
2.5. The Lysozyme Moieties: NMR Results
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FTIR | Fourier Transform Infrared Spectroscopy |
| NMR | Nuclear Magnetic Resonance |
| FWHM | Full Width at Half Maximum |
References
- Šali, A.; Shakhnovich, E.; Karplus, M. How does a protein fold? Nature 1994, 369, 248–251. [Google Scholar] [PubMed]
- Schaeffer, R.D.; Daggett, V. Protein folds and protein folding. Protein Eng. Des. Sel. 2011, 24, 11–19. [Google Scholar] [CrossRef] [PubMed]
- Karplus, M. Behind the folding funnel diagram. Nat. Chem. Biol. 2011, 7, 401–404. [Google Scholar] [CrossRef] [PubMed]
- Levinthal, C. Are there pathways for protein folding? J. Chim. Phys. 1968, 65, 44–45. [Google Scholar] [CrossRef]
- Wolynes, P.G. Evolution, energy landscapes and the paradoxes of protein folding. Biochimie 2015, 119, 218–230. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Finkelstein, A.V.; Badretdin, A.J.; Galzitskaya, O.V.; Ivankov, D.N.; Bogatyreva, N.S.; Garbuzynskiy, S.O. There and back again: Two views on the protein folding puzzle. Phys. Life Rev. 2017, 21, 56–71. [Google Scholar] [CrossRef] [PubMed]
- Baldwin, R.L. Protein folding. Matching speed and stability. Nature 1994, 369, 183–184. [Google Scholar] [CrossRef] [PubMed]
- Dill, K.A.; MacCallum, J.L. The Protein-Folding Problem, 50 Years On. Science 2012, 338, 1042–1046. [Google Scholar] [CrossRef] [PubMed]
- Barducci, A.; Bonomi, M.; Prakash, M.K.; Parrinello, M. Free-energy landscape of protein oligomerization from atomistic simulations. Proc. Natl. Acad. Sci. USA 2013, 110, E4708–E4713. [Google Scholar] [CrossRef] [PubMed]
- Salvetti, G.; Tombari, E.; Mikheeva, L.; Johari, G.P. The Endothermic Effects during Denaturation of Lysozyme by Temperature Modulated Calorimetry and an Intermediate Reaction Equilibrium. J. Phys. Chem. B 2002, 106, 6081–6087. [Google Scholar] [CrossRef]
- Mallamace, F.; Corsaro, C.; Mallamace, D.; Vasi, S.; Vasi, C.; Baglioni, P.; Buldyrev, S.V.; Chen, S.H.; Stanley, H.E. Energy landscape in protein folding and unfolding. Proc. Natl. Acad. Sci. USA 2016, 105, 536. [Google Scholar] [CrossRef] [PubMed]
- McDonald, C.C.; Phillips, W.D.; Glickson, J.D. Nuclear magnetic resonance study of the mechanism of reversible denaturation of lysozyme. J. Am. Chem. Soc. 1971, 93, 235–246. [Google Scholar] [CrossRef] [PubMed]
- Ball, P. Water as an Active Constituent in Cell Biology. Chem. Rev. 2008, 108, 74–108. [Google Scholar] [CrossRef] [PubMed]
- Tsytlonok, M.; Itzhaki, L.S. The how’s and why’s of protein folding intermediates. Arch. Biochem. Biophys. 2013, 531, 14–23. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.J.; Xi, X.K.; Kleinhammes, A.; Wu, Y. Temperature-Induced Hydrophobic-Hydrophilic Transition Observed by Water Adsorption. Science 2008, 322, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Dinner, A.R.; Sali, A.; Smith, L.J.; Dobson, C.M.; Karplus, M. Understanding protein folding via free-energy surfaces from theory and experiment. Trends Biochem. Sci. 2000, 25, 331–339. [Google Scholar] [CrossRef]
- Stirling, P.C.; Lundin, V.F.; Leroux, M.R. Getting a grip on non-native proteins. EMBO Rep. 2003, 4, 565–570. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Daggett, V. Molecular Dynamics Simulations of the Protein Unfolding/Folding Reaction. Acc. Chem. Res. 2002, 35, 422–429. [Google Scholar] [CrossRef] [PubMed]
- Chiti, F.; Dobson, C.M. Protein Misfolding, Amyloid Formation, and Human Disease: A Summary of Progress over the Last Decade. Annu. Rev. Biochem. 2017, 86, 27–68. [Google Scholar] [CrossRef] [PubMed]
- Lapidus, L. Protein unfolding mechanisms and their effects on folding experiments [version 1; referees: 2 approved]. F1000Research 2017, 6, 1723. [Google Scholar] [CrossRef] [PubMed]
- Laage, D.; Elsaesser, T.; Hynes, J.T. Water Dynamics in the Hydration Shells of Biomolecules. Chem. Rev. 2017, 117, 10694–10725. [Google Scholar] [CrossRef] [PubMed]
- Careri, G. Cooperative charge fluctuations by migrating protons in globular proteins. Prog. Biophys. Mol. Biol. 1998, 70, 223–249. [Google Scholar] [CrossRef]
- Nakagawa, H.; Kataoka, M. Percolation of Hydration Water as a Control of Protein Dynamics. J. Phys. Soc. Jpn. 2010, 79, 083801. [Google Scholar] [CrossRef]
- Nakasako, M. Water–protein interactions from high-resolution protein crystallography. Philos. Trans. R. Soc. Lond. B 2004, 359, 1191–1206. [Google Scholar] [CrossRef] [PubMed]
- Frauenfelder, H.; Fenimore, P.W.; Young, R.D. Protein dynamics and function: Insights from the energy landscape and solvent slaving. IUBMB Life 2008, 59, 506–512. [Google Scholar] [CrossRef] [PubMed]
- Bellissent-Funel, M.C.; Hassanali, A.; Havenith, M.; Henchman, R.; Pohl, P.; Sterpone, F.; van der Spoel, D.; Xu, Y.; Garcia, A.E. Water Determines the Structure and Dynamics of Proteins. Chem. Rev. 2016, 116, 7673–7697. [Google Scholar] [CrossRef] [PubMed]
- Köhler, M.H.; Barbosa, R.C.; da Silva, L.B.; Barbosa, M.C. Role of the hydrophobic and hydrophilic sites in the dynamic crossover of the protein-hydration water. Phys. A Stat. Mech. Appl. 2017, 468, 733–739. [Google Scholar] [CrossRef]
- Maruyama, Y.; Harano, Y. Does water drive protein folding? Chem. Phys. Lett. 2013, 581, 85–90. [Google Scholar] [CrossRef]
- Levy, Y.; Onuchic, J.N. Water and proteins: A love–hate relationship. Proc. Natl. Acad. Sci. USA 2004, 101, 3325–3326. [Google Scholar] [CrossRef] [PubMed]
- Eisenberg, D. The discovery of the α-helix and β-sheet, the principal structural features of proteins. Proc. Natl. Acad. Sci. USA 2003, 100, 11207–11210. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jefferson, R.E.; Min, D.; Corin, K.; Wang, J.Y.; Bowie, J.U. Applications of Single-Molecule Methods to Membrane Protein Folding Studies. J. Mol. Biol. 2018, 430, 424–437. [Google Scholar] [CrossRef] [PubMed]
- Min, D.; Jefferson, R.E.; Bowie, J.U.; Yoon, T.Y. Mapping the energy landscape for second-stage folding of a single membrane protein. Nat. Chem. Biol. 2015, 11, 981. [Google Scholar] [CrossRef] [PubMed]
- Ball, P. Water is an active matrix of life for cell and molecular biology. Proc. Natl. Acad. Sci. USA 2017. [Google Scholar] [CrossRef] [PubMed]
- Cheung, M.S.; García, A.E.; Onuchic, J.N. Protein folding mediated by solvation: Water expulsion and formation of the hydrophobic core occur after the structural collapse. Proc. Natl. Acad. Sci. USA 2002, 99, 685–690. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mallamace, F.; Corsaro, C.; Mallamace, D.; Stanley, H.E.; Chen, S.H. Water and Biological Macromolecules. In Liquid Polymorphism: Advances in Chemical Physics, 1st ed.; Stanley, H.E., Ed.; IOS Press: Amsterdam, The Netherlands, 1999; Volume 152, pp. 263–308. [Google Scholar]
- Berg, J.M.; Tymoczko, J.L.; Stryer, L. Protein Structure and Function. In Biochemistry, 15th ed.; W. H. Freeman: New York, NY, USA, 2002. [Google Scholar]
- Tseng, Y.Y.; Li, W.H. Classification of protein functional surfaces using structural characteristics. Proc. Natl. Acad. Sci. USA 2012, 109, 1170–1175. [Google Scholar] [CrossRef] [PubMed]
- Orengo, C.A.; Todd, A.E.; Thornton, J.M. From protein structure to function. Curr. Opin. Struct. Biol. 1999, 9, 374–382. [Google Scholar] [CrossRef]
- Chen, M.; Lin, X.; Zheng, W.; Onuchic, J.N.; Wolynes, P.G. Protein Folding and Structure Prediction from the Ground Up: The Atomistic Associative Memory, Water Mediated, Structure and Energy Model. J. Phys. Chem. B 2016, 120, 8557–8565. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Onuchic, J.N.; Luthey-Schulten, Z.; Wolynes, P.G. THEORY OF PROTEIN FOLDING: The Energy Landscape Perspective. Annu. Rev. Phys. Chem. 1997, 48, 545–600. [Google Scholar] [CrossRef] [PubMed]
- Debenedetti, P.G.; Stillinger, F.H. Supercooled liquids and the glass transition. Nature 2001, 410, 259–267. [Google Scholar] [CrossRef] [PubMed]
- Yip, S. Understanding the viscosity of supercooled liquids and the glass transition through molecular simulations. Mol. Simul. 2016, 42, 1330–1342. [Google Scholar] [CrossRef]
- Yip, S.; Short, M.P. Escaping free-energy minima. Nat. Mater. 2013, 12, 774–777. [Google Scholar] [CrossRef] [PubMed]
- Stillinger, F.H. Energy Landscapes, Inherent Structures, and Condensed-Matter Phenomena; Princeton University Press: Princeton, NJ, USA, 2016. [Google Scholar]
- Dobson, C.M.; Šali, A.; Karplus, M. Protein Folding: A Perspective from Theory and Experiment. Angew. Chem. Int. Ed. 1998, 837, 868–893. [Google Scholar] [CrossRef]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Camisasca, G.; De Marzio, M.; Corradini, D.; Gallo, P. Two structural relaxations in protein hydration water and their dynamic crossovers. J. Chem. Phys. 2016, 145, 044503. [Google Scholar] [CrossRef] [PubMed]
- Boyd, J.; Dobson, C.M.; Redfield, C. Assignment of resonances in the 1H NMR spectrum of human lysozyme. Eur. J. Biochem. 1985, 153, 383–396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jana, B.; Pal, S.; Bagchi, B. Hydration dynamics of protein molecules in aqueous solution: Unity among diversity. J. Chem. Sci. 2012, 124, 317–325. [Google Scholar] [CrossRef]
- Corsaro, C.; Mallamace, D. A Nuclear Magnetic Resonance study of the reversible denaturation of hydrated lysozyme. Phys. A Stat. Mecha. Appl. 2011, 390, 2904–2908. [Google Scholar] [CrossRef]
- Mallamace, F.; Corsaro, C.; Mallamace, D.; Baglioni, P.; Stanley, H.E.; Chen, S.H. A Possible Role of Water in the Protein Folding Process. J. Phys. Chem. B 2011, 115, 14280. [Google Scholar] [CrossRef] [PubMed]
- Mallamace, F.; Corsaro, C.; Mallamace, D.; Vasi, S.; Vasi, C.; Dugo, G. The role of water in protein’s behavior: The two dynamical crossovers studied by NMR and FTIR techniques. Comput. Struct. Biotechnol. J. 2015, 13, 33–37. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.H.; Liu, L.; Fratini, E.; Baglioni, P.; Faraone, A.; Mamantov, E. Observation of fragile-to-strong dynamic crossover in protein hydration water. Proc. Natl. Acad. Sci. USA 2006, 103, 9012–9016. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Lagi, M.; Liu, D.; Mallamace, F.; Fratini, E.; Baglioni, P.; Mamontov, E.; Hagen, M.; Chen, S.H. Observation of high-temperature dynamic crossover in protein hydration water and its relation to reversible denaturation of lysozyme. J. Chem. Phys. 2009, 130, 135101. [Google Scholar] [CrossRef] [PubMed]
- Rupley, J.A.; Careri, G. Protein hydration and function. Adv. Protein Chem. 1991, 41, 37–172. [Google Scholar] [PubMed]
- Kurkal, V.; Daniel, R.; Finney, J.L.; Tehei, M.; Dunn, R.; Smith, J.C. Enzyme Activity and Flexibility at Very Low Hydration. Biophys. J. 2005, 89, 1282–1287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rupley, J.A.; Yang, P.H.; Tollin, G. Thermodynamic and Related Studies of Water Interacting with Proteins. In Water in Polymers; Rowland, S.P., Ed.; ACS Symposium Volume 127; American Chemical Society: Washington, DC, USA, 1980; pp. 111–132. [Google Scholar]
- Fomina, M.; Schirò, G.; Cupane, A. Hydration dependence of myoglobin dynamics studied with elastic neutron scattering, differential scanning calorimetry and broadband dielectric spectroscopy. Biophys. Chem. 2014, 185, 25–31. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mallamace, F.; Corsaro, C.; Mallamace, D.; Vasi, S.; Vasi, C.; Stanley, H.E. Thermodynamic properties of bulk and confined water. J. Chem. Phys. 2014, 141, 18C504. [Google Scholar] [CrossRef] [PubMed]
- Mallamace, F.; Corsaro, C.; Mallamace, D.; Vasi, S.; Vasi, C.; Stanley, H.E.; Chen, S.H. Some thermodynamical aspects of protein hydration water. J. Chem. Phys. 2015, 142, 215103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mallamace, F.; Corsaro, C.; Broccio, M.; Branca, C.; Gonzalez-Segredo, N.; Spooren, J.; Chen, S.H.; Stanley, H.E. NMR evidence of a sharp change in a measure of local order in deeply supercooled confined water. Proc. Natl. Acad. Sci. USA 2008, 105, 12725–12729. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mallamace, F.; Corsaro, C.; Mallamace, D.; Vasi, C.; Stanley, H.E. The thermodynamical response functions and the origin of the anomalous behavior of liquid water. Faraday Discuss. 2013, 167, 95–108. [Google Scholar] [CrossRef] [PubMed]
- Adam, G.; Gibbs, J. On the Temperature Dependence of Cooperative Relaxation Properties in Glass-Forming Liquids. J. Chem. Phys. 1965, 43, 139. [Google Scholar] [CrossRef]
- Mallamace, F.; Chen, S.H.; Broccio, M.; Corsaro, C.; Crupi, V.; Majolino, D.; Venuti, V.; Baglioni, P.; Fratini, E.; Vannucci, C.; Stanley, H.E. Role of the solvent in the dynamical transitions of proteins: The case of the lysozyme-water system. J. Chem. Phys. 2007, 127, 045104. [Google Scholar] [CrossRef] [PubMed]
- Schirò, G.; Fomina, M.; Cupane, A. Communication: Protein dynamical transition vs. liquid-liquid phase transition in protein hydration water. J. Chem. Phys. 2013, 139. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Doster, W.; Settles, M. Protein–water displacement distributions. Biochimica et Biophysica Acta (BBA) Proteins Proteom. 2005, 1749, 173–186. [Google Scholar] [CrossRef] [PubMed]
- Mallamace, F.; Baglioni, P.; Corsaro, C.; Chen, S.H.; Mallamace, D.; Vasi, C.; Stanley, H.E. The influence of water on protein properties. J. Chem. Phys. 2014, 141, 165104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, S.H.; Liu, L.; Chu, X.; Zhang, Y.; Fratini, E.; Baglioni, P.; Faraone, A.; Mamontov, E. Experimental evidence of fragile-to-strong dynamic crossover in DNA hydration water. J. Chem. Phys. 2006, 125, 171103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nilsson, L. Molecular Dynamics and NMR Shed Light on Motions Underpinning Dynamical Transitions in Biomolecules. Biophys. J. 2015, 108, 2755–2756. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Yan, Z.; Mazza, M.G.; Buldyrev, S.V.; Chen, S.H.; Sastry, S.; Stanley, H.E. Glass Transition in Biomolecules and the Liquid-Liquid Critical Point of Water. Phys. Rev. Lett. 2006, 97, 177802. [Google Scholar] [CrossRef] [PubMed]
- Schiro, G.; Natali, F.; Cupane, A. Physical Origin of Anharmonic Dynamics in Proteins: New Insights From Resolution-Dependent Neutron Scattering on Homomeric Polypeptides. Phys. Rev. Lett. 2012, 109. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khodadadi, S.; Sokolov, A. Protein dynamics: From rattling in a cage to structural relaxation. Soft Matter 2015, 11, 4984–4998. [Google Scholar] [CrossRef] [PubMed]
- Ngai, K.; Capaccioli, S.; Paciaroni, A. Nature of the water specific relaxation in hydrated proteins and aqueous mixtures. Chem. Phys. 2013, 424, 37–44. [Google Scholar] [CrossRef]
- Doster, W.; Busch, S.; Gaspar, A.M.; Appavou, M.S.; Wuttke, J.; Scheer, H. Dynamical Transition of Protein-Hydration Water. Phys. Rev. Lett. 2010, 104, 098101. [Google Scholar] [CrossRef] [PubMed]
- Mallamace, F. The liquid water polymorphism. Proc. Natl. Acad. Sci. USA 2009, 106, 15097–15098. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Poole, P.H.; Sciortino, F.; Essmann, U.; Stanley, H.E. Phase behaviour of metastable water. Nature 1992, 360, 324–328. [Google Scholar] [CrossRef]
- Stanley, H.; Angell, C.; Essmann, U.; Hemmati, M.; Poole, P.; Sciortino, F. Is there a second critical point in liquid water? Phys. A Stat. Mech. Appl. 1994, 205, 122–139. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.H.; Späh, A.; Pathak, H.; Perakis, F.; Mariedahl, D.; Amann-Winkel, K.; Sellberg, J.A.; Lee, J.H.; Kim, S.; Park, J.; et al. Maxima in the thermodynamic response and correlation functions of deeply supercooled water. Science 2017, 358, 1589–1593. [Google Scholar] [CrossRef] [PubMed]
- Mallamace, F.; Corsaro, C.; Mallamace, D.; Cicero, N.; Vasi, S.; Dugo, G.; Stanley, H.E. Dynamical changes in hydration water accompanying lysozyme thermal denaturation. Front. Phys. 2015, 10, 106104. [Google Scholar] [CrossRef]
- Mallamace, F.; Corsaro, C.; Stanley, H.E. Transport properties in supercooled confined water. Sci. Rep. 2012, 2, 993. [Google Scholar] [CrossRef] [PubMed]
- Prielmeier, F.X.; Lang, E.W.; Speedy, R.J.; Lüdemann, H.D. The Pressure Dependence of Self Diffusion in Supercooled Light and Heavy Water. Berichte der Bunsengesellschaft für Physikalische Chemie 1988, 92, 1111–1117. [Google Scholar] [CrossRef] [Green Version]
- Göetze, W.; Sjoegren, L. The essentials of the mode-coupling theory for glassy dynamics. Condens. Matter Phys. 1998, 1, 873–904. [Google Scholar] [CrossRef]
- Chong, S.H.; Chen, S.H.; Mallamace, F. A possible scenario for the fragile-to-strong dynamic crossover predicted by the extended mode-coupling theory for glass transition. J. Phys. Condens. Matter 2009, 21, 504101. [Google Scholar] [CrossRef] [PubMed]
- Mallamace, F.; Corsaro, C.; Mallamace, D.; Vasi, C.; Cicero, N.; Stanley, H.E. Water and lysozyme: Some results from the bending and stretching vibrational modes. Front. Phys. 2015, 10, 106105. [Google Scholar] [CrossRef]
- Mallamace, F.; Broccio, M.; Corsaro, C.; Faraone, A.; Majolino, D.; Venuti, V.; Liu, L.; Mou, C.Y.; Chen, S.H. Evidence of the existence of the low-density liquid phase in supercooled, confined water. Proc. Natl. Acad. Sci. USA 2007, 104, 424–427. [Google Scholar] [CrossRef] [PubMed]
- Schirò, G.; Caronna, C.; Natali, F.; Koza, M.M.; Cupane, A. The “Protein Dynamical Transition” Does Not Require the Protein Polypeptide Chain. J. Phys. Chem. Lett. 2011, 2, 2275–2279. [Google Scholar] [CrossRef] [Green Version]
- Sceats, M.G.; Rice, S.A. TAmorphous Solid Water and Its Relationship to Liquid Water: A Random Network Model for Water. In Water and Aqueous Solutions at Subzero Temperatures; Franks, F., Ed.; Springer US: New York, NY, USA, 1982; pp. 83–214. [Google Scholar]
- Pelton, J.T.; McLean, L.R. Spectroscopic Methods for Analysis of Protein Secondary Structure. Anal. Biochem. 2000, 277, 167–176. [Google Scholar] [CrossRef] [PubMed]
- Barth, A. Infrared spectroscopy of proteins. Biochim. Biophys. Acta Bioenerg. 2007, 1767, 1073–1101. [Google Scholar] [CrossRef] [PubMed]
- Fabian, H.; Naumann, D. (Eds.) Protein Folding and Misfolding; Springer-Verlag: Berlin, Germany, 2012. [Google Scholar] [CrossRef]
- Mallamace, D.; Corsaro, C.; Vasi, C.; Vasi, S.; Dugo, G.; Mallamace, F. The protein irreversible denaturation studied by means of the bending vibrational mode. Phys. A Stat. Mech. Appl. 2014, 412, 39–44. [Google Scholar] [CrossRef]
- Cruzeiro, L. Why are proteins with glutamine- and asparagine-rich regions associated with protein misfolding diseases? J. Phys. Condens. Matter 2005, 17, 7833. [Google Scholar] [CrossRef]
- Adams, S.; Higgins, A.M.; Jones, R.A.L. Surface-Mediated Folding and Misfolding of Proteins at Lipid/Water Interfaces. Langmuir 2002, 18, 4854–4861. [Google Scholar] [CrossRef]
- Cooper, A. Heat capacity effects in protein folding and ligand binding: A re-evaluation of the role of water in biomolecular thermodynamics. Biophys. Chem. 2005, 115, 89–97. [Google Scholar] [CrossRef] [PubMed]
- Walsh, S.T.; Cheng, R.P.; Wright, W.W.; Alonso, D.O.; Daggett, V.; Vanderkooi, J.M.; DeGrado, W.F. The hydration of amides in helices: A comprehensive picture from molecular dynamics, IR, and NMR. Protein Sci. 2003, 12, 520–531. [Google Scholar] [CrossRef] [PubMed]
- Makhatadze, G.I.; Privalov, P.L. Energetics of Protein Structure. In Advances in Protein Chemistry; Academic Press: Cambridge, MA, USA, 1995; Volume 47, pp. 307–425. [Google Scholar] [CrossRef]
- Fitch, W.L.; Detre, G.; Holmes, C.P.; Shoolery, J.N.; Keifer, P.A. High-Resolution 1H NMR in Solid-Phase Organic Synthesis. J. Organ. Chem. 1994, 59, 7955–7956. [Google Scholar] [CrossRef]
- Corsaro, C.; Mallamace, D.; Vasi, S.; Pietronero, L.; Mallamace, F.; Missori, M. The role of water in the degradation process of paper using 1H HR-MAS NMR spectroscopy. Phys. Chem. Chem. Phys. 2016, 18, 33335–33343. [Google Scholar] [CrossRef] [PubMed]
- Torre, A.; Trischitta, F.; Corsaro, C.; Mallamace, D.; Faggio, C. Digestive cells from Mytilus galloprovincialis show a partial regulatory volume decrease following acute hypotonic stress through mechanisms involving inorganic ions. Cell Biochem. Funct. 2013, 31, 489–495. [Google Scholar] [CrossRef] [PubMed]
- Moestue, S.; Sitter, B.; Bathen, T.F.; Tessem, M.B.; Gribbestad, I.S. HR MAS MR Spectroscopy in Metabolic Characterization of Cancer. Curr. Top. Med. Chem. 2011, 11, 2–26. [Google Scholar] [CrossRef] [PubMed]
- Corsaro, C.; Cicero, N.; Mallamace, D.; Vasi, S.; Naccari, C.; Salvo, A.; Giofrè, S.V.; Dugo, G. HR-MAS and NMR towards Foodomics. Food Res. Int. 2016, 89, 1085–1094. [Google Scholar] [CrossRef]
- Mukaiyama, A.; Takano, K. Slow unfolding of monomeric proteins from hyperthermophiles with reversible unfolding. Int. J. Mol. Sci. 2009, 10, 1369–1385. [Google Scholar] [CrossRef] [PubMed]
- Gallo, P.; Amann-Winkel, K.; Angell, C.A.; Anisimov, M.A.; Caupin, F.; Chakravarty, C.; Lascaris, E.; Loerting, T.; Panagiotopoulos, A.Z.; Russo, J.; et al. A Tale of Two Liquids. Chem. Rev. 2016, 116, 7463–7500. [Google Scholar] [CrossRef] [PubMed]
- Corradini, D.; Strekalova, E.G.; Stanley, H.E.; Gallo, P. Microscopic mechanism of protein cryopreservation in an aqueous solution with trehalose. Sci. Rep. 2013, 3, 1218. [Google Scholar] [CrossRef] [PubMed]

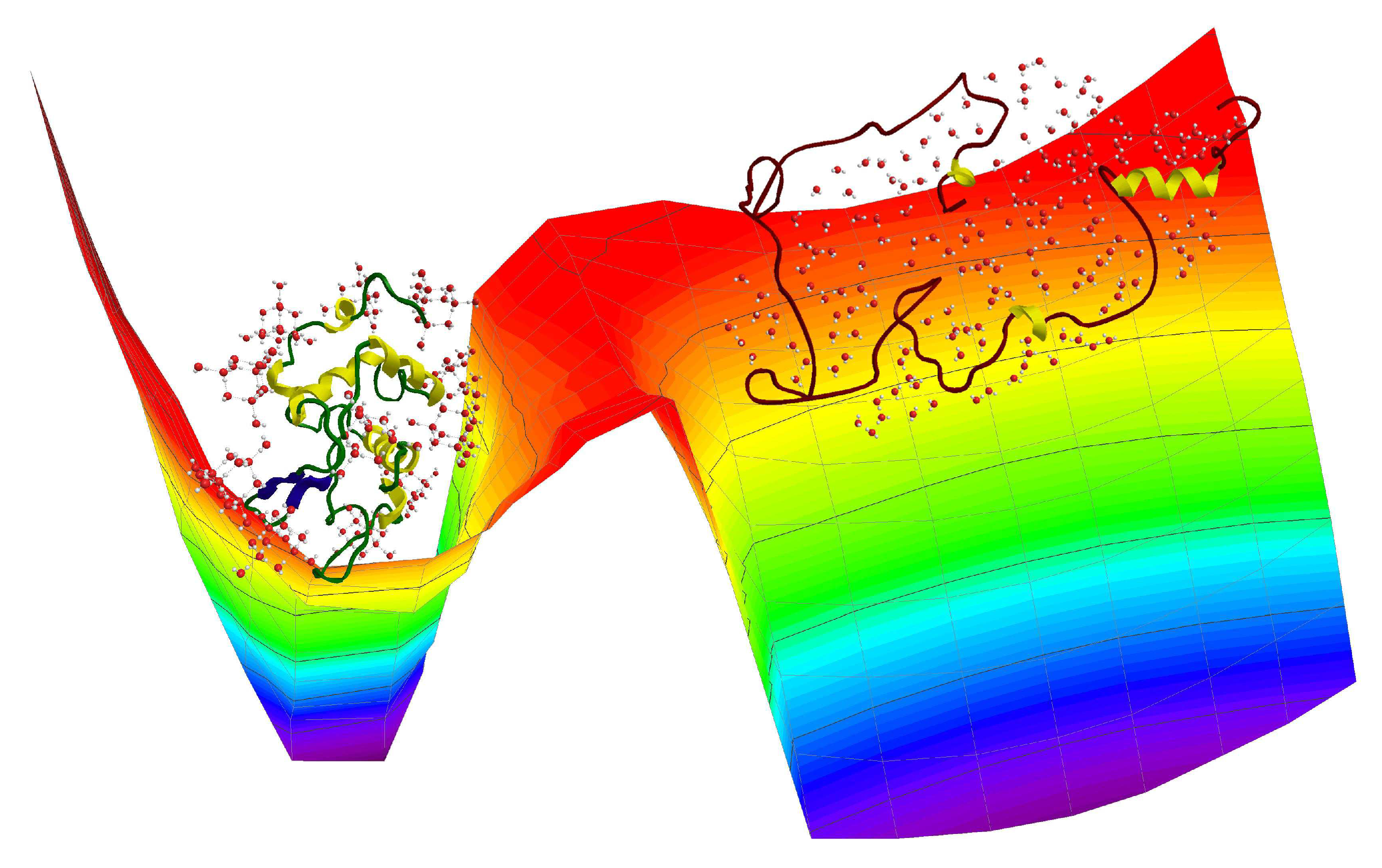

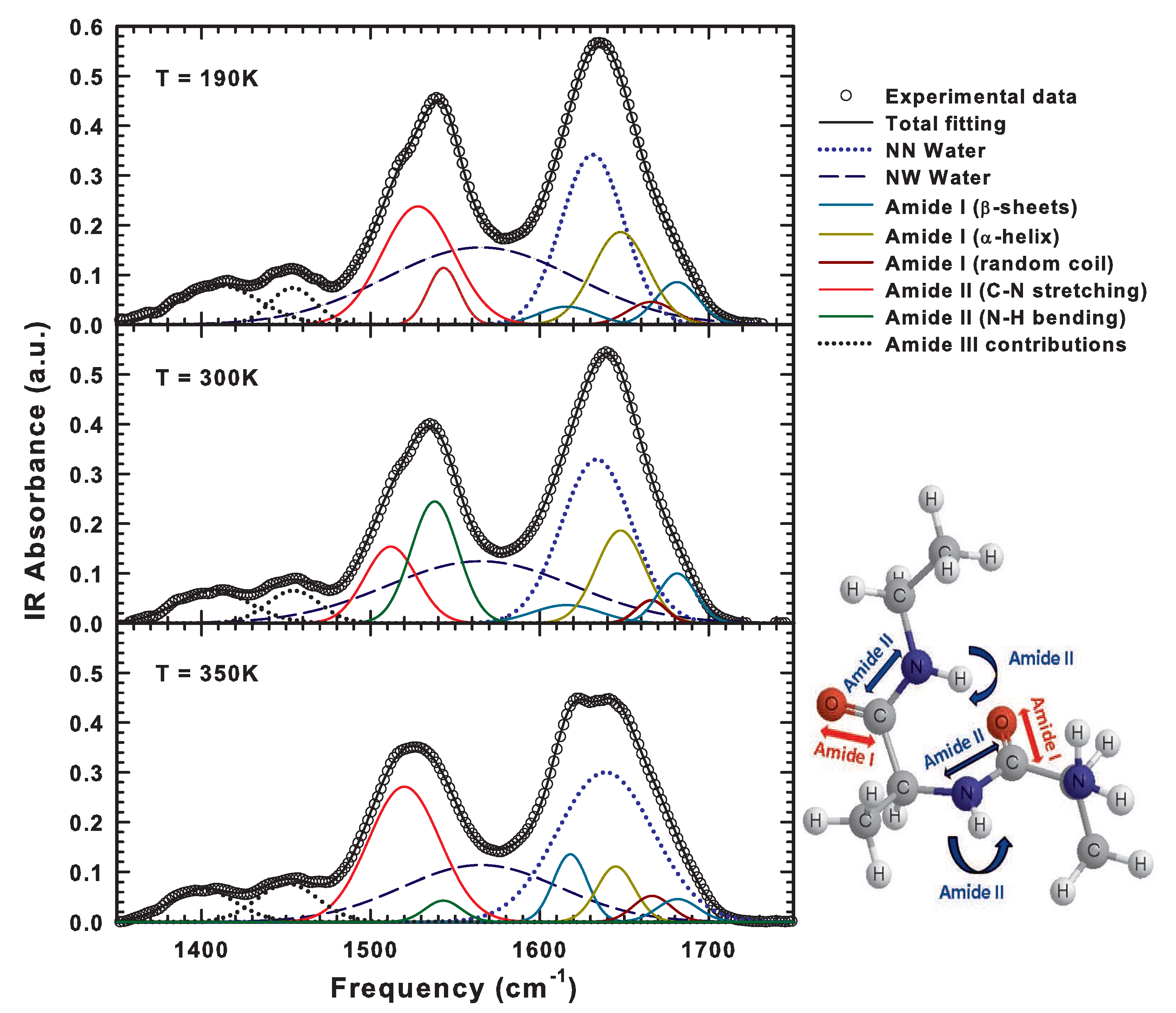


| IR Frequency (cm) | Conformation | Assignment |
|---|---|---|
| 1680–1696 | Antiparallel -sheets | C=O Stretching |
| 1655–1675 | Random coil | C=O Stretching |
| 1650–1657 | -helix | C=O Stretching |
| ≈1640 | Free water molecules | O–H Bending |
| 1612–1630 | Antiparallel -sheets | C=O Stretching |
| ≈1560 | Hydrogen-bonded water molecules | O–H Bending |
| ≈1540 | Peptide backbone | N–H Bending |
| ≈1520 | Peptide backbone | C–N Stretching |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mallamace, D.; Fazio, E.; Mallamace, F.; Corsaro, C. The Role of Hydrogen Bonding in the Folding/Unfolding Process of Hydrated Lysozyme: A Review of Recent NMR and FTIR Results. Int. J. Mol. Sci. 2018, 19, 3825. https://0-doi-org.brum.beds.ac.uk/10.3390/ijms19123825
Mallamace D, Fazio E, Mallamace F, Corsaro C. The Role of Hydrogen Bonding in the Folding/Unfolding Process of Hydrated Lysozyme: A Review of Recent NMR and FTIR Results. International Journal of Molecular Sciences. 2018; 19(12):3825. https://0-doi-org.brum.beds.ac.uk/10.3390/ijms19123825
Chicago/Turabian StyleMallamace, Domenico, Enza Fazio, Francesco Mallamace, and Carmelo Corsaro. 2018. "The Role of Hydrogen Bonding in the Folding/Unfolding Process of Hydrated Lysozyme: A Review of Recent NMR and FTIR Results" International Journal of Molecular Sciences 19, no. 12: 3825. https://0-doi-org.brum.beds.ac.uk/10.3390/ijms19123825