Multi-Scale Multivariate Models for Small Area Health Survey Data: A Chilean Example
Abstract
:1. Introduction
1.1. Objectives
1.2. Data Background and Availability
2. Methods
2.1. Joint Scale Models
2.2. Missingness and Imputation
2.3. Joint Outcome Modelling
2.4. Model Fitting and Goodness of fit
2.5. Posterior Risk Exceedance
2.6. Descriptive Statistics
3. Results of the Joint Modeling
Linear Model Parameter Estimates
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Region | Nr | Province | Mean | Sd | 2.50% | 97.50% | >= 9.4% |
|---|---|---|---|---|---|---|---|
| Arica y Parinacota | 1 | Parinacota | 13.12% | 6.36% | 4.67% | 29.04% | 74.09% |
| 2 | Arica | 10.91% | 1.33% | 8.42% | 13.65% | 87.87% | |
| Tarapaca | 3 | Iquique | 11.23% | 1.37% | 8.78% | 14.14% | 91.99% |
| 4 | Tamarugal | 12.17% | 2.53% | 8.24% | 18.18% | 90.05% | |
| Antofagasta | 5 | Tocopilla | 10.36% | 1.95% | 7.04% | 14.92% | 67.75% |
| 6 | El Loa | 9.03% | 1.77% | 5.98% | 12.97% | 38.03% | |
| 7 | Antofagasta | 10.56% | 1.48% | 7.98% | 13.82% | 77.99% | |
| Atacama | 8 | Chanaral | 12.72% | 6.13% | 4.39% | 28.23% | 72.01% |
| 9 | Copiapo | 10.33% | 1.42% | 7.61% | 13.22% | 74.90% | |
| 10 | Huasco | 11.90% | 1.96% | 8.20% | 16.08% | 90.33% | |
| Coquimbo | 11 | Elqui | 10.51% | 1.49% | 8.00% | 13.87% | 76.80% |
| 12 | Limari | 12.81% | 2.14% | 9.26% | 17.70% | 97.02% | |
| 13 | Choapa | 9.70% | 1.78% | 6.11% | 13.20% | 57.78% | |
| Valparaiso | 14 | San Antonio | 9.37% | 2.09% | 5.59% | 13.89% | 47.25% |
| 15 | Petorca | 13.02% | 3.01% | 8.29% | 20.00% | 92.05% | |
| 16 | Valparaiso | 11.53% | 1.51% | 8.64% | 14.54% | 92.25% | |
| 17 | Quillota | 12.39% | 1.99% | 8.74% | 16.75% | 94.13% | |
| 18 | Los Andes | 10.97% | 2.13% | 7.42% | 15.88% | 78.08% | |
| 19 | San Felipe de Aconcagua | 15.45% | 3.35% | 10.61% | 23.80% | 99.63% | |
| Metropolitana | 20 | Chacabuco | 6.23% | 1.94% | 3.02% | 10.53% | 6.24% |
| 21 | Santiago | 9.87% | 0.96% | 8.08% | 11.79% | 68.00% | |
| 22 | Melipilla | 14.23% | 3.19% | 9.28% | 21.94% | 97.19% | |
| 23 | Talagante | 11.19% | 5.14% | 3.85% | 23.94% | 57.26% | |
| 24 | Maipo | 10.19% | 1.83% | 6.79% | 14.12% | 66.56% | |
| 25 | Cordillera | 8.73% | 1.61% | 5.81% | 12.23% | 31.43% | |
| O’Higgins | 26 | Cardenal Caro | 11.54% | 5.79% | 4.14% | 25.96% | 62.77% |
| 27 | Cachapoal | 10.64% | 1.34% | 8.05% | 13.28% | 81.97% | |
| 28 | Colchagua | 12.96% | 2.15% | 9.01% | 17.50% | 95.99% | |
| Maule | 29 | Cauquenes | 16.27% | 3.73% | 9.83% | 24.52% | 98.30% |
| 30 | Curico | 13.72% | 2.27% | 10.18% | 18.95% | 99.31% | |
| 31 | Linares | 9.80% | 1.53% | 7.10% | 13.16% | 58.38% | |
| 32 | Talca | 7.79% | 1.35% | 5.16% | 10.51% | 11.15% | |
| Biobio | 33 | Arauco | 11.94% | 2.07% | 8.55% | 16.68% | 92.13% |
| 34 | Concepcion | 13.03% | 2.19% | 9.56% | 18.02% | 98.15% | |
| 35 | Nuble | 8.67% | 1.93% | 5.04% | 12.58% | 34.00% | |
| 36 | Biobio | 10.97% | 2.01% | 6.94% | 14.96% | 78.73% | |
| Araucania | 37 | Malleco | 12.32% | 2.70% | 7.52% | 18.01% | 86.75% |
| 38 | Cautin | 12.10% | 1.46% | 9.61% | 15.30% | 98.49% | |
| Rios | 39 | Ranco | 11.17% | 1.78% | 7.93% | 15.09% | 85.17% |
| 40 | Valdivia | 10.78% | 1.41% | 8.19% | 13.83% | 83.66% | |
| Lagos | 41 | Chiloe | 9.87% | 1.64% | 6.50% | 13.04% | 63.11% |
| 42 | Llanquihue | 10.84% | 1.66% | 7.77% | 14.39% | 81.12% | |
| 43 | Palena | 10.32% | 5.19% | 3.60% | 22.95% | 50.33% | |
| 44 | Osorno | 10.30% | 1.67% | 7.16% | 13.85% | 70.61% | |
| Aysen | 45 | Coyhaique | 7.89% | 1.40% | 5.30% | 10.79% | 13.88% |
| 46 | General Carrera | 5.84% | 1.70% | 3.02% | 9.65% | 3.24% | |
| 47 | Aisen | 10.20% | 5.04% | 3.50% | 22.88% | 49.23% | |
| 48 | Capitan Prat | 10.24% | 5.30% | 3.49% | 23.05% | 48.79% | |
| Magallanes | 49 | Antartica Chilena | 11.53% | 10.18% | 0.79% | 38.62% | 46.47% |
| 50 | Ultima Esperanza | 10.37% | 2.18% | 6.46% | 14.92% | 66.17% | |
| 51 | Magallanes | 10.14% | 1.45% | 7.49% | 13.20% | 68.81% | |
| 52 | Tierra del Fuego | 10.02% | 7.59% | 0.93% | 30.10% | 43.23% |
| Region | Nr | Province | Mean | Sd | 2.50% | 97.5% | >= 25.1% |
|---|---|---|---|---|---|---|---|
| Arica y Parinacota | 1 | Parinacota | 26.78% | 8.04% | 12.72% | 44.93% | 55.31% |
| 2 | Arica | 27.56% | 2.21% | 23.31% | 32.03% | 86.87% | |
| Tarapaca | 3 | Iquique | 20.13% | 2.10% | 16.15% | 24.31% | 1.10% |
| 4 | Tamarugal | 25.16% | 4.51% | 17.05% | 34.94% | 48.28% | |
| Antofagasta | 5 | Tocopilla | 29.75% | 4.57% | 21.69% | 39.63% | 85.25% |
| 6 | El Loa | 26.58% | 3.60% | 19.96% | 33.88% | 64.71% | |
| 7 | Antofagasta | 29.27% | 2.67% | 24.19% | 34.61% | 94.48% | |
| Atacama | 8 | Chanaral | 28.05% | 8.11% | 13.66% | 45.79% | 62.97% |
| 9 | Copiapo | 31.07% | 2.59% | 26.04% | 36.32% | 99.06% | |
| 10 | Huasco | 25.55% | 3.48% | 19.02% | 32.66% | 53.45% | |
| Coquimbo | 11 | Elqui | 31.02% | 2.83% | 25.63% | 36.85% | 98.51% |
| 12 | Limari | 19.42% | 3.29% | 13.28% | 26.08% | 4.38% | |
| 13 | Choapa | 21.32% | 3.72% | 14.27% | 28.89% | 15.34% | |
| Valparaiso | 14 | San Antonio | 25.54% | 4.50% | 17.32% | 35.01% | 51.71% |
| 15 | Petorca | 25.98% | 5.24% | 16.52% | 36.87% | 54.40% | |
| 16 | Valparaiso | 24.07% | 2.47% | 19.36% | 29.06% | 32.85% | |
| 17 | Quillota | 28.66% | 4.16% | 21.21% | 37.69% | 80.42% | |
| 18 | Los Andes | 25.62% | 4.40% | 17.56% | 35.02% | 52.64% | |
| 19 | San Felipe de Aconcagua | 31.03% | 5.26% | 21.90% | 42.40% | 87.65% | |
| Metropolitana | 20 | Chacabuco | 31.00% | 6.38% | 19.88% | 44.79% | 82.27% |
| 21 | Santiago | 23.76% | 1.50% | 20.91% | 26.74% | 18.82% | |
| 22 | Melipilla | 25.59% | 4.65% | 17.09% | 35.46% | 52.14% | |
| 23 | Talagante | 28.56% | 7.58% | 15.11% | 44.83% | 65.43% | |
| 24 | Maipo | 31.41% | 4.72% | 23.19% | 41.38% | 92.34% | |
| 25 | Cordillera | 25.57% | 3.46% | 19.09% | 32.72% | 54.29% | |
| O’Higgins | 26 | Cardenal Caro | 26.95% | 7.71% | 12.97% | 44.19% | 57.30% |
| 27 | Cachapoal | 25.51% | 2.34% | 21.08% | 30.35% | 55.86% | |
| 28 | Colchagua | 20.36% | 3.04% | 14.65% | 26.59% | 6.44% | |
| Maule | 29 | Cauquenes | 27.40% | 5.54% | 17.43% | 38.99% | 64.62% |
| 30 | Curico | 28.48% | 3.60% | 21.76% | 35.87% | 82.54% | |
| 31 | Linares | 35.18% | 3.67% | 28.25% | 42.72% | 99.86% | |
| 32 | Talca | 29.70% | 3.14% | 23.79% | 36.13% | 93.31% | |
| Biobio | 33 | Arauco | 36.04% | 4.40% | 27.91% | 45.27% | 99.70% |
| 34 | Concepcion | 28.41% | 3.18% | 22.42% | 34.85% | 85.14% | |
| 35 | Nuble | 27.06% | 4.38% | 18.77% | 35.99% | 66.45% | |
| 36 | Biobio | 38.28% | 4.88% | 29.40% | 48.44% | 99.83% | |
| Araucania | 37 | Malleco | 32.71% | 4.50% | 24.41% | 41.91% | 96.12% |
| 38 | Cautin | 36.05% | 2.52% | 31.22% | 40.95% | 100.0% | |
| Rios | 39 | Ranco | 33.18% | 3.94% | 25.66% | 41.02% | 98.29% |
| 40 | Valdivia | 36.70% | 2.77% | 31.39% | 42.25% | 100.0% | |
| Lagos | 41 | Chiloe | 31.38% | 3.60% | 24.77% | 38.92% | 96.85% |
| 42 | Llanquihue | 29.43% | 3.10% | 23.42% | 35.65% | 92.21% | |
| 43 | Palena | 34.23% | 8.99% | 17.55% | 53.47% | 86.27% | |
| 44 | Osorno | 37.03% | 3.82% | 29.84% | 44.70% | 99.96% | |
| Aysen | 45 | Coyhaique | 32.59% | 2.98% | 26.81% | 38.54% | 99.61% |
| 46 | General Carrera | 37.74% | 4.47% | 29.34% | 46.83% | 99.87% | |
| 47 | Aisen | 35.06% | 9.11% | 17.98% | 54.83% | 88.13% | |
| 48 | Capitan Prat | 35.46% | 9.02% | 18.53% | 54.36% | 88.76% | |
| Magallanes | 49 | Antartica Chilena | 40.60% | 16.12% | 12.75% | 74.23% | 81.67% |
| 50 | Ultima Esperanza | 36.02% | 4.80% | 26.72% | 45.82% | 99.06% | |
| 51 | Magallanes | 38.52% | 2.66% | 33.37% | 43.79% | 100.0% | |
| 52 | Tierra del Fuego | 39.59% | 12.42% | 17.18% | 64.96% | 87.56% |
| Region | Nr | Province | Mean | Sd | 2.50% | 97.5% | >= 6.9% |
|---|---|---|---|---|---|---|---|
| Arica y Parinacota | 1 | Parinacota | 30.98% | 10.7% | 14.0% | 56.98% | 60.55% |
| 2 | Arica | 26.29% | 2.07% | 22.2% | 30.28% | 37.92% | |
| Tarapaca | 3 | Iquique | 28.26% | 2.07% | 24.3% | 32.43% | 74.40% |
| 4 | Tamarugal | 28.99% | 3.56% | 22.7% | 36.87% | 71.65% | |
| Antofagasta | 5 | Tocopilla | 27.65% | 3.22% | 22.1% | 34.94% | 55.83% |
| 6 | El Loa | 21.82% | 2.70% | 16.8% | 27.56% | 4.16% | |
| 7 | Antofagasta | 27.59% | 2.30% | 23.3% | 32.35% | 60.34% | |
| Atacama | 8 | Chanaral | 33.29% | 10.6% | 16.1% | 57.77% | 71.07% |
| 9 | Copiapo | 31.35% | 2.40% | 26.7% | 36.16% | 96.99% | |
| 10 | Huasco | 37.98% | 3.34% | 31.4% | 44.58% | 99.99% | |
| Coquimbo | 11 | Elqui | 32.75% | 2.57% | 27.9% | 38.02% | 99.27% |
| 12 | Limari | 39.20% | 3.38% | 32.6% | 45.94% | 100.0% | |
| 13 | Choapa | 34.48% | 3.50% | 27.3% | 41.25% | 98.05% | |
| Valparaiso | 14 | San Antonio | 32.69% | 3.89% | 25.1% | 40.47% | 93.46% |
| 15 | Petorca | 43.10% | 4.78% | 34.1% | 53.06% | 99.99% | |
| 16 | Valparaiso | 43.42% | 2.59% | 38.4% | 48.70% | 100.0% | |
| 17 | Quillota | 44.17% | 3.43% | 37.2% | 50.79% | 100.0% | |
| 18 | Los Andes | 34.27% | 3.60% | 26.8% | 41.02% | 97.45% | |
| 19 | San Felipe de Aconcagua | 49.71% | 4.01% | 42.3% | 58.24% | 100.0% | |
| Metropolitana | 20 | Chacabuco | 19.94% | 3.75% | 13.4% | 28.16% | 4.25% |
| 21 | Santiago | 32.11% | 1.63% | 28.9% | 35.36% | 99.96% | |
| 22 | Melipilla | 44.93% | 4.53% | 36.6% | 54.68% | 100.0% | |
| 23 | Talagante | 24.46% | 6.65% | 13.2% | 39.20% | 32.86% | |
| 24 | Maipo | 35.08% | 3.28% | 29.0% | 42.06% | 99.65% | |
| 25 | Cordillera | 28.95% | 2.90% | 23.4% | 34.86% | 76.37% | |
| O’Higgins | 26 | Cardenal Caro | 40.45% | 11.4% | 21.1% | 66.95% | 90.67% |
| 27 | Cachapoal | 42.41% | 2.37% | 37.9% | 47.25% | 100.0% | |
| 28 | Colchagua | 54.27% | 3.40% | 47.6% | 60.89% | 100.0% | |
| Maule | 29 | Cauquenes | 57.14% | 5.03% | 46.6% | 66.67% | 100.0% |
| 30 | Curico | 43.80% | 3.21% | 37.2% | 49.89% | 100.0% | |
| 31 | Linares | 35.05% | 2.95% | 29.1% | 40.84% | 99.65% | |
| 32 | Talca | 33.00% | 2.79% | 27.7% | 38.66% | 98.82% | |
| Biobio | 33 | Arauco | 42.95% | 3.49% | 36.3% | 49.99% | 100.0% |
| 34 | Concepcion | 39.90% | 2.91% | 34.3% | 45.73% | 100.0% | |
| 35 | Nuble | 31.93% | 3.45% | 25.4% | 38.97% | 93.32% | |
| 36 | Biobio | 45.97% | 3.84% | 39.1% | 54.16% | 100.0% | |
| Araucania | 37 | Malleco | 55.48% | 4.28% | 46.9% | 63.95% | 100.0% |
| 38 | Cautin | 41.86% | 2.30% | 37.4% | 46.44% | 100.0% | |
| Rios | 39 | Ranco | 43.22% | 3.35% | 36.9% | 50.03% | 100.0% |
| 40 | Valdivia | 36.74% | 2.57% | 31.7% | 41.80% | 99.99% | |
| Lagos | 41 | Chiloe | 37.79% | 3.07% | 32.5% | 44.80% | 100.0% |
| 42 | Llanquihue | 40.20% | 2.95% | 34.4% | 46.03% | 100.0% | |
| 43 | Palena | 37.63% | 10.9% | 18.8% | 62.70% | 85.39% | |
| 44 | Osorno | 41.31% | 3.20% | 34.9% | 47.55% | 100.0% | |
| Aysen | 45 | Coyhaique | 35.13% | 2.75% | 29.9% | 40.73% | 99.94% |
| 46 | General Carrera | 25.98% | 3.66% | 19.2% | 33.50% | 38.48% | |
| 47 | Aisen | 37.11% | 11.0% | 18.6% | 62.63% | 83.58% | |
| 48 | Capitan Prat | 36.50% | 11.0% | 17.9% | 61.74% | 81.35% | |
| Magallanes | 49 | Antartica Chilena | 21.46% | 13.1% | 3.92% | 53.47% | 28.10% |
| 50 | Ultima Esperanza | 44.71% | 4.14% | 36.7% | 53.02% | 100.0% | |
| 51 | Magallanes | 34.74% | 2.53% | 29.8% | 39.73% | 99.94% | |
| 52 | Tierra del Fuego | 17.54% | 9.04% | 4.24% | 39.02% | 15.05% |
| Region | Nr | Province | Mean | Sd | 2.50% | 97.50% | >= 22.7% |
|---|---|---|---|---|---|---|---|
| Arica y Parinacota | 1 | Parinacota | 31.28% | 11.00% | 13.0% | 57.03% | 79.12% |
| 2 | Arica | 26.55% | 2.95% | 20.9% | 32.58% | 90.67% | |
| Tarapaca | 3 | Iquique | 32.05% | 3.08% | 26.1% | 38.25% | 99.94% |
| 4 | Tamarugal | 32.24% | 6.37% | 20.6% | 45.62% | 94.34% | |
| Antofagasta | 5 | Tocopilla | 35.08% | 6.60% | 23.9% | 50.18% | 98.60% |
| 6 | El Loa | 28.04% | 5.06% | 18.9% | 38.90% | 85.45% | |
| 7 | Antofagasta | 25.39% | 3.32% | 19.0% | 31.97% | 78.74% | |
| Atacama | 8 | Chanaral | 31.46% | 10.89% | 13.1% | 56.28% | 79.48% |
| 9 | Copiapo | 37.15% | 3.73% | 30.1% | 44.60% | 100.00% | |
| 10 | Huasco | 32.22% | 4.73% | 23.2% | 41.95% | 98.29% | |
| Coquimbo | 11 | Elqui | 23.41% | 3.46% | 16.9% | 30.50% | 57.46% |
| 12 | Limari | 31.65% | 5.11% | 22.1% | 42.35% | 96.66% | |
| 13 | Choapa | 24.43% | 4.70% | 15.7% | 33.96% | 63.39% | |
| Valparaiso | 14 | San Antonio | 27.66% | 6.25% | 17.0% | 41.47% | 78.12% |
| 15 | Petorca | 29.60% | 6.42% | 18.4% | 43.65% | 86.55% | |
| 16 | Valparaiso | 32.69% | 4.26% | 24.8% | 41.49% | 99.49% | |
| 17 | Quillota | 27.66% | 5.62% | 17.1% | 39.04% | 81.23% | |
| 18 | Los Andes | 24.60% | 5.60% | 14.4% | 36.82% | 61.88% | |
| 19 | San Felipe de Aconcagua | 28.63% | 5.91% | 17.4% | 40.53% | 84.15% | |
| Metropolitana | 20 | Chacabuco | 18.36% | 6.19% | 8.67% | 32.94% | 21.41% |
| 21 | Santiago | 21.62% | 1.92% | 18.0% | 25.52% | 28.35% | |
| 22 | Melipilla | 22.94% | 5.86% | 12.1% | 35.33% | 49.74% | |
| 23 | Talagante | 17.94% | 7.82% | 6.16% | 36.79% | 23.61% | |
| 24 | Maipo | 21.72% | 4.56% | 13.5% | 31.52% | 38.96% | |
| 25 | Cordillera | 17.19% | 3.93% | 10.1% | 25.48% | 8.82% | |
| O’Higgins | 26 | Cardenal Caro | 27.64% | 10.16% | 11.1% | 51.62% | 67.34% |
| 27 | Cachapoal | 27.54% | 3.51% | 20.9% | 34.74% | 91.92% | |
| 28 | Colchagua | 28.15% | 4.70% | 19.2% | 37.80% | 87.74% | |
| Maule | 29 | Cauquenes | 38.11% | 7.30% | 24.3% | 53.16% | 98.61% |
| 30 | Curico | 28.09% | 4.27% | 20.0% | 36.80% | 90.05% | |
| 31 | Linares | 23.97% | 3.90% | 16.6% | 31.96% | 62.41% | |
| 32 | Talca | 23.57% | 3.28% | 17.5% | 30.35% | 59.41% | |
| Biobio | 33 | Arauco | 29.18% | 4.61% | 20.5% | 38.68% | 92.55% |
| 34 | Concepcion | 28.95% | 4.01% | 21.5% | 37.29% | 94.71% | |
| 35 | Nuble | 18.49% | 4.61% | 10.2% | 28.28% | 17.57% | |
| 36 | Biobio | 33.47% | 5.73% | 23.3% | 45.66% | 98.26% | |
| Araucania | 37 | Malleco | 37.51% | 5.83% | 26.5% | 49.18% | 99.74% |
| 38 | Cautin | 40.06% | 3.78% | 32.8% | 47.69% | 100.00% | |
| Rios | 39 | Ranco | 32.08% | 4.64% | 23.3% | 41.45% | 98.33% |
| 40 | Valdivia | 26.19% | 3.29% | 20.0% | 32.74% | 85.61% | |
| Lagos | 41 | Chiloe | 40.28% | 5.84% | 29.8% | 52.48% | 100.00% |
| 42 | Llanquihue | 32.40% | 3.76% | 25.3% | 39.86% | 99.63% | |
| 43 | Palena | 31.80% | 10.87% | 13.3% | 56.29% | 80.81% | |
| 44 | Osorno | 30.01% | 4.40% | 21.6% | 39.08% | 95.58% | |
| Aysen | 45 | Coyhaique | 32.14% | 4.34% | 24.0% | 41.11% | 98.94% |
| 46 | General Carrera | 27.71% | 4.70% | 19.1% | 37.26% | 85.61% | |
| 47 | Aisen | 32.16% | 11.16% | 13.3% | 58.58% | 81.17% | |
| 48 | Capitan Prat | 32.20% | 11.28% | 13.3% | 58.78% | 81.19% | |
| Magallanes | 49 | Antartica Chilena | 37.17% | 18.31% | 7.79% | 76.28% | 75.29% |
| 50 | Ultima Esperanza | 41.79% | 6.27% | 30.2% | 54.65% | 99.96% | |
| 51 | Magallanes | 31.45% | 3.41% | 24.9% | 38.19% | 99.74% | |
| 52 | Tierra del Fuego | 34.33% | 13.49% | 11.5% | 62.79% | 78.95% |
References
- Vandendijck, Y.; Faes, C.; Kirby, R.S.; Lawson, A.; Hens, N. Model-based inference for small area estimation with sampling weights. Spat. Stat. 2016, 18, 455–473. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Watjou, K.; Faes, C.; Lawson, A.; Kirby, R.S.; Aregay, M.; Carroll, R.; Vandendijck, Y. Spatial small area smoothing models for handling survey data with nonresponse. Stat. Med. 2017, 36, 3708–3745. [Google Scholar] [CrossRef] [PubMed]
- Raghunathan, T.E.; Xie, D.; Schenker, N.; Parsons, V.L.; Davis, W.W.; Dodd, K.W.; Feuer, E.J. Combining information from two surveys to estimate county-level prevalence rates of cancer risk factors and screening. J. Am. Stat. Assoc. 2007, 102, 474–486. [Google Scholar] [CrossRef] [Green Version]
- Mercer, L.; Wakefield, J.; Chen, C.; Lumley, T. A comparison of spatial smoothing methods for small area estimation with sampling weights. Spat. Stat. 2014, 8, 69–85. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, C.; Wakefield, J.; Lumley, T. The use of sampling weights in Bayesian hierarchical models for small area estimation. Spat. Patio Temporal Epidemiol. 2014, 11, 33–43. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kolaczyk, E.D. Multiscale statisticstal models for hierarchical spatal aggregation. Stat. Med. 2001, 33, 95–118. [Google Scholar]
- Louie, M.M. A multiscale method for disease mapping in spatial epidemiology. Stat. Med. 2006, 25, 1287–1306. [Google Scholar]
- Aregay, M.; Lawson, A.B.; Faes, C.; Kirby, R.S.; Carroll, R.; Watjou, K. Comparing multilevel and multiscale convolution models for small area aggregated health data. Spat. Spatio Temporal Epidemiol. 2017, 22, 39–49. [Google Scholar] [CrossRef] [PubMed]
- Aregay, M.; Lawson, A.B.; Faes, C.; Kirby, R.S. Bayesian multi-scale modeling for aggregated disease mapping data. Stat. Methods Med. Res. 2017, 26, 2726–2742. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lawson, A.B. Bayesian Disease Mapping: Hierarchical Modeling in Spatial Epidemiology, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Clark-Núñez, X. Compendio Estadístico; Instituto Nacional de Estadísticas Chile: Santiago, Chile, 2017.
- Salud, M.D. National Health Survey Chile 2009–2010, Results; Departamento de Epidemiología. Ministerio de Salud: Santiago, Chile, 2011.
- Besag, J. Bayesian image restoration with two applications in spatial statistics. Ann. Inst. Stat. Math. 1991, 43, 1–59. [Google Scholar] [CrossRef]
- Lunn, D.J.; Thomas, A.; Best, N.; Spiegelhalter, D. WinBUGS—A Bayesian modelling framework: Concepts, structure, and extensibility. Stat. Comput. 2000, 10, 325–337. [Google Scholar] [CrossRef]
- Tennekes, M. tmap: Thematic Maps. J. Stat. Softw. 2018, 84, 6. [Google Scholar] [CrossRef] [Green Version]
- Lunn, D.; Spiegelhalter, D.; Thomas, A.; Best, N. The BUGS project: Evolution, critique and future directions. Stat. Med. 2009, 28, 3049–3067. [Google Scholar] [CrossRef] [PubMed]
- Lunn, D.; Jackson, C.; Best, N.; Thomas, A.; Spiegelhalter, D. The BUGS Book: A Practical Introduction to Bayesian Analysis; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Brooks, S.P.; Gelman, A. General Methods for Monitoring Convergence of Iterative Simulations. J. Comput. Graph. Stat. 1998, 7, 434–455. [Google Scholar] [CrossRef] [Green Version]
- Gelman, A.; Rubin, D.B. Inference from Iterative Simulation Using Multiple Sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Lawson, A.B.; Browne, W.J.; Rodeiro, C.L.V. Disease Mapping with WinBUGS and MLwiN; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Spiegelhalter, D.; Best, N.; Carlin, B.P. Bayesian Deviance, the Effective Number of Parameters, and the Comparison of Arbitrarily Complex Models; Tech Report 98-009 Division of Biostatistics; University of Minnesota: Minneapolis, MN, USA, 1998. [Google Scholar]
- Lawson, A.B. Hotspot detection and clustering: Ways and means. Environ. Ecol. Stat. 2010, 17, 231–245. [Google Scholar] [CrossRef]
- Lawson, A.B.; Rotejanaprasert, C. Childhood brain cancer in Florida: A Bayesian clustering approach. Stat. Public Policy 2014, 1, 99–107. [Google Scholar] [CrossRef]
- Richardson, S.; Thomson, A.; Best, N.; Elliott, P. Interpreting Posterior Relative Risk Estimates in Disease-Mapping Studies. Environ. Health Perspect. 2004, 112, 1016–1025. [Google Scholar] [CrossRef] [PubMed]
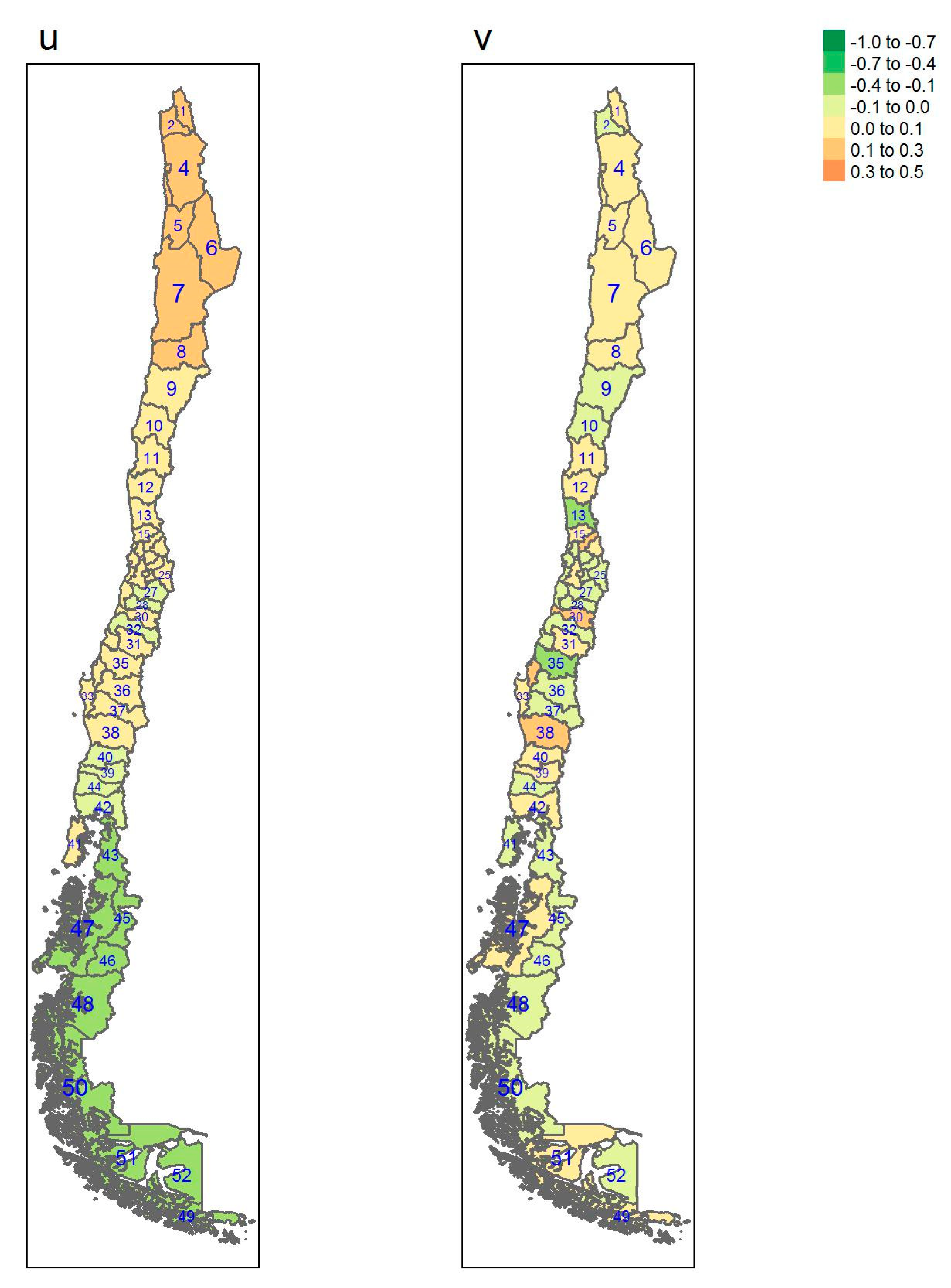
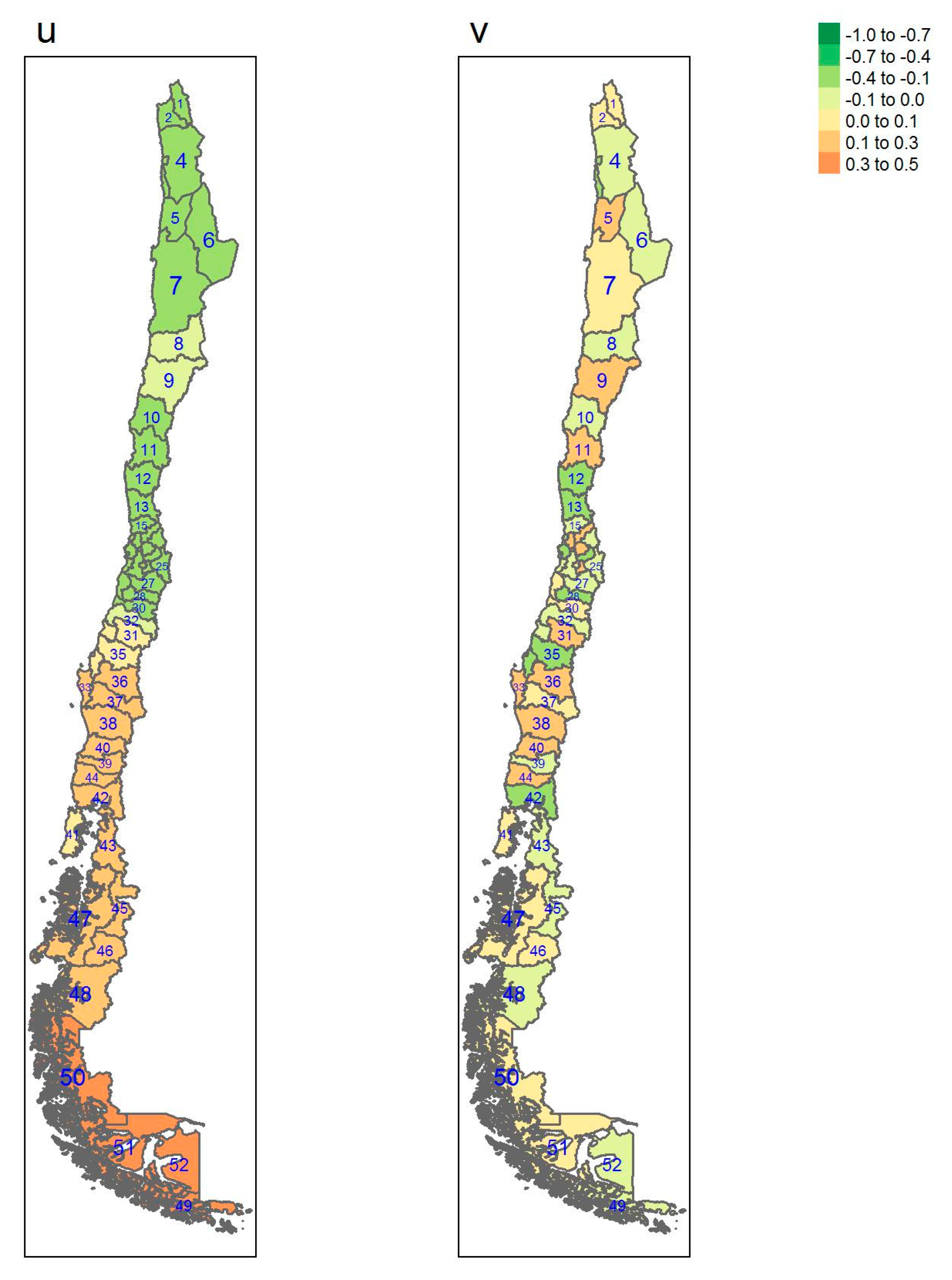
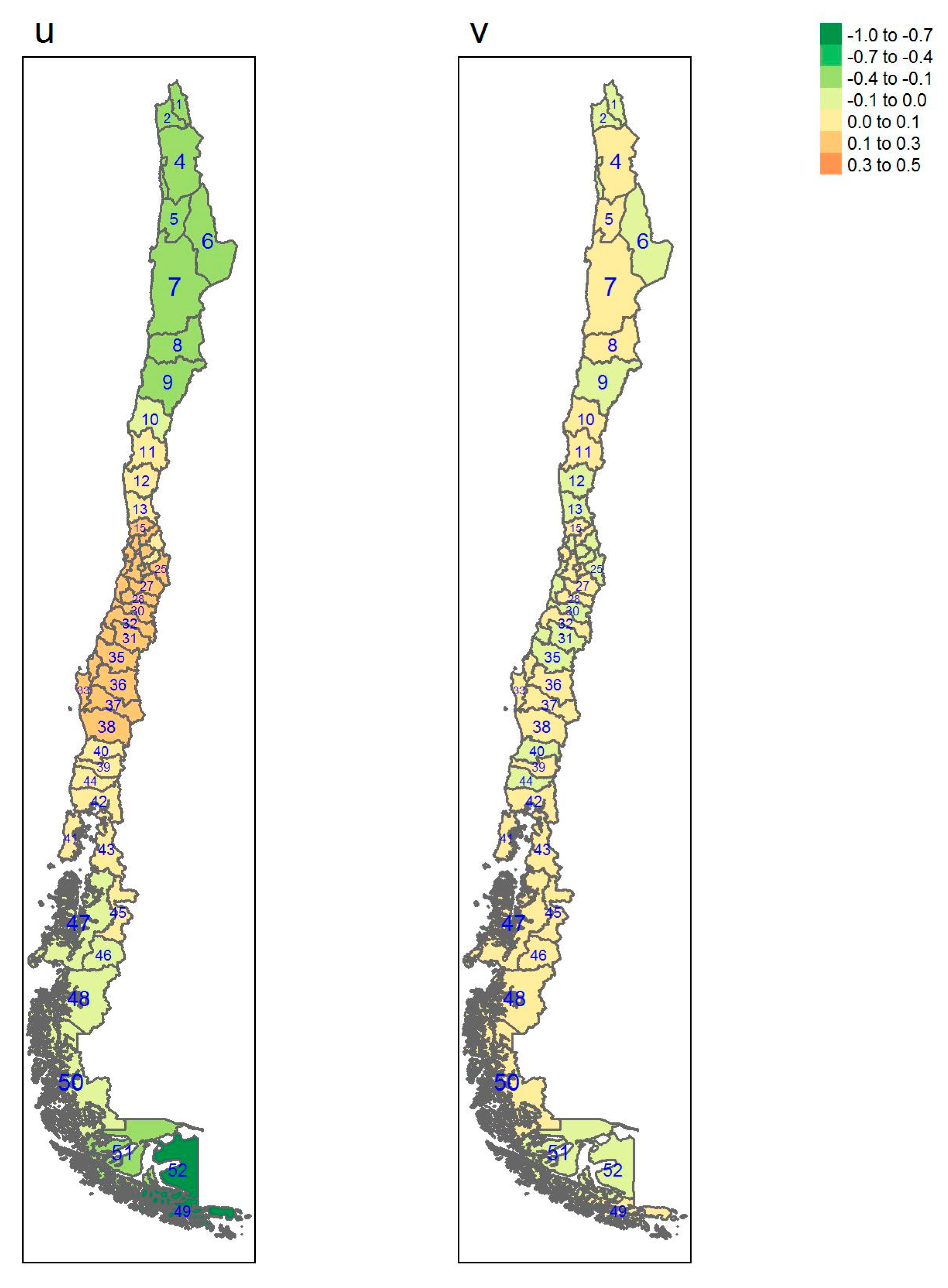
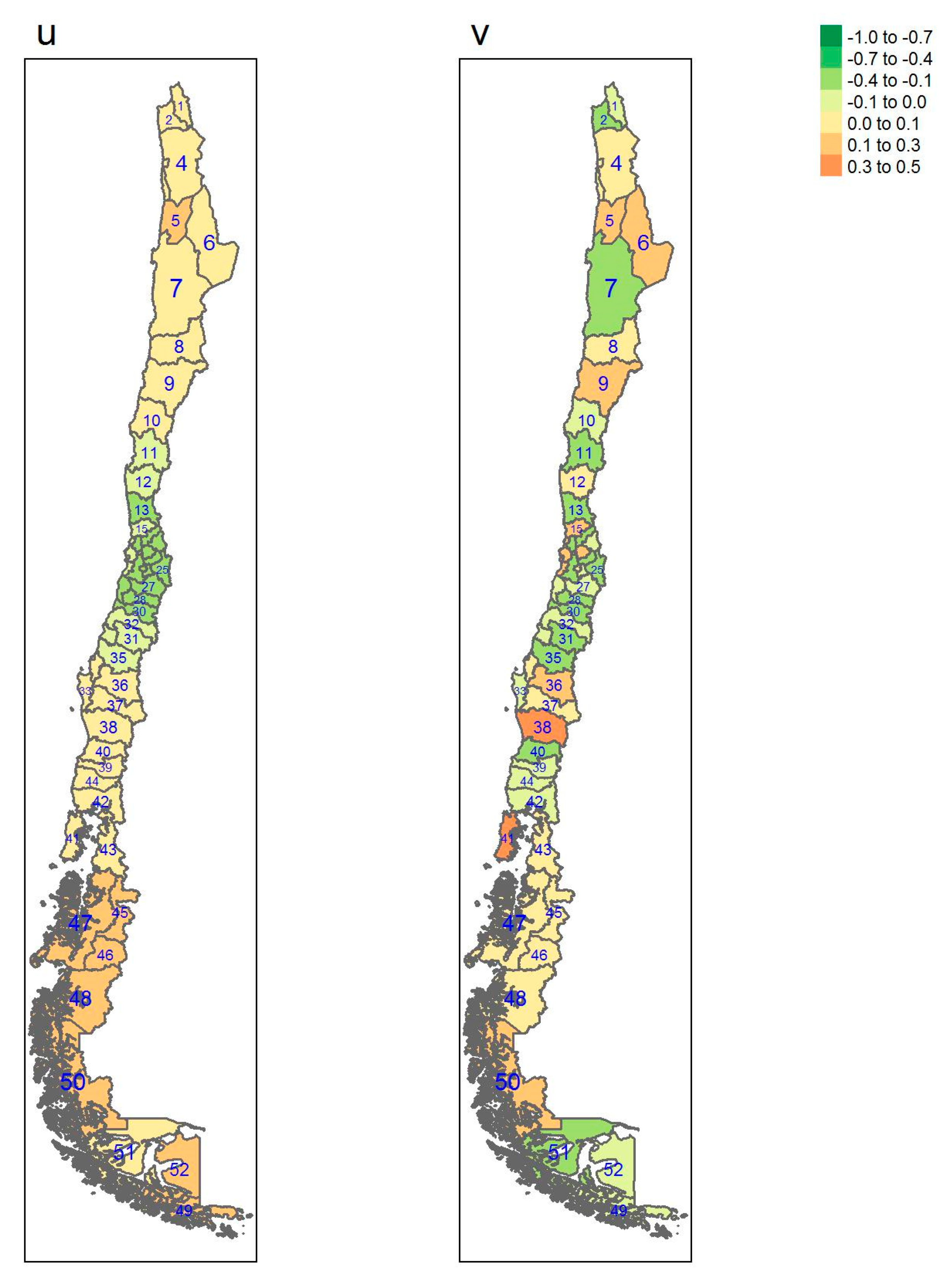
| Regions | Area (km2) a | Inhabitants/km2 a | GDP/Capita USD a | Provinces (Number) | Sampled |
|---|---|---|---|---|---|
| North | |||||
| Arica y Parinacota | 16,873 | 14.6 | 9848 | Parinacota (1) | 0 |
| Arica (2) | 311 | ||||
| Tarapacá | 42,226 | 8.4 | 27,604 | Iquique (3) | 289 |
| Tamarugal (4) | 24 | ||||
| Antofagasta | 126,049 | 5.1 | 63,402 | Tocopilla (5) | 34 |
| El Loa (6) | 88 | ||||
| Antofagasta (7) | 183 | ||||
| Atacama | 75,176 | 4.3 | 27,882 | Chañaral (8) | 0 |
| Copiapó (9) | 226 | ||||
| Huasco (10) | 81 | ||||
| Coquimbo | 40,580 | 19.6 | 14,800 | Elqui (11) | 185 |
| Limarí (12) | 72 | ||||
| Choapa (13) | 49 | ||||
| Center | |||||
| Valparaíso | 16,396 | 113.4 | 17,009 | San Antonio (14) | 34 |
| Petorca (15) | 17 | ||||
| Valparaíso (16) | 187 | ||||
| Quillota (17) | 48 | ||||
| Los Andes (18) | 25 | ||||
| San Felipe de Aconcagua (19) | 34 | ||||
| Metropolitana | 15,403 | 485.8 | 24,224 | Chacabuco (20) | 13 |
| Santiago (21) | 728 | ||||
| Melipilla (22) | 26 | ||||
| Talagante (23) | 18 | ||||
| Maipo (24) | 49 | ||||
| Cordillera (25) | 77 | ||||
| O’Higgins | 16,387 | 57 | 17,985 | Cardenal Caro (26) | 0 |
| Cachapoal (27) | 211 | ||||
| Colchagua (28) | 102 | ||||
| Maule | 30,296 | 34.9 | 10,620 | Cauquenes (29) | 19 |
| Curicó (30) | 85 | ||||
| Linares (31) | 108 | ||||
| Talca (32) | 139 | ||||
| Biobío | 37,069 | 57.8 | 12,582 | Arauco (33) | 51 |
| Concepción (34) | 134 | ||||
| Ñuble (35) | 57 | ||||
| Biobío (36) | 49 | ||||
| South | |||||
| Araucanía | 31,842 | 31.5 | 8,376 | Malleco (37) | 67 |
| Cautín (38) | 261 | ||||
| Los Ríos | 18,430 | 22.3 | 11,711 | Ranco (39) | 71 |
| Valdivia (40) | 228 | ||||
| Los Lagos | 48,584 | 17.6 | 13,335 | Chiloé (41) | 74 |
| Llanquihue (42) | 151 | ||||
| Palena (43) | 0 | ||||
| Osorno (44) | 92 | ||||
| Far South | |||||
| Aysén | 108,494 | 1 | 19,851 | Coyhaique (45) | 185 |
| General Carrera (46) | 98 | ||||
| Aysén (47) | 0 | ||||
| Capitan Prat (48) | 0 | ||||
| Magallanes | 1,382,291 | 0.1 | 18,447 | Antártica Chilena (49) | 0 |
| Última Esperanza (50) | 56 | ||||
| Magallanes (51) | 243 | ||||
| Tierra del Fuego (52) | 14 |
| Disease Outcome | Model | Parameters | Mean | SD | 2.50% | 97.50% |
|---|---|---|---|---|---|---|
| Diabetes | Individual level model | Intercept | −4.088 | 0.508 | −5.242 | −3.222 |
| Survey weight | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Age | 0.081 | 0.011 | 0.063 | 0.105 | ||
| Sex male | −0.027 | 0.149 | −0.348 | 0.266 | ||
| Age * Sex male | 0.006 | 0.009 | −0.010 | 0.023 | ||
| Aggregated model (per province) | Intercept | −2.365 | 0.336 | −3.063 | −1.722 | |
| Mean Survey weight | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Mean Age | 0.097 | 0.098 | −0.077 | 0.303 | ||
| Proportion Male | 0.375 | 0.791 | −1.161 | 2.051 | ||
| Mean age * proportion male | −0.112 | 0.231 | −0.599 | 0.304 | ||
| Obesity | Individual level model | Intercept | −1.182 | 0.174 | −1.557 | −0.894 |
| Survey weight | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Age | 0.029 | 0.005 | 0.020 | 0.041 | ||
| Sex male | −0.793 | 0.148 | −1.111 | −0.536 | ||
| Age * Sex male | −0.005 | 0.006 | −0.018 | 0.006 | ||
| Aggregated model (per province) | Intercept | −0.826 | 0.281 | −1.364 | −0.224 | |
| Mean Survey weight | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Mean Age | −0.008 | 0.068 | −0.148 | 0.129 | ||
| Proportion Male | −0.142 | 0.665 | −1.567 | 1.142 | ||
| Mean age * proportion male | 0.011 | 0.159 | -0.310 | 0.345 | ||
| Cholesterol | Individual level model | Intercept | −2.410 | 0.330 | −3.145 | −1.839 |
| Survey weight | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Age | 0.102 | 0.014 | 0.078 | 0.134 | ||
| Sex male | 1.118 | 0.227 | 0.709 | 1.608 | ||
| Age * Sex male | −0.005 | 0.010 | −0.025 | 0.013 | ||
| Aggregated model (per province) | Intercept | −0.895 | 0.340 | −1.586 | −0.204 | |
| Mean Survey weight | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Mean Age | 0.063 | 0.090 | −0.109 | 0.261 | ||
| Proportion Male | 0.144 | 0.812 | −1.517 | 1.813 | ||
| Mean age * proportion male | −0.043 | 0.213 | −0.511 | 0.363 | ||
| Hypertension | Individual level model | Intercept | −1.542 | 0.137 | −1.848 | −1.313 |
| Survey weight | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Age | 0.142 | 0.010 | 0.127 | 0.168 | ||
| Sex male | 0.501 | 0.118 | 0.274 | 0.734 | ||
| Age * Sex male | −0.022 | 0.007 | −0.037 | −0.008 | ||
| Aggregated model (per province) | Intercept | −0.890 | 0.253 | −1.396 | −0.424 | |
| Mean Survey weight | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Mean Age | 0.052 | 0.063 | −0.071 | 0.183 | ||
| Proportion Male | 0.742 | 0.612 | −0.345 | 1.982 | ||
| Mean age * proportion male | 0.044 | 0.149 | −0.268 | 0.339 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lawson, A.; Schritz, A.; Villarroel, L.; Aguayo, G.A. Multi-Scale Multivariate Models for Small Area Health Survey Data: A Chilean Example. Int. J. Environ. Res. Public Health 2020, 17, 1682. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph17051682
Lawson A, Schritz A, Villarroel L, Aguayo GA. Multi-Scale Multivariate Models for Small Area Health Survey Data: A Chilean Example. International Journal of Environmental Research and Public Health. 2020; 17(5):1682. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph17051682
Chicago/Turabian StyleLawson, Andrew, Anna Schritz, Luis Villarroel, and Gloria A. Aguayo. 2020. "Multi-Scale Multivariate Models for Small Area Health Survey Data: A Chilean Example" International Journal of Environmental Research and Public Health 17, no. 5: 1682. https://0-doi-org.brum.beds.ac.uk/10.3390/ijerph17051682





