Centroid Error Analysis of Beacon Tracking under Atmospheric Turbulence for Optical Communication Links
Abstract
:1. Introduction
2. System and Channel Model
2.1. Link Equation
2.2. Turbulence-Induced Beam Spreading
2.3. Log-Normal Tracking Channel
3. Centroid Error Analysis
3.1. Signal-to-Noise Ratio
3.2. Centroid Error under Atmospheric Turbulence
3.3. Fade Probability
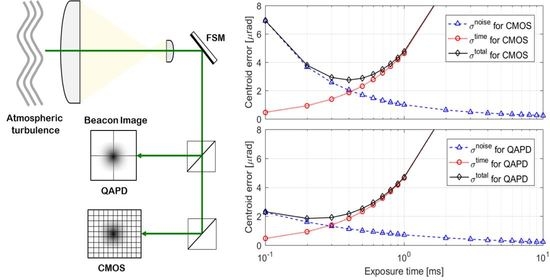
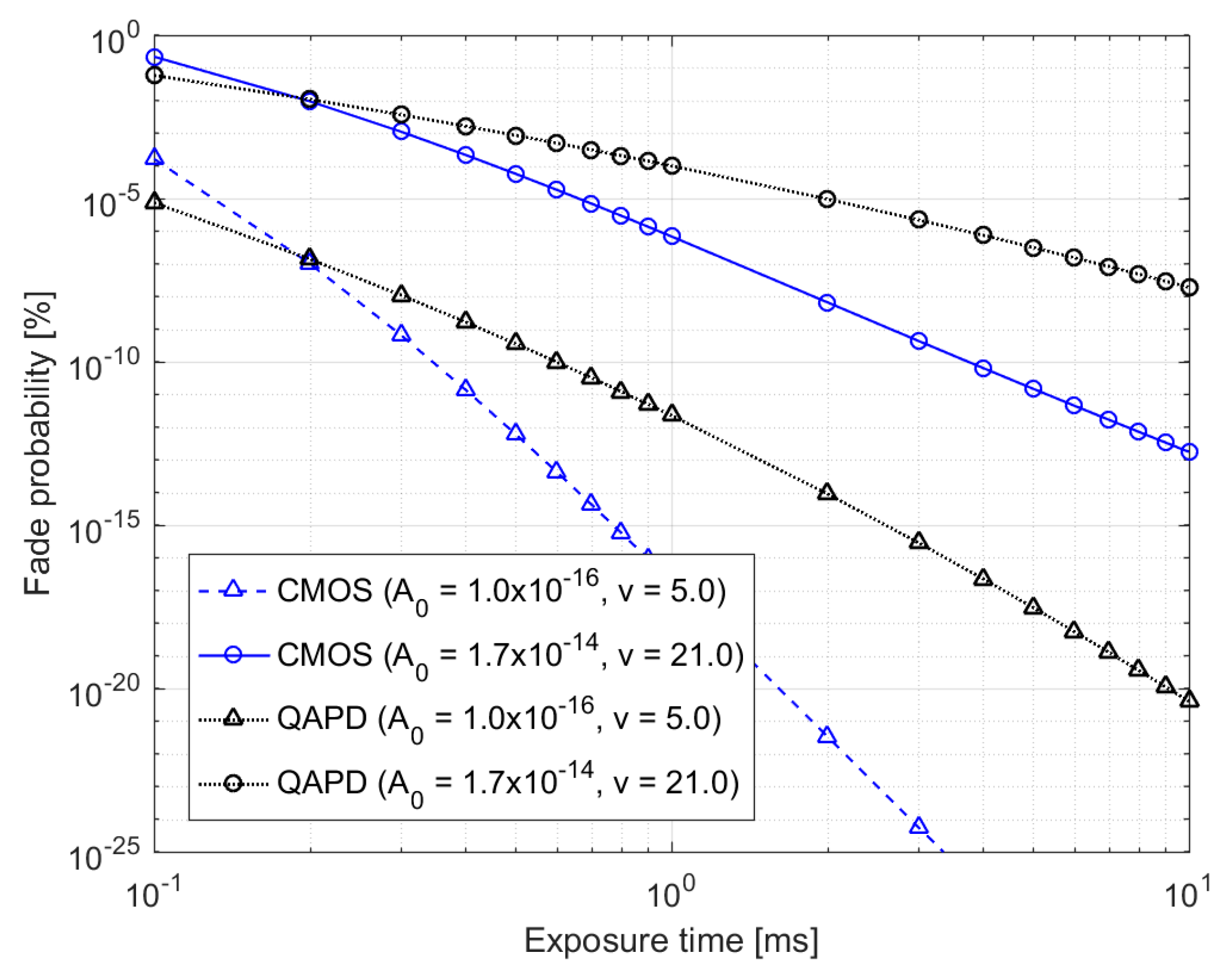
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Toyoshima, M.; Leeb, W.R.; Kunimori, H. Comparison of microwave and light wave communication systems in space application. Opt. Eng. 2005, 46, 1–12. [Google Scholar]
- Li, X.; Yu, S.; Ma, J. Analytical expression and optimization of spatial acquisition for intersatellite optical communications. Opt. Exp. 2011, 19, 2381–2390. [Google Scholar] [CrossRef]
- Ma, J.; Li, K.; Tan, L.; Yu, S.; Cao, Y. Performance analysis of satellite-to-ground downlink coherent optical communications with spatial diversity over Gamma- Gamma atmospheric turbulence. Appl. Opt. 2015, 54, 7575–7585. [Google Scholar] [CrossRef]
- Kaushal, H.; Kaddoum, G. Optical communication in space: Challenges and mitigation techniques. IEEE Commun. Surv. Tutor. 2016, 19, 57–96. [Google Scholar] [CrossRef] [Green Version]
- Lim, H.-C.; Park, J.U.; Choi, M.; Choi, C.-S.; Choi, J.-D.; Kim, J. Performance analysis of DPSK optical communication for LEO-to-Ground Relay link via a GEO Satellite. J. Astron. Space Sci. 2020, 37, 11–18. [Google Scholar]
- Meynants, G.; Lepage, G.; Bogaerts, J.; Vanhorebeek, G.; Wang, X. Limitations to the frame rate of high speed image sensors. In Proceedings of the 2009 International Image Sensor Workshop, Bergen, Norway, 22–28 June 2009. [Google Scholar]
- Cierny, O. Precision Closed-Loop Laser Pointing System for the Nanosatellite Optical Downlink Experiment. Master’s Thesis, Lulea University of Technology, Lulea, Sweden, 2017. [Google Scholar]
- Anugu, N.; Amorim, A.; Gordo, P.; Eisenhauer, F.; Pfuhl, O.; Haug, M.; Wieprecht, E.; Wiezorrek, E.; Lima, J.; Perrin, G.; et al. Methods for multiple-telescope beam imaging and guiding in the near-infrared. MNRAS 2018, 476, 459–468. [Google Scholar] [CrossRef] [Green Version]
- Ivan, I.A.; Ardeleanu, M.; Laurent, G.J. High dynamics and precision optical measurement using a position sensitive Detector (PSD) in reflection-mode: Application to 2D object tracking over a smart surface. Sensors 2012, 12, 16771–16784. [Google Scholar] [CrossRef] [PubMed]
- Toyoshima, M. Trends in satellite communications and the role of optical free-space communications. J. Opt. Netw. 2005, 4, 300–311. [Google Scholar] [CrossRef]
- Buske, I.; Riede, W. Sub-μrad laser beam tracking. In Technologies for Optical Countermeasures III, Proceedings of the Optics/Photonics in Security and Defence, Stockholm, Sweden, 11–14 September 2016; SPIE: Cardiff, Wales, UK, 2006. [Google Scholar]
- Hemmati, H. Near-Earth Laser Communications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Leeb, W. Space laser communications: Systems, technologies, and applications. Rev. Laser Eng. 2000, 28, 804–808. [Google Scholar] [CrossRef] [Green Version]
- Kaminow, I.P.; Li, T.; Willner, A.E. Optical Fiber Telecommunications VIB; Elsevier Inc.: Waltham, MA, USA, 2013. [Google Scholar]
- Carrasco-Casado, A.; Biswas, A.; Fields, R.; Grefenstette, B.; Harrison, F.; Sburlan, S.; Toyoshima, M. Optical communication on CubeSats—Enabling the next era in space science. In Proceedings of the 2017 IEEE International Conference on Space Optical Systems and Applications (ICSOS), Okinawa, Japan, 14–16 November 2017. [Google Scholar]
- Dios, F.; Rubio, J.A.; Rodriguez, A.; Comeron, A. Scintillation and beam-wander analysis in an optical ground station-satellite uplink. Appl. Opt. 2004, 43, 3866–3873. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cui, A. Analysis of angle of arrival fluctuations for optical wave’s propagation through weak anisotropic non-Kolmogorov turbulence. Opt. Exp. 2015, 23, 6313–6325. [Google Scholar] [CrossRef] [PubMed]
- Lim, H.-C.; Zhang, Z.-P.; Sung, K.-P.; Park, J.U.; Kim, S.; Choi, C.-S.; Choi, M. Modeling and analysis of an echo laser pulse waveform for the orientation determination of space debris. Remote Sens. 2020, 12, 1659. [Google Scholar] [CrossRef]
- Nguyen, T.N. Laser Beacon Tracking for Free-space Optical Communication on Small-Satellite Platforms in Low-Earth Orbit. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2013. [Google Scholar]
- Tyler, G.A.; Fried, D.L. Image-position error associated with a quadrant detector. J. Opt. Soc. Am. 1982, 72, 804–808. [Google Scholar] [CrossRef]
- Lee, S. Pointing accuracy improvement using model-based noise reduction method. In Free-Space Laser Communication Technologies XIV, Proceedings of the High-Power Lasers and Applications, San Jose, CA, USA, 20–25 January 2002; SPIE: Cardiff, Wales, UK, 2002. [Google Scholar]
- Hemmati, H. Deep Space Optical Communications; Jet Propulsion Laboratory: Pasadena, CA, USA, 2005. [Google Scholar]
- Sandler, D.G.; Stahl, S.; Angel, J.R.P.; Lloyd-Hart, M.; McCarthy, D. Adaptive optics for diffraction-limited infrared imaging with 8-m telescopes. J. Opt. Soc. Am. A 1994, 11, 925–945. [Google Scholar] [CrossRef]
- Colucci, D.; Lloyd-Hart, M.; Wittman, D.; Angel, R.; Ghez, A.; Mcleod, B. A reflective shack-hartmann wave-front sensor for adaptive optics. Publ. Astron. Soc. Pac. 1994, 106, 1104–1110. [Google Scholar] [CrossRef]
- Thomas, S.; Fusco, T.; Tokovinin, A.; Nicolle, M.; Michau, V.; Rousset, G. Comparison of centroid computation algorithms in a Shack-Hartmann sensor. Mon. Not. R. Astron. Soc. 2006, 371, 323–336. [Google Scholar] [CrossRef] [Green Version]
- Nightingale, A.M.; Gordeyev, S. Shack-Hartmann wavefront sensor image analysis: A comparison of centroiding methods and image-processing techniques. Opt. Eng. 2013, 52, 071413. [Google Scholar] [CrossRef]
- Li, C.; Xian, H.; Rao, C.; Jiang, W. Measuring statistical error of Shack–Hartmann wavefront sensor with discrete detector arrays. J. Mod. Opt. 2008, 55, 2243–2255. [Google Scholar] [CrossRef]
- Tsiftsis, T.A.; Sandalidis, H.G.; Karagiannidis, G.K.; Uysal, M. Optical wireless links with spatial diversity over strong atmospheric turbulence channels. IEEE Trans. Wirel. Commun. 2009, 8, 951–957. [Google Scholar] [CrossRef] [Green Version]
- Mishra, N.; Kumar, D.S. Outage analysis of relay assisted FSO systems over K-distribution turbulence channel. In Proceedings of the 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennei, India, 3–5 March 2016; pp. 2965–2967. [Google Scholar]
- Al-Habash, M.A.; Andrews, L.C.; Phillips, R.L. Mathematical model for the irradiance probability density function of a laser beam propagating through turbulent media. Opt. Eng. 2001, 40, 1554–1562. [Google Scholar] [CrossRef]
- Kiasaleh, K. Performance of APD-based, PPM free-space optical communication systems in atmospheric turbulence. IEEE Trans. Commun. 2005, 53, 1455–1461. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media; SPIE Press: Bellingham, WA, USA, 2005. [Google Scholar]
- Nistazakis, H.E.; Tsiftsis, T.A.; Tombras, G.S. Performance analysis of free-space optical communication systems over atmospheric turbulence channels. IET Commun. 2009, 3, 1402–1409. [Google Scholar] [CrossRef]
- Johnson, S.E. Effect of target surface orientation on the range precision of laser detection and ranging systems. J. Appl. Remote Sens. 2009, 3, 033564. [Google Scholar] [CrossRef]
- Degnan, J.J. Milimeter accuracy satellite laser ranging: A review. Geodyn. Ser. 1993, 25, 133–162. [Google Scholar]
- Shen, H.; Yu, L.; Fan, C. Temporal spectrum of atmospheric scintillation and the effects of aperture averaging and time averaging. Opt. Commun. 2014, 330, 160–164. [Google Scholar] [CrossRef]
- Ghassemlooy, Z.; Popoola, W.; Rajbhandari, S. Optical Wireless Communications: System and Channel Modelling with MATLAB.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Gunderson, K.; Thomas, N.; Rohner, M. A Laser altimeter performance model and its application to BELA. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3308–3319. [Google Scholar] [CrossRef]
- Ma, X.; Rao, C.; Zheng, H. Error analysis of CCD-based point source centroid computation under the background light. Opt. Exp. 2009, 17, 8525–8541. [Google Scholar] [CrossRef]
- Barry, J.D.; Mecherle, G.S. Beam pointing error as a significant design parameter for satellite-borne, free-space optical communication systems. Opt. Eng. 1985, 24, 1049–1054. [Google Scholar] [CrossRef]
- Tyler, G.A. Bandwidth considerations for tracking through turbulence. J. Opt. Soc. Am. A 1994, 11, 358–367. [Google Scholar] [CrossRef]
- Roddier, R. The effects of atmospheric turbulence in optical astronomy. Prog. Opt. 1981, 19, 281–376. [Google Scholar]
- Riesing, K.M. Development of a Pointing, Acquisition, and Tracking System for a Nanosatellite Laser Communication Module. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2013. [Google Scholar]
- Toyoda, M.; Araki, K.; Suzuki, Y. Measurement of the characteristics of a quadrant avalanche photodiode and its application to a laser tracking system. Opt. Eng. 2002, 41, 145–149. [Google Scholar] [CrossRef]
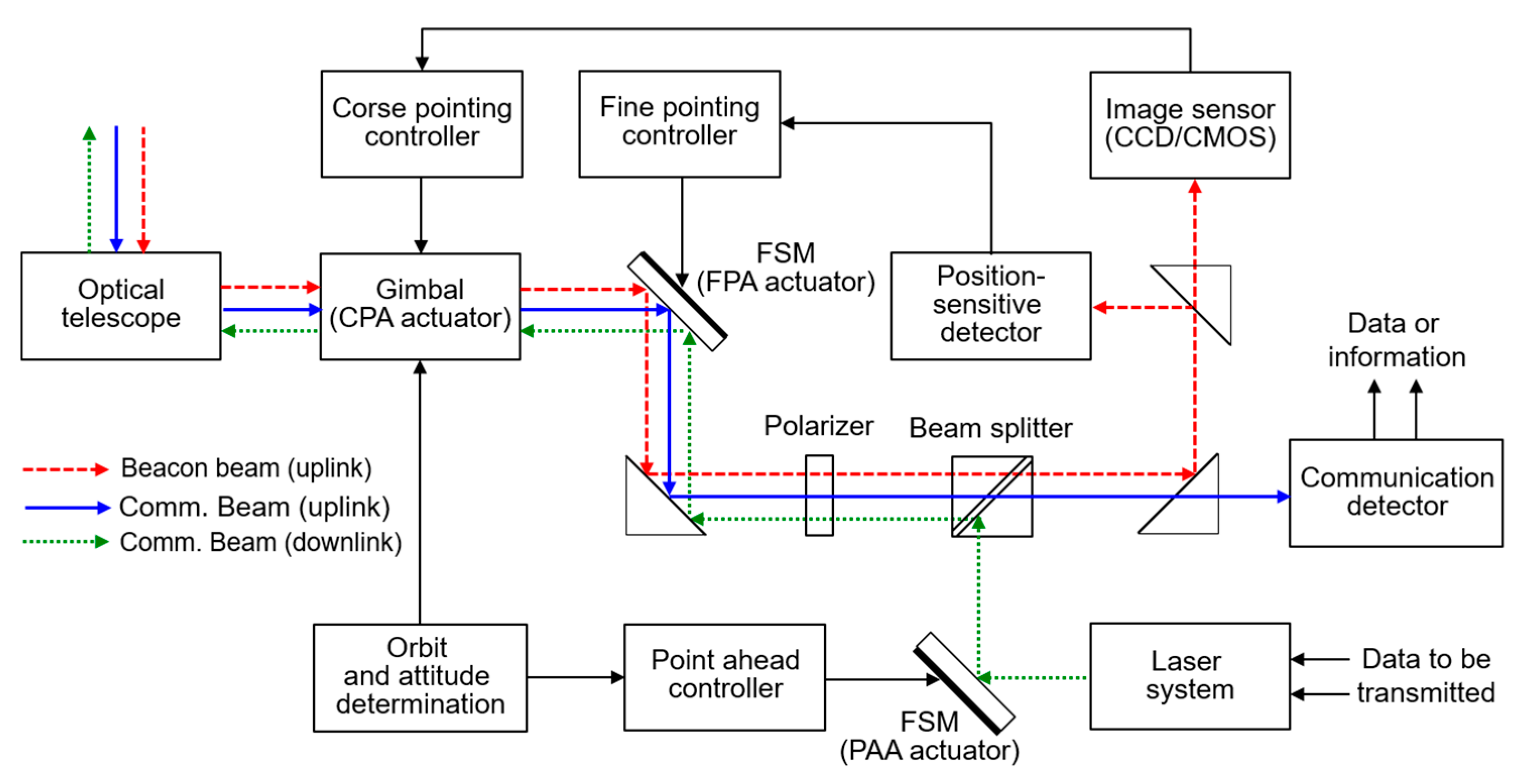

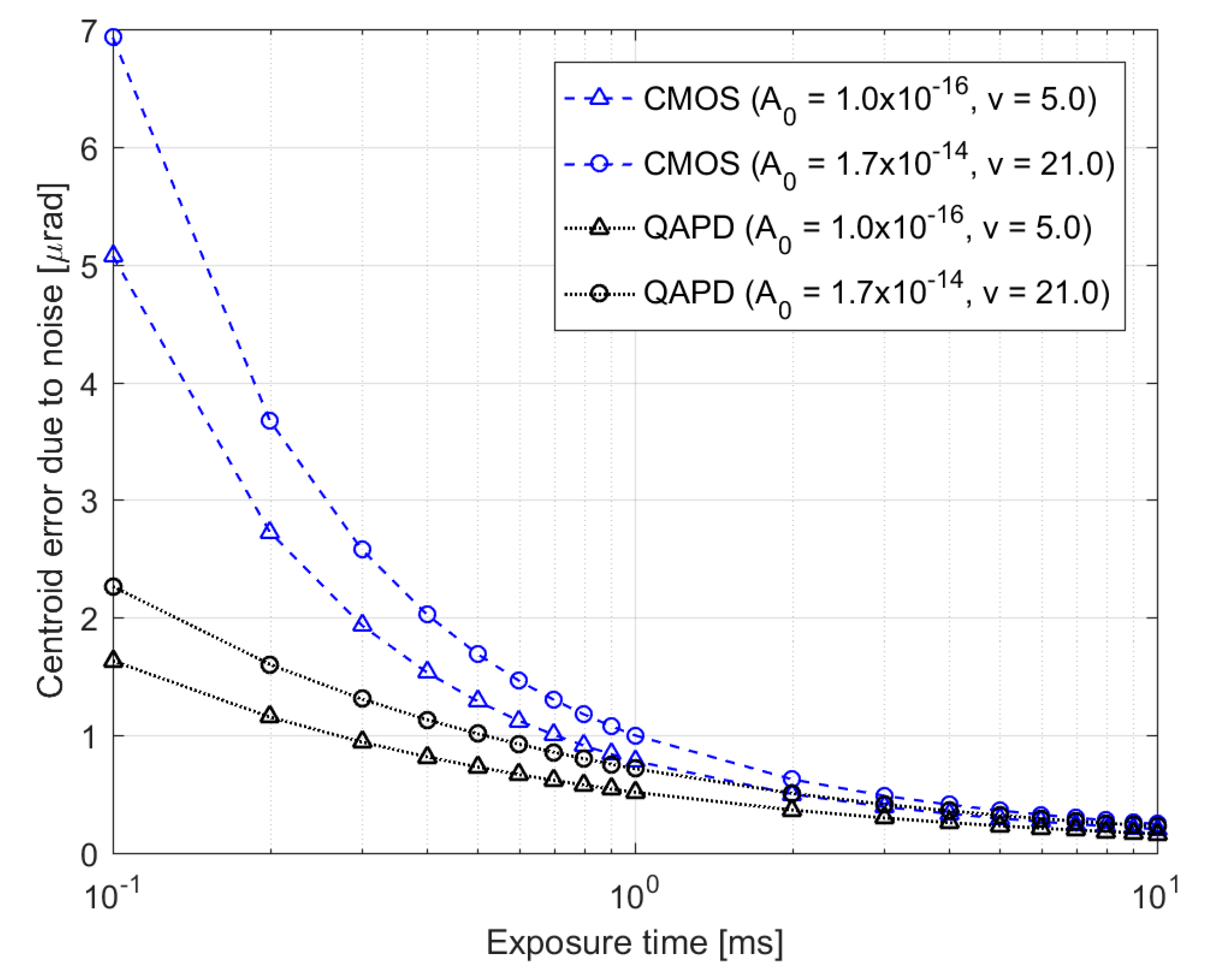


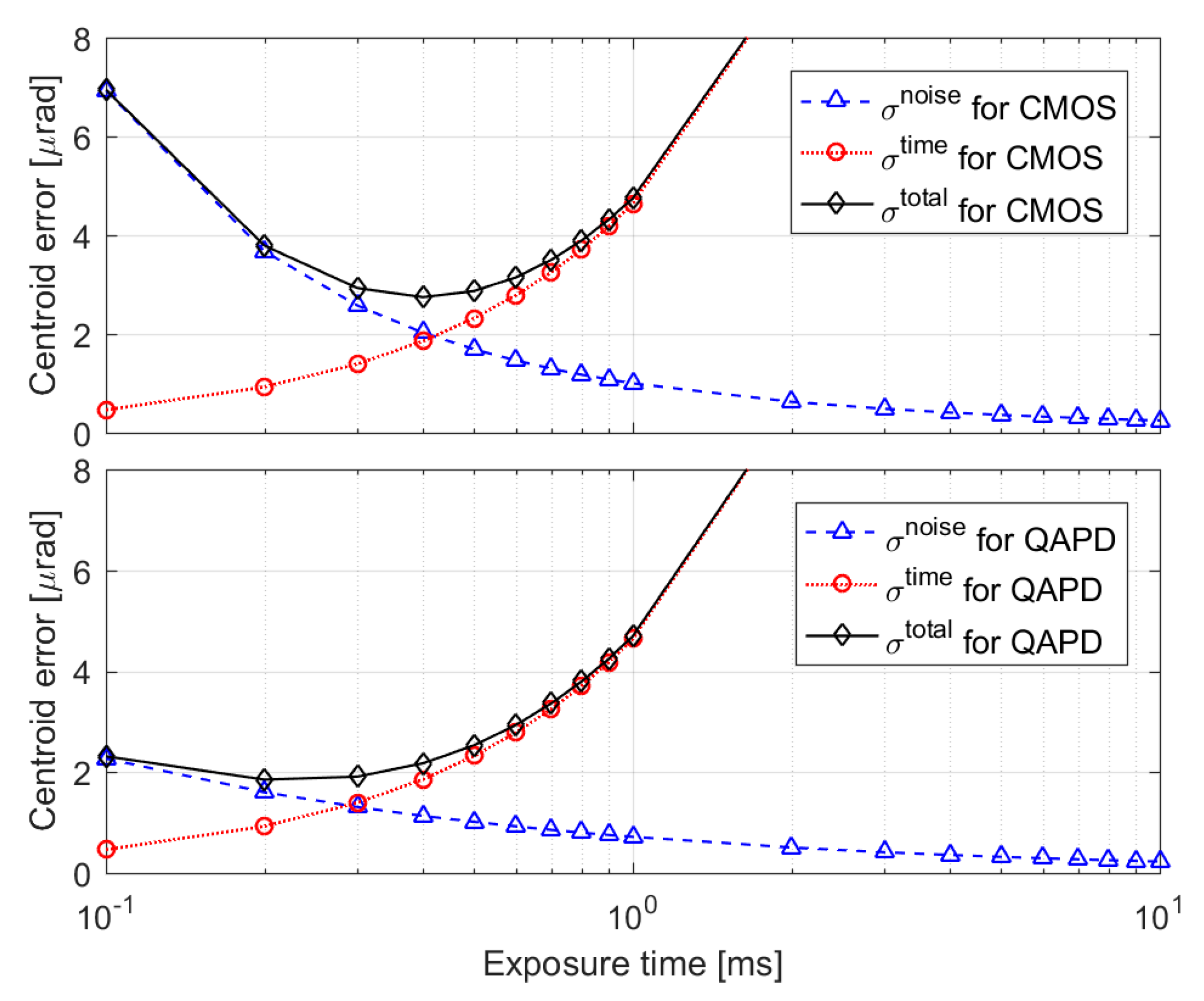
| Parameter | Symbol | CMOS | QAPD |
|---|---|---|---|
| Rx aperture | 2.5 cm | ||
| Rx optical efficiency | 0.68 | ||
| Optical filter bandwidth | 4 nm | ||
| Quantum efficiency | 0.15 | 0.7 | |
| Focal length | 4.1 cm | 7.9 cm | |
| Active pixels | 2592 × 1944 | 4 | |
| Active area | 5.7 × 4.28 mm2 | 1.77 mm2 | |
| Pixel size | 2.2 × 2.2 μm2 | 0.44 mm2 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, H.-C.; Choi, C.-S.; Sung, K.-P.; Park, J.-U.; Choi, M. Centroid Error Analysis of Beacon Tracking under Atmospheric Turbulence for Optical Communication Links. Remote Sens. 2021, 13, 1931. https://0-doi-org.brum.beds.ac.uk/10.3390/rs13101931
Lim H-C, Choi C-S, Sung K-P, Park J-U, Choi M. Centroid Error Analysis of Beacon Tracking under Atmospheric Turbulence for Optical Communication Links. Remote Sensing. 2021; 13(10):1931. https://0-doi-org.brum.beds.ac.uk/10.3390/rs13101931
Chicago/Turabian StyleLim, Hyung-Chul, Chul-Sung Choi, Ki-Pyoung Sung, Jong-Uk Park, and Mansoo Choi. 2021. "Centroid Error Analysis of Beacon Tracking under Atmospheric Turbulence for Optical Communication Links" Remote Sensing 13, no. 10: 1931. https://0-doi-org.brum.beds.ac.uk/10.3390/rs13101931