1. Introduction
Spatiotemporal big data analysis is a hot topic in the field of geospatial information. Recently, deep learning has provided a solution for the pattern recognition of a single type of geospatial data, such as land-use classification based on optical remote sensing image data [
1,
2,
3]. However, it is typically necessary to use multiple data types. For example, in the analysis of earthquake precursors, the data concerning the time and space of earthquakes include atmospheric anomalies and historical earthquakes. Multi-type geospatial information integration analysis challenges the existing spatiotemporal data organization model and the analysis model based on deep learning.
Before the popularization of big data, the standard methods primarily included earthquake warnings based on earthquake mechanisms, mechanical models, and earthquake precursor analysis using statistics. For example, UCERF [
4], which established a fault model for California in the United States, is based on earthquake mechanisms. The attributes of each study-area raster grid cell are a series of mechanical and statistical characteristics based on the fault model. However, UCERF only provides the possibility of earthquake occurrence on a very rough time scale (~10 years), showing the complexity of earthquake mechanical mechanisms. By analyzing the spatiotemporal correlation between earthquakes and their possible precursors, the relationship between them was established and then an earthquake warning system was developed. The earliest work in this field was the Gutenberg–Richter (GR) law [
5]. This model gives the relationship between a certain magnitude threshold and the total number of earthquakes with magnitudes exceeding the threshold in a specific region and time. The GR law shows a strong correlation between earthquakes and historical earthquakes, thus the historical earthquakes can be the precursors of new earthquakes in the same region. The parameter b of the GR law is an important statistical feature. Some follow-up studies have further designed statistical features on the basis of parameter b, assigning these statistical features to each grid cell on the basis of raster data organization and used historical earthquakes to predict new earthquakes [
6] or used the data of the main shock to predict possible aftershocks [
7].
Some researchers have also combined a model based on earthquake mechanisms with a model based on statistics. The representative literature in this field is Zhou et al. [
8]. Based on historical earthquake data, the author carried out further feature engineering on the earthquake catalog with a dynamic model. Taking the average value of the earthquake time interval and earthquake magnitude as the input information, statistical machine learning methods, such as the support vector machine (SVM), can be used for earthquake early warning. In recent years, studies of earthquake prediction based on statistics have found that the geographical phenomena with strong spatiotemporal correlation with earthquakes include not only historical earthquakes but also geothermal anomalies [
9], geomagnetic anomalies [
10], and atmospheric anomalies [
11]. However, unlike earthquakes and historical earthquakes, the statistical relationship between these spatiotemporal phenomena and earthquakes has not been established as the general formula of the GR law, which is not suitable for the raster data model that requires statistical characteristics as grid attributes. The data are arranged according to a hierarchical organizational model based on a vector point model. Therefore, these studies primarily analyze the original earthquake and its precursor data, and the data organization is based on the hierarchical organization model of the vector point.
Research on earthquake prediction based on the traditional non-deep learning analysis model shows a highly non-linear spatiotemporal correlation between earthquake precursors and earthquakes, and a more complex analysis model can improve earthquake early warning reliability. Therefore, in recent years, with the emergence of deep learning with higher model complexity, many studies are exploring deep learning for earthquake prediction. In a study by Alves [
12] based on historical earthquake data, some indexes, such as the moving average of historical earthquake times, are designed as inputs and the fully connected neural network (FCNN) is used for earthquake prediction. The predicted earthquake was accurate to the space area with a longitude–latitude span of approximately 2° and a time window with a time span of approximately one year. The difference between the predicted and actual magnitudes was approximately a value of one. Based on historical earthquakes and the GR law, various characteristics reflecting seismic mechanical properties, energy, and time distribution were designed as inputs in studies by Asencio-Cortés et al. [
13] and Reyes et al. [
14], and FCNN was used for earthquake prediction. The desired prediction concerned whether two cities in Chile would have an earthquake of a magnitude of >4.5 in a five-day time window. Devries et al. [
15] did not use historical earthquakes but designed a series of mechanical characteristics based on the fault zone model as the input of the FCNN to predict aftershocks in each 5 km × 5 km sub-region of areas where major earthquakes have occurred. The prediction accuracy index of the experimental results reached an AUC of 0.85. In earthquake predictions using FCNN, the researchers primarily studied the relationship between earthquakes and historical data and used a hierarchical model based on vector point objects to organize the spatiotemporal data of earthquakes. Mosavi et al. [
16] used historical earthquake data from Iran and a radial basis function neural network to predict the time interval of large earthquakes in this dataset. Asencio-Cortés et al. [
17] used historical earthquake data from Japan and FCNN to predict whether an earthquake with a magnitude of >5 would occur within seven days. The results showed that the prediction accuracy of FCNN was higher than that of some traditional machine learning methods, such as SVM and K-nearest neighbor.
In a study by Panakkat and Adeli [
18], in addition to FCNN, the input historical earthquake data were organized and entered into the recurrent neural network (RNN) according to the time sequence to predict the maximum earthquake magnitude likely to occur in the next month at specific locations. The experiment revealed that RNN’s prediction ability was better than FCNN’s in this case. The seismic features used by Panakkat and Adeli [
18], Asencio-Cortés et al. [
13], and Reyes et al. [
14] are different. Martínez-Álvarez et al. [
19] analyzed the importance of different features in earthquake prediction using FCNN and seismic data from Chile and the Iberian Peninsula. It was found that these features had a similar order of importance in the two different study areas and the feature based on the GR law was the most important. In a study by Asim and Martínez-Álvarez [
20], historical earthquakes and RNN were used to predict whether earthquakes with magnitudes of >5.5 would occur within the next month in the Hindu Kush Mountains and the prediction accuracy reached 71% in the test set. In Wang et al. [
21], historical earthquake data were input into a long short-term memory (LSTM) network, that is, an improved RNN. Earthquake prediction was based on two simulation datasets. The above-mentioned earthquake prediction using RNN was primarily based on the hierarchical model of vector point objects to organize the spatiotemporal data of earthquakes. Huang et al. [
22] organized the historical earthquake data of the entire Taiwan Province using the raster model. The study area was divided into 256 × 256 square sub-regions. The accumulated data of every 120 days formed a 256 × 256 raster map and the value of each raster grid represented the maximum magnitude of the corresponding sub-region over the past 120 days. Convolution neural networks (CNNs) can predict whether earthquakes with magnitudes of >6 will occur in the Taiwan Province over the next 30 days. The R-score was used to evaluate the prediction accuracy and the R-score of the prediction model was approximately 0.3. Although far from ideal, the accuracy of the earthquake prediction (R-score is close to 1) is significantly higher than that obtained using random input data (R-score is 0.065).
Compared with the use of historical earthquakes to predict new earthquakes, research on earthquake prediction based on atmospheric anomalies is still in its infancy and primarily focuses on the statistical correlation between different types of atmospheric anomalies and earthquakes. Shah et al. [
23] conducted a correlation analysis between three large earthquakes (magnitude of 6 or above) in Pakistan and Iran, and the atmospheric observation data at that time. It was found that there were significant anomalies in different atmospheric parameters, including long-wave radiation, surface temperature, and nitrogen dioxide, which could be observed in a minimum of 5 days and a maximum of 21 days before the earthquake. However, the time difference between the anomalies and earthquake occurrence shows conspicuous differences in different areas. In Fujiwara et al. [
11], 29 earthquakes with magnitudes of >4.8 in Japan and the atmospheric observation data at that time were analyzed, and it was found that these earthquakes had a strong correlation with the electromagnetic wave anomalies in the five days before the earthquake.
Deep learning can automatically learn and extract characteristics from the original data and CNN, a representative deep learning model, uses a spatial window to explore the spatial association information between data [
24], which is suitable for grid data. In earthquake precursor analysis, deep learning analysis of the earthquake precursor based on multi-layer and multi-source spatial data is in its early stages and there is little related research. The deep learning frontier for multi-layer data is concentrated around traditional computer vision and remote sensing data analysis. With non-uniform multi-layer input gridded data, the existing methods primarily design the branch structure of the CNN, in which each branch network processes a layer and the results of different branches are summarized at the neural network’s end. Land-use classification based on multi-source remote sensing data [
25,
26] is a typical challenge. Chen et al. [
27] designed a CNN with two branches to process and integrate multispectral optical remote sensing image data and (light detection and ranging) LiDAR data. Xu et al. [
28] designed a CNN with three branches to process and integrate the hyperspectral remote sensing image, digital elevation model, and LiDAR data for land-use classification. Ienco et al. [
29] designed a CNN with four branches to fuse the multi-temporal remote sensing image data of Sentinel-1 and Sentinel-2 satellites. In Hang et al. [
30], a CNN with two branches was designed to fuse hyperspectral and LiDAR remote sensing images, and parameter-sharing technology was used for some parameters of the two branches, reducing the complexity of the model. Hong et al. [
31] summarized the design ideas of branching neural networks in several studies and proposed that different branches of the neural network adopt different architectures. For example, one branch could use FCNN and the other branch could use CNN.
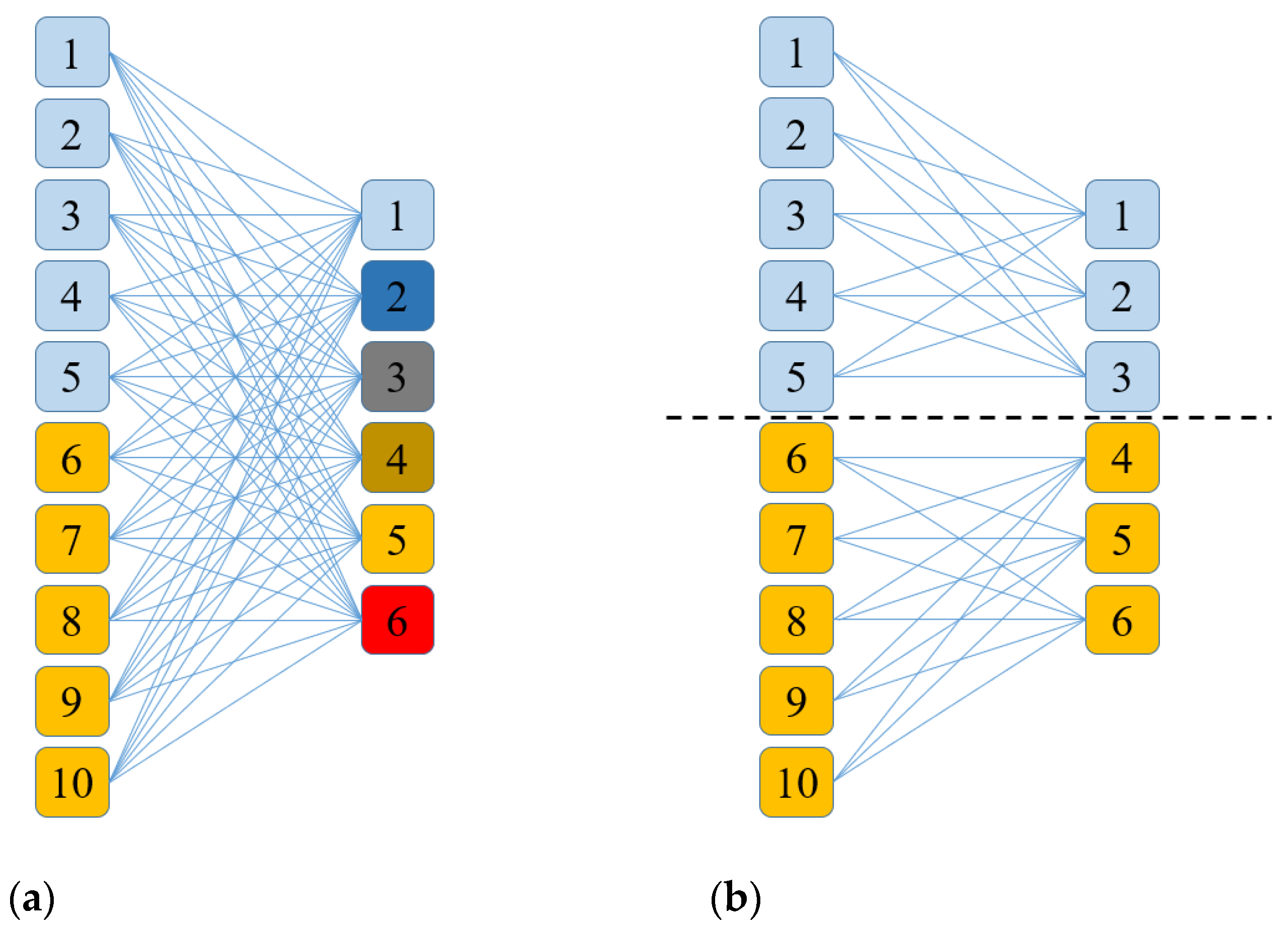
For the branching CNN for multi-layer data integration, the data matrix and data unit sizes can differ on different branches and there is no direct superposition between layer features on different branches. However, the structure of a branching neural network is complex. More data layers mean more branches and a more complex model. Therefore, the branch network is unsuitable for earthquake prediction involving multiple data types. Compared with a branching neural network, the structure of a neural network with only one backbone is simple and the costs of both network design and calculation are low. However, using a single backbone neural network for multi-layer data analysis requires overcoming the problems of correspondence between the different layers in data organization and feature integration of multi-source data in the analysis. Regarding data organization, for multi-layer data, the input data of CNN is block data with a unified matrix structure (layer number C, image height H, image width W). The data matrix formed by the different layers should be consistent in the H and W dimensions. Therefore, in terms of data organization, the gridding of different vector layers requires the different layers to form a unified H and W. This creates a relationship between the upper and lower layers, and a single-layer data slice can then form a multi-layer data block. Concerning data analysis, the calculation results of different layers are superimposed in the CNN. When different layers represent different data types, the data of different layers have different meanings. Therefore, this type of direct superposition is meaningless and should be avoided.
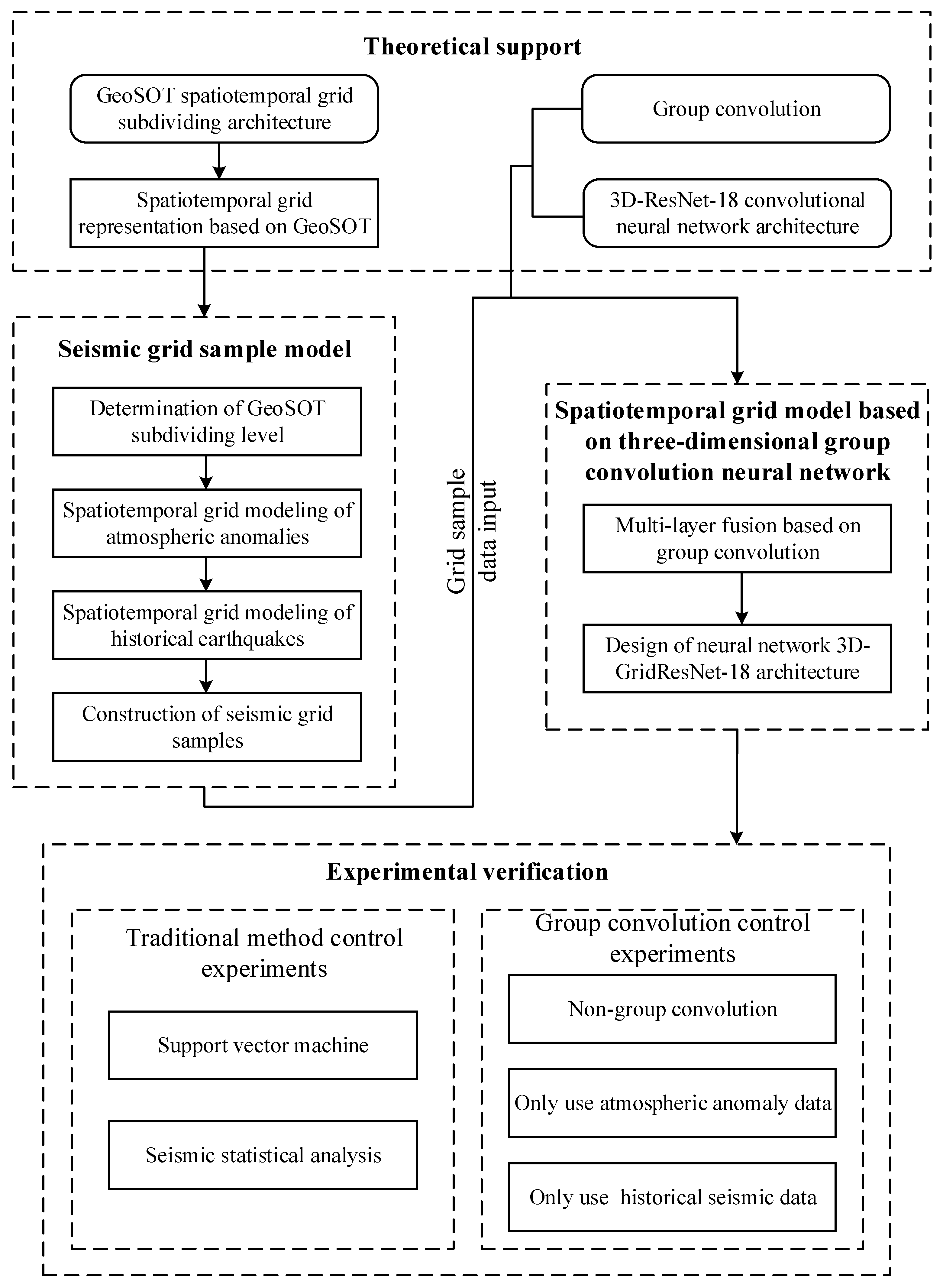
In summary, this study focuses on the deep learning of multiple spatial information in spatiotemporal big data, as shown in
Figure 1. For earthquake warnings, this study proposes a seismic grid sample model (SGSM) organizing multiple single-layer data slice spatial information data to form a multi-layer data block with a consistent data structure oriented to the deep learning model. Furthermore, the study proposes a spatiotemporal grid model based on a three-dimensional group convolution neural network (3DGCNN-SGM) to improve the learning effect of the integration analysis of multiple spatial information.
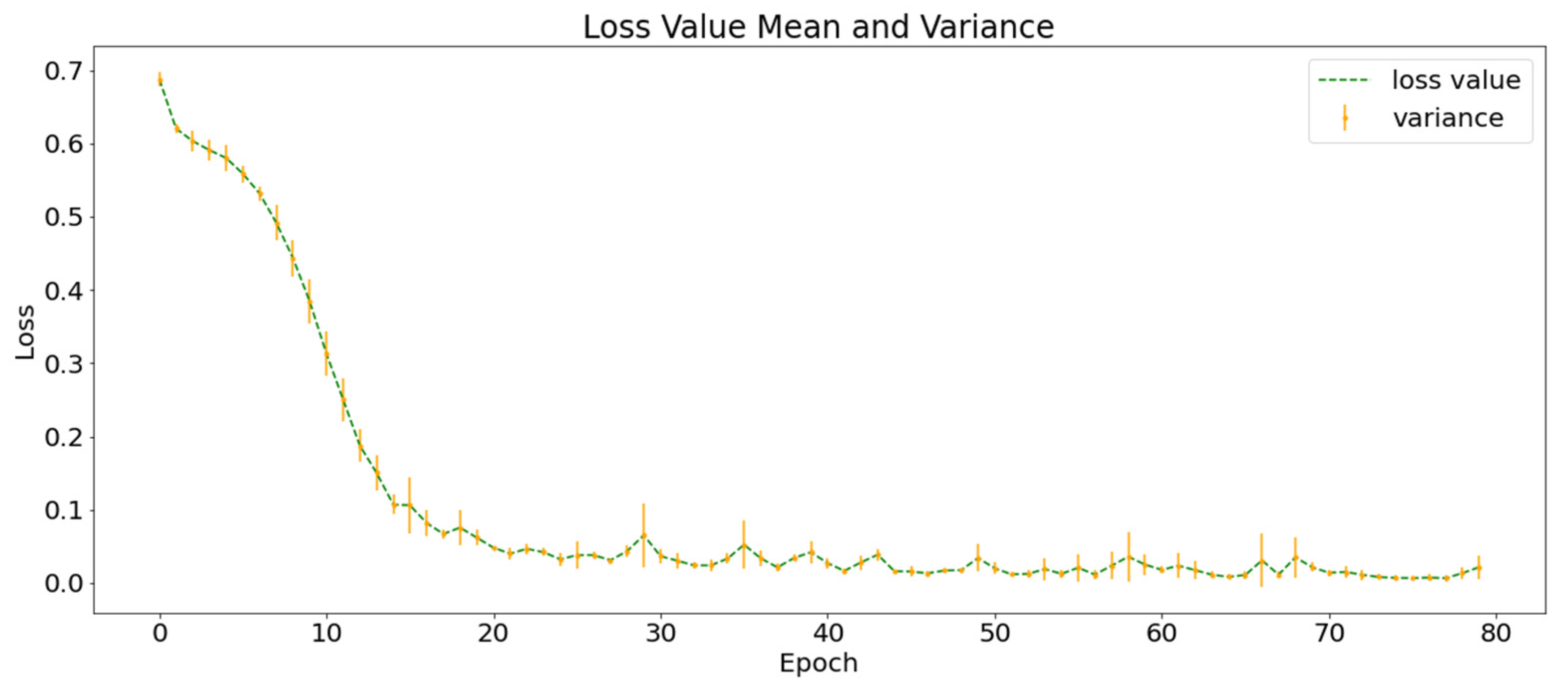
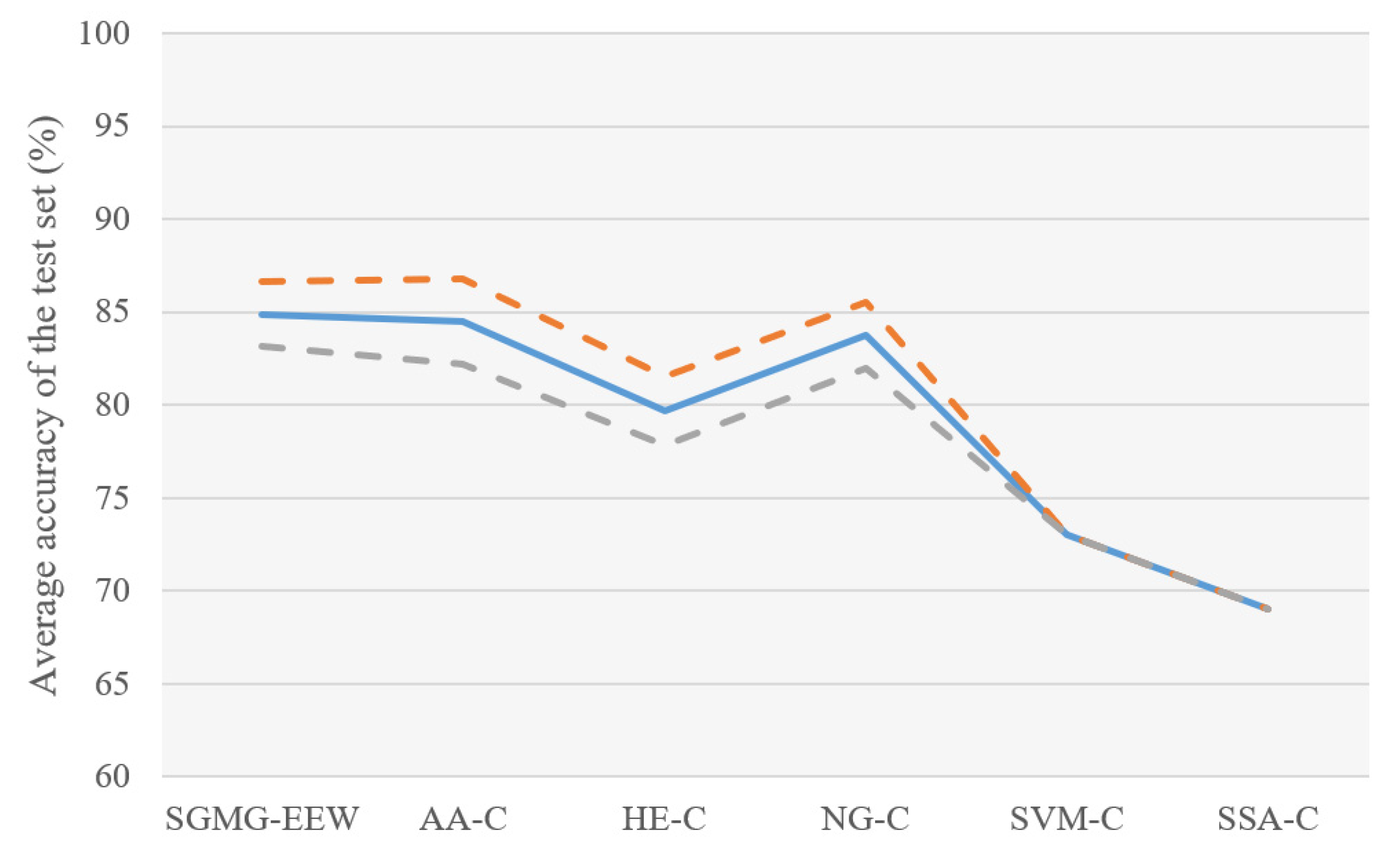
4. Discussion
As shown in
Figure 11, the SGMG-EEW has the highest
(84.89 ± 1.76%). It uses multi-source spatiotemporal data (atmospheric anomalies and historical earthquakes) and group convolution, as well as strongly demonstrates the effectiveness of SGSM and 3DGCNN-SGM.
The of AA-C (84.47 ± 2.30%) > of NG-C (83.74 ± 1.76%) > of HE-C (79.67 ± 1.85%); that is, the accuracy of the classification using traditional convolution was between those of the two control groups using one type of data. This shows that the superposition calculation of all layers in the traditional convolution is likely to negatively impact the classification and supports the improvement of group convolution, which is conducive to multi-layer data integration in deep learning.
The of SVM-C was lower than that of the three control groups using deep learning (AA-C, HE-C and NG-C). The results showed that the complex spatiotemporal correlation between earthquake and precursor data is probably behind the low recall rate of earthquake warnings. The of SSA-C (the control group without SGSM) was lower than that of the four control groups using SGSM, supporting the necessity of SGSM. In addition, the experimental results of SGMG-EEW, AA-C, HE-C, and NG-C show that SGSM is a suitable deep learning-oriented geographic information data organization model. Indeed, SGSM not only supports the deep learning of traditional single-layer data but also the deep learning of multi-layer data.
Figure 12 shows the earthquake prediction results of the trained SGMG-EEW on 21 July 2019 and 22 July 2019. Notably, the data for these two days do not belong to the dataset and have not been trained and tested. The results show that earthquake reports are missing in the prediction, consistent with the higher accuracy rate and lower recall rate in the experiment. However, although the accuracy of the earthquake prediction on the test set can reach 85%, the prediction accuracy of the new data is not ideal and there is still room for improvement.