Computational Analysis of Air Lubrication System for Commercial Shipping and Impacts on Fuel Consumption
Abstract
:1. Introduction
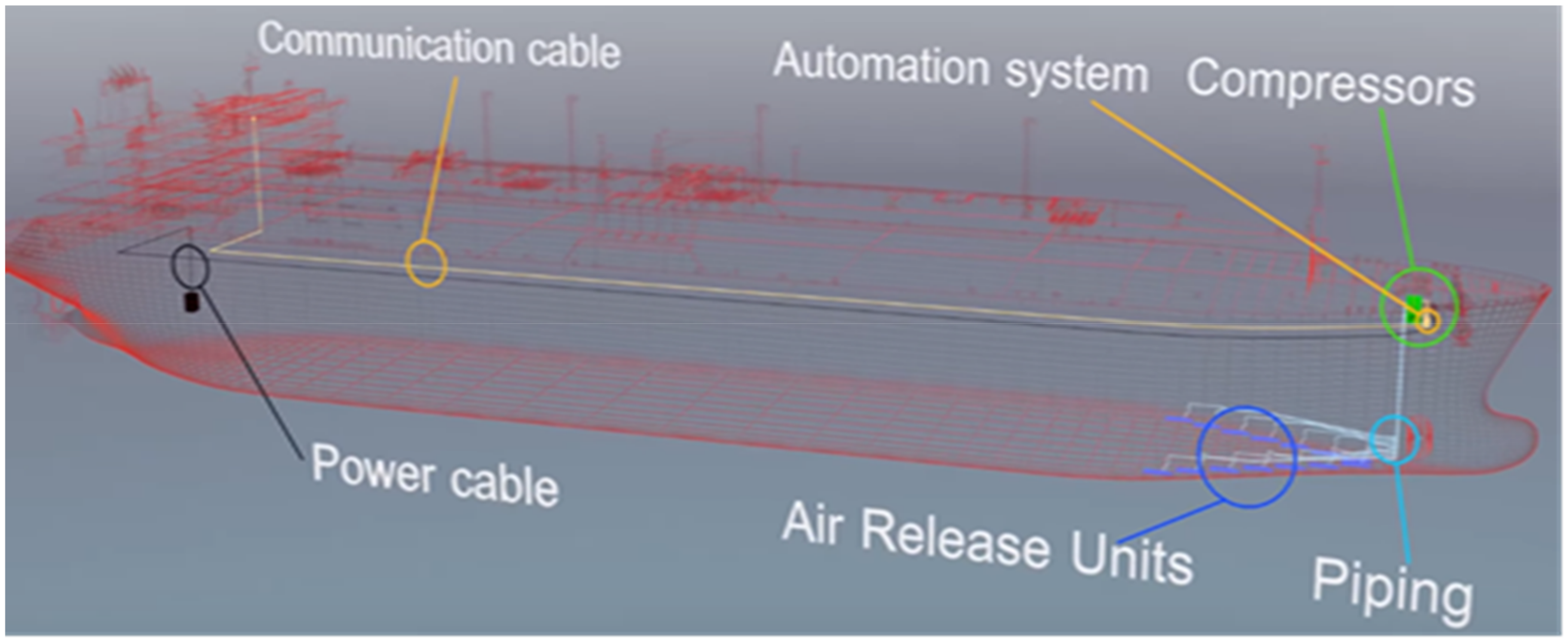
2. Computational Analysis
3. Results
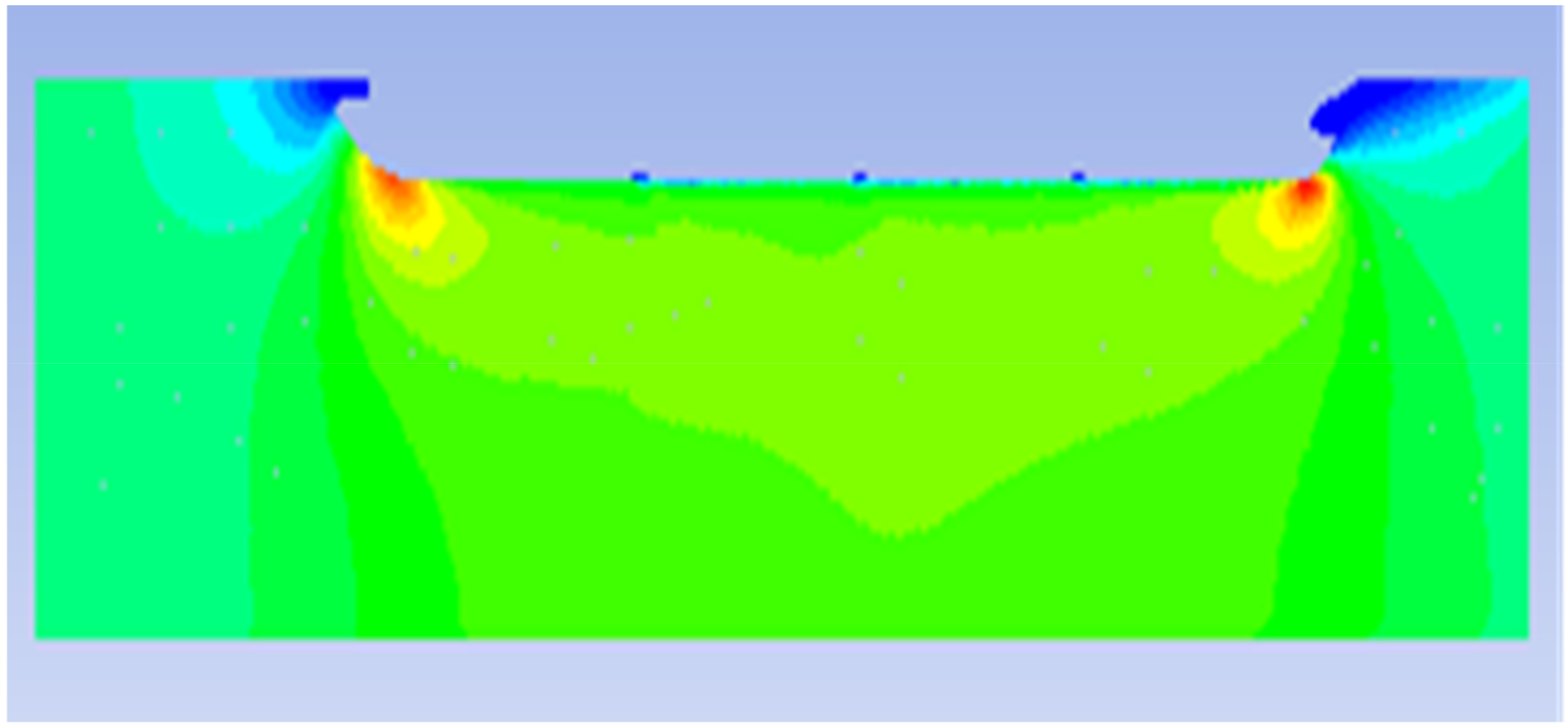
3.1. Results without Air Lubrication
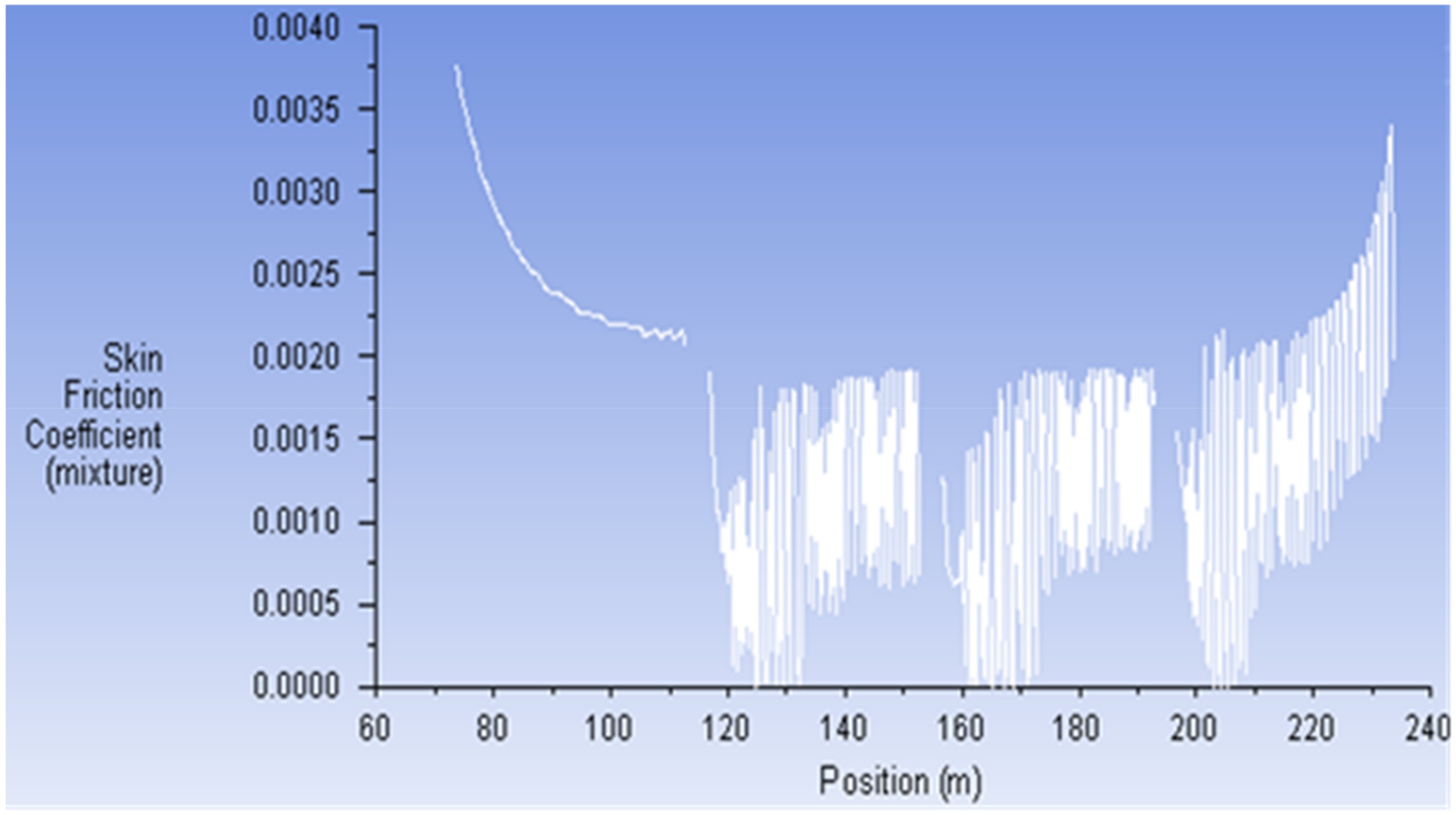
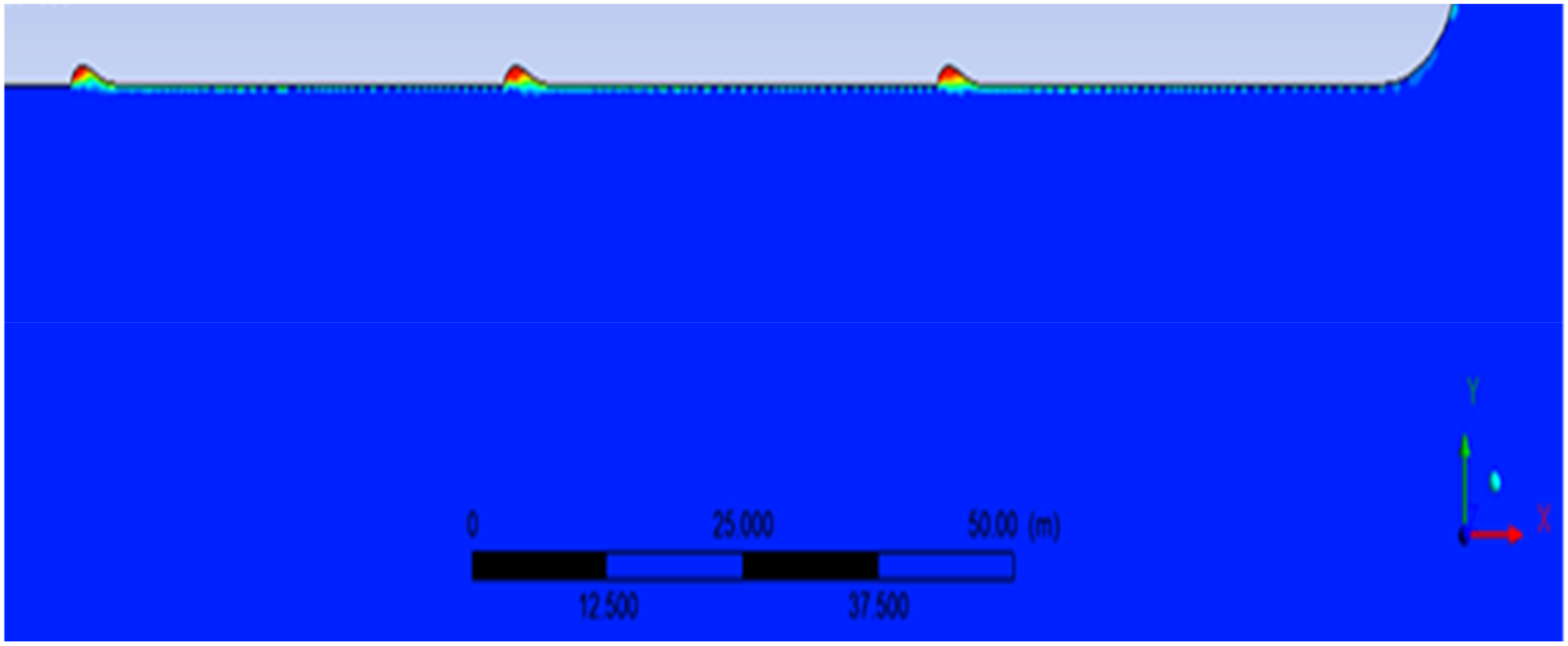
3.2. Results with Air Lubrication
3.3. Fuel Consumption and Emissions
3.3.1. Engine Features and Fuel Consumption
3.3.2. Decrease in Consumption
- CA = −0.00350,
- CAA = 0.00055,
- CR = 0.00400,
- For Cf = 0.0023 > CT = 0.00335
- For Cf = 0.0020 > CT = 0.00305 > 8.9% decrease between two CT coefficients,
3.3.3. Decrease in CO2 Emissions
4. Discussion and Conclusions
4.1. Technical Remarks
4.2. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Info Sheet No. 30—Modern Ship Size Definitions. 2010. Available online: https://books.google.gr/books?id=3XZr_gMA1F0C&pg=PA110&dq=Info+Sheet+No.30%E2%80%94Modern+Ship+Size+Definitions;+Lloyd%27s+Register:+2010&hl=el&sa=X&ved=0ahUKEwiG2MTPvobpAhXEeZoKHejEBVIQ6AEIMTAB (accessed on 27 April 2020).
- Foeth, E.J. Decreasing frictional resistance by air lubrication. In Proceedings of the 20th International Hiswa Symposium on Yacht Design and Yacht Construction, Decreasing Frictional Resistance by Air Lubrication, Amsterdam, The Netherlands, 17–18 November 2008. [Google Scholar]
- Reynolds, W.C. Fundamentals of Turbulence for Turbulence Modeling and Simulation; Lecture Note No 755; Mechanical Engineering, Stanford University: Stanford, CA, USA, 1987. [Google Scholar]
- Takahashi, T.; Kakugawa, A.; Nagaya, S.; Yanagihara, T.; Kodama, Y. Mechanisms and Scale Effects of Skin Friction Reduction by Microbubbles. 2001. Available online: https://pdfs.semanticscholar.org/13d4/357f5a8cd83a1d3e792fc20264dafd9fc332.pdf (accessed on 23 April 2020).
- Kawabuchi, M.; Kawakita, C.; Mizokami, S.; Higasa, S.; Kodan, Y.; Takano, S. CFD Predictions of Bubbly Flow Around an Energy-Saving Ship with Mitsubishi Air Lubrication System. Mitsubishi Heavy Ind. Tech. Rev. 2011, 48, 53. [Google Scholar]
- Park, S.H.; Lee, I. Optimization of drag reduction effect of air lubrication for a tanker model. Int. J. Nav. Arch. Ocean Eng. 2018, 10, 427–438. [Google Scholar] [CrossRef]
- Douvi, E.C.; Margaris, D.P. Reducing the Shear Stress between the Ship’s Hull and Seawater by Means of Air Cavity Lubrication System. In Proceedings of the 6th International Conference on “Experiments/Process/System Modelling/Simulation/Optimization”, Athens, Greece, 8–11 July 2015. [Google Scholar]
- Granville, P.S. The Viscous Resistance of Surface Vessels and the Skin Friction of Flat Plates. Trans. Soc. Naval Archit. Mar. Eng. 1956, 64, 209–240. [Google Scholar]
- DK Group. Improving Efficiency by Retrofitting of an Existing Vessel with ACS Air Lubrication System, Silverstream Technologies; American Bureau of Shipping: Houston, TX, USA, 2017; Available online: https://ww2.eagle.org/content/dam/eagle/advisories-and-debriefs/Air%20Lubrication%20Technology.pdf (accessed on 23 April 2020).
- Wartsila-46df. Available online: https://www.wartsila.com/marine/build/engines-and-generating-sets/dual-fuel-engines/wartsila-46df (accessed on 23 April 2020).
- Principles of Naval Architecture, Propulsion and Vibration; The Society of Naval Architects and Marine Engineers: Jersey City, NJ, USA, 1998.
- Voxakis, P. Ship Hull Resistance Calculations Using CFD Methods. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2012. [Google Scholar]
- Resistance, Propulsion & Machinery, ITTC-57, ITTC-78 Methods, Valerian Albanov. Available online: https://wiki.aalto.fi/download/attachments/97622265/2%20Resistance,%20Propulsion%20and%20machinery.pdf?version=1&modificationDate=1412079381365&api=v2 (accessed on 23 April 2020).
- Coşofreţ, D.; Bunea, M.; Popa, C. The Computing Methods for CO2 Emissions in Maritime Transports. In Proceedings of the International Conference Knowledge-Based Organization; Walter de Gruyter GmbH: Berlin, Germany, 2016; pp. 622–627. [Google Scholar]
- Carbon Emissions All at Sea, Shayne MacLachlan. OECD Environment Directorate. Available online: http://oecdinsights.org/2016/05/04/carbon-emissions-all-at-sea-why-was-shipping-left-out-of-the-paris-climate-agreement/ (accessed on 27 April 2020).
- Contact-Cooled Rotary Screw Air Compressors R-Series 90–160 kW/125–200. Available online: http://ingersollrand.jp/pdf/air/air_catalog_08.pdf (accessed on 23 April 2020).
- Silverstream Technologies. 2017. Available online: https://www.silverstream-tech.com/ (accessed on 23 April 2020).









| CT | Total Resistance Coefficient |
|---|---|
| Cf | Hull’s skin friction coefficient |
| CA | Increase in resistance due to the ship’s volume |
| CAA | Air resistance coefficient |
| CR | Residual resistance coefficient |
| SFC | Specific Fuel Consumption of engine |
| FT | Total propulsive resistance |
| P | Propulsive power |
| FC | Fuel consumption |
| M | Amount of money spent |
| E | Amount of CO2 emissions calculated |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fotopoulos, A.G.; Margaris, D.P. Computational Analysis of Air Lubrication System for Commercial Shipping and Impacts on Fuel Consumption. Computation 2020, 8, 38. https://0-doi-org.brum.beds.ac.uk/10.3390/computation8020038
Fotopoulos AG, Margaris DP. Computational Analysis of Air Lubrication System for Commercial Shipping and Impacts on Fuel Consumption. Computation. 2020; 8(2):38. https://0-doi-org.brum.beds.ac.uk/10.3390/computation8020038
Chicago/Turabian StyleFotopoulos, Andreas G., and Dionissios P. Margaris. 2020. "Computational Analysis of Air Lubrication System for Commercial Shipping and Impacts on Fuel Consumption" Computation 8, no. 2: 38. https://0-doi-org.brum.beds.ac.uk/10.3390/computation8020038





