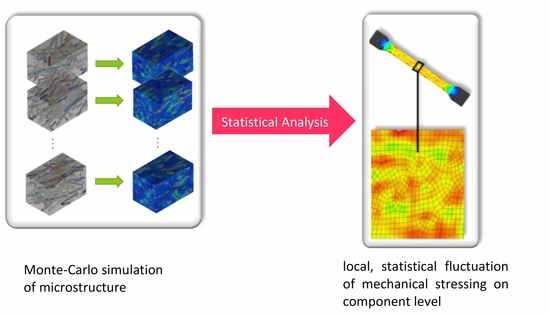
Statistical Analysis of Mechanical Stressing in Short Fiber Reinforced Composites by Means of Statistical and Representative Volume Elements
Abstract
:1. Introduction
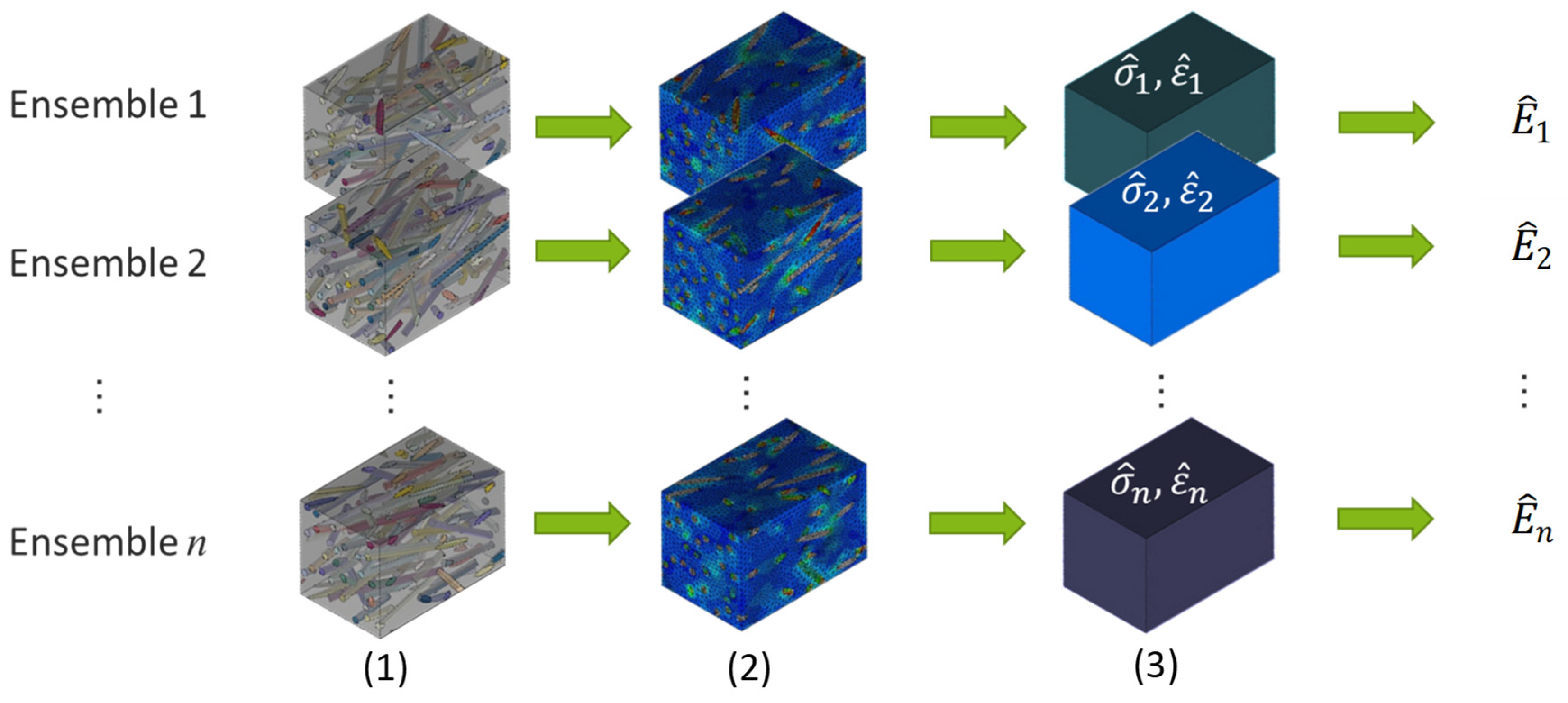
2. Materials and Methods
3. Results
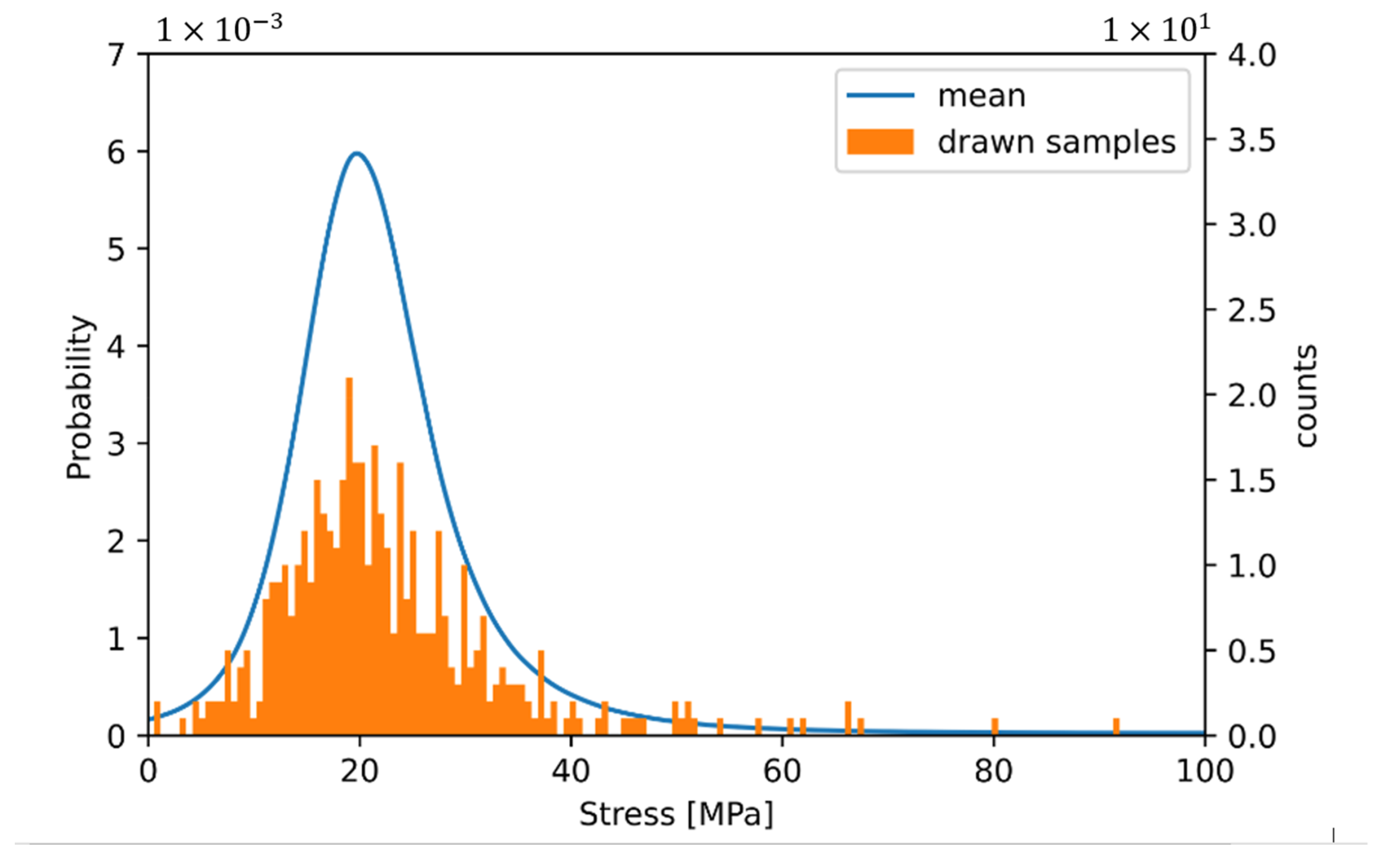
3.1. Influence of Finite Volume Approaches
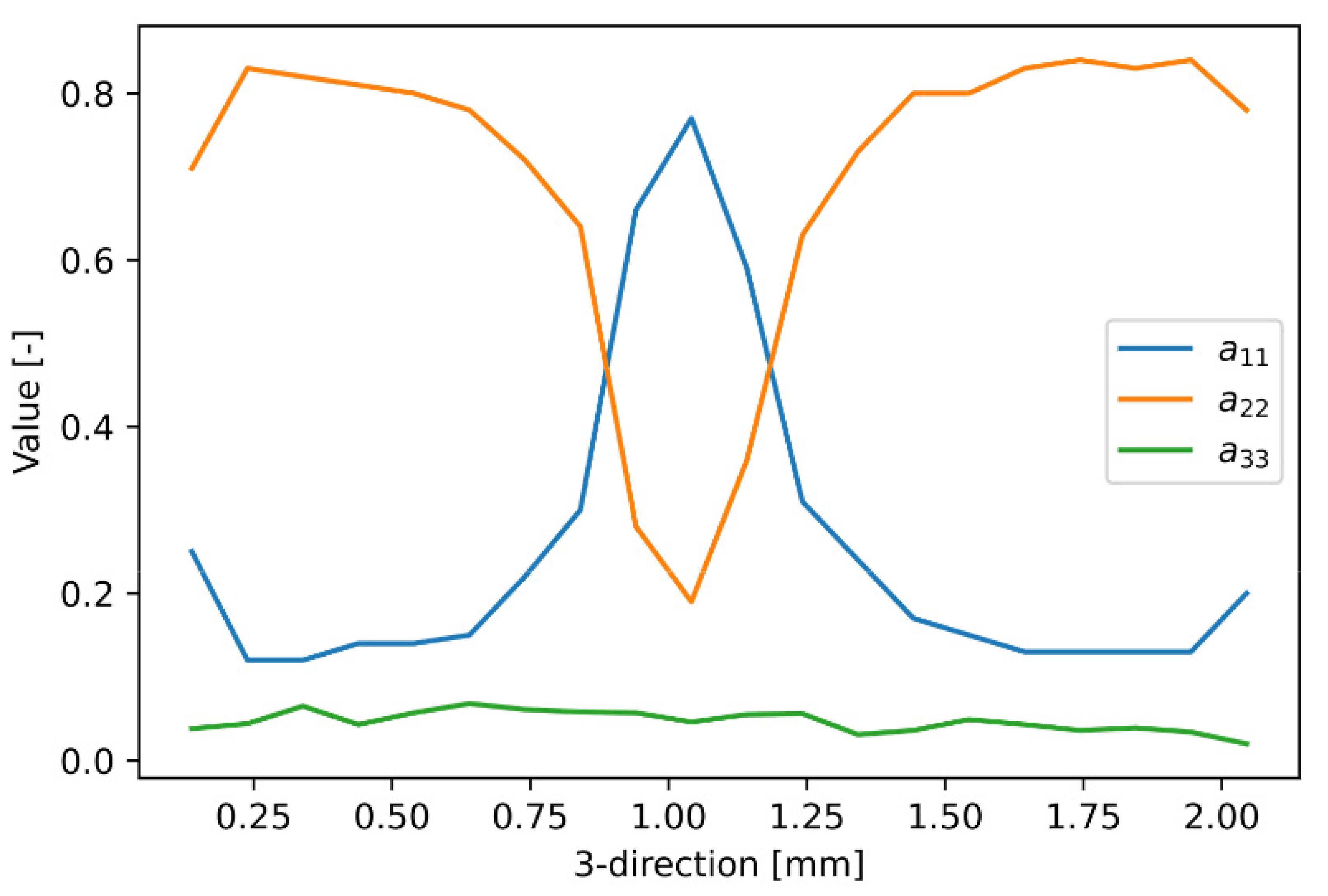
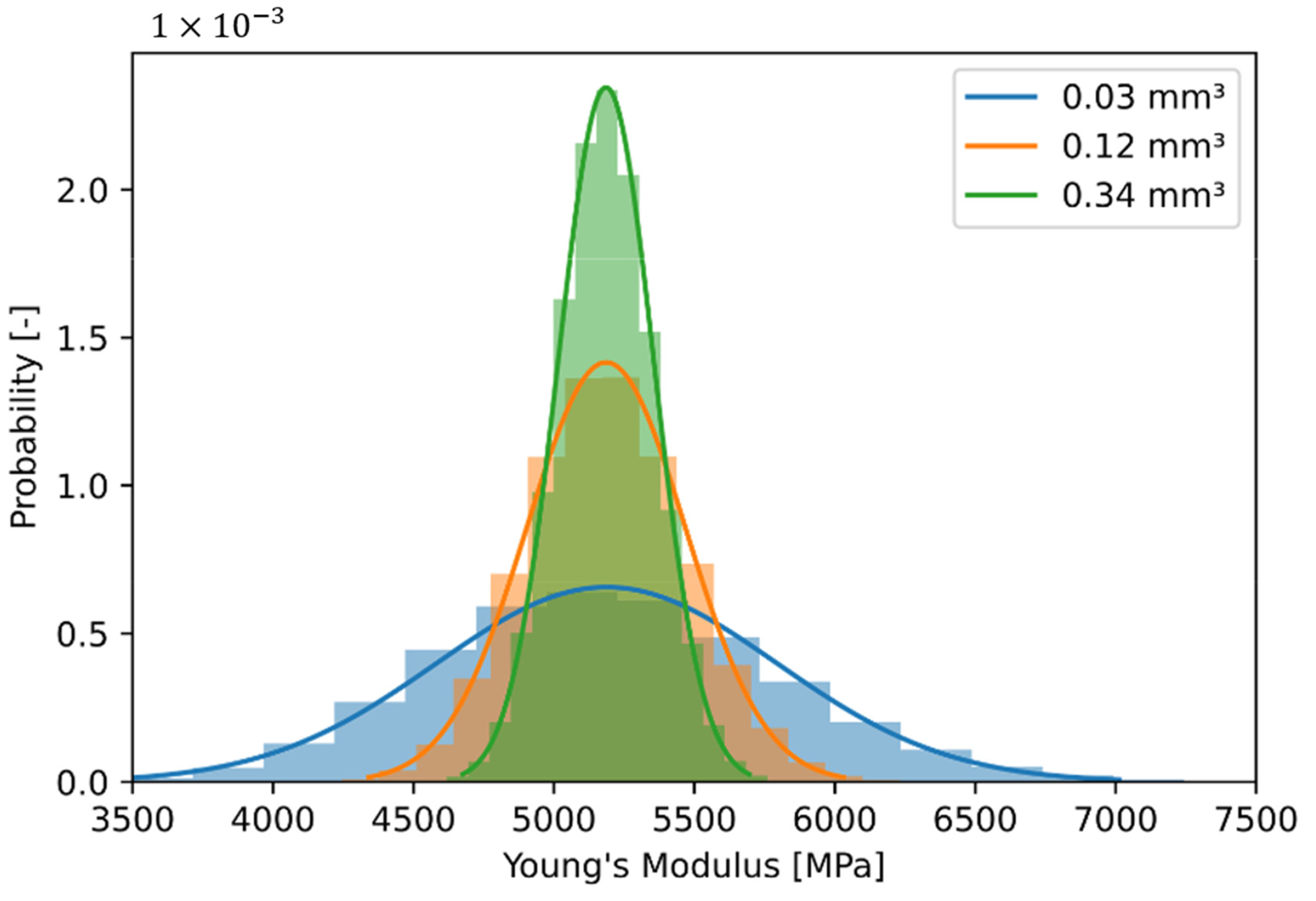
3.2. Influence of Finite Volume Size
- Sampling stress values from a statistical population;
- Calculating mean value of samples;
- Calculating stiffness out of mean of samples with global strain;
- Repeating steps 1–3 several times to achieve stiffness distribution;
- Repeating steps 1–4 for different volumes.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Duschlbauer, D.; Pettermann, H.E.; Böhm, H.J. Mori–Tanaka based evaluation of inclusion stresses in composites with nonaligned reinforcements. Scr. Mater. 2003, 48, 223–228. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Benveniste, Y. A new approach to the application of Mori-Tanaka’s theory in composite materials. Mech. Mater. 1987, 6, 147–157. [Google Scholar] [CrossRef]
- Doghri, I.; Quar, A. Homogenization of two-phase elasto-plastic composite materials and structures: Study of tangent operators, cyclic plasticity and numerical algorithms. Int. J. Solids Struct. 2003, 40, 1681–1712. [Google Scholar] [CrossRef]
- Eshelby, J.D. The Determination of the Elastic Field of an Ellipsoidal Inclusion, and Related Problems. Proc. R. Soc. Lon. Ser. A 1957, 241, 376–396. [Google Scholar]
- Sun, C.T.; Vaidya, R.S. Prediction of composite properties from a representative volume element. Compos. Sci. Technol. 1996, 56, 171–179. [Google Scholar] [CrossRef]
- Sab, K. On the homogenization and the simulation of random materials. Eur. J. Mech. A Solids 1992, 11, 585–607. [Google Scholar]
- Akpoyomare, A.I.; Okereke, M.I.; Bingley, M.S. Virtual testing of composites: Imposing periodic boundary conditions on general finite element meshes. Compos. Struct. 2017, 160, 983–994. [Google Scholar] [CrossRef]
- Gusev, A.A. Representative volume element size for elastic composites: A numerical study. J. Mech. Phys. Solids 1997, 45, 1449–1459. [Google Scholar] [CrossRef]
- Okereke, M.I.; Akpoyomare, A.I. A virtual framework for prediction of full-field elastic response of unidirectional composites. Comput. Mater. Sci. 2013, 70, 82–99. [Google Scholar] [CrossRef]
- Schneider, M.; Ospald, F.; Kabel, M. Computational homogenization of elasticity on a staggered grid. Int. J. Numer. Methods Eng. 2016, 105, 693–720. [Google Scholar] [CrossRef]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Drugan, W.J.; Willis, J.R. A micromechanics-based nonlocal constitutive equation and estimates of representative volume element size for elastic composites. J. Mech. Phys. Solids 1996, 44, 497–524. [Google Scholar] [CrossRef]
- Gitman, I.M.; Askes, H.; Sluys, L.J. Representative volume: Existence and size determination. Eng. Fract. Mech. 2007, 74, 2518–2534. [Google Scholar] [CrossRef]
- Brisard, S.; Dormieux, L. FFT-based methods for the mechanics of composites: A general variational framework. Comput. Mater. Sci. 2010, 49, 663–671. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Smith, D.E. Numerical analysis on viscoelastic creep responses of aligned short fiber reinforced composites. Compos. Struct. 2019, 229, 111394. [Google Scholar] [CrossRef]
- Babu, K.P.; Mohite, P.M.; Upadhyay, C.S. Development of an RVE and its stiffness predictions based on mathematical homogenization theory for short fibre composites. Int. J. Solids Struct. 2018, 130–131, 80–104. [Google Scholar] [CrossRef]
- Berger, H.; Kari, S.; Gabbert, U.; Rodríguez-Ramos, R.; Bravo-Castillero, J.; Guinovart-Díaz, R. Evaluation of effective material properties of randomly distributed short cylindrical fiber composites using a numerical homogenization technique. J. Mech. Mater. Struct. 2007, 2, 1561–1570. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Gu, B.; Tao, J.; Zhou, J. The average response and isotropy of 3D representative volume elements for random distributed short fibers reinforced elastomer. Compos. Struct. 2019, 216, 279–289. [Google Scholar] [CrossRef]
- Pan, Y.; Iorga, L.; Pelegri, A.A. Analysis of 3D random chopped fiber reinforced composites using FEM and random sequential adsorption. Comput. Mater. Sci. 2008, 43, 450–461. [Google Scholar] [CrossRef]
- Chen, L.; Gu, B.; Zhou, J.; Tao, J. Study of the Effectiveness of the RVEs for Random Short Fiber Reinforced Elastomer Composites. Fibers Polym. 2019, 20, 1467–1479. [Google Scholar] [CrossRef]
- Pan, Y.; Iorga, L.; Pelegri, A.A. Numerical generation of a random chopped fiber composite RVE and its elastic properties. Compos. Sci. Technol. 2008, 68, 2792–2798. [Google Scholar] [CrossRef]
- Burgarella, B.; Maurel-Pantel, A.; Lahellec, N.; Bouvard, J.-L.; Billon, N.; Moulinec, H.; Lebon, F. Effective viscoelastic behavior of short fibers composites using virtual DMA experiments. Mech. Time-Depend. Mater. 2019, 23, 337–360. [Google Scholar] [CrossRef]
- Wang, L.; Nygren, G.; Karkkainen, R.L.; Yang, Q. A multiscale approach for virtual testing of highly aligned short carbon fiber composites. Compos. Struct. 2019, 230, 111462. [Google Scholar] [CrossRef]
- Breuer, K.; Stommel, M. RVE modelling of short fiber reinforced thermoplastics with discrete fiber orientation and fiber length distribution. SN Appl. Sci. 2019, 2, 91. [Google Scholar] [CrossRef] [Green Version]
- Görthofer, J.; Schneider, M.; Ospald, F.; Hrymak, A.; Böhlke, T. Computational homogenization of sheet molding compound composites based on high fidelity representative volume elements. Comput. Mater. Sci. 2020, 174, 109456. [Google Scholar] [CrossRef]
- Greco, A. FEM analysis of the elastic behavior of composites and nanocomposites with arbitrarily oriented reinforcements. Compos. Struct. 2020, 241, 112095. [Google Scholar] [CrossRef]
- Huet, C. Application of variational concepts to size effects in elastic heterogeneous bodies. J. Mech. Phys. Solids 1990, 38, 813–841. [Google Scholar] [CrossRef]
- Hazanov, S.; Huet, C. Order relationships for boundary conditions effect in heterogeneous bodies smaller than the representative volume. J. Mech. Phys. Solids 1994, 42, 1995–2011. [Google Scholar] [CrossRef]
- Kanit, T.; Forest, S.; Galliet, I.; Mounoury, V.; Jeulin, D. Determination of the size of the representative volume element for random composites: Statistical and numerical approach. Int. J. Solids Struct. 2003, 40, 3647–3679. [Google Scholar] [CrossRef]
- Celanese. Celanex 2300 GV1/20 Datasheet. Available online: http://catalog.ides.com/Datasheet.aspx?I=26793&E=73487 (accessed on 28 April 2021).
- Kaiser, J.-M.; Stommel, M. Modified mean-field formulations for the improved simulation of short fiber reinforced thermoplastics. Compos. Sci. Technol. 2014, 99, 75–81. [Google Scholar] [CrossRef]
- Parra-Venegas, E.J.; Campos-Venegas, K.; Martinez-Sanchez, R.; Herrera-Ramirez, J.M.; Rodriguez-Miranda, A. The Tensile Behavior of E-glass fibers. Microsc. Microanal. 2012, 18, 784–785. [Google Scholar] [CrossRef]
- Breuer, K.; Stommel, M.; Korte, W. Analysis and Evaluation of Fiber Orientation Reconstruction Methods. J. Compos. Sci. 2019, 3, 67. [Google Scholar] [CrossRef] [Green Version]
- D’Agostino, R.B. An omnibus test of normality for moderate and large sample size. Biometrika 1971, 58, 341–348. [Google Scholar] [CrossRef]
- D’Agostino, R.B.; Pearson, E.S. Tests for departure from normality. Biometrika 1973, 60, 613–622. [Google Scholar]
- Gandhi, U.N.; Goris, S.; Osswald, T.A.; Song, Y.-Y. Discontinuous Fiber-Reinforced Composites, 1st ed.; Hanser: Munich, Germany, 2020. [Google Scholar]

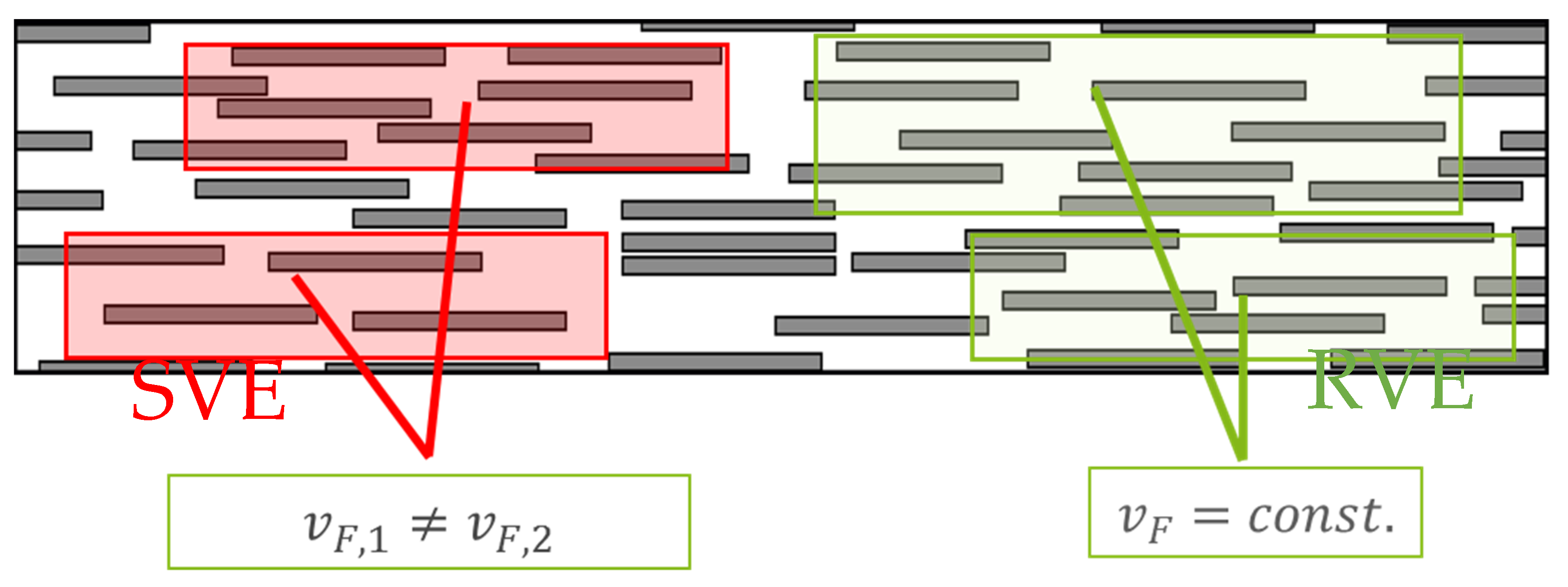

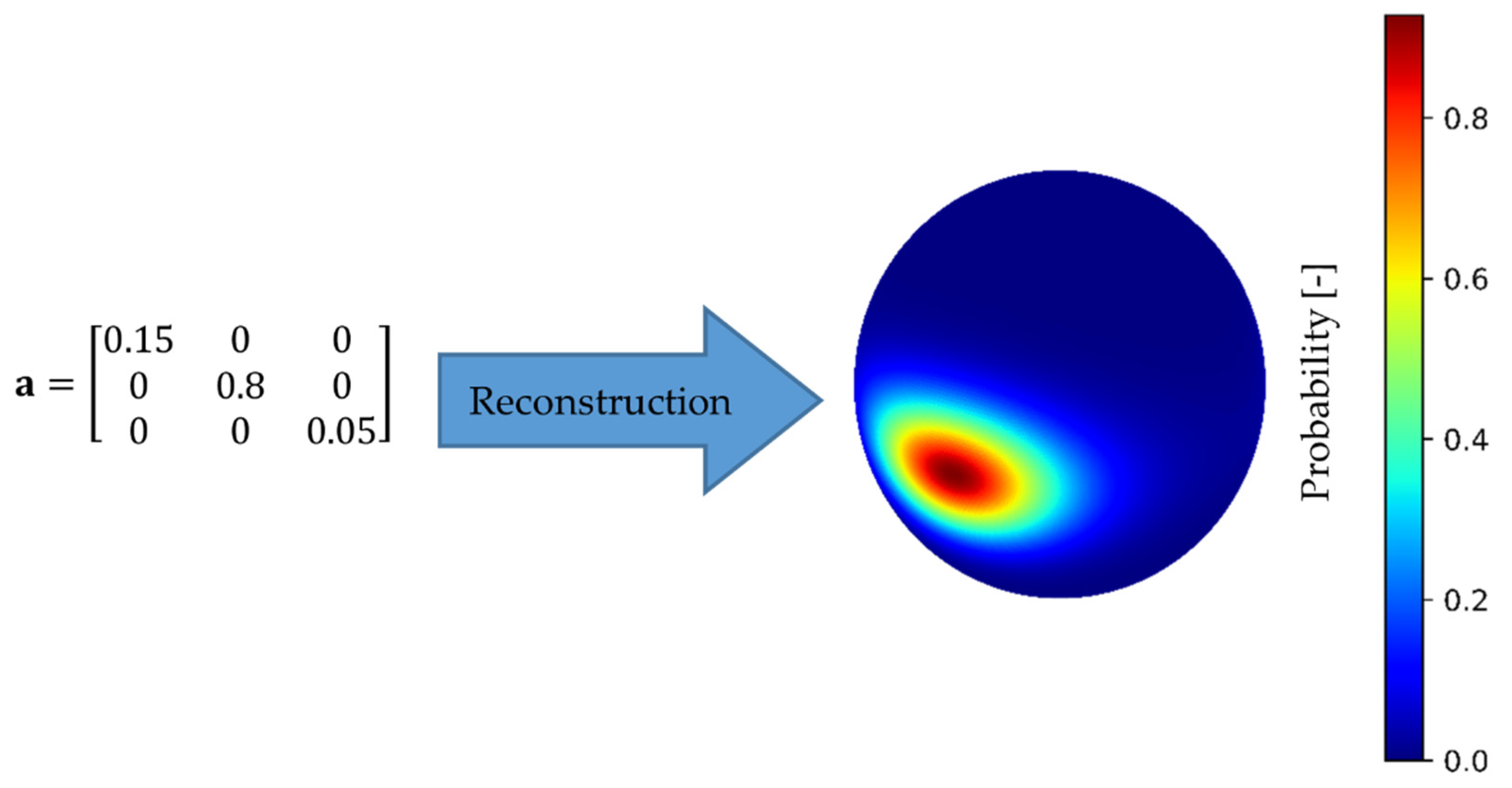

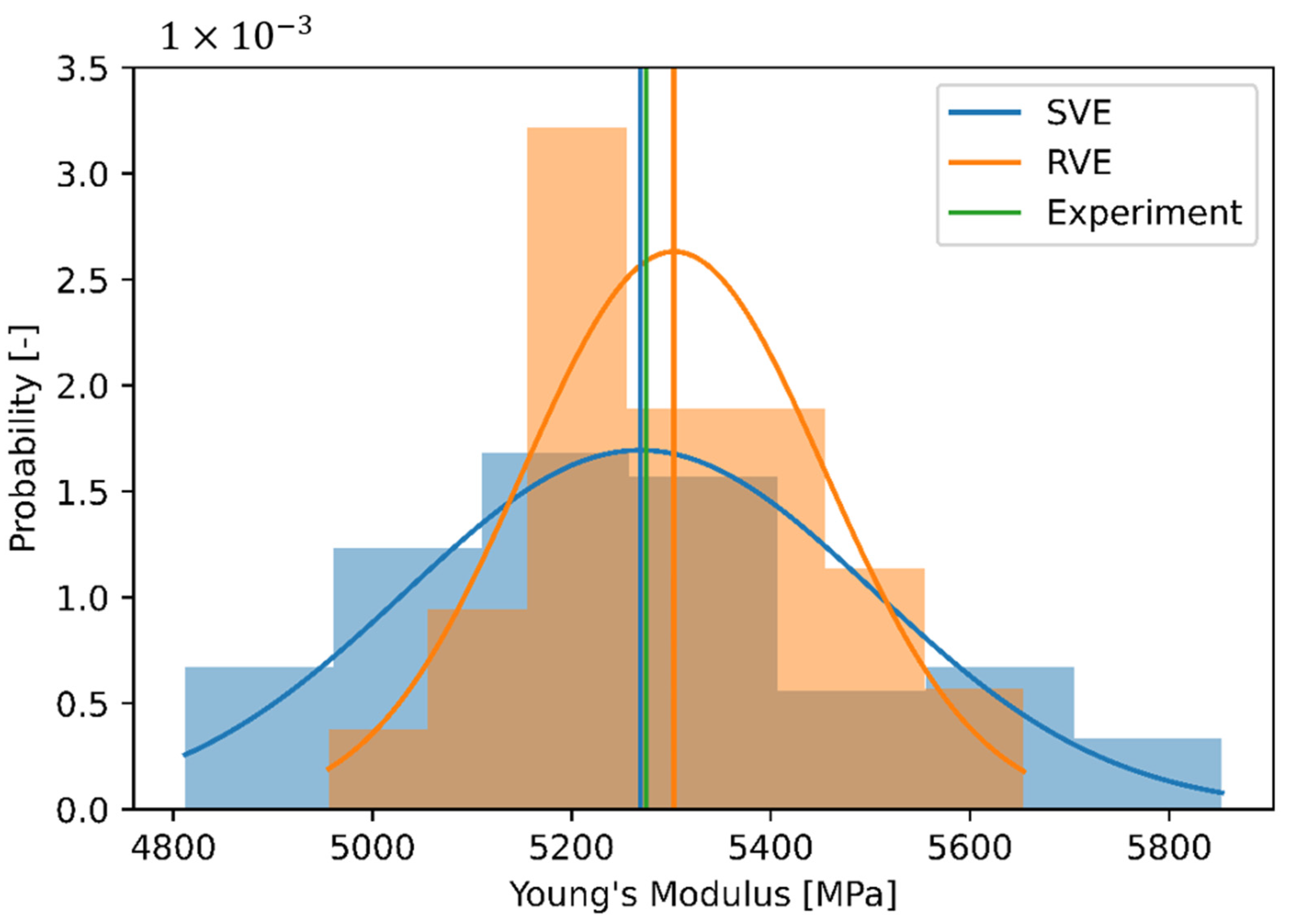

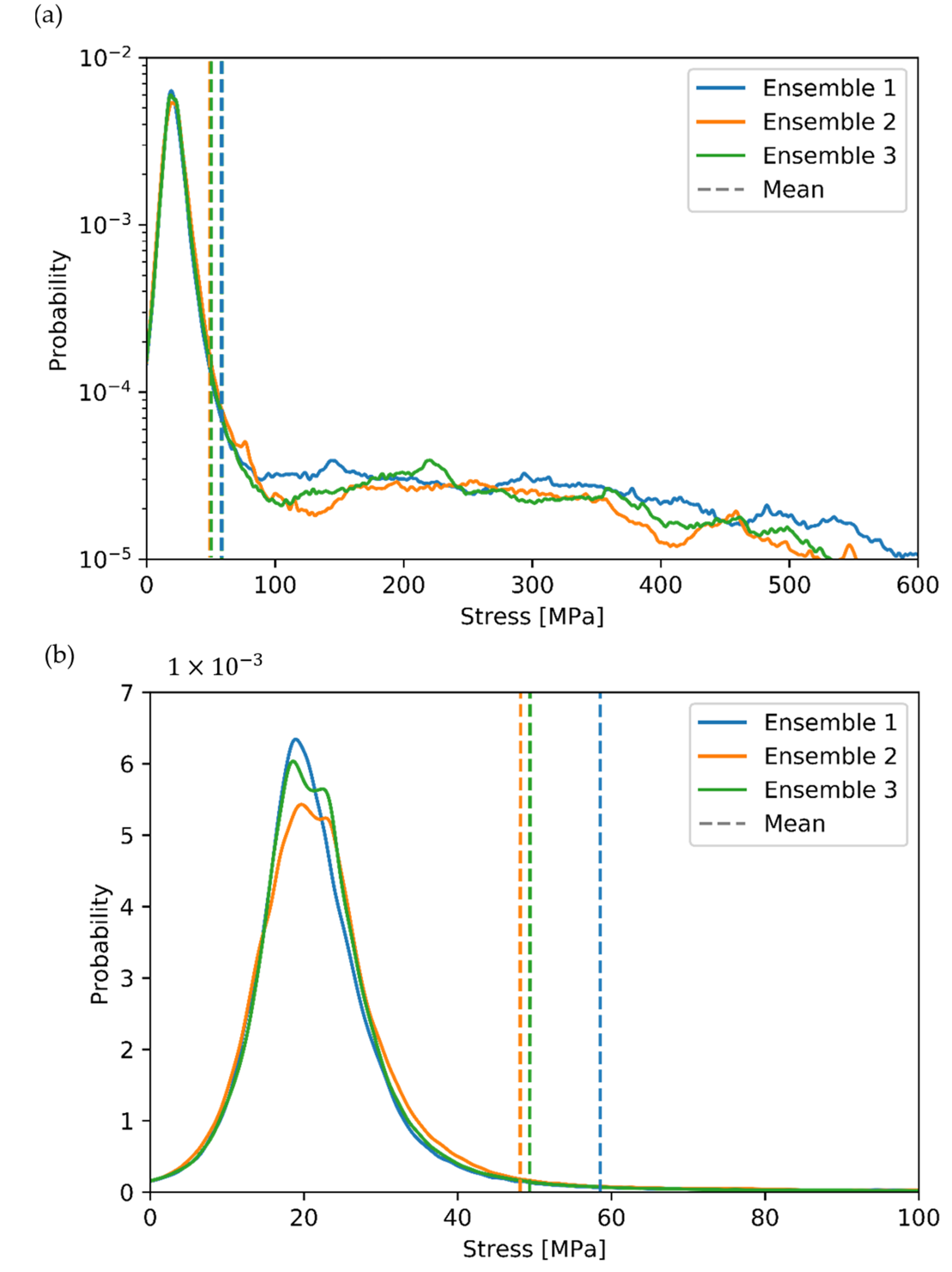
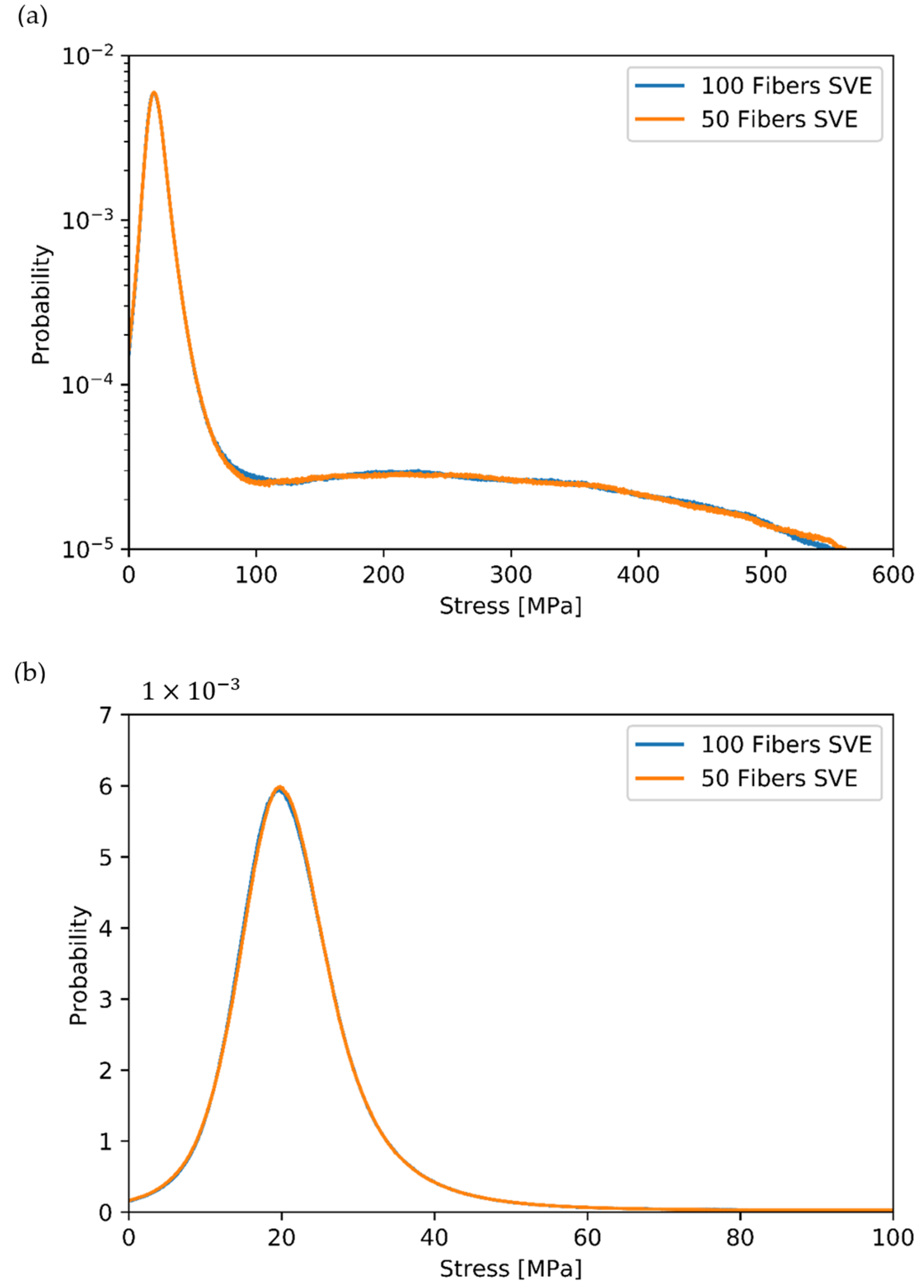


| Parameter | SVE | RVE |
|---|---|---|
| number of fibers | constant | constant |
| fiber geometry | constant | constant |
| fiber length | defined by LDF | defined by LDF |
| fiber volume fraction | defined by fibers and total volume | constant |
| total volume | constant | defined by fibers and fiber volume fraction |
| fiber orientation | defined by ODF | defined by ODF |
| fiber arrangement | random | random |
| phase properties | constant | constant |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Breuer, K.; Spickenheuer, A.; Stommel, M. Statistical Analysis of Mechanical Stressing in Short Fiber Reinforced Composites by Means of Statistical and Representative Volume Elements. Fibers 2021, 9, 32. https://0-doi-org.brum.beds.ac.uk/10.3390/fib9050032
Breuer K, Spickenheuer A, Stommel M. Statistical Analysis of Mechanical Stressing in Short Fiber Reinforced Composites by Means of Statistical and Representative Volume Elements. Fibers. 2021; 9(5):32. https://0-doi-org.brum.beds.ac.uk/10.3390/fib9050032
Chicago/Turabian StyleBreuer, Kevin, Axel Spickenheuer, and Markus Stommel. 2021. "Statistical Analysis of Mechanical Stressing in Short Fiber Reinforced Composites by Means of Statistical and Representative Volume Elements" Fibers 9, no. 5: 32. https://0-doi-org.brum.beds.ac.uk/10.3390/fib9050032