The XSTAR Atomic Database
Abstract
:1. Introduction
2. XSTAR Atomic Database
- 01 .
- Ground state ionization
- 03 .
- Bound–bound collision
- 04 .
- Bound–bound radiative
- 05 .
- Bound–free collision (level)
- 06 .
- Total recombination
- 07 .
- Bound–free radiative (level)
- 08 .
- Total recombination forcing normalization
- 09 .
- Two-photon decay
- 11 .
- Element data
- 12 .
- Ion data
- 13 .
- Level data
- 14 .
- Bound–bound radiative, superlevel to spectroscopic level
- 15 .
- Collisional ionization total rate
- 40 .
- Bound–bound collisional, superlevel to spectroscopic level
- 41 .
- Non-radiative Auger transition
- 42 .
- Inner-shell photoabsorption followed by autoionization.
- Since the datasets are compiled from diverse sources, the original data structures and units are explicitly kept in the database records to be transcribed and unified at runtime. For instance, level energies are specified in eV but the photoionization cross-sections are usually tabulated in Rydbergs. Levels in some atomic models are listed in intermediate coupling (fine structure) while in others terms are adopted. These format differences are accounted for by defining data types, each of which adheres to its own set of rules for data tabulation.
- As new data and processes are included in the database, new data types may be defined. Thus, photoionization cross-sections can be specified in more than one data type—valence shell and K shell, say—if the tabulation for each energy region comes from different sources. They are then concatenated and adjusted at runtime.
3. Computation of Atomic Data for K-Line Diagnostics
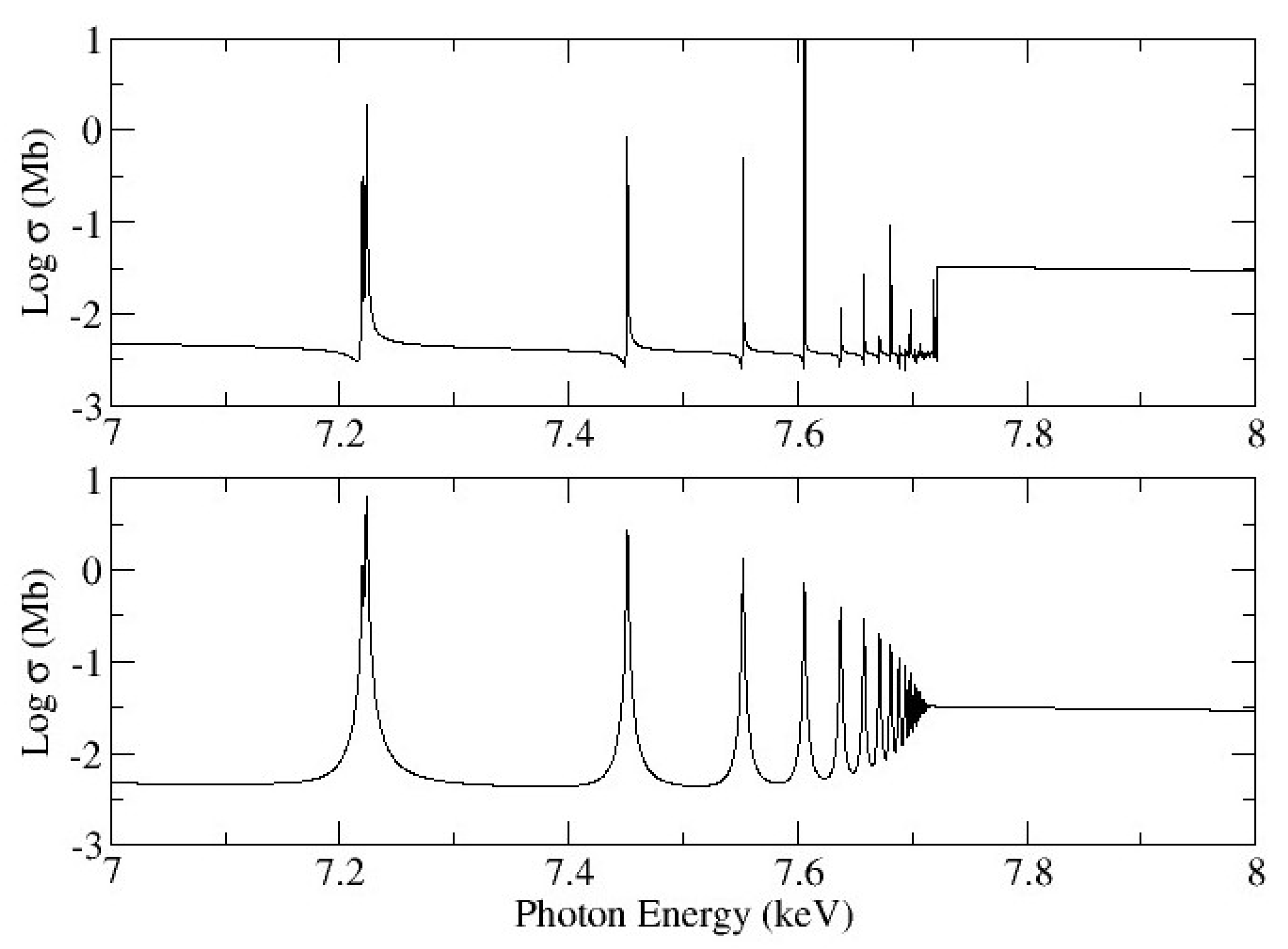
3.1. Radiative and Auger Damping
3.2. Orbital Relaxation
4. Photoabsorption Cross-Section Benchmarks
4.1. Carbon Sequence
4.2. Oxygen Sequence
4.3. Neon
4.4. Magnesium
4.5. Silicon
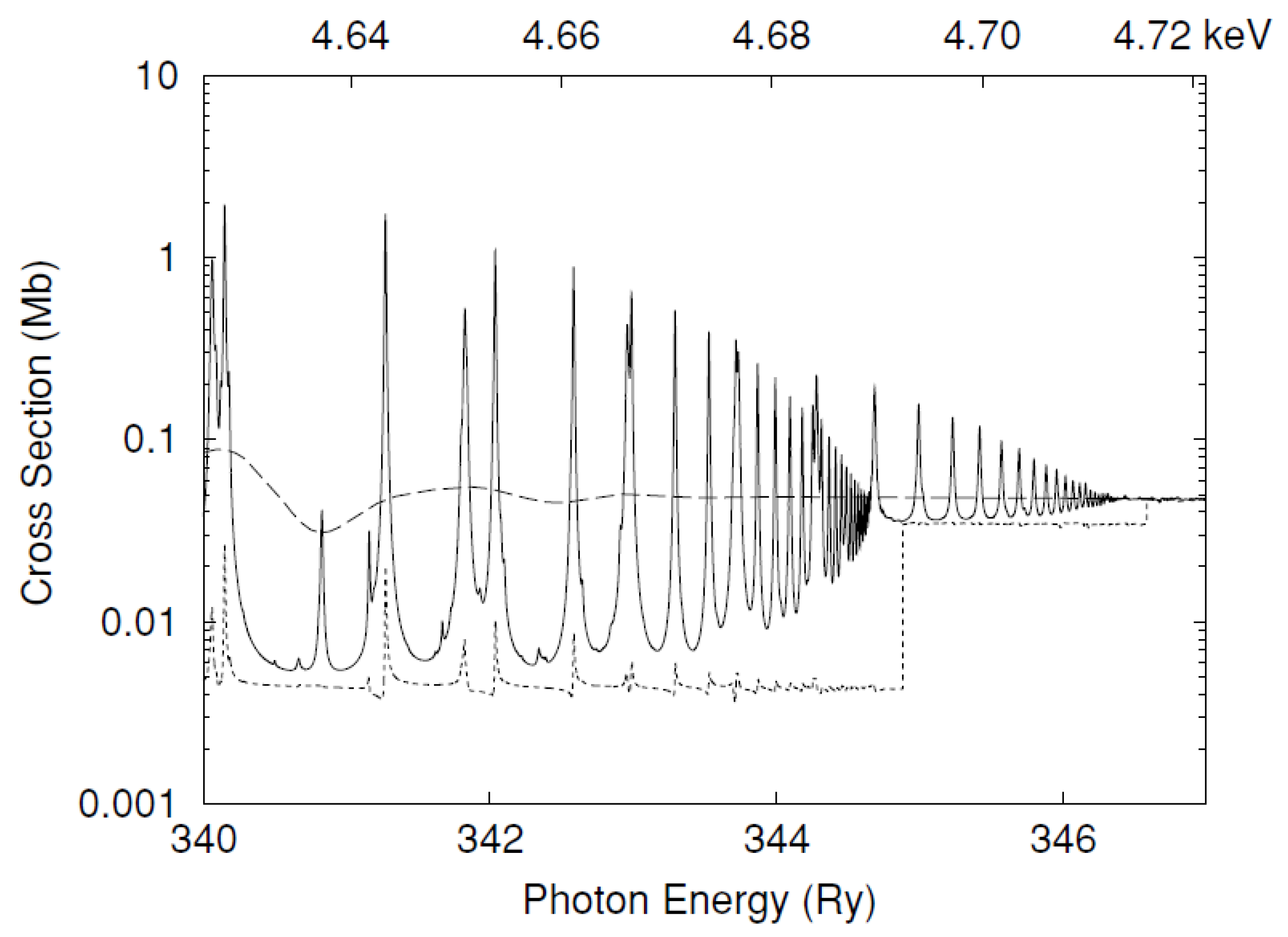
5. High-Density Effects on Atomic Parameters
5.1. Continuum Lowering
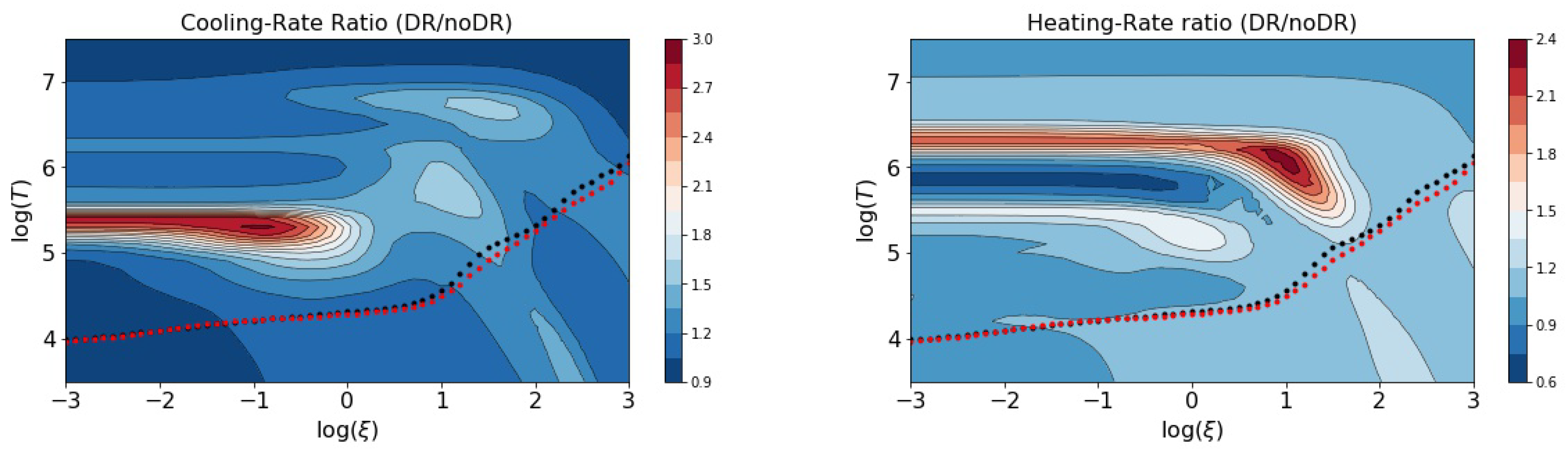
5.2. DR Suppression
6. Database Curation
6.1. Atomic Models
6.2. Metastable Levels
6.3. Database Pointers
6.4. Metadata
6.5. Relational Integrity
6.6. Atomic Data Accuracy
7. ISMabs
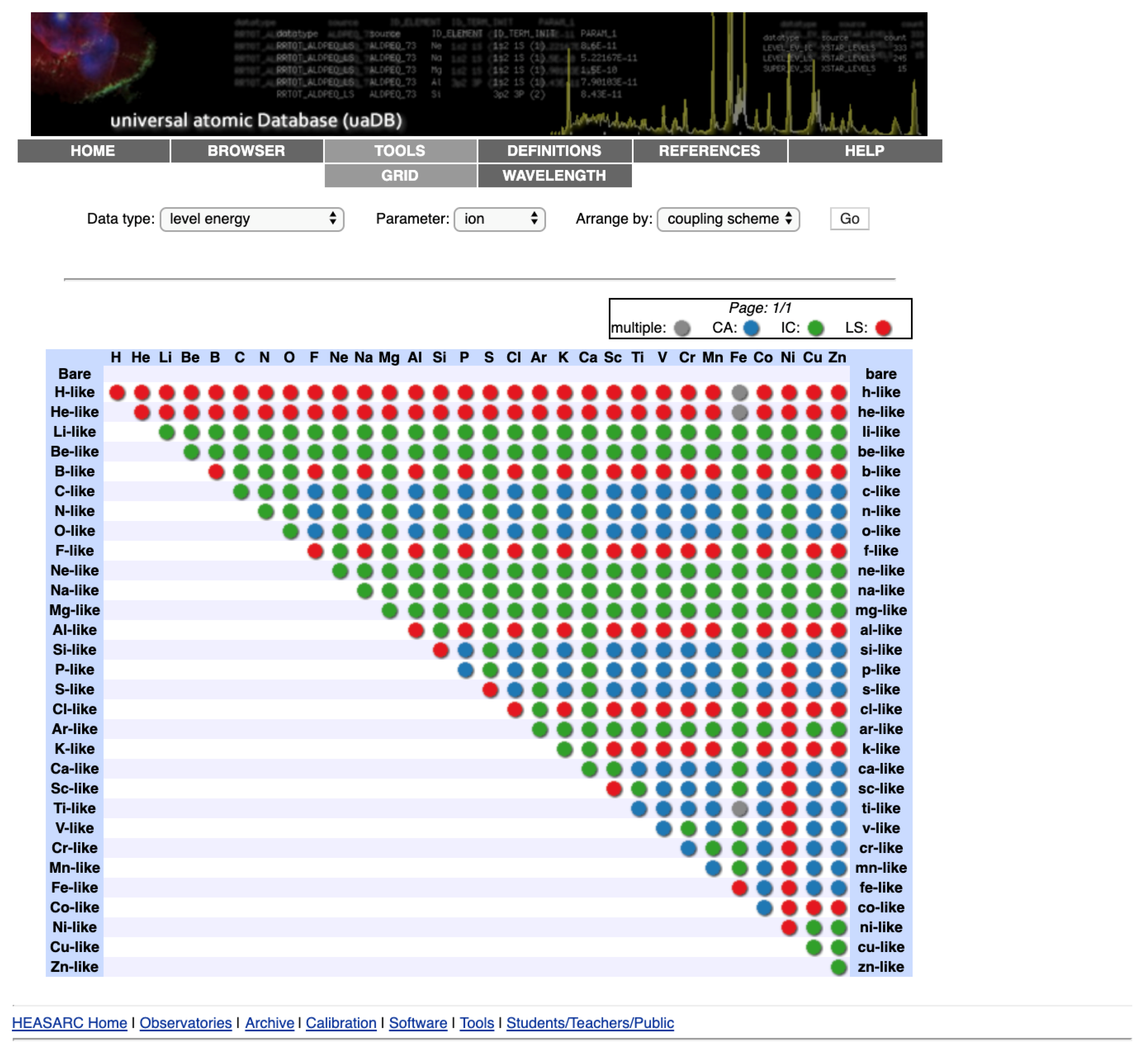
8. Universal Atomic Database (uaDB)
- Each dataset contains a reference to the source paper(s);
- Data are stored in the original format and units as published;
- Multiple entries can exist for the same quantity (e.g., theoretical vs. measured energy levels);
- The coupling scheme of atomic states is built into the database structure;
- Data collections exist that define a complete model; no duplicate data exist within a collection.
9. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADAS | Atomic Data and Analysis Structure |
| ADS | Astrophysics Data System |
| ALS | Advanced Light Source |
| AMDPP | Atomic and Molecular Diagnostic Processes in Plasmas |
| FITS | Flexible Image Transport System |
| GSFC | Goddard Space Flight Center |
| HZB | Helmholtz-Zentrum Berlin |
| IPNAS | Institut de Physique Nucléaire, Atomique et de Spectrométrie |
| LTE | Local Thermodynamic Equilibrium |
| NASA | National Aeronautics and Space Administration |
| NIST | National Institute of Standards and Technology |
| PP95 | Atomic Data for the Analysis of Emission Lines |
| SQL | Structured Query Language |
| WSRC | Wisconsin Synchrotron Radiation Center |
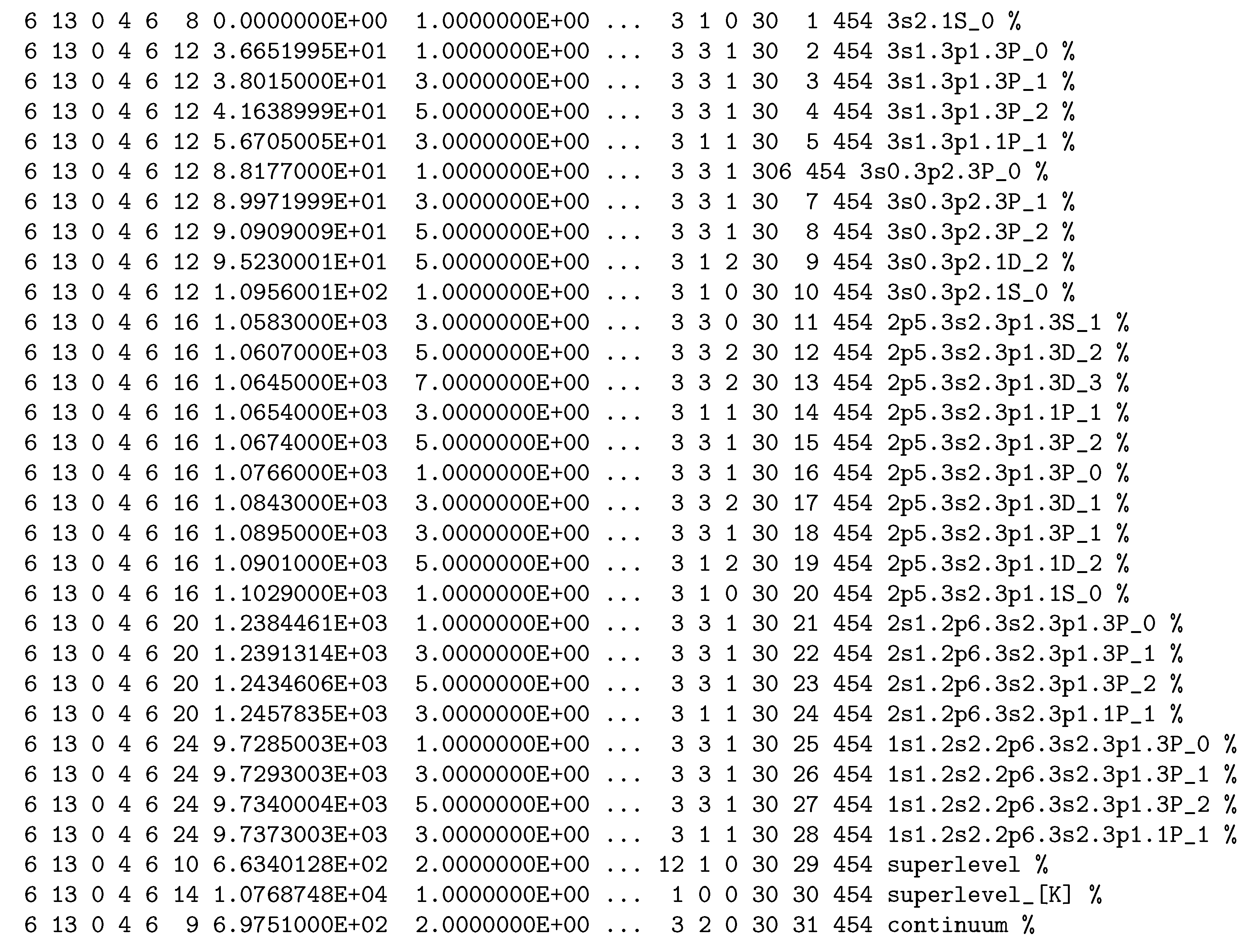
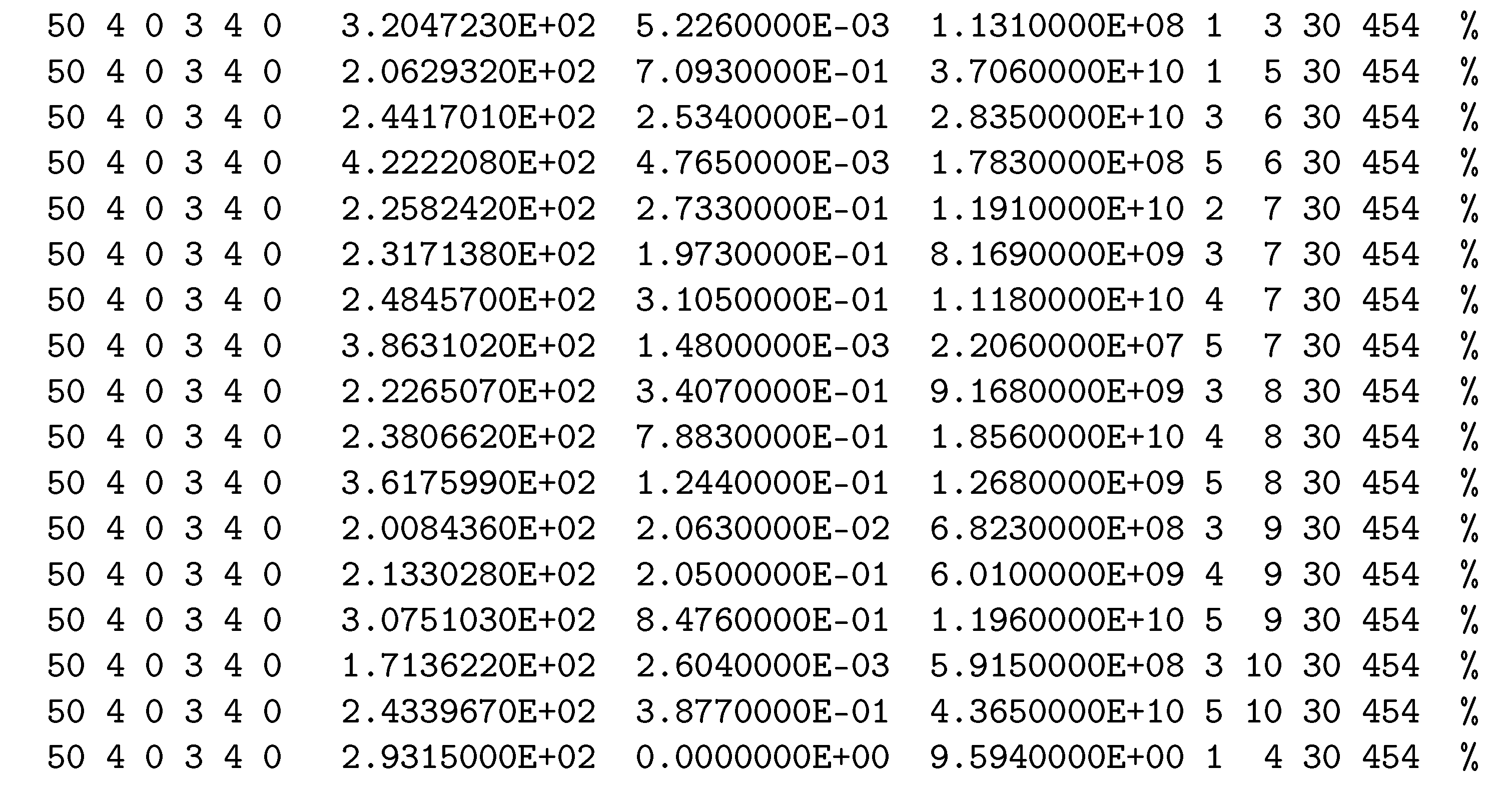
Appendix A. Data Types
- 01 .
- 02 .
- H charge exchange rate coefficient of N-electron recombined ion [98]: ( cm s); ; ; ; (K); (K); ( K); ; recombining ion identifier.
- 06 .
- Data attributes of the ith level of N-electron ion: (eV); ; (effective quantum number); (eV); ; ; ; ; ; ; level assignment (electron configuration and spectroscopic term).
- 07 .
- 14 .
- Ionization potential of N-electron ion: (eV); ; ; ; ion identifier.
- 22 .
- Dielectronic recombination rate coefficient of the N-electron recombined ion [99]: ; ; ; ; ; .
- 30 .
- Total radiative recombination rate (hydrogenic) for N-electron recombined ion [100]: ; .
- 38 .
- Total radiative recombination rate coefficient of N-electron recombined ion [http://amdpp.phys.strath.ac.uk/tamoc/DATA/RR/]: (cm s; ; (K); (K); ; (K); ; ; ; ; .
- 39 .
- Total dielectronic recombination rate coefficient of N-electron recombined ion [http://amdpp.phys.strath.ac.uk/tamoc/DATA/DR/]: (cm s K); (K); ; ; ; , .
- 49 .
- Partial photoionization cross-section of th level of the N-electron ion leaving the ()-electron ion in the th level: (Energy in Ryd relative to , cross-section in Mb); ; ; ; ; ; ; ; .
- 50 .
- Line () radiation rates of N-electron ion: (Å); ; (s); (lower level); (upper level); ; .
- 51 .
- 53 .
- TOPbase partial photoionization cross-section (resonance averaged) of th level of the N-electron ion leaving the ()-electron ion in the th level: (Energy in Ryd relative to , cross-section in Mb); ; ; ; ; ; ; ; .
- 54 .
- Radiative transition probability for the transition of N-electron ion computed by quantum defect theory (or hydrogenic): E+0; (lower level); (upper level); ; .
- 56 .
- Electron-impact effective collision strengths for the transition of N-electron ion: (K); (effective collision strength); (lower level); (upper level); ; .
- 57 .
- Effective ion charge for ith level of N-electron ion used in collisional ionization rates: ; ; ; ; ;
- 59 .
- Partial photoionization cross-section of th level of the N-electron ion leaving the ()-electron ion in the th level [102]: (eV); (eV); (Mb); ; ; ; ; (shell principal quantum number); (subshell orbital quantum number); ; ; ; ; shell–ion identifier.
- 60 .
- Analytic fits for effective collision strengths in H-like ions [103]: coefficients; (lower level); (upper level); ; ; Transition.
- 62 .
- Analytic fits for effective collision strengths in H-like ions [103]: coefficients; (lower level); (upper level); ; ; Transition.
- 63 .
- Collisional transition probability for N-electron ion computed by quantum defect theory (or hydrogenic): (lower level); (upper level); ; .
- 66 .
- Fits to fine-structure collision strengths for He-like ions [104]: coefficients; (lower level); (upper level); ; .
- 67 .
- Analytic fits for effective collision strengths in He-like ions [105]: coefficients; (lower level); (upper level); ; .
- 68 .
- Analytic fits for effective collision strengths in He-like ions [106]: coefficients; (lower level); (upper level); ; .
- 69 .
- Fits to collision strengths for He-like ions [104]: coefficients; (lower level); (upper level); ; .
- 70 .
- Coefficients for recombination and photoionization cross-sections of superlevels: = (cm); ;;= (Ryd, Mb); ; ; ; ; ; ; ; ; ; ; .
- 71 .
- Radiative transition rates from superlevels to spectroscopic levels: (cm); ; (s); (Å); ; ; (lower level); (upper level); ; .
- 72 .
- Autoionization rates for satellite levels: (s); (eV above ionization limit); ; ; ; (level); (continuum level); ; ; level configuration.
- 73 .
- Fit to effective collision strengths for satellite levels of He-like ions [107]: fit coefficients; (lower level); (upper level); ; .
- 74 .
- Delta functions to add to photoionization cross-sections to match ADAS DR rates: (Ryd); (Ryd); (cm); ; ; ; ; ; ; ; .
- 75 .
- Autoionization rates for Fe xxiv satellites [5]: (s); (eV above ionization limit); , ; ; ; .
- 76 .
- Two-photon radiation rate for () transition of N-electron ion: (s); (lower level); (upper level); ; ; transition.
- 77 .
- Collision transition rates from superlevels to spectroscopic levels: (cm); ; (s); (Å); ; ; (lower level); (upper level); ; .
- 81 .
- Collision strengths for Fe xix [108]: ; (lower level); (upper level); ; .
- 82 .
- Decay rates for Fe UTA [109]: (Å); (eV); ; (s); (s); (lower level); (upper level); .
- 83 .
- Level data for Fe UTA [109]: (eV); ; ; ; ; (level); ; level configuration assignment.
- 85 .
- Photoionization cross-sections for Fe ions obtained by summation of resonances near the K edge [3]: ; (Ryd); ; ; scaling factor; ; ; ; ; ; ; ; .
- 86 .
- Auger and radiative widths of th K-vacancy level: (eV, relative to ); (s); (s); (s); ; ; ; ; .
- 88 .
- Photoionization cross-section damped excess of th level of the N-electron ion leaving the ()-electron ion in superlevel_[K] : (Energy in Ryd relative to , cross-section in Mb); ; ; ; ; ; ; .
- 91 .
- APED line () radiation rates [110]: (Å); ; (s); (lower level); (upper level); ; .
- 92 .
- APED collision strengths [110]: (K); (K); (K); ; (lower level); (upper level); ; ; .
- 95 .
- Collisional ionization rates for N-electron ion [111]: (eV); (K); (effective collision strength); (level); .
- 98 .
- 99 .
- Coefficients for recombination and photoionization cross-sections of superlevels: (cm); ; ;(Ryd, Mb); ; ; ; ; ; ; ; ; ; ; .
Appendix B. Ion Models
| Z | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | ||||||||||||||||
| 1 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | |
| 2 | 46 | 32 | 32 | 32 | 56 | 58 | 241 | 52 | 54 | 52 | 58 | 52 | 58 | 52 | ||
| 3 | 3 | 3 | 3 | 26 | 43 | 43 | 22 | 43 | 22 | 43 | 22 | 43 | 22 | |||
| 4 | 3 | 3 | 22 | 53 | 53 | 43 | 79 | 43 | 79 | 43 | 79 | 43 | ||||
| 5 | 3 | 22 | 58 | 163 | 53 | 163 | 53 | 163 | 53 | 163 | 53 | |||||
| 6 | 8 | 61 | 79 | 53 | 79 | 53 | 79 | 53 | 79 | 53 | ||||||
| 7 | 82 | 34 | 34 | 34 | 34 | 34 | 63 | 34 | 34 | |||||||
| 8 | 19 | 3 | 19 | 19 | 19 | 57 | 19 | 19 | ||||||||
| 9 | 3 | 118 | 7 | 7 | 7 | 7 | 7 | |||||||||
| 10 | 4 | 3 | 46 | 46 | 46 | 50 | ||||||||||
| 11 | 3 | 24 | 4 | 60 | 42 | |||||||||||
| 12 | 3 | 4 | 57 | 31 | ||||||||||||
| 13 | 3 | 18 | 55 | |||||||||||||
| 14 | 3 | 3 | ||||||||||||||
| 15 | 3 | |||||||||||||||
| Z | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| N | ||||||||||||||||
| 1 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | |
| 2 | 58 | 52 | 38 | 52 | 46 | 52 | 52 | 52 | 52 | 52 | 50 | 52 | 43 | 52 | 52 | |
| 3 | 43 | 22 | 43 | 22 | 43 | 22 | 22 | 22 | 22 | 22 | 52 | 22 | 53 | 22 | 22 | |
| 4 | 79 | 43 | 79 | 43 | 79 | 43 | 43 | 43 | 43 | 43 | 199 | 43 | 79 | 43 | 43 | |
| 5 | 163 | 53 | 163 | 53 | 163 | 53 | 53 | 53 | 53 | 53 | 551 | 53 | 163 | 53 | 53 | |
| 6 | 79 | 53 | 53 | 53 | 53 | 53 | 53 | 53 | 53 | 53 | 623 | 53 | 53 | 53 | 53 | |
| 7 | 34 | 34 | 34 | 34 | 34 | 34 | 34 | 34 | 34 | 34 | 744 | 34 | 34 | 34 | 34 | |
| 8 | 19 | 19 | 19 | 19 | 29 | 19 | 19 | 19 | 19 | 19 | 639 | 19 | 67 | 19 | 19 | |
| 9 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 340 | 7 | 117 | 7 | 7 | |
| 10 | 46 | 50 | 72 | 50 | 78 | 50 | 50 | 50 | 50 | 50 | 276 | 50 | 98 | 50 | 50 | |
| 11 | 60 | 42 | 208 | 42 | 208 | 42 | 42 | 42 | 42 | 42 | 85 | 42 | 216 | 42 | 42 | |
| 12 | 53 | 31 | 153 | 31 | 149 | 31 | 31 | 31 | 31 | 31 | 146 | 31 | 171 | 31 | 31 | |
| 13 | 76 | 55 | 208 | 55 | 208 | 55 | 55 | 55 | 55 | 55 | 55 | 55 | 235 | 55 | 55 | |
| 14 | 82 | 71 | 249 | 71 | 249 | 71 | 71 | 71 | 71 | 71 | 68 | 71 | 269 | 71 | 71 | |
| 15 | 31 | 55 | 211 | 55 | 211 | 55 | 55 | 55 | 55 | 55 | 78 | 55 | 219 | 55 | 55 | |
| 16 | 3 | 3 | 143 | 31 | 143 | 31 | 31 | 31 | 31 | 31 | 70 | 31 | 145 | 31 | 31 | |
| 17 | 3 | 62 | 10 | 62 | 10 | 10 | 10 | 10 | 10 | 62 | 10 | 63 | 10 | 10 | ||
| 18 | 3 | 3 | 3 | 54 | 54 | 54 | 54 | 54 | 31 | 54 | 40 | 54 | 54 | |||
| 19 | 3 | 5 | 221 | 221 | 221 | 221 | 221 | 170 | 221 | 143 | 221 | 221 | ||||
| 20 | 3 | 32 | 258 | 258 | 258 | 258 | 54 | 258 | 258 | 258 | 258 | |||||
| 21 | 3 | 84 | 441 | 441 | 441 | 55 | 441 | 441 | 441 | 441 | ||||||
| 22 | 3 | 3 | 537 | 537 | 33 | 537 | 537 | 537 | 537 | |||||||
| 23 | 3 | 163 | 463 | 70 | 463 | 463 | 463 | 463 | ||||||||
| 24 | 3 | 160 | 73 | 295 | 295 | 295 | 295 | |||||||||
| 25 | 3 | 197 | 128 | 128 | 128 | 128 | ||||||||||
| 26 | 3 | 3 | 40 | 40 | 40 | |||||||||||
| 27 | 3 | 3 | 3 | 3 | ||||||||||||
| 28 | 3 | 3 | 3 | |||||||||||||
| 29 | 3 | 3 | ||||||||||||||
| 30 | 3 | |||||||||||||||
Appendix C. Atomic Data Provenance
| ID | Code | rt | dt | References | |
|---|---|---|---|---|---|
| ac81 | 1000 | 3 | 56 | [112] | |
| ac92 | 1001 | 3 | 56 | [113] | |
| ak91 | 1002 | 3 | 56 | [114] | |
| ak91a | 1003 | 3 | 56 | [115] | |
| ak92 | 1004 | 3 | 56 | [116] | |
| ak92a | 1005 | 3 | 56 | [117] | |
| ak93 | 1006 | 3 | 56 | [118] | |
| ba00 | 1007 | 4 | 50 | [91] | |
| bm98 | 1008 | 3 | 56 | [119], chianti ([120,121]) | |
| bn00 | 1009 | 3 | 56 | [122], chianti ([123]) | |
| bp98 | 1010 | 3 | 56 | [90] | |
| ch00 | 1011 | 3 | 51 | , , , | chianti |
| ch00 | 1012 | 4 | 50 | , ,, | chianti |
| , | |||||
| ch01 | 1013 | 3 | 51 | chianti ([124]) | |
| ch01 | 1014 | 4 | 50 | chianti ([125,126]) | |
| ch02 | 1015 | 4 | 50 | chianti ([126,127]) | |
| ch02 | 1016 | 3 | 51 | chianti ([127]) | |
| ch04 | 1017 | 3 | 51 | chianti ([128,129]) | |
| ch04 | 1018 | 4 | 50 | chianti ([130,131,132]) | |
| ch05 | 1019 | 3 | 51 | chianti ([133]) | |
| ch05 | 1020 | 4 | 50 | chianti, chianti ([131]) | |
| ch06 | 1021 | 3 | 51 | chianti ([132,134]) | |
| ch06 | 1022 | 4 | 50 | chianti ([130,132]) | |
| ch07 | 1023 | 3 | 51 | chianti ([131,132]) | |
| ch07 | 1024 | 4 | 50 | chianti ([135,136,137]), nist | |
| ch08 | 1025 | 3 | 51 | chianti ([138]) | |
| ch08 | 1026 | 4 | 50 | chianti ([139,140]) | |
| ch09 | 1027 | 4 | 50 | chianti ([135]) | |
| ch09 | 1028 | 3 | 51 | chianti ([141,142]) | |
| ch10 | 1029 | 4 | 50 | chianti ([135,143]) | |
| ch10 | 1030 | 3 | 51 | chianti ([144]) | |
| ch11 | 1031 | 3 | 51 | chianti ([145]) | |
| ch11 | 1032 | 4 | 50 | chianti ([145]) | |
| ch12 | 1033 | 4 | 50 | chianti ([135,143,145]) | |
| ch12 | 1034 | 3 | 51 | chianti ([141,142]) | |
| ch13 | 1035 | 4 | 50 | chianti, chianti ([146]) | |
| ch13 | 1036 | 3 | 51 | chianti ([147,148,149,150]) | |
| ch14 | 1037 | 4 | 50 | chianti ([149]) | |
| ch14 | 1038 | 3 | 51 | chianti ([150,151,152]) | |
| ch15 | 1039 | 4 | 50 | chianti ([152,153]) | |
| ch15 | 1040 | 3 | 51 | chianti ([154]) | |
| ch16 | 1041 | 3 | 51 | chianti ([152,153] | |
| ch16 | 1042 | 4 | 50 | chianti ([155]) | |
| ch17 | 1043 | 4 | 50 | chianti ([156] | |
| ch17 | 1044 | 3 | 51 | chianti ([155,157]) | |
| ch18 | 1045 | 3 | 51 | chianti ([156]) | |
| ch18 | 1046 | 4 | 50 | chianti ([158]) | |
| ch19 | 1047 | 3 | 51 | chianti ([159,160]) | |
| ch19 | 1048 | 4 | 50 | chianti ([161]) | |
| ch20 | 1049 | 4 | 50 | chianti ([162]) | |
| ch20 | 1050 | 3 | 51 | chianti ([163,164]) | |
| ch21 | 1051 | 4 | 50 | chianti ([165]) | |
| ch21 | 1052 | 3 | 51 | chianti ([166]) | |
| ch22 | 1053 | 3 | 51 | chianti ([161]) | |
| ch22 | 1054 | 4 | 50 | chianti ([167]) | |
| ch23 | 1055 | 3 | 51 | chianti ([161,162]) | |
| ch24 | 1056 | 4 | 50 | chianti ([168]), nist | |
| ch24 | 1057 | 3 | 51 | chianti ([169]) | |
| ch25 | 1058 | 3 | 51 | chianti ([165]) | |
| ch25 | 1059 | 4 | 50 | chianti ([168,170,171]), nist | |
| ch26 | 1060 | 4 | 50 | chianti ([172]) | |
| ch26 | 1061 | 3 | 51 | chianti ([167]) | |
| ch27 | 1062 | 4 | 50 | chianti ([173]) | |
| ch27 | 1063 | 3 | 51 | chianti ([174]) | |
| ch28 | 1064 | 3 | 51 | chianti ([174,175]) | |
| ch28 | 1065 | 4 | 50 | chianti ([173,176]) | |
| ch29 | 1066 | 4 | 50 | chianti ([177]) | |
| ch29 | 1067 | 3 | 51 | chianti ([174,178]) | |
| ch30 | 1068 | 3 | 51 | chianti ([174,179]) | |
| ch30 | 1069 | 4 | 50 | chianti ([125,180]) | |
| ch31 | 1070 | 4 | 50 | chianti, chianti ([181]) | |
| ch31 | 1071 | 3 | 51 | chianti ([174,182]) | |
| ch32 | 1072 | 3 | 51 | chianti ([172]) | |
| ch32 | 1073 | 4 | 50 | chianti ([183]), nist | |
| ch33 | 1074 | 4 | 50 | chianti, chianti ([184]) | |
| ch33 | 1075 | 3 | 51 | chianti ([185]) | |
| ch34 | 1076 | 4 | 50 | chianti ([186,187]) | |
| ch34 | 1077 | 3 | 51 | chianti ([176]) | |
| ch35 | 1078 | 3 | 51 | chianti ([177]) | |
| ch35 | 1079 | 4 | 50 | chianti ([188]) | |
| ch36 | 1080 | 4 | 50 | chianti ([189,190]), nist | |
| ch36 | 1081 | 3 | 51 | chianti ([180]) | |
| ch37 | 1082 | 3 | 51 | chianti ([191]) | |
| ch37 | 1083 | 4 | 50 | chianti ([192]) | |
| ch38 | 1084 | 3 | 51 | chianti ([183]) | |
| ch39 | 1085 | 3 | 51 | chianti ([193]) | |
| ch40 | 1086 | 3 | 51 | chianti ([186,187,194]) | |
| ch41 | 1087 | 3 | 51 | chianti ([195,196]) | |
| ch42 | 1088 | 3 | 51 | chianti ([189,197]) | |
| ch43 | 1089 | 3 | 51 | chianti ([196,198]) | |
| cj94 | 1090 | 3 | 56 | [103,199] | |
| cp99 | 1091 | 4 | 50 | [200] | |
| cp99 | 1092 | 3 | 56 | [200] | |
| eg99 | 1093 | 3 | 56 | [180,201] | |
| ei99 | 1094 | 3 | 56 | chianti, [202] | |
| fe01 | 1095 | 4 | 50 | [203,204,205,206] | |
| fe10 | 1096 | 3 | 56 | chianti, [207] | |
| fe24 | 1097 | 3 | 56 | [127,208] | |
| gr58 | 1098 | 4 | 50 | [209] | |
| im | 1099 | 3 | 63 | , | Impact parameter method |
| kh84 | 1100 | 4 | 50 | [210] | |
| km87 | 1101 | 3 | 56 | [105,106,107,211] | |
| kn89 | 1102 | 3 | 69 | [104] | |
| kn89b | 1103 | 3 | 69 | [104,107,211] | |
| kn89c | 1104 | 3 | 69 | [104,105,106,107,211] | |
| mg05 | 1105 | 4 | 50 | PP95 ([212]), [213,214] | |
| ne01 | 1106 | 4 | 50 | chianti, PP95 ([212,215]) | |
| ne02 | 1107 | 4 | 50 | chianti, PP95 ([212,214]) | |
| np96 | 1108 | 4 | 50 | [216] | |
| ny01 | 1109 | 4 | 50 | [217,218,219] | |
| ox01 | 1110 | 4 | 50 | PP95 ([212,220]), chianti ([149]) | |
| ox02 | 1111 | 4 | 50 | chianti, PP95 ([212,215]) | |
| ox03 | 1112 | 4 | 50 | [218,219], PP95 ([212,214] | |
| pb95 | 1113 | 3 | 56 | [207] | |
| pp01 | 1114 | 4 | 50 | PP95 ([136,212,213]) | |
| pp01 | 1115 | 3 | 56 | PP95 ([221,222,223]) | |
| pp02 | 1116 | 3 | 56 | PP95 ([224,225]) | |
| pp03 | 1117 | 3 | 56 | PP95 ([225,226]) | |
| pp04 | 1118 | 3 | 56 | PP95 ([214]) | |
| pp05 | 1119 | 4 | 50 | PP95 ([212,214]) | |
| pp05 | 1120 | 3 | 56 | , | PP95 ([214]) |
| pp06 | 1121 | 3 | 56 | PP95 ([227]) | |
| pp06 | 1122 | 4 | 50 | , | PP95 ([212]) |
| pp07 | 1123 | 3 | 56 | PP95 ([228]) | |
| pp07 | 1124 | 4 | 50 | PP95 ([212,229,230]) | |
| pp08 | 1125 | 4 | 50 | PP95 ([212,231]) | |
| pp09 | 1126 | 4 | 50 | PP95 ([214]) | |
| pp10 | 1127 | 4 | 50 | PP95 ([232]) | |
| pp11 | 1128 | 4 | 50 | PP95 ([187,212]) | |
| rb96 | 1129 | 3 | 56 | [233], chianti ([234]) | |
| sm00 | 1130 | 3 | 51 | [235] | |
| ss01 | 1131 | 4 | 50 | chianti | |
| ss96 | 1132 | 3 | 56 | [236] | |
| tb93 | 1133 | 4 | 50 | [60] | |
| zh96 | 1134 | 3 | 56 | [237] | |
| zp97 | 1135 | 3 | 56 | [238] | |
| zs87 | 1136 | 3 | 56 | [106] | |
| bm01 | 1137 | 3 | 56 | [5] | |
| bm01 | 1138 | 4 | 50 | [5] | |
| bm02 | 1139 | 3 | 56 | [8] | |
| pm01 | 1140 | 4 | 50 | [6] | |
| pm02 | 1141 | 4 | 50 | [7] | |
| mk01 | 1142 | 4 | 50 | [9] | |
| gm01 | 1143 | 4 | 50 | [11] | |
| gk01 | 1144 | 4 | 50 | [17] | |
| pm03 | 1145 | 4 | 50 | [14] | |
| pq01 | 1146 | 4 | 50 | [15] | |
| pq02 | 1147 | 4 | 50 | [16] | |
| pq03 | 1148 | 4 | 50 | [22] | |
| pq04 | 1149 | 4 | 50 | [26] | |
| mb01 | 1150 | 3 | 56 | , | Unpublished |
| , | |||||
| fj01 | 1151 | 3 | 56 | [110] | |
| fj01 | 1152 | 4 | 50 | [110] | |
| gu01 | 1153 | 4 | 50 | [109] | |
| gu01 | 1154 | 13 | 6 | [109] | |
| kf01 | 1155 | 5 | 25 | , | [98] |
| , | |||||
| , | |||||
| , | |||||
| bb01 | 1156 | 5, 15 | 95 | [111] | |
| tb01 | 1157 | 7 | 53 | , , | Hydrogenic |
| tb02 | 1158 | 7 | 53 | [239] | |
| tb03 | 1159 | 7 | 53 | [240] | |
| tb04 | 1160 | 7 | 53 | [241] | |
| tb05 | 1161 | 7 | 53 | [242] | |
| tb06 | 1162 | 7 | 53 | [243] | |
| tb07 | 1163 | 7 | 53 | [60] | |
| tb08 | 1164 | 7 | 53 | [60] | |
| tb09 | 1165 | 7 | 53 | [60] | |
| tb10 | 1166 | 7 | 53 | [244] | |
| tb11 | 1167 | 7 | 53 | [60] | |
| tb12 | 1168 | 7 | 53 | [245] | |
| tb13 | 1169 | 7 | 53 | [246] | |
| tb14 | 1170 | 7 | 53 | [60,247] | |
| tb15 | 1171 | 7 | 53 | , , | [60] |
| tb16 | 1172 | 7 | 53 | [248] | |
| tb17 | 1173 | 7 | 53 | [249] | |
| tb18 | 1174 | 7 | 53 | [250] | |
| tb19 | 1175 | 7 | 53 | [251] | |
| tb20 | 1176 | 7 | 53 | [252] | |
| tb21 | 1177 | 7 | 53 | [218] | |
| vy01 | 1178 | 1, 7 | 59 | , | [102] |
| , , | |||||
| , , , | |||||
| , , | |||||
| kp01 | 1179 | 7 | 53 | [3,5,8,10] | |
| gg01 | 1180 | 7 | 53 | [21,37] | |
| gm01 | 1181 | 7 | 53 | [11] | |
| gg02 | 1182 | 7 | 49 | [23,32,33] | |
| gk01 | 1183 | 7 | 53 | [17] | |
| wk01 | 1184 | 7 | 49 | [18] | |
| gg03 | 1185 | 7 | 49 | [13,35,253] | |
| wk02 | 1186 | 7 | 49 | [19] | |
| gg04 | 1187 | 7 | 49 | [25] | |
| wk03 | 1188 | 7 | 49 | [24] | |
| wk04 | 1189 | 7 | 49 | [20] | |
| tr01 | 1190 | 7 | 49 | , | [27] |
| tr02 | 1191 | 7 | 49 | , | [28] |
| tr03 | 1192 | 7 | 49 | , | [29] |
| , | |||||
| ap01 | 1193 | 8 | 1 | , | [89,97] |
| ap01 | 1194 | 8 | 7 | , , | [89,97] |
| ad01 | 1195 | 8 | 38 | , | AMDPP ([65]) |
| ad01 | 1196 | 8 | 39 | , , | AMDPP ([64]) |
| , | |||||
| ns01 | 1197 | 8 | 22 | , | [99] |
| gt01 | 1198 | 8 | 30 | [100] |
References
- Kallman, T.; Bautista, M. Photoionization and High-Density Gas. Astrophys. J. Suppl. Ser. 2001, 133, 221–253. [Google Scholar] [CrossRef]
- Bautista, M.A.; Kallman, T.R. The XSTAR Atomic Database. Astrophys. J. Suppl. Ser. 2001, 134, 139–149. [Google Scholar] [CrossRef]
- Palmeri, P.; Mendoza, C.; Kallman, T.R.; Bautista, M.A. On the Structure of the Iron K Edge. Astrophys. J. 2002, 577, L119–L122. [Google Scholar] [CrossRef]
- Palmeri, P.; Mendoza, C.; Kallman, T.; Bautista, M. Photoionization of the Fe Ions: Structure of the K-Edge. In X-ray and Inner-Shell Processes; Bianconi, A., Marcelli, A., Saini, N.L., Eds.; American Institute of Physics: College Park, MD, USA, 2003; AIP Conf. Proc.; Volume 652, pp. 159–164. [Google Scholar] [CrossRef]
- Bautista, M.A.; Mendoza, C.; Kallman, T.R.; Palmeri, P. Atomic data for the K-vacancy states of Fe XXIV. Astron. Astrophys. 2003, 403, 339–355. [Google Scholar] [CrossRef] [Green Version]
- Palmeri, P.; Mendoza, C.; Kallman, T.R.; Bautista, M.A. A complete set of radiative and Auger rates for K-vacancy states in Fe XVIII-Fe XXV. Astron. Astrophys. 2003, 403, 1175–1184. [Google Scholar] [CrossRef]
- Palmeri, P.; Mendoza, C.; Kallman, T.R.; Bautista, M.A.; Meléndez, M. Modeling of iron K lines: Radiative and Auger decay data for Fe II-Fe IX. Astron. Astrophys. 2003, 410, 359–364. [Google Scholar] [CrossRef] [Green Version]
- Bautista, M.A.; Mendoza, C.; Kallman, T.R.; Palmeri, P. K-shell photoionization and electron impact excitation of Fe XVII-Fe XXIII. Astrophys. J. Suppl. Ser. 2004, 418, 1171–1178. [Google Scholar] [CrossRef] [Green Version]
- Mendoza, C.; Kallman, T.R.; Bautista, M.A.; Palmeri, P. Decay properties of K-vacancy states in Fe X-Fe XVII. Astron. Astrophys. 2004, 414, 377–388. [Google Scholar] [CrossRef]
- Kallman, T.R.; Palmeri, P.; Bautista, M.A.; Mendoza, C.; Krolik, J.H. Photoionization Modeling and the K Lines of Iron. Astrophys. J. Suppl. Ser. 2004, 155, 675–701. [Google Scholar] [CrossRef] [Green Version]
- García, J.; Mendoza, C.; Bautista, M.A.; Gorczyca, T.W.; Kallman, T.R.; Palmeri, P. K-Shell Photoabsorption of Oxygen Ions. Astrophys. J. Suppl. Ser. 2005, 158, 68–79. [Google Scholar] [CrossRef] [Green Version]
- Palmeri, P.; Kallman, T.R.; Mendoza, C.; Bautista, M.A.; Krolik, J.H. Photoionization Modeling: the K Lines and Edges of Iron. In X-ray Diagnostics of Astrophysical Plasmas: Theory, Experiment, and Observation; Smith, R., Ed.; American Institute of Physics: College Park, MD, USA, 2005; AIP Conf. Proc.; Volume 774, pp. 75–82. [Google Scholar] [CrossRef]
- Juett, A.M.; Schulz, N.S.; Chakrabarty, D.; Gorczyca, T.W. High-Resolution X-ray Spectroscopy of the Interstellar Medium. II. Neon and Iron Absorption Edges. Astrophys. J. 2006, 648, 1066–1078. [Google Scholar] [CrossRef] [Green Version]
- Palmeri, P.; Mendoza, C.; Bautista, M.A.; García, J.; Kallman, T.R. K lines in the sulphur isonuclear sequence. Rad. Phys. Chem. 2006, 75, 1465–1470. [Google Scholar] [CrossRef]
- Palmeri, P.; Quinet, P.; Mendoza, C.; Bautista, M.A.; García, J.; Kallman, T.R. Radiative and Auger Decay of K-Vacancy Levels in the Ne, Mg, Si, S, Ar, and Ca Isonuclear Sequences. Astrophys. J. Suppl. Ser. 2008, 177, 408–416. [Google Scholar] [CrossRef] [Green Version]
- Palmeri, P.; Quinet, P.; Mendoza, C.; Bautista, M.A.; García, J.; Witthoeft, M.C.; Kallman, T.R. Radiative and Auger Decay Data for Modeling Nickel K Lines. Astrophys. J. Suppl. Ser. 2008, 179, 542–552. [Google Scholar] [CrossRef] [Green Version]
- García, J.; Kallman, T.R.; Witthoeft, M.; Behar, E.; Mendoza, C.; Palmeri, P.; Quinet, P.; Bautista, M.A.; Klapisch, M. Nitrogen K-Shell Photoabsorption. Astrophys. J. Suppl. Ser. 2009, 185, 477–485. [Google Scholar] [CrossRef] [Green Version]
- Witthoeft, M.C.; Bautista, M.A.; Mendoza, C.; Kallman, T.R.; Palmeri, P.; Quinet, P. K-Shell Photoionization and Photoabsorption of Ne, Mg, Si, S, Ar, and Ca. Astrophys. J. Suppl. Ser. 2009, 182, 127–130. [Google Scholar] [CrossRef] [Green Version]
- Witthoeft, M.C.; García, J.; Kallman, T.R.; Bautista, M.A.; Mendoza, C.; Palmeri, P.; Quinet, P. K-shell Photoionization of Na-like to Cl-like Ions of Mg, Si, S, Ar, and Ca. Astrophys. J. Suppl. Ser. 2011, 192, 7. [Google Scholar] [CrossRef] [Green Version]
- Witthoeft, M.C.; Bautista, M.A.; García, J.; Kallman, T.R.; Mendoza, C.; Palmeri, P.; Quinet, P. K-shell Photoionization of Nickel Ions using R-matrix. Astrophys. J. Suppl. Ser. 2011, 196, 7. [Google Scholar] [CrossRef] [Green Version]
- Hasoglu, M.F.; Abdel-Naby, S.A.; Gorczyca, T.W.; Drake, J.J.; McLaughlin, B.M. K-shell Photoabsorption Studies of the Carbon Isonuclear Sequence. Astrophys. J. 2010, 724, 1296–1304. [Google Scholar] [CrossRef]
- Palmeri, P.; Quinet, P.; Mendoza, C.; Bautista, M.A.; García, J.; Witthoeft, M.C.; Kallman, T.R. Atomic decay data for modeling the Al K lines. Astron. Astrophys. 2011, 525, A59. [Google Scholar] [CrossRef] [Green Version]
- Gorczyca, T.W.; Bautista, M.A.; Hasoglu, M.F.; García, J.; Gatuzz, E.; Kaastra, J.S.; Kallman, T.R.; Manson, S.T.; Mendoza, C.; Raassen, A.J.J.; et al. A Comprehensive X-ray Absorption Model for Atomic Oxygen. Astrophys. J. 2013, 779, 78. [Google Scholar] [CrossRef] [Green Version]
- Witthoeft, M.C.; Bautista, M.A.; García, J.; Kallman, T.R.; Mendoza, C.; Palmeri, P.; Quinet, P. Photoionization and photoabsorption cross sections for the aluminum iso-nuclear sequence. At. Data Nucl. Data Tables 2013, 99, 53–61. [Google Scholar] [CrossRef]
- Hasoğlu, M.F.; Abdel-Naby, S.A.; Gatuzz, E.; García, J.; Kallman, T.R.; Mendoza, C.; Gorczyca, T.W. K-shell Photoabsorption of Magnesium Ions. Astrophys. J. Suppl. Ser. 2014, 214, 8. [Google Scholar] [CrossRef] [Green Version]
- Palmeri, P.; Quinet, P.; Mendoza, C.; Bautista, M.A.; García, J.; Witthoeft, M.C.; Kallman, T.R. Atomic decay data for modeling K lines of iron peak and light odd-Z elements. Astron. Astrophys. 2012, 543, A44. [Google Scholar] [CrossRef] [Green Version]
- Palmeri, P.; Quinet, P.; Mendoza, C.; Bautista, M.A.; Witthoeft, M.C.; Kallman, T.R. K-shell photoabsorption and photoionisation of trace elements. I. Isoelectronic sequences with electron number 3 ≤ N ≤ 11. Astron. Astrophys. 2016, 589, A137. [Google Scholar] [CrossRef] [Green Version]
- Mendoza, C.; Bautista, M.A.; Palmeri, P.; Quinet, P.; Witthoeft, M.C.; Kallman, T.R. K-shell photoabsorption and photoionization of trace elements. II. Isoelectronic sequences with electron number 12 ≤ N ≤ 18. Astron. Astrophys. 2017, 604, A63. [Google Scholar] [CrossRef] [Green Version]
- Mendoza, C.; Bautista, M.A.; Palmeri, P.; Quinet, P.; Witthoeft, M.C.; Kallman, T.R. K-shell photoabsorption and photoionization of trace elements. III. Isoelectronic sequences with electron number 19 ≤ N ≤ 26. Astron. Astrophys. 2018, 616, A62. [Google Scholar] [CrossRef]
- Kallman, T.R.; Bautista, M.A.; Goriely, S.; Mendoza, C.; Miller, J.M.; Palmeri, P.; Quinet, P.; Raymond, J. Spectrum Synthesis Modeling of the X-ray Spectrum of GRO J1655-40 Taken During the 2005 Outburst. Astrophys. J. 2009, 701, 865–884. [Google Scholar] [CrossRef]
- García, J.; Ramírez, J.M.; Kallman, T.R.; Witthoeft, M.; Bautista, M.A.; Mendoza, C.; Palmeri, P.; Quinet, P. Modeling the Oxygen K Absorption in the Interstellar Medium: An XMM-Newton View of Sco X-1. Astrophys. J. 2011, 731, L15. [Google Scholar] [CrossRef] [Green Version]
- Gatuzz, E.; García, J.; Mendoza, C.; Kallman, T.R.; Witthoeft, M.; Lohfink, A.; Bautista, M.A.; Palmeri, P.; Quinet, P. Photoionization Modeling of Oxygen K Absorption in the Interstellar Medium: The Chandra Grating Spectra of XTE J1817-330. Astrophys. J. 2013, 768, 60. [Google Scholar] [CrossRef] [Green Version]
- Gatuzz, E.; García, J.; Mendoza, C.; Kallman, T.R.; Witthoeft, M.; Lohfink, A.; Bautista, M.A.; Palmeri, P.; Quinet, P. Erratum: “Photoionization Modeling of Oxygen K Absorption in the Interstellar Medium, the Chandra Grating Spectra of XTE J1817-330” (2013, ApJ, 768, 60). Astrophys. J. 2013, 778, 83. [Google Scholar] [CrossRef] [Green Version]
- Gatuzz, E.; García, J.; Mendoza, C.; Kallman, T.R.; Bautista, M.A.; Gorczyca, T.W. Physical Properties of the Interstellar Medium Using High-resolution Chandra Spectra: O K-edge Absorption. Astrophys J. 2014, 790, 131. [Google Scholar] [CrossRef] [Green Version]
- Gatuzz, E.; García, J.; Kallman, T.R.; Mendoza, C.; Gorczyca, T.W. ISMabs: A Comprehensive X-ray Absorption Model for the Interstellar Medium. Astrophys. J. 2015, 800, 29. [Google Scholar] [CrossRef]
- Gatuzz, E.; García, J.A.; Kallman, T.R.; Mendoza, C. Oxygen, neon, and iron X-ray absorption in the local interstellar medium. Astron. Astrophys. 2016, 588, A111. [Google Scholar] [CrossRef] [Green Version]
- Gatuzz, E.; Ness, J.U.; Gorczyca, T.W.; Hasoglu, M.F.; Kallman, T.R.; García, J.A. Carbon X-ray absorption in the local ISM: Fingerprints in X-ray Novae spectra. Mon. Not. R. Astron. Soc. 2018, 479, 2457–2463. [Google Scholar] [CrossRef]
- Gatuzz, E.; García, J.A.; Kallman, T.R. On the discrepancy between the X-ray and UV absorption measurements of O VI in the local ISM. Mon. Not. R. Astron. Soc. 2019, 483, L75–L79. [Google Scholar] [CrossRef]
- Gatuzz, E.; Gorczyca, T.W.; Hasoglu, M.F.; Schulz, N.S.; Corrales, L.; Mendoza, C. Silicon ISM X-ray absorption: The gaseous component. Mon. Not. R. Astron. Soc. 2020, 498, L20–L24. [Google Scholar] [CrossRef]
- Deprince, J.; Palmeri, P.; Quinet, P.; Fritzsche, S.; Bautista, M.; Mendoza, C.; Kallman, T.R.; García, J.A. Plasma-Environment Effects on the Atomic Structure and K Lines of He- and Li-like Oxygen Ions. In Workshop on Astrophysical Opacities; Astronomical Society of the Pacific: San Francisco, CA, USA, 2018; AIP Conf. Ser.; Volume 515, p. 289. [Google Scholar]
- Deprince, J.; Bautista, M.A.; Fritzsche, S.; García, J.A.; Kallman, T.R.; Mendoza, C.; Palmeri, P.; Quinet, P. Plasma environment effects on K lines of astrophysical interest. I. Atomic structure, radiative rates, and Auger widths of oxygen ions. Astron. Astrophys. 2019, 624, A74. [Google Scholar] [CrossRef] [Green Version]
- Deprince, J.; Bautista, M.A.; Fritzsche, S.; García, J.A.; Kallman, T.; Mendoza, C.; Palmeri, P.; Quinet, P. Plasma environment effects on K lines of astrophysical interest. II. Ionization potentials, K thresholds, radiative rates, and Auger widths in Ne- through He-like iron ions (Fe XVII–Fe XXV). Astron. Astrophys. 2019, 626, A83. [Google Scholar] [CrossRef] [Green Version]
- Deprince, J.; Bautista, M.A.; Fritzsche, S.; García, J.A.; Kallman, T.R.; Mendoza, C.; Palmeri, P.; Quinet, P. Plasma-environment effects on K lines of astrophysical interest. III. IPs, K thresholds, radiative rates, and Auger widths in Fe IX–Fe XVI. Astron. Astrophys. 2020, 635, A70. [Google Scholar] [CrossRef]
- Deprince, J.; Bautista, M.; Fritzsche, S.; García, J.; Kallman, T.; Mendoza, C.; Palmeri, P.; Quinet, P. K-line X-ray fluorescence from highly charged iron ions under dense astrophysical plasma conditions. X-ray Spectrom. 2020, 49, 29–32. [Google Scholar] [CrossRef]
- Deprince, J.; Bautista, M.A.; Fritzsche, S.; García, J.A.; Kallman, T.R.; Mendoza, C.; Palmeri, P.; Quinet, P. Plasma environment effects on K lines of astrophysical interest. IV. IPs, K thresholds, radiative rates, and Auger widths in Fe II-Fe VIII. Astron. Astrophys. 2020, 643, A57. [Google Scholar] [CrossRef]
- Kallman, T.; Bautista, M.; Deprince, J.; Garcia, J.A.; Mendoza, C.; Ogorzalek, A.; Palmeri, P.; Quinet, P. Photoionization Models for High Density Gas. arXiv 2020, arXiv:2011.10603. [Google Scholar]
- Hitomi Collaboration; Aharonian, F.; Akamatsu, H.; Akimoto, F.; Allen, S.W.; Anabuki, N.; Angelini, L.; Arnaud, K.; Audard, M.; Awaki, H.; et al. The quiescent intracluster medium in the core of the Perseus cluster. Nature 2016, 535, 117–121. [Google Scholar] [CrossRef] [Green Version]
- Nikolić, D.; Gorczyca, T.W.; Korista, K.T.; Ferland, G.J.; Badnell, N.R. Suppression of Dielectronic Recombination due to Finite Density Effects. Astrophys. J. 2013, 768, 82. [Google Scholar] [CrossRef] [Green Version]
- Nikolić, D.; Gorczyca, T.W.; Korista, K.T.; Chatzikos, M.; Ferland, G.J.; Guzmán, F.; van Hoof, P.A.M.; Williams, R.J.R.; Badnell, N.R. Suppression of Dielectronic Recombination Due to Finite Density Effects. II. Analytical Refinement and Application to Density-dependent Ionization Balances and AGN Broad-line Emission. Astrophys. J. Suppl. 2018, 237, 41. [Google Scholar] [CrossRef] [Green Version]
- García, J.A.; Fabian, A.C.; Kallman, T.R.; Dauser, T.; Parker, M.L.; McClintock, J.E.; Steiner, J.F.; Wilms, J. The effects of high density on the X-ray spectrum reflected from accretion discs around black holes. Mon. Not. R. Astron. Soc. 2016, 462, 751–760. [Google Scholar] [CrossRef] [Green Version]
- García, J.A.; Kallman, T.R.; Bautista, M.; Mendoza, C.; Deprince, J.; Palmeri, P.; Quinet, P. The Problem of the High Iron Abundance in Accretion Disks around Black Holes. In Workshop on Astrophysical Opacities; Astronomical Society of the Pacific: San Francisco, CA, USA, 2018; AIP Conf. Ser.; Volume 515, p. 282. [Google Scholar]
- Leutenegger, M.A.; Kühn, S.; Micke, P.; Steinbrügge, R.; Stierhof, J.; Shah, C.; Hell, N.; Bissinger, M.; Hirsch, M.; Ballhausen, R.; et al. High-Precision Determination of Oxygen Kα Transition Energy Excludes Incongruent Motion of Interstellar Oxygen. Phys. Rev. Lett. 2020, 125, 243001. [Google Scholar] [CrossRef] [PubMed]
- Greisen, E.W. FITS: A Remarkable Achievement in Information Exchange. In Information Handling in Astronomy—Historical Vistas; Heck, A., Ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003; Astrophysics and Space Science Library; Volume 285, p. 71. [Google Scholar] [CrossRef] [Green Version]
- Pence, W.D.; Chiappetti, L.; Page, C.G.; Shaw, R.A.; Stobie, E. Definition of the Flexible Image Transport System (FITS), version 3.0. Astron. Astrophys. 2010, 524, A42. [Google Scholar] [CrossRef] [Green Version]
- Cowan, R.D. The Theory of Atomic Structure and Spectra; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
- Berrington, K.A.; Eissner, W.B.; Norrington, P.H. RMATRX1: Belfast atomic R-matrix codes. Comput. Phys. Commun. 1995, 92, 290–420. [Google Scholar] [CrossRef]
- Burke, P.G. R-Matrix Theory of Atomic Collisions; Springer: New York, NY, USA, 2011. [Google Scholar]
- Gorczyca, T.W.; Robicheaux, F. Auger decay of the photoexcited 2p-1nl Rydberg series in argon. Phys. Rev. A 1999, 60, 1216–1225. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2020. Available online: https://physics.nist.gov/asd (accessed on 15 November 2020).
- Cunto, W.; Mendoza, C.; Ochsenbein, F.; Zeippen, C.J. TOPbase at the CDS. Astron. Astrophys. 1993, 275, L5–L8. [Google Scholar]
- Dere, K.P.; Landi, E.; Mason, H.E.; Monsignori Fossi, B.C.; Young, P.R. CHIANTI—An atomic database for emission lines. Astron. Astrophys. Suppl. Ser. 1997, 125, 149–173. [Google Scholar] [CrossRef] [Green Version]
- Hummer, D.G.; Berrington, K.A.; Eissner, W.; Pradhan, A.K.; Saraph, H.E.; Tully, J.A. Atomic data from the IRON project. I. Goals and methods. Astron. Astrophys. 1993, 279, 298–309. [Google Scholar]
- Pradhan, A.K.; Peng, J. Atomic Data For The Analysis of Emission Lines. In The Analysis of Emission Lines; Williams, R.E.W., Livio, M., Eds.; Space Institute Symposium Series; Cambridge University Press: Cambridge, UK, 1995; Volume 8, pp. 8–34. [Google Scholar]
- Badnell, N.R.; O’Mullane, M.G.; Summers, H.P.; Altun, Z.; Bautista, M.A.; Colgan, J.; Gorczyca, T.W.; Mitnik, D.M.; Pindzola, M.S.; Zatsarinny, O. Dielectronic recombination data for dynamic finite-density plasmas. I. Goals and methodology. Astron. Astrophys. 2003, 406, 1151–1165. [Google Scholar] [CrossRef]
- Badnell, N.R. Radiative Recombination Data for Modeling Dynamic Finite-Density Plasmas. Astrophys. J. Suppl. Ser. 2006, 167, 334–342. [Google Scholar] [CrossRef] [Green Version]
- Eissner, W.; Jones, M.; Nussbaumer, H. Techniques for the calculation of atomic structures and radiative data including relativistic corrections. Comput. Phys. Commun. 1974, 8, 270–306. [Google Scholar] [CrossRef]
- Badnell, N.R. A Breit-Pauli distorted wave implementation for AUTOSTRUCTURE. Comput. Phys. Commun. 2011, 182, 1528–1535. [Google Scholar] [CrossRef]
- Parpia, F.A.; Fischer, C.F.; Grant, I.P. GRASP92: A package for large-scale relativistic atomic structure calculations. Comput. Phys. Commun. 1996, 94, 249–271. [Google Scholar] [CrossRef]
- Hickman, A.P. Complex potential model for dielectronic recombination. J. Phys. B At. Mol. Phys. 1984, 17, L101–L106. [Google Scholar] [CrossRef]
- Robicheaux, F.; Gorczyca, T.W.; Pindzola, M.S.; Badnell, N.R. Inclusion of radiation damping in the close-coupling equations for electron-atom scattering. Phys. Rev. A 1995, 52, 1319–1333. [Google Scholar] [CrossRef] [PubMed]
- Davies, P.C.W.; Seaton, M.J. Radiation damping in the optical continuum. J. Phys. B At. Mol. Phys. 1969, 2, 757–765. [Google Scholar] [CrossRef]
- Bell, R.H.; Seaton, M.J. Dielectronic recombination. I. General theory. J. Phys. B At. Mol. Phys. 1985, 18, 1589–1629. [Google Scholar] [CrossRef]
- Froese Fischer, C. The Hartree-Fock Method for Atom; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Froese Fischer, C. A general multi-configuration Hartree-Fock program. Comput. Phys. Commun. 1991, 64, 431–454. [Google Scholar] [CrossRef]
- Froese Fischer, C.; Brage, T.; Jönsson, P. Computational Atomic Structure: An MCHF Approach; Institute of Physics Publ.: Bristol, UK, 1997. [Google Scholar]
- Stolte, W.C.; Lu, Y.; Samson, J.A.R.; Hemmers, O.; Hansen, D.L.; Whitfield, S.B.; Wang, H.; Glans, P.; Lindle, D.W. The K-shell Auger decay of atomic oxygen. J. Phys. B At. Mol. Phys. 1997, 30, 4489–4497. [Google Scholar] [CrossRef]
- Liao, J.Y.; Zhang, S.N.; Yao, Y. Wavelength Measurements of K Transitions of Oxygen, Neon, and Magnesium with X-ray Absorption Lines. Astrophys. J. 2013, 774, 116. [Google Scholar] [CrossRef] [Green Version]
- Juett, A.M.; Schulz, N.S.; Chakrabarty, D. High-Resolution X-ray Spectroscopy of the Interstellar Medium: Structure at the Oxygen Absorption Edge. Astrophys. J. 2004, 612, 308–318. [Google Scholar] [CrossRef] [Green Version]
- McLaughlin, B.M.; Ballance, C.P.; Bowen, K.P.; Gardenghi, D.J.; Stolte, W.C. High Precision K-shell Photoabsorption Cross Sections for Atomic Oxygen: Experiment and Theory. Astrophys. J. 2013, 771, L8. [Google Scholar] [CrossRef] [Green Version]
- McLaughlin, B.M.; Ballance, C.P.; Bowen, K.P.; Gardenghi, D.J.; Stolte, W.C. Erratum: “High Precision K-Shell Photoabsorption Cross Sections for Atomic Oxygen: Experiment and Theory” (2013, ApJL, 771, l8). Astrophys. J. 2013, 779, L31. [Google Scholar] [CrossRef] [Green Version]
- Menzel, A.; Benzaid, S.; Krause, M.O.; Caldwell, C.D.; Hergenhahn, U.; Bissen, M. Natural widths in open-shell atoms: The K absorption spectrum of atomic oxygen. Phys. Rev. A 1996, 54, R991–R994. [Google Scholar] [CrossRef]
- Caldwell, C.; Schaphorst, S.; Krause, M.; Jiménez-Mier, J. Photoexcited K Auger spectra of atomic and molecular oxygen. JESRP 1994, 67, 243–259. [Google Scholar] [CrossRef]
- Fabian, A.C.; Ross, R.R. X-ray Reflection. Space Sci. Rev. 2010, 157, 167–176. [Google Scholar] [CrossRef]
- Badnell, N.R.; Pindzola, M.S.; Dickson, W.J.; Summers, H.P.; Griffin, D.C.; Lang, J. Electric Field Effects on Dielectronic Recombination in a Collisional-Radiative Model. Astrophys. J. 1993, 407, L91. [Google Scholar] [CrossRef]
- Nahar, S.N.; Pradhan, A.K. Electron-ion recombination in the close-coupling approximation. Phys. Rev. Lett. 1992, 68, 1488–1491. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nahar, S.N.; Pradhan, A.K. Unified treatment of electron-ion recombination in the close-coupling approximation. Phys. Rev A 1994, 49, 1816–1835. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- García, J.; Kallman, T.R. X-ray Reflected Spectra from Accretion Disk Models. I. Constant Density Atmospheres. Astrophys. J. 2010, 718, 695–706. [Google Scholar] [CrossRef] [Green Version]
- García, J.; Dauser, T.; Reynolds, C.S.; Kallman, T.R.; McClintock, J.E.; Wilms, J.; Eikmann, W. X-ray Reflected Spectra from Accretion Disk Models. III. A Complete Grid of Ionized Reflection Calculations. Astrophys. J. 2013, 768, 146. [Google Scholar] [CrossRef] [Green Version]
- Aldrovandi, S.M.V.; Pequignot, D. Radiative and Dielectronic Recombination Coefficients for Complex Ions. Astron. Astrophys. 1973, 25, 137. [Google Scholar]
- Bautista, M.A.; Pradhan, A.K. Ionization Structure and Spectra of Iron in Gaseous Nebulae. Astrophys. J. 1998, 492, 650–676. [Google Scholar] [CrossRef] [Green Version]
- Bautista, M.A. Theoretical Calculations of Atomic Data for Spectroscopy. In Atomic Data Needs for X-ray Astronomy; Bautista, M.A., Kallman, T.R., Pradhan, A.K., Eds.; NASA/CP-2000-209968; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2000; pp. 25–40. [Google Scholar]
- Ralchenko, Y.; Kramida, A. Development of NIST Atomic Databases and Online Tools. Atoms 2020, 8, 56. [Google Scholar] [CrossRef]
- Albert, D.; Antony, B.K.; Ba, Y.A.; Babikov, Y.L.; Bollard, P.; Boudon, V.; Delahaye, F.; Del Zanna, G.; Dimitrijević, M.S.; Drouin, B.J.; et al. A Decade with VAMDC: Results and Ambitions. Atoms 2020, 8, 76. [Google Scholar] [CrossRef]
- Mendoza, C.; Boswell, J.; Ajoku, D.; Bautista, M. AtomPy: An Open Atomic Data Curation Environment for Astrophysical Applications. Atoms 2014, 2, 123–156. [Google Scholar] [CrossRef] [Green Version]
- Juan de Dios, L.; Rodríguez, M. The impact of atomic data selection on nebular abundance determinations. Mon. Not. R. Astron. Soc. 2017, 469, 1036–1053. [Google Scholar] [CrossRef] [Green Version]
- Morisset, C.; Luridiana, V.; García-Rojas, J.; Gómez-Llanos, V.; Bautista, M. Atomic Data Assessment with PyNeb. Atoms 2020, 8, 66. [Google Scholar] [CrossRef]
- Aldrovandi, S.M.V.; Pequignot, D. Erratum; Radiative and Dielectronic Recombination Coefficients for Complex Ions. Astron. Astrophys. 1976, 47, 321. [Google Scholar]
- Kingdon, J.B.; Ferland, G.J. Rate Coefficients for Charge Transfer between Hydrogen and the First 30 Elements. Astrophys. J. Suppl. Ser. 1996, 106, 205. [Google Scholar] [CrossRef] [Green Version]
- Nussbaumer, H.; Storey, P.J. Dielectronic recombination at low temperatures. III—Recombination coefficients for Mg, Al, Si. Astron. Astrophys. Suppl. Ser. 1986, 64, 545–555. [Google Scholar]
- Gould, R.J.; Thakur, R.K. Atomic processes in a low-density hydrogen-helium plasma. Ann. Phys. 1970, 61, 351–386. [Google Scholar] [CrossRef]
- Burgess, A.; Tully, J.A. On the analysis of collision strengths and rate coefficients. Astron. Astrophys. 1992, 254, 436–453. [Google Scholar]
- Verner, D.A.; Yakovlev, D.G. Analytic FITS for partial photoionization cross sections. Astron. Astrophys. Suppl. Ser. 1995, 109, 125–133. [Google Scholar]
- Callaway, J. Effective Collision Strengths for Hydrogen and Hydrogen-Like Ions. At. Data Nucl. Data Tables 1994, 57, 9–20. [Google Scholar] [CrossRef]
- Kato, T.; Nakazaki, S. Recommended Data for Excitation Rate Coefficients of Helium Atoms and Helium-like Ions by Electron Impact. Atom. Data Nucl. Data Tables 1989, 42, 313. [Google Scholar] [CrossRef]
- Keenan, F.P.; McCann, S.M.; Kingston, A.E. Electron Impact Excitation Rates for Transitions from the Ground State to the n = 2 and 3 levels in Helium-Like Ions. Phys. Scr. 1987, 35, 432–436. [Google Scholar] [CrossRef]
- Zhang, H.; Sampson, D.H. Collision Rates for Excitation of Helium-like Ions with Inclusion of Resonance Effects. Astrophys. J. Suppl. Ser. 1987, 63, 487. [Google Scholar] [CrossRef]
- Sampson, D.H.; Goett, S.J.; Clark, R.E.H. Electron-Impact Collision Strengths for Inner-Shell Excitation of Doubly Excited Levels from Singly Excited Levels in He-like Ions. At. Data Nucl. Data Tables 1983, 28, 299. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Fawcett, B.C.; Phillips, K.J.H.; Lemen, J.R.; Mason, H.E. A comparison of theoretical and solar-flare intensity ratios for the Fe XIX X-ray lines. Mon. Not. R. Astron. Soc. 1989, 240, 421–444. [Google Scholar] [CrossRef] [Green Version]
- Gu, M.F.; Holczer, T.; Behar, E.; Kahn, S.M. Inner-Shell Absorption Lines of Fe VI-Fe XVI: A Many-Body Perturbation Theory Approach. Astrophys. J. 2006, 641, 1227–1232. [Google Scholar] [CrossRef] [Green Version]
- Foster, A.R.; Ji, L.; Smith, R.K.; Brickhouse, N.S. Updated Atomic Data and Calculations for X-ray Spectroscopy. Astrophys. J. 2012, 756, 128. [Google Scholar] [CrossRef] [Green Version]
- Bryans, P.; Badnell, N.R.; Gorczyca, T.W.; Laming, J.M.; Mitthumsiri, W.; Savin, D.W. Collisional Ionization Equilibrium for Optically Thin Plasmas. I. Updated Recombination Rate Coefficients for Bare through Sodium-like Ions. Astrophys. J. Suppl. Ser. 2006, 167, 343–356. [Google Scholar] [CrossRef] [Green Version]
- Abu-Salbi, N.; Callaway, J. Electron-impact excitation of hydrogenic ions. Phys. Rev. A 1981, 24, 2372–2386. [Google Scholar] [CrossRef]
- Aggarwal, K.M.; Callaway, J.; Kingston, A.E.; Unnikrishnan, K. Excitation Rate Coefficients for Transitions among the N = 1, 2, and 3 Levels of He+. Astrophys. J. Suppl. Ser. 1992, 80, 473. [Google Scholar] [CrossRef]
- Aggarwal, K.M.; Kingston, A.E. Electron impact excitation of C VI: Collision strengths and rate coefficients. J. Phys. B At. Mol. Phys. 1991, 24, 4583–4602. [Google Scholar] [CrossRef]
- Aggarwal, K.M.; Kingston, A.E. Electron impact excitation of Ne X: Collision strengths and rate coefficients. Phys. Scr. 1991, 44, 517–527. [Google Scholar] [CrossRef]
- Aggarwal, K.M.; Kingston, A.E. Electron impact excitation of Si XIV: Collision strengths and rate coefficients. Phys. Scr. 1992, 46, 193–201. [Google Scholar] [CrossRef]
- Aggarwal, K.M.; Kingston, A.E. Electron impact excitation of Ca XX: Collision strengths and rate coefficients. J. Phys. B At. Mol. Phys. 1992, 25, 751–771. [Google Scholar] [CrossRef]
- Aggarwal, K.M.; Kingston, A.E. Electron Impact Excitation of Fe xxvi: Collision Strengths and Rate Coefficients. Astrophys J. Suppl. 1993, 85, 187. [Google Scholar] [CrossRef]
- Binello, A.M.; Mason, H.E.; Storey, P.J. Atomic data from the IRON Project. XXV. Electron impact excitation of fine-structure transitions in the ground configuration of Fe XII. Astron. Astrophys. Suppl. Ser. 1998, 127, 545–553. [Google Scholar] [CrossRef] [Green Version]
- Flower, D.R. Excitation of the Fe XII spectrum in the solar corona. Astron. Astrophys. 1977, 54, 163–166. [Google Scholar]
- Tayal, S.S.; Henry, R.J.W.; Pradhan, A.K. Electron Excitation of Fine-Structure Transitions within the Ground 3s23p3 Configuration in Fe XII. Astrophys. J. 1987, 319, 951. [Google Scholar] [CrossRef]
- Berrington, K.A.; Nakazaki, S.; Norrington, P.H. Atomic data from the IRON Project. XLI. Electron excitation rates among the 3d2 fine-structure levels of Ca-like Fe VII. Astron. Astrophys. Suppl. Ser. 2000, 142, 313–316. [Google Scholar] [CrossRef] [Green Version]
- Keenan, F.P.; Norrington, P.H. Relative emission line strengths for Fe VII in astrophysical plasmas. Astron. Astrophys. 1987, 181, 370–372. [Google Scholar]
- Gau, J.N.; Henry, R.J.W. Excitation of lithiumlike ions by electron impact. Phys. Rev. A 1977, 16, 986–990. [Google Scholar] [CrossRef]
- Wiese, W.L.; Smith, M.W.; Glennon, B.M. Atomic Transition Probabilities. Vol.: Hydrogen through Neon. A Critical Data Compilation; US Government Printing Office: Washington, DC, USA, 1966.
- Martin, I.; Karwowski, J.; Diercksen, G.H.F.; Barrientos, C. Transition probabilities in the lithium sequence. Astron. Astrophys. Suppl. Ser. 1993, 100, 595–605. [Google Scholar]
- Zhang, H.L.; Sampson, D.H.; Fontes, C.J. Relativistic Distorted-Wave Collision Strengths for the 85 Li-like Ions with 8 <= Z <= 92. At. Data Nucl. Data Tables 1990, 44, 31. [Google Scholar] [CrossRef]
- Berrington, K.A.; Burke, P.G.; Dufton, P.L.; Kingston, A.E. Electron-Impact-Excitation Collision Strengths for Be-like Ions. II. Intermediate-Energy Region and Collision Rates. At. Data Nucl. Data Tables 1985, 33, 195. [Google Scholar] [CrossRef]
- Berrington, K.A.; Burke, V.M.; Burke, P.G.; Scialla, S. Electron impact excitation of n = 3 states of C III: An application of a new R-matrix package. J. Phys. B At. Mol. Phys. 1989, 22, 665–676. [Google Scholar] [CrossRef]
- Muehlethaler, H.P.; Nussbaumer, H. Transition probabilities within 2s2-2s2p-2p2 in the Be I sequence, Be I—Ni XXV. Astron. Astrophys. 1976, 48, 109–114. [Google Scholar]
- Sampson, D.H.; Goett, S.J.; Clark, R.E.H. Collision Strengths and Line Strengths for Fine-Structure Transitions between the 2la2lb Configurations and the 2l′a3l′b Configurations in Be-like Ions. At. Data Nucl. Data Tables 1984, 30, 125. [Google Scholar] [CrossRef]
- Zhang, H.L.; Sampson, D.H. Relativistic Distorted-Wave Collision Strengths and Oscillator Strengths for the 45 Δn =0 Transitions with n = 2 in the 85 Be-like Ions with 8 <= Z <= 92. At. Data Nucl. Data Tables 1992, 52, 143. [Google Scholar] [CrossRef]
- Ramsbottom, C.A.; Berrington, K.A.; Hibbert, A.; Bell, K.L. Electron impact excitation rates for transitions involving the n = 2 and n = 3 levels of beryllium-like N IV. Phys. Scr. 1994, 50, 246–253. [Google Scholar] [CrossRef]
- Kato, T.; Lang, J.; Berrington, K.A. Intensity Ratios of Emission Lines for O V Ions for Temperature and Density Diagnostics, and Recommended Excitation Rate Coefficients. At. Data Nucl. Data Tables 1990, 44, 133. [Google Scholar] [CrossRef]
- Dankwort, W.; Trefftz, E. Breit-Pauli approximation for highly ionized boron-like ions, up to Fe XXII. Astron. Astrophys. 1978, 65, 93–98. [Google Scholar]
- Nussbaumer, H.; Storey, P.J. C II two-electron transitions. Astron. Astrophys. 1981, 96, 91–95. [Google Scholar]
- Lennon, D.J.; Dufton, P.L.; Hibbert, A.; Kingston, A.E. C II emission lines formed in optically thin plasmas. Astrophys. J. 1985, 294, 200–206. [Google Scholar] [CrossRef]
- Blum, R.D.; Pradhan, A.K. Rate Coefficients for the Excitation of Infrared and Ultraviolet Lines in C II, N III, and O IV. Astrophys. J. Suppl. Ser. 1992, 80, 425. [Google Scholar] [CrossRef]
- Nussbaumer, H.; Storey, P.J. N III lines for solar diagnostics. Astron. Astrophys. 1979, 71, L5–L8. [Google Scholar]
- Stafford, R.P.; Hibbert, A.; Bell, K.L. Accurate transition probabilities for spectral lines of N III. Mon. Not. R. Astron. Soc. 1993, 260, L11–L14. [Google Scholar] [CrossRef] [Green Version]
- Stafford, R.P.; Bell, K.L.; Hibbert, A. Electron impact excitation of N III—Fine-structure collision strengths and Maxwellian-averaged rate coefficients. Mon. Not. R. Astron. Soc. 1994, 266, 715. [Google Scholar] [CrossRef] [Green Version]
- Stafford, R.P.; Bell, K.L.; Hibbert, A.; Wijesundera, W.P. Electron Impact Excitation of NII—Fine Structure Collision Strengths and Maxwellian-Averaged Rate Coefficients. Mon. Not. R. Astron. Soc. 1994, 268, 816. [Google Scholar] [CrossRef] [Green Version]
- Bhatia, A.K.; Feldman, U.; Seely, J.F. Atomic Data and Spectral Line Intensities for the Boron Isoelectronic Sequence (Ar XIV through Kr XXXII). At. Data Nucl. Data Tables 1986, 35, 319. [Google Scholar] [CrossRef]
- Zhang, H.L.; Graziani, M.; Pradhan, A.K. Atomic Data from the Iron Project: III. Rate Coefficients for Electron Impact Excitation of Boron-like Ions: NE VI, MG VIII, AL IX, SI X, S XII, AR XIV, CA XVI and Fe XXII. Astron. Astrophys. 1994, 283, 319. [Google Scholar]
- Sampson, D.H.; Weaver, G.M.; Goett, S.J.; Zhang, H.; Clark, R.E.H. Collision Strengths and Line Strengths for All Transitions among the Levels of the 1s22s22p, 1s22s2p2, and 1s22p3, Configurations of Boron-like Ions. At. Data Nucl. Data Tables 1986, 35, 223. [Google Scholar] [CrossRef]
- Bell, K.L.; Hibbert, A.; Stafford, R.P. Transition probabilities for some spectral lines of singly ionised nitrogen. Phys. Scr. 1995, 52, 240–251. [Google Scholar] [CrossRef]
- Aggarwal, K.M. Electron excitation rates among fine structure levels in O III. Astrophys. J. Suppl. Ser. 1983, 52, 387–398. [Google Scholar] [CrossRef]
- Aggarwal, K.M. Line intensity ratios for transitions in O III. Astron. Astrophys. 1985, 146, 149–158. [Google Scholar]
- Bhatia, A.K.; Kastner, S.O. Collision Strengths and Transition Rates for O III. At. Data Nucl. Data Tables 1993, 54, 133–164. [Google Scholar] [CrossRef]
- Lennon, D.J.; Burke, V.M. Atomic data from the IRON project. II. Effective collision strengths for infrared transitions in carbon-like ions. Astron. Astrophys. Suppl. Ser. 1994, 103, 273–277. [Google Scholar]
- Aggarwal, K.M. Electron impact excitation rates for fine-structure transitions in NE V and SI IX—An R-matrix approach. Astrophys. J. Suppl. Ser. 1984, 54, 1–15. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Doschek, G.A. Atomic Data and Spectral Line Intensities for C-like Ne V. At. Data Nucl. Data Tables 1993, 55, 315–348. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Doschek, G.A. Atomic Data and Spectral Line Intensities for C-Like Si IX. At. Data Nucl. Data Tables 1993, 55, 281–314. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Doschek, G.A. Atomic Data and Spectral Line Intensities for C-like Mg VII. At. Data Nucl. Data Tables 1995, 60, 145. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Kastner, S.O. Atomic parameters for carbon-like S XI. J. Quant. Spectros. Radiat. Transf. 1987, 37, 527–529. [Google Scholar] [CrossRef]
- Dere, K.P.; Mason, H.E.; Widing, K.G.; Bhatia, A.K. XUV electron density diagnostics for solar flares. Astrophys. J. Suppl. Ser. 1979, 40, 341–364. [Google Scholar] [CrossRef]
- Mason, H.E.; Bhatia, A.K. Theoretical intensity ratios for the UV lines of Mg VII, Si IX and S XI. Mon. Not. R. Astron. Soc. 1978, 184, 423–437. [Google Scholar] [CrossRef] [Green Version]
- Froese Fischer, C.; Saha, H.P. Multiconfiguration Hartree-Fock Results with Breit-Pauli Corrections for Transitions in the Carbon Sequence. Phys. Scr. 1985, 32, 181–194. [Google Scholar] [CrossRef]
- Aggarwal, K.M.; Berrington, K.A.; Keenan, F.P. Effective Collision Strengths among Fine-Structure Levels of CA XV. Astrophys. J. Suppl. Ser. 1990, 72, 815. [Google Scholar] [CrossRef]
- Aggarwal, K.M.; Berrington, K.A.; Keenan, F.P. Effective collision strengths among fine-structure levels of CA XV: Erratum. Astrophys. J. Suppl. Ser. 1991, 77, 441–449. [Google Scholar] [CrossRef] [Green Version]
- Bhatia, A.K.; Mason, H.E. Theoretical atomic structure and electron scattering data for ions in the nitrogen isoelectronic sequence—MG VI, SI VIII, S X, A XII and CA XIV. Mon. Not. R. Astron. Soc. 1980, 190, 925–929. [Google Scholar] [CrossRef] [Green Version]
- Bhatia, A.K.; Seely, J.F.; Feldman, U. Atomic Data and Spectral Line Intensities for the Nitrogen Isoelectronic Sequence (Ar XII through Kr XXX). At. Data Nucl. Data Tables 1989, 43, 99. [Google Scholar] [CrossRef]
- Mason, H.E.; Bhatia, A.K.; Doschek, G.A.; Feldman, U. Fe XXI as an electron density diagnostic in solar flares. Astron. Astrophys. 1979, 73, 74–81. [Google Scholar]
- Aggarwal, K.M. Collision Strengths and Excitation Rate Coefficients for Transitions in Fe XXI. Astrophys. J. Suppl. Ser. 1991, 77, 677. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Feldman, U.; Doschek, G.A. New atomic data for Si/6+/, S/8+/ and Ar/10+/. Astron. Astrophys. 1979, 80, 22–26. [Google Scholar]
- McLaughlin, B.M.; Bell, K.L. Analytical FITS for Electron Collisionally Excited Effective Collision Strengths of O II. Astrophys. J. Suppl. Ser. 1994, 94, 825. [Google Scholar] [CrossRef]
- Loulergue, M.; Mason, H.E.; Nussbaumer, H.; Storey, P.J. Fe XIX transitions within the N = 2 complex. Astron. Astrophys. 1985, 150, 246–250. [Google Scholar]
- Blackford, H.M.S.; Hibbert, A. Transitions in Fluorine-Like Ions. At. Data Nucl. Data Tables 1994, 58, 101–164. [Google Scholar] [CrossRef]
- Butler, K.; Zeippen, C.J. Atomic data from the IRON Project. V. Effective collision strengths for transitions in the ground configuration of oxygen-like ions. Astron. Astrophys. Suppl. Ser. 1994, 108, 1–8. [Google Scholar]
- Sampson, D.H.; Zhang, H.L.; Fontes, C.J. Relativistic Distorted-Wave Collision Strengths and Oscillator Strengths for F-like Ions with 22 <= Z <= 92. At. Data Nucl. Data Tables 1991, 48, 25. [Google Scholar] [CrossRef]
- Cornille, M.; Dubau, J.; Loulergue, M.; Bely-Dubau, F.; Faucher, P. Theoretical analysis of the Fe XVIII X-ray spectrum and application to solar coronal observations. Astron. Astrophys. 1992, 259, 669–681. [Google Scholar]
- Bhatia, A.K.; Feldman, U.; Seely, J.F. Atomic Data and Spectral Line Intensities for the Neon Isoelectronic Sequence (Si V through Kr XXVII). At. Data Nucl. Data Tables 1985, 32, 435. [Google Scholar] [CrossRef]
- Hibbert, A.; Ledourneuf, M.; Mohan, M. Energies, Oscillator Strengths, and Lifetimes for Neon-like Ions Up to Kr XXVII. At. Data Nucl. Data Tables 1993, 53, 23–112. [Google Scholar] [CrossRef]
- Saraph, H.E.; Tully, J.A. Atomic data from the IRON project. IV. Electron excitation of the 2P3/2∘–2P1/2∘ fine structure transition in fluorine-like ions. Astron. Astrophys. Suppl. Ser. 1994, 107, 29–38. [Google Scholar]
- Mohan, M.; Baluja, K.L.; Hibbert, A. Electron-impact excitation of MG IV using the R-matrix method. Phys. Scr. 1988, 38, 699–701. [Google Scholar] [CrossRef]
- Zhang, H.; Sampson, D.H.; Clark, R.E.H.; Mann, J.B. Collision Strengths and Oscillator Strengths for Excitation to the n = 3 and 4 Levels of Neon-like Ions. At. Data Nucl. Data Tables 1987, 37, 17. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Doschek, G.A. Atomic Data and Spectral Line Intensities for Ne-like Fe XVII. At. Data Nucl. Data Tables 1992, 52, 1. [Google Scholar] [CrossRef]
- Mohan, M.; Le Dourneuf, M. Electron-impact excitation from the Si(5+) ground state, using the R-matrix method. Astron. Astrophys. 1990, 227, 285–288. [Google Scholar]
- Mohan, M.; Hibbert, A.; Baluja, K.L. Electron impact excitation of S VIII from its ground state. J. Phys. B At. Mol. Phys. 1987, 20, 2565–2570. [Google Scholar] [CrossRef]
- Sampson, D.H.; Zhang, H.L.; Fontes, C.J. Relativistic Distorted-Wave Collision Strengths and Oscillator Strengths for the 71 Na-like Ions with 22 <= Z <= 92. At. Data Nucl. Data Tables 1990, 44, 209. [Google Scholar] [CrossRef]
- Dufton, P.L.; Hibbert, A.; Kingston, A.E.; Doschek, G.A. Si III line ratios in the Sun. Astrophys. J. 1983, 274, 420–428. [Google Scholar] [CrossRef]
- Mason, H.E. The excitation of several iron and calcium lines in the visible spectrum of the solar corona. Mon. Not. R. Astron. Soc. 1975, 170, 651–689. [Google Scholar] [CrossRef]
- Christensen, R.B.; Norcross, D.W.; Pradhan, A.K. Electron-impact excitation of ions in the magnesium sequence. II. S v, Ar vii, Ca ix, Cr xiii, and Ni xvii. Phys. Rev. A 1986, 34, 4704–4715. [Google Scholar] [CrossRef]
- Lanzafame, A.C. Si II resonance multiplets in the Sun. Astron. Astrophys. 1994, 287, 972–981. [Google Scholar]
- Mohan, M.; Hibbert, A.; Berrington, K.A.; Burke, P.G. Electron impact excitation of neon-like S VII from its ground state. J. Phys. B At. Mol. Phys. 1990, 23, 989–996. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Doschek, G.A.; Feldman, U. Atomic data for S IV and solar observations of the 3s23p2P–3s3p24P multiplet. Astron. Astrophys. 1980, 86, 32–35. [Google Scholar]
- Dufton, P.L.; Hibbert, A.; Kingston, A.E.; Doschek, G.A. S IV emission-line ratios in the sun. Astrophys. J. 1982, 257, 338–344. [Google Scholar] [CrossRef]
- Fischer, C.F.; Liu, B. Energy Levels, Lifetimes, Wavelengths, and Transition Probabilities of Fe XIV. At. Data Nucl. Data Tables 1986, 34, 261. [Google Scholar] [CrossRef]
- Czyzak, S.J.; Krueger, T.K. On the Excited Levels of Fe VIII. Astrophys. J. 1966, 144, 381. [Google Scholar] [CrossRef]
- Fawcett, B.C. Computed Oscillator Strengths and Energy Levels for Potassium-like Ions V V, Cr VI, Mn VII, Fe VIII, Co IX, Ni X, and Cu XI with Calculated Wavelengths and Wavelengths Derived from Established Data. At. Data Nucl. Data Tables 1989, 43, 71. [Google Scholar] [CrossRef]
- Dufton, P.L.; Kingston, A.E. Effective collision strengths for Si III. Mon. Not. R. Astron. Soc. 1989, 241, 209–214. [Google Scholar] [CrossRef] [Green Version]
- Nussbaumer, H.; Storey, P.J.; Storey, P.J. Forbidden emission lines of Fe VII. Astron. Astrophys. 1982, 113, 21–26. [Google Scholar]
- Dufton, P.L.; Kingston, A.E. Effective collision strengths for Si II. Mon. Not. R. Astron. Soc. 1991, 248, 827–828. [Google Scholar] [CrossRef] [Green Version]
- Bhadra, K.; Henry, R.J.W. Oscillator strengths and collision strengths for S IV. Astrophys. J. 1980, 240, 368–373. [Google Scholar] [CrossRef]
- Fawcett, B.C.; Mason, H.E. Collision Strengths and Oscillator Strengths for Fe IX. At. Data Nucl. Data Tables 1991, 47, 17. [Google Scholar] [CrossRef]
- Mason, H.E. An Assessment of Theoretical Electron Excitation Data for Fe IX-Fe XIV. At. Data Nucl. Data Tables 1994, 57, 305–328. [Google Scholar] [CrossRef]
- Pindzola, M.S.; Griffin, D.C.; Bottcher, C. Coupling effects for electron-impact excitation in the potassium isoelectronic sequence. Phys. Rev. A 1989, 39, 2385–2391. [Google Scholar] [CrossRef]
- Fawcett, B.C.; Mason, H.E. A Slater Parameter Optimization Method Applied to the Computation of Collision Strengths for Fe XIII. At. Data Nucl. Data Tables 1989, 43, 245. [Google Scholar] [CrossRef]
- Aggarwal, K.M.; Berrington, K.A.; Burke, P.G.; Kingston, A.E.; Pathak, A. Electron collision cross sections at low energies for all transitions between the n=1, 2, 3, 4 and 5 levels of atomic hydrogen. J. Phys. B At. Mol. Phys. 1991, 24, 1385–1410. [Google Scholar] [CrossRef]
- Chen, G.X.; Pradhan, A.K. Atomic data from the Iron Project. XXXVII. Electron impact excitation collision strengths and rate coefficients for Fe VI. Astron. Astrophys. Suppl. Ser. 1999, 136, 395–403. [Google Scholar] [CrossRef]
- Eissner, W.; Galavís, M.E.; Mendoza, C.; Zeippen, C.J. Atomic data from the IRON Project. XXXIV. Electron impact excitation of Fe XVI. Astron. Astrophys. Suppl. Ser. 1999, 136, 385–394. [Google Scholar] [CrossRef] [Green Version]
- Eissner, W.; Galavís, M.E.; Mendoza, C.; Zeippen, C.J. Atomic data from the IRON Project. XXXVIII. Electron impact excitation of the fine-structure transitions in the n = 3 complex of Fe XV. Astron. Astrophys. Suppl. Ser. 1999, 137, 165–173. [Google Scholar] [CrossRef]
- Garstang, R.H. Transition probabilities for forbidden lines of Fe II. Mon. Not. R. Astron. Soc. 1962, 124, 321. [Google Scholar] [CrossRef]
- Nussbaumer, H.; Storey, P.J. Transition probabilities for Fe II infrared lines. Astron. Astrophys. 1988, 193, 327–333. [Google Scholar]
- Giridhar, S.; Arellano Ferro, A. A Critical Compilation of Oscillator Strengths for Fe II Lines. Rev. Mex. Astron. Astrofis. 1995, 31, 23–37. [Google Scholar]
- Nahar, S.N. Atomic data from the Iron Project. VII. Radiative dipole transition probabilities for Fe II. Astron. Astrophys. 1995, 293, 967–977. [Google Scholar]
- Pelan, J.; Berrington, K.A. Atomic data from the IRON Project. IX. Electron excitation of the 2P3/2∘–2P1/2∘ fine-structure transition in chlorine-like ions, from AR II to NI XII. Astron. Astrophys. Suppl. Ser. 1995, 110, 209. [Google Scholar]
- Berrington, K.A.; Tully, J.A. Atomic data from the IRON Project. XXIV. Electron excitation of Li-like Fe XXIV between the N = 2 and n′ = 2, 3, 4 fine-structure levels. Astron. Astrophys. Suppl. Ser. 1997, 126, 105–111. [Google Scholar] [CrossRef] [Green Version]
- Garstang, R.H. Energy levels and transition probabilities of Fe IV. Mon. Not. R. Astron. Soc. 1958, 118, 572. [Google Scholar] [CrossRef] [Green Version]
- Kono, A.; Hattori, S. Accurate oscillator strengths for neutral helium. Phys. Rev. A 1984, 29, 2981–2988. [Google Scholar] [CrossRef]
- Goett, S.J.; Sampson, D.H.; Clark, R.E.H. Intermediate-Coupling Collision Strengths for Transitions between Doubly Excited Levels Produced by Electron Impact on Highly Charged He-like Ions. At. Data Nucl. Data Tables 1983, 28, 279. [Google Scholar] [CrossRef]
- Kaufman, V.; Sugar, J. Forbidden Lines in ns2npk Ground Configurations and nsnp Excited Configurations of Beryllium through Molybdenum Atoms and Ions. J. Phys. Chem. Ref. Data 1986, 15, 321–426. [Google Scholar] [CrossRef]
- Nussbaumer, H.; Rusca, C. Forbidden transitions in the C I sequence. Astron. Astrophys. 1979, 72, 129–133. [Google Scholar] [CrossRef]
- Mendoza, C. Recent advances in atomic calculations and experiments of interest in the study of planetary nebulae. In Planetary Nebulae; Flower, D.R., Ed.; D. Reidel Publishing Co.: Dordrecht, Holland, 1983; IAU Symposium 103; pp. 143–172. [Google Scholar]
- Zeippen, C.J. Transition probabilities for forbidden lines in the 2p3 configuration. Mon. Not. R. Astron. Soc. 1982, 198, 111–125. [Google Scholar] [CrossRef] [Green Version]
- Nahar, S.N.; Pradhan, A.K. Atomic data from the Iron Project. XVII. Radiative transition probabilities for dipole allowed and forbidden transitions in Fe III. Astron. Astrophys. Suppl. Ser. 1996, 119, 509–522. [Google Scholar] [CrossRef]
- Butler, K.; Zeippen, C.J. N I forbidden lines revisited. Astron. Astrophys. 1984, 141, 274–278. [Google Scholar]
- Bautista, M.A. Atomic data from the Iron Project. XXXIX. Photoionization cross sections and oscillator strengths for NI II. Astron. Astrophys. Suppl. Ser. 1999, 137, 529–535. [Google Scholar] [CrossRef] [Green Version]
- Bautista, M.A. Continuum Fluorescence Excitation of [N I] and [O I] Lines in Gaseous Nebulae. Astrophys. J. 1999, 527, 474–478. [Google Scholar] [CrossRef]
- Moore, C.E. Selected Tables of Atomic Spectra. Atomic Energy Levels and Multiplet Table O III; US Government Printing Office: Washington, DC, USA, 1985. [Google Scholar]
- Thomas, L.D.; Nesbet, R.K. Low-energy electron scattering by atomic carbon. Phys. Rev. A 1975, 12, 2378–2382. [Google Scholar] [CrossRef]
- Pequignot, D.; Aldrovandi, S.M.V. Effective collision strengths for the forbidden emission lines of neutral carbon, nitrogen and oxygen. Astron. Astrophys. 1976, 50, 141–144. [Google Scholar]
- Johnson, C.T.; Burke, P.G.; Kingston, A.E. Electron scattering from the fine structure levels within the 1s22s22p23Pe ground state of C I. J. Phys. B At. Mol. Phys. 1987, 20, 2553–2563. [Google Scholar] [CrossRef]
- Dopita, M.A.; Mason, D.J.; Robb, W.D. Atomic nitrogen as a probe of physical conditions in the interstellar medium. Astrophys. J. 1976, 207, 102–109. [Google Scholar] [CrossRef]
- Berrington, K.A.; Burke, P.G. Effective collision strengths for forbidden transitions in e-N and e-O scattering. Planet. Space Sci. 1981, 29, 377–381. [Google Scholar] [CrossRef]
- LeDourneuf, M.; Nesbet, R.K. Electron impact excitation of fine-structure levels of atomic oxygen. J. Phys. B At. Mol. Phys. 1976, 9, L241–L243. [Google Scholar] [CrossRef]
- Zeippen, C.J.; Butler, K.; Le Bourlot, J. Effective collision strengths for fine-structure forbidden transitions in the 3p3 configuration of AR IV. Astron. Astrophys. 1987, 188, 251–257. [Google Scholar]
- Krueger, T.K.; Czyzak, S.J. Excitation of Forbidden Lines in Gaseous Nebulae. II. Calculations for 3pq Ions. Proc. R. Soc. Lon. Ser. A 1970, 318, 531–539. [Google Scholar] [CrossRef]
- Mendoza, C.; Zeippen, C.J. Transition probabilities for forbidden lines in the 3p2 configuration-II. Mon. Not. R. Astron. Soc. 1982, 199, 1025–1032. [Google Scholar] [CrossRef] [Green Version]
- Hayes, M.A. The S III intercombination multiplet—Radiative and electron excitation data. J. Phys. B At. Mol. Phys. 1986, 19, 1853–1862. [Google Scholar] [CrossRef]
- Mendoza, C.; Zeippen, C.J. Transition probabilities for forbidden lines in the 3p3 configuration. Mon. Not. R. Astron. Soc. 1982, 198, 127–139. [Google Scholar] [CrossRef] [Green Version]
- Fuhr, J.R.; Wiese, W.L. RCR Handbook of Chemistry and Physics, 71st ed.; CRC Press: Boca Raton, FL, USA, 1990. [Google Scholar]
- Ramsbottom, C.A.; Bell, K.L.; Stafford, R.P. Effective Collision Strengths for Electron Impact Excitation of Singly Ionized Sulfur. At. Data Nucl. Data Tables 1996, 63, 57. [Google Scholar] [CrossRef]
- Cai, W.; Pradhan, A.K. Excitation Rate Coefficients and Line Ratios for the Optical and Ultraviolet Transitions in S II. Astrophys. J. Suppl. Ser. 1993, 88, 329. [Google Scholar] [CrossRef]
- Storey, P.J.; Mason, H.E.; Young, P.R. Atomic data from the IRON Project. XL. Electron impact excitation of the Fe XIV EUV transitions. Astron. Astrophys. Suppl. Ser. 2000, 141, 285–296. [Google Scholar] [CrossRef] [Green Version]
- Saraph, H.E.; Storey, P.J. Atomic data from the IRON Project. XI. The 2P1/2∘–2P3/2∘ fine-structure lines of AR VI, K VII and CA VIII. Astron. Astrophys. Suppl. Ser. 1996, 115, 151. [Google Scholar]
- Zhang, H. Atomic data from the Iron Project. XVIII. Electron impact excitation collision strengths and rate coefficients for Fe III. Astron. Astrophys. 1996, 119, 523–528. [Google Scholar] [CrossRef]
- Zhang, H.L.; Pradhan, A.K. Atomic data from the Iron Project. XXVII. Electron impact excitation collision strengths and rate coefficients for Fe IV. Astron. Astrophys. Suppl. Ser. 1997, 126, 373–378. [Google Scholar] [CrossRef] [Green Version]
- Fernley, J.A.; Seaton, M.J.; Taylor, K.T. Atomic data for opacity calculations. VII. Energy levels, f values and photoionisation cross sections for He-like ions. J. Phys. B At. Mol. Phys. 1987, 20, 6457–6476. [Google Scholar] [CrossRef]
- Peach, G.; Saraph, H.E.; Seaton, M.J. Atomic data for opacity calculations. IX. The lithium isoelectronic sequence. J. Phys. B At. Mol. Phys. 1988, 21, 3669–3683. [Google Scholar] [CrossRef]
- Tully, J.A.; Seaton, M.J.; Berrington, K.A. Atomic data for opacity calculations. XIV. The beryllium sequence. J. Phys. B At. Mol. Phys. 1990, 23, 3811–3837. [Google Scholar] [CrossRef]
- Fernley, J.A.; Hibbert, A.; Kingston, A.E.; Seaton, M.J. Atomic data for opacity calculations: XXIV. The boron-like sequence. J. Phys. B At. Mol. Phys. 1999, 32, 5507–5522. [Google Scholar] [CrossRef]
- Luo, D.; Pradhan, A.K. Atomic data for opacity calculations. XI. The carbon isoelectronic sequence. J. Phys. B At. Mol. Phys. 1989, 22, 3377–3395. [Google Scholar] [CrossRef]
- Hibbert, A.; Scott, M.P. Atomic data for opacity calculations. XXI. The neon sequence. J. Phys. B At. Mol. Phys. 1994, 27, 1315–1323. [Google Scholar] [CrossRef]
- Butler, K.; Mendoza, C.; Zeippen, C.J. Atomic data for opacity calculations. XIX. The magnesium isoelectronic sequence. J. Phys. B At. Mol. Phys. 1993, 26, 4409–4423. [Google Scholar] [CrossRef]
- Mendoza, C.; Eissner, W.; LeDourneuf, M.; Zeippen, C.J. Atomic data for opacity calculations. XXIII. The aluminium isoelectronic sequence. J. Phys. B At. Mol. Phys. 1995, 28, 3485–3504. [Google Scholar] [CrossRef]
- Nahar, S.N.; Pradhan, A.K. Atomic data for opacity calculations. XVIII. Photoionization and oscillator strengths of Si-like ions Si0, S2+, Ar4+, Ca6+. J. Phys. B At. Mol. Phys. 1993, 26, 1109–1127. [Google Scholar] [CrossRef]
- Bautista, M.A. Atomic data from the Iron Project. XVI. Photoionization cross sections and oscillator strengths for Fe V. Astron. Astrophys. Suppl. Ser. 1996, 119, 105–110. [Google Scholar] [CrossRef] [Green Version]
- Bautista, M.A.; Pradhan, A.K. Atomic data from the Iron Project. XXVI. Photoionization cross sections and oscillator strengths for Fe IV. Astron. Astrophys. Suppl. Ser. 1997, 126, 365–371. [Google Scholar] [CrossRef] [Green Version]
- Nahar, S.N. Photoionization cross sections and oscillator strengths for Fe III. Phys. Rev. A 1996, 53, 1545–1552. [Google Scholar] [CrossRef] [Green Version]
- Nahar, S.N.; Pradhan, A.K. Atomic data for opacity calculations: XX. Photoionization cross sections and oscillator strengths for Fe II. J. Phys. B At. Mol. Phys. 1994, 27, 429–446. [Google Scholar] [CrossRef] [Green Version]
- Bautista, M.A. Atomic data from the IRON Project. XX. Photoionization cross sections and oscillator strengths for Fe I. Astron. Astrophys. Suppl. Ser. 1997, 122, 167–176. [Google Scholar] [CrossRef] [Green Version]
- Gorczyca, T.W. Auger decay of the photoexcited 1s-1np Rydberg series in neon. Phys. Rev. A 2000, 61, 024702. [Google Scholar] [CrossRef]





| Method | Source | |||
|---|---|---|---|---|
| Astronomical observations | XMM-Newton, Mrk 421 [23] | 527.30(5) | 541.95(28) | 14.65(33) |
| Chandra, 7 sources [23] | 527.44(9) | 541.72(18) | 14.28(21) | |
| Chandra, shifted [23] | 527.26(9) | |||
| Chandra, 11 sources [77] | 527.39(2) | |||
| Chandra, 6 sources [78] | 527.41(18) | 541.77(40) | 14.36(58) | |
| Laboratory measurements | HZB [52] | 527.26(4) | 541.645(12) | |
| ALS [79,80] | 526.79(4) | 541.19(4) | 14.40(8) | |
| ALS [76] | 526.79(4) | 541.20(4) | 14.41(8) | |
| WSRC [81] | 527.85(10) | 541.27(15) | 13.41(25) | |
| Auger spectroscopy [82] | 527.20(30) | |||
| mchf converged result | mchf [23] | 527.49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mendoza, C.; Bautista, M.A.; Deprince, J.; García, J.A.; Gatuzz, E.; Gorczyca, T.W.; Kallman, T.R.; Palmeri, P.; Quinet, P.; Witthoeft, M.C. The XSTAR Atomic Database. Atoms 2021, 9, 12. https://0-doi-org.brum.beds.ac.uk/10.3390/atoms9010012
Mendoza C, Bautista MA, Deprince J, García JA, Gatuzz E, Gorczyca TW, Kallman TR, Palmeri P, Quinet P, Witthoeft MC. The XSTAR Atomic Database. Atoms. 2021; 9(1):12. https://0-doi-org.brum.beds.ac.uk/10.3390/atoms9010012
Chicago/Turabian StyleMendoza, Claudio, Manuel A. Bautista, Jérôme Deprince, Javier A. García, Efraín Gatuzz, Thomas W. Gorczyca, Timothy R. Kallman, Patrick Palmeri, Pascal Quinet, and Michael C. Witthoeft. 2021. "The XSTAR Atomic Database" Atoms 9, no. 1: 12. https://0-doi-org.brum.beds.ac.uk/10.3390/atoms9010012






