Street Centralities and Land Use Intensities Based on Points of Interest (POI) in Shenzhen, China
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
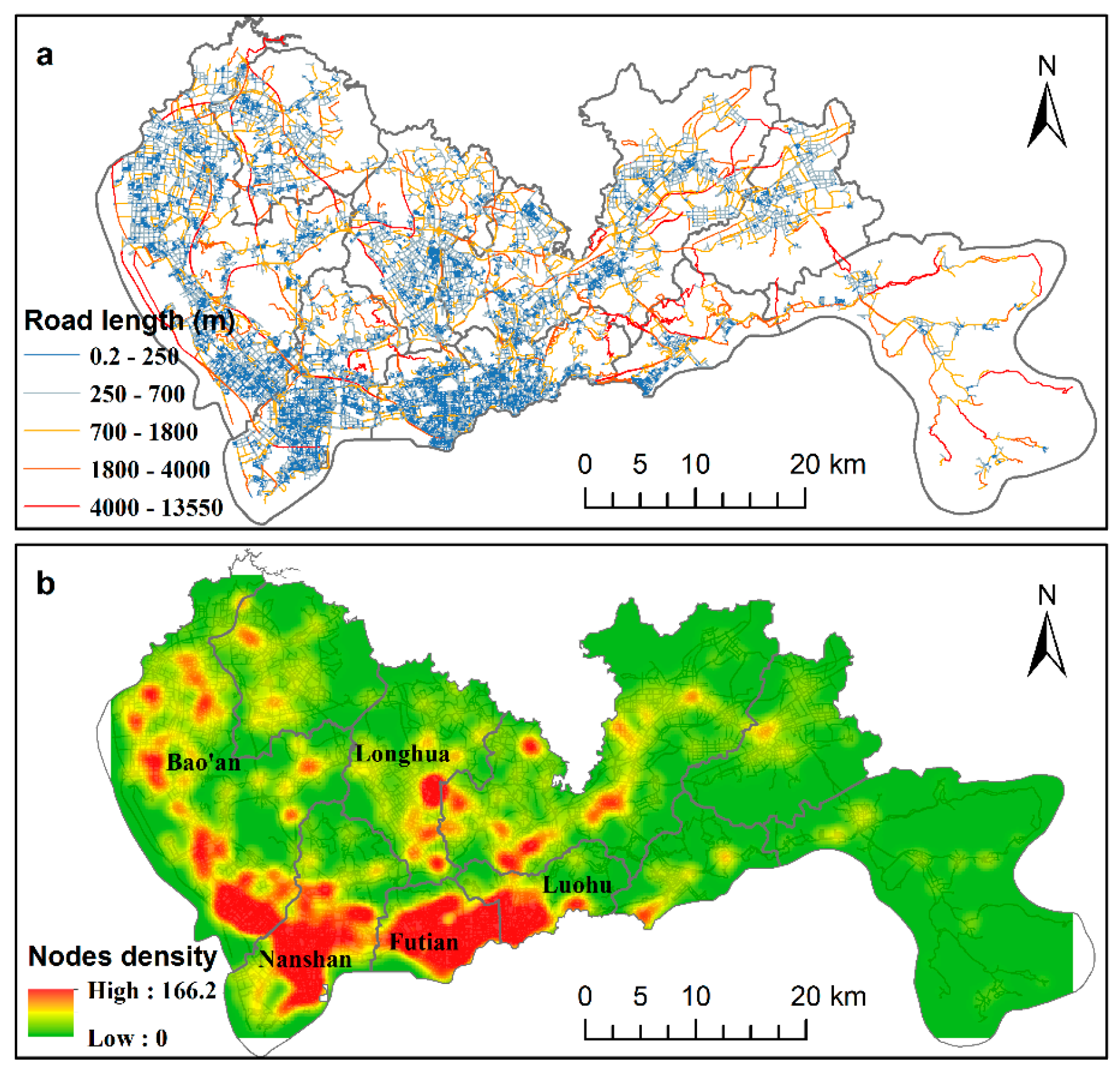
2.2. Street Network
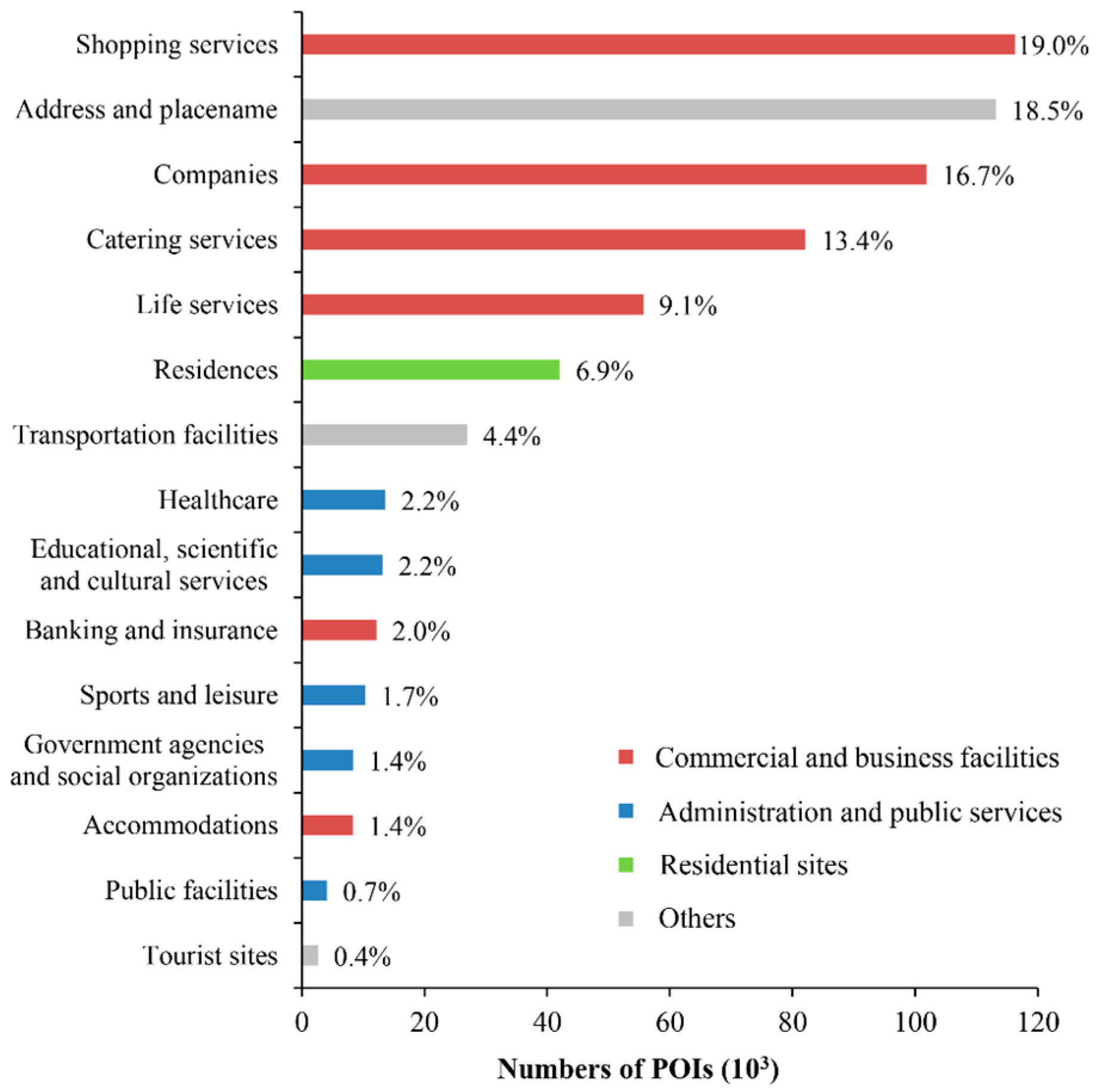
2.3. Points of Interest (POI)
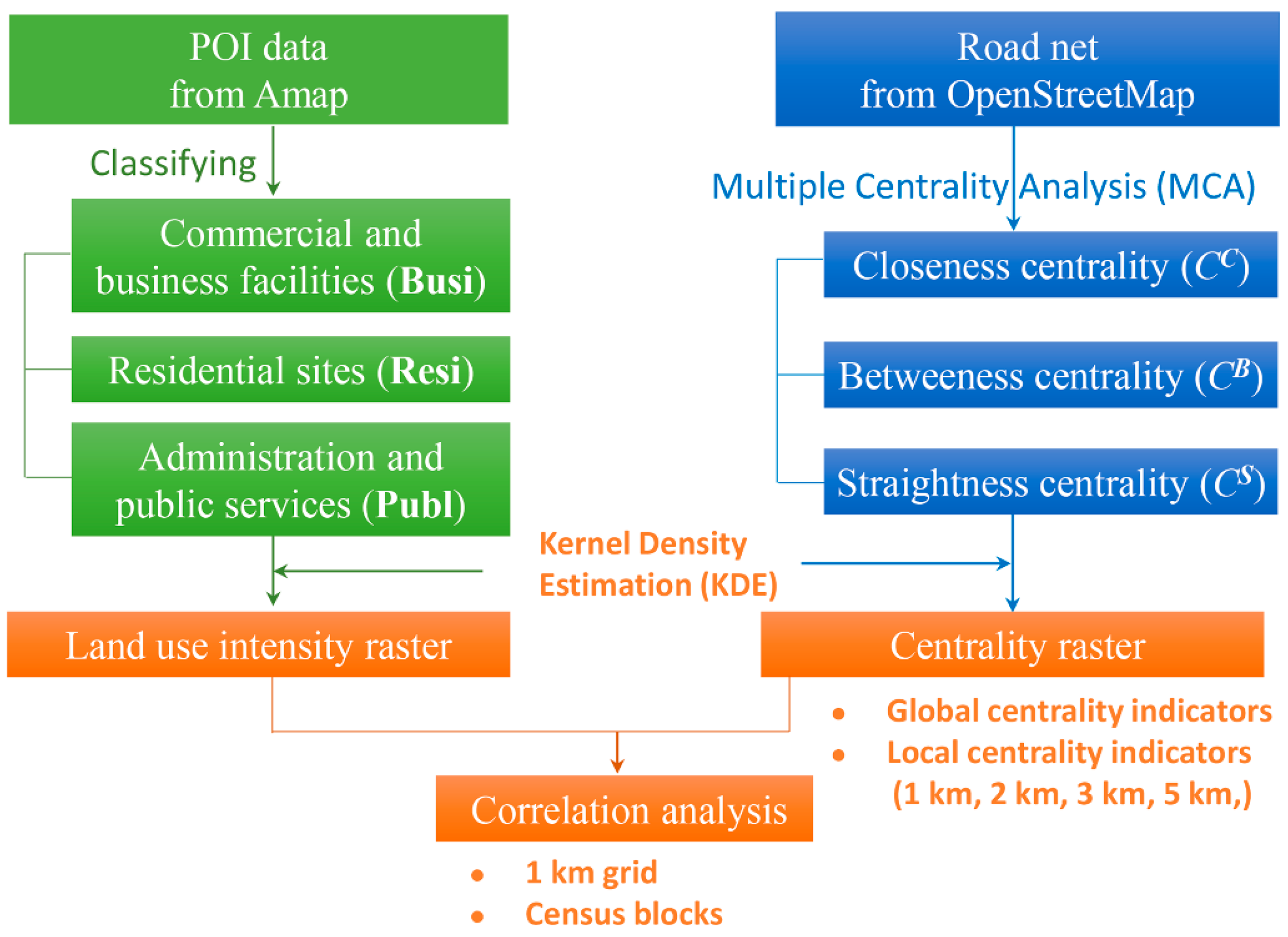
3. Methods
3.1. Street Centrality Measures
3.2. Kernel Density Estimation (KDE)
4. Results
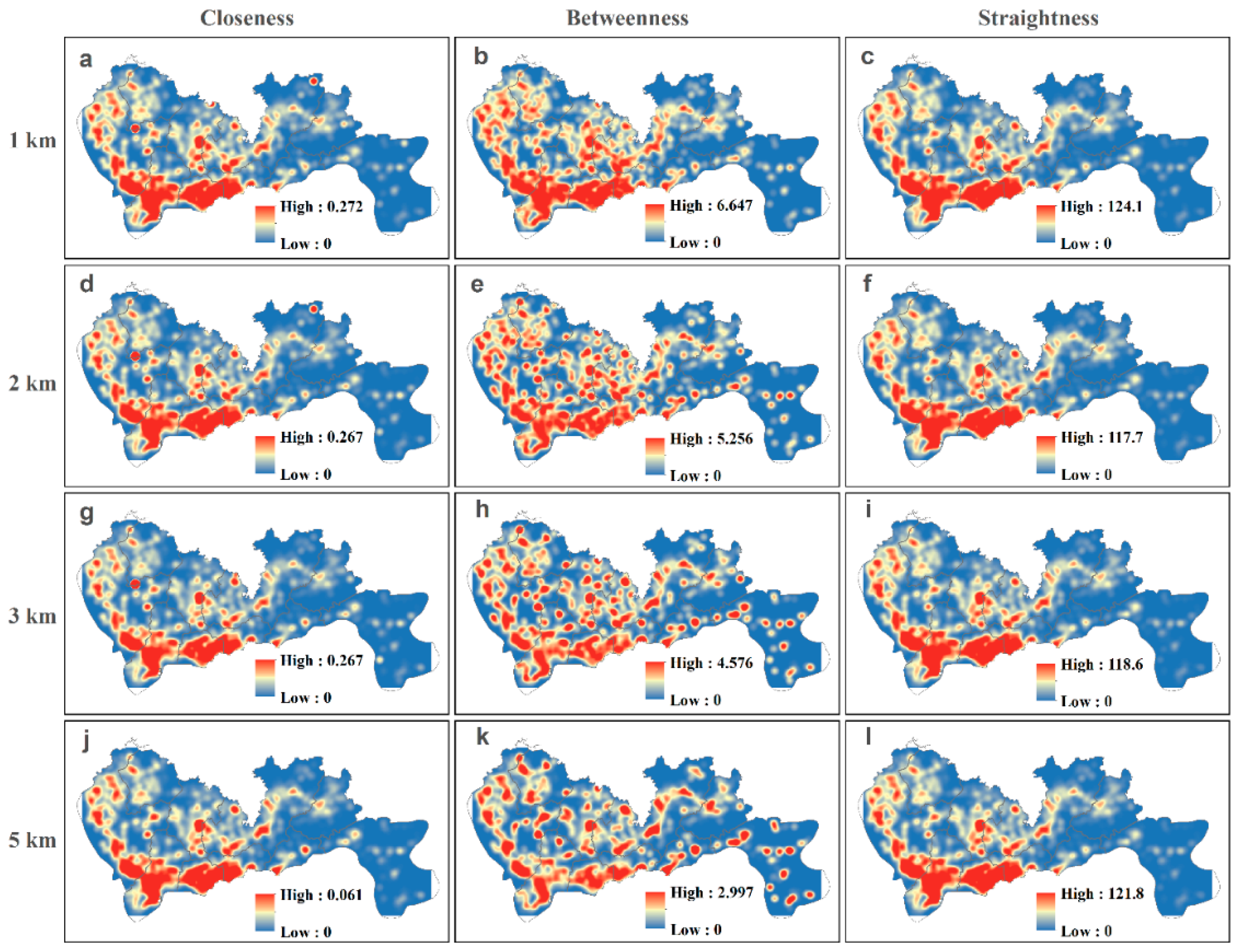
4.1. Spatial Patterns of Street Centralities
4.2. Spatial Distributions of Urban Land Use Intensities
4.3. Correlations between Street Centrality and Land Use Intensity
5. Discussion
5.1. Local Street Centralities
5.2. Effect of Statistical Units
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Badoe, D.A.; Miller, E.J. Transportation-land-use interaction: Empirical findings in North America, and their implications for modeling. Transp. Res. Part D 2000, 5, 235–263. [Google Scholar] [CrossRef]
- Cao, X. Land use and transportation in China. Transp. Res. Part D 2017, 52, 423–427. [Google Scholar] [CrossRef]
- Wang, Y.; Monzon, A.; Ciommo, F.D. Assessing the accessibility impact of transport policy by a land-use and transport interaction model—The case of Madrid. Comput. Environ. Urban Syst. 2015, 49, 126–135. [Google Scholar] [CrossRef] [Green Version]
- Hansen, W.G. How accessibility shapes land use. J. Am. Inst. Plan. 1959, 25, 73–76. [Google Scholar] [CrossRef]
- Sultana, S. Transportation and land use. In International Encyclopedia of Geography; John Wiley & Sons, Ltd.: New York, NY, USA, 2016. [Google Scholar]
- Van Wee, B. Evaluating the impact of land use on travel behaviour: The environment versus accessibility. J. Transp. Geogr. 2011, 19, 1530–1533. [Google Scholar] [CrossRef]
- Lee, M.; Barbosa, H.; Youn, H.; Holme, P.; Ghoshal, G. Morphology of travel routes and the organization of cities. Nat. Commun. 2017, 8, 2229. [Google Scholar] [CrossRef] [PubMed]
- Jaarsma, C.F. Approaches for the planning of rural road networks according to sustainable land use planning. Landsc. Urban Plan. 1997, 39, 47–54. [Google Scholar] [CrossRef]
- Shen, Y.; Karimi, K. The economic value of streets: Mix-scale spatio-functional interaction and housing price patterns. Appl. Geogr. 2017, 79, 187–202. [Google Scholar] [CrossRef]
- Van Oort, F.; Burger, M.; Raspe, O. On the economic foundation of the urban network paradigm: Spatial integration, functional integration and economic complementarities within the Dutch Randstad. Urban Stud. 2010, 47, 725–748. [Google Scholar] [CrossRef]
- Lin, J.; Ban, Y. Comparative analysis on topological structures of urban street networks. ISPRS Int. J. Geo-Inf. 2017, 6, 295. [Google Scholar]
- Porta, S.; Crucitti, P.; Latora, V. The network analysis of urban streets: A dual approach. Physica A 2006, 369, 853–866. [Google Scholar] [CrossRef] [Green Version]
- Porta, S.; Crucitti, P.; Latora, V. The network analysis of urban streets: A primal approach. Environ. Plan. B 2006, 33, 705–725. [Google Scholar] [CrossRef]
- Crucitti, P.; Latora, V.; Porta, S. Centrality measures in spatial networks of urban streets. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2006, 73, 036125. [Google Scholar] [CrossRef] [PubMed]
- Crucitti, P.; Latora, V.; Porta, S. Centrality in networks of urban streets. Chaos 2006, 16, 015113. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Antipova, A.; Porta, S. Street centrality and land use intensity in Baton rouge, Louisiana. J. Transp. Geogr. 2011, 19, 285–293. [Google Scholar] [CrossRef] [Green Version]
- Porta, S.; Strano, E.; Iacoviello, V.; Messora, R.; Latora, V.; Cardillo, A.; Wang, F.H.; Scellato, S. Street centrality and densities of retail and services in Bologna, Italy. Environ. Plan. B 2009, 36, 450–465. [Google Scholar] [CrossRef]
- Porta, S.; Latora, V.; Wang, F.; Rueda, S.; Strano, E.; Scellato, S.; Cardillo, A.; Belli, E.; Càrdenas, F.; Cormenzana, B. Street centrality and the location of economic activities in Barcelona. Urban Stud. 2012, 49, 1471–1488. [Google Scholar] [CrossRef]
- Wang, F.; Chen, C.; Xiu, C.; Zhang, P. Location analysis of retail stores in Changchun, China: A street centrality perspective. Cities 2014, 41, 54–63. [Google Scholar] [CrossRef]
- Rui, Y.; Ban, Y. Exploring the relationship between street centrality and land use in Stockholm. Int. J. Geogr. Inf. Sci. 2014, 28, 1425–1438. [Google Scholar] [CrossRef]
- Chaudhuri, G.; Clarke, K.C. On the spatiotemporal dynamics of the coupling between land use and road networks: Does political history matter? Environ. Plan. B 2015, 42, 133–156. [Google Scholar] [CrossRef]
- Pei, T.; Sobolevsky, S.; Ratti, C.; Shaw, S.-L.; Li, T.; Zhou, C. A new insight into land use classification based on aggregated mobile phone data. J. Geogr. Inf. Sci. 2014, 28, 1988–2007. [Google Scholar] [CrossRef] [Green Version]
- Zhou, M.; Yue, Y.; Li, Q.; Wang, D. Portraying temporal dynamics of urban spatial divisions with mobile phone positioning data: A complex network approach. ISPRS Int. J. Geo-Inf. 2016, 5, 240. [Google Scholar] [CrossRef]
- Huang, B.; Zhao, B.; Song, Y. Urban land-use mapping using a deep convolutional neural network with high spatial resolution multispectral remote sensing imagery. Remote Sens. Environ. 2018, 214, 73–86. [Google Scholar] [CrossRef]
- Yao, Y.; Li, X.; Liu, X.; Liu, P.; Liang, Z.; Zhang, J.; Mai, K. Sensing spatial distribution of urban land use by integrating points-of-interest and Google word2vec model. J. Geogr. Inf. Sci. 2016, 31, 825–848. [Google Scholar] [CrossRef]
- Jiang, S.; Alves, A.; Rodrigues, F.; Ferreira, J.; Pereira, F.C. Mining point-of-interest data from social networks for urban land use classification and disaggregation. Comput. Environ. Urban Syst. 2015, 53, 36–46. [Google Scholar] [CrossRef]
- Liu, X.; Long, Y. Automated identification and characterization of parcels with openstreetmap and points of interest. Environ. Plan. B 2015, 43, 341–360. [Google Scholar] [CrossRef]
- Gao, S.; Janowicz, K.; Couclelis, H. Extracting urban functional regions from points of interest and human activities on location-based social networks. Trans. GIS 2017, 21, 446–467. [Google Scholar] [CrossRef]
- Shen, Y.; Karimi, K. Urban function connectivity: Characterisation of functional urban streets with social media check-in data. Cities 2016, 55, 9–21. [Google Scholar] [CrossRef] [Green Version]
- Yuan, J.; Zheng, Y.; Xie, X. Discovering Regions of Different Functions in a City Using Human Mobility and POIs. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; ACM: New York, NY, USA, 2012; pp. 186–194. [Google Scholar]
- Wang, Y.; Gu, Y.; Dou, M.; Qiao, M. Using spatial semantics and interactions to identify urban functional regions. ISPRS Int. J. Geo-Inf. 2018, 7, 130. [Google Scholar] [CrossRef]
- Yue, Y.; Zhuang, Y.; Yeh, A.G.O.; Xie, J.-Y.; Ma, C.-L.; Li, Q.-Q. Measurements of POI-based mixed use and their relationships with neighbourhood vibrancy. J. Geogr. Inf. Sci. 2016, 31, 658–675. [Google Scholar] [CrossRef]
- Beruea of Statistics of Shenzhen. Statistical Communique of Shenzhen on Economic and Social Development in 2016. 2017. Available online: http://www.sz.gov.cn/cn/xxgk/zfxxgj/tjsj/tjgb/201705/t20170502_6199402.htm (accessed on 20 October 2018). (In Chinese)
- Yao, Y.; Liu, X.; Li, X.; Liu, P.; Hong, Y.; Zhang, Y.; Mai, K. Simulating urban land-use changes at a large scale by integrating dynamic land parcel subdivision and vector-based cellular automata. J. Geogr. Inf. Sci. 2017, 31, 2452–2479. [Google Scholar] [CrossRef]
- Tu, W.; Cao, J.; Yue, Y.; Shaw, S.-L.; Zhou, M.; Wang, Z.; Chang, X.; Xu, Y.; Li, Q. Coupling mobile phone and social media data: A new approach to understanding urban functions and diurnal patterns. J. Geogr. Inf. Sci. 2017, 31, 2331–2358. [Google Scholar] [CrossRef]
- Haklay, M.; Weber, P. Openstreetmap: User-generated street maps. IEEE Pervasive Comput. 2008, 7, 12–18. [Google Scholar] [CrossRef]
- Haklay, M. How good is volunteered geographical information? A comparative study of openstreetmap and ordnance survey datasets. Environ. Plan. B 2010, 37, 682–703. [Google Scholar] [CrossRef]
- Boeing, G. Osmnx: New methods for acquiring, constructing, analyzing, and visualizing complex street networks. Comput. Environ. Urban Syst. 2017, 65, 126–139. [Google Scholar] [CrossRef]
- Grippa, T.; Georganos, S.; Zarougui, S.; Bognounou, P.; Diboulo, E.; Forget, Y.; Lennert, M.; Vanhuysse, S.; Mboga, N.; Wolff, E. Mapping urban land use at street block level using openstreetmap, remote sensing data, and spatial metrics. ISPRS Int. J. Geo-Inf. 2018, 7, 246. [Google Scholar] [CrossRef]
- Hacar, M.; Kılıç, B.; Şahbaz, K. Analyzing openstreetmap road data and characterizing the behavior of contributors in Ankara, Turkey. ISPRS Int. J. Geo-Inf. 2018, 7, 400. [Google Scholar] [CrossRef]
- Sevtsuk, A.; Mekonnen, M. Urban network analysis. A new toolbox for arcgis. Revue Int. Géomat. 2012, 22, 287–305. [Google Scholar] [CrossRef]
- Gil, J. Street network analysis “edge effects”: Examining the sensitivity of centrality measures to boundary conditions. Environ. Plan. B 2016, 44, 819–836. [Google Scholar] [CrossRef]





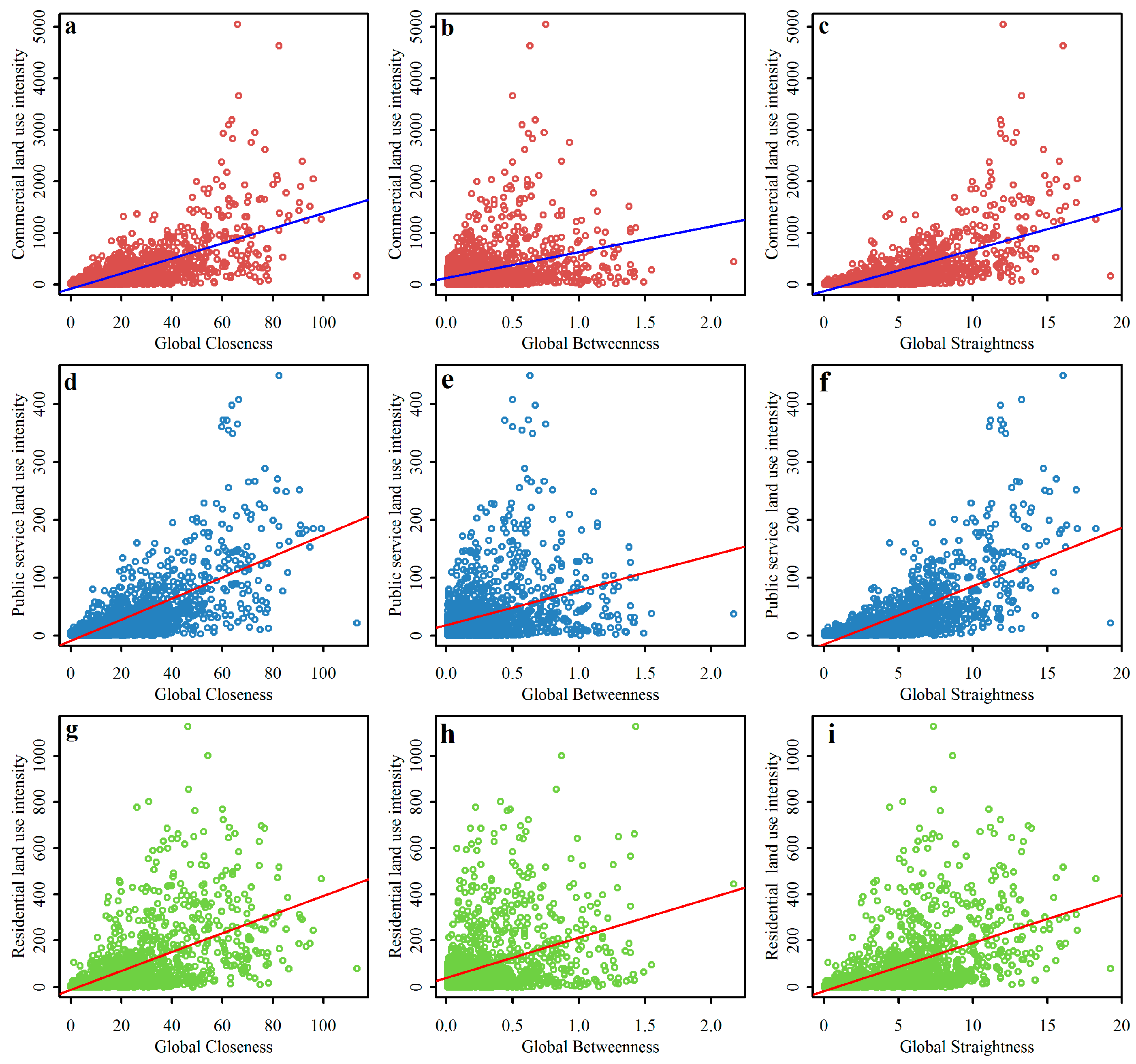

| Centralities | Comm # | Publ # | Resi # | Ln(Comm) | Ln(Publ) | Ln(Resi) |
|---|---|---|---|---|---|---|
| Glob CC | 0.670 ** | 0.701 ** | 0.585 ** | 0.679 ** | 0.677 ** | 0.648 ** |
| Glob CB | 0.343 ** | 0.350 ** | 0.381 ** | 0.386 ** | 0.374 ** | 0.391 ** |
| Glob CS | 0.665 ** | 0.700 ** | 0.540 ** | 0.733 ** | 0.729 ** | 0.668 ** |
| Ln(Glob CC) | 0.428 ** | 0.463 ** | 0.428 ** | 0.737 ** | 0.725 ** | 0.694 ** |
| Ln(Glob CB) | 0.360 ** | 0.375 ** | 0.381 ** | 0.456 ** | 0.441 ** | 0.447 ** |
| Ln(Glob CS) | 0.426 ** | 0.461 ** | 0.400 ** | 0.753 ** | 0.738 ** | 0.684 ** |
| Centralities | Comm # | Publ | Resi |
|---|---|---|---|
| Global CC ## | 0.675 ** | 0.706 ** | 0.592 ** |
| Local CC1km | 0.698 ** | 0.734 ** | 0.541 ** |
| Local CC2km | 0.654 ** | 0.688 ** | 0.501 ** |
| Local CC3km | 0.597 ** | 0.629 ** | 0.452 ** |
| Local CC5km | 0.316 ** | 0.344 ** | 0.255 ** |
| Global CB | 0.405 ** | 0.413 ** | 0.433 ** |
| Local CB1km | 0.296 ** | 0.325 ** | 0.264 ** |
| Local CB2km | 0.248 ** | 0.272 ** | 0.232 ** |
| Local CB3km | 0.215 ** | 0.239 ** | 0.201 ** |
| Local CB5km | 0.195 ** | 0.223 ** | 0.169 ** |
| Global CS | 0.669 ** | 0.703 ** | 0.549 ** |
| Local CS1km | 0.733 ** | 0.771 ** | 0.563 ** |
| Local CS2km | 0.740 ** | 0.779 ** | 0.563 ** |
| Local CS3km | 0.744 ** | 0.783 ** | 0.565 ** |
| Local CS5km | 0.747 ** | 0.785 ** | 0.569 ** |
| Centralities | Comm # | Publ | Resi |
|---|---|---|---|
| Local CC1km | 0.794 ** | 0.849 ** | 0.749 ** |
| Global CB | 0.518 ** | 0.573 ** | 0.521 ** |
| Local CS5km | 0.819 ** | 0.872 ** | 0.753 ** |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Xu, G.; Guo, Q. Street Centralities and Land Use Intensities Based on Points of Interest (POI) in Shenzhen, China. ISPRS Int. J. Geo-Inf. 2018, 7, 425. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi7110425
Wang S, Xu G, Guo Q. Street Centralities and Land Use Intensities Based on Points of Interest (POI) in Shenzhen, China. ISPRS International Journal of Geo-Information. 2018; 7(11):425. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi7110425
Chicago/Turabian StyleWang, Shuai, Gang Xu, and Qingsheng Guo. 2018. "Street Centralities and Land Use Intensities Based on Points of Interest (POI) in Shenzhen, China" ISPRS International Journal of Geo-Information 7, no. 11: 425. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi7110425





