DEM-Based Vs30 Map and Terrain Surface Classification in Nationwide Scale—A Case Study in Iran
Abstract
:1. Introduction
2. Study Area
2.1. Seismotectonic Setting
2.2. Iranian Strong Motion Network (ISMN)
3. Data
3.1. Vs30 Measurements
3.2. SRTM 30c and ASTER 1c
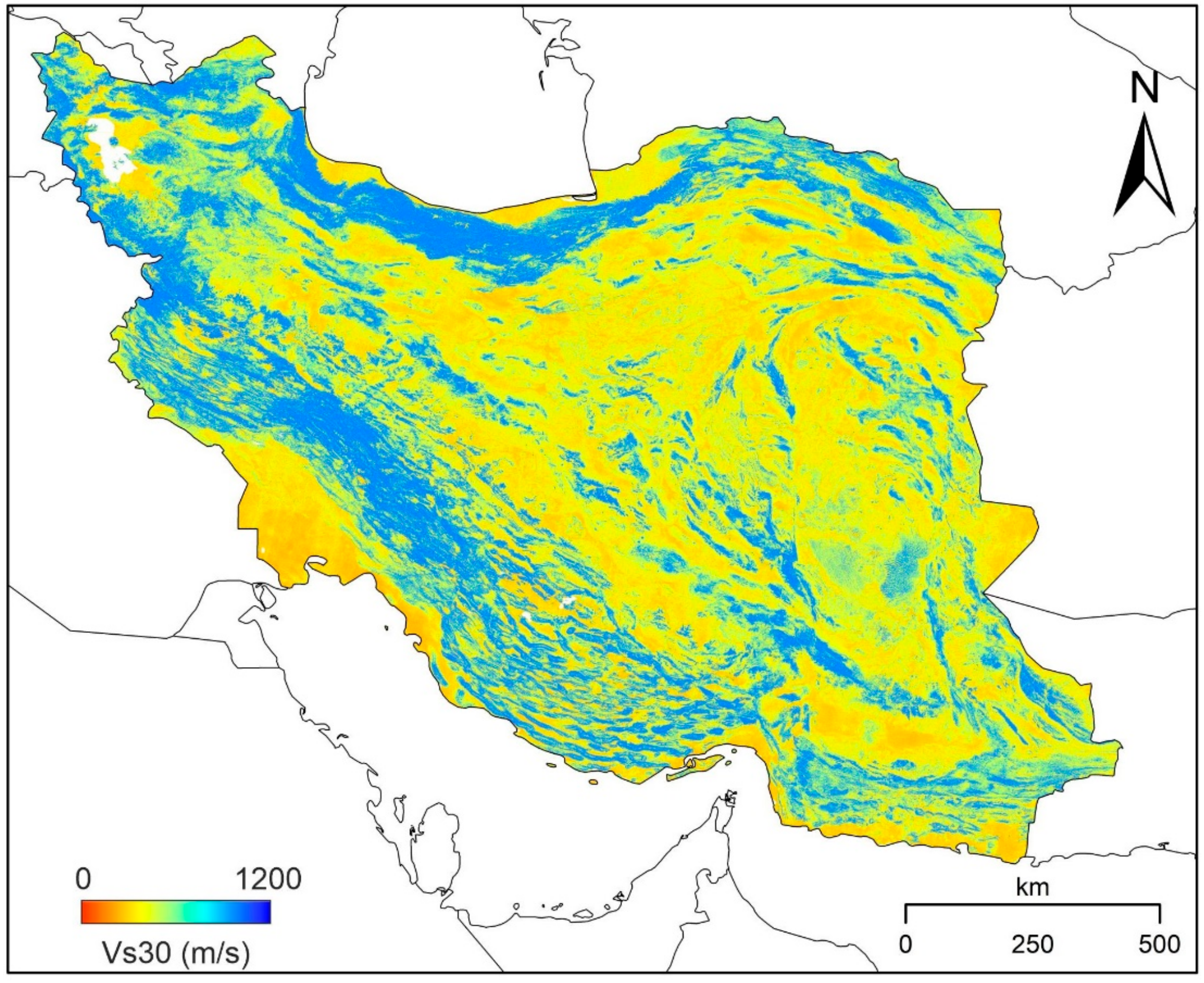
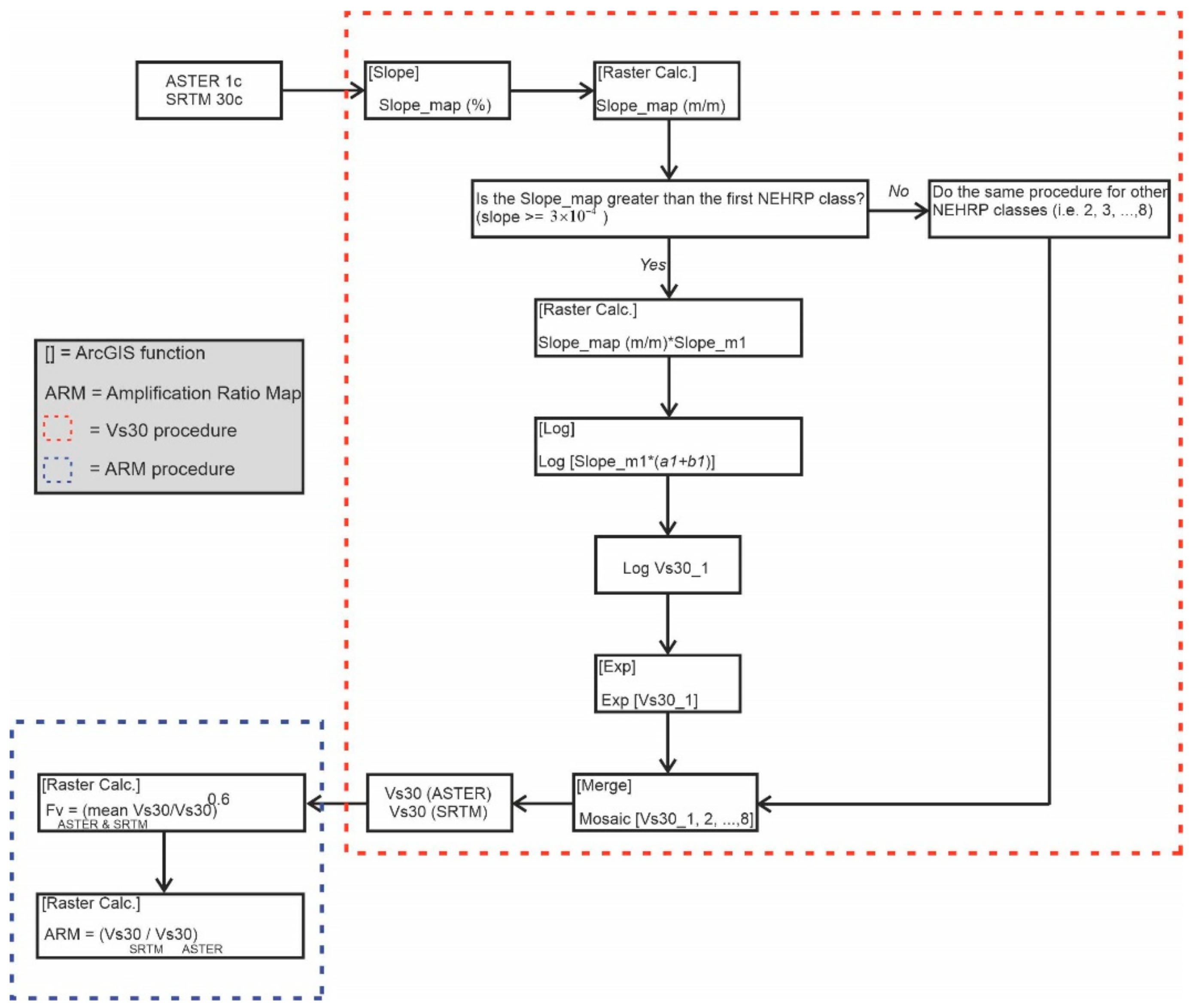
4. Vs30 Proxy Map
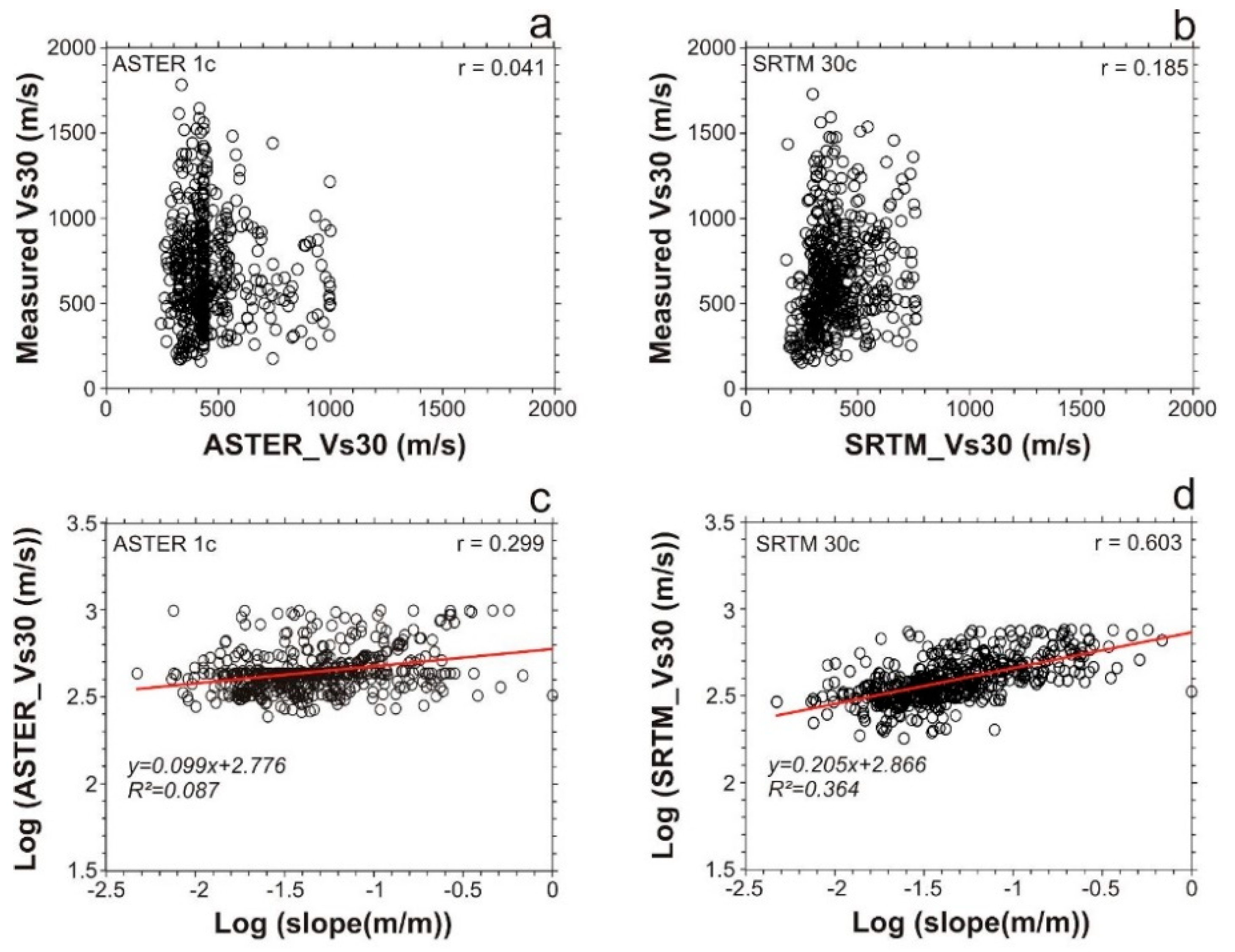
4.1. Regression Analysis and Vs30 Estimation
4.2. Vs30 and Amplifiation Map
4.3. Vs30 Results
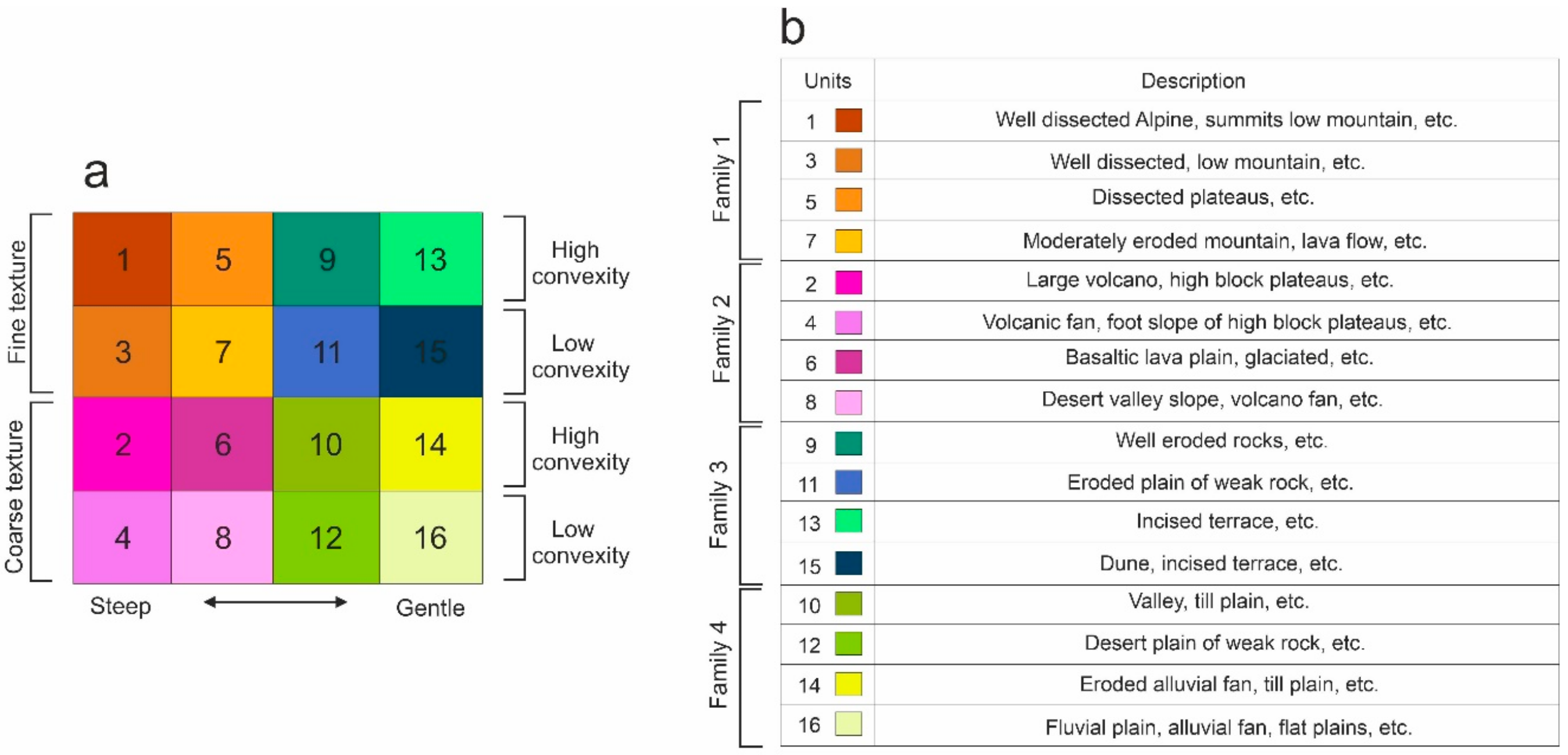
5. Terrain Classification and Site Characterization
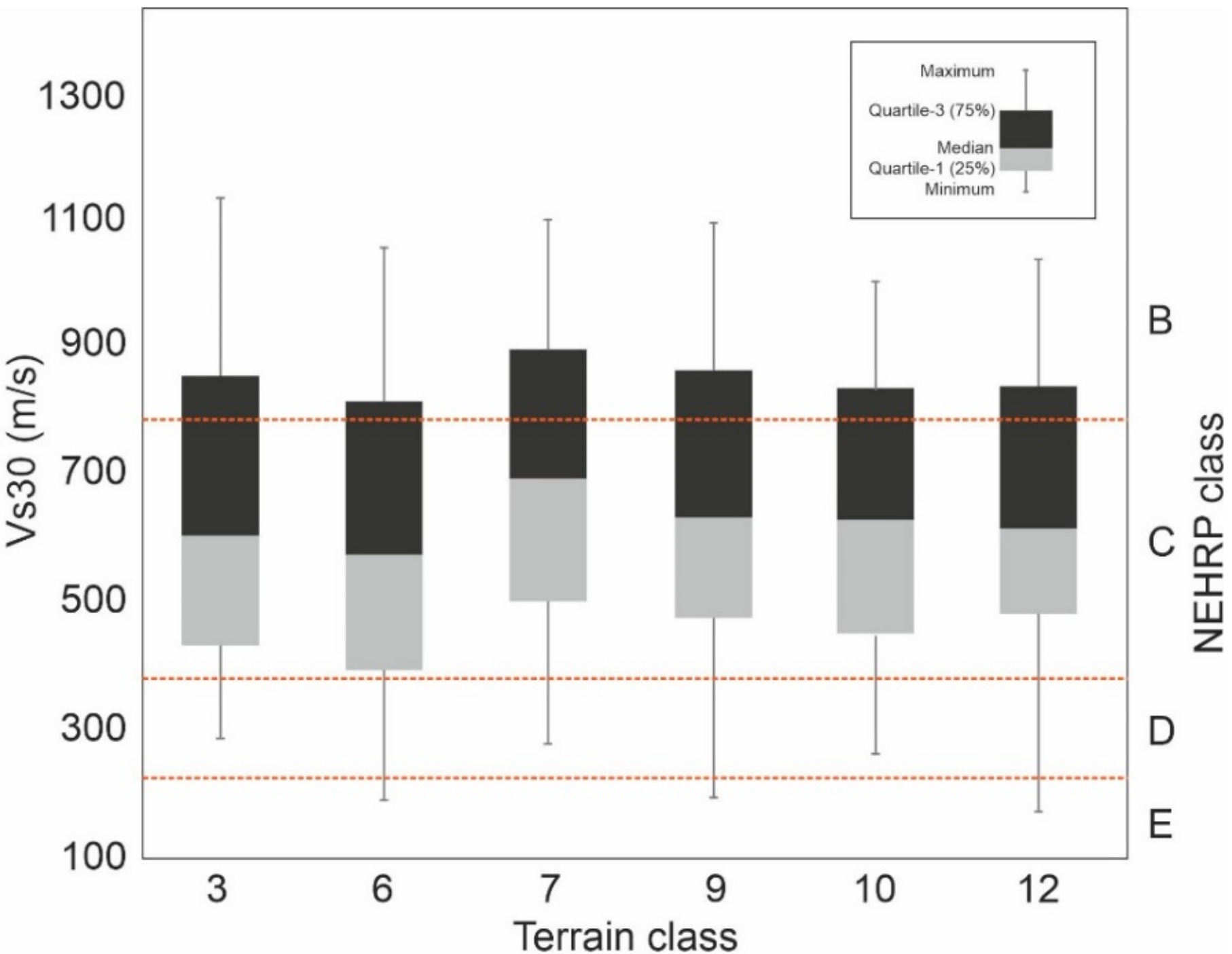
6. Terrain Classification Results
7. Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hassanzadeh, R.; Zorica, N.; Razavi, A.A.; Norouzzadeh, M.; Hodhodkian, H. Interactive approach for GIS-based earthquake scenario development and resource estimation (Karmania hazard model). Comput. Geosci. 2013, 51, 324–338. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Miyajima, M.; Hassanzadeh, R.; Amiraslanzadeh, R.; Kamel, B.A. GIS-based seismic hazard, building vulnerability and human loss assessment for the earthquake scenario in Tabriz. Soil Dyn. Earthq. Eng. 2014, 66, 263–280. [Google Scholar] [CrossRef]
- Hassanzadeh, R.; Zorica, N. Where to go first: Prioritization of damaged areas for allocation of Urban Search and Rescue (USAR) operations (PI-USAR model). Geomat. Nat. Hazards Risk 2015, 7, 1337–1366. [Google Scholar] [CrossRef]
- Matsuoka, M.; Wakamatsu, K.; Fujimoto, K.; Midorikawa, S. Nationwide site amplification zoning using GIS-based Japan Engineering Geomorphologic Classification Map. In Proceedings of the ICOSSAR, Millpress, Bethlehem, PA, USA, 19 June 2005; pp. 239–246. [Google Scholar]
- Matsuoka, M.; Wakamatsu, K.; Fujimoto, K.; Midorikawa, S. Average shear-wave velocity mapping using Japan Engineering Geomorphologic Classification Map. J. Struct. Mech. Earthq. Eng. 2006, 23, 57s–68s. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Miyajima, M.; Kamel, B.; Pessina, V. A fast topographic characterization of seismic station locations in Iran, through integrated use of Digital Elevation Models and GIS. J. Seismol. 2015, 19, 949–967. [Google Scholar] [CrossRef]
- Karimzadeh, S. Characterization of land subsidence in Tabriz basin (NW Iran) using InSAR and watershed analyses. Acta Geod. Geophys. 2015, 51, 181–195. [Google Scholar] [CrossRef]
- Iwahashi, J.; Kamiya, I.; Matsuoka, M. Regression analysis of Vs30 using topographic attributes from a 50-m DEM. Geomorphology 2010, 117, 202–205. [Google Scholar] [CrossRef]
- Lemoine, A.; Douglas, J.; Cotton, F. Testing the Applicability of Correlations between Topographic Slope and Vs30 for Europe. Bull. Seismol. Soc. Am. 2012, 102, 2585–2599. [Google Scholar] [CrossRef]
- Burjanek, J.; Edwards, B.; Fah, D. Empirical evidence of local seismic effects at sites with pronounced topography: A systematic approach. Geophys. J. Int. 2014, 197, 608–619. [Google Scholar] [CrossRef]
- Kwok, A.; Chiu, H. Developing correlation relationships of Vs30 for use in site classification in Taiwan. In Proceedings of the Tenth US National Conference on Earthquake Engineering Frontiers of Earthquake Engineering, Alaska, AK, USA, 21–25 July 2014. [Google Scholar]
- Wills, C.J.; Petersen, M.D.; Bryant, W.A.; Reichle, S.; Saucedo, G.J.; Tan, S.S.; Taylor, G.C.; Treiman, J.A. A site conditions map for California based on geology and shear wave velocity. Bull. Seismol. Soc. Am. 2000, 90, S187–S208. [Google Scholar] [CrossRef]
- Kawase, H. Site effects on strong ground motions. In International Handbook of Earthquake and Engineering Seismology; Academic Press: New York, NY, USA, 2003; pp. 1013–1030. [Google Scholar]
- Holzer, T.L.; Padovani, A.C.; Bennett, M.J.; Noce, T.E.; Tinsley, J.C. Mapping NEHRP VS30 site classes. Earthq. Spectra 2005, 2, 353–370. [Google Scholar] [CrossRef]
- Wald, D.J.; Allen, T.I. Topographic slope as a proxy for seismic site conditions and amplification. Bull. Seismol. Soc. Am. 2007, 97, 1379–1395. [Google Scholar] [CrossRef]
- Allen, T.I.; Wald, D.J. On the Use of High-Resolution Topographic Data as a Proxy for Seismic Site Conditions (VS30). Bull. Seismol. Soc. Am. 2009, 99, 935–943. [Google Scholar] [CrossRef]
- Allen, T.I.; Wald, D.J. Topographic Slope as a Proxy for SeismicSite-Conditions (VS30) and Amplification around the Globe; Open-File Report, 1357 U.S.; Geological Survey Reston: Virginia, VA, USA, 2007. [Google Scholar]
- Chung, J.W.; Rogers, D. Seismic Site Classifications for the St. Louis Urban Area. Bull. Seismol. Soc. Am. 2012, 102, 980–990. [Google Scholar] [CrossRef]
- Iranian Code of Practice for Seismic Resistance Design of Buildings, 4th ed.; Iranian building codes and standards, standard no. 2800; Building and Housing Research Center (BHRC): Tehran, Iran, 2014.
- NEHRP Recommended Seismic Provisions for New Buildings and Other Structures Volume I: Part 1 Provisions, Part 2 Commentary FEMA; A council of the National Institute of Building Sciences: Washington, DC, USA, 2015.
- Matsuoka, M.; Yamamoto, N. Web-based Quick Estimation System of Strong Ground Motion Maps Using Engineering Geomorphologic Classification Map and Observed Seismic Records. In Proceedings of the 15th World Conference on Earthquake Engineering, Portuguese Association for Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012; p. 10. [Google Scholar]
- Forte, G.; Chioccarelli, E.; De Falco, M.; Cito, P.; Santo, A.; Iervolino, I. Seismic soil classification of Italy based on surface geology and shear-wave velocity measurements. Soil Dyn. Earthq. Eng. 2019, 122, 79–93. [Google Scholar] [CrossRef]
- Stewart, J.P.; Klimis, N.; Savvaidis, A.; Theodoulidis, N.; Zargli, E.; Athanasopoulos, G.; Pelekis, P.; Mylonakis, G.; Margaris, B. Compilation of a local vs. profile database and its application for inference of VS30 from geologic- and terrain-based proxies. Bull. Seismol. Soc. Am. 2014, 104, 2827–2841. [Google Scholar] [CrossRef]
- Yong, A. Comparison of measured and proxy-based VS30 values in California. Earthq. Spectra 2016, 32, 171–192. [Google Scholar] [CrossRef]
- Vernant, P.; Nilforoushan, F.; Hatzfeld, D.; Abbassi, M.R.; Vigny, C.; Masson, F.; Nankali, H.; Martinod, J.; Ghafory-Ashtiany, M.; Bayer, R.; et al. Present-Day Crustal Deformation and Plate Kinematics in the Middle East Constrained by GPS Measurements in Iran and Northern Oman. Geophys. J. Int. 2004, 157, 381–398. [Google Scholar] [CrossRef]
- Nowroozi, A.A. Seismotectonic provinces of Iran. Bull. Seismol. Soc. Am. 1976, 66, 1249–1276. [Google Scholar]
- Berberian, M. Discussion of the paper A.A. Nowroozi, 1976 “Seismotectonic provinces of Iran”. Bull. Seismol. Soc. Am. 1979, 69, 293–297. [Google Scholar]
- Mirzaei, N.; Mengtan, G.; Yantai, C. Seismic source regionalization for seismic zoning of Iran: Major seismotectonic provinces. J. Earthq. Predict. Res. 1998, 7, 465–495. [Google Scholar]
- Mojarab, M.; Memarian, H.; Zare, M.; Morshedy, A.H.; Pishahang, M.H. Modeling of the seismotectonic provinces of Iran using the self-organizing map algorithm. Comput. Geosci. 2014, 67, 150–162. [Google Scholar] [CrossRef]
- Yazdani, A.; Kowsari, M. Bayesian estimation of seismic hazards in Iran. Sci. Iran. 2013, 20, 422–430. [Google Scholar]
- Mirzaei, H.; Farzanegan, E. Iran Strong Motion Network (Technical Note). Asian J. Civ. Eng. Build. Hous. 2003, 4, 173–186. [Google Scholar]
- Mousavi, M.; Zafarani, H.; Rahpeyma, S.; Azarbakht, A. Test of Goodness of the NGA Ground-Motion Equations to Predict the Strong Motions of the 2012 Ahar–Varzaghan Dual Earthquakes in Northwestern Iran. Bull. Seismol. Soc. Am. 2014, 104, 2512–2528. [Google Scholar] [CrossRef]
- Wills, C.J.; Clahan, K.B. Developing a map of geologically defined site-condition categories for California. Bull. Seismol. Soc. Am. 2006, 96, 1483–1501. [Google Scholar] [CrossRef]
- Nikolakopoulos, K.G.; Kamaratakis, E.K.; Chrysoulakis, N. SRTM vs. ASTER elevation products. Comparison for two regions in Crete, Greece. Int. J. Remote Sens. 2006, 27, 4819–4838. [Google Scholar] [CrossRef]
- Raster Tutorial; ESRI: Redlands, CA, USA, 2010; pp. 8–21. Available online: http://help.arcgis.com/en/arcgisdesktop/10.0/pdf/raster-tutorial.pdf (accessed on 01 October 2018).
- Wald, D.J.; Earle, P.S.; Quitoriano, V. Topographic Slope as a Proxy for Seismic Site Correction and Amplification. EOS Trans AGU 2004, 85, F1424. [Google Scholar]
- Karimzadeh, S.; Feizizadeh, B.; Matsuoka, M. From a GIS-based hybrid site condition map to an earthquake damage assessment in Iran: Methods and trends. Int. J. Disaster Risk Reduct. 2017, 22, 23–36. [Google Scholar] [CrossRef]
- Borcherdt, R.D. Estimates of site-dependent response spectra for design (methodology and justification). Earthq. Spectra 1994, 10, 617–653. [Google Scholar] [CrossRef]
- Iwahashi, J.; Pike, R.J. Automated classification of topography from DEMs by an unsupervised nested-means algorithm and a three-part geometric signature. Geomorphology 2007, 86, 409–440. [Google Scholar] [CrossRef]
- Iwahashi, J.; Kamiya, I.; Matsuoka, M.; Yamazaki, D. Global terrain classification using 280 m DEMs: Segmentation, clustering, and reclassification. Prog. Earth Planet. Sci. 2018, 5, 1. [Google Scholar] [CrossRef]
- Thamarux, P.; Matsuoka, M.; Poovarodom, N.; Iwahashi, J. VS30 Seismic Microzoning Based on a Geomorphology Map: Experimental Case Study of Chiang Mai, Chiang Rai, and Lamphun, Thailand. ISPRS Int. J. Geo-Inf. 2019, 8, 309. [Google Scholar] [CrossRef] [Green Version]







| NEHRP Site Classification | Vs30 Range (m/s) | Slope Range (m/m) | General Description | |
|---|---|---|---|---|
| Active Tectonic Regions | Craton Regions | |||
| Soil profile with soft clay | ||||
| Stiff soil | ||||
| Stiff soil | ||||
| Stiff soil | ||||
| Very dense soil and soft rock | ||||
| Very dense soil and soft rock | ||||
| Very dense soil and soft rock | ||||
| Rock & Hard rock | ||||
| Slope Range (m/m) | Vs30 Range (m/s) | |||
|---|---|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karimzadeh, S.; Feizizadeh, B.; Matsuoka, M. DEM-Based Vs30 Map and Terrain Surface Classification in Nationwide Scale—A Case Study in Iran. ISPRS Int. J. Geo-Inf. 2019, 8, 537. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi8120537
Karimzadeh S, Feizizadeh B, Matsuoka M. DEM-Based Vs30 Map and Terrain Surface Classification in Nationwide Scale—A Case Study in Iran. ISPRS International Journal of Geo-Information. 2019; 8(12):537. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi8120537
Chicago/Turabian StyleKarimzadeh, Sadra, Bakhtiar Feizizadeh, and Masashi Matsuoka. 2019. "DEM-Based Vs30 Map and Terrain Surface Classification in Nationwide Scale—A Case Study in Iran" ISPRS International Journal of Geo-Information 8, no. 12: 537. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi8120537







