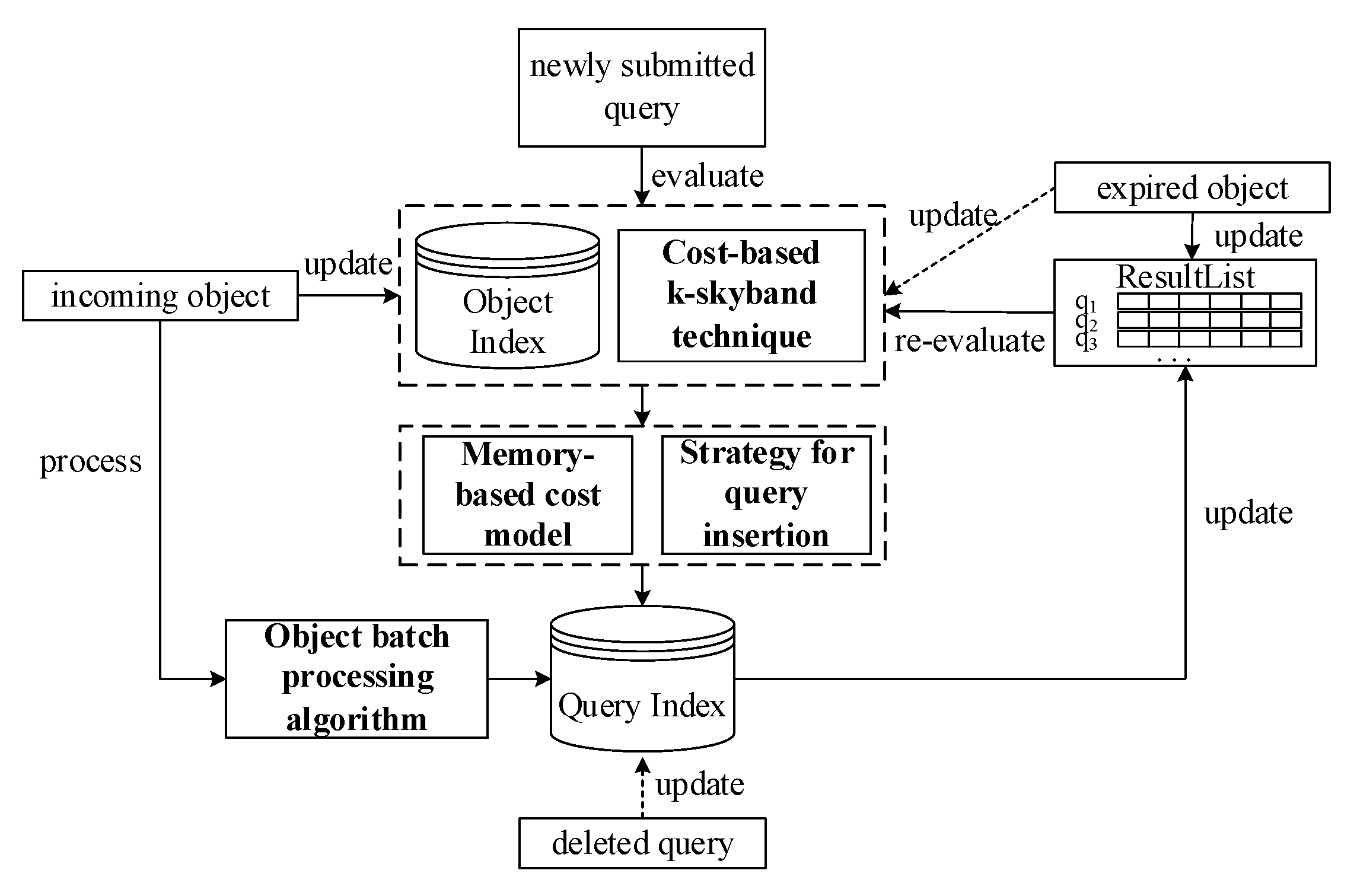
3.1. Motivations
Organizing the search range of CkQST. The first issue of using a quadtree to organize the search range of CkQST is how to map the search range to the quadtree nodes. Given that , can be mapped to any set of quadtree nodes , only if the union of the spatial region corresponding to these nodes in covers , which is also called that is associated with . Associating a query with the quadtree nodes is challenging because it affects two computation costs: (1) Verification cost, i.e., the cost of verifying the query with the objects falling in the associated nodes. (2) Update cost, i.e., the cost of inserting or deleting the query in or from the associated nodes. If the search range is organized by nodes with large regions, the index update cost is small, and the verification cost is large; otherwise, if multiple nodes with small regions are used, the situation is reversed. Therefore, a cost model is required to trade off the verification cost and update cost, and find the optimal associated nodes for CkQST.
Organizing the keywords of CkQST. When new objects arrive, the cost of verifying these objects with queries in spatial nodes is expensive. How to reduce the verification cost is the key to improve the filtering ability of the index. We discuss three aspects of constructing an inverted index. (1) For an inverted index, queries in posting lists are usually unordered. For the five queries in
Figure 1, we attached them to the posting list of a single keyword.
Figure 3a is the inverted index in which queries are attached to the posting list corresponding to the first query keyword, and
Figure 3b is the ranked-key inverted index in which queries are attached to the posting list corresponding to the least frequent keyword. If the incoming objects contain the corresponding term, all queries in posting lists are verified [
1,
2], which is inefficient. In this work, we use an ordered, inverted index to solve the above problem.
Figure 3c is the ordered, inverted index if queries are attached to the posting list corresponding to the first keyword, i.e., queries in posting lists are organized in the ascending order according to the keywords. When
with keywords
arrives, the posting list corresponding to
is verified. When
is verified with
, its keywords are smaller than
, so we can terminate the verification early and speed up processing objects.
(2) Compared with the ordered, inverted index constructed by single keyword, the ordered, inverted index constructed by multiple keywords has more advantages. The length is shorter and the verification probability is smaller. As
Figure 3d shows,
is verified with the first two posting lists and contains all the keywords of the queries in these posting lists. However, the number of posting lists might grow sharply. If the number of terms contained in vocabulary set
is 1 M, and the number of query keywords are not more than 5, total 10
6×5 posting lists are required, which is difficult to implement by hash table due to the need for large continuous memory. Like other works in [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12], this paper uses the Map class in Microsoft Visual Studio [
19] to build the ordered, inverted index. Lemma 1 describes the verification efficiency with the number of keywords for constructing the ordered, inverted index.
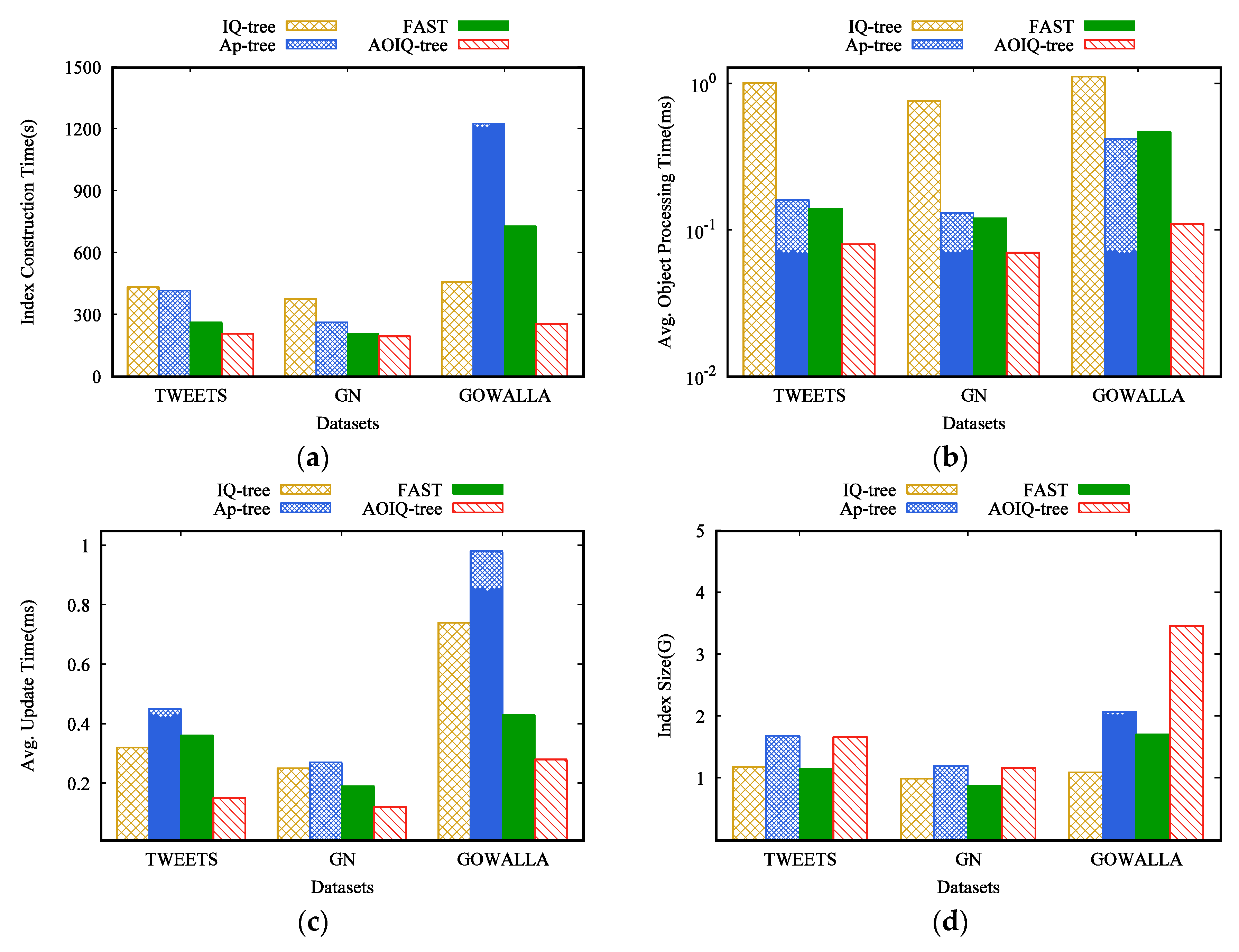
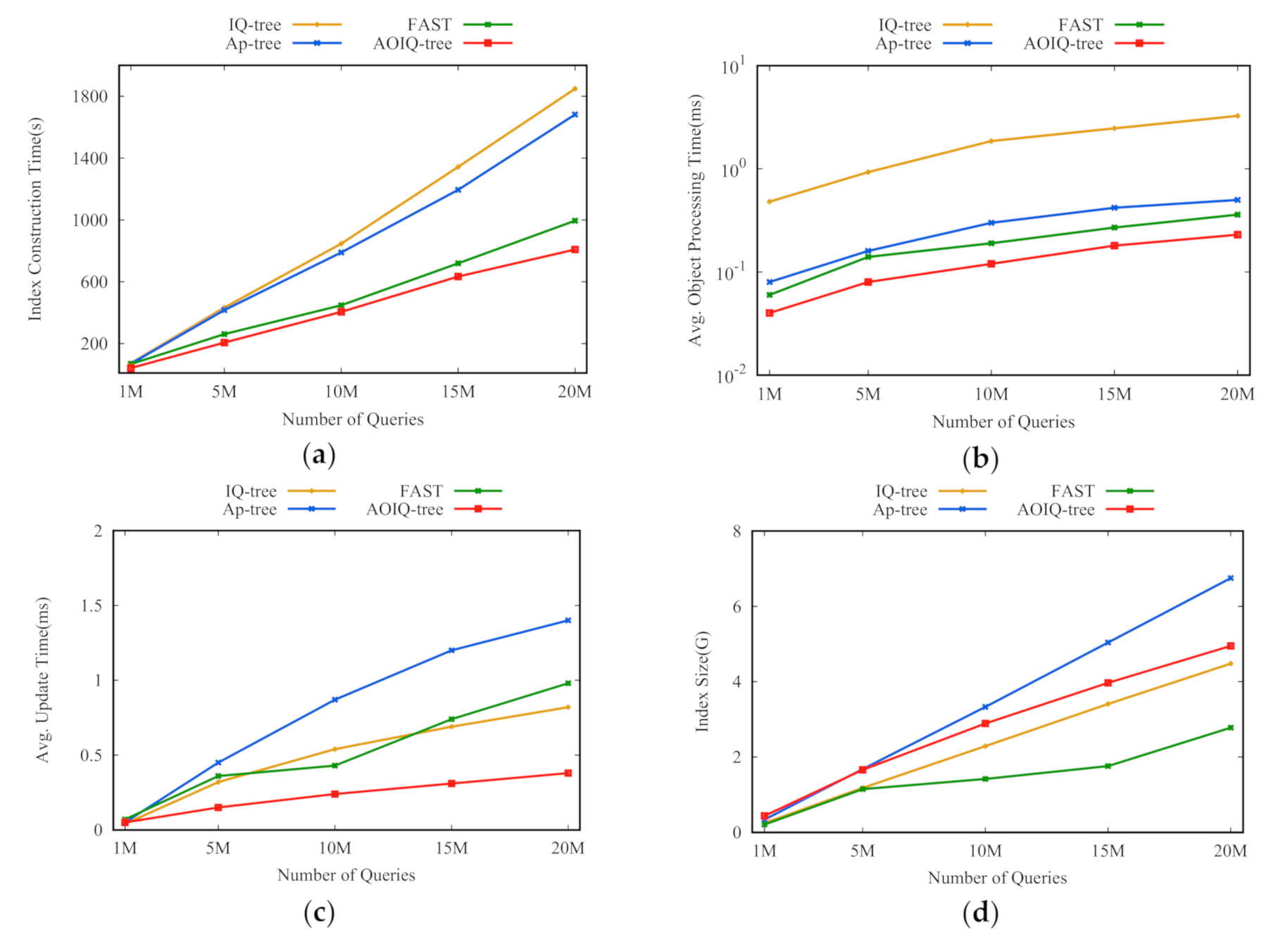
Section 4.2 verifies this lemma through experiments. Based on the discussions, we select two keywords to construct the ordered, inverted index.
(3) Usually, there are many queries in posting lists, but only a small number match the incoming objects. Therefore, quickly locating the queries to be verified in posting lists is another way to improve the efficiency of evaluating CkQST. The queries in posting list are partitioned into multiple blocks such that objects are verified with the queries in a few blocks rather than the whole posting list. The only problem is how to partition these queries in posting lists. It is inefficient to have too many or too few queries in a block. An adaptive insertion strategy is proposed in
Section 3.3.
3.2. Ordered, Inverted Index
The formal definition of an ordered, inverted index constructed using two keywords follows. Queries are attached to the posting list of their first two keywords, and arranged in ascending order according to their keywords.
Definition 1 (Ordered Posting List/Ordered, Inverted Index). Given a set of queries to be inserted into a quadtree node, if , and , the posting list determined by the two terms at the node is denoted as , in which these queries are successively inserted. is called an ordered posting list. Specifically, if these queries only contain one keyword, the corresponding posting list is denoted as. All the ordered posting lists constitute the ordered, inverted index.
Hereafter the ordered posting list is abbreviated as posting list, if there is no ambiguity. To quickly locate the queries to be verified, posting lists are divided into multiple blocks.
Definition 2 (Block). Given any ordered posting list ,, is the block of . For any query in,, where , . denotes all the keywords satisfying . Specially, if only contains one or two keywords, it is inserted into the block of the corresponding posting list.
Lemma 1. If the number of keywords for constructing an ordered, inverted index is
, there are at mostposting lists at a node. For any object containing more than two keywords, the verification cost can be estimated by Equation (1). Where is the number of blocks in a posting list, is the number of queries in , contains queries whose keywords are contained in , and the number of keywords is less than .
The proof is shown in Appendix A. For
, the verification probability, denoted as
, is maintained, i.e., the probability of verifying these queries subjected to
in
. For
, the verifying probability, denoted as
, is maintained, i.e., the probability that the block
is verified, which can be estimated by Equation (2).
The following theorems claim that the incoming object is verified with few queries in posting lists. For any incoming object, the blocks being verified can be located according to block keyword interval (see Theorem 1). The object verification with a block or a posting list can be terminated if the keywords are smaller than that of some query being verified. (see Theorem 2).
Theorem 1. Givenand a posting listbeing verified with, forin, ifin, contains all keywords of, only if, .
Proof. Suppose that contains all the keywords of , but there is no term in satisfying . Based on Definition 2, , does not contain the third keyword of , so does not contain all the keywords of . It is contradicted by the hypothesis, so the theorem is proved. □
Theorem 2. Givenand a posting listbeing verified with, forin, we have the following conclusions. (1) If, is not the result of queries in the blocks starting from, andcan be terminated verifying. Specifically, for in , if , can be terminated verifying. (2) If , is not the result of queries in .
Proof. (1) If , i.e., for any in , does not contain its third keyword, is not the result of . So does the block , since . Similarly, for any in , , is not the result of queries after .
(2) If , is not the result of the queries in . □
3.3. Adaptive Query Insertion Algorithm
Given any posting list at a node, we consider two extreme situations: (1) the posting list only contains a block which contains all queries; (2) the posting list contains many blocks, each of which only contain one query. The former has poor filtering ability and the latter has high update cost. Neither is what we expect. In the real world, people are concerned with different interests and often pay high attention to the breaking news or topical issues, so the keywords of the queries and objects vary over time. For each query, we adaptively insert it into the posting lists according to the historical queries and objects. We expect that the increase of the verification cost and update cost of the posting list is minimal after the query being inserted.
Given a posting list
, the update cost is denoted as
, and the verification cost is denoted as
, which can be estimated by Equation (3), where
represents the verification cost of the block
in
.
Theorem 3. Letbe the query to be inserted into, , hasblocks, is the increase of verification cost ofafterbeing inserted. We have the following conclusions.
Case 1: If satisfies , is inserted into . .
Case 2: If satisfies , but satisfies , is inserted into the tail of . The updated block is denoted as . .
Case 3: Similar to case 2, if satisfies , but satisfies , is inserted into the head of the . .
Case 4: If satisfies , a new block is constructed in , and is inserted into ..
Proof. (1) Case 1: If
is inserted into
, the verifying probability
does not change since
, but the number of queries in
increases by 1.
(3) Similar to case 2.
(4) Case 4: For any
in
,
,
Theorem 3 shows all the cases where the verification costs increase if a query is inserted into the posting list. The increase of update costs corresponding to the above four cases are , , , and respectively. To compare the verification costs and update costs, we introduce a normalization parameter to represent the ratio of the update operation to the verification operation, i.e., if a query is inserted into a node, there will be objects being verified with it. A query is adaptively inserted into the posting list according to the following theorem. □
Theorem 4. Let be the query to be inserted into, . Ifin satisfies , is inserted into. Otherwise, the minimumof the cases 2–4 is taken.
| Algorithm 1: |
| 1 if then |
| 2 construct new block b in insert q into b; return;
|
| 3 ;
|
| 4 if then q is inserted into br; return;
|
| 5 if and then
|
| 6 q is inserted into br−1; return;
|
| 7 if then compute on ;
|
| 8 if r == 1 then compute ;
|
| 9 if r > 1 then compute ;
|
| 10 if case 2 then q is inserted into the tail of br−1;
|
| 11 if case 3 then q is inserted into the head of br;
|
| 12 if case 4 inserted into a new block.
|
Given , if contains no more than two keywords, it is directly inserted into the of the corresponding posting list. Algorithm 1 shows how a query containing more than two keywords is adaptively inserted into a posting list. If does not exist, a new block is constructed, and is inserted into (lines 1–2). Otherwise, a block in is found for to minimize (lines 3–12). First, we find the block, denoted as , whose is the smallest—no smaller than (line 3). If , is inserted into (line 4). If (), is inserted into block (lines 5–6). Otherwise, we compute according to cases 2–4 in Theorem 3 and select the minimum case (lines 7–12). It is worth noting that when compared with the first block of the list, there are only cases 3–4, and if is larger than of all the blocks, there are only cases 2 and 4.
Computation complexity. In the worst case, the computation cost of Algorithm 1 is shown as Lemma 1. That is, in posting lists constructed by two keywords, the complexity of inserting a query at a node is . The algorithm can adaptively adjust and .
3.4. The Memory-Based Cost Model
A memory-based cost model associates queries with the optimal quadtree nodes. Given the search range of CkQST, the model traversals the quadtree from the root node, compares the sum of the verification cost and index update cost if the query is associated with the current node and its child nodes, and selects the smaller one. The verification cost is the product of the number of verified objects and the expectation of the verification cost, and the update cost is the expectation of the update cost if the query is inserted into the corresponding block of the posting list.
Definition 3 (Minimum Bounding Node). Given
and search range , if ,, and for any child node of ,, is the minimum bounding node of , where , are the region where and locate respectively. The minimum bounding node of is the node, which covers its search range, but any of its child nodes cannot completely cover the search range.
Verification cost. Given
and its minimum bounding node
,
, if
is associated with
, the verification cost within unit time interval, denoted as
, can be estimated by Equation (4). We assume that the query and object contain more than two keywords, and the average verification cost is unit time.
Specifically, if the query or the object contains one or two keywords, the verification cost is estimated by Equation (5). This case is simple, so we omit the details.
where
is the number of objects falling in
within the unit time interval.
is the probability that
is verified if it is inserted into
in
, i.e., the probability that the objects contain the terms
, and
, and can be estimated by Equation (6).
where
is the number of keywords contained in
.
is the verification cost if
is inserted into
in
, and can be estimated with the expectation of verification cost of the queries in
, i.e., Equation (7).
where
is the number of queries subjected to
in
. Similarly, if the query
is associated with a set of non-overlapping nodes, denoted as
, the verification cost is denoted as
and can be estimated by Equation (8).
For
, we find the optimal associated nodes starting from its minimum bounding node, and check whether the query is associated with the current node or associated with its child nodes. The difference of two verification costs is estimated by Equation (9).
where
keeps the intermediate result,
contains the child nodes of
that intersect with the search range of the query. It is worth noting that if
, we terminate the iteration.
Update cost. When inserting or deleting queries in nodes, it will incur an index update cost. We delay deleting queries until these queries are accessed again, so the deletion cost is ignored. If a query
is associated with its minimum bounding node
, and is inserted into a block
of posting list
in
, the insertion cost consists of two parts, the time to find the corresponding block and the time to find the insertion position. The update cost, denoted as
, can be estimated by Equation (10).
If
is associated with a set of non-overlapping nodes, denoted as
, the update cost is denoted as
and can be estimated by Equation (11).
Similarly to
, the difference of two update costs between the query being associated with the node and associated with the child nodes is estimated by Equation (12).
Given and search range , we start from the minimum bounding node, and computes and between the query being associated with the node and associated with the child nodes. If , the child nodes are the optimal. Otherwise the node is optimal. The computation cost consists of two parts, finding the minimum bounding node of , and finding an optimal association in the descendant nodes of minimum bounding node. The computation cost of the first part is , and the second part is , i.e., in the worst case, the node will be partitioned until the leaf node, where is the height of the quadtree.
3.5. Processing Objects in Batches
For these objects being verified with the same posting list, an object processing algorithm, which is a group matching technique that follows the filtering and verification strategy, is proposed to process objects in batches.
A data structure is defined to group the objects being verified with the same posting list, where is the block id, is a term, is a set of objects being verified with block and containing . For the convenience of the description, is a set of terms satisfying , is a set of objects which are verified with the queries in block and contain .
Algorithm 2 describes how to process a set of objects represented by , which are verified with the queries in the posting list . If is , the queries in is verified with the objects in (lines 1–5). Otherwise, for any term in , according to Theorem 2, if , we check the next term (line 7); if , we check the next block (line 8); otherwise, for each query in , if , we check the next term (line 10); if , we check the next query (line 11); otherwise, we verify whether the object is the results of . If yes, is added to (lines 12–13). Moreover, the result list and search range of are updated.
Computation complexity. Algorithm 2 describes how to process objects in batches in an ordered posting list. In the worst case, objects are processed individually. As Lemma 1 shows, in posting lists constructed by two keywords, for an object, the time complexity of finding the qualified queries at a node is .
| Algorithm 2: .
|
![Ijgi 09 00694 i001]() |
3.6. Cost-Based k-Skyband Technique
To reduce the re-evaluation cost, a cost-based k-skyband technique is proposed to judiciously determine an optimal search range for CkQST such that the overall cost defined in the cost model can be minimized. Specifically, for , three parameters are defined: an extended search range is denoted as , where ; a k-skyband, i.e., an extended result list, denoted as , where ; the number of objects containing all query keywords within in the initial timestamp is denoted as , where .
Definition 4 (Loose Matching). Given and , loosely matches only if and . All the objects that loosely match aredenoted as .
Definition 5 (Dominance). Given and two objects ,, which loosely match , dominates only if and or and .
Definition 6 (k-skyband/Extended Result list). Given , for any incoming object , we insert it into the k-skyband only if: (1) loosely matches ; (2) is dominated by less than other objects. For, ifan object loosely matches , and there are objects in dominating,would not be a result at any timestamp. Therefore, we would not insert these objects into the result list.
Theorem 5. Given and an extended search range, we always have the following conclusions. (1); (2); (3)iff.
Proof. (1) At any timestamp, for , we have and , i.e., loosely matches , and less than objects dominate . So . (2) According to Definition 4, for , loosely matches , so , . (3) Since , if , we have . On the other hand, if , , i.e., and , which means loosely matches , but is dominated by more than other objects, which is contradicted by . The theorem is proved. □
According to Theorem 5, the extended result list is the super set of the exact result list, from which we can extract the kNN objects, and the number of objects in extended result list is less than only if the number of objects in is less than .
Given , an extended search range , and the corresponding extended result list , three costs are defined in the cost-based k-skyband technique: the verification cost of within , the update cost of , and the re-evaluation cost.
Verification cost. The verification cost of
within
, within the unit time interval, denoted as
, is estimated by Equation (13), i.e., the verification cost if
is inserted into all the leaf nodes that intersect with
.
Update cost. Similarly to
, the extended result list
is organized by a linked list. For
, a dominance counter is defined to count the number of objects dominating
. If an incoming object
is inserted into
, the dominance counters of all the objects in
with
and
, or
and
will increase by 1, and the objects with dominance counter equal to
will be evicted, which can be processed in
time. When an object in
expires, it is deleted from
until it is accessed again. The cost is negligible. The update cost of
within unit time interval, denoted as
, is estimated by Equation (14). Where
is the number of object updates within unit time interval,
is the probability that the objects loosely match
within the search range
, and is estimated by
,
is the probability that a qualified object arrival,
can be estimated by
.
Re-evaluation cost. The re-evaluation cost within the unit time interval is denoted as . Where is the re-evaluation period, i.e., the shortest time required between two consecutive independent evaluations, and is the frequency of re-evaluation. is the re-evaluation cost, and is approximated to the verification cost in , i.e., .
The overall cost in the cost-based k-skyband technique, denoted as
, is shown in Equation (15). When
is minimal, the search range is optimal.
In the following, we discuss how to get
.
is the re-evaluation period, i.e., the shortest time that
is reduced to
since the last re-evaluation. For
, the update process of number of objects in
can be modeled as a simple random walk, which is a stochastic sequence
, with
being the original status, defined by
, where
is the object update, which is an independent and identically distributed random variable. In
, if an object is inserted,
; if an object expires or is dominated,
; otherwise
. It’s difficult to estimate
due to the eviction of objects by the dominance relationship in
. For example, an object is inserted, but the number of objects decreases due to the eviction of objects with dominance counters reaching
. According to Theorem 5, the number of objects in
is less than
only if the number of objects in
is less than
, and the objects in
don’t dominate each other. Therefore we estimate the shortest time that
is reduced to
, denoted as
, where
. The object update in
at any timestamp can be estimated as Equation (16).
The number of object updates required to reduce the number of objects from
to
in
, denoted as
, is estimated by Equation (17).
is estimated by
.
For , the variables in Equation (15) are and . To minimize Equation (15), we employ the incremental estimation algorithm to compute the optimal and the corresponding .
To accommodate our extended search range with the objects processing algorithm and index construction and maintenance algorithm, we replace with and replace with .