Analyzing Links between Spatio-Temporal Metrics of Built-Up Areas and Socio-Economic Indicators on a Semi-Global Scale
Abstract
:1. Introduction
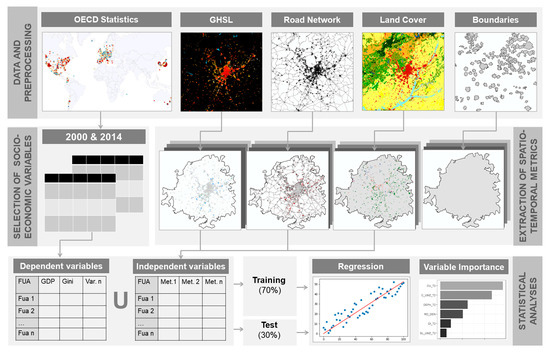
2. Materials and Methods
2.1. Socio-Economic, EO-Derived and Ancillary Datasets
2.1.1. Global Human Settlement Layer (GHSL)
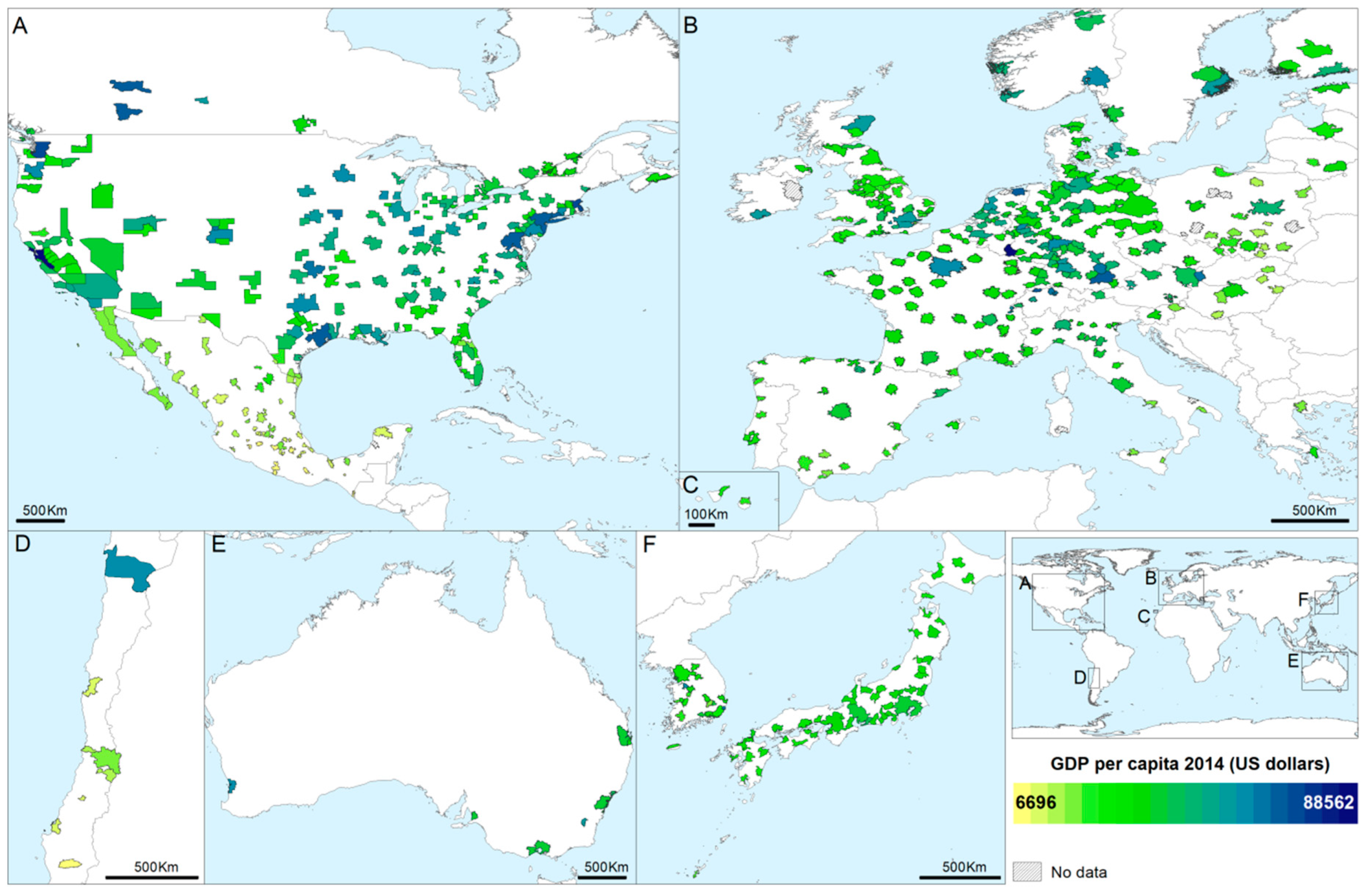
2.1.2. OECD Regional Statistics
2.1.3. Boundaries of EU-OECD FUAs
2.1.4. Climate Change Initiative Land Cover
2.1.5. Road Network
2.2. Preprocessing and Harmonization of Datasets
- The boundaries of the EU-OECD FUAs from each country were merged in a shapefile, and only those FUAs with statistical information in the metropolitan area dataset were kept. Colombian FUAs were not included in the analysis due to GHSL underclassification, cloud presence or a lack of socio-economic variables.
- The European region of the GRIP dataset was georeferenced using control points from OpenStreetMaps, as it was originally displaced (about 100 m).
- Then, two built-up epochs were extracted from the GHSL. Categories 4 to 6 represent the built-up area in 2000, and categories 3 to 6, that in 2014. This generated two built-up maps.
- Regarding the CCI-LC, two bands corresponding to the years 2000 and 2014 were extracted (bands 9 and 23). The legend of the CCI-LC was grouped into seven major land cover types, as follows: agricultural areas (categories from 10 to 30, both included), high semi-/natural vegetation (40–100 and 160–180), low semi-natural/natural vegetation (110–153), urban areas (190), bare areas (200–202), water bodies (210) and permanent snow (220). To see the original legend and the link between the categories and land covers, refer to the European Space Agency (ESA) [41]. This process generated two land cover maps.
- The resulting global built-up and land cover maps and road network dataset were clipped using the boundaries of the FUAs in the CRS of the dataset to be clipped, transforming the FUA boundaries when necessary.
- After that, the built-up and land cover maps in their original spatial resolutions were vectorized to shapefile format, since the tool used for the extraction of the metrics works with vector data.
- Finally, the data were transformed to a local projected CRS to allow the measurement of areas and distances, which are basic attributes in most of the spatial metrics. To do so, the centroid of the FUA was used to determine the EPSG code to project the data to their Universal Transverse Mercator (UTM) zone (e.g., Madrid has the EPSG code 32630, which corresponds to the CRS WGS84/UTM zone 30N). Thus, all the FUAs have similar adapted and local CRSs in the same units, meters.
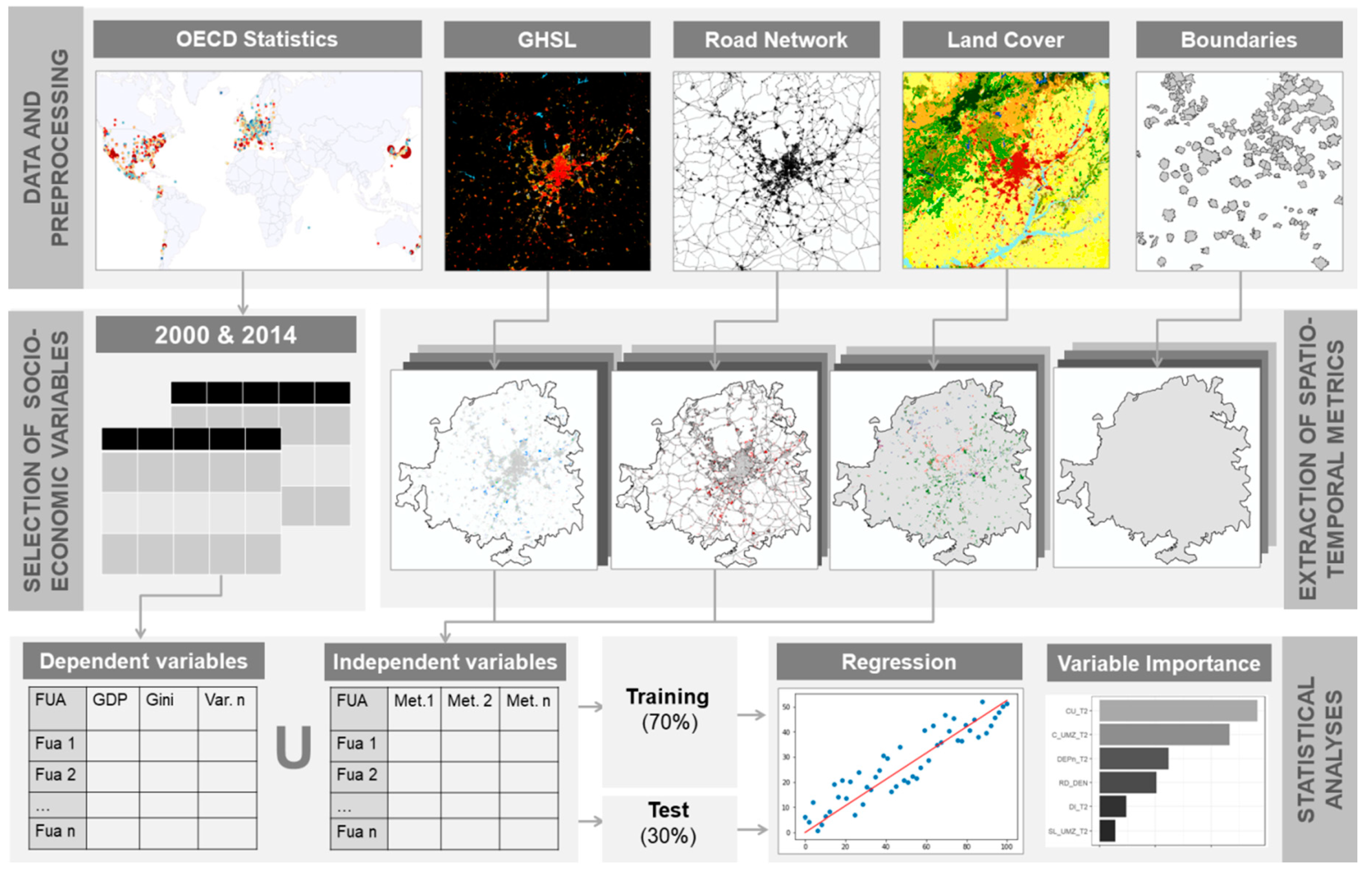
2.3. Extraction of Spatio-Temporal Metrics
2.3.1. Spatial Metrics (2000 and 2014)
- The urban compactness (C) measures the complexity and fragmentation of the built-up area; it is for both the FUAs and for the largest urban core (CUC). High values show a more compact shape and aggregated distribution; it ranges from 0 to 100.
- The dispersion index (DI) is the ratio between the normalized number of patches and the proportion of built-up area occupied by the largest patch [54]. Low values indicate coalescence, while high values represent dispersion.
- The normalized area-weighted standard distance (AWSD) measures the centrality of the built-up area, quantifying the degree to which objects are concentrated around their centroid. It is normalized to the shape and size of the FUA by means of the “maximum distance”, measured as the standard distance of a regular grid covering the FUA extension to the centroid. Normalized values range from 0 to 100, where lower distances show a concentrated distribution of built-up patches around the core, and higher values show built-up patches homogeneously distributed across the entire FUA, without a special clustering around the center.
- The density is the percentage of built-up area (DU) and other land covers (D) relative to the total FUA area.
- The percentage of the urban core (LUC) is the percentage of the built-up area that occupies the largest core. When the value is high, it shows a monocentric form. Since the spatial metric is highly correlated to the DI, only the change was computed and included as a multi-temporal metric.
- The second largest urban core (SLUC) is the percentage of the built-up area that occupies the second largest core. When the value is close to LUC, it suggests a polycentric form.
- The elongation ratio (ERUC) of the largest urban core quantifies the elongation shape of the urban core. This metric is commonly used in hydrology [55]; it measures the elongation, dividing the diameter of the circumference with the same area as the core by the largest side of the core. It ranges from 0 to 1. Values closer to zero show elongated shapes, i.e., a linear urban form.
- The density of road network (D road) is the total length of roads per square kilometer.
2.3.2. Multi-Temporal Metrics (2000–2014)
- We calculated the following metrics as the differences between the spatial metrics for the two different years, 2000 and 2014: the change in urban compactness (CCH), urban core compactness (CUC CH), dispersion index (DICH), normalized area-weighted standard distance (AWSDCH), density (DUCH, DCH), percentage of the urban core (LUC CH), second largest urban core (SLUC CH) and elongation ratio (ERUC CH).
- The urban change rate (UCR) is the percentage of built-up growth relative to the built-up area for the first date.
- The area-weighted mean expansion index (AWMEI) is equal to the sum of adjacencies to the built-up area across all the new patches weighted by their area. It quantifies the aggregation and densification of growth. It ranges from 0 to 100. A high value indicates a densification (infilling growth) and therefore a more compact growth pattern, and an intermediate value shows expansive growth, while a low value represents scattered growth.
- The area-weighted mean accessibility index (AWMAI) quantifies the accessibility of new built-up patches to the road network. This is measured with the mean of the inverse distance between the new built-up patches and their closest roads, weighted by the areas of the patches. It ranges from 0 to 100. Higher values show shorter distances to roads and better accessibility.
- The population and urban growth imbalance index (PUGI) it measures the inequality between the increase in the built-up area with respect to population growth or decline (based on population counts from Table 1). It provides information related to the land consumption per capita (i.e., the amount of built-up land per population change) and the degree of sprawl in the urbanization process [56]. Positive values show more urban growth, zero means equal growth, and negative values mean higher population growth.
- The change proportion (CP) of the land cover is the ratio representing the change in a particular land cover with respect to the total area of the FUA, and it measures the relative area of change.
2.4. Regression Models and Identifying Spatio-Temporal Metrics’ Relevance
3. Results
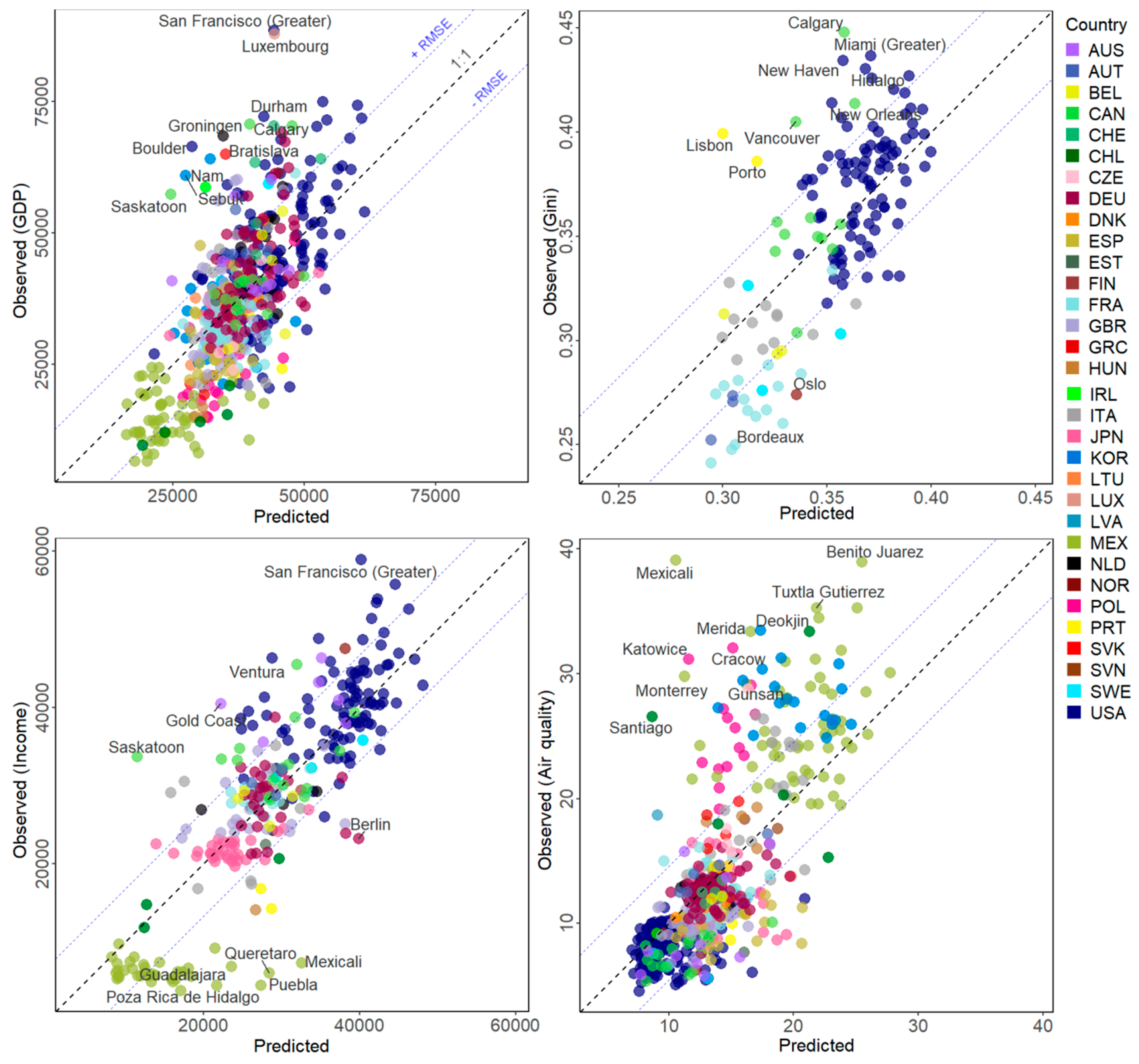
3.1. Estimation of Socio-Economic Variables
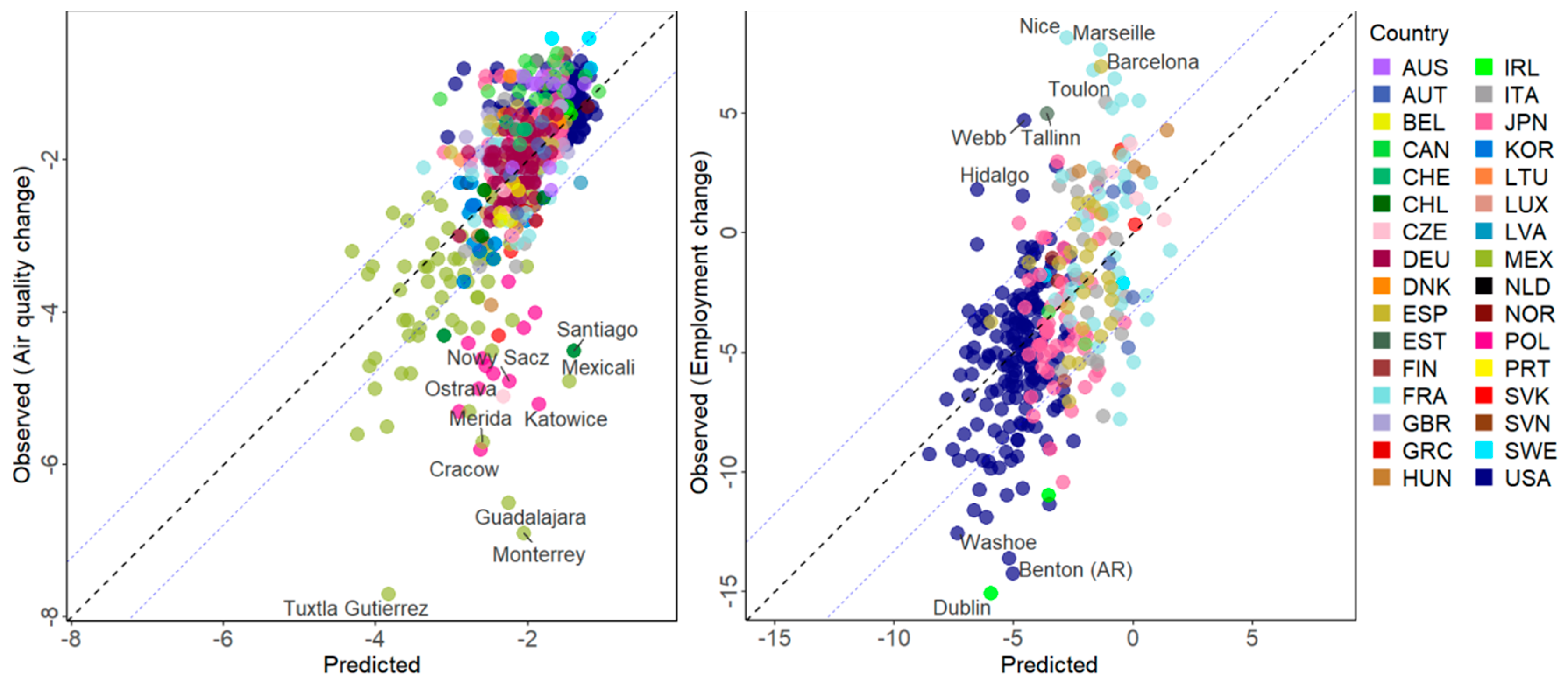
3.2. Estimation of the Variation of Socio-Economic Variables
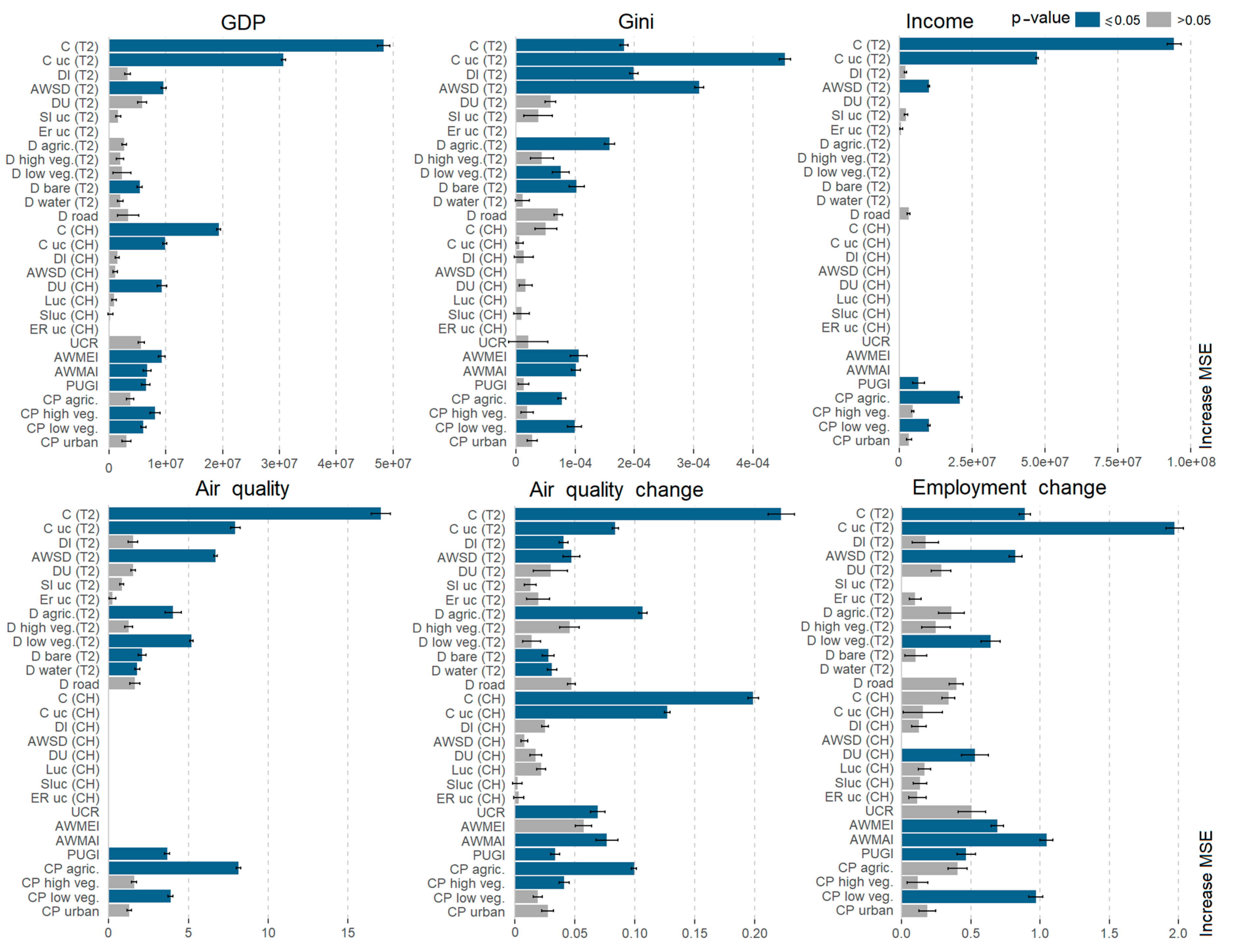
3.3. Relevance of Spatio-Temporal Metrics
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Tonkiss, F. Cities by Design: The Social Life of Urban Form; Polity Press: Cambridge, UK, 2013. [Google Scholar]
- Zhu, Z.; Zhou, Y.; Seto, K.C.; Stokes, E.C.; Deng, C.; Pickett, S.T.A.; Taubenböck, H. Understanding an urbanizing planet: Strategic directions for remote sensing. Remote Sens. Environ. 2019, 228, 164–182. [Google Scholar] [CrossRef]
- United Nations (UN). Department of Economic and Social Affairs, Population Division; World Urbanization Prospects: New York, NY, USA, 2019. [Google Scholar]
- Wentz, E.A.; York, A.M.; Alberti, M.; Conrow, L.; Fischer, H.; Inostroza, L.; Jantz, C.; Pickett, S.T.A.; Seto, K.C.; Taubenböck, H. Six fundamental aspects for conceptualizing multidimensional urban form: A spatial mapping perspective. Landsc. Urban Plan. 2018, 179, 55–62. [Google Scholar] [CrossRef]
- Wentz, E.A.; Anderson, S.; Fragkias, M.; Netzband, M.; Mesev, V.; Myint, S.W.; Quattrochi, D.; Rahman, A.; Seto, K.C. Supporting Global Environmental Change Research: A Review of Trends and Knowledge Gaps in Urban Remote Sensing. Remote Sens. 2014, 6, 3879–3905. [Google Scholar] [CrossRef] [Green Version]
- Allen, L.; Williams, J.; Townsend, N.; Mikkelsen, B.; Roberts, N.; Foster, C.; Wickramasinghe, K. Socioeconomic status and non-communicable disease behavioural risk factors in low-income and lower-middle-income countries: A systematic review. Lancet Glob. Health 2017, 5, e277–e289. [Google Scholar] [CrossRef] [Green Version]
- Belsky, D.W.; Caspi, A.; Arseneault, L.; Corcoran, D.L.; Domingue, B.W.; Harris, K.M.; Houts, R.M.; Mill, J.D.; Moffitt, T.E.; Prinz, J.; et al. Genetics and the geography of health, behaviour and attainment. Nat. Hum. Behav. 2019, 3, 576–586. [Google Scholar] [CrossRef] [PubMed]
- Villeneuve, P.J.; Jerrett, M.; Su, J.G.; Burnett, R.T.; Chen, H.; Wheeler, A.J.; Goldberg, M.S. A cohort study relating urban green space with mortality in Ontario, Canada. Environ. Res. 2012, 115, 51–58. [Google Scholar] [CrossRef]
- Patz, J.A.; Daszak, P.; Tabor, G.M.; Aguirre, A.A.; Pearl, M.; Epstein, J.; Wolfe, N.D.; Kilpatrick, A.M.; Foufopoulos, J.; Molyneux, D.; et al. Unhealthy landscapes: Policy recommendations on land use change and infectious disease emergence. Environ. Health Perspect. 2004, 112, 1092–1098. [Google Scholar] [CrossRef] [Green Version]
- Wilkinson, D.A.; Marshall, J.C.; French, N.P.; Hayman, D.T.S. Habitat fragmentation, biodiversity loss and the risk of novel infectious disease emergence. J. R. Soc. Interface 2018, 15, 20180403. [Google Scholar] [CrossRef] [Green Version]
- Zohdy, S.; Schwartz, T.S.; Oaks, J.R. The coevolution effect as a driver of spillover. Trends Parasitol. 2019, 35, 399–408. [Google Scholar] [CrossRef]
- Watmough, G.R.; Atkinson, P.M.; Saikia, A.; Hutton, C.W. Understanding the evidence base for poverty–environment relationships using remotely sensed satellite data: An example from Assam, India. World Dev. 2016, 78, 188–203. [Google Scholar] [CrossRef]
- Duque, J.C.; Patino, J.E.; Ruiz, L.A.; Pardo-Pascual, J.E. Measuring intra-urban poverty using land cover and texture metrics derived from remote sensing data. Landsc. Urban Plan. 2015, 135, 11–21. [Google Scholar] [CrossRef]
- Venerandi, A.; Quattrone, G.; Capra, L. A scalable method to quantify the relationship between urban form and socio-economic indexes. EPJ Data Sci. 2018, 7, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Arribas-Bel, D.; Patino, J.E.; Duque, J.C. Remote sensing-based measurement of Living Environment Deprivation: Improving classical approaches with machine learning. PLoS ONE 2017, 12, e0176684. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Faisal, K.; Shaker, A.; Habbani, S. Modeling the relationship between the gross domestic product and built-up area using remote sensing and GIS data: A case study of seven major cities in Canada. ISPRS Int. J. Geo-Inf. 2016, 5, 23. [Google Scholar] [CrossRef] [Green Version]
- Liang, H.; Guo, Z.; Wu, J.; Chen, Z. GDP spatialization in Ningbo City based on NPP/VIIRS night-time light and auxiliary data using random forest regression. Adv. Space Res. 2020, 65, 481–493. [Google Scholar] [CrossRef]
- Weigand, M.; Wurm, M.; Dech, S.; Taubenböck, H. Remote sensing in environmental justice research—A review. ISPRS Int. J. Geo-Inf. 2019, 8, 20. [Google Scholar] [CrossRef] [Green Version]
- McCarty, J.; Kaza, N. Urban form and air quality in the United States. Landsc. Urban Plan. 2015, 139, 168–179. [Google Scholar] [CrossRef]
- Hankey, S.; Marshall, J.D. Urban form, air pollution, and health. Curr. Environ. Health Rep. 2017, 4, 491–503. [Google Scholar] [CrossRef]
- Olsen, J.R.; Nicholls, N.; Mitchell, R. Are urban landscapes associated with reported life satisfaction and inequalities in life satisfaction at the city level? A cross-sectional study of 66 European cities. Soc. Sci. Med. 2019, 226, 263–274. [Google Scholar] [CrossRef]
- Sapena, M.; Ruiz, L.A.; Goerlich, F.J. Analysing relationships between urban land use fragmentation metrics and socio-economic variables. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2016, XLI-B8, 1029–1036. [Google Scholar] [CrossRef]
- Stokes, E.C.; Seto, K.C. Characterizing and measuring urban landscapes for sustainability. Environ. Res. Lett. 2019, 14, 045002. [Google Scholar] [CrossRef]
- Mveyange, A. Night Lights and Regional Income Inequality in Africa; The United Nations University World Institute for Development Economics Research (UNU-WIDER): Helsinki, Finland, 2015. [Google Scholar]
- De Leeuw, J.; Georgiadou, Y.; Kerle, N.; De Gier, A.; Inoue, Y.; Ferwerda, J.; Smies, M.; Narantuya, D. The Function of Remote Sensing in Support of Environmental Policy. Remote Sens. 2010, 2, 1731–1750. [Google Scholar] [CrossRef] [Green Version]
- Taubenböck, H.; Ferstl, J.; Dech, S. Regions set in stone—Delimiting and categorizing regions in Europe by settlement patterns derived from EO-data. ISPRS Int. J. Geo-Inf. 2017, 6, 55. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Nordhaus, W.D. Using luminosity data as a proxy for economic statistics. Proc. Natl. Acad. Sci. USA 2011, 108, 8589–8594. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rimal, B.; Zhang, L.; Keshtkar, H.; Wang, N.; Lin, Y. Monitoring and Modeling of Spatiotemporal Urban Expansion and Land-Use/Land-Cover Change Using Integrated Markov Chain Cellular Automata Model. ISPRS Int. J. Geo-Inf. 2017, 6, 288. [Google Scholar] [CrossRef] [Green Version]
- Oldekop, J.A.; Sims, K.R.; Karna, B.K.; Whittingham, M.J.; Agrawal, A. Reductions in deforestation and poverty from decentralized forest management in Nepal. Nat. Sustain. 2019, 2, 421–428. [Google Scholar] [CrossRef] [Green Version]
- Sims, K.R.; Thompson, J.R.; Meyer, S.R.; Nolte, C.; Plisinski, J.S. Assessing the local economic impacts of land protection. Conserv. Biol. 2019, 33, 1035–1044. [Google Scholar] [CrossRef]
- Lobo, J.; Alberti, M.; Allen-Dumas, M.; Arcaute, E.; Barthelemy, M.; Bojorquez-Tapia, L.A.; Brail, S.; Bettencourt, L.; Beukes, A.; Chen, W.; et al. Urban science: Integrated theory from the first cities to sustainable metropolises. SSRN Electron. J. 2020, (in press). [Google Scholar] [CrossRef]
- Seto, K.C.; Golden, J.S.; Alberti, M.; Turner, B.L. Sustainability in an urbanizing planet. Proc. Natl. Acad. Sci. USA 2017, 114, 8935–8938. [Google Scholar] [CrossRef] [Green Version]
- Eurostat. Cities (Urban Audit). 2016. Available online: https://ec.europa.eu/eurostat/web/cities/background (accessed on 15 April 2020).
- OECD. Metropolitan Areas, OECD Regional Statistics [Database]. 2019. Available online: http://0-dx-doi-org.brum.beds.ac.uk/10.1787/data-00531-en (accessed on 22 November 2019).
- GEOSTAT. Eurostat, Geographical Information and Maps. 2020. Available online: https://ec.europa.eu/eurostat/web/gisco/gisco-activities/integrating-statistics-geospatial-information/geostat-initiative (accessed on 15 April 2020).
- SEDAC. NASA Socioeconomic Data and Applications Center. U.S. Census Grids. 2020. Available online: https://sedac.ciesin.columbia.edu/ (accessed on 15 April 2020).
- Esch, T.; Taubenböck, H.; Roth, A.; Heldens, W.; Felbier, A.; Thiel, M.; Schmidt, M.; Müller, A.; Dech, S. TanDEM-X mission: New perspectives for the inventory and monitoring of global settlement patterns. J. Appl. Remote Sens. 2012, 6, 061702. [Google Scholar] [CrossRef]
- Corbane, C.; Florczyk, A.; Pesaresi, M.; Politis, P.; Syrris, V. GHS-BUILT R2018A—GHS Built-Up Grid, Derived from Landsat, Multitemporal (1975-1990-2000-2014). European Commission, Joint Research Centre (JRC) [Dataset]. 2018. Available online: http://data.europa.eu/89h/jrc-ghsl-10007 (accessed on 2 January 2020).
- Angel, S.; Blei, A.M.; Parent, J.; Lamson-Hall, P.; Galarza-Sánchez, N.; Civco, D.L.; Qian, L.R.; Thom, K. Atlas of Urban Expansion; Lincoln Institute of Land Policy: Cambridge, MA, USA, 2016. [Google Scholar]
- Chen, J.; Cao, X.; Peng, S.; Ren, H. Analysis and applications of GlobeLand30: A review. ISPRS Int. J. Geo-Inf. 2017, 6, 230. [Google Scholar] [CrossRef] [Green Version]
- ESA. Land Cover CCI Product User Guide Version 2. 2017. Available online: http://maps.elie.ucl.ac.be/CCI/viewer/download/ESACCI-LC-Ph2-PUGv2_2.0.pdf (accessed on 7 February 2020).
- Bechtel, B.; Alexander, P.; Böhner, J.; Ching, J.; Conrad, O.; Feddema, J.; Mills, G.; See, L.; Stewart, I. Mapping local climate zones for a worldwide database of form and function of cities. ISPRS Int. J. Geo-Inf. 2015, 4, 199–219. [Google Scholar] [CrossRef] [Green Version]
- Cao, W.; Dong, L.; Wu, L.; Liu, Y. Quantifying urban areas with multi-source data based on percolation theory. Remote Sens. Environ. 2020, 241, 111730. [Google Scholar] [CrossRef] [Green Version]
- Qiu, C.; Schmitt, M.; Geiß, C.; Chen, T.H.K.; Zhu, X.X. A framework for large-scale mapping of human settlement extent from Sentinel-2 images via fully convolutional neural networks. ISPRS J. Photogramm. Remote Sens. 2020, 163, 152–170. [Google Scholar] [CrossRef] [PubMed]
- OECD. The Metropolitan Database. Metadata and Release Notes. 2019. Available online: http://stats.oecd.org/wbos/fileview2.aspx?IDFile=4aed3009-6020-48f3-8eeb-e01a8e5f61c4 (accessed on 7 February 2020).
- OECD. Gross Domestic Product (GDP) (Indicator). 2020. Available online: https://0-doi-org.brum.beds.ac.uk/10.1787/dc2f7aec-en (accessed on 1 May 2020).
- OECD. Income Inequality (Indicator). 2020. Available online: https://0-doi-org.brum.beds.ac.uk/10.1787/459aa7f1-en (accessed on 1 May 2020).
- OECD. Air pollution Exposure (Indicator). 2020. Available online: https://0-doi-org.brum.beds.ac.uk/10.1787/8d9dcc33-en (accessed on 1 May 2020).
- OECD. Employment Rate (Indicator). 2020. Available online: https://0-doi-org.brum.beds.ac.uk/10.1787/1de68a9b-en (accessed on 1 May 2020).
- OECD. Redefining “Urban”: A New Way to Measure Metropolitan Areas, OECD Publishing. 2012. Available online: https://0-doi-org.brum.beds.ac.uk/10.1787/9789264174108-en (accessed on 1 May 2020).
- Meijer, J.R.; Huijbregts, M.A.; Schotten, K.C.; Schipper, A.M. Global patterns of current and future road infrastructure. Environ. Res. Lett. 2018, 13, 064006. [Google Scholar] [CrossRef] [Green Version]
- Sapena, M.; Ruiz, L.A. Description and extraction of urban fragmentation indices: The Indifrag tool. Rev. Teledetección 2015, 43, 77–89. [Google Scholar] [CrossRef] [Green Version]
- EEA. Urban morphological zones 2006. European Environment Agency. 2014. Available online: https://www.eea.europa.eu/data-and-maps/data/urban-morphological-zones-2006-1 (accessed on 3 June 2020).
- Taubenböck, H.; Wiesner, M.; Felbier, A.; Marconcini, M.; Esch, T.; Dech, S. New dimensions of urban landscapes: The spatio-temporal evolution from a polynuclei area to a mega-region based on remote sensing data. Appl. Geogr. 2014, 47, 137–153. [Google Scholar] [CrossRef]
- Schumm, S.A. Evolution of Drainage Systems and Slopes in Badlands at Perth Amboy, New Jersey. Geol. Soc. Am. Bull. 1956, 67, 597–646. [Google Scholar] [CrossRef]
- Sapena, M.; Ruiz, L.A. Analysis of land use/land cover spatio-temporal metrics and population dynamics for urban growth characterization. Comput. Environ. Urban Syst. 2019, 73, 27–39. [Google Scholar] [CrossRef]
- Breiman, L. Statistcal modeling: The two cultures. Stat. Sci. 2001, 16, 199–231. [Google Scholar] [CrossRef]
- Gonzalez, J.J.; Leboulluec, A. Crime Prediction and Socio-Demographic Factors: A Comparative Study of Machine Learning Regression-Based Algorithms. J. Appl. Comput. Sci. Math. 2019, 13, 13–18. [Google Scholar] [CrossRef]
- Paul, S.S.; Coops, N.C.; Johnson, M.S.; Krzic, M.; Chandna, A.; Smukler, S.M. Mapping soil organic carbon and clay using remote sensing to predict soil workability for enhanced climate change adaptation. Geoderma 2020, 363, 114177. [Google Scholar] [CrossRef]
- Breiman, L. Random Forest. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Otto, S.A. How to Normalize the RMSE. 2019. Available online: https://www.marinedatascience.co/blog/2019/01/07/normalizing-the-rmse/ (accessed on 20 January 2020).
- Probst, P.; Wright, M.N.; Boulesteix, A.L. Hyperparameters and tuning strategies for random forest. Wires Data Min. Knowl. 2019, 9, e1301. [Google Scholar] [CrossRef] [Green Version]
- Salvati, L.; Carlucci, M. Patterns of Sprawl: The Socioeconomic and Territorial Profile of Dispersed Urban Areas in Italy. Reg. Stud. 2015, 50, 1346–1359. [Google Scholar] [CrossRef]
- Angel, S.; Parent, J.; Civco, D.L.; Blei, A.M. Making Room for a Planet of Cities; Lincoln Institute of Land Policy: Cambridge, MA, USA, 2011. [Google Scholar]
- Boulant, J.; Brezzi, M.; Veneri, P. Income Levels and Inequality in Metropolitan Areas: A Comparative Approach in OECD Countries. In OECD Regional Development Working Papers; OECD Publishing: Paris, France, 2016. [Google Scholar]
- Weilenmann, B.; Seidl, I.; Schulz, T. The socio-economic determinants of urban sprawl between 1980 and 2010 in Switzerland. Landsc. Urban Plan. 2017, 157, 468–482. [Google Scholar] [CrossRef]
- Huang, J.; Lu, X.X.; Sellers, J.M. A global comparative analysis of urban form: Applying spatial metrics and remote sensing. Landsc. Urban Plan. 2007, 82, 184–197. [Google Scholar] [CrossRef]
- Angel, S.; Arango Franco, S.; Liu, Y.; Blei, A.M. The shape compactness of urban footprints. Prog. Plan. 2020, 139, 100429. [Google Scholar] [CrossRef]
- Bechle, M.J.; Millet, D.B.; Marshall, J.D. Effects of Income and Urban Form on Urban NO2: Global Evidence from Satellites. Environ. Sci. Technol. 2011, 45, 4914–4919. [Google Scholar] [CrossRef]
- Meneses, B.M.; Reis, E.; Pereira, S.; Vale, M.J.; Reis, R. Understanding Driving Forces and Implications Associated with the Land Use and Land Cover Changes in Portugal. Sustainability 2017, 9, 351. [Google Scholar] [CrossRef] [Green Version]
- Ahlfeldt, G.; Pietrostefani, E.; Schumann, A.; Matsumoto, T. Demystifying compact urban growth: Evidence from 300 studies from across the world. In OECD Regional Development Working Papers; OECD Publishing: Paris, France, 2018. [Google Scholar]
- Corbane, C.; Pesaresi, M.; Kemper, T.; Politis, P.; Florczyk, A.J.; Syrris, V.; Melchiorri, M.; Sabo, F.; Soille, P. Automated global delineation of human settlements from 40 years of Landsat satellite data archives. Big Earth Data 2019, 3, 140–169. [Google Scholar] [CrossRef]

| Variable | Description | Year/s |
|---|---|---|
| GDP | Gross domestic product per capita (GDP) is the value added created through the production of goods and services during a certain period per capita. It is expressed in United State dollars (USD) constant prices and constant Purchasing Power Parities (PPPs) with the base year 2010 (i.e., differences in price levels between countries are eliminated based on PPP rates). The GDP is less suitable for comparisons over time, as growth is affected by changes in prices and dollars per capita [46]. | 2014 |
| Gini | It is an indicator of income inequality among individuals. The Gini coefficient is based on the comparison of the cumulative proportions of the population against the cumulative proportions of income they receive; this ratio ranges from 0 in the case of perfect equality to 1 in the case of perfect inequality [47]. | 2014 |
| Income | It is defined as household disposable income in a particular year measured in USD. It consists of earnings, self-employment and capital income and public cash transfers; taxes and contributions are deducted [47]. | 2014 |
| Air quality | Fine particulate matter (PM2.5) is the air pollutant that poses the greatest risk to health, affecting more people than any other pollutant. Chronic exposure to PM2.5 increases the risk of respiratory and cardiovascular diseases. Average level in µg/m3 [48]. | 2014 2000/2014 |
| Employment rate | Employment rate measures the extent to which available labor resources (people available to work) are being used, calculated as the ratio of the employed to the working age population (aged 15 or over) [49]. | 2000/2014 |
| Population | Population, all ages. It is used to derive a spatio-temporal metric. | 2000/2014 |
| Variable (unit) | FUAs | R2 | MSE | RMSE | sd-NRMSE | range-NRMSE |
|---|---|---|---|---|---|---|
| GDP (USD) | 597 | 43.97 | 102,028,574 | 10,101 | 0.7479 | 0.1234 |
| Gini (ratio) | 142 | 52.2 | 0.0011 | 0.0326 | 0.689 | 0.1577 |
| Income (USD) | 280 | 68.07 | 45,985,090 | 6781 | 0.564 | 0.1232 |
| Air quality (µg/m3) | 599 | 52.9 | 20.8591 | 4.5672 | 0.6857 | 0.1324 |
| Variable (unit) | FUAs | R2 | MSE | RMSE | sd-NRMSE | range-NRMSE |
|---|---|---|---|---|---|---|
| Air quality change (µg/m3) | 599 | 41.16 | 0.6172 | 0.7856 | 0.7664 | 0.1076 |
| Employment change (%) | 313 | 31.56 | 10.7334 | 3.2762 | 0.826 | 0.1413 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sapena, M.; Ruiz, L.A.; Taubenböck, H. Analyzing Links between Spatio-Temporal Metrics of Built-Up Areas and Socio-Economic Indicators on a Semi-Global Scale. ISPRS Int. J. Geo-Inf. 2020, 9, 436. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9070436
Sapena M, Ruiz LA, Taubenböck H. Analyzing Links between Spatio-Temporal Metrics of Built-Up Areas and Socio-Economic Indicators on a Semi-Global Scale. ISPRS International Journal of Geo-Information. 2020; 9(7):436. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9070436
Chicago/Turabian StyleSapena, Marta, Luis A. Ruiz, and Hannes Taubenböck. 2020. "Analyzing Links between Spatio-Temporal Metrics of Built-Up Areas and Socio-Economic Indicators on a Semi-Global Scale" ISPRS International Journal of Geo-Information 9, no. 7: 436. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9070436