Thermodynamics and Kinetics of Glycolytic Reactions. Part I: Kinetic Modeling Based on Irreversible Thermodynamics and Validation by Calorimetry
Abstract
:1. Introduction
2. Results
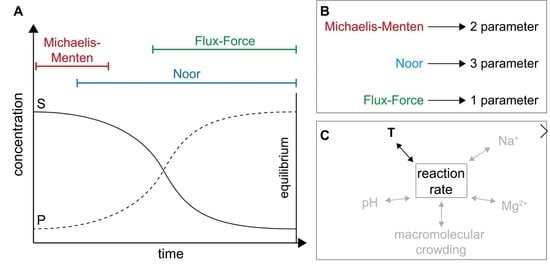
2.1. Definitions and Specifications
2.2. Application of Irreversible Thermodynamics for Kinetic Evaluation
2.3. ITC Results
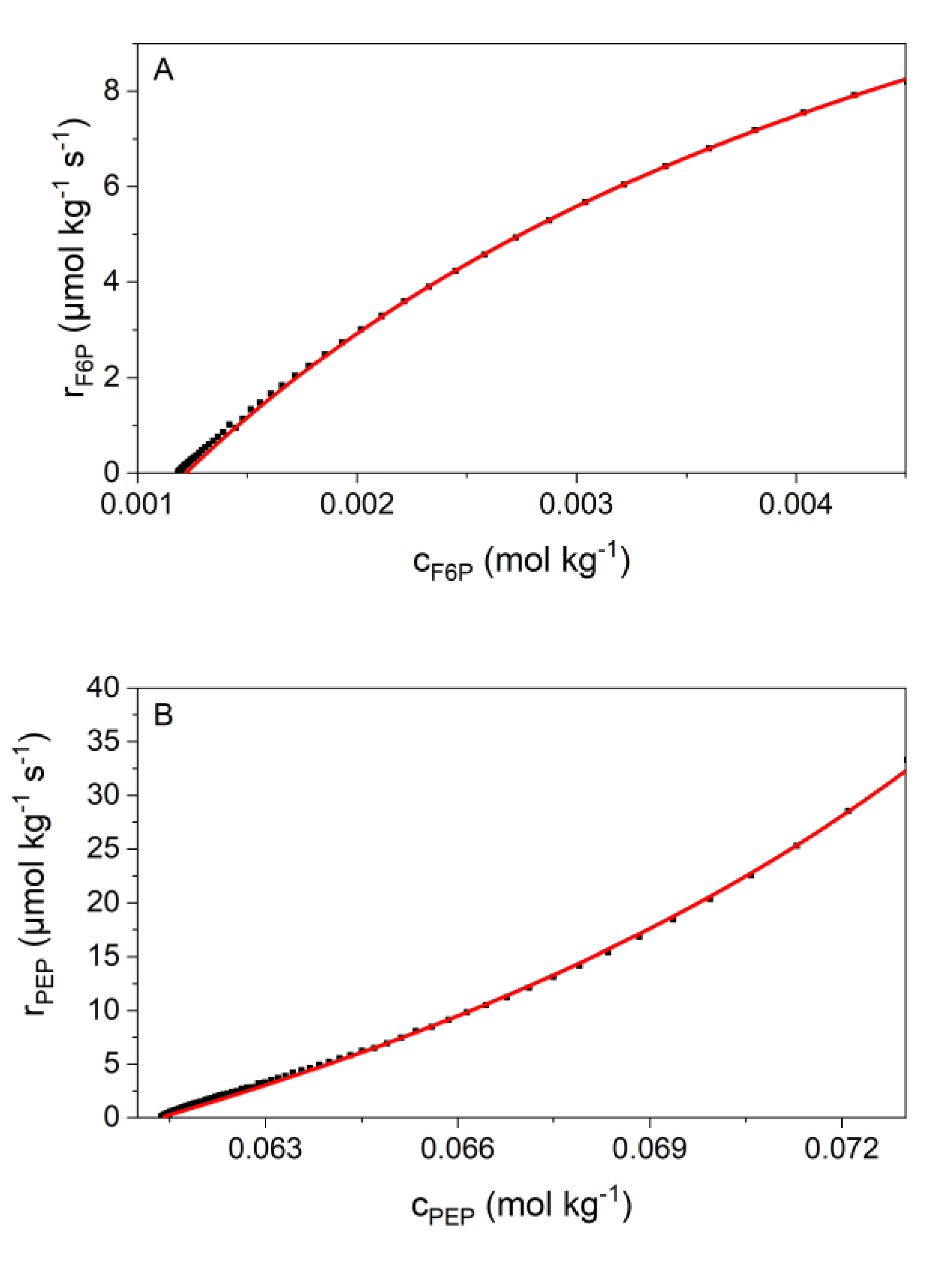
2.4. Kinetic Analyses
3. Discussion
3.1. Thermodynamic Data for Reaction 2
3.2. Validation of Kinetic Models by the New Calorimetric Data
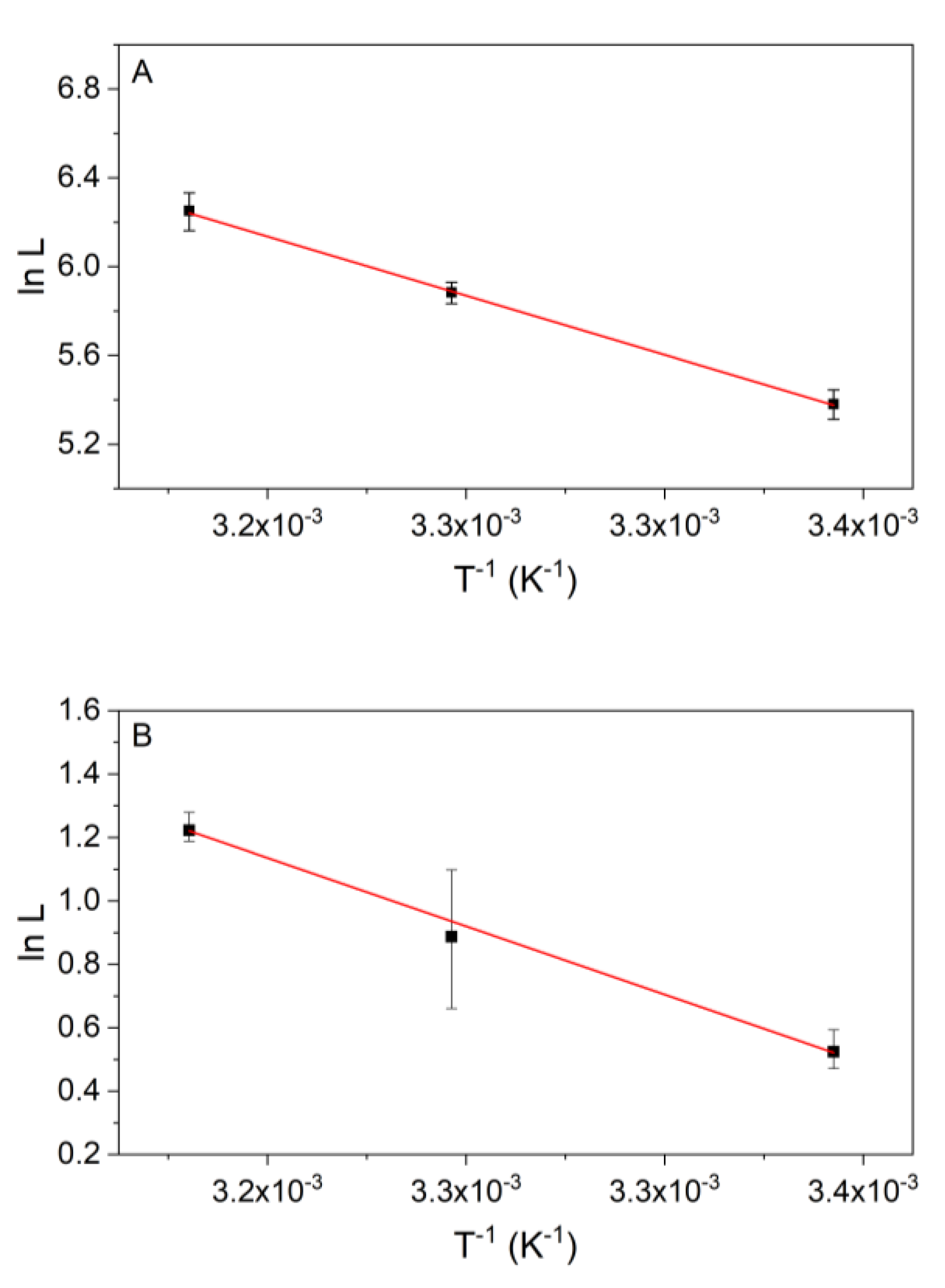
3.3. Temperature Dependency of the Kinetics of Reaction 2
3.4. Temperature Dependency of Reaction 9
4. Materials and Methods
4.1. Chemicals
4.2. Sample Preparation for ITC Measurement
4.3. ITC Measurements
4.3.1. Reaction 2 (Phosphoglucose Isomerase Reaction)
4.3.2. Reaction 9 (Enolase Reaction)
4.4. Determination of Reaction Enthalpy and Equilibrium Constant
4.5. Kinetic Investigations
4.6. Statistics
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ITC | isothermal titration calorimetry |
| G6P | glucose-6-phosphate |
| F6P | fructose-6-phosphate |
| 2PG | 2-phosphoglycerate |
| PEP | phosphoenolpyruvate |
| PGI | phosphoglucose isomerase |
References
- Brown, A.J. XXXVI.—Enzyme action. J. Chem. Soc. Perkin 1 1902, 81, 373–388. [Google Scholar] [CrossRef] [Green Version]
- Henri, V. Lois Générales De L’action Des Diastases; Librairie Scientifique A.: Hermann, MO, USA, 1903. [Google Scholar]
- Henri, V. Théorie Générale De L’action De Quelques Diastases; Gauthier-Villars: Paris, France, 1902. [Google Scholar]
- Michaelis, L.; Menton, M.L. Kinetik der Invertinwirkung. Biochem. Z. 1913, 49, 333. [Google Scholar]
- Miller, W.G.; Alberty, R.A. Kinetics of the reversible Michaelis-Menten mechanism and the applicability of the steady-state approximation. J. Am. Chem. Soc. 1958, 80, 5146–5151. [Google Scholar] [CrossRef]
- Paul, S.; Gangopadhyay, G. Power law kinetics in reversible enzyme-catalyzed reaction due to diffusion. J. Chem. Phys. 2003, 119, 3501–3508. [Google Scholar] [CrossRef]
- Voet, D.; Voet, J.G. Biochemistry, 4th ed.; W. Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Cornish-Bowden, A.; Cardenas, M.L. Information transfer in metabolic pathways. Effects of irreversible steps in computer models. Eur. J. Biochem. 2001, 268, 6616–6624. [Google Scholar] [CrossRef]
- Noor, E.; Flamholz, A.; Liebermeister, W.; Bar-Even, A.; Milo, R. A note on the kinetics of enzyme action: A decomposition that highlights thermodynamic effects. FEBS Lett. 2013, 587, 2772–2777. [Google Scholar] [CrossRef] [Green Version]
- Cornish-Bowden, A. Fundamentals of Enzyme Kinetics; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Imperial, S.; Centelles, J.J. Enzyme Kinetic Equations of Irreversible and Reversible Reactions in Metabolism. J. Biosci. Med. 2014, 2, 24–29. [Google Scholar] [CrossRef]
- Rohwer, J.M.; Postma, P.W.; Kholodenko, B.N.; Westerhoff, H.V. Implications of macromolecular crowding for signal transduction and metabolite channeling. Proc. Natl. Acad. Sci. USA 1998, 95, 10547–10552. [Google Scholar] [CrossRef] [Green Version]
- Smith, W.G. In Vivo Kinetics and the Reversible Michaelis-Menten Model. J. Chem. Educ. 1992, 69, 981–984. [Google Scholar] [CrossRef]
- Hoh, C.Y.; CordRuwisch, R. A practical kinetic model that considers endproduct inhibition in anaerobic digestion processes by including the equilibrium constant. Biotechnol. Bioeng. 1996, 51, 597–604. [Google Scholar] [CrossRef]
- Keleti, T. Two rules of enzyme kinetics for reversible Michaelis-Menten mechanisms. FEBS Lett. 1986, 208, 109–112. [Google Scholar] [CrossRef] [Green Version]
- Lee, L.W.; Yin, L.; Zhu, X.M.; Ao, P. Generic enzymatic rate equation under living conditions. J. Biol. Syst. 2007, 15, 495–514. [Google Scholar] [CrossRef] [Green Version]
- Brooks, S.P.J.; Storey, K.B. A kinetic description of sequential, reversible, Michaelis-Menten reactions: Practical application of theory to metabolic pathways. Mol. Cell. Biochem. 1992, 115, 43–48. [Google Scholar] [CrossRef]
- Cha, S. A Simple Method for Derivation of Rate Equations for Enzyme-catalyzed Reactions under the Rapid Equilibrium Assumption or Combined Assumptions of Equilibrium and Steady State. J. Biol. Chem. 1968, 243, 820–825. [Google Scholar]
- Zadvornyy, O.A.; Boyd, E.S.; Posewitz, M.C.; Zorin, N.A.; Peters, J.W. Biochemical and structural characterization of enolase from Chloroflexus aurantiacus: Evidence for a thermophilic origin. Front. Bioeng. Biotechnol. 2015, 3, 74. [Google Scholar] [CrossRef] [Green Version]
- Pancholi, V.; Fischetti, V.A. Alpha-enolase, a novel strong plasmin(ogen) binding protein on the surface of pathogenic streptococci. J. Biol. Chem. 1998, 273, 14503–14515. [Google Scholar] [CrossRef] [Green Version]
- Wold, F.; Ballou, C.E. Studies on the enzyme enolase II. kinetic studies. J. Biol. Chem. 1957, 227, 313–328. [Google Scholar]
- Westhead, E.W.; Malmstrom, B.G. The chemical kinetics of the enolase reaction with special reference to the use of mixed solvents. J. Biol. Chem. 1957, 228, 655–671. [Google Scholar] [PubMed]
- Kornblatt, M.J.; Musil, R. The Inhibition of Yeast Enolase by Li+ and Na+. Arch. Biochem. Biophys. 1990, 277, 301–305. [Google Scholar] [CrossRef]
- Dyson, J.E.; Noltmann, E.A. The effect of pH and temperature on the kinetic parameters of phosphoglucose isomerase. Participation of histidine and lysine in a proposed dual function mechanism. J. Biol. Chem. 1968, 243, 1401–1414. [Google Scholar]
- Zera, A.J. Temperature-dependent kinetic variation among phosphoglucose isomerase allozymes from the whing-polymorphic water strider, Limnoporus Canaliculatus. Mol. Biol. Evol. 1987, 4, 266–285. [Google Scholar]
- Grosch, J.H.; Wagner, D.; Nistelkas, V.; Spiess, A.C. Thermodynamic activity-based intrinsic enzyme kinetic sheds light on enzyme-solvent interactions. Biotechnol. Prog. 2017, 33, 96–103. [Google Scholar] [CrossRef]
- Pleiss, J. Thermodynamic activity-based interpretation of enzyme kinetics. Trends Biotechnol. 2017, 35, 379–382. [Google Scholar] [CrossRef]
- Gopal, S.M.; Klumpers, F.; Herrmann, C.; Schafer, L.V. Solvent effects on ligand binding to a serine protease. Phys. Chem. Chem. Phys. 2017, 19, 10753–10766. [Google Scholar] [CrossRef] [Green Version]
- Knierbein, M.; Wangler, A.; Luong, T.Q.; Winter, R.; Held, C.; Sadowski, G. Combined co-solvent and pressure effect on kinetics of a peptide hydrolysis: An activity-based approach. Phys. Chem. Chem. Phys. 2019, 21, 22224–22229. [Google Scholar] [CrossRef]
- Wangler, A.; Held, C.; Sadowski, G. Thermodynamic activity-based solvent design for bioreactors. Trends Biotechnol. 2019, 37, 1038–1041. [Google Scholar] [CrossRef] [PubMed]
- Lonhienne, T.G.; Winzor, D.J. A potential role for isothermal calorimetry in studies of the effects of thermodynamic non-ideality in enzyme-catalyzed reactions. J. Mol. Recognit. 2004, 17, 351–361. [Google Scholar] [CrossRef]
- van Eunen, K.; Bakker, B.M. The importance and challenges of in vivo-like enzyme kinetics. Perspect. Sci. 2014, 1, 126–130. [Google Scholar] [CrossRef] [Green Version]
- Beard, D.A.; Qian, H. Relationship between thermodynamic driving force and one-way fluxes in reversible processes. PLoS ONE 2007, 2, e144. [Google Scholar] [CrossRef] [Green Version]
- Maskow, T.; Paufler, S. What does calorimetry and thermodynamics of living cells tell us? Methods 2015, 76, 3–10. [Google Scholar] [CrossRef]
- Todd, M.J.; Gomez, J. Enzyme kinetics determined using calorimetry: A general assay for enzyme activity? Anal. Biochem. 2001, 296, 179–187. [Google Scholar] [CrossRef] [Green Version]
- Westerhoff, H.V. Thermodynamics and Control. of Biological Free-Energy Transduction; Elsevier Science Ltd.: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Stitt, M. Control of sucrose synthesis: Estimation of free energy changes, investigation of the contribution of equilibrium and non-equilibrium reactions, and estimation of elasticities and flux control coefficients. In Techniques and New Developments in Photosynthesis Research; Springer: Berlin, Germany, 1989; pp. 365–391. [Google Scholar]
- Arrhenius, S. Über die Reaktionsgeschwindigkeit bei der Inversion von Rohrzucker durch Säuren. Z. für Phys. Chem. 1889, 4U, 226–248. [Google Scholar]
- Mazzei, L.; Ciurli, S.; Zambelli, B. Hot Biological Catalysis: Isothermal Titration Calorimetry to Characterize Enzymatic Reactions. J. Vis. Exp. 2014, 86, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vogel, K.; Greinert, T.; Harms, H.; Sadowski, G.; Held, C.; Maskow, T. Influence of cytosolic conditions on the reaction equilibrium and the reaction enthalpy of the enolase reaction accessed by calorimetry and van ‘t HOFF. Biochim. Biophys. Gen. Subj. 2020, 1864, 129675. [Google Scholar] [CrossRef] [PubMed]
- Tewari, Y.B.; Steckler, D.K.; Goldberg, R.N. Thermodynamics of isomerization reactions involving sugar phosphates. J. Biol. Chem. 1988, 263, 3664–3669. [Google Scholar]
- Hoffmann, P.; Held, C.; Maskow, T.; Sadowski, G. A thermodynamic investigation of the glucose-6-phosphate isomerization. Biophys. Chem. 2014, 195, 22–31. [Google Scholar] [CrossRef]
- Hines, M.C.; Wolfe, R.G. Phosphoglucose isomerase. 2. Influence of pH on kinetic parameters. Biochemistry 1963, 2, 770–775. [Google Scholar] [CrossRef]
- Ruijter, G.J.G.; Visser, J. Characterization of Aspergillus niger phosphoglucose isomerase. Use for quantitative determination of erythrose 4-phosphate. Biochimie 1999, 81, 267–272. [Google Scholar] [CrossRef]
- Staples, J.F.; Suarez, R.K. Honeybee flight muscle phosphoglucose isomerase: Matching enzyme capacities to flux requirements at a near-equilibrium reaction. J. Exp. Biol. 1997, 200, 1247–1254. [Google Scholar]
- Holt, A.; Wold, F. The isolation and characterization of rabbit muscle enolase. J. Biol. Chem. 1961, 236, 3227–3231. [Google Scholar] [PubMed]
- Lowry, O.H.; Passonneau, J.V. The relationships between substrates ad enzymes of glycolysis in brain. J. Biol. Chem. 1964, 239, 31–42. [Google Scholar] [PubMed]
- Vinarov, D.A.; Nowak, T. pH Dependence of the reaction catalyzed by yeast Mg−enolase. Biochemistry. 1998, 37, 15238–15246. [Google Scholar] [CrossRef]
- Stuart, C.C.P. A study of temperature-coeffcients and van ‘t Hoff’s rule. KNAW Proc. 1912, 14, 1159–1173. [Google Scholar]
- Sangwan, R.S.; Singh, R. Characterization of amyloplastic phosphohexose isomerase from immature wheat (Triticum aestivum L.) endosperm. Indian J. Biochem. Biophys. 1990, 27, 23–27. [Google Scholar]
- Westhead, E.W.; McLain, G. A purification of brewers’ and baker’s yeast enolase yielding a single active component. J. Biol. Chem. 1964, 239, 2464–2468. [Google Scholar]
- Schurig, H.; Rutkat, K.; Rachel, R.; Jaenicke, R. Octameric enolase from the hyperthermophilic baxcterium Thermotoga maritima—purification, characterization, and image processing. Protein Sci. 1995, 4, 228–236. [Google Scholar] [CrossRef] [Green Version]
- Hansen, L.D.; Transtrum, M.K.; Quinn, C.; Demarse, N. Enzyme-catalyzed and binding reaction kinetics determined by titration calorimetry. Biochim. Biophys. Gen. Subj. 2016, 1860, 957–966. [Google Scholar] [CrossRef]




| Symbol | Property | Unit |
|---|---|---|
| A | pre-exponential factor | s−1 |
| activity of component | - | |
| concentration of component | mol kg−1 | |
| concentration of component at time 0 | mol kg−1 | |
| equilibrium concentration of component | mol kg−1 | |
| product concentration | mol kg−1 | |
| substrate concentration | mol kg−1 | |
| activation energy | J mol−1 | |
| Gibbs energy of biochemical reaction | J mol−1 | |
| standard Gibbs energy of biochemical reaction | J mol−1 | |
| enthalpy of biochemical reaction | J mol−1 | |
| J | flux | mol L−1 s−1 |
| thermodynamic equilibrium constant of biochemical reaction | - | |
| apparent equilibrium-molality ratio of biochemical reaction | −/mol kg−1 | |
| kinetic constant of reaction | s−1 | |
| Michaelis constant for substrate/product | mol kg−1 | |
| activity-coefficient ratio of biochemical reaction | −/mol kg−1 | |
| L | phenomenological coefficient/kinetic parameter | s−1 |
| m | mass | kg |
| P | heat production rate | W |
| Q | heat | J |
| universal gas constant (8.314 J mol−1 K−1) | J mol−1 K−1 | |
| r | reaction rate | mol L−1 s−1 |
| maximum reaction rate | mol L−1 s−1 | |
| temperature | K | |
| α | correlation factor | mol kg−1 s−1 |
| Λ | kinetic parameter | s−1 |
| thermodynamic driving force | - | |
| rational activity coefficient of component on molality base | - |
| Buffer | |
|---|---|
| HEPES | 9.7 ± 0.3 |
| Potassium phosphate | 9.6 ± 0.2 |
| MOPS | 11.1 ± 0.5 |
| Reaction 2 | Reaction 9 [40] | |||||
|---|---|---|---|---|---|---|
| Temperature (K) | Q (mJ) | Q (mJ) | ||||
| 298.15 | 7.63 ± 0.14 | 0.285 | 10.3 ± 0.2 | 8.15 ± 0.72 | 239.4 | 2.4 ± 0.2 |
| 305.15 | 7.63 ± 0.07 | 0.318 | 10.6 ± 0.1 | 7.85 ± 0.17 | 245.9 | 2.4 ± 0.1 |
| 310.15 | 7.86 ± 0.33 | 0.343 | 11.1 ± 0.5 | 7.64 ± 0.22 | 251.3 | 2.4 ± 0.1 |
| Temperature (K) | Reaction 2 | Reaction 9 | ||
|---|---|---|---|---|
(µmol kg−1s−1) | (mmol kg−1) | (ms−1) | (mmol kg−1) | |
| 298.15 | 7.03 ± 0.58 | 4.35 ± 0.64 | 0.34 ± 0.01 | 10.2 ± 0.92 |
| 305.15 | 10.30 ± 0.88 | 3.41 ± 0.39 | 0.44 ± 0.13 | 13.8 ± 3.35 |
| 310.15 | 13.21 ± 1.20 | 3.26 ± 0.09 | 0.57 ± 0.03 | 16.5 ± 0.48 |
| Temperature (K) | Reaction 2 | Reaction 9 |
|---|---|---|
| L Value (s−1) | L Value (s−1) | |
| 298.15 | 217.18 ± 14.27 | 10.13 ± 0.65 |
| 305.15 | 358.80 ± 17.29 | 14.57 ± 3.20 |
| 310.15 | 518.44 ± 43.84 | 20.37 ± 1.03 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vogel, K.; Greinert, T.; Reichard, M.; Held, C.; Harms, H.; Maskow, T. Thermodynamics and Kinetics of Glycolytic Reactions. Part I: Kinetic Modeling Based on Irreversible Thermodynamics and Validation by Calorimetry. Int. J. Mol. Sci. 2020, 21, 8341. https://0-doi-org.brum.beds.ac.uk/10.3390/ijms21218341
Vogel K, Greinert T, Reichard M, Held C, Harms H, Maskow T. Thermodynamics and Kinetics of Glycolytic Reactions. Part I: Kinetic Modeling Based on Irreversible Thermodynamics and Validation by Calorimetry. International Journal of Molecular Sciences. 2020; 21(21):8341. https://0-doi-org.brum.beds.ac.uk/10.3390/ijms21218341
Chicago/Turabian StyleVogel, Kristina, Thorsten Greinert, Monique Reichard, Christoph Held, Hauke Harms, and Thomas Maskow. 2020. "Thermodynamics and Kinetics of Glycolytic Reactions. Part I: Kinetic Modeling Based on Irreversible Thermodynamics and Validation by Calorimetry" International Journal of Molecular Sciences 21, no. 21: 8341. https://0-doi-org.brum.beds.ac.uk/10.3390/ijms21218341