Advanced Construction of the Dynamic Matrix in Numerically Efficient Fuzzy MPC Algorithms
Abstract
:1. Introduction
1.1. MPC Algorithms Based on Linear Models
1.2. MPC Algorithms Based on Nonlinear Models
2. Efficient Fuzzy MPC Algorithms with the Advanced Construction of the Dynamic Matrix
2.1. Generation of the Free Response
2.2. Generation of the Dynamic Matrix
2.2.1. Fuzzy Model Used to Obtain the Dynamic Matrix
2.2.2. Standard Dynamic Matrix
2.2.3. Advanced Dynamic Matrix Generation
2.3. Optimization Problem in the Numerical and Analytical Versions of the Algorithms
2.3.1. Optimization with the Classical Performance Index
2.3.2. Optimization with the Modified Performance Index
2.3.3. Utilization of Analytical Versions of the Algorithms
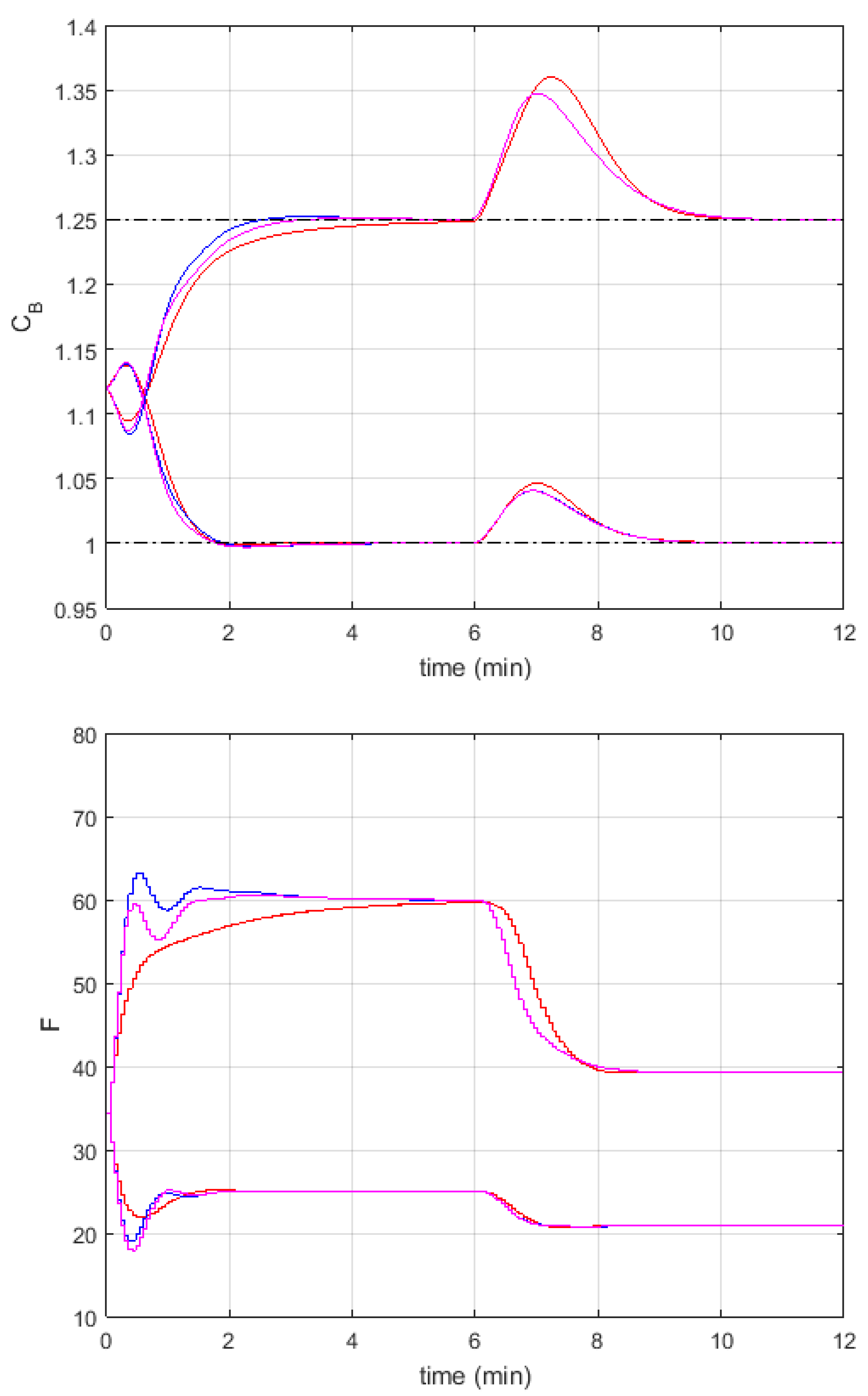
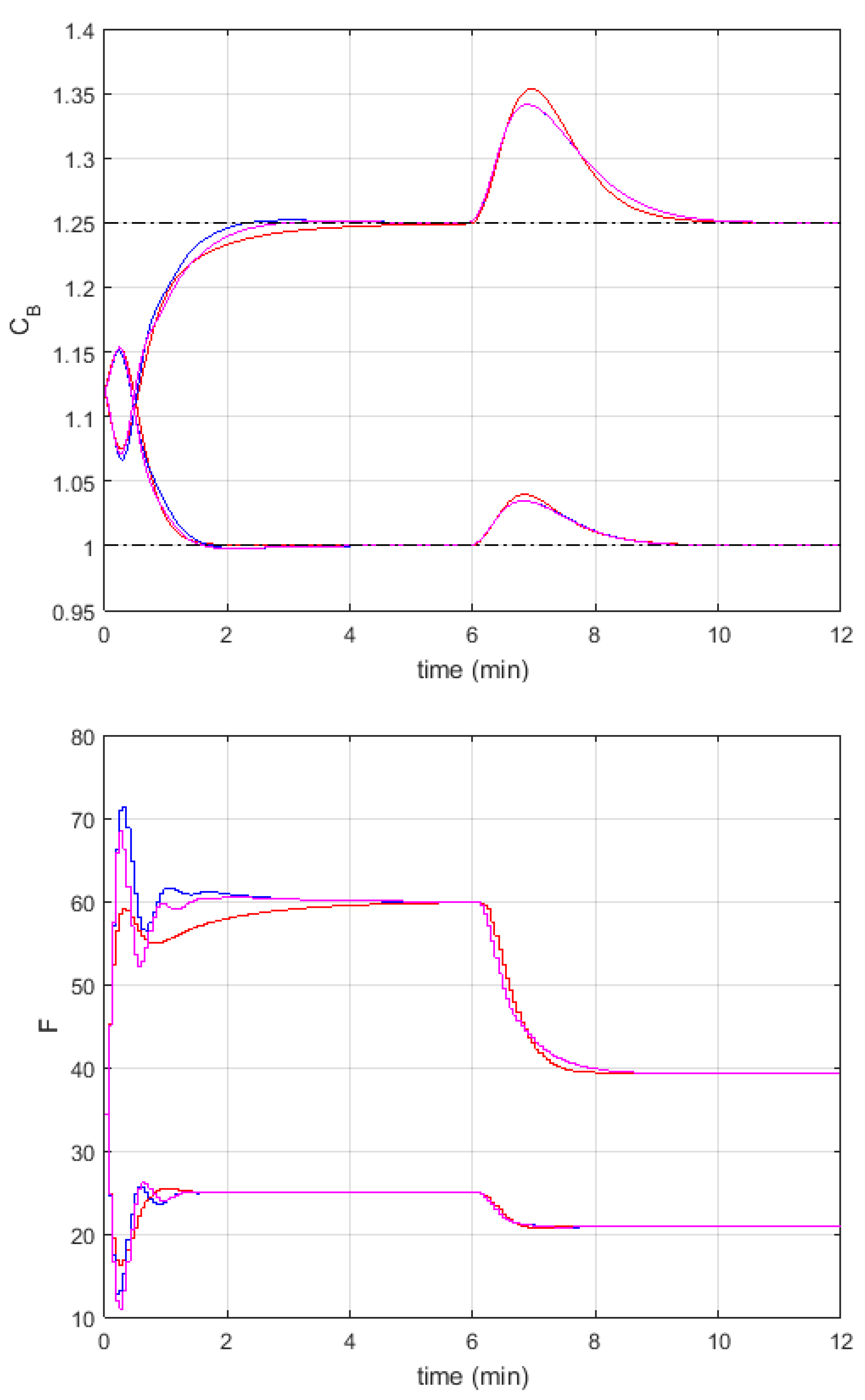
3. Example
3.1. Control Plant
- R1 0.91 mol/L, 2.18 mol/L, 20 L/h;
- R2 1.12 mol/L, 3 mol/L, 34.3 L/h;
- R3 1.22 mol/L, 3.66 mol/L, 50 L/h.
3.2. Experiments
- -
- NMPC—based on the nonlinear model and nonlinear optimization and numerically efficient FMPC algorithms with advanced free response generation, proposed in [12], and:
- -
- FMPC1 with the conventional dynamic matrix and the classical performance index,
- -
- FMPC2 with the conventional dynamic matrix and the modified performance index,
- -
- FMPC1a with the advanced dynamic matrix and the classical performance index,
- -
- FMPC2a with the advanced dynamic matrix and the modified performance index.
4. Conclusions
Funding
Conflicts of Interest
Abbreviations
| CSTR | Continuous Stirred-Tank Reactor |
| DMC | Dynamic Matrix Control |
| FMPC | Fuzzy Model Predictive Control |
| LMPC | Linear Model Predictive Control |
| LMIs | Linear Matrix Inequalities |
| MPC | Model Predictive Control |
| MIMO | Multiple-Input Multiple-Output |
| NMPC | Nonlinear Model Predictive Control |
| SSE | Sum of Squared Errors |
References
- Camacho, E.F.; Bordons, C. Model Predictive Control; Springer: London, UK, 1999. [Google Scholar]
- Domański, P.D. Performance Assessment of Predictive Control—A Survey. Algorithms 2020, 13, 97. [Google Scholar] [CrossRef] [Green Version]
- El Youssef, J.; Castle, J.; Ward, W.K. A Review of Closed—Loop Algorithms for Glycemic Control in the Treatment of Type 1 Diabetes. Algorithms 2009, 2, 518. [Google Scholar] [CrossRef] [Green Version]
- Maciejowski, J.M. Predictive Control with Constraints; Prentice Hall: Harlow, UK, 2002. [Google Scholar]
- Nebeluk, R.; Marusak, P. Efficient MPC algorithms with variable trajectories of parameters weighting predicted control errors. Arch. Control Sci. 2020, 30, 325–363. [Google Scholar]
- Plamowski, S.; Kephart, R.W. The Model Order Reduction Method as an Effective Way to Implement GPC Controller for Multidimensional Objects. Algorithms 2020, 13, 178. [Google Scholar] [CrossRef]
- Rossiter, J.A. Model–Based Predictive Control: A Practical Approach; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Sands, T. Comparison and Interpretation Methods for Predictive Control of Mechanics. Algorithms 2019, 12, 232. [Google Scholar] [CrossRef] [Green Version]
- Tatjewski, P. Advanced Control of Industrial Processes; Structures and Algorithms; Springer: London, UK, 2007. [Google Scholar]
- Blevins, T.L.; McMillan, G.K.; Wojsznis, W.K.; Brown, M.W. Advanced Control Unleashed; The ISA Society: Research Triangle Park, NC, USA, 2003. [Google Scholar]
- Ławryńczuk, M.; Marusak, P.; Tatjewski, P. Cooperation of model predictive control with steady–state economic optimisation. Control Cybern. 2008, 37, 133–158. [Google Scholar]
- Marusak, P. Numerically Efficient Fuzzy MPC Algorithm with Advanced Generation of Prediction: Application to a Chemical Reactor. Algorithms 2020, 13, 143. [Google Scholar] [CrossRef]
- Tatjewski, P. Disturbance modeling and state estimation for offset–free predictive control with state–spaced process models. Int. J. Appl. Math. Comput. Sci. 2014, 24, 313–323. [Google Scholar] [CrossRef] [Green Version]
- Abdelaal, M.; Schön, S. Predictive Path Following and Collision Avoidance of Autonomous Connected Vehicles. Algorithms 2020, 13, 52. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Allgöwer, F. A Quasi-Infinite Horizon Nonlinear Model Predictive Control Scheme with Guaranteed Stability. Automatica 1998, 34, 1205–1217. [Google Scholar] [CrossRef]
- Tatjewski, P. Offset–free nonlinear model predictive control with state–space process models. Arch. Control Sci. 2017, 27, 595–615. [Google Scholar] [CrossRef] [Green Version]
- Diehl, M.; Bock, H.G.; Schlöder, J.P.; Findeisen, R.; Nagy, Z.; Allgöwer, F. Real–time optimization and nonlinear model predictive control of processes governed by differential–algebraic equations. J. Process Control 2002, 12, 577–585. [Google Scholar] [CrossRef]
- Schäfer, A.; Kühl, P.; Diehl, M.; Schlöder, J.; Bock, H.G. Fast reduced multiple shooting methods for nonlinear model predictive control. Chem. Eng. Process. 2007, 46, 1200–1214. [Google Scholar] [CrossRef]
- Zavala, V.M.; Laird, C.D.; Biegler, L.T. A fast moving horizon estimation algorithm based on nonlinear programming sensitivity. J. Process Control 2008, 18, 876–884. [Google Scholar] [CrossRef] [Green Version]
- Dominguez, L.F.; Pistikopoulos, E.N. A Novel mp-NLP Algorithm for Explicit/Multi-parametric NMPC. In Proceedings of the 8th IFAC Symposium on Nonlinear Control Systems, Bologna, Italy, 1–3 September 2010. [Google Scholar]
- Johansen, T.A. On multi–parametric nonlinear programming and explicit nonlinear model predictive control. In Proceedings of the 41st IEEE Conf Decision and Control, Las Vegas, NV, USA, 10–13 December 2002; Volume 3, pp. 2768–2773. [Google Scholar]
- Johansen, T.A. Approximate explicit receding horizon control of constrained nonlinear systems. Automatica 2004, 40, 293–300. [Google Scholar] [CrossRef] [Green Version]
- Pistikopoulos, E.N.; Dua, V.; Bozinis, N.A.; Bemporad, A.; Morari, M. On–line optimization via off–line parametric optimization tools. Comput. Chem. Eng. 2002, 26, 175–185. [Google Scholar] [CrossRef]
- Bemporad, A.; Morari, M.; Dua, V.; Pistikopoulos, E.N. The explicit linear quadratic regulator for constrained systems. Automatica 2002, 38, 3–20. [Google Scholar] [CrossRef]
- Bemporad, A.; Borrelli, F.; Morari, M. Piecewise linear optimal controllers for hybrid systems. In Proceedings of the 2000 American Control Conference, Chicago, IL, USA, 28–30 June 2000; Volume 2, pp. 1190–1194. [Google Scholar]
- Khooban, M.H.; Vafam, N.; Niknam, T. Optimal partitioning of a boiler–turbine unit for Fuzzy model predictive control. ISA Trans. 2016, 64, 231–240. [Google Scholar] [CrossRef]
- Kong, L.; Yuan, J. Disturbance–observer–based fuzzy model predictive control for nonlinear processes with disturbances and input constraints. ISA Trans. 2019, 90, 74–88. [Google Scholar] [CrossRef]
- Kong, L.; Yuan, J. Generalized Discrete–time Nonlinear Disturbance Observer Based Fuzzy Model Predictive Control for Boiler–Turbine Systems. ISA Trans. 2019, 90, 89–106. [Google Scholar] [CrossRef] [PubMed]
- Shen, D.; Lim, C.-C.; Shi, P. Robust fuzzy model predictive control for energy management systems in fuel cell vehicles. Control Eng. Pract. 2020, 98, 104364. [Google Scholar] [CrossRef]
- Wu, X.; Shen, J.; Li, Y.; Lee, K.Y. Fuzzy modeling and predictive control of superheater steam temperature for power plant. ISA Trans. 2015, 56, 241–251. [Google Scholar] [CrossRef] [PubMed]
- Marusak, P.; Tatjewski, P. Stability analysis of nonlinear control systems with unconstrained fuzzy predictive controllers. Arch. Control Sci. 2002, 12, 267–288. [Google Scholar]
- Killian, M.; Kozek, M. T–S fuzzy model predictive speed control of electrical vehicles. IFAC-Pap. Line 2017, 50, 2011–2016. [Google Scholar] [CrossRef]
- Marusak, P. Efficient model predictive control algorithm with fuzzy approximations of nonlinear models. LNCS 2009, 5495, 448–457. [Google Scholar]
- Ławryńczuk, M. Computationally Efficient Model Predictive Control Algorithms: A Neural Network Approach; Springer: Heidelberg, Germany, 2014. [Google Scholar]
- Morari, M.; Lee, J.H. Model predictive control: Past, present and future. Comput. Chem. Eng. 1999, 23, 667–682. [Google Scholar] [CrossRef]
- Boulkaibet, I.; Belarbi, K.; Bououden, S.; Marwala, T.; Chadli, M. A new T–S fuzzy model predictive control for nonlinear processes. Expert Syst. Appl. 2017, 88, 132–151. [Google Scholar] [CrossRef]
- Essien, E.; Ibrahim, H.; Mehrandezh, M.; Idem, R. Adaptive neuro-fuzzy inference system (ANFIS)—Based model predictive control (MPC) for carbon dioxide reforming of methane (CDRM) in a plug flow tubular reactor for hydrogen production. Therm. Sci. Eng. Prog. 2019, 9, 148–161. [Google Scholar] [CrossRef]
- Ławryńczuk, M. Nonlinear state–space predictive control with on–line linearisation and state estimation. Int. J. Appl. Math. Comput. Sci. 2015, 25, 833–847. [Google Scholar] [CrossRef] [Green Version]
- Marusak, P. Advantages of an easy to design fuzzy predictive algorithm in control systems of nonlinear chemical reactors. Appl. Soft Comput. 2009, 9, 1111–1125. [Google Scholar] [CrossRef]
- Lu, J.; Cao, Z.; Zhang, R.; Gao, F. Nonlinear Monotonically Convergent Iterative Learning Control for Batch Processes. IEEE Trans. Ind. Electron. 2018, 65, 5826–5836. [Google Scholar] [CrossRef]
- Lu, J.; Cao, Z.; Gao, F. 110th Anniversary: An Overview on Learning–Based Model Predictive Control for Batch Processes. Ind. Eng. Chem. Res. 2019, 58, 17164–17173. [Google Scholar] [CrossRef]
- Lu, J.; Cao, Z.; Zhao, C.; Gao, F. Multipoint Iterative Learning Model Predictive Control. IEEE Trans. Ind. Electron. 2019, 66, 6230–6240. [Google Scholar] [CrossRef]
- Marusak, P. Disturbance Measurement Utilization in the Efficient MPC Algorithm with Fuzzy Approximations of Nonlinear Models. LNCS 2013, 7824, 307–316. [Google Scholar]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its application to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Piegat, A. Fuzzy Modeling and Control; Physica–Verlag: Heidelberg, Germany, 2001. [Google Scholar]
- Marusak, P. Efficient fuzzy predictive algorithms with integrated economic optimization: A case study. IFAC Proc. Vol. 2007, 40, 61–66. [Google Scholar] [CrossRef]
- Marusak, P. Easily reconfigurable analytical fuzzy predictive controllers: Actuator faults handling. LNCS 2008, 5370, 396–405. [Google Scholar]
- Ribeiro, L.M.; Secchi, A.R. A methodology to obtain analytical models that reduce the computational complexity faced in real time implementation of NMPC controllers. Braz. J. Chem. Eng. 2019, 36, 1255–1277. [Google Scholar] [CrossRef] [Green Version]
- Mate, S.; Kodamana, H.; Bhartiya, S.; Nataraj, P.S.V. A Stabilizing Sub–Optimal Model Predictive Control for Quasi–Linear Parameter Varying Systems. IEEE Control Syst. Lett. 2020, 4, 402–407. [Google Scholar] [CrossRef]
- Jain, A.; Taparia, R. Laguerre function based model predictive control for van–de–vusse reactor. In Proceedings of the 2nd IEEE Int. Conf. Power Electronics, Intelligent Control and Energy Systems, ICPEICES 2018, Delhi, India, 22–24 October 2018; Volume 3, pp. 1010–1015. [Google Scholar]
- Uçak, K. A Runge–Kutta neural network-based control method for nonlinear MIMO systems. Soft Comput. 2019, 23, 7769–7803. [Google Scholar] [CrossRef]
- Uçak, K. A Novel Model Predictive Runge–Kutta Neural Network Controller for Nonlinear MIMO Systems. Neural Process. Lett. 2020, 51, 1789–1833. [Google Scholar] [CrossRef]
- Sang Nguyen, T.; Hoang, N.H.; Hussain, M.A. Tracking error plus damping injection control of non-minimum phase processes. IFAC-Pap. Line 2018, 51, 643–648. [Google Scholar] [CrossRef]
- Doyle, F.; Ogunnaike, B.A.; Pearson, R.K. Nonlinear model–based control using second–order Volterra models. Automatica 1995, 31, 697–714. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marusak, P.M. Advanced Construction of the Dynamic Matrix in Numerically Efficient Fuzzy MPC Algorithms. Algorithms 2021, 14, 25. https://0-doi-org.brum.beds.ac.uk/10.3390/a14010025
Marusak PM. Advanced Construction of the Dynamic Matrix in Numerically Efficient Fuzzy MPC Algorithms. Algorithms. 2021; 14(1):25. https://0-doi-org.brum.beds.ac.uk/10.3390/a14010025
Chicago/Turabian StyleMarusak, Piotr M. 2021. "Advanced Construction of the Dynamic Matrix in Numerically Efficient Fuzzy MPC Algorithms" Algorithms 14, no. 1: 25. https://0-doi-org.brum.beds.ac.uk/10.3390/a14010025




