Hardness of an Asymmetric 2-Player Stackelberg Network Pricing Game †
Abstract
:1. Introduction
1.1. Stackelberg Network Pricing Games
1.2. Asymmetric SNPGs
- Instance: A directed graph , a function , and a source node .
- Leader feasible solution: A pricing .
- –
- Follower feasible solution: A spanning arborescence of G rooted at r (after edges in P have been priced).
- –
- Follower objective: Find a feasible solution minimizing the sum of all the path costs in T from r to any node in G, namely, denoting by the number of paths in T emanating from r and using e, minimize
- Leader objective: Find a feasible pricing maximizing the revenue w.r.t. an optimal solution, say , selected by the follower, namely minimize
1.3. Our Results
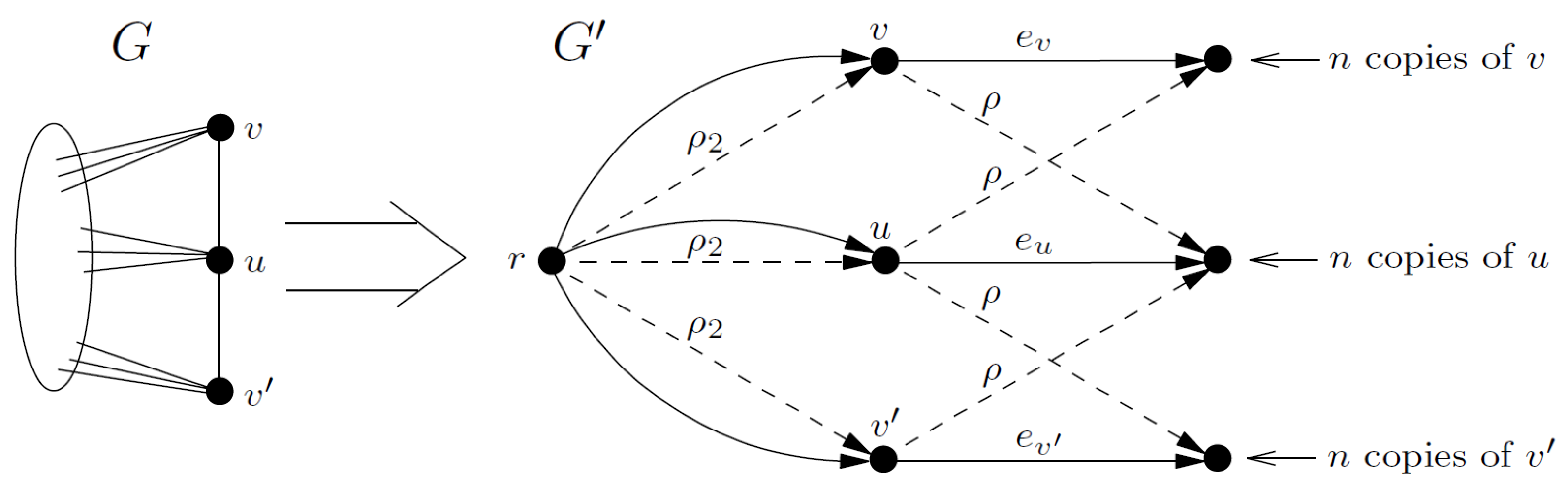
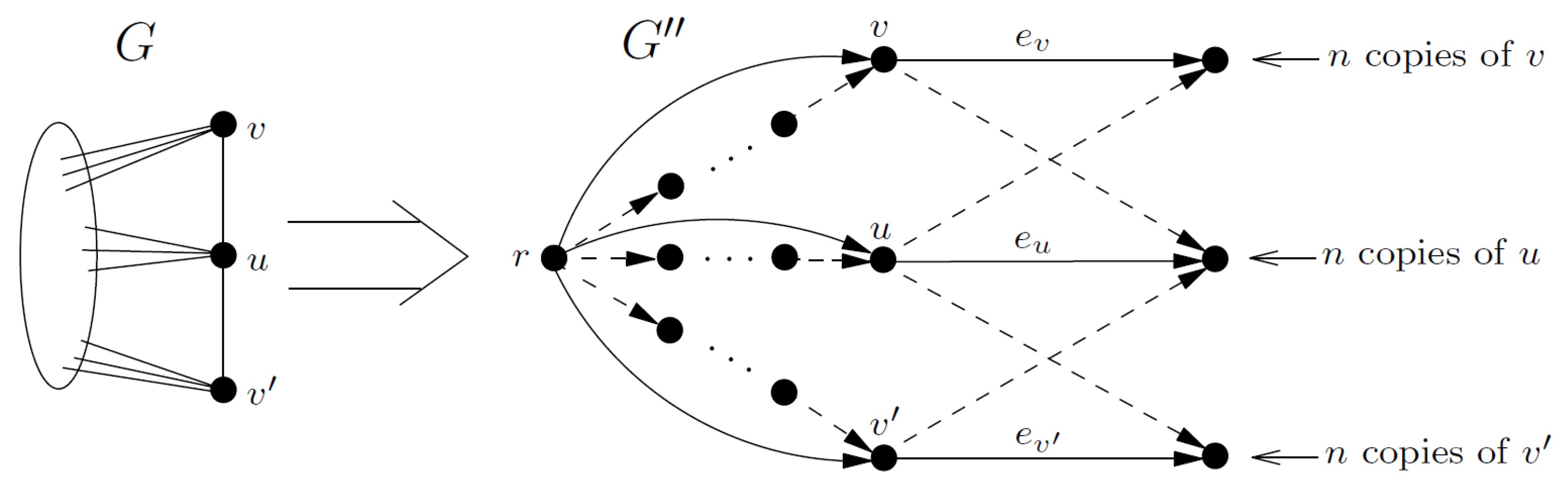
2. Non-Approximability Results
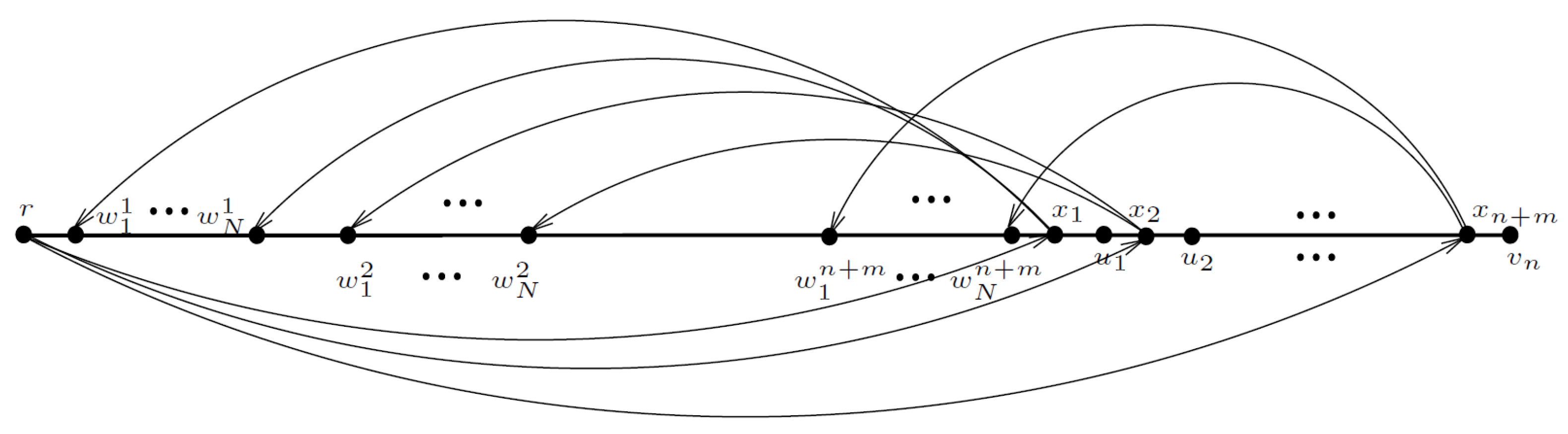
3. A Strongly Polynomial -Approximation Algorithm
4. Dealing with Basic Network Topologies
4.1. Unweigthed Stars
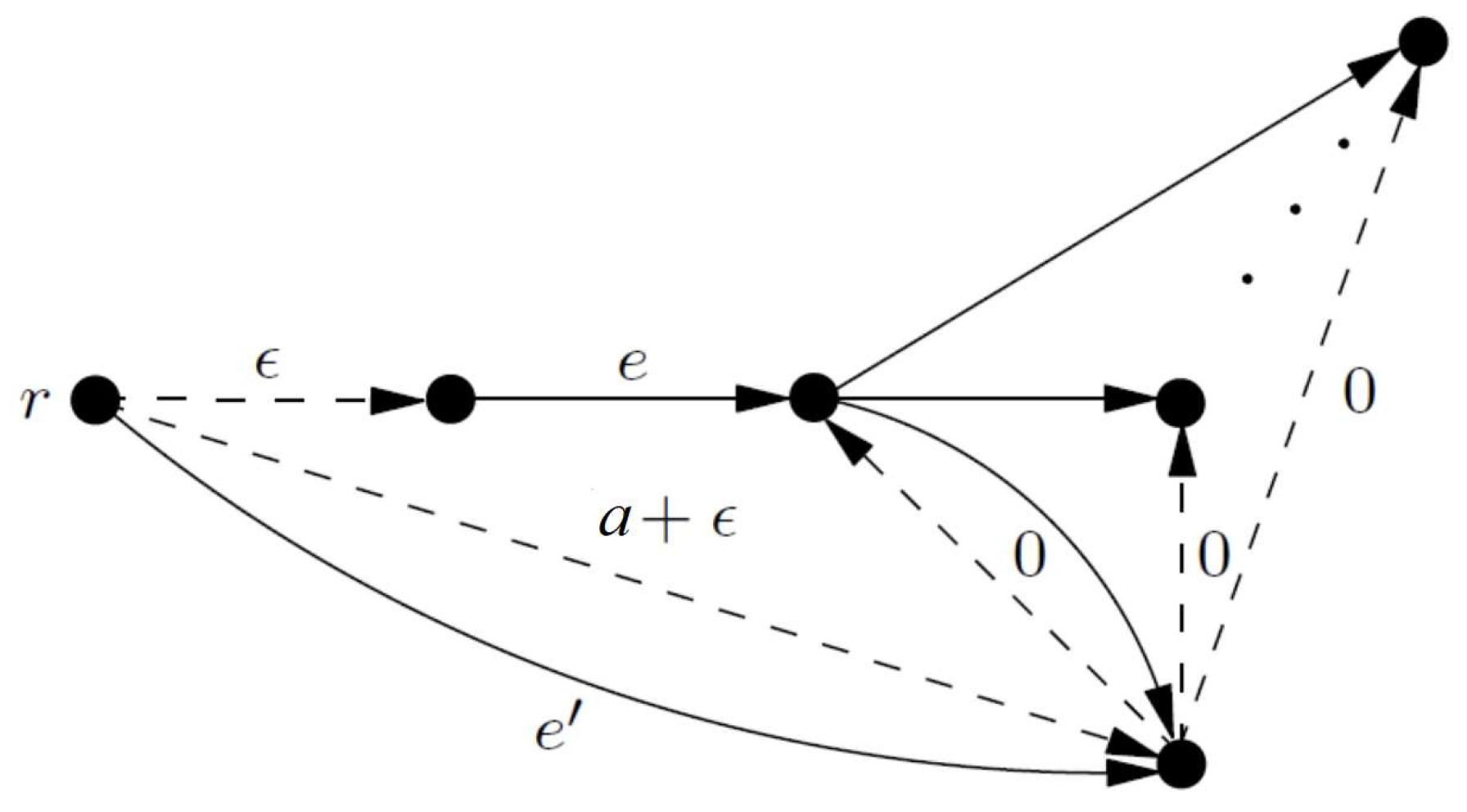
4.2. Unweigthed Chains
- Case
- Since is in and since , we have . Moreover, since the price of every edge increased by at least a, we have that which is strictly greater than when .
- Case
- When , no edge was selected in . As a consequence, we have which is strictly greater than when , since .Otherwise, when , we have that no edge with was selected in . Hence, since the price of every edge with has been increased by at least a, we have that , which is strictly greater than when .
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kolev, S. Heinrich von Stackelberg, Market Structure and Equilibrium. J. Hist. Econ. Thought 2016, 38, 557–560. [Google Scholar] [CrossRef]
- Cole, R.; Dodis, Y.; Roughgarden, T. Pricing network edges for heterogeneous selfish users. In Proceedings of the 35th Annual ACM Symposium on Theory of Computing, San Diego, CA, USA, 9–11 June 2003; Larmore, L.L., Goemans, M.X., Eds.; ACM: New York, NY, USA, 2003; pp. 521–530. [Google Scholar] [CrossRef] [Green Version]
- Van Hoesel, C. An overview of Stackelberg pricing in networks. In Research Memorandum 043; Maastricht University, Maastricht Research School of Economics of Technology and Organization (METEOR): Maastricht, The Netherlands, 2006. [Google Scholar]
- Joret, G. Stackelberg network pricing is hard to approximate. Networks 2011, 57, 117–120. [Google Scholar] [CrossRef] [Green Version]
- Briest, P.; Chalermsook, P.; Khanna, S.; Laekhanukit, B.; Nanongkai, D. Improved Hardness of Approximation for Stackelberg Shortest-Path Pricing. In Internet and Network Economics; Saberi, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 444–454. [Google Scholar]
- Roch, S.; Savard, G.; Marcotte, P. An approximation algorithm for Stackelberg network pricing. Networks 2005, 46, 57–67. [Google Scholar] [CrossRef] [Green Version]
- Labbé, M.; Marcotte, P.; Savard, G. A Bilevel Model of Taxation and Its Application to Optimal Highway Pricing. Manag. Sci. 1998, 44, 1608–1622. [Google Scholar] [CrossRef] [Green Version]
- Grigoriev, A.; van Hoesel, S.P.M.; van der Kraaij, A.F.; Uetz, M.; Bouhtou, M. Pricing Network Edges to Cross a River. In Proceedings of the Approximation and Online Algorithms, Second International Workshop, WAOA 2004, Bergen, Norway, 14–16 September 2004; Revised Selected Papers; Lecture Notes in Computer Science; Persiano, G., Solis-Oba, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3351, pp. 140–153. [Google Scholar] [CrossRef] [Green Version]
- Cardinal, J.; Demaine, E.D.; Fiorini, S.; Joret, G.; Newman, I.; Weimann, O. The Stackelberg minimum spanning tree game on planar and bounded-treewidth graphs. J. Comb. Optim. 2013, 25, 19–46. [Google Scholar] [CrossRef] [Green Version]
- Bilò, D.; Gualà, L.; Leucci, S.; Proietti, G. Specializations and generalizations of the Stackelberg minimum spanning tree game. Theor. Comput. Sci. 2015, 562, 643–657. [Google Scholar] [CrossRef]
- Briest, P.; Hoefer, M.; Krysta, P. Stackelberg Network Pricing Games. Algorithmica 2012, 62, 733–753. [Google Scholar] [CrossRef]
- Briest, P.; Gualà, L.; Hoefer, M.; Ventre, C. On stackelberg pricing with computationally bounded customers. Networks 2012, 60, 31–44. [Google Scholar] [CrossRef]
- Vinci, C.; Bilò, V. On the Stackelberg fuel pricing problem. In Proceedings of the 15th Italian Conference on Theoretical Computer Science, Perugia, Italy, 17–19 September 2014; Bistarelli, S., Formisano, A., Eds.; CEUR Workshop Proceedings; CEUR-WS.org: Bari, Italy, 2014; Volume 1231, pp. 213–224. [Google Scholar]
- Baïou, M.; Barahona, F. Stackelberg Bipartite Vertex Cover and the Preflow Algorithm. Algorithmica 2016, 74, 1174–1183. [Google Scholar] [CrossRef]
- Grandoni, F.; Rothvoß, T. Pricing on Paths: A PTAS for the Highway Problem. SIAM J. Comput. 2016, 45, 216–231. [Google Scholar] [CrossRef]
- Böhnlein, T.; Kratsch, S.; Schaudt, O. Revenue Maximization in Stackelberg Pricing Games: Beyond the Combinatorial Setting. In Proceedings of the 44th International Colloquium on Automata, Languages, and Programming, ICALP 2017, Warsaw, Poland, 10–14 July 2017; Chatzigiannakis, I., Indyk, P., Kuhn, F., Muscholl, A., Eds.; LIPIcs; Schloss Dagstuhl—Leibniz-Zentrum für Informatik: Boston, MA, USA, 2017; Volume 80, pp. 46:1–46:13. [Google Scholar] [CrossRef]
- Böhnlein, T.; Schaudt, O.; Schauer, J. Stackelberg Packing Games. In Proceedings of the Algorithms and Data Structures—16th International Symposium, WADS 2019, Edmonton, AB, Canada, 5–7 August 2019; Friggstad, Z., Sack, J., Salavatipour, M.R., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2019; Volume 11646, pp. 239–253. [Google Scholar] [CrossRef]
- Böhnlein, T.; Schaudt, O. On the Complexity of Stackelberg Matroid Pricing Problems. In Proceedings of the Combinatorial Algorithms—31st International Workshop, IWOCA 2020, Bordeaux, France, 8–10 June 2020; Gasieniec, L., Klasing, R., Radzik, T., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2020; Volume 12126, pp. 83–96. [Google Scholar] [CrossRef]
- Bilò, D.; Gualà, L.; Proietti, G.; Widmayer, P. Computational Aspects of a 2-Player Stackelberg Shortest Paths Tree Game. In Proceedings of the Internet and Network Economics, 4th International Workshop, WINE 2008, Shanghai, China, 17–20 December 2008; Papadimitriou, C.H., Zhang, S., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5385, pp. 251–262. [Google Scholar] [CrossRef]
- Cabello, S. Stackelberg Shortest Path Tree Game, Revisited. arXiv 2012, arXiv:1207.2317. [Google Scholar]
- Daligault, J.; Thomassé, S. On Finding Directed Trees with Many Leaves. In Proceedings of the Parameterized and Exact Computation, 4th International Workshop, IWPEC 2009, Copenhagen, Denmark, 10–11 September 2009; Chen, J., Fomin, F.V., Eds.; Revised Selected Papers; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5917, pp. 86–97. [Google Scholar] [CrossRef] [Green Version]
- Alon, N.; Fomin, F.V.; Gutin, G.Z.; Krivelevich, M.; Saurabh, S. Spanning Directed Trees with Many Leaves. SIAM J. Discret. Math. 2009, 23, 466–476. [Google Scholar] [CrossRef] [Green Version]
- Zuckerman, D. Linear Degree Extractors and the Inapproximability of Max Clique and Chromatic Number. Theory Comput. 2007, 3, 103–128. [Google Scholar] [CrossRef]
- Galbiati, G.; Maffioli, F.; Morzenti, A. A short note on the approximability of the maximum leaves spanning tree problem. Inf. Process. Lett. 1994, 52, 45–49. [Google Scholar] [CrossRef]
- Raz, R.; Safra, S. A Sub-Constant Error-Probability Low-Degree Test, and a Sub-Constant Error-Probability PCP Characterization of NP. In Proceedings of the Twenty-Ninth Annual ACM Symposium on the Theory of Computing, El Paso, TX, USA, 4–6 May 1997; Leighton, F.T., Shor, P.W., Eds.; ACM: New York, NY, USA, 1997; pp. 475–484. [Google Scholar] [CrossRef]
- Alimonti, P.; Kann, V. Some APX-completeness results for cubic graphs. Theor. Comput. Sci. 2000, 237, 123–134. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bilò, D.; Gualà, L.; Proietti, G. Hardness of an Asymmetric 2-Player Stackelberg Network Pricing Game. Algorithms 2021, 14, 8. https://0-doi-org.brum.beds.ac.uk/10.3390/a14010008
Bilò D, Gualà L, Proietti G. Hardness of an Asymmetric 2-Player Stackelberg Network Pricing Game. Algorithms. 2021; 14(1):8. https://0-doi-org.brum.beds.ac.uk/10.3390/a14010008
Chicago/Turabian StyleBilò, Davide, Luciano Gualà, and Guido Proietti. 2021. "Hardness of an Asymmetric 2-Player Stackelberg Network Pricing Game" Algorithms 14, no. 1: 8. https://0-doi-org.brum.beds.ac.uk/10.3390/a14010008




