Simulation of Sentinel-2 Bottom of Atmosphere Reflectance Using Shadow Parameters on a Deciduous Forest in Thailand
Abstract
:1. Introduction
2. Methodology
2.1. Flow Chart of This Study
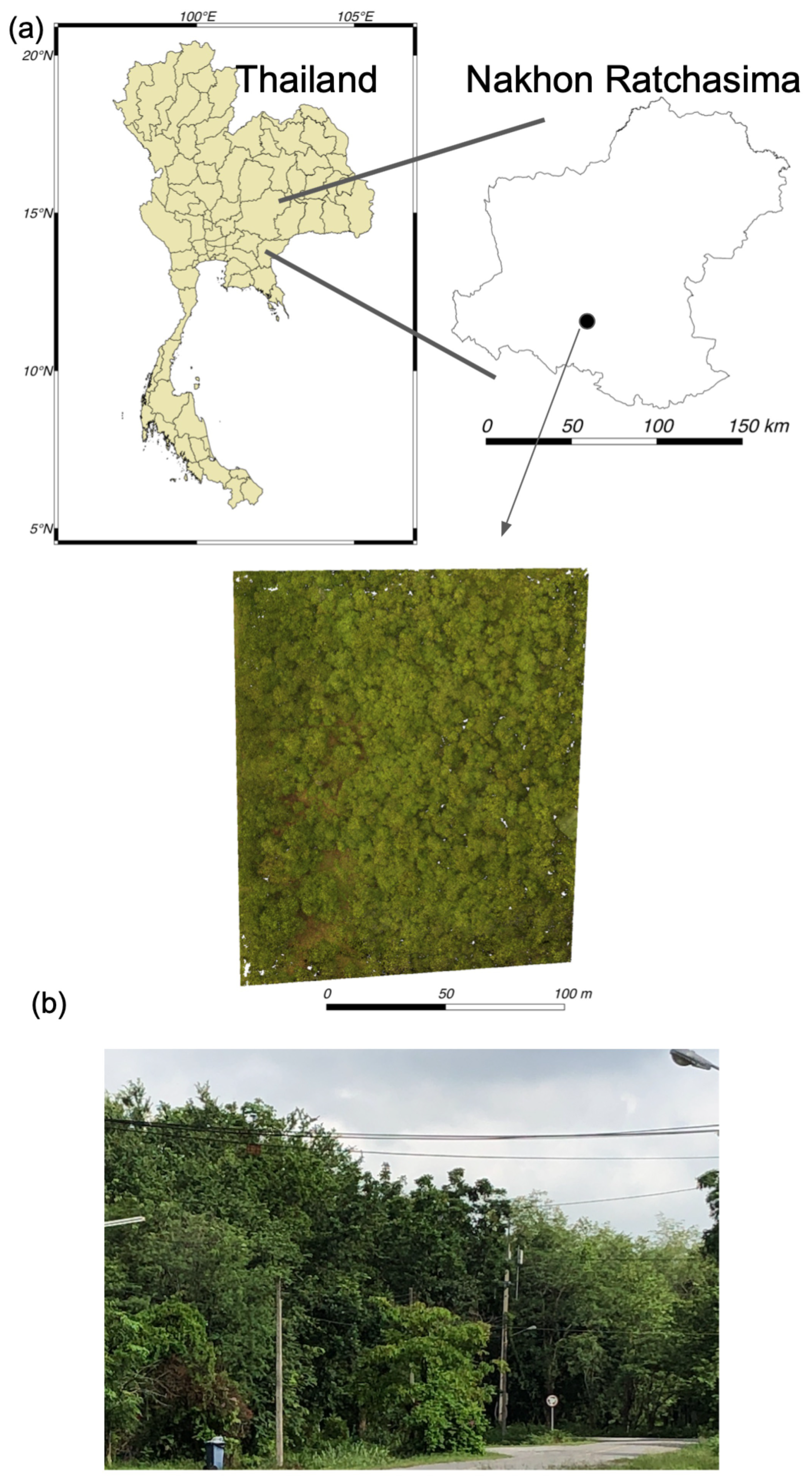
2.2. Study Site
2.3. Data Collection
2.3.1. UAV Observation
2.3.2. Sentinel-2 Image and Its Spectral Response Function
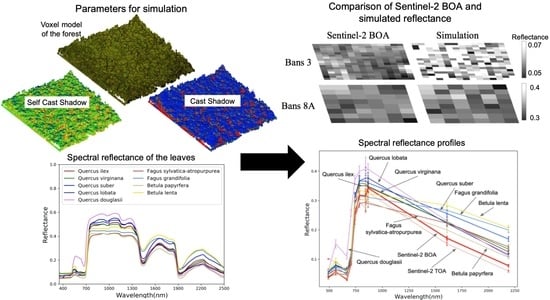
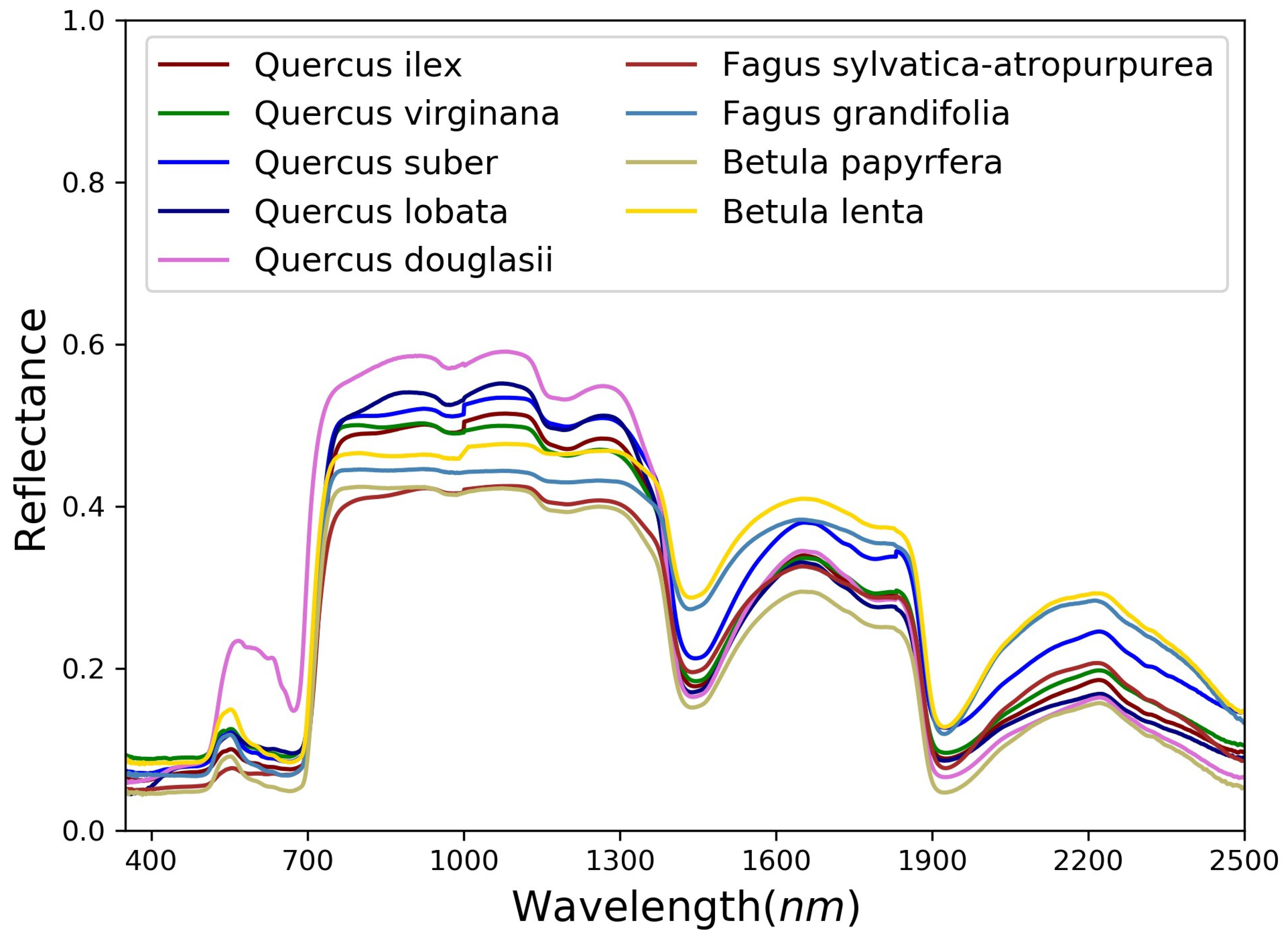
2.3.3. Spectral Reflectance of the Leaves
2.4. Voxel Model Creation
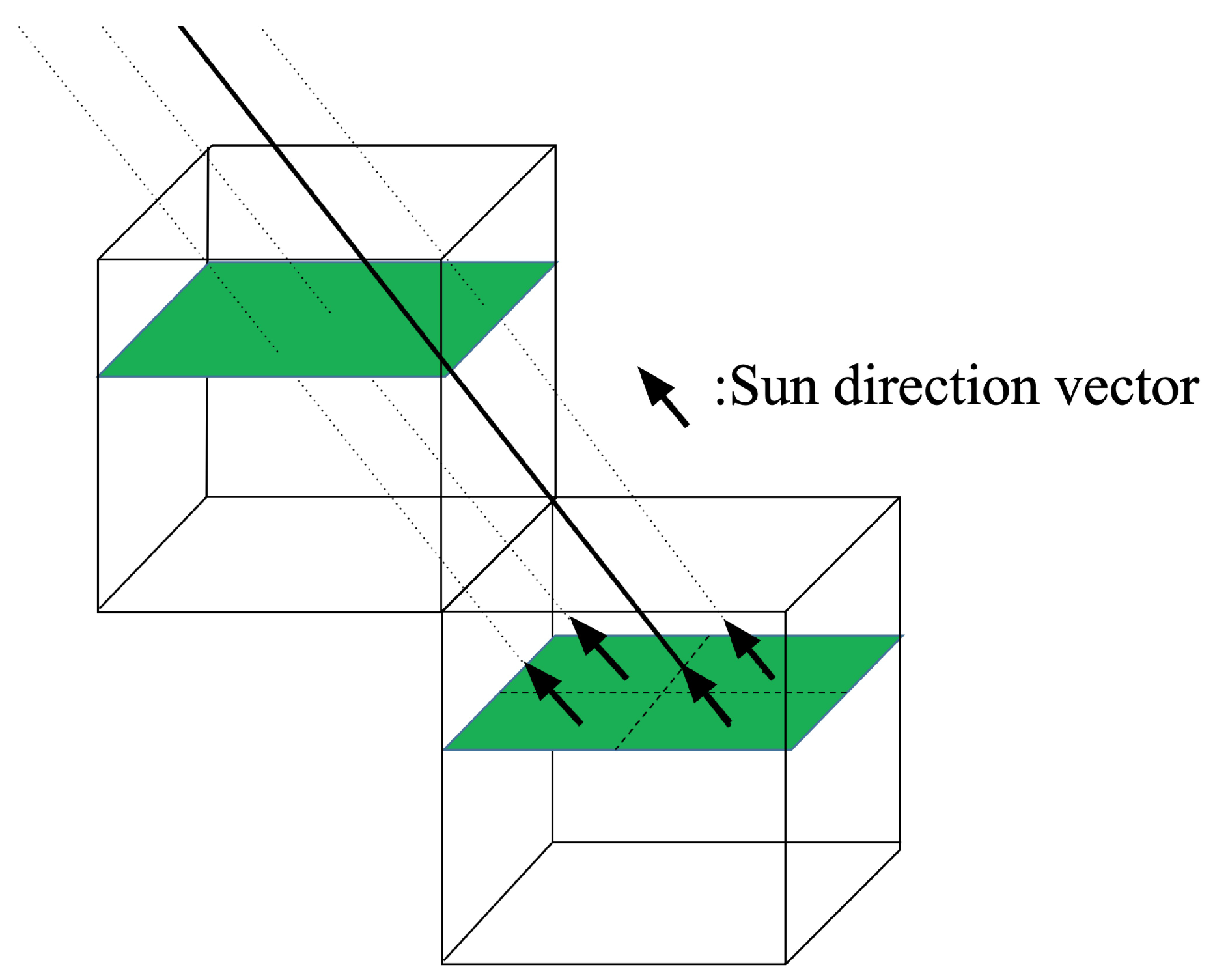
2.4.1. Voxel Based Computation of Self Cast Shadow
2.4.2. Voxel Based Computation of Cast Shadow
2.5. Reflectance Simulation Using a Shadow Parameters
3. Results and Discussion
3.1. Point Cloud Profile and Voxel Size Determination
3.2. Spatial Variation of Cast and Self Cast Shadow
3.3. Result of Simulated Sentinel-2 BOA Reflectance
3.4. Effect of Voxel Size on a Simulated Reflectance
3.5. Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lachérade, S.; Miesch, C.; Boldo, D.; Briottet, X.; Valorge, C.; Le Men, H. ICARE: A Physically-Based Model to Correct Atmospheric and Geometric Effects from High Spatial and Spectral Remote Sensing Images over 3D Urban Areas. Meteorol. Atmos. Phys. 2008, 102, 209–222. [Google Scholar] [CrossRef]
- Leblon, B.; Gallant, L.; Granberg, H. Effects of shadowing types on ground-measured visible and near-infrared shadow reflectances. Remote Sens. Environ. 1996, 58, 322–328. [Google Scholar] [CrossRef]
- Cameron, M.; Kumar, L. Diffuse skylight as a surrogate for shadow detection in high-resolution imagery acquired under clear sky conditions. Remote Sens. 2018, 10, 1185. [Google Scholar] [CrossRef] [Green Version]
- Shahtahmassebi, A.; Yang, N.; Wang, K.; Moore, N.; Shen, Z. Review of shadow detection and de-shadowing methods in remote sensing. Chin. Geogr. Sci. 2013, 23, 403–420. [Google Scholar] [CrossRef] [Green Version]
- Shimabukuro, Y.E.; Haertel, V.F.A.; Smith, J.A. Landsat Derived Shade Images of Forested Areas. Proc. ISPRS 1988, 27, 534–543. [Google Scholar]
- Hodul, M.; Knudby, A.; Ho, H.C. Estimation of Continuous Urban Sky View Factor from Landsat Data Using Shadow Detection. Remote Sens. 2016, 8, 568. [Google Scholar] [CrossRef] [Green Version]
- Ono, A.; Takeuchi, W.; Hayashida, S. Estimation of forest canopy height using MODIS shadow index. In Proceedings of the 36th Asian Conference on Remote Sensing (ACRS), Manilla, Philippines, 20 October 2015. [Google Scholar]
- Cui, L.; Jiao, Z.; Dong, Y.; Zhang, X.; Sun, M.; Yin, S.; Chang, Y.; He, D.; Ding, A. Forest Vertical Structure from MODIS BRDF Shape Indicators. In Proceedings of the 2018 IEEE International Symposium on Geoscience and Remote Sensing IGARSS, Valencia, Spain, 22–27 July 2018; pp. 5911–5914. [Google Scholar] [CrossRef]
- Cui, L.; Jiao, Z.; Dong, Y.; Sun, M.; Zhang, X.; Yin, S.; Ding, A.; Chang, Y.; Guo, J.; Xie, R. Estimating Forest Canopy Height Using MODIS BRDF Data Emphasizing Typical-Angle Reflectances. Remote Sens. 2019, 11, 2239. [Google Scholar] [CrossRef] [Green Version]
- Roy, D.P.; Zhang, H.K.; Ju, J.; Gomez-Dans, J.L.; Lewis, P.E.; Schaaf, C.B.; Sun, Q.; Li, J.; Huang, H.; Kovalskyy, V. A general method to normalize Landsat reflectance data to nadir BRDF adjusted reflectance. Remote Sens. Environ. 2016, 176, 255–271. [Google Scholar] [CrossRef] [Green Version]
- Li, F.; Jupp, D.L.B.; Paget, M.; Briggs, P.R.; Thankappan, M.; Lewis, A.; Held, A. Improving BRDF normalisation for Landsat data using statistical relationships between MODIS BRDF shape and vegetation structure in the Australian continent. Remote Sens. Environ. 2017, 195, 275–296. [Google Scholar] [CrossRef]
- Franch, B.; Vermote, E.; Skakun, S.; Roger, J.-C.; Masek, J.; Ju, J.; Villaescusa-Nadal, J.L.; Santamaria-Artigas, A. A Method for Landsat and Sentinel 2 (HLS) BRDF Normalization. Remote Sens. 2019, 11, 632. [Google Scholar] [CrossRef] [Green Version]
- Lucht, W.; Schaaf, C.B.; Strahler, A.H. An algorithm for the retrieval of albedo from space using semiempirical BRDF models. IEEE Trans. Geosci. Remote Sens. 2000, 38, 977–998. [Google Scholar] [CrossRef] [Green Version]
- Hall, F.G.; Hilker, T.; Coops, N.C.; Lyapustin, A.; Huemmrich, K.F.; Middleton, E.; Margolis, H.; Drolet, G.; Black, T.A. Multi-angle remote sensing of forest light use efficiency by observing PRI variation with canopy shadow fraction. Remote Sens. Environ. 2008, 112, 3201–3211. [Google Scholar] [CrossRef] [Green Version]
- Li, F.; Cohen, S.; Naor, A.; Shaozong, K.; Erez, A. Studies of canopy structure and water use of apple trees on three rootstocks. Agric. Water Manag. 2002, 55, 1–14. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.P.; Demarez, V.; Pinel, V.; Zagolski, F. Modeling radiative transfer in heterogeneous 3-D vegetation canopies. Remote Sens. Environ. 1996, 58, 131–156. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, H.; Iwabuchi, H. A coupled 1-D atmosphere and 3-D canopy radiative transfer model for canopy reflectance, light environment, and photosynthesis simulation in a heterogeneous landscape. Remote Sens. Environ. 2008, 112, 173–185. [Google Scholar] [CrossRef]
- Qin, W.W.; Gerstl, S.W. 3-D Scene Modeling of Semidesert Vegetation Cover and its Radiation Regime. Remote Sens. Environ. 2000, 74, 145–162. [Google Scholar] [CrossRef]
- Lau, A.; Bentley, L.P.; Martius, C.; Shenkin, A.; Bartholomeus, H.; Raumonen, P.; Malhi, Y.; Jackson, T.; Herold, M. Quantifying Branch Architecture of Tropical Trees Using Terrestrial Lidar and 3D Modelling. Trees 2018, 32, 1219–1231. [Google Scholar] [CrossRef] [Green Version]
- Vicari, M.B.; Pisek, J.; Disney, M. New estimates of leaf angle distribution from terrestrial LiDAR: Comparison with measured and modelled estimates from nine broadleaf tree species. Agric. For. Meteorol. 2019, 264, 322–333. [Google Scholar] [CrossRef]
- Itakura, K.; Hosoi, F. Voxel-based leaf area estimation from three-dimensional plant images. J. Agric. Meteorol. 2019, 75, 211–216. [Google Scholar] [CrossRef] [Green Version]
- Gorte, B.; Pfeifer, N. Structuring laser-scanned trees using 3D mathematical morphology. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 35, 929–933. [Google Scholar]
- Hosoi, F.; Omasa, K. Voxel-Based 3-D Modeling of Individual Trees for Estimating Leaf Area Density Using High-Resolution Portable Scanning Lidar. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3610–3618. [Google Scholar] [CrossRef]
- Bienert, A.; Hess, C.; Maas, H.-G.; von Oheimb, G. A voxel-based technique to estimate the volume of trees from terrestrial laser scanner data. In Proceedings of the The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, ISPRS Technical Commission V Symposium, Riva Del Garda, Italy, 23–25 June 2014; Volume XL-5. [Google Scholar] [CrossRef] [Green Version]
- Itakura, K.; Hosoi, F. Estimation of leaf inclination angle in three-dimensional plant images obtained from lidar. Remote Sens. 2019, 11, 344. [Google Scholar] [CrossRef] [Green Version]
- Sakai, Y.; Kobayashi, H.; Kato, T. FLiES-SIF ver. 1.0: Three-dimensional radiative transfer model for estimating solar induced fluorescence. Geosci. Model Dev. Discuss. 2020, 1–36. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Zheng, G.; Yun, Z.; Xu, Z.; Moskal, L.; Tian, Q. Characterizing the Spatial Variations of Forest Sunlit and Shaded Components Using Discrete Aerial Lidar. Remote Sens. 2020, 12, 1071. [Google Scholar] [CrossRef] [Green Version]
- Arévalo, V.; Gonzáez, J.; Ambrosio, G. Shadow detection in color high-resolution satellite images. Int. J. Remote Sens. 2008, 29, 1945–1963. [Google Scholar] [CrossRef]
- Krishna Moorthy, S.M.; Bao, Y.; Calders, K.; Schnitzer, S.A.; Verbeeck, H. Semi-automatic extraction of liana stems from terrestrial LiDAR point clouds of tropical rainforests. ISPRS J. Photogramm. Remote Sens. 2019, 154, 114–126. [Google Scholar] [CrossRef] [PubMed]
- Wassihun, A.N.; Hussin, Y.A.; Van Leeuwen, L.M.; Latif, Z.A. Effect of forest stand density on the estimation of above ground biomass/carbon stock using airborne and terrestrial LIDAR derived tree parameters in tropical rainforest, Malaysia. Environ. Syst. Res. 2019, 8. [Google Scholar] [CrossRef] [Green Version]
- Pix4D Support. Available online: https://support.pix4d.com/hc/en-us (accessed on 1 June 2020).
- Müller-Wilm, U. Sentinel-2 MSI–Level-2A Prototype Processor Installation and User Manual. Available online: http://step.esa.int/thirdparties/sen2cor/2.2.1/S2PAD-VEGA-SUM-0001-2.2.pdf (accessed on 1 July 2020).
- Watson, I.D.; Johnson, G.T. Short communication. Graphical estimation of Sky View-Factors in urban environments. J. Climatol. 1987, 7, 193–197. [Google Scholar] [CrossRef]
- Holmer, B.; Postgȧrd, U.; Eriksson, M. Sky view factors in forest canopies calculated with IDRISI. Theor. Appl. Climatol. 2001, 68, 33–40. [Google Scholar] [CrossRef]
- Yuan, C.; Chen, L. Mitigating urban heat island effects in high-density cities based on sky view factor and urban morphological understanding: A study of Hong Kong. Arch. Sci. Rev. 2011, 54, 305–315. [Google Scholar] [CrossRef]
- Fujiwara, T.; Akatsuka, S.; Takagi, M. Estimation of PAR in a forest floor using a voxel model. Jpn. Soc. Photogramm. Remote Sens. 2018, 57, 4–12. [Google Scholar] [CrossRef] [Green Version]
- Fujiwara, T.; Takagi, M. Simulation of reflected sunlight using a voxel model in a forest. Jpn. Soc. Photogramm. Remote Sens. 2019, 58, 184–195. [Google Scholar] [CrossRef]
- Gueymard, C.A. SMARTS Code, Version 2.9.5. USER’S MANUAL for Linux. Available online: https://www.solarconsultingservices.com/SMARTS295_Users_Manual_Linux.pdf (accessed on 25 March 2020).
- Shettle, E.P.; Fenn, R.W. Models for the Aerosols of the Lower Atmosphere and the Effects of Humidity Variations on Their Optical Properties; Report AFGL-TR-79-0214; Air Force Geophysics Laboratory: Hanscom, MA, USA, 1979. [Google Scholar]
- Cao, L.; Liu, H.; Fu, X.; Zhang, Z.; Shen, X.; Ruan, H. Comparison of UAV LiDAR and Digital Aerial Photogrammetry Point Clouds for Estimating Forest Structural Attributes in Subtropical Planted Forests. Forests 2019, 10, 145. [Google Scholar] [CrossRef] [Green Version]
- Nesbit, P.R.; Hugenholtz, C.H. Enhancing UAV-SfM 3D Model Accuracy in High-Relief Landscapes by Incorporating Oblique Images. Remote Sens. 2019, 11, 239. [Google Scholar] [CrossRef] [Green Version]
- Moriyama, M.; Honda, Y.; Ono, A. GCOM?C1/SGLI Shadow Index Algorithm Theoretical Basis Document. Available online: https://suzaku.eorc.jaxa.jp/GCOM_C/data/ATBD/ver2/V2ATBD_T2A_SDI_Moriyama.pdf (accessed on 25 May 2020).
- Ulsig, L.; Nichol, C.J.; Huemmrich, K.F.; Landis, D.R.; Middleton, E.M.; Lyapustin, A.I.; Mammarella, I.; Levula, J.; Porcar-Castell, A. Detecting inter-annual variations in the phenology of evergreen conifers using long-term modis vegetation index time series. Remote Sens. 2017, 9, 49. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Liu, Z.; Zhou, Y.; Liu, Y.; An, S.; Tang, J. Comparison of phenology estimated from reflectance-based indices and solar-induced chlorophyll fluorescence (SIF) observations in a temperate forest using GPP-based phenology as the standard. Remote Sens. 2018, 10, 932. [Google Scholar] [CrossRef] [Green Version]
- Rengarajan, R.; Schott, J.R. Modeling and Simulation of Deciduous Forest Canopy and Its Anisotropic Reflectance Properties Using the Digital Image and Remote Sensing Image Generation (DIRSIG) Tool. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4805–4817. [Google Scholar] [CrossRef]
- Li, Y.; Chen, J.; Ma, Q.; Zhang, H.; Liu, J. Evaluation of Sentinel-2A Surface Reflectance Derived Using Sen2Cor in North America. IEEE J. Sel. Top. Appl. Earth Obs. 2018, 11, 1997–2021. [Google Scholar] [CrossRef]
- Seelig, H.D.; Hoehn, A.; Stodieck, L.; Klaus, D.; Adams, W., III; Emery, W. The assessment of leaf water content using leaf reflectance ratios in the visible, near-, and short-wave-infrared. Int. J. Remote Sens. 2008, 29, 3701–3713. [Google Scholar] [CrossRef]
- Zou, X.; Mõttus, M. Sensitivity of Common Vegetation Indices to the Canopy Structure of Field Crops. Remote Sens. 2017, 9, 994. [Google Scholar] [CrossRef] [Green Version]






| Parameter | Range | Increment/Grid Points |
|---|---|---|
| Solar zenith angle | 0–70 | 10 |
| Sensor view angle | 0–10 | 10 |
| Relative azimuth angle | 0–180 | 30 (180 = backscatter) |
| Ground elevation | 0–2.5 km | 0.5 km |
| Visibility | 5–120 km | 5, 7, 10, 15, 23, 40, 80, 120 km |
| Water vapor, summer | 0.4–5.5 cm | 0.4, 1.0, 2.0, 2.9, 4.0, 5.0 cm |
| Water vapor, winter | 0.2–1.5 cm | 0.2, 0.4, 0.8, 1.1 cm |
| Input Condition | Values | Remarks |
|---|---|---|
| Station Pressure | 1013.25 mb | Basic value |
| Altitude | 0 km | Sea level |
| Reference Atmosphere | Tropical | Water Vapor, Ozone, Gas absorption and pollution |
| Carbon Dioxide | 370ppmv | Basic value |
| Aerosol Model | Rural | Shettle and Fenn [39] |
| Atmospheric Turbidity | Aerosol Optical Depth at 500 nm = 0.084 | Basic value |
| Albedo | 1.0 | Totally reflect |
| Spectral Range | 400 to 4000 nm | |
| Solar Constant | 1366.1 W/m2 | Basic value |
| Solar geometry | Zenith angle 34.2 Azimuth angle 134.0 |
| Leaf | B02 | B03 | B04 | B05 | B06 | B07 | B08 | B8A | B11 | B12 | Mean | StD |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Quercus ilex | 0.012 | 0.010 | 0.022 | 0.007 | 0.035 | 0.037 | 0.050 | 0.017 | 0.056 | 0.048 | 0.029 | 0.018 |
| Quercus virginana | 0.024 | 0.025 | 0.033 | 0.029 | 0.058 | 0.046 | 0.054 | 0.018 | 0.055 | 0.057 | 0.040 | 0.016 |
| Quercus suber | 0.017 | 0.021 | 0.028 | 0.026 | 0.061 | 0.052 | 0.063 | 0.024 | 0.085 | 0.091 | 0.047 | 0.027 |
| Quercus lobata | 0.019 | 0.022 | 0.036 | 0.029 | 0.054 | 0.053 | 0.072 | 0.038 | 0.052 | 0.038 | 0.041 | 0.016 |
| Quercus douglasii | 0.022 | 0.096 | 0.080 | 0.175 | 0.118 | 0.084 | 0.101 | 0.067 | 0.060 | 0.032 | 0.084 | 0.044 |
| Fagus sylvatica-atropurpurea | 0.005 | 0.009 | 0.017 | 0.016 | 0.013 | 0.031 | 0.036 | 0.055 | 0.052 | 0.065 | 0.030 | 0.021 |
| Fagus grandifolia | 0.010 | 0.018 | 0.017 | 0.027 | 0.037 | 0.016 | 0.032 | 0.035 | 0.096 | 0.122 | 0.041 | 0.037 |
| Betula papyrfera | 0.006 | 0.006 | 0.005 | 0.005 | 0.020 | 0.020 | 0.033 | 0.049 | 0.030 | 0.029 | 0.020 | 0.015 |
| Betula lenta | 0.022 | 0.038 | 0.028 | 0.048 | 0.053 | 0.024 | 0.037 | 0.025 | 0.113 | 0.129 | 0.052 | 0.038 |
| Band | 50 cm | 100 cm | 200 cm |
|---|---|---|---|
| 2 | 1.02 | 1.10 | 1.17 |
| 3 | 1.02 | 1.09 | 1.17 |
| 4 | 1.04 | 1.10 | 1.19 |
| 5 | 1.04 | 1.11 | 1.18 |
| 6 | 1.04 | 1.10 | 1.18 |
| 7 | 1.03 | 1.10 | 1.18 |
| 8 | 1.04 | 1.10 | 1.17 |
| 8A | 1.03 | 1.10 | 1.18 |
| 11 | 1.02 | 1.10 | 1.17 |
| 12 | 1.04 | 1.10 | 1.19 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fujiwara, T.; Takeuchi, W. Simulation of Sentinel-2 Bottom of Atmosphere Reflectance Using Shadow Parameters on a Deciduous Forest in Thailand. ISPRS Int. J. Geo-Inf. 2020, 9, 582. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9100582
Fujiwara T, Takeuchi W. Simulation of Sentinel-2 Bottom of Atmosphere Reflectance Using Shadow Parameters on a Deciduous Forest in Thailand. ISPRS International Journal of Geo-Information. 2020; 9(10):582. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9100582
Chicago/Turabian StyleFujiwara, Takumi, and Wataru Takeuchi. 2020. "Simulation of Sentinel-2 Bottom of Atmosphere Reflectance Using Shadow Parameters on a Deciduous Forest in Thailand" ISPRS International Journal of Geo-Information 9, no. 10: 582. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9100582